Abstract
Reward expectation and reward prediction errors are thought to be critical for dynamic adjustments in decision-making and reward-seeking behavior, but little is known about their representation in the brain during uncertainty and risk-taking. Furthermore, little is known about what role individual differences might play in such reinforcement processes. In this study, it is shown behavioral and neural responses during a decision-making task can be characterized by a computational reinforcement learning model and that individual differences in learning parameters in the model are critical for elucidating these processes. In the fMRI experiment, subjects chose between high- and low-risk rewards. A computational reinforcement learning model computed expected values and prediction errors that each subject might experience on each trial. These outputs predicted subjects’ trial-to-trial choice strategies and neural activity in several limbic and prefrontal regions during the task. Individual differences in estimated reinforcement learning parameters proved critical for characterizing these processes, because models that incorporated individual learning parameters explained significantly more variance in the fMRI data than did a model using fixed learning parameters. These findings suggest that the brain engages a reinforcement learning process during risk-taking and that individual differences play a crucial role in modeling this process.
Keywords: reward prediction error, reward expectation, fMRI, decision-making, reinforcement learning, risk-taking
INTRODUCTION
In order to maximize rewards during decision-making, organisms can estimate expected rewards, or value, of various decision options and continually update their expectations according to outcomes of their decisions. In the past half century, reinforcement learning theory has emerged as a powerful tool to characterize how organisms acquire such reward expectations and how they can use outcomes of their decisions to adjust those expectations (Sutton and Barto, 1998; Camerer, 2003; Schultz, 2004). In typical reinforcement learning models, ‘weights’ represent expected outcomes of each decision option, and thus decision options with stronger weights become preferred and are more likely to be chosen than are decision options with relatively weaker weights. The difference between the expected outcome (e.g. reward) and the received outcome is termed a prediction error, and can be used to adjust decision option weights so they better reflect the true reward value of the chosen decision. Thus, these two variables—weights and prediction errors—are distinct but related, and together form a simple mechanism by which organisms can dynamically adjust their decision-making based on reinforcements (Cohen and Ranganath, under review).
Neuroscientists have suggested that reward prediction errors are encoded in structures including midbrain dopamine regions, the cingulate cortex and ventral striatum. In particular, phasic increases in activity are observed when reinforcements are better than expected (a positive prediction error), and phasic decreases in activity are observed when reinforcements are worse than expected or not given (a negative prediction error) (Schultz et al., 1997; Waelti et al., 2001; Daw et al., 2002; Holroyd and Coles, 2002; O’Doherty et al., 2003; Schultz, 2004; Seymour et al., 2004; Rodriguez et al., 2005; Abler et al., 2006).
In contrast, neural representations of expected rewards (termed ‘weights’ in reinforcement learning models) are thought to be housed in the orbitofrontal cortex and amygdala: activity in these regions is sensitive to the relative preference of rewards, suggesting that these regions might encode the expected values or relative motivational significance of different decision options (Tremblay and Schultz, 1999; Hikosaka and Watanabe, 2000; Hollerman et al., 2000; Kringelbach et al., 2003). Together, these findings suggest a neuroanatomical distinction between prediction errors and expected rewards (Haruno and Kawato, 2006). Thus, the first goal of this study was to test whether a reinforcement learning model could be used to uncover representations of expected rewards and reward prediction errors in an environment that involved decision-making under uncertainty.
The second goal of this study was to test the role of individual differences in these processes. Specifically, reinforcement learning models have learning rates that describe how the prediction error adjusts the weights (equations provided in the ‘Methods’ section): a large learning rate means that the prediction error strongly influences the adjustment of the weight, whereas a small learning rate (e.g. close to 0) means that the prediction error only slightly influences the weights. These parameters are typically selected a priori and fixed across subjects (e.g. O’Doherty et al., 2003; Seymour et al., 2004). These models have provided powerful insights into the neural computations of a prediction error, although they are traditionally tested either in passive learning or in simple choice tasks in which there is a ‘best’ or correct response. However, fixing these parameters to be constant across all subjects might not be appropriate in more complex situations, such as those that involve decision-making under uncertainty or risk, in which different individuals might interpret the same reinforcement in different ways. For example, after losing a high-risk gamble, some people might avoid another high-risk gamble, whereas others might continue seeking high-risk gambles (Cohen and Ranganath, 2005). Reinforcement learning models with fixed learning parameters do not capture this inter-subject variability because fixed learning parameters assume that all subjects interpret and use reinforcements in the same way to update weights of decision options. However, these parameters can be empirically estimated for each subject based on their behavioral data and used to characterize behavioral and neural processes (e.g. Paulus and Frank, 2006). Here, the performance of models that used fixed or individually derived learning rates to determine the importance of individual differences in reinforcement learning processes are compared.
METHODS
Task
Seventeen subjects (aged 22–27 years, eight males) were scanned while engaged in a decision-making task in which on each trial they chose either a high-risk (40% chance of $2.50 and 60% chance of $0.00) or a low-risk (80% chance of $1.25 and 20% chance of $0.00) decision option. Subjects were told the probabilities and amounts of each decision option prior to the start of the experiment, and they practiced for several minutes before scanning began. This training minimized early learning and guessing processes that may have affected performance and brain activity during the early phases of the task. Thus, this task is useful for studying how reinforcements are used to adjust behavior on the trial-by-trial level rather than examining how learning optimal response patterns occurs over a longer time scale.
On each trial, subjects first saw a visual cue for 400 ms that indicated that the trial began. They indicted their decision to choose the high- or low-risk decision option either by pressing a button or withholding a response, depending on the shape of the cue (press to indicate high-risk decision if the cue was a square, or withhold a response to indicate a high-risk decision if the cue was a circle). This was done to prevent subjects from planning their motor responses before the trial began. Results did not differ according to this manipulation, and these conditions were thus collapsed. Additional control trials were included in which subjects simply made a response (i.e. no decision was involved). These trials are not discussed in the present article. An inter-trial interval of 2–8 s (jittered) separated each trial. There were 300 trials spaced over eight scanning runs. Other, nonoverlapping results from this data set are reported elsewhere (Cohen and Ranganath, 2005).
MRI acquisition and processing
MRI data were collected on a 1.5T GE Signa scanner at the UC Davis Research Imaging Center. Functional imaging was done with a gradient echo planar imaging (EPI) sequence (TR = 2000, TE = 40, FOV = 220, 64 × 64 matrix, voxel size = 3.475 × 3.475 × 5 mm3, 22 oblique axial slices). Coplanar and high-resolution T1 weighted images were acquired from each subject. EPI data were realigned to the first volume, coregistered with the anatomical scan, spatially normalized to Montreal Neurological Institute (MNI) space (Brett et al., 2002) resampled to 3.5 mm isotropic voxels, and spatially smoothed with an 8 mm FWHM kernel using SPM99 software.
Model
The model contains the following components: (1) Weights for each decision option (whigh-risk and wlow-risk for high- and low-risk decision options). Weights are thought to index expected rewards or subjective values, but are here termed weights for consistency with the machine learning literature (Sutton and Barto, 1998); (2) A prediction error signal (δ) generator. The prediction error node takes as input the weight of the chosen decision option and the actual reward received, and sends the difference between these two as output back to the weights (equation in the following paragraph). Thus, outcomes that are ‘better than expected’ yield positive prediction errors and increase the weight of the chosen decision option, and outcomes that are ‘worse than expected’ yield negative prediction errors and thus decrease the weight of the chosen decision option.
The model adjusts its weights as follows: The weight on trial t + 1 is the weight on trial t plus the prediction error on trial t : w(t + 1) = α × w(t) + η × δ(t). Thus, when the prediction error is positive (which occurs after a reward is received), the weight on the next trial (w (t + 1)) increases. Importantly, the weight is scaled by α, a discount parameter (sometimes called a ‘forgetting’ parameter), and the prediction error is scaled by η, the learning rate. These parameters can be estimated based on subjects’ behavioral data (see the following text). The learning rate associated with each weight can take on one of three values on each trial: 0 when the decision option was not chosen, and, when the decision option was chosen, ηreward and ηnon-reward for trials in which subjects received or did not receive a reward, respectively. Having separate parameters provides flexibility for the model to respond to different outcomes in different ways. In other words, high-risk wins need not be treated as equal to low-risk wins. Values of 1.25, 2.5 and 0 were used to represent low-risk rewards, high-risk rewards and non-rewards, respectively. Although the relative scaling of the two rewards is important (because the magnitude of the high-risk reward is twice as much as that of the low-risk reward), the actual numerical values are arbitrary with respect to the fMRI analyses, and the results would not be different if reward values were, for example, 125 and 250.
Three models were compared: a model in which all parameters were estimated individually for each subject (the ‘individual differences’ model), a model that used the average parameters across all subjects (the ‘group’ model) such that parameters were empirically estimated but were fixed across all subjects (parameters were: high-risk/reward: 0.033; high-risk/nonreward: 0.213; low-risk/reward: 0.201; low-risk/nonreward’: 0.137; discount: 0.753); finally, a model that used fixed, a priori selected parameters for all subjects (the ‘fixed’ model). For the fixed model, α was set to 0.99 and η was set to 0.7. These parameters have been used previously (O’Doherty et al., 2003). The purpose of comparing these models was to evaluate the results that would be obtained if one used the model in different ways.
To estimate these parameters for each subject, an iterative maximum likelihood minimization procedure (Luce, 1999; Barraclough et al., 2004; Cohen and Ranganath, 2005) was implemented in MATLAB. On each iteration, the model takes the behavioral choices and outcomes for each subject and computes the probability of the subject choosing the high-risk decision on each trial as the difference of the logarithm of the weights:
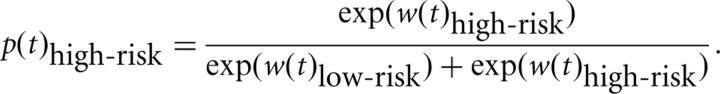 |
The procedure uses the nonlinear, unconstrained NelderMead simplex method (Lagarias et al., 1998) to find values of the learning parameters that maximize the sum of p(t)high-risk or p(t)high-risk across the experiment (depending on the decision made by the subject on trial t). Learning parameters are adjusted on each iteration until further iterations and adjustments do not improve the model. Weights are each set to 1 at the start of each iteration, and 0.5 is used as starting values for all parameters, although the initial values had negligible effects on their final estimates. There was an average of 479.2 iterations (SD: 259.8, range: 218–1034) until convergence. Note that the criteria for optimizing learning rates does not involve directly comparing weights or prediction errors and actual decisions made by the subjects, and is completely orthogonal to the fMRI data, and so comparing results from the models is not redundant with how the parameters were estimated.
FMRI analyses
To examine putative neural representations of prediction errors and weights, each model was fed the unique history of decisions and reinforcements from each subject, and calculated a reward prediction error and difference in the weights for the two decision options on each trial of the experiment.1 In this study, the difference between the weights, rather than the weights themselves, is used because decision options were not associated with unique behavioral responses, and the brain likely does not house separable representations for ‘high-risk’ and ‘low-risk’ decision options. Because the two decision options have equal mathematical expected values (i.e. the magnitude of reward times the probability of reward is one dollar for each option), this difference term may correspond to trial-by-trial changes in relative subjective value or motivational significance of the two decision options. These vectors of model outputs were then convolved with each subject's empirically derived hemodynamic response function (obtained from a separate visual-motor response task) (Aguirre et al., 1998; Handwerker et al., 2004) to produce a unique expected blood oxygenation-level dependent (BOLD) response to these terms for each subject. The procedure is illustrated in Figure 1. To the extent that the BOLD response in a particular voxel correlates with this independent variable, the voxel covers tissue in which activity may reflect or be modulated by prediction errors as defined by the model. This method has been previously used to study the putative neural correlates of prediction errors (O’Doherty et al., 2003; O’Doherty et al., 2004; Seymour et al., 2004; Tanaka et al., 2004; Glascher and Buchel, 2005; Haruno and Kawato, 2006).
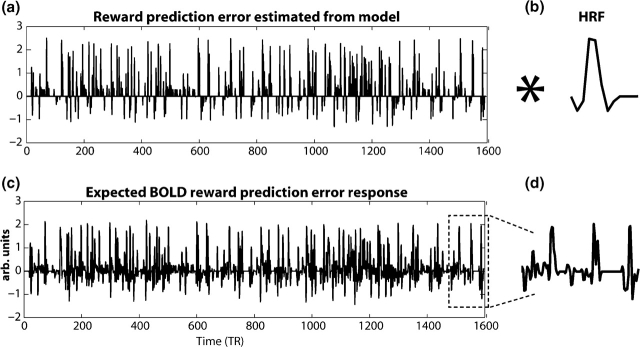
Fig. 1.
Illustration of prediction error independent variable used in fMRI GLM. (a) shows the unit-length prediction errors across the entire experiment for one subject calculated by the model. This vector of prediction errors is then convolved with the subject's hemodynamic response HRF; (b) to create a vector of an expected hemodynamic response to prediction errors (c). This vector is entered into the GLM analysis as an independent variable (see ‘Methods’ section). (d) shows an enlarged section of the expected BOLD response to reward prediction errors.
In the analysis, all of the task variables (combinations of high- and low-risk rewards and nonreward and a no-decision control condition) and the vectors calculated by the model were included as independent variables. The task variables were included to remove any possible shared variance between normal task covariates and the prediction error and weight regressors. All variables were centered on a mean of zero. Separate general linear models (GLMs) were conducted for each model. Results of single-subject analyses were maps of statistical values, where the value at each voxel is the parameter estimate (unstandardized β) of the relation between the BOLD response in that voxel and the independent variable (e.g. prediction error). In the present analyses, two maps were of interest: the prediction error and difference in weights. Group-level analyses were conducted by entering these maps into a one sample t-test, in which the β-estimate at each voxel across subjects was tested against zero, and subject was treated as a random variable. Significant activations were identified with a two-tailed threshold of P < 0.001 and a cluster threshold of five contiguous voxels. In the fMRI behavior correlation, one subject was removed from analyses because the behavior β-value was over three SDs above the mean (Figure 2c). However, results with this subject included were very similar.
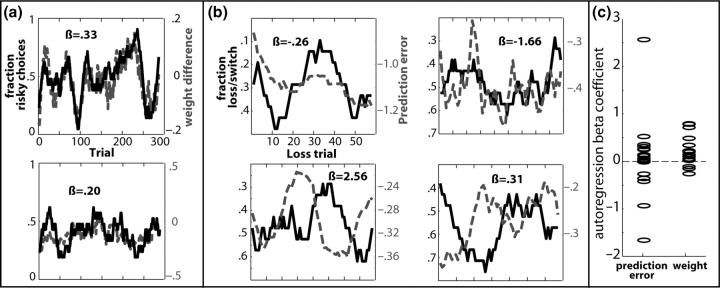
Fig. 2.
Model outputs predict behavioral choice data. Plotted are the local fraction of choosing the high-risk option (a) and choosing the opposite decision following nonrewards (b) represented as the solid black line, and the difference in the model's high- vs low-risk decision option weights (a) and the prediction error on each trial (b) represented as the dotted gray line. Results are displayed from six separate subjects. (c) Displays the β-coefficients for each subject.
Behavioral analyses
To examine the correspondence between the model and subjects’ behavioral choices, behavioral responses were compared with prediction errors and weights generated by the individual differences and fixed models. Responses were coded as 0 (safe decision) or 1 (risky decision) and were smoothed with a running-average filter with a 10-trial kernel to produce a continuous vector that reflects the local fraction of choices selected. Such methods are often used to examine correspondence between model predictions and behavioral selections (Sugrue et al., 2004; Bayer and Glimcher, 2005; Samejima et al., 2005). Because of autocorrelations induced by the smoothing, data were analyzed with autoregression, which estimates both the autocorrelation coefficient [using AR(1)] and the regression parameters that are independent of autocorrelation present in the data. Greenhouse–Geisser corrections to degrees of freedom were used in ANOVAs of behavioral fits.
RESULTS
Behavioral results
If subjects chose the decision option with the stronger weight, as reinforcement learning theory suggests, the model's calculated weights should correlate with subjects’ trial-to-trial choices. This was tested by computing the autoregression with each subject's local fraction of high-risk choices and the model's calculated weight of the high-risk option for each trial. This β-coefficient was significantly greater than zero across subjects (average β = 0.20, t16 = 2.6, P = 0.01) (Figure 2a and c). The average β for the analysis with the fixed model was smaller, although still significant across the group (average β = 0.09, t16 = 2.5, P = 0.01). The average β for the analysis with the group model was not different from zero (average β = −0.08, t16 = 2, P = 0.054). A repeated-measures ANOVA on these β-values using ‘model’ as factor revealed that these fits were significantly different (F1.4,22.8 = 7.04, P = 0.008), such that the individual differences model yielded greater β-values than those of the group model (P = 0.01) and the fixed model yielded greater β-values that those of the group model (P = 0.01).
It was further predicted that prediction error signals are used to guide decision-making (Cohen and Ranganath, under review). In particular, if negative prediction errors indicate that reinforcements are worse than expected, these negative prediction errors might signal a need for adjustments in behavior; larger prediction errors should therefore signal greater need for behavioral adjustments. If this is the case, the model's calculated prediction error on each nonreward trial should predict subjects’ choices in the subsequent trial. This was operationalized as whether, following each nonreward, subjects chose the same vs the opposite decision option on the following trial as on the current one (e.g. when not receiving a high-risk reward on trial n, does the subject choose another high-risk reward or a low-risk reward on trial n + 1?). The β-coefficient between this trial-to-trial strategy and the model's calculated prediction error on each of these trials was not significantly different from zero across subjects (average β = 0.78; t16 = 0.32). This occurred because for some subjects the β-coefficient was positive and for other subjects this β-coefficient was negative (Figure 2b and c). That is, for some subjects, larger prediction errors following nonrewards were associated with an increased probability of behavioral switches, whereas for others the opposite was the case. This seemingly counterintuitive variability is significantly related to individual variability in the neural correlates of the prediction error, as described in the following section. The fixed model also showed no significant β-coefficient across subjects (average β = −0.0003; t16 = −0.0008). The group model, however, showed a significant β-coefficient across subjects (average β = 0.581; t16 = 4.26, P = 0.001). A repeated-measures ANOVA revealed that these fits were significantly different (F1.3,21.4 = 5.8, P = 0.017) such that the group model yielded greater β-values than those of the individual differences model (P = 0.037), and of the fixed model (P < 0.001).
FMRI results
Neural correlates of value (i.e. difference of weights)
For the individual differences model, activations were observed in the right amygdala extending into the hippocampus, right orbitofrontal cortex extending into the ventral striatum, bilateral caudate, bilateral thalamus/putamen, bilateral dorsolateral prefrontal cortex and cerebellum (Figure 3d). Figure 4a displays an example BOLD time course and weight vector (convolved with a hemodynamic response) to illustrate the correlation. No deactivations (i.e. more activity for the weight of the low-risk option compared to the high-risk option) were observed. Table 1 lists activation foci for this and all other analyses reported here.
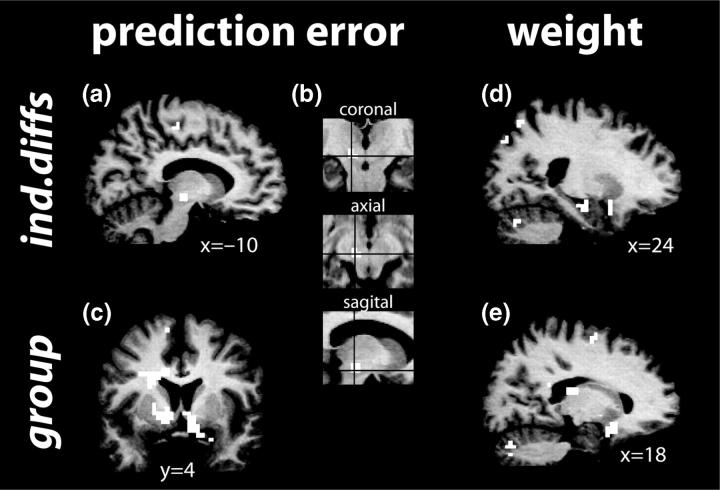
Fig. 3.
Group activation maps depicting brain regions in which activity correlated with the prediction error term (a–c) and difference in weights (d,e) for the model using individual differences in learning parameters (a,b,d) or group-defined parameters (c,e). Insets in (b) show precise location of midbrain activation.
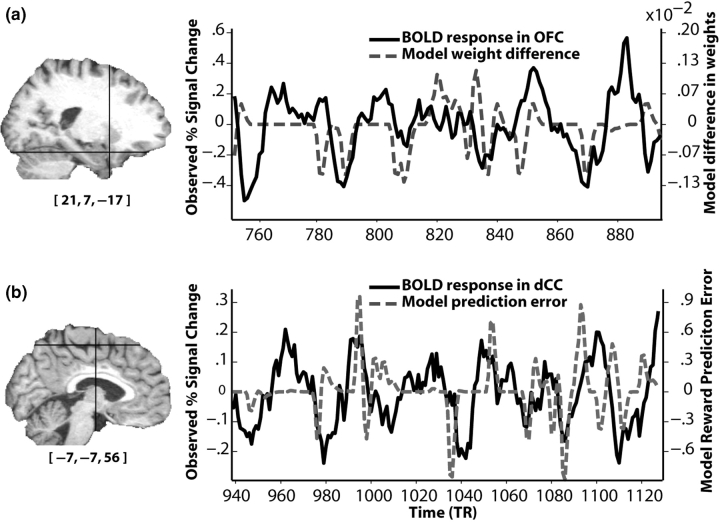
Fig. 4.
BOLD responses from a single subject correlate with variables predicted by the individual differences model. (a) Correspondence between BOLD signal from the maximally significant voxel in orbitofrontal cortex (OFC; solid black line) and the difference of the high- and low-risk weights calculated by the model (dotted gray line). (b) The BOLD response from the maximally significant voxel in dorsal cingulate cortex (dCC; solid black line) and the model's prediction error, convolved with a hemodynamic response function (dotted gray line). Cross-hairs in the T1 display the position of the voxel (MNI coordinates displayed under the T1). BOLD responses are low-pass filtered for illustration purposes.
Table 1.
List of activation clusters
| Region | X, Y, Z | t | Brodmann Area (BA) |
|---|---|---|---|
| Difference of weights | |||
| Individual differences model | |||
| R. amygdala/hippocampus | 24, −13, −12 | 4.60 | |
| R. posterior orbital gyrus | 14, 14, −12 | 5.01 | 11 |
| L. putamen | −24, −20, 12 | 4.90 | |
| R. putamen | 21, −14, 13 | 5.97 | |
| L. caudate | −17, 3, 14 | 4.28 | |
| R. caudate | 13, −14, 19 | 4.47 | |
| R. dorsal cingulate | 7, −27, 33 | 4.06 | 23 |
| L. superior frontal gyrus | −43, 15, 43 | 4.67 | 9/44 |
| R. superior parietal gyrus | 23, −64, 57 | 4.53 | 7 |
| L. superior parietal gyrus | −26, −65, 53 | 4.50 | 7 |
| R. cerebellum | 24, −70, −28 | 4.78 | |
| L. cerebellum | −24, −74, −34 | 4.60 | |
| R. middle temporal gyrus | 46, −58, −8 | 4.61 | 37 |
| Group model | |||
| L. posterior orbital gyrus | −28, 11, −20 | 4.62 | 38 |
| R. posterior orbital gyrus | 18, 12, −18 | 6.90 | 11 |
| R. caudate | 10, 2, 7 | 4.07 | |
| R. collateral sulcus | 38, −56, −14 | 5.41 | 37 |
| R. inferior frontal gyrus | 42, 50, −5 | 7.04 | 46 |
| R. anterior insula | 29, 19, 7 | 6.66 | 48 |
| L. thalamus | −11, −24, 12 | 5.17 | |
| R. posterior cingulate | 10, −44, 26 | 5.36 | 23/26 |
| R. medial frontal gyrus | 36, 30, 34 | 4.83 | 46 |
| L. medial frontal gyrus | −46, 19, 36 | 4.88 | 44/46 |
| R. superior frontal gyrus | 21, −4, 66 | 5.36 | 6 |
| L. precuneus/angular gyrus | −36, −64, 53 | 4.57 | 7 |
| R. precuneus/angular gyrus | 38, −56, 53 | 5.24 | 40 |
| R. cerebellum | 27, −77, −34 | 5.51 | |
| L. cerebellum | −21, −78, −31 | 4.43 | |
| Fixed model | |||
| R. middle temporal gyrus | 45, −54, −16 | 4.59 | 37 |
| L. middle frontal gyrus | −46, 50, 4 | 4.60 | 46 |
| R. superior parietal gyrus | 26, −64, 58 | 5.67 | 7 |
| Individual differences–fixed | |||
| R. thalamus | −12, −19, 14 | 5.11 | |
| R. cerebellum | 38, −65, −35 | 5.78 | |
| Group–fixed | |||
| R. cerebellum | 14, −79, −33 | 5.55 | |
| Cerebellar vermis | 0, −54, −17 | 5.10 | |
| R. posterior orbital gyrus | 18, 12, −17 | 7.34 | 11 |
| L. posterior orbital gyrus | −19, 8, −19 | 4.16 | 48 |
| R. middle frontal gyrus | 42, 51, −6 | 6.19 | 46 |
| L. middle frontal gyrus | −46, 50, −4 | 5.42 | 46 |
| R. collateral sulcus | 42, −56, −12 | 5.04 | 37 |
| R. anterior insula | 33, 22, 4 | 4.93 | 47/48 |
| R. caudate | 10, −2, 12 | 5.95 | |
| L. thalamus | −14, 9, 12 | 5.55 | |
| R. posterior cingulate | 11, −48, 26 | 4.91 | 23 |
| L. middle frontal gyrus | −36, 12, 40 | 6.77 | 44 |
| R. middle frontal gyrus | 34, 9, 47 | 4.40 | 6 |
| L. precuneus/angular gyrus | −35, −69, 55 | 5.09 | 7 |
| R. precuneus/angular gyrus | 35, −61, 52 | 5.28 | 7/40 |
| Prediction error | |||
| Individual differences model | |||
| L. substantia nigra/midbrain | −10, −18, −9 | 4.73 | |
| L. dorsal cingulate | −10, −24, 54 | 4.63 | 4/6 |
| L. middle frontal gyrus | −40, −9, 54 | 4.94 | 6 |
| R. middle frontal gyrus | 40, −11, 49 | 5.16 | 6 |
| R. superior frontal gyrus | 14, −9, 71 | 4.67 | 6 |
| R. cuneus | 15, −86, 19 | 4.53 | 18/19 |
| R. caudate | 17, −16, 23 | −4.49 | |
| L. middle temporal gyrus | −56, −44, −5 | −5.43 | 21 |
| L. angular gyrus | −46, −70, 33 | −4.55 | 39 |
| Group model | |||
| L. hippocampus/amygdala | −21, −13, −26 | 4.86 | 36 |
| R. amygdala | 21, 0, −23 | 5.53 | 28 |
| R. ventral striatum | 8, 2, −4 | 5.94 | |
| L. ventral striatum | −10, 3, −5 | 5.86 | |
| R. middle occipital gyrus | 39, −87, −11 | 5.16 | 19 |
| L. medial orbital gyrus | −8, 36, 0 | 4.77 | 11 |
| L. middle occipital gyrus | −38, 91, 5 | 4.58 | 18 |
| Posterior cingulate | 5, −52, 28 | 5.11 | 23 |
| L. cingulate sulcus | −7, 32, 29 | 5.08 | 32 |
| L. precentral sulcus | −39, −13, 35 | 4.86 | 3 |
| L. superior frontal gyrus | −10, 45, 47 | 6.25 | 9 |
| R. superior frontal gyrus | 15, 35, 40 | 5.55 | 32/9 |
| Fixed model | |||
| L. middle frontal gyrus | −48, 43, 1 | −5.94 | 45 |
| Individual differences−fixed | |||
| L. dorsal cingulate | −7, −27, 49 | 4.89 | 23 |
| L. middle frontal gyrus | −45, −13, 55 | 4.37 | 6 |
| L. anterior insula | −36, 22, 9 | 4.81 | 48 |
| L. superior frontal gyrus | −7, 1, 61 | 5.05 | 6 |
| L. cuneus | −13, 82, 16 | 4.29 | 19 |
| R. cuneus | 14, −85, 19 | 4.17 | 18/19 |
| Group–fixed | |||
| L. posterior orbital gyrus | −24, 17, 18 | 4.12 | 48 |
| L. middle temporal gyrus | −62, −51, −18 | 4.91 | 37 |
| L. ventral striatum | −10, 3, −4 | 5.51 | |
| L. middle frontal gyrus | −46, 9, 36 | 4.61 | 44 |
| L. superior frontal gyrus | −21, 11, 66 | 6.88 | 6 |
| R. caudate | 14, −5, 21 | 5.54 | |
| R. angular gyrus | 37, −78, 34 | 4.88 | 19 |
| R. superior frontal gyrus | 8, 25, 46 | 7.10 | 8 |
| Individual differences correlation with prediction error | |||
| Individual differences model | |||
| L. lateral orbitofrontal cortex | −31, 28, −23 | 5.97 | 47/11 |
| R. lateral orbitofrontal cortex | 21, 25, −21 | 8.40 | 11 |
| R. ventral striatum | 12, 19, 1 | 5.26 | |
| L. ventral striatum | −17, 26, −2 | 5.50 | |
| L. thalamus | −3, −16, 1 | 6.20 | |
| R. superior frontal gyrus | 17, 60, 22 | 7.84 | 10 |
| L. superior frontal gyrus | −3, 63, 19 | 6.01 | 10 |
| Posterior cingulate | 3, −27, 26 | 8.97 | 23 |
| R. middle frontal gyrus | 27, 23, 55 | 7.37 | 8 |
| R. superior parietal gyrus | 18, −78, 57 | 5.68 | 7 |
| L. superior parietal gyrus | −25, −68, 64 | 6.43 | 7 |
| R. caudate | 17, 8, 18 | 4.37 |
The group model yielded activations that were largely overlapping with those observed for the individual differences model: bilateral posterior orbitofrontal cortex/subgenual cingulate (BA 11/25) as well as anterior orbitofrontal cortex (BA 11), right ventrolateral prefrontal cortex (BA 47), bilateral thalamus, bilateral dorsal prefrontal cortex (BA 44/45) and parietal cortex (BA 39) (Figure 3e).
Finally, for the fixed model, activations were observed in right temporal cortex and left dorsolateral prefrontal cortex (BA 46) and right middle temporal gyrus and superior parietal gyrus.
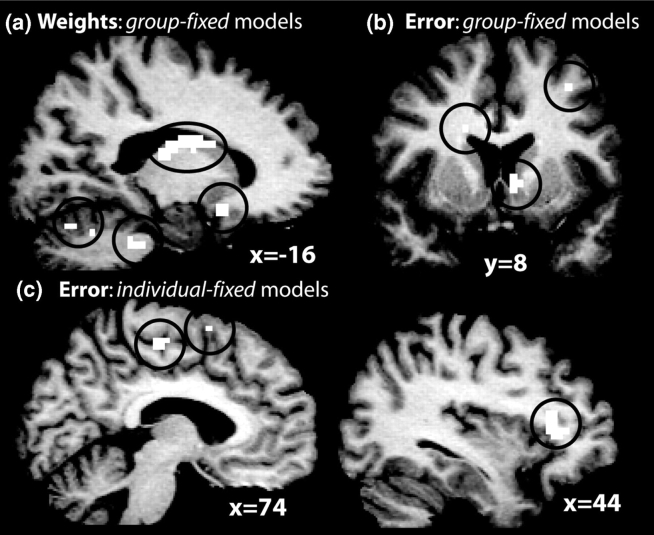
Next, the performance of the models is formally compared by testing whether the difference between β-values at each voxel produced by different models (e.g. group model results − fixed model results) was significantly greater or less than zero. There were no differences between the individual differences and group maps. Comparing the individual differences and fixed maps revealed regions with significantly higher β's in the left cerebellum and right thalamus. Comparing the group and fixed models revealed several regions with higher β-values for the group model, including bilateral caudate, posterior orbitofrontal cortex, cerebellum, thalamus and bilateral prefrontal cortex (Figure 5a).
Fig. 5.
Regions in which the group (a–b) and individual differences (c) models provided significantly higher parameter estimates than did the fixed model for neural correlates of a reward prediction error (b–c) and the weights (a). Black circles enclose activations for ease in viewing.
Neural correlates of reward prediction error signal
For the individual differences model, activity in several regions was significantly positively correlated with the reward prediction error signal, including the left midbrain (anatomically consistent with a source in the substantia nigra), dorsal cingulate cortex, bilateral prefrontal cortex (BA 6) and right cuneus (BA 18/19) (Figure 3a and b). Figure 4b displays an example BOLD time course and reward prediction error vector (convolved with a hemodynamic response) to illustrate the correlation. In addition to activations (i.e. positive correlations with the reward prediction error signal), there were also deactivations (i.e. inverse correlations with the reward prediction error signal) in the head of the right caudate, left middle temporal gyrus (BA 21) and left angular gyrus.
For the group model, activations were observed in bilateral amygdala, ventral striatum extending in the caudate in the left hemisphere, anterior cingulate and medial supplementary motor cortex, posterior cingulate and anterior prefrontal cortex (BA 10) (Figure 3c).
Finally, the fixed model produced no significant activations, but a deactivation was observed in ventrolateral prefrontal cortex (PFC) (BA 47).
Next the performance of the models was directly compared. There were no differences between the individual differences and group maps. However, comparing the individual differences and fixed maps revealed regions with significantly higher β's in the dorsal cingulate and ventrolateral prefrontal cortex (Figure 5c). Comparing the group and fixed models yielded largely similar results, although additional regions exhibited higher β-values for the group model including the right ventral striatum and orbitofrontal cortex (Figure 5b).
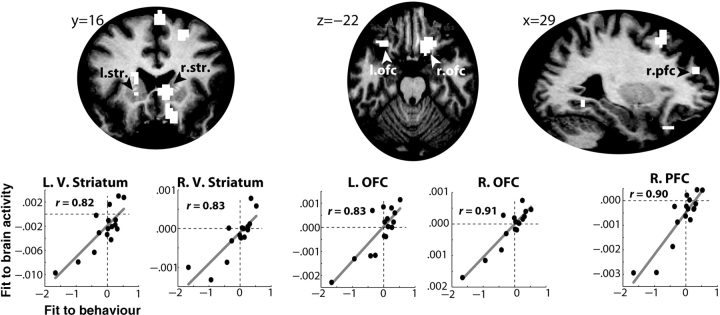
The variability in the relationship between prediction errors and behavioral strategies (Figure 2c) suggests that individuals differed in how they used the prediction error signal to guide decision-making. Thus, these individual differences might reflect differences in the neural representation of the prediction error signal. To test this, the β-value is used between the prediction error term and the local fraction of stay/switch choices of the subjects (e.g. the relationships depicted in Figure 2b) as an independent variable in a regression with the statistical brain activation maps of correlates of the prediction error. Cross-subject variability in each of these analyses reflects differences in the representation and use of prediction errors during the task, and thus significant brain activations in this analysis indicate that differences in how prediction errors guide behavior predict differences in how prediction errors might be represented in the brain. As seen in Figure 6, the behavioral correlation significantly predicted the model's fit to the fMRI data in bilateral ventral striatum, orbitofrontal cortex and prefrontal cortex.2
Fig. 6.
The model fit to behavior predicted the model fit to brain activity in striatum and prefrontal cortex. The top row displays a selection of brain regions in which this correlation was significant. Scatter plots depict the relationship between model fit to behavior (unstandardized β-coefficient between model's prediction errors and subjects’ stay/switch decisions; X-axis) and model fit to brain activity (average unstandardized parameter estimates from all voxels in the indicated region; Y-axis) in selected regions. Note that the X- and Y-axes display unstandardized β-coefficients and are thus their magnitudes are not directly comparable. L, left; R, right; V, ventral; str., striatum; OFC, orbitofrontal cortex; PFC, prefrontal cortex.
Next, this individual differences correlation analysis was run using β-coefficients between the group model's prediction errors and subjects’ stay/switch behaviors. In contrast to the findings obtained from the individual differences model, no activations were observed, even at a liberal threshold of P < 0.01, uncorrected. Finally, no significant activations were observed for the fixed model.
DISCUSSION
Here, evidence is provided suggesting that, during decision-making under uncertainty, two variables predicted by reinforcement learning theory and estimated using computational modeling—reward prediction errors and decision option weights—are encoded in a network of cortical and subcortical brain structures and used to guide decision-making. Consideration of individual differences proved central to elucidating the behavioral and neural correlates of reinforcement learning because the individual differences and group models explained significantly more variance in the fMRI data than did the fixed model.
Neural representation of value
Activity in several regions including the amygdala, orbitofrontal cortex/ventral striatum and caudate nucleus correlated with the model-derived estimate of the difference in weights. Neurons in these regions are known to encode the relative value of rewards as well as expectations of rewards. For example, orbitofrontal and amygdala neurons show increased firing rates to preferred rewards compared to less preferred rewards (Everitt et al., 1991; Tremblay and Schultz, 1999; Hikosaka and Watanabe, 2000; Baxter and Murray, 2002; Gilbert et al., 2003). Thus, these regions may compute online assessments of the relative value of competing decision options, and may guide behavior by indicating which option is the most valuable or worthy of pursuit. Consistent with this interpretation, patients with damage to orbitofrontal cortex and amygdala have impairments in reward-based decision-making and often continue to prefer risky decision options even when this behavior leads to long-term losses (Bechara et al., 1997, 2000, 2003). Among their impairments may be inability to compute or utilize computations of relative value to guide their decision-making.
In this study, the difference between the weights of the high- and low-risk decision options is used, rather than the weights themselves, because in this study there were no unique behavioral responses associated with choosing high- vs low-risk decision options, and so specific motor representations of the high- and low-risk decision options could not be formed. Thus, what is represented by the difference vector, and what the brain activations may reflect, is not representations of decision options or value per se but of the difference in value or motivational significance between two competing decision options. Other studies have demonstrated that when specific decisions are linked with specific behaviors (e.g. eye movements or left- vs right-hand button presses), activity in neural structures that represent those behaviors is influenced by the value of that decision option (Schall, 1995; Gold and Shadlen, 2000; Sugrue et al., 2004; Samejima et al., 2005; Cohen and Ranganath, under review). Thus, value might be encoded in the brain both as strength of action representations and as relative activation of neurons in orbitofrontal cortex and amygdala, among other regions.
Neural representation of prediction errors
The prediction errors generated by the model correlated with activity in the midbrain, dorsal cingulate cortex and prefrontal cortex for the individual differences model, and the ventral striatum, amygdala, dorsal cingulate cortex and prefrontal cortex for the group model. These activations confirm those reported in previous studies (Schultz et al., 1997; Waelti et al., 2001; Daw et al., 2002; Holroyd and Coles, 2002; O’Doherty et al., 2003; Schultz, 2004; Seymour et al., 2004; Rodriguez et al., 2005; Abler et al., 2006). Although precise localization of activation in the midbrain is difficult, this activation appears to be centered in the substantia nigra, the origin of the nigrostriatal dopamine pathway. The location of this activation is also consistent with coordinates reported in previous fMRI studies of reinforcement learning processes (Seymour et al., 2004; O’Doherty et al., 2006) and with direct recordings of single unit activity in monkeys (Schultz, 1998; Bayer and Glimcher, 2005).
In the individual differences model, a deactivation (i.e. inverse correlations with the prediction error) was observed in the caudate nucleus. Although such deactivations have not been previously reported, previous investigations of the neural bases of reward prediction error signals did not test for deactivations, instead using one-tailed statistical tests that would only reveal positive correlations with the prediction error signal (O’Doherty et al., 2003; Seymour et al., 2004). Thus, deactivations would not have been identified even if they were present in the data. However, this finding seems consistent with the presumed role of the caudate as the ‘actor’ in actor–critic models of reinforcement learning (Montague et al., 1996; O’Doherty et al., 2004). Specifically, the ‘critic’ (thought to be the ventral striatum or midbrain) uses prediction errors to associate reinforcements with events or actions that preceded them, and the ‘actor’ uses prediction errors to guide appropriate behavioral responses. Thus, the actor may use an inverse prediction error term to help motivate behavior (i.e. larger negative prediction errors means more motivation to adjust behavior) (Joel et al., 2002; Worgotter and Porr, 2005).
The variance in the relation between the prediction errors and stay/switch strategies following losses suggested that different subjects used or calculated the prediction error differently. This seems counterintuitive because reinforcement learning theory suggests that larger prediction errors signal a greater need to change behavior. In other words, it appears as if in some cases, observed behavior is ‘opposite’ to what the model suggests behavior should be. Given that there is no optimal policy or correct strategy, it is possible that some subjects viewed choosing a nonrewarded decision a second time as a strategy ‘switch’, which would mean they actually were using prediction errors as reinforcement learning suggests, but that their conceptualization of strategy was different from how it was modeled. This could occur, for example, if some subjects thought that when a decision option did not provide a reward in the current trial, it would in the next trial. Regardless, this variance proved to be meaningful because the prediction error–behavioral strategy β-coefficients explained variance in the prediction error–brain activation correlations. Such relationships were observed primarily in the ventral striatum and orbitofrontal cortex, consistent with previous reports that these regions are sensitive to prediction errors (McClure et al., 2003; O’Doherty et al., 2003; Abler et al., 2006; Haruno and Kawato, 2006; Jensen et al., 2006). There were no similar correlations with the group and fixed models, even at more liberal statistical thresholds. This dissociation suggests that models incorporating individual differences provide maximal sensitivity to uncovering further individual differences. Interestingly, the regions that exhibited significant correlations with the individual differences model overlapped considerably with the regions identified in the group analysis, in particular the ventral striatum.
The importance of individual differences naturally leads to the question of their origins. Differences in risk-taking preferences have been linked to a number of neurobiological and psychosocial factors such as the concentration of dopamine D2 receptors in the limbic system (Noble, 1998, 2003), socioeconomic status (Diala et al., 2004), or personality (Craig, 1979; Zuckerman and Kuhlman, 2000; Petry, 2001). Lee and colleagues (Barraclough et al., 2004; Lee et al., 2005) found that reinforcement learning parameters in monkeys are highly stable over many testing sessions of the same experiment, suggesting that these learning parameters reflect stable individual differences. Stability of learning parameters across multiple settings and over time is especially relevant to the present study, because the same individuals might have different learning rates in different tasks, such as those in which some strategies provide a greater cumulative reward in the long run. Regardless of their origins and generalizability, however, characterizing how individual differences modulate these processes may prove critical to elucidating the neural mechanisms of reinforcement learning and decision-making.
However, it is not suggested that choosing learning parameters a priori to be the same for all subjects is incorrect or inappropriate. Indeed, without measuring choice behavior over time it is impossible to empirically estimate learning parameters how they were estimated here. Fixed parameters might be appropriate in passive learning experiments or in simple decision-making situations in which the optimal response is always to maintain rewarded behaviors and avoid punished behaviors. However, in more complex situations in which different individuals evaluate and utilize reinforcements in different ways, models with a priori chosen parameters may not adequately characterize reinforcement learning processes.
Relations to other reinforcement learning models
Nearly all reinforcement learning models contain the same basic components: representations of each decision option or stimulus (weights, in this study), and a means to adjust those representations (typically a prediction error). Many variants of reinforcement learning models exist and could be related to behavioral and neuroimaging data, but differences between different models are typically minor and more related to the experimental paradigm than to the interpretation of model parameters and output (see Sutton and Barto, 1998, for an extensive comparison of the similarities and differences between various reinforcement learning models). The model used in the present study is of course not the only possible model that could be applied to this data set; indeed, one could propose a new model specifically designed to capture behavior in this task. However, the model used here was selected because (1) it is widely used in neuroscience to study reinforcement learning (see Montague and Berns, 2002, for a review) and (2) it has a proposed biological basis and is used to investigate neuroanatomical correlates of reinforcement learning and decision-making (Schultz et al., 1997; Barraclough et al., 2004; Montague et al., 2004). Typical uses of such models typically involve passive learning (Seymour et al., 2004) or very simple decision-making situations in which one response is optimal and another suboptimal (O’Doherty et al., 2004). The fact that this simple reinforcement learning model is capable of modeling behavior and brain activity during more complex situations that involve risk and uncertainty with no optimal response is a strength of the reinforcement learning model approach to understanding dynamic changes in brain activity.
Acknowledgments
This work was supported by an Extramural Research Grant from the Institute for Research on Pathological Gambling and Related Disorders. The author thanks Charan Ranganath and Chris Moore for their help.
Conflict of Interest
None declared.
1 It would be ideal to separate the hemodynamic response from the decision and feedback phases of the trial, as prediction errors may be differentially represented during these phases. Unfortunately, the rapid event-related design combined with the sluggishness of the hemodynamic response precludes such a distinction from the present analyses. Thus, each trial was treated as a single event.
2 This relationship could not be explained by the use of a win/stay–lose/switch strategy, because the probability of using this strategy did not correlate with any of the learning parameters (all P > 0.05), nor did it correlate with activation in any of the regions identified in this analysis (all P > 0.5).
REFERENCES
- Abler B, Walter H, Erk S, Kammerer H, Spitzer M. Prediction error as a linear function of reward probability is coded in human nucleus accumbens. Neuroimage. 2006;31:790–5. doi: 10.1016/j.neuroimage.2006.01.001. [DOI] [PubMed] [Google Scholar]
- Aguirre GK, Zarahn E, D'Esposito M. The variability of human, BOLD hemodynamic responses. Neuroimage. 1998;8:360–9. doi: 10.1006/nimg.1998.0369. [DOI] [PubMed] [Google Scholar]
- Barraclough DJ, Conroy ML, Lee D. Prefrontal cortex and decision making in a mixed-strategy game. Nature Neuroscience. 2004;7:404–10. doi: 10.1038/nn1209. [DOI] [PubMed] [Google Scholar]
- Baxter MG, Murray EA. The amygdala and reward. Nature Reviews. Neuroscience. 2002;3:563–73. doi: 10.1038/nrn875. [DOI] [PubMed] [Google Scholar]
- Bayer HM, Glimcher PW. Midbrain dopamine neurons encode a quantitative reward prediction error signal. Neuron. 2005;47:129–41. doi: 10.1016/j.neuron.2005.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR. Emotion, decision making and the orbitofrontal cortex. Cerebal Cortex. 2000;10:295–307. doi: 10.1093/cercor/10.3.295. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Damasio AR. Role of the amygdala in decision-making. Annals of the New York Academy of Sciences. 2003;985:356–69. doi: 10.1111/j.1749-6632.2003.tb07094.x. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Tranel D, Damasio AR. Deciding advantageously before knowing the advantageous strategy. Science. 1997;275:1293–5. doi: 10.1126/science.275.5304.1293. [DOI] [PubMed] [Google Scholar]
- Brett M, Johnsrude IS, Owen AM. The problem of functional localization in the human brain. Nature Reviews Neuroscience. 2002;3:243–9. doi: 10.1038/nrn756. [DOI] [PubMed] [Google Scholar]
- Camerer CF. Behavioral Game Theory: Experiments in Strategic Interaction. Princeton: Princeton University Press; 2003. [Google Scholar]
- Cohen MX, Ranganath C. Behavioral and Neural Predictors of Upcoming Decisions. Cognitive, Affective & Behavioral Neuroscience. 2005;5:117–26. doi: 10.3758/cabn.5.2.117. [DOI] [PubMed] [Google Scholar]
- Cohen MX, Ranganath C. Reinforcement learning signals predict future decisions. doi: 10.1523/JNEUROSCI.4421-06.2007. (under review). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig RJ. Personality characteristics of heroin addicts: a review of the empirical literature with critique—part II. The International Journal of the Addictions. 1979;14:607–26. doi: 10.3109/10826087909041894. [DOI] [PubMed] [Google Scholar]
- Daw ND, Kakade S, Dayan P. Opponent interactions between serotonin and dopamine. Neural Network. 2002;15:603–16. doi: 10.1016/s0893-6080(02)00052-7. [DOI] [PubMed] [Google Scholar]
- Diala CC, Muntaner C, Walrath C. Gender, occupational, and socioeconomic correlates of alcohol and drug abuse among U.S. rural, metropolitan, and urban residents. The American Journal of Drug and Alcohol Abuse. 2004;30:409–28. doi: 10.1081/ada-120037385. [DOI] [PubMed] [Google Scholar]
- Everitt BJ, Morris KA, O'Brien A, Robbins TW. The basolateral amygdala-ventral striatal system and conditioned place preference: further evidence of limbic-striatal interactions underlying reward-related processes. Neuroscience. 1991;42:1–18. doi: 10.1016/0306-4522(91)90145-e. [DOI] [PubMed] [Google Scholar]
- Gilbert PE, Campbell A, Kesner RP. The role of the amygdala in conditioned flavor preference. Neurobiology of Learning and Memory. 2003;79:118–21. doi: 10.1016/s1074-7427(02)00013-8. [DOI] [PubMed] [Google Scholar]
- Glascher J, Buchel C. Formal learning theory dissociates brain regions with different temporal integration. Neuron. 2005;47:295–306. doi: 10.1016/j.neuron.2005.06.008. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Representation of a perceptual decision in developing oculomotor commands. Nature. 2000;404:390–4. doi: 10.1038/35006062. [DOI] [PubMed] [Google Scholar]
- Handwerker DA, Ollinger JM, D'Esposito M. Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage. 2004;21:1639–51. doi: 10.1016/j.neuroimage.2003.11.029. [DOI] [PubMed] [Google Scholar]
- Haruno M, Kawato M. Different neural correlates of reward expectation and reward expectation error in the putamen and caudate nucleus during stimulus-action-reward association learning. Journal of Neurophysiology. 2006;95:948–59. doi: 10.1152/jn.00382.2005. [DOI] [PubMed] [Google Scholar]
- Hikosaka K, Watanabe M. Delay activity of orbital and lateral prefrontal neurons of the monkey varying with different rewards. Cerebral Cortex. 2000;10:263–71. doi: 10.1093/cercor/10.3.263. [DOI] [PubMed] [Google Scholar]
- Hollerman JR, Tremblay L, Schultz W. Involvement of basal ganglia and orbitofrontal cortex in goal-directed behavior. Progress in Brain Research. 2000;126:193–215. doi: 10.1016/S0079-6123(00)26015-9. [DOI] [PubMed] [Google Scholar]
- Holroyd CB, Coles MG. The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. Psychological Review. 2002;109:679–709. doi: 10.1037/0033-295X.109.4.679. [DOI] [PubMed] [Google Scholar]
- Jensen J, Smith AJ, Willeit M, et al. Separate brain regions code for salience vs. valence during reward prediction in humans. Human Brain Mapping. 2006 doi: 10.1002/hbm.20274. [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joel D, Niv Y, Ruppin E. Actor-critic models of the basal ganglia: new anatomical and computational perspectives. Neural Network. 2002;15:535–47. doi: 10.1016/s0893-6080(02)00047-3. [DOI] [PubMed] [Google Scholar]
- Kringelbach ML, O'Doherty J, Rolls ET, Andrews C. Activation of the human orbitofrontal cortex to a liquid food stimulus is correlated with its subjective pleasantness. Cerebral Cortex. 2003;13:1064–71. doi: 10.1093/cercor/13.10.1064. [DOI] [PubMed] [Google Scholar]
- Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM Journal of Optimization. 1998;9:112–47. [Google Scholar]
- Lee D, McGreevy BP, Barraclough DJ. Learning and decision making in monkeys during a rock-paper-scissors game. Brain Research. Cognitive Brain Research. 2005 doi: 10.1016/j.cogbrainres.2005.07.003. [DOI] [PubMed] [Google Scholar]
- Luce DP. Individual Choice Behavior. New York: Wiley; 1999. [Google Scholar]
- McClure SM, Berns GS, Montague PR. Temporal prediction errors in a passive learning task activate human striatum. Neuron. 2003;38:339–46. doi: 10.1016/s0896-6273(03)00154-5. [DOI] [PubMed] [Google Scholar]
- Montague PR, Berns GS. Neural economics and the biological substrates of valuation. Neuron. 2002;36:265–84. doi: 10.1016/s0896-6273(02)00974-1. [DOI] [PubMed] [Google Scholar]
- Montague PR, Dayan P, Sejnowski TJ. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. Journal of Neuroscience. 1996;16:1936–47. doi: 10.1523/JNEUROSCI.16-05-01936.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montague PR, Hyman SE, Cohen JD. Computational roles for dopamine in behavioural control. Nature. 2004;431:760–7. doi: 10.1038/nature03015. [DOI] [PubMed] [Google Scholar]
- Noble EP. The D2 dopamine receptor gene: a review of association studies in alcoholism and phenotypes. Alcohol. 1998;16:33–45. doi: 10.1016/s0741-8329(97)00175-4. [DOI] [PubMed] [Google Scholar]
- Noble EP. D2 dopamine receptor gene in psychiatric and neurologic disorders and its phenotypes. American Journal of Medical Genetics. 2003;116B:103–25. doi: 10.1002/ajmg.b.10005. [DOI] [PubMed] [Google Scholar]
- O'Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;304:452–4. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP, Buchanan TW, Seymour B, Dolan RJ. Predictive neural coding of reward preference involves dissociable responses in human ventral midbrain and ventral striatum. Neuron. 2006;49:157–66. doi: 10.1016/j.neuron.2005.11.014. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003;38:329–37. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- Paulus MP, Frank LR. Anterior cingulate activity modulates nonlinear decision weight function of uncertain prospects. Neuroimage. 2006;30:668–77. doi: 10.1016/j.neuroimage.2005.09.061. [DOI] [PubMed] [Google Scholar]
- Petry NM. Substance abuse, pathological gambling, and impulsiveness. Drug and Alcohol Dependence. 2001;63:29–38. doi: 10.1016/s0376-8716(00)00188-5. [DOI] [PubMed] [Google Scholar]
- Rodriguez PF, Aron AR, Poldrack RA. Ventral-striatal/nucleus-accumbens sensitivity to prediction errors during classification learning. Human Brain Mapping. 2006;27:306–13. doi: 10.1002/hbm.20186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samejima K, Ueda Y, Doya K, Kimura M. Representation of action-specific reward values in the striatum. Science. 2005;310:1337–40. doi: 10.1126/science.1115270. [DOI] [PubMed] [Google Scholar]
- Schall JD. Neural basis of saccade target selection. Reviews in Neuroscience. 1995;6:63–85. doi: 10.1515/revneuro.1995.6.1.63. [DOI] [PubMed] [Google Scholar]
- Schultz W. Predictive reward signal of dopamine neurons. Journal of Neurophysiology. 1998;80:1–27. doi: 10.1152/jn.1998.80.1.1. [DOI] [PubMed] [Google Scholar]
- Schultz W. Neural coding of basic reward terms of animal learning theory, game theory, microeconomics and behavioural ecology. Current Opinion in Neurobiology. 2004;14:139–47. doi: 10.1016/j.conb.2004.03.017. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275:1593–9. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seymour B, O'Doherty JP, Dayan P, et al. Temporal difference models describe higher-order learning in humans. Nature. 2004;429:664–7. doi: 10.1038/nature02581. [DOI] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Matching behavior and the representation of value in the parietal cortex. Science. 2004;304:1782–7. doi: 10.1126/science.1094765. [DOI] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement Learning. Cambrige: MIT Press; 1998. [Google Scholar]
- Tanaka SC, Doya K, Okada G, Ueda K, Okamoto Y, Yamawaki S. Prediction of immediate and future rewards differentially recruits cortico-basal ganglia loops. Nature Neuroscience. 2004;7:887–93. doi: 10.1038/nn1279. [DOI] [PubMed] [Google Scholar]
- Tremblay L, Schultz W. Relative reward preference in primate orbitofrontal cortex. Nature. 1999;398:704–8. doi: 10.1038/19525. [DOI] [PubMed] [Google Scholar]
- Waelti P, Dickinson A, Schultz W. Dopamine responses comply with basic assumptions of formal learning theory. Nature. 2001;412:43–8. doi: 10.1038/35083500. [DOI] [PubMed] [Google Scholar]
- Worgotter F, Porr B. Temporal sequence learning, prediction, and control: a review of different models and their relation to biological mechanisms. Neural Computation. 2005;17:245–319. doi: 10.1162/0899766053011555. [DOI] [PubMed] [Google Scholar]
- Zuckerman M, Kuhlman DM. Personality and risk-taking: common biosocial factors. Journal of Personality. 2000;68:999–1029. doi: 10.1111/1467-6494.00124. [DOI] [PubMed] [Google Scholar]