Estimation of Number of Independent Brain Electric Sources from the scalp EEGs

Abstract

In electromagnetic source analysis, many source localization strategies require the number of sources as an input parameter (e.g., spatio-temporal dipole fitting and the multiple signal classification). In the present study, an information criterion method, in which the penalty functions are selected based on the spatio-temporal source model, has been developed to estimate the number of independent dipole sources from electromagnetic measurements such as the electroencephalogram (EEG). Computer simulations were conducted to evaluate the effects of various parameters on the estimation of the source number. A three-concentric-spheres head model was used to approximate the head volume conductor. Three kinds of typical signal sources, i.e. the damped sinusoid sources, sinusoid sources with one frequency band and sinusoid sources with two separated frequency bands, were used to simulate the oscillation characteristics of brain electric sources. The simulation results suggest that the present method can provide a good estimate of the number of independent dipole sources from the EEG measurements. In addition, the present simulation results suggest that choosing the optimal penalty function can successfully reduce the effect of noise on the estimation of number of independent sources. The present study suggests that the information criterion method may provide a useful means in estimating the number of independent brain electrical sources from EEG/MEG measurements.

I. Introduction

The reconstruction of brain electric activity from measured electromagnetic signals, such as electroencephalogram (EEG) or magnetoencephalogram (MEG), is referred to as the brain electromagnetic inverse problem and generally has no unique solution [1]. It is necessary to construct a model of electrical sources describing the brain electric activity in order to solve this inverse problem [1], [2]. Many such source models have been reported, for example, the point-like dipole [3]–[7], the cortical dipole layers [2], [8], [9], and the distributed model [10], [11]. Many inverse methods based on the point-like dipole model have been developed to reconstruct brain activity, ranging from spatio-temporal dipole source localization [12], multiple signal classification (MUSIC) [13] and first principal vectors (FINE) [14]. However, in these source estimation approaches, accurate estimates of dipole sources can be obtained only if the number of dipole sources is known a priori. In order to use the aforementioned methods, assumptions need to be made with regard to the number of dipole sources.

Efforts have been made to rationally estimate the number of independent electrical sources from bioelectromagnetic measurements. The information criterion (IC) method and the threshold (TH) method had been applied to detect the number of independent signal sources in multilead electrocardiograms [15], [16]. The merits of these two methods are that the number of independent dipole sources can be determined by only analyzing the eigenvalues of the covariance matrix of the measured data, thus avoiding solving the time-consuming inverse problem. Their results suggested that the IC method is effective in identifying the number of signal sources [16]. Knösche et al. [17] used the IC method to determine the number of independent dipole sources of the scalp EEGs. Nine types of information criteria have been used to estimate the number of independent dipole sources. In addition, the effects of the number of electrodes and time points on these information criteria were also considered in their computer simulations. However, the influence of the penalty functions on the identification of source number has not been addressed in [17]. Another interesting study was reported by Waldorp et al. [18], [19], in which the authors addressed the identification of dipole source number from MEG measurements made at each time point. However, there is no treatment in [18], [19] using the spatio-temporal dipole source model.

In the present study, we first present the spatio-temporal signal model and characteristics of the eigenvalues of the covariance matrix of the scalp EEG. Then, we describe the principles of the Information Criterion method and show how to implement it with five well-known penalty functions for two widely used log likelihood functions of the Information Criterion method. Lastly, we evaluate the proposed method for three kinds of typical signal sources, i.e. the damped sinusoid sources, sinusoid sources with one frequency band (9.9 Hz, 10 Hz and 10.1 Hz) and sinusoid sources with two separated frequency bands (9.9 Hz, 10 Hz, 39.9 Hz and 40 Hz) that are used to simulate epileptic sources for ictal and interictal activities. Particularly, the optimal penalty function is chosen from five well-known penalty functions for these typical signals for a 64-electrode system. For EEG signals with color noise, a pre-whitening [13], [14], [17] method is used in the computer simulations.

II. Theory and Methods

A. Signal model

We assume an array of m electrodes sensing signals from K dipole sources, and denote the received m-dimensional signal vector at time instance t by v(t). The dipole sources are related to the scalp EEG signal vector through a gain matrix G. The head volume conductor model is incorporated into G. The scalp EEG measurement vector can be described as a superposition of the contributions from dipole sources and additive noise as follows:

$$\mathbf{v}(t)=\mathbf{G}(\mathbf{R})\mathbf{Q}(t)+\mathbf{n}(t),$$ (1)

where G(R) is the m×3K gain matrix, e.g., G(R) = [g₁(r₁) ··· g_K (r_K )]. Each dipole source is associated with an m×3 submatrix g_i (r_i ) in G(R). R is K×3 vector of locations of K dipole sources:

$$\mathbf{R}={[{\mathbf{r}}_1\cdots {\mathbf{r}}_k]}^T\hspace{0.17em}\text{with\hspace{0.17em}}\hspace{0.17em}{\mathbf{r}}_i=[r_i^x\hspace{0.17em}{r}_i^y\hspace{0.17em}{r}_i^z],$$ (2)

Q(t) is a 3K×1 column vector that represents the moments of K dipole sources:

$$\mathbf{Q}(t)={[{\mathbf{q}}_1(t)\cdots {\mathbf{q}}_k(t)]}^T\hspace{0.17em}\hspace{0.17em}\text{with\hspace{0.17em}}\hspace{0.17em}{\mathbf{q}}_i(t)={[q_i^x(t)\hspace{0.17em}{q}_i^y\hspace{0.17em}{q}_i^z(t)]}^T,$$ (3)

and n(t) is m×1 vector of the additive noise at time instance t.

Instead of considering each time point separately, the spatio-temporal model combines the scalp EEG recordings at all the w time points to form a spatio-temporal data matrix V, V = [v(t₁ ) ··· v(t_w ) ][12]. There are two types of spatio-temporal models. In the unconstrained orientation spatio-temporal model that contains 3K + 3Kw source parameters, the moment magnitudes and orientations can vary throughout the measurement interval while the locations are fixed. Another spatio-temporal model, in which both the location and orientation are fixed throughout the measurement interval, contains K×(5+w) source parameters. In the present study, we consider the fixed location and orientation spatio-temporal model. Thus, the ith dipole source moment vector can be represented by q_i = m_is_i(t), where m_i denotes a 3×1 unit orientation vector and s_i(t) is a time varying amplitude of the moment of the ith dipole source. The fixed location and orientation spatio-temporal model can be represented as follows:

$$\mathbf{V}=\mathbf{A}(\mathbf{R},\hspace{0.17em}\mathbf{M})\mathbf{S}+\mathbf{N},$$ (4)

where S is a K×w scalar matrix, e.g. S = [s₁ ··· s_K]^T , s_i expresses the time varying scalar moment of the ith dipole source, s_i = [s_i (t₁) ··· s_i (t_w )]. A is the m×K transform matrix, A(R, M) = G(R)M, where M is a 3K×K matrix consisting of orientation vectors m_i, i = 1 ··· K , e.g.,

$$\mathbf{M}=\left[\begin{array}{ccc}{\mathbf{m}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{m}}_k\end{array}\right].$$ (5)

N is an m×w matrix, which contains additive noise at all the w time points.

In the above spatio-temporal model, the following assumptions, which are also necessary for subspace algorithms such as MUSIC or FINE [13], [14] to work appropriately, are made: 1) the time series from the different dipole sources are linearly independent, i.e. less than 100% mutually correlated; 2) the number of time samples is greater than the number of scalp electrodes; 3) the number of dipole sources is smaller than the number of scalp electrodes; and 4) the matrix A is of full rank. [13], [14].

According to the signal processing [20] and biomedical literature [15]–[17], the problem of detection of number of independent sources can be defined as analyzing the structure of the covariance matrix of the observation matrix V. From the above assumptions and equation (4), the covariance matrix C of the observation matrix V can be expressed as

$$\mathbf{C}={\mathbf{C}}_s+{\mathbf{C}}_n,$$ (6)

where C_s and C_n are the covariance of the source signal AS and the noise N. It follows that the rank of C_s is K, with the smallest m-K eigenvalues being equal to zero.

In the case of white noise, the covariance matrix C_n can be expressed as ${\mathbf{C}}_n={\sigma }_n^2\mathbf{I}$, where ${\sigma }_n^2$ is an unknown constant and I is the identity matrix. Therefore, equation (6) can be changed to

$$\mathbf{C}={\mathbf{C}}_s+{\sigma }^2\mathbf{I}.$$ (7)

The eigenvalues of C can be expressed as ${\lambda }_1\ge \cdots \ge {\lambda }_K\ge {\lambda }_{K+1}=\cdots ={\lambda }_m={\sigma }_n^2.$ The smallest m-K eigenvalues of C are equal to ${\sigma }_n^2$. It follows from equation (7) that the number of sources may be determined from the smallest m-K eigenvalues of C. Unfortunately; the exact form of covariance C is usually unknown. Instead, the sample covariance estimated from a finite sample set needs to be used. In this case, all eigenvalues of C are different. In order to search the smallest eigenvalues, a better way is to determine the number of sources from the finite measurement set, by means of the IC method [15]–[17].

In case of the color noise, the similar methods can be applied if the noise covariance is known apart from ${\sigma }_n^2$. The noise covariance matrix is a symmetric positive definite matrix $C_n={\sigma }_n^2\mathrm{\Psi }$. Then, a non-singular square matrix ψ exists such as Ψ = ψψ^T, where ψ is a non-singular m×m matrix. The measurement covariance matrix can be transformed from equation (6) to the following

$${\psi }^{-1}\mathbf{C}{({\psi }^T)}^{-1}={\psi }^{-1}{\mathbf{C}}_s{({\psi }^T)}^{-1}+{\sigma }_n^2\mathbf{I}.$$ (8)

For both the white and color noise, the eigenvalues can be calculated from the left hand sides of equations (7) and (8), respectively, and then these eigenvalues can be analyzed by the information theoretic criterion [16], [17] to estimate the number of independent sources.

B. Information-theoretic criteria

The information theoretic criterion consists of two parts. The first part is the likelihood function representing the information gained from the measured data which are dependent on the assumed number of sources. The second part is the penalty term, a function of the number of snapshots (data points in the time domain). It increases with the number of free parameters in the probability model and represents the penalty for the uncertainty introduced by the unknown parameters. Thus the information theoretic criteria for the determination of the number of signals can generally be expressed as

$$IC=-logf(\mathbf{X}|\stackrel{\sim }{\mathrm{\Xi }}(k))+C_f(w)\cdot P_f,$$ (9)

where f(•) is a family of conditional probability density functions (pdf) depending on the assumed number of signals k, X is the given set of w observations, Ξ(k) is a system function of k parameters, $\stackrel{\sim }{\mathrm{\Xi }}(k)$ is the maximum likelihood estimate of Ξ(k) , P_f is the number of free parameters in Ξ, and C_f(w), the coefficient of the penalty function, which are dependent on the number of snapshots w [20], [21].

While some different log likelihood functions in (9) have been studied to determine the number of independent sources [17], in the present study, we selected two widely used log likelihood functions for detecting the number of brain electrical sources. Wax and Kailath [22] proposed an approach based on the information and the minimum descriptive length (MDL) criterion to detect the number of independent signal sources. The number of sources can be determined by analyzing the eigenvalues of covariance matrix of observation set. In the Wax and Kailath’s proposal, the measured data X = {x₁, ··· ,x_w} obtained from w observations and m channels can be described in the following model

$$\mathbf{X}=\mathbf{Y}\mathbf{Z}+\mathbf{N}$$ (10)

where Y is a m×K transfer matrix, Z is the K×w signal matrix and N is the m×w matrix of Gaussian noise. The covariance C of X has K largest eigenvalues and m-K smallest eigenvalues ${\mu }_1\ge \cdots \ge {\mu }_K\ge {\mu }_{K+1}=\cdots ={\mu }_m={\sigma }_n^2,$ which represent K signal sources and m-K noise sources, respectively. The problem is changed to determine the number of largest eigenvalues. The IC value (10) can be represented by (11)

$$IC=-\frac{w}{2}(log|{\mathbf{C}}^{(k)}|+\text{tr}{({\mathbf{C}}^{(k)})}^{-1}\mathbf{C})+d(k,m)C_f(w)$$ (11)

where C^{(k )} is the covariance of model of k signal sources, k is the number of assumed signal sources and d(k,m) is the number of free parameters of model of k signal sources. As shown in [22], the first term of (11) can be expressed completely in terms of estimated eigenvalues of C. Comparing (4) with (10), it is noted that the model functions, the structure of covariance of observation matrix are similar. A, Y and S, Z are equivalent respectively. The identification of number of dipole sources can thus be equivalent to the identification of signal sources. The dipole source with fixed location and orientation can be equivalent to single signal source, and dipole source with only fixed location can be equivalent to three signal sources.

Based on the signal model (4), the IC value derived by Wax and Kailath [22] can be obtained from eigenvalues λ_i of C as follows [17, 22]

$$IC=w(m-k)log\frac{1}{m-k}\sum _{i=k+1}^m{\lambda }_1-w\sum _{i=k+1}^{m}log{\lambda }_1+2d(k,m)C_f(w),$$ (12)

where d(k, m) = k(2m − k+1)/2, k is the number of assumed dipole sources. Here, the noise level ${\sigma }_n^2$ is unknown and is estimated from the eigenvalues of sample covariance matrix. Reference [17] extended this approach and proposed a criterion that is based on the distribution of the noise eigenvalues. Based on the signal model (4), the IC value can also be obtained from eigenvalues λ_i of C as follows [17]

$$\begin{array}{l}IC=-\left(w-1-k-\frac{2{(m-k)}^2+m-k+2}{6(m-k)}+\sum _{i=1}^k\frac{{\overline{\lambda }}_{m-k}^2}{{({\lambda }_i-{\overline{\lambda }}_{m-k})}^2}\right).\\ log\left({\overline{\lambda }}_{m-k}^{-(m-k)}\prod _{i=k+1}^m{\lambda }_i\right)+2d(k,m)C_f(w-1)\end{array}$$ (13)

where d(k, m) = k(m − k+2)(m − k − 1)/2, k is the number of assumed dipole sources, ${\overline{\lambda }}_{m-k}$ is the average of the m-k smallest eigenvalues. Knösche et al [17] suggested, based on their computer simulations, that if the noise information is accurate, it is better to use (12); and if the noise information is not accurate, the good candidate is (13). In 1969, Akaike [23] proposed the AIC, a statistic incorporating Kullback-Leibler information with the use of maximum likelihood principles and negative entropy. Several penalty functions based on AIC have also been reported [24]. In the present study, we consider the penalty function C_f(h) (h = w or w − 1) as one of the following:

1. C₁ = 2 ;

2. C₂ = 2log(log(h)) ;

3. C₃ = log(h) ;

4. C₄ = 2log(h) ;

5. C₅ = 3log(h) .

C. Detection algorithm

The proposed algorithm for detecting the number of independent sources from EEG or MEG involves the following steps:

1. Calculating the covariance matrix C from the measured data matrix V.

2. Using SVD to decompose the covariance matrix C, and get all eigenvalues such as, λ₁ > … > λ_m.

3. Calculating the information criterion value with eigenvalues of the covariance matrix C. The information criterion (IC_k) can be calculated using equations (12) and (13).

4. According to the rule of the IC method, the number of sources with minimum information criterion IC is selected as the estimated number of sources.

III. Computer simulation

The performance of the present method in determining the number of sources was assessed via computer simulations. In the forward procedure, a three-concentric-spheres head model consisting of three compartments with an outer radius of 10 cm and standard thickness (8.7 cm and 9.2 cm) was used to approximate the head volume conductor [25]. Recent studies suggest that the brain-skull-conductivity ratio ranges from 15 [26] to 25 [27]. In the present study, a brain-to-skull conductivity ratio of 20 is used. The corresponding conductivity values for the various tissue types are 0.33s/m, 0.0165s/m, and 0.33s/m, respectively.

The scalp potentials were simulated over the outermost sphere at 64 electrode sites, which were uniformly distributed over the upper hemisphere. The number of sources was varied from one to five in a row. For each set of sources, 500 samples were generated. Some restrictions were placed for the locations, moment magnitudes and orientations of the source dipoles as follows.

• The locations were generated randomly under the constraint that the distance between any two dipoles was larger than 1.0cm.

• The orientations were generated randomly.

• The moment magnitudes were less than 0.8.

The sampling rate was 1,000 Hz and 100 time samples (=100ms) were obtained in the forward simulations [14], [16], [17]. Three simulations with different time functions were performed to consider the influence of the temporal dynamics of sources. The three kinds of sources shown in Fig. 1 include the damped sinusoid sources (Case A), sinusoid sources (Case B) with one frequency bands (9.9 Hz, 10 Hz and 10.1 Hz), and sinusoid sources (Case C) with two separated frequency bands (9.9 Hz, 10 Hz, 39.9 Hz and 40 Hz) [28]–[30]. The correlation coefficients (CC) of two adjacent time series in each Case were used to assess the performance of identification of the source number. Here, the CC ρ is denoted as follows:

Fig. 1.

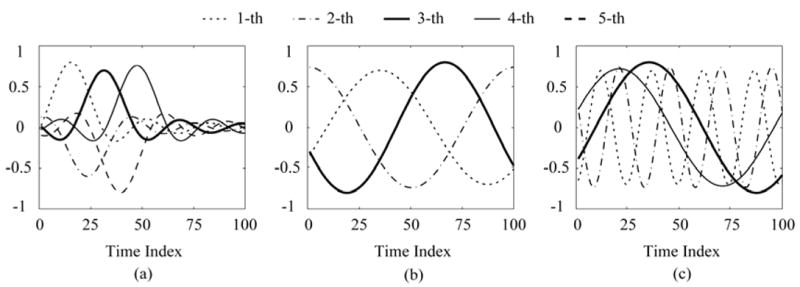
Examples of source waveforms (three sources) used in the present simulation. (a) Case A: the damped sinusoid sources, (b) Case B: sinusoid sources with one frequency band (9.9 Hz, 10 Hz and 10.1 Hz), (c) Case C: sinusoid sources with two separated frequency bands (9.9 Hz, 10 Hz, 39.9 Hz and 40 Hz). The CCs of three cases are (a) ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅: 0.62, 0.62, 0.62, 0.62; (b) ρ₁₂, ρ₂₃: 0.5, 0.6; (c) ρ_12, ρ₂₃, ρ₃₄: 0.6, 0.02, 0.6, respectively.

$${\rho }_{g,h}=\frac{|\sum _{i=1}^w{s}_g(i)s_h(i)|}{\sqrt{\sum _{i=1}^w{s}_g^2(i)}\sqrt{\sum _{i=1}^w{s}_h^2(i)}},$$ (14)

where w represents the number of the time samples, s_g and s_h are the gth and hth time series respectively. This equation implies that when two time series are orthogonal, they are uncorrelated and ρ_gh is 0; when two time series are identical or only different by a scalar; they are completely correlated and ρ_gh is 1. For three cases, some CCs are chosen as follows,

• Case A: four groups (ρ₁₂, ρ ₂₃, ρ₃₄, ρ₄₅) were used, e.g., (0.42, 0.42, 0.42, 0.42), (0.52, 0.52, 0.52, 0.52), (0.62, 0.62, 0.62, 0.62) and (0.72, 0.72, 0.72, 0.72).

• Case B: three groups (ρ₁₂, ρ₂₃) were used, e.g., (0.5, 0.5), (0.5, 0.6) and (0.5, 0.7).

• Case C: four groups (ρ₁₂, ρ ₂₃, ρ ₃₄) were chosen, e.g., (0.4, 0.02, 0.4), (0.5, 0.02, 0.5), (0.6, 0.02, 0.6) and (0.7, 0.02, 0.7).

In Fig. 1, CCs of three cases are (0.62, 0.62, 0.62, 0.62) (Case A: Fig. 1(a)), (0.5, 0.6) (Case B: Fig. 1(b)) and (0.6, 0.02, 0.6) (Case C: Fig. 1(c)), respectively.

For each of the three source models, effects of the white and color noise were assessed. For the white noise, we used three sets of normally distributed noise with different noise levels (5%, 10% and 20%), where the noise level was defined as the percentage ratio of the root mean square value of the noise to that of the potential data in single time slice (w time points) [14]. For the color noise, the white noise was generated in the same way as described above. It was then multiplied by an m×m matrix T. For the white noise, this matrix T is diagonal and its elements are uniformly equal to 1. For the spatially correlated noise, when i is equal to j, T_ij = 1; when i is not equal to j; the elements of T are T_ij = 0.5 for all electrodes adjacent to the electrode of interest, and T_ij = 0 for all non-adjacent electrodes [17]. In the Case A, B and C, for (12), it is assumed that the noise covariance matrix is known exactly. All simulations were performed with this accuracy noise information for the pre-whitening; for (13), all simulations were performed with inaccurate noise information for the pre-whitening. To simulate inaccurate noise information, a certain amount of Gaussian noise D_ij is added to each element of the noise covariance matrix T_ij. The noise inaccuracy κ_i of each row of the noise covariance matrix is defined as

$${\kappa }_i=\sqrt{\sum _{i=1}^m{D}_{ij}/\sum _{i=1}^m{T}_{ij}}\times 100\%$$ (15)

Two κ_i values, e.g., 1% and 7% were used in the computer simulation using (13) in the Case A, B and C [17].

IV. Results

A. Case A - Damped sinusoid sources

Fig. 2 shows the eigenvalues of the covariance matrix of EEG data generated by three sources for both the 20% white noise and color noise (ρ₁₂, ρ ₂₃, ρ ₃₄, ρ ₄₅ are 0.62, 0.62, 0.62, 0.62.). Fig. 2(a) shows that the elbow of the eigenvalue curve is clear, suggesting that one can determine the number of independent sources from the eigenvalue curve. On the contrary the elbow point is not clear in the case with color noise [Fig. 2(b)]. Therefore it becomes difficult to identify the number of independent sources from visual inspection of the eigenvalue curve. Fig. 3(a) shows the IC values of the aforementioned example of source configuration adding 20% white noise using (12). According to the rule of the IC method, the detected dipole source numbers of the five curves are 3, 3, 3, 2 and 2 for C₁ to C₅ in Fig. 3(a). The estimated source number with C₄ and C₅ are incorrect. Figs. 3(b) and (c) show the IC values of the aforementioned example of source configuration (20% color noise) with pre-whitening using (12), where it is assumed that the exact noise variances are known. According to the rule of the IC method, the detected source number using the five penalty functions can be different, e.g., 3, 2, 2, 2 and 2 for C₁ to C₅, respectively. The estimated source number with C₂, C₃, C₄ and C₅ are incorrect. Fig. 3 suggests that the penalty function plays an important role in the IC method.

Fig. 2.

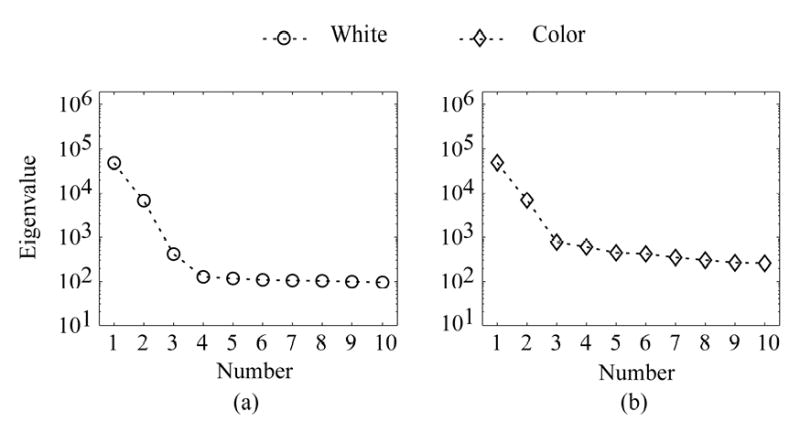
Eigenvalues of the covariance matrix of the scalp EEG data simulated from three dipole sources. (a) Case A and 20% white noise. (b) Case A and 20% color noise. The CCs among the three sources are 0.62.

Fig. 3.

IC values of the data shown in Fig. 2 using (12). (a) Case A and 20% white noise. (b) Case A and 20% color noise with pre-whitening, (c) enlarged display of (b) for C_1, C₂ and C_3. The estimated source number with the five penalty functions (C₁, C₂, C₃, C₄, C₅) are (a) 3, 3, 3, 2 and 2; (b) 3, 2, 2, 2 and 2, respectively.

Note that the noise level may affect the eigenvalue curve [see Section II-A]. Hence, it can also influence the identification of source number. To consider the effect of the noise level, we obtained the accuracy of identification for the five penalty functions. Fig. 4 summarizes the corresponding identification results of (12) for the color noise with pre-whitening (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅ are 0.62, 0.62, 0.62, 0.62.): (a) 5% noise; (b) 10% noise; and (c) 20% noise, where it is assumed that the exact noise variances are known. The accuracies (in %) in the cases from one to five dipoles are shown, where the accuracy is defined as the percentage of the correctly estimated samples in all the samples. It shows that the detected source number is not affected by the choice of different penalty functions when the real source number is equal to or smaller than three. If the real dipole sources are equal to or more than four, the number of the detected dipole sources may depend on the choice of the penalty function. Fig. 4 suggests that using C₁ for (12) obtains the best results. When the number of the detected dipoles is five or fewer, the accuracy is 97% in 10% color noise with pre-whitening.

Fig. 4.

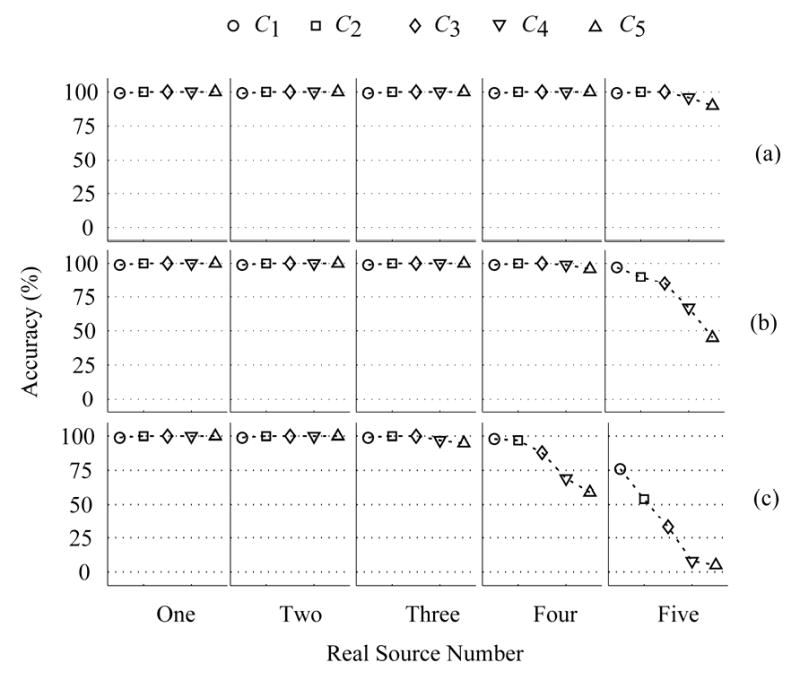
Identification accuracies of five cases with the proposed method with (12) for Case A and the color noise with pre-whitening, where it is assumed that the exact noise information is known. The accuracy (%) is a percent ratio between the correct samples and all of samples, where the correct sample refers to the situation where the estimated number of dipole sources is the same as the number of real sources. (a) 5% color noise, (b) 10% color noise, (c) 20% color noise. The CCs ρ₁₂, ρ₂₃, ρ₃₄ and ρ₄₅ are 0.42.

The accuracies of C₁ with (12) are summarized in Table 1, where source activities are shown in Fig.1a and different correlations of each two source activities are used. These results indicate that accuracies are not affected by the change of the noise level and the CC (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅) when the real dipole number is equal to or smaller than three. When the number of real sources is up to four, the corresponding identification accuracies reduce if the CC (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅) or the noise level increases. The accuracies of the four-source and five-source cases can be up to 88% for 10% color noise (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅ are 0.72, 0.72, 0.72, 0.72) and 85% for 10% color noise (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅ are 0.52, 0.52, 0.52, 0.52), respectively. Only when the noise level and the CC are over 10% and 0.52, the accuracies of the five-source case are lower than 80% under the color noise with pre-whitening.

TABLE 1.

The accuracy (in %) of identification by the IC method with the optimal penalty function C₁ for (12) and C₄ for (13). The EEG signals under the color noise with pre-whitening are used with Case A of source configuration (Fig. 1(a)): the damped sinusoid sources. The CCs: ρ₁₂, ρ ₂₃, ρ ₃₄ and ρ₄₅ are used from four groups, e.g., (0.42, 0.42, 0.42, 0.42), (0.52, 0.52, 0.52, 0.52), (0.62, 0.62, 0.62, 0.62) and (0.72, 0.72, 0.72, 0.72). In the simulations of (12), the noise information is accuracy. In the simulations of (13), two noise inaccuracy values are considered, e.g., κ = 1% and 7%. NL: Noise level.

	Accuracy (%): (12) and C1
NL	5%	10%	20%
One Dipole	99	99	99
ρ12, ρ23, ρ34, ρ45	0.42, 0.42, 0.42, 0.42			0.52, 0.52, 0.52, 0.52			0.62, 0.62, 0.62, 0.62			0.72, 0.72, 0.72, 0.72
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	99	99	99	99	99	99	99	99	99	99	99	99
Three Dipoles	99	99	99	99	99	99	99	99	99	99	99	97
Four Dipoles	99	99	98	99	99	93	99	99	79	99	88	51
Five Dipoles	99	97	76	99	85	36	88	49	7	56	8	2
	Accuracy (%) : (13), C4 and κ =1%
NL	5%	10%	20%
One Dipole	100	100	100
ρ12, ρ23, ρ34, ρ45	0.42, 0.42, 0.42, 0.42			0.52, 0.52, 0.52, 0.52			0.62, 0.62, 0.62, 0.62			0.72, 0.72, 0.72, 0.72
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	100	100	100	100	100	100	100	100	100	100	100	100
Three Dipoles	100	100	96	100	98	94	100	98	90	100	96	77
Four Dipoles	100	98	66	100	85	34	98	66	17	78	27	3
Five Dipoles	94	56	7	69	11	1	20	2	0	3	0	0
	Accuracy (%): (13), C4 and κ= 7%
NL	5%	10%	20%
One Dipole	100	100	100
ρ12, ρ23, ρ34, ρ45	0.42, 0.42, 0.42, 0.42			0.52, 0.52, 0.52, 0.52			0.62, 0.62, 0.62, 0.62			0.72, 0.72, 0.72, 0.72
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	100	100	100	100	100	100	100	100	100	100	100	100
Three Dipoles	100	99	96	100	99	94	100	98	90	100	97	81
Four Dipoles	100	98	67	100	85	35	98	68	18	79	29	4
Five Dipoles	94	59	8	68	10	1	22	1	0	3	0	0

Considering the effect of the noise information inaccuracy, equation (13) was used to test the identification accuracy with different penalty functions for Case A. Two different noise inaccuracies κ, e.g., 1% and 7%, were used in the simulations. Fig.5 summarizes the corresponding identification results of (13) for the color noise with pre-whitening (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅ are 0.42, 0.42, 0.42, and 0.42.): (a) 5% noise; (b) 10% noise; and (c) 20% noise, and noise inaccuracy κ : 1%. Fig.6 summarizes corresponding identification results of (13) for the noise inaccuracy κ : 7% and other conditions are the same as Fig.5. Comparing Fig.5 with Fig.6, the accuracy of C₁, C₂ and C₃ for one and two sources decreases significantly when the noise information is inaccurate. The accuracy of C₁ for three sources also shows a small decrease. Fig.5 and Fig.6 suggest that using C₄ for (13) can provide the best performance and robustness again the noise. The accuracies of C₄ with (13) are also summarized in Table 1. The results indicate that the accuracies with C₄ are not affected by the change of the noise inaccuracy for different dipole-cases, but are affected by the variation in the noise level and the CC (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅) when the real dipole number is equal to or larger than three. When the number of real sources is equal to three or four, the corresponding identification accuracies are sensitive to the CC (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅) or the noise level. The accuracies of the four-source and five-source cases for 7% noise inaccuracy can be up to 85% for 10% color noise (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅ are 0.52, 0.52, 0.52, 0.52) and 94% for 5% color noise (ρ₁₂, ρ₂₃, ρ₃₄, ρ₄₅ are 0.42, 0.42, 0.42, 0.42) respectively.

Fig. 5.

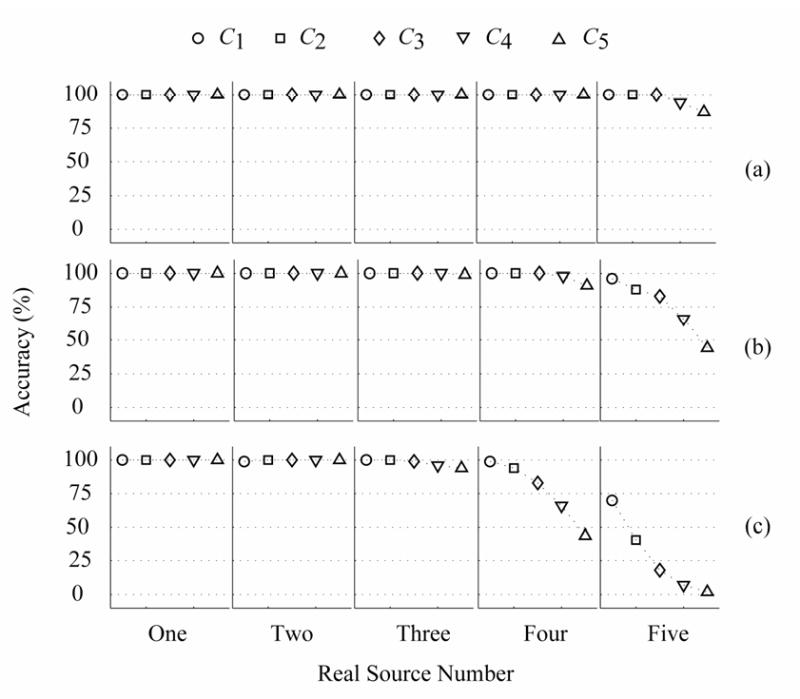
Identification accuracies of five cases with the proposed method with (13) for Case A and the color noise with pre-whitening, where 1% inaccuracy noise information is added. The accuracy (%) is a percent ratio between the correct samples and all of samples, where the correct sample refers to the situation where the estimated number of dipole sources is the same as the number of real sources. (a) 5% color noise, (b) 10% color noise, (c) 20% color noise. The CCs ρ₁₂, ρ₂₃, ρ₃₄ and ρ₄₅ are 0.42.

Fig. 6.

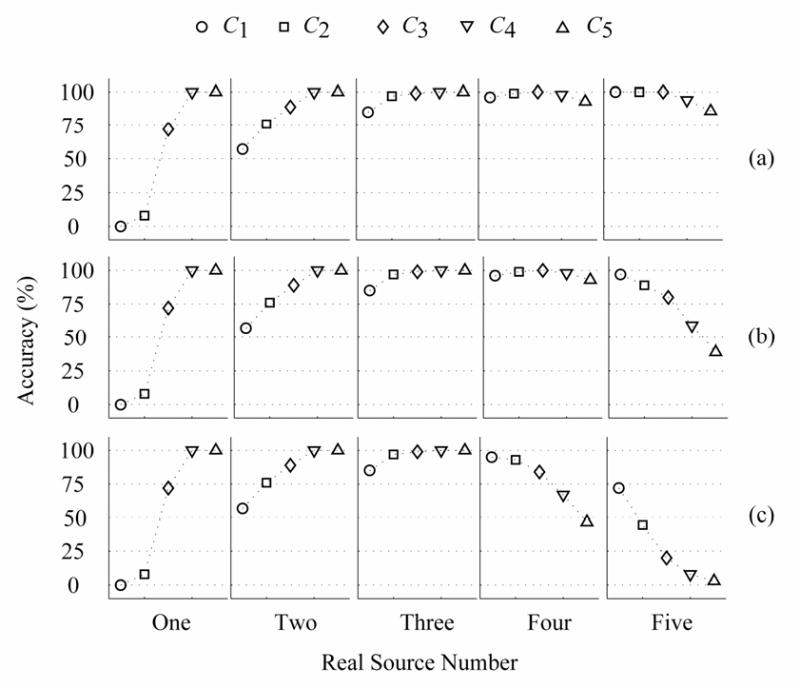
Identification accuracies of five cases with the proposed method with (13) for Case A and the color noise with pre-whitening, where 7% inaccuracy noise information is added. The accuracy (%) is a percent ratio between the correct samples and all of samples, where the correct sample refers to the situation where the estimated number of dipole sources is the same as the number of real sources. (a) 5% color noise, (b) 10% color noise, (c) 20% color noise. The CCs ρ₁₂, ρ₂₃, ρ₃₄ and ρ₄₅ are 0.42.

B. Case B

In this simulation, the frequencies of the sinusoid sources were 9.9 Hz, 10 Hz and 10.1 Hz. If the sources are more than three or the CC ρ of any pairs of two dipole sources is greater than 0.7, it will be difficult to identify the source number by the present method. Therefore, we placed at most three sources in the simulations. We found that C₁ is the optimal functions with (12) for the color noise with pre-whitening. The accuracies of C₁ with (12) are summarized in Table 2, where source activities are shown in Fig. 1(b) and different correlations of every two source activities are used. The results show that the accuracies of identification are not affected by the noise level and the CC (ρ₁₂, ρ₂₃) when the source number is equal to or smaller than two. The accuracies for one- and two- dipole cases are 99%. When the source number is three, the identification accuracies became sensitive to the noise level. The best performance for 10% and 20% color noise with pre-whitening, with correlation coefficients of (0.7, 0.5) and (0.5, 0.5), can be up to 94% and 80%, respectively, for three sources.

TABLE 2.

The accuracy (in %) of identification by the IC method with the optimal penalty function C₁ for (12) and C₄ for (13). The EEG signals under the color noise with pre-whitening are used with source configuration of Case B (Fig. 1(b)): sinusoid sources with close frequency band (9.9 Hz, 10 Hz and 10.1 Hz). Three groups (ρ₁₂, ρ₂₃) are used, e.g., (0.5, 0.5), (0.5, 0.6) and (0.5, 0.7). ). In the simulations of (12), the noise information is accuracy. In the simulations of (13), two noise inaccuracy values are considered, e.g., κ = 1% and 7%. NL: Noise level.

	Accuracy (%): (12) and C1
NL	5%	10%	20%
One Dipole	99	99	99
ρ12, ρ23	0.5, 0.5			0.6, 0.5			0.7, 0.5
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	99	99	99	99	99	99	99	99	99
Three Dipoles	99	96	80	99	95	75	99	94	67
	Accuracy (%) : (13), C4 and κ= 1%
NL	5%	10%	20%
One Dipole	100	100	100
ρ12, ρ23	0.5, 0.5			0.6, 0.5			0.7, 0.5
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	100	100	100	100	100	100	100	100	100
Three Dipoles	95	62	18	95	57	12	90	52	9
	Accuracy (%): (13), C4 and κ = 7%
NL	5%	10%	20%
One Dipole	100	100	100
ρ12, ρ23	0.5, 0.5			0.6, 0.5			0.7, 0.5
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	100	100	100	100	100	100	100	100	100
Three Dipoles	95	68	31	94	66	26	89	57	18

The accuracies of C₄ with (13) are also summarized in Table 2 for sinusoid sources, where two noise inaccuracies κ : 1% and 7% are used in the pre-whitening. Table 2 suggests that the accuracies of identification using C₄ for (13) are stable when the noise inaccuracy is lower than 7%. The simulation results also indicate that the accuracies of identification are not affected by the noise level and the CC (ρ₁₂, ρ₂₃) when the source number is equal or smaller than two (the accuracies for one- and two- dipole cases are 100%). When the source number is three, the identification accuracies are sensitive to the noise level. The best performance for 5% color noise with pre-whitening and noise inaccuracy 7%, with CC of (0.7, 0.5) and (0.5, 0.5), can be up to 89% and 95%, respectively.

C. Case C

In the present simulation, four sources with two different frequency bands (9.9 Hz, 10 Hz, 39.9 Hz and 40 Hz) were used. The corresponding results with the color noise are summarized in Table 3, where source activities are shown in Fig. 1(c) and different correlations of each two source activities are used. C₁ is found to be the optimal functions of (12) for the color noise. For all four cases, the influence of correlation coefficients is negligible. When the noise level and the CC (ρ₁₂, ρ₂₃, ρ₃₄) are up to 20% and (0.7, 0.02, 0.7), the accuracies for four-dipole case still remain at 99%.

TABLE 3.

The accuracy (in %) of identification by the IC method with the optimal penalty function C₁ for (12) and C₄ for (13). The EEG signals under the color noise with pre-whitening are used with source configuration of Case C (Fig. 1(c)): sinusoid sources within two separated frequency bands (9.9 Hz, 10 Hz, 39.9 Hz and 40 Hz). Four groups (ρ₁₂, ρ₂₃, ρ₃₄) are chosen, e.g., (0.4, 0.02, 0.4), (0.5, 0.02, 0.5), (0.6, 0.02, 0.6) and (0.7, 0.02, 0.7). ). In the simulations of (12), the noise information is accuracy. In the simulations of (13), two noise inaccuracy values are considered, e.g., κ= 1% and 7%. NL: Noise level.

	Accuracy (%): (12) and C1
NL	5%	10%	20%
One Dipole	99	99	99
ρ12, ρ23, ρ34	0.4, 0.02, 0.4			0.5, 0.02, 0.5			0.6, 0.02, 0.6			0.7, 0.02, 0.7
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	99	100	100	99	99	99	99	99	99	99	99	99
Three Dipoles	100	99	99	99	99	99	100	99	99	99	99	99
Four Dipoles	99	99	99	99	99	99	99	99	99	99	99	99
	Accuracy (%) : (13), C4 and κ= 1%
NL	5%	10%	20%
One Dipole	100	100	100
ρ12, ρ23, ρ34	0.4, 0.02, 0.4			0.5, 0.02, 0.5			0.6, 0.02, 0.6			0.7, 0.02, 0.7
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	100	100	100	100	100	100	100	100	100	100	100	100
Three Dipoles	100	100	99	100	100	99	100	100	99	100	100	97
Four Dipoles	100	100	98	100	100	95	100	100	90	100	100	87
	Accuracy (%): (13), C4 and κ= 7%
NL	5%	10%	20%
One Dipole	100	100	100
ρ12, ρ23, ρ34	0.4, 0.02, 0.4			0.5, 0.02, 0.5			0.6, 0.02, 0.6			0.7, 0.02, 0.7
NL	5%	10%	20%	5%	10%	20%	5%	10%	20%	5%	10%	20%
Two Dipoles	100	100	100	100	100	100	100	100	100	100	100	100
Three Dipoles	100	100	99	100	100	99	100	100	99	100	100	97
Four Dipoles	100	100	97	100	100	93	100	100	90	100	100	81

The accuracies of C₄ with (13) are also summarized in Table 3 for two types of sinusoid sources. When the noise level and the dipole number are up to 20% and three respectively, the CC is the most important factor influencing the accuracies of identification. When the CC (ρ₁₂, ρ₂₃, ρ₃₄) and noise inaccuracy are up to (0.7, 0.02, and 0.7) and 7%, the accuracy for the four-dipole case is up to 81%.

V. Discussion

In order to detect the number of equivalent dipoles from EEG and MEG, Waldorp et al. [19] suggested using the Bayes information criterion and Wald test to determine the dipole number for the multiple-equivalent dipoles inverse problem from MEG signals measured at a single time point. Our previous work [31] extended the information criterion method to select optimal penalty functions for increasing the identification accuracy and robustness against noise. Recently, Waldorp et al. [32] extended these methods to the spatio-temporal head model. However, the inverse problem must be solved for detecting the number of dipoles by these methods [19], [31], [32]. In the present study, we have developed a noninvasive method to determine the number of independent sources in the spatio-temporal model by means of the Information Criterion method. We have also searched for the optimal penalty function for both white and color noise. The present simulation results are promising, suggesting that the present method can estimate the number of sources by only analyzing the eigenvalues of the covariance matrix of observation data without solving the inverse problem. This is an important improvement over our previous work [31] in which a multiple equivalent dipole inverse problem has to be solved.

Knösche et al. [17] compared nine log likelihood functions about the detecting accuracy and robustness against noise. Knösche et al. suggested that if the noise information is accurate, it is better to use (12), and if the noise information is not accurate, the good candidate is (13). Based on the results of [17], we selected two widely used log likelihood functions (Eq. (12) and (13)) with five penalty functions for detecting the number of EEG sources.

Our main results of numerical simulations are as follows. Firstly, the choice of penalty functions in the IC method can affect markedly the identification accuracy for multi-source cases. The optimal penalty functions in the IC method can be determined by the simulations, given the forward model and the electrode configuration. Secondly, the source configuration also affects the accuracy of identification substantially. For the damped sinusoid sources (Case A), the sinusoid sources (Case B) and the sinusoid sources (Case C), the number of independent dipole sources can be up to five, three and four, respectively. Lastly, we found that the optimal penalty function of (12) and (13) for the 64-electrode configuration is C₁ and C₄, respectively, for the source configurations studied. Knösche et al. [17] used 8 different dipole combinations with 2, 3, or 5 independent components in the simulation. Their results suggested that C₁ in (12) is useful with stronger noise levels and relatively accurate estimations of the covariance matrix and C₃ in (13) is better when the noise level is not so high or the covariance estimate is quite inaccurate. For these three types of source activities and 64-electrode configuration, the present study indicates that C₁ for (12) is still optimal penalty function, but C₄ for (13) is better than C₃.

Note that the present results are based on the use of a simplified spherical head model. Further investigations using realistic geometry head models would improve the accuracy of the identification. However, since the identification of source number is essential involved with the inverse algorithm, but it is anticipated that the results would not be significantly changed.

While three source configurations used in the present simulation are designed to attempt to represent a wide range of brain electrical sources, it is not intended to serve as an exhaustive list of possible sources within the brain. Rather, the purpose of the present study is to demonstrate the applicability and performance of the present method in representative source configurations.

Due to the large number of simulations involved, we have limited our simulation to a particular number of scalp electrodes, i.e. 64. The reason to choose this number is because of its wide use in EEG systems. Therefore, if different numbers of scalp electrodes are to be used, then exploration of the optimal penalty function should be conducted with respect to the specific number of scalp electrodes. However, the present method as demonstrated in the present simulation study shall be applicable to any number of scalp electrodes.

In summary, the present promising results suggest that the proposed IC method can provide a convenient means of estimating the number of sources in brain source localization from the scalp EEG. The method should also be applicable to MEG source localization.