From task parameters to motor synergies: A hierarchical framework for approximately-optimal control of redundant manipulators

Abstract

We present a hierarchical framework for approximately-optimal control of redundant manipulators. The plant is augmented with a low-level feedback controller, designed to yield input-output behavior that captures the task-relevant aspects of plant dynamics but has reduced dimensionality. This makes it possible to reformulate the optimal control problem in terms of the augmented dynamics, and optimize a high-level feedback controller without running into the curse of dimensionality. The resulting control hierarchy compares favorably to existing methods in robotics. Furthermore we demonstrate a number of similarities to (non-hierarchical) optimal feedback control. Besides its engineering applications, the new framework addresses a key unresolved problem in the neural control of movement. It has long been hypothesized that coordination involves selective control of task parameters via muscle synergies, but the link between these parameters and the synergies capable of controlling them has remained elusive. Our framework provides this missing link.

1 Introduction

The control of complex redundant systems is a challenging problem, of interest in both robotics and biological motor control. The nonlinear dynamics and high-dimensional state and control spaces of such systems prevent the use of many traditional methods for controller design. One way to tackle very complex problems is through divide-and-conquer strategies. Indeed, the most advanced control system known to date –the nervous system –appears to rely on such strategies. Sensorimotor control occurs simultaneously on many levels [1–3]. Lower-level circuits interact with the musculoskeletal system directly: they receive rich sensory input, and generate corresponding motor output before the rest of the brain has had time to react to that input. Higher-level circuits interact with an augmented plant, that consists of the lower levels and the musculoskeletal system. The lower levels perform a (not well understood) transformation, allowing higher levels to operate on increasingly more abstract and more goal-related movement representations [4].

Here we propose a hierarchical control scheme inspired by this general organization of the sensorimotor system, as well as by prior work on hierarchical control in robotics [5–7]. We focus on two-level feedback control hierarchies as illustrated in Fig 1. The low-level controller receives information about the plant state x, and generates an abstract and more compact state representation y (x) that is sent to the high level. The high-level controller monitors task progress, and issues commands v (y) which in general specify how y should change. The job of the low-level controller is to compute energy-efficient controls u (v, x) consistent with v. Thus the low-level controller does not solve a specific sub-task (as usually assumed in hierarchical reinforcement learning [8,9]), but instead performs an instantaneous feedback transformation. This enables the high level to control y unencumbered by the full details of the plant.

Figure 1.

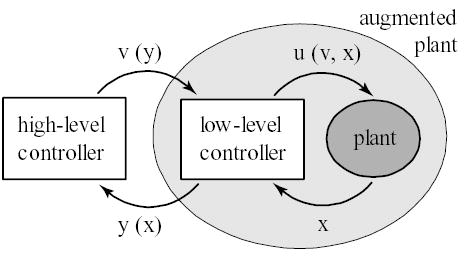
schematic illustration of the proposed framework.

While the proposed scheme is designed to resemble the sensorimotor system on a structural level, achieving functional resemblance is equally important. Functionally, sensorimotor control is best described as being near-optimal [10]. It may seem surprising that a hierarchical controller can closely approximate an optimal controller. But as we have shown elsewhere [11, 12], optimal feedback controllers for redundant systems exhibit hierarchical organization similar to Fig 1, even when such organization is not imposed by design. This finding provides yet another motivation for the present scheme: if full-blown optimization on redundant tasks is known to yield hierarchical structure, it makes sense to restrict the optimization to an (appropriately chosen) family of hierarchical controllers.

The general idea that the brain monitors a small number of task parameters y instead of the full state x, generates abstract commands v, and maps them into muscle activations u using motor synergies, has been around for a long time [26, 28]. A number of concrete models of end-effector control have been formulated in the context of reaching tasks [29–34]. The high-level state in such models is assumed to be hand position, the abstract command is desired velocity in hand space or in joint space, and the high-level controller is a simple positional servo. While these models are related to our work, in some sense they leave all the hard questions unanswered: it is unclear how the task parameters are actually controlled (i.e. what the corresponding muscle synergies are), and whether this choice of task parameters can yield satisfactory performance. We address these questions here.

Our framework is related in interesting ways to input-output feedback linearization [13, 14] as well as to the operational space formulation [6] – which also fit in the general scheme in Fig 1. These methods yield linear dynamics on the high level, by cancelling the plant nonlinearities at the low level. However, many systems of interest cannot be linearized, and furthermore it is not clear that linearization is desirable in the first place. Suppressing the natural plant dynamics may require large control signals –which are energetically expensive, and also increase error in systems subject to control-multiplicative noise (which is a universal characteristic of biological movement [15–17]). In contrast, we summarize the plant dynamics on the high level and thus create opportunities for exploiting them. Recent work in biped locomotion [18] underscores the potential of such approaches. In general, our objective is dimensionality reduction rather than linearization. This is because we are pursuing optimality, and what makes optimal control hard is the curse of dimensionality. We are also pursuing neurobiological relevance, and it is clear that a number of behaviors (including locomotion [19] and arm movements [20]) are optimized with respect to the nonlinear musculoskeletal dynamics.

The rest of the paper is organized as follows. Section 2 summarizes our previous findings relating optimal feedback control to hierarchical control, introduces relevant concepts from biological motor control, and illustrates them with experimental data. This motivates the formal development of the new framework in Section 3. The relation to existing methodologies is elaborated in Section 4. Numerical comparisons to robotic control methods as well as to optimal control are presented in Section 5. Preliminary results have been reported in conference proceedings [21].

2 Biological motivation, and relation to optimal control

Optimal control models of biological movement have a long history, and provide satisfying computational accounts of many behavioral phenomena [10]. The majority of these models are formulated in open loop, and plan a desired trajectory while ignoring the role of online feedback. Desired trajectory planning implies that the neural processing in the mosaic of brain areas involved in online sensorimotor control does little more than play a prerecorded movement tape –which is unlikely [4]. Consequently, we and others [11,22–25] have focused on optimal feedback control models, that predict not only average behavior but also the task-specific sensorimotor contingencies used to generate intelligent adjustments online. Such adjustments enable biological systems to “solve a control problem repeatedly rather than repeat its solution” [26], and thus afford remarkable levels of performance in the presence of noise, delays, internal fluctuations, and unpredictable changes in the environment. The latter models have significantly extended the range of phenomena addressed by open-loop optimization [10]. Some of the key results from this line of work are directly relevant to hierarchical control, as described next.

2.1 Minimal intervention, synergies, and uncontrolled manifolds

Our work on motor coordination [11, 12] revealed that when the task is redundant, the optimal feedback controller exhibits hierarchical structure even though it is not specifically designed to be hierarchical. Fig 2 illustrates this finding in the context of a simple redundant task –where two state variables x₁, x₂ with dynamics x_i (t + 1) = ax_i (t) + u_i (t) (1 + ε_i (t)), i = 1, 2, have to be controlled so that x₁ + x₂ equals a given target T. The noise model is control-multiplicative; details can be found in [11]. The optimal controller pushes the system state towards the nearest point on the manifold of acceptable states (“redundant direction” in Fig 2). This clearly requires less control energy compared to pushing towards a predefined point (say x₁ = x₂ = T/2).

Figure 2.

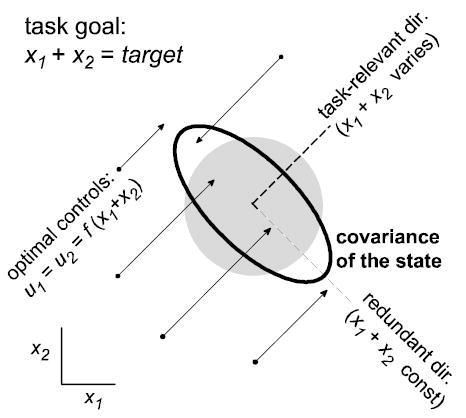
properties of optimal feedback controllers in redundant tasks (from ref. 10)

It also causes less variability in the direction that matters (compare state covariance to gray circle). Note however that variability in the redundant direction is increased –because the optimal controller is not correcting deviations in that direction. Analysis of optimal value functions for stochastic nonlinear control problems has shown that the structure in Fig 2 is a general property of optimal feedback controllers: deviations from the average behavior are corrected selectively, only when they compromise task performance [11]. We have called this the minimal intervention principle.

This is an important result because redundancy is ubiquitous in the motor system. The phenomenon of increased variability along redundant directions (illustrated below) has been observed in a wide range of behaviors [11], and has been quantified via the “uncontrolled manifold” method for comparing task-relevant and task-irrelevant variance [27]. It implies that the substantial yet structured variability of biological movements is not due to sloppiness, but on the contrary, is a signature of an exceptionally well-designed sensorimotor system.

The hierarchical nature of the optimal controller is evident in Fig 2: u₁, u₂ are coupled, and equal to some function of x₁ +x₂ rather than being functions of the individual state variables x₁, x₂. In the terminology of Fig 1, the high-level state is y = x₁ + x₂, the high-level control is v = f (y), and the vector of actual control signals is u = [v; v]. In more complex tasks our analysis has shown that the optimal control law still has this property, but for a high-level state y which may not be easy to guess. This is because y is related to the shape of the optimal value function (defined as the sum of future costs under an optimal control law) rather than the cost function, and the optimal value function is hard to compute. Nevertheless, these results [11,12] provide strong motivation for hierarchical approximations to optimal control in redundant tasks.

2.2 Empirical illustration of structured motor variability

Selective control of task-relevant parameters –which is a signature of both optimal feedback control and hierarchical control schemes –implies increased variability in task-irrelevant parameters. This phenomenon is illustrated here with data from the following experiment. Six subjects were asked to move repeatedly between three targets attached to their body (one target on each leg, and one on the left upper arm). Subjects held a 25cm wooden pointer in their right hand, and always used the same tip (TIP 1) to touch the center of the targets. We measured the position and orientation of the center of the pointer with a Polhemus Liberty sensor (240Hz sampling rate), which allowed us to calculate the positions of both TIP 1 and TIP 2. The experimental setup is shown in Fig 3a. The goal of the experiment was to quantify the positional variance of the movement paths.

Figure 3.

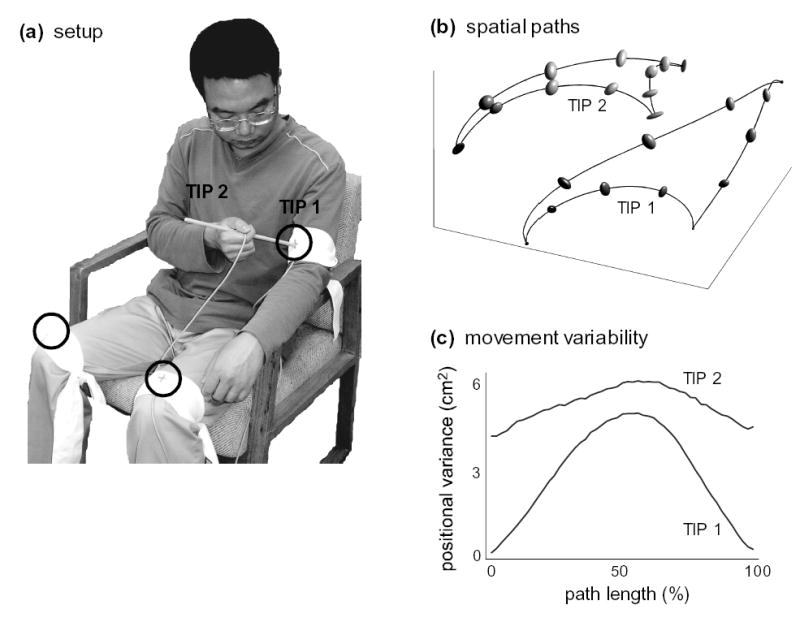
experimental illustration of increased variability in redundant dimensions.

The data were analyzed as follows. The start and end times of each movement were found using a velocity threshold, applied when TIP 1 was within 10cm of a target. Outlier movements, that failed to reach within 10cm of their target, were eliminated. Each movement was resampled in space, at equal intervals with length 2% of the total path length for that movement (this resampling is needed to suppress temporal misalignment). The mean and covariance for each sample point were computed, separately for each subject and movement target. Positional variance was defined as the trace of the covariance matrix. The means and covariances were then averaged over subjects, and plotted in Fig 3b (±1 standard deviation ellipsoids are shown at 25% intervals). To facilitate comparison, we further averaged over the three targets and plotted the positional variances of the two tips of the pointer in Fig 3c.

The main result shown in Fig 3c nicely illustrates the typical structure of motor variability. The position of the task-relevant TIP 1 is less variable than the task-irrelevant TIP 2. Furthermore, both variances are smaller in the task-relevant portions of the movement (when the pointer approaches the target) compared to the middle of the movement. The latter effect is much stronger for the task-relevant TIP 1.

These observations make it clear that the nervous system is not using the classic robotics approach – which is to plan a trajectory in joint space, and then execute that trajectory using some combination of computed torque and servo control. This is not surprising. Since a joint-space trajectory plan contains no information regarding task relevance, the execution system would have no choice but to track faithfully all details of the plan –including the irrelevant ones. This would result in increased energy consumption, and increased errors due to control-dependent noise.

3 Hierarchical control framework

Key to our framework is the low-level controller u (v, x) –whose design we address first, assuming that the high-level parameters y (x) and their desired dynamics have been given. We pay specific attention to the case when the controls u do not affect the high-level parameters y instantaneously. We then discuss how the desired y-dynamics can be adapted to the natural plant dynamics, and how the high-level controller v (y) can be designed using optimal control techniques.

3.1 Low-level controller design

Consider the dynamical system

$$\dot{\mathbf{x}}(t)=\mathbf{a}(\mathbf{x}(t))+B(\mathbf{x}(t))\mathbf{u}(t)$$ (1)

where x ∈ R^n_x is the state vector, u ∈ R^n_u is the control vector, a (x) are the passive dynamics, and B (x) u are the control-dependent dynamics (assumed linear in the control). We are interested in controllers that achieve low cumulative cost, for a cost-per-step function of the form

$$\ell (t,\mathbf{x}(t),\mathbf{u}(t))=q(t,\mathbf{x}(t))+r(\mathbf{u}(t),\mathbf{x}(t))$$ (2)

The high-level state vector y ∈ R^n_y, n_y ≤ n_x, is a static function of the plant state:

$$\mathbf{y}=\mathbf{h}(\mathbf{x})$$ (3)

The function h defining the high-level state y is supplied by the user. What we provide is a way to “control” y, that is, to generate controls u which affect x in such a way that the corresponding changes in y are as desired. We assume that y contains enough information to compute the state-dependent cost q (t, x); in other words, there exists a function $\tilde{q}$ such that

$$\tilde{q}(t,\mathbf{h}(\mathbf{x}))=q(t,\mathbf{x})$$ (4)

Other than that, the function h should be chosen to yield the lowest-dimensional representation which allows satisfactory control. Different choices of h will be explored later. The control cost r (u, x) cannot be represented exactly on the high level, because it typically contains independent contributions from all components of u. This is the reason why the proposed hierarchical scheme is only an approximation to optimal control.

Differentiating (3) w.r.t. t and using (1), the dynamics of y become

$$\dot{\mathbf{y}}=H(\mathbf{x})(\mathbf{a}(\mathbf{x})+B(\mathbf{x})\mathbf{u})$$ (5)

where $H(\mathbf{x})=\frac{\partial \mathbf{h}(\mathbf{x})}{\partial \mathbf{x}}$ is the Jacobian of the function h. Note that y will often contain more information than end-effector position.

Our design method seeks to create an augmented system with prescribed high-level dynamics

$$\dot{\mathbf{y}}=\mathbf{f}(\mathbf{y})+G(\mathbf{y})\mathbf{v}$$ (6)

where v ∈ R^n_v is the high-level control signal generated by some high-level controller. The functions f, G define the meaning of the high-level control v, as discussed later. For now we simply assume that f, G are some known functions.

The low-level controller design problem is the following: choose u (v, x) so that the prescribed (6) and actual (5) y-dynamics are identical; when multiple solutions exist, use the control cost r (u; x) to resolve redundancy. The control u is thus defined at each time t as the solution to the following constrained optimization problem:

$$\begin{array}{l}\text{given\hspace{0.17em}}\mathbf{v}\hspace{0.17em}\text{and\hspace{0.17em}}\mathbf{x},\hspace{0.17em}\text{find\hspace{0.17em}}\mathbf{u}\hspace{0.17em}\text{that\hspace{0.17em}minimizes\hspace{0.17em}}r(\mathbf{u},\mathbf{x})\hspace{0.17em}\text{subject\hspace{0.17em}to}\\ H(\mathbf{x})B(\mathbf{x})\mathbf{u}=\mathbf{f}(\mathbf{y})+G(\mathbf{y})\mathbf{v}–H(\mathbf{x})\mathbf{a}(\mathbf{x})\end{array}$$ (7)

In addition to the above equality constraint, we can incorporate inequality constraints on u. The latter are particularly important in biological movement control where muscle activations are always non-negative. For a general r (u, x), problem (7) has to be solved numerically at each time step (using Sequential Quadratic Programming, or another efficient method). Since the solution is likely to be similar from one time step to the next, we can use the current solution to initialize the search for the next solution.

In practice, the control cost will normally have the quadratic form

$$r(\mathbf{u},\mathbf{x})=\frac{1}{2}{\mathbf{u}}^{\text{T}}R(\mathbf{x})\mathbf{u}$$ (8)

where R(x) is a symmetric positive-definite matrix (often proportional to the identify matrix). When r (u, x) is in the form (8), and control inequality constraints are absent, we can solve (7) explicitly. The solution relies on the following fact:

$$\text{the\hspace{0.17em}minimum\hspace{0.17em}of\hspace{0.17em}}\frac{1}{2}{\mathbf{u}}^{\text{T}}W\mathbf{u}\hspace{0.17em}\text{subject\hspace{0.17em}to\hspace{0.17em}}X\mathbf{u}=\mathbf{c}\hspace{0.17em}\text{is\hspace{0.17em}}\mathbf{u}=X_W^{†}\mathbf{c}$$ (9)

The weighted pseudo-inverse is defined as

$$X_W^{†}=W^{–1}{X}^{\text{T}}{(X{W}^{–1}{X}^{\text{T}})}^{–1}$$ (10)

where W is symmetric positive-definite, and X has full row-rank. Note that X^†_I is the Moore-Penrose pseudo-inverse X^T (XX^T)⁻¹; in that case we use the shorthand X^†.

Applying this to problem (7) for a cost in the form (8), and assuming that H (x)B (x) has full row-rank (a condition which we will return to), the unique solution is

$$\mathbf{u}(\mathbf{v},\mathbf{x})={(H(\mathbf{x})B(\mathbf{x}))}_{R(\mathbf{x})}^{†}(\mathbf{f}(\mathbf{y})+G(\mathbf{y})\mathbf{v}–H(\mathbf{x})\mathbf{a}(\mathbf{x}))$$ (11)

In case of inequality constraints on u we cannot obtain an explicit solution, and have to resort to numerical optimization. But the quadratic form (8) of the control cost allows us to use Quadratic Programming – which is numerically very efficient when the cost is convex.

Another form of cost function, that can be used on the low level to resolve redundancy, is

$$r(\mathbf{u},\mathbf{x})=\frac{1}{2}{\mathbf{u}}^{\text{T}}R(\mathbf{x})\mathbf{u}+{(\mathbf{a}(\mathbf{x})+B(\mathbf{x})\mathbf{u})}^{\text{T}}{\nabla }_{\mathbf{x}g}(\mathbf{x})$$ (12)

The new term encourages movement against the gradient of some potential function g (x). With this r (u, x) problem (7) can still be solved explicitly, using the following fact:

$$\begin{array}{l}\text{the\hspace{0.17em}minimum\hspace{0.17em}of\hspace{0.17em}}\frac{1}{2}{\mathbf{u}}^{\text{T}}W\mathbf{u}+{\mathbf{u}}^{\text{T}}\mathbf{d}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{subject\hspace{0.17em}to\hspace{0.17em}}\hspace{0.17em}\hspace{0.17em}X\mathbf{u}=\mathbf{c}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{is}\\ \mathbf{u}={\left[\begin{array}{c}X\\ N_X^{\text{T}}W\end{array}\right]}^{–1}\left[\begin{array}{c}\mathbf{c}\\ –N_X^{\text{T}}\mathbf{d}\end{array}\right]=X_W^{†}\mathbf{c}–N_X{(N_X^{\text{T}}W{N}_X)}^{–1}{N}_X^{\text{T}}\mathbf{d}\end{array}$$ (13)

where N_X is a matrix whose columns form an orthonormal basis for the null-space of X. Note that solving the system [X;N^T_XW] u = [c; − N^T_Xd] with a linear solver is numerically preferable to explicit computation of the pseudo-inverses in (13). A similar point has been made in [35] regarding velocity control methods.

Applying (13) to our problem in the case when control inequality constraints are absent, and suppressing the functional dependencies for clarity, we have

$$\mathbf{u}={(HB)}_R^{†}(\mathbf{f}+G\mathbf{v}–H\mathbf{a})–N_{HB}{(N_{HB}^{\text{T}}R{N}_{HB})}^{–1}{N}_{HB}^{\text{T}}{B}^{\text{T}}{\nabla }_{\mathbf{x}g}$$ (14)

In comparison to (11), the controller in (14) has an extra term acting in the redundant subspace where variations in x do not affect y. Thus g (x) can be used to modify the behavior of the controlled system in that subspace; the choice of g (x) is presently left to the user.

An alternative way of computing u (v, x) is to transform the above constrained optimization problem into an unconstrained one, and use a mixed cost that absorbs all constraints. Let c (u, x) be a potential function replacing any control inequality constraints: c (u, x) = 0 when u satisfies those constraints and c (u, x) > 0 when it does not. Then we can define u at each time t as the solution to the following unconstrained optimization problem:

$$\begin{array}{l}\text{given\hspace{0.17em}}\mathbf{v}\hspace{0.17em}\text{and\hspace{0.17em}}\mathbf{x},\hspace{0.17em}\text{find\hspace{0.17em}}\mathbf{u}\hspace{0.17em}\text{that\hspace{0.17em}minimizes}\\ {\lambda }_1\parallel \mathbf{f}(\mathbf{y})+G(\mathbf{y})\mathbf{v}–H(\mathbf{x})\mathbf{a}(\mathbf{x})–H(\mathbf{x})B(\mathbf{x})\mathbf{u}{\parallel }^2+{\lambda }_{2}c(\mathbf{u},\mathbf{x})+r(\mathbf{u},\mathbf{x})\end{array}$$ (15)

The constants λ₁, λ₂ set the relative importance of satisfying constraints versus minimizing energy. For large λ’s the solution to this problem is numerically indistinguishable from the solution to the constrained problem, in the case when all constraints can be satisfied. However, the advantage of (15) is that it applies even when the constraints on u cannot be satisfied – which can happen when H (x)B (x) becomes row-rank-defficient, or when the high-level control v calls for a low-level control u exceeding its allowed range.

3.2 Dynamic compatibility between levels of control

A potential problem with the above method is lack of “dynamic compatibility” between the two levels. This occurs when $\dot{\mathbf{y}}$ does not explicitly depend on u, and leads to H (x)B (x) = 0. For example, suppose y is end-effector position, v is end-effector velocity, and u is joint torque. This is problematic because torque cannot affect velocity instantaneously. However torque has a predictable effect when applied over time, suggesting that the “instantaneous” a, B should be replaced with functions $\tilde{\mathbf{a}},\tilde{B}$ incorporating temporal prediction. Next we present a method for doing so.

Consider the discrete-time representation of system (1) with time step Δ:

$$\mathbf{x}(t+\mathrm{\Delta })=\mathbf{x}(t)+\mathrm{\Delta }(\mathbf{a}(\mathbf{x}(t))+B(\mathbf{x}(t))\mathbf{u}(t))$$ (16)

We now analyze this system within a single step, from time t to time t + Δ. Define the shortcut notation x_τ = x (t + τ), τ ∈ [0, Δ], so that x₀ = x (t). The control term b = B (x (t)) u (t) will be treated as constant, while the changes in a (x) will be captured to first order through the linearization

$${\mathbf{a}({\mathbf{x}}_{\tau })\approx \mathbf{a}({\mathbf{x}}_0)+A({\mathbf{x}}_{\tau }-{\mathbf{x}}_0),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}A=\frac{\partial \mathbf{a}(\mathbf{x})}{\partial \mathbf{x}}\mid }_{\mathbf{x}={\mathbf{x}}_0}$$ (17)

Then we have continuous dynamics

$${\dot{\mathbf{x}}}_{\tau }=A{\mathbf{x}}_{\tau }+(\mathbf{a}({\mathbf{x}}_0)+\mathbf{b}–A{\mathbf{x}}_0)$$ (18)

where the term in the brackets is constant. In the case when x, a, b, A = a′ (x₀) are scalar we can solve this initial-value ODE analytically, and after some rearrangement obtain

$$x_{\mathrm{\Delta }}=x_0+\frac{exp(\mathrm{\Delta }{a}^{\prime }(x_0))–1}{a^{\prime }(x_0)}(a(x_0)+b)$$ (19)

This scalar result indicates that in the vector case we can expect a similar solution involving a matrix exponential and an inverse, and we can also expect complications when A is singular.

We will now solve (18) in the vector case, by performing Euler integration in n smaller time steps of duration d = Δ/n each, and then taking the limit n → ∞. Each step k < n is in the form

$${\mathbf{x}}_{d(k+1)}=(\text{I}+dA){\mathbf{x}}_{dk}+d(\mathbf{a}({\mathbf{x}}_0)–A{\mathbf{x}}_0+\mathbf{b})$$ (20)

Applying this recursion n times, and noting that x_dn = x_Δ, we have

$${\mathbf{x}}_{\mathrm{\Delta }}={(\text{I}+dA)}^n{\mathbf{x}}_0+(\text{I}+(\text{I}+dA)+\cdots +{(\text{I}+dA)}^{n–1})\hspace{0.17em}d\hspace{0.17em}(\mathbf{a}({\mathbf{x}}_0)–A{\mathbf{x}}_0+\mathbf{b})$$ (21)

Using the identity (I + X + · · · + Xⁿ⁻¹)(X − I) = (Xn − I) along with dAx₀ = ((I + dA) − I) x₀, the above equality simplifies to

$${\mathbf{x}}_{\mathrm{\Delta }}={\mathbf{x}}_0+\mathrm{\Delta }T(\mathrm{\Delta }A,n)(\mathbf{a}({\mathbf{x}}_0)+\mathbf{b})$$ (22)

where the matrix function T is defined as

$$T(X,n)=\frac{1}{n}\left(\text{I}+\left(\text{I}+\frac{X}{n}\right)+\cdots +{\left(\text{I}+\frac{X}{n}\right)}^{n–1}\right)$$ (23)

When X is invertible, T further simplifies to

$$T(X,n)=\left({\left(\text{I}+\frac{X}{n}\right)}^n–\text{I}\right)X^{–1}$$ (24)

In the limit n → ∞, the identity $\underset{n\to \infty }{lim}{(\text{I}+X/n)}^n=exp(X)$ can be used to obtain

$$T(X,\infty )=(exp(X)–\text{I})X^{–1}$$ (25)

When X is singular we can approximate T (X, ∞) by either adding ∊I to X and applying (25), or by using T (X, n) evaluated with a large n. Numerically we have found that T (X, n) converges even for singular X, although we do not have a closed-form solution in that case.

Switching back to continuous notation, we have the following modified integration scheme

$$\mathbf{x}(t+\mathrm{\Delta })=\mathbf{x}(t)+\mathrm{\Delta }T(\mathrm{\Delta }A,\infty )(\mathbf{a}(\mathbf{x}(t))+B(\mathbf{x}(t))\mathbf{u}(t))$$ (26)

which differs from Euler integration (16) only by T. This motivates the construction of the “predictive” dynamics $\tilde{\mathbf{a}},\tilde{B}$ from the following condition: Euler integration (16) with $\tilde{\mathbf{a}},\tilde{B}$ should be equivalent to the modified scheme (26) with the original a, B. This condition is satisfied by

$$\begin{array}{l}\tilde{\mathbf{a}}(\mathbf{x})=T(\mathrm{\Delta }A,\infty )\mathbf{a}(\mathbf{x})\\ \tilde{B}(\mathbf{x})=T(\mathrm{\Delta }A,\infty )B(\mathbf{x})\end{array}$$ (27)

Explicit integration of the functions $\tilde{\mathbf{a}},\tilde{B}$ resembles implicit integration of the original a, B. To see the relationship to implicit integration, consider the implicit Euler scheme

$${\mathbf{x}}_{\mathrm{\Delta }}={\mathbf{x}}_0+\mathrm{\Delta }(\mathbf{a}({\mathbf{x}}_{\mathrm{\Delta }})+\mathbf{b})$$ (28)

where x_Δ is now the unknown in a non-linear equation. One way to approximate the solution is to linearize a around x₀ as we did before, yielding

$${\mathbf{x}}_{\mathrm{\Delta }}={\mathbf{x}}_0+\mathrm{\Delta }(\mathbf{a}({\mathbf{x}}_0)+A{\mathbf{x}}_{\mathrm{\Delta }}–A{\mathbf{x}}_0+\mathbf{b})$$ (29)

Moving ΔAx_Δ to the left hand side and left-multiplying by (I − ΔA)⁻¹, the solution is

$${\mathbf{x}}_{\mathrm{\Delta }}={\mathbf{x}}_0+\mathrm{\Delta }\overline{T}(\mathrm{\Delta }A)(\mathbf{a}({\mathbf{x}}_0)+\mathbf{b})$$ (30)

where the matrix function $\overline{T}$ is defined as

$$\overline{T}(X)={(\text{I}–X)}^{–1}$$ (31)

This is very similar to (22), except that $\overline{T}$ now replaces T. However (25) is preferable to (31), because it captures the exact solution of the linearized ODE (18) while the implicit Euler method relies on a finite-difference approximation. Note that implicit integration is in general more stable and accurate, so the functions $\tilde{\mathbf{a}},\tilde{B}$ can be used instead of a, B even when dynamic compatibility is not an issue. Their only drawback is the increased computational cost per step – which may be offset by the larger time steps that implicit integrators can safely take.

Here is a simple example of how (27) can enforce dynamic compatibility. Suppose p and v are the position and velocity of a 1D point with mass 1, and u is the applied force, so that $\dot{v}=u$. The plant state is x = [p; v]. Let the high-level state be y = p. Then the dynamics functions are a (x) = [v; 0] and B = [0; 1]. Therefore H = ∂y=∂x = [1, 0], and so HB = 0. To apply (27) we first compute A = ∂a=∂x = [0, 1; 0, 0]. Numerically T (ΔA; ∞) converges to the matrix [1, Δ/2; 0, 1]. Thus the modified dynamics are $\tilde{\mathbf{a}}(\mathbf{x})=\mathbf{a}(\mathbf{x})$ and $\tilde{B}=[\mathrm{\Delta }/2;1]$, yielding $H\tilde{B}=\mathrm{\Delta }/2$. The fact that $H\tilde{B}\ne 0$ makes it possible to design the low-level controller using (11).

3.3 High-level dynamics and cost models

It is clear from (11) that as long as H (x)B (x) has full row-rank, we can choose f, G arbitrarily and thereby instantiate whatever high-level dynamics we desire. But what should we desire? One possibility is to choose f (y) linear and G(y) constant – which yields linear y-dynamics, and is related to feedback linearization as discussed below. However we believe that the y-dynamics should mimic the x-dynamics to the extent possible, so that the high-level controller can exploit the natural plant dynamics while operating on a lower-dimensional system. Matching the passive dynamics in (5) and (6) yields

$$\mathbf{f}(\mathbf{h}(\mathbf{x})\approx H(\mathbf{x})\mathbf{a}(\mathbf{x})$$ (32)

Matching the control-dependent terms in (5) and (6) yields

$$G(\mathbf{h}(\mathbf{x}))\tilde{\mathbf{v}}(\mathbf{u},\mathbf{x})\approx H(\mathbf{x})B(\mathbf{x})\mathbf{u}$$ (33)

where the function $\tilde{\mathbf{v}}(\mathbf{u},\mathbf{x})$ remains to be defined. In addition, optimization of the high-level controller will be facilitated if the cost function can be captured on the high level. The state-dependent cost term q (t, x) is by definition computable given y = h (x), but we would also like (an approximation to) the control energy term r (u, x). This requires a function $\tilde{r}$ such that

$$\tilde{r}(\tilde{\mathbf{v}}(\mathbf{u},\mathbf{x}),\mathbf{h}(\mathbf{x}))\approx r(\mathbf{u},\mathbf{x})$$ (34)

Functions f, G, $\tilde{r}$ that approximately satisfy (32,33,34) can be constructed by choosing a suitable parameterization (basis functions, neural networks, etc.), collecting data, and fitting a model using supervised learning procedures. The dataset consists of observation pairs (x^(k), u^(k)), where u^(k) is the signal generated by some existing controller when the plant is in state x^(k). Given x^(k) and u^(k), we can compute learning targets for f, G, $\tilde{r}$ by evaluating the right hand sides of (32,33,34). Thus the application of supervised learning is straightforward –as long as we define the function $\tilde{\mathbf{v}}(\mathbf{u},\mathbf{x})$. This function corresponds to the meaning of the high-level control signals, and should be chosen using physical intuition. For example, if u is joint torque and y is end-effector position and velocity, $\tilde{\mathbf{v}}(\mathbf{u},\mathbf{x})$ could be either end-effector acceleration or force. In the former case G will be constant and will not capture anything about plant dynamics. In the latter case G will be related to inverse inertia in end-effector space. Regardless of how we choose the function $\tilde{\mathbf{v}}$ after learning we will have $\tilde{\mathbf{v}}(\mathbf{u}(\mathbf{v},\mathbf{x}),\mathbf{x})\approx \mathbf{v}$. Note that whenever the functions f, G change (through learning or otherwise) the low-level controller must be redesigned.

It is interesting to ask under what conditions (32,33,34) can be satisfied exactly. We focus on the passive dynamics (32), which do not depend on our choice of $\tilde{\mathbf{v}}(\mathbf{u},\mathbf{x})$ and are also likely to be the most worthwhile fitting. Since $\mathbf{x}\stackrel{\mathbf{h}}{\to }\mathbf{y}$ is a many-to-one mapping, a function f satisfying (32) does not always exist. The necessary and sufficient condition for the existence of f is

$$H({\mathbf{x}}_1)\mathbf{a}({\mathbf{x}}_1)=H({\mathbf{x}}_2)\mathbf{a}({\mathbf{x}}_2)\hspace{0.17em}\hspace{0.17em}\text{whenever\hspace{0.17em}}\hspace{0.17em}\mathbf{h}\text{(}{\mathbf{x}}_{\text{1}})=\mathbf{h}({\mathbf{x}}_2)$$ (35)

Define the set ℳ[x₀] = {x : h (x) = h (x₀)} and suppose h is such that ℳ is a smooth manifold. This is the redundant (or uncontrolled) manifold where the plant state x can fluctuate without affecting the high-level state y. If the passive dynamics act within this manifold, i.e. a (x) ∈ T_xℳ [x], then H (x) a (x) = 0 and (35) is trivially satisfied. Therefore (35) can only be violated by the component of the vector field a normal to ℳ. In particular, note that the row vectors of the matrix H (x) span the subspace normal to ℳ[x], and so H (x) a (x) is a form of projection of the vector field in the normal subspace. For nonlinear h (x) this projection is difficult to understand because H (x) varies with x, but in the linear case h (x) = Hx condition (35) becomes

$$H(\mathbf{a}({\mathbf{x}}_1)–\mathbf{a}({\mathbf{x}}_2))=0\hspace{0.17em}\hspace{0.17em}\text{whenever\hspace{0.17em}}\hspace{0.17em}H({\mathbf{x}}_1–{\mathbf{x}}_2)=0$$ (36)

The latter condition has a simple interpretation: if the difference between two states lies within the redundant subspace, then the difference in the passive dynamics between these states should also lie within the redundant subspace.

3.4 High-level controller optimization

A high-level dynamics model together with an (approximate) high-level cost model lead to an optimal control problem formulated on the high level. This problem can be solved via standard techniques, or via a new implicit method (see below) that is specific to hierarchical control schemes.

While a survey of standard techniques for optimal controller design is beyond the scope of this paper, three points are in order. First, mapping the original control problem to the high level reduces dimensionality, and thereby facilitates the application of numerical methods for optimal control that suffer from the curse of dimensionality. Second, a high-level dynamics model is required in order to design the low-level controller, even if the high-level controller is built via model-free methods (such as proportional-derivative control, or reinforcement learning). Third, it may be advantageous to use iterative design: start with some high-level model, design the two-level control scheme and apply it, use the resulting data to fit a high-level model more compatible with the plant dynamics, and iterate. The need to iterate comes from the fact that the approximation (32,33,34) depends on what regions of the state and control spaces are visited, and that in turn depends on what controller is being used during data collection.

In addition to standard techniques, the hierarchical framework allows a novel implicit method for optimal controller design. In this method, the passive dynamics are no longer modeled explicitly on the high level and the discrepancy between f (y) and H (x) a (x) is no longer compensated on the low level. Instead, the high-level controller is given online access to H (x) a (x) and is responsible for dealing with that term. The constraint in (7) simplifies to H (x) B (x) u = G (y) v, and the low-level controller (11) becomes

$$\mathbf{u}(\mathbf{v},\mathbf{x})={(H(\mathbf{x})B(\mathbf{x}))}_{R(\mathbf{x})}^{†}G(\mathbf{y})\mathbf{v}$$ (37)

When condition (35) is violated the input-output behavior of the augmented plant resulting from (37) is no longer autonomous in terms of y, but instead can depend on the specific value of x –because H (x) a (x) can vary while y remains constant. In that case f (y) can still be computed as long as the plant state x is known. But how can we know x when $\mathbf{x}\stackrel{\mathbf{h}}{\to }\mathbf{y}$ is a many-to-one mapping? We cannot if all we are given is an arbitrarily chosen y. However, suppose that we reached y by initializing the plant in some state x (0), applying some high-level control sequence v (t), computing the low-level controls from (37), and integrating the plant dynamics. Then we always have a unique underlying state x. Implicit computation of f (y) can be used in conjunction with trajectory-based methods for optimal control –such as ODE methods [36], differential dynamic programming [37], or the iterative linear-quadratic-Gaussian method [38] we have developed (illustrated later). This modified version of our hierarchical scheme is likely to yield better performance, but comes at the price of not having an explicit high-level controller v (y) that is independent of the initial x and its trajectory. When condition (35) is satisfied, and an exact passive dynamics model f (y) = H (x) a (x) is available, the implicit method does not improve performance.

4 Relation to existing approaches

Hierarchical control is an appealing idea which has been pursued in a number of fields. Consequently, several existing approaches are related to ours. Some are related only in spirit (and are summarized first), while others allow formal comparisons developed in the sub-sections below.

In reinforcement learning, researchers have attempted to alleviate the curse of dimensionality via autonomous low-level control policies [8, 9] that solve specific sub-problems over time (such as exiting a room in a maze). In contrast our low-level controller performs an instantaneous feedback transformation of plant dynamics, and is continuously driven by high-level commands. We believe this is more appropriate for control of complex redundant manipulators (and is a more plausible model of biological sensorimotor control) while hierarchical reinforcement learning is more appropriate for non-articulated “agents” solving navigation problems.

In control theory, there is increasing interest in hybrid systems [39–41] with continuous low-level dynamics and discrete event-driven high-level dynamics. In contrast, the high-level dynamics we instantiate are continuous. Consider for example a walking mechanism. Our framework can be applied to yield augmented dynamics in terms of the center-of-mass and feet positions. The resulting high level could be further decomposed via a hybrid systems approach, with ground contacts being the discrete events. Thus the two approaches are in some cases complementary, and a closer examination of the link between them is needed.

In robotics, examples of hierarchical control include the subsumption architecture [5] as well as virtual model control [42]. The latter is similar to our approach in terms of overall strategy –which is to design high-level feedback controllers without considering the full details of the plant. However virtual model control is a kinematic method: it maps forces produced by virtual actuators into real actuator commands, and does not exploit knowledge of plant dynamics. Another difference is that the high-level controller design is intuitive rather than model-based, and furthermore a model of high-level dynamics independent of the specific high-level controller is not available. Finally, virtual model control takes dynamic compatibility for granted and does not readily apply to biomechanical systems with higher-order dynamics.

4.1 Feedback linearization

There are interesting parallels between our method and feedback linearization (FL) –which is one of the few general methods for nonlinear control [13,14]. For comparison purposes, we first give a brief summary of input-output FL in the single-input-single-output case. Consider the system

$$\begin{array}{l}\dot{\mathbf{x}}=\mathbf{a}(\mathbf{x})+\mathbf{b}(\mathbf{x})u\\ y=h(\mathbf{x})\end{array}$$ (38)

where the control u is now called “input”, the high-level state y is “output”, the high-level control v is “external reference input”, and u, y, v are for simplicity scalar. Define the Lie derivative of a function h (x) with respect to a vector field a (x) as the directional derivative of h along a:

$$L_{\mathbf{a}}h=\frac{\partial h(\mathbf{x})}{\partial \mathbf{x}}\mathbf{a}(\mathbf{x})$$ (39)

System (38) is said to have relative degree r in a region D if for all x ε D we have

$$\begin{array}{l}{L}_{\mathbf{b}}{L}_{\mathbf{a}}^{k}h(\mathbf{x})=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for\hspace{0.17em}all\hspace{0.17em}}k<r–1\\ L_{\mathbf{b}}{L}_{\mathbf{a}}^{r–1}h(\mathbf{x})\ne 0\end{array}$$ (40)

Then the low-level control law (called “state feedback control”) given by

$$u(v,\mathbf{x})=\frac{1}{L_{\mathbf{b}}{L}_{\mathbf{a}}^{r–1}h(\mathbf{x})}(v–L_{\mathbf{a}}^{r}h(\mathbf{x}))$$ (41)

yields linear y-dynamics of the form y^(r) = v, where y^(r) is the r-th order time derivative of y.

To see the similarity to our method, note that definition (39) implies L_ah (x) = H (x) a (x) and similarly for L_b. Now, in the case r = 1 we have L_a^r−1h = h, and the control law (41) becomes

$$u(v,\mathbf{x})=\frac{1}{H(\mathbf{x})\mathbf{b}(\mathbf{x})}(v–H(\mathbf{x})\mathbf{a}(\mathbf{x}))$$ (42)

which is identical to our control law (11) for prescribed high-level dynamics f (y) = 0, G (y) = 1 and control cost R (x) = 1. The parallels between the two methods can be summarized as follows:

• The objective of FL is to make the y-dynamics linear, in the form y^(r) = v, while our objective is to make it low-dimensional yet similar to the x-dynamics. Our method can instantiate any desired y-dynamics.

• The dynamic compatibility problem discussed above corresponds to a system with relative degree greater than one. FL handles this case by augmenting y with its first r 31 derivatives. We could do the same, but that may defeat the purpose of our method because dimensionality is increased. Instead, we prefer to use the predictive version $\tilde{\mathbf{a}},\tilde{B}$ of plant dynamics.

• Most of FL theory is developed for systems with equal numbers of inputs and outputs, while redundant manipulators tend to have many more inputs than task-relevant outputs. Our method does not impose any such restriction. We deal with the mismatch in dimensionality by formulating an optimization problem –which yields a weighted pseudo-inverse solution.

• There is an important step in FL which was omitted in the above summary. It has to do with finding an explicit parameterization of the redundant manifold ℳ defined above. Such a parameterization is analytically interesting, but does not facilitate the design of a high-level controller (and the low-level controller has already been designed).

4.2 Operational space formulation

Our framework also turns out to have a number of interesting similarities and differences with the operational space (OS) formulation [6] –which is another hierarchical scheme aiming to decouple task-level control from details of plant dynamics. For comparison purposes, we summarize the OS scheme here. Let q be the generalized coordinates of a redundant manipulator. The end-effector coordinates p are related to q by the forward kinematics function p = k (q), with Jacobian $J(\mathbf{q})=\frac{\partial \mathbf{k}(\mathbf{q})}{\partial \mathbf{q}}$. The equations of motion are

$$\tau =M(\mathbf{q})\ddot{\mathbf{q}}+\mathbf{n}(\mathbf{q},\dot{\mathbf{q}})$$ (43)

where M (q) is the (symmetric positive-definite) generalized inertia matrix, and n are Coriolis, centripetal, gravitational, and viscoelastic forces. The end-effector inertia matrix is

$$\mathrm{\Lambda }(\mathbf{q})={\left(J(\mathbf{q})M{(\mathbf{q})}^{–1}J{(\mathbf{q})}^{\text{T}}\right)}^{–1}$$ (44)

The OS low-level controller maps desired end-effector accelerations $\ddot{\mathbf{p}}\ast$ to generalized forces τ as

$$\tau =J{(\mathbf{q})}^{\text{T}}\mathrm{\Lambda }(\mathbf{q})(\ddot{\mathbf{p}}\ast –\dot{J}(\mathbf{q})\dot{\mathbf{q}})+\mathbf{n}(\mathbf{q},\dot{\mathbf{q}})$$ (45)

The OS scheme leaves the high-level controller unspecified – as long as that controller can issue desired end-effector accelerations. The high-level dynamics correspond to a point mass $(\ddot{\mathbf{p}}=\ddot{\mathbf{p}}\ast )$, therefore the operational space formulation is an instance of feedback linearization.

Let us now apply our method to the same plant. Note that our method is formulated using general first-order dynamics, and so the plant state contains both generalized coordinates and their derivatives. We have $\mathbf{x}=[\mathbf{q};\dot{\mathbf{q}}],\hspace{0.17em}y=[\mathbf{p};\dot{\mathbf{p}}]$, and therefore

$$\mathbf{h}(\mathbf{x})=\left[\begin{array}{c}\mathbf{k}(\mathbf{q})\\ J(\mathbf{q})\dot{\mathbf{q}}\end{array}\right]$$ (46)

The second row in the above equation comes from the identity

$$\dot{\mathbf{p}}=J(\mathbf{q})\dot{\mathbf{q}}$$ (47)

The Jacobian of h differs from the Jacobian of the forward kinematics function, and is given by

$$H(\mathbf{x})=\left[\begin{array}{cc}J(\mathbf{q})& 0\\ \frac{\partial }{\partial \mathbf{q}}(J(\mathbf{q})\dot{\mathbf{q}})& J(\mathbf{q})\end{array}\right]$$ (48)

where the above partial derivative term can be written as $\dot{J}(\mathbf{q})$. This is because

$$\frac{\partial }{\partial \mathbf{q}}(J(\mathbf{q})\dot{\mathbf{q}})=\frac{\partial }{\partial \mathbf{q}}\left(\frac{\partial \mathbf{k}}{\partial \mathbf{q}}\frac{d\mathbf{q}}{dt}\right)=\frac{\partial }{\partial \mathbf{q}}\left(\frac{d\mathbf{k}}{dt}\right)=\frac{d}{dt}\left(\frac{\partial \mathbf{k}}{\partial \mathbf{q}}\right)=\frac{d}{dt}(J(\mathbf{q}))=\dot{J}(\mathbf{q})$$ (49)

From (43), the passive and control-dependent plant dynamics expressed in first-order form are

$$\mathbf{a}(\mathbf{x})=\left[\begin{array}{c}\dot{\mathbf{q}}\\ –M{(\mathbf{q})}^{–1}\mathbf{n}(\mathbf{q},\dot{\mathbf{q}})\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}B(\mathbf{x})=\left[\begin{array}{c}0\\ M{(\mathbf{q})}^{–1}\end{array}\right]$$ (50)

Suppose the prescribed high-level dynamics correspond to a point mass $(\ddot{\mathbf{p}}=\mathbf{v})$ so that

$$\mathbf{f}(\mathbf{y})=\left[\begin{array}{c}\dot{\mathbf{p}}\\ 0\end{array}\right],\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}G(\mathbf{y})=\left[\begin{array}{c}0\\ 1\end{array}\right]$$ (51)

Let R (x) = I, so the control cost is $\frac{1}{2}{\mathbf{u}}^{\text{T}}\mathbf{u}$. Then the constraint in (7) becomes

$$\left[\begin{array}{c}0\\ J(\mathbf{q})M{(\mathbf{q})}^{–1}\end{array}\right]\mathbf{u}=\left[\begin{array}{c}\dot{\mathbf{p}}\\ \mathbf{v}\end{array}\right]–\left[\begin{array}{c}J(\mathbf{q})\dot{\mathbf{q}}\\ \dot{J}(\mathbf{q})\dot{\mathbf{q}}–J{(\mathbf{q})}^{–1}\mathbf{n}(\mathbf{q},\dot{\mathbf{q}})\end{array}\right]$$ (52)

The first row is always satisfied because of (47). Thus the effective constraint on u is given by the second row of the above equation. Replacing the general u, v with their specific to this example values τ, $\ddot{\mathbf{p}}\ast$, the solution produced by our method is

$$\tau ={\left(J(\mathbf{q})M{(\mathbf{q})}^{–1}\right)}^{†}\left(\ddot{\mathbf{p}}\ast –\dot{J}(\mathbf{q})\dot{\mathbf{q}}+J(\mathbf{q})M{(\mathbf{q})}^{–1}\mathbf{n}(\mathbf{q},\dot{\mathbf{q}})\right)$$ (53)

To make the relationship to the operational space formulation more explicit, we omit the dependence for clarity, and observe that the definition of the weighted pseudo-inverse implies (JM−1)† = MJM2† JTΛ = MJM†. The two methods can then be rewritten as

$$\begin{array}{l}\text{operational\hspace{0.17em}space}:\hspace{0.17em}\hspace{0.17em}\tau =M{J}_M^{†}\left(\ddot{\mathbf{p}}\ast –\dot{J}\dot{\mathbf{q}}\right)+\mathbf{n}\\ \text{hierarchical\hspace{0.17em}control}:\hspace{0.17em}\hspace{0.17em}\tau =M{J}_{M^2}^{†}\left(\ddot{\mathbf{p}}\ast –\dot{J}\dot{\mathbf{q}}\right)+{\left(J{M}^{–1}\right)}^{†}\left(J{M}^{–1}\right)\mathbf{n}\end{array}$$ (54)

The overall form is very similar, but there are two differences. First, the torques $\mathbf{n}(\mathbf{q},\dot{\mathbf{q}})$ are fully cancelled in the OS method, while our method only cancels the component acting in end-effector space. Second, the Jacobian pseudo-inverses being used are weighted differently (see next section). Note that when J is invertible, both formulas reduce to the inverse dynamics (43), and map desired accelerations to forces. To see this, differentiate (47) to obtain $J(\mathbf{q})\ddot{\mathbf{q}}=\ddot{\mathbf{p}}–\dot{J}(\mathbf{q})\dot{\mathbf{q}}$.

Despite the similarity, our framework is more general than the operational space formulation –in two ways that are obscured by this example. First, it can handle systems other than second-order, without any modification. Indeed we will later illustrate the control of a third-order system (a model of the human arm). Second, our framework is not constrained to point-mass high-level dynamics in the form (51), but can be used with other high-level models that are better adapted to the natural plant dynamics. Below we will see an example where adapting the high-level dynamics makes a difference in terms of performance.

4.3 Kinematic redundancy elimination

A number of kinematic planning methods that map desired end-effector velocities into joint velocities have been studied. Such methods start from the identity (47) and look for ways to invert J (q). The majority of available methods lead to solutions of the form

$$\dot{\mathbf{q}}=J{(\mathbf{q})}_{W(\mathbf{q})}^{†}\dot{\mathbf{p}}\ast$$ (55)

and can be interpreted as minimizing $\frac{1}{2}{\dot{\mathbf{q}}}^{\text{T}}W(\mathbf{q})\dot{\mathbf{q}}$ subject to the constraint (47). We will explore numerically three such pseudo-inverses:

$$\begin{array}{l}\text{Moore-Penrose:\hspace{0.17em}}W(\mathbf{q})=\text{I}\\ \text{dynamically\hspace{0.17em}consistent}:W(\mathbf{q})=M(\mathbf{q})\\ \text{impedance\hspace{0.17em}control}:W(\mathbf{q})=\mathbf{I}-\frac{\partial }{\partial \mathbf{q}}\left(J{(\mathbf{q})}^{\text{T}}\overline{\mathbf{f}}\right),\overline{\mathbf{f}}={\left(J{(\mathbf{q})}^{\text{T}}\right)}^{†}({\mathbf{q}}_0–\mathbf{q})\end{array}$$ (56)

The Moore-Penrose pseudo-inverse minimizes joint velocity, while the “dynamically consistent” one minimizes kinetic energy [43]. The pseudo-inverse labeled “impedance control” minimizes a quantity that does not have a name, but has an integrability property which yields repeatable joint motion [44]. In our implementation of that method $\overline{\mathbf{f}}$ is the end-effector force resulting from joint stiffness I and joint displacement q₀ − q, where q₀ is the configuration illustrated in Fig 4a.

Figure 4.

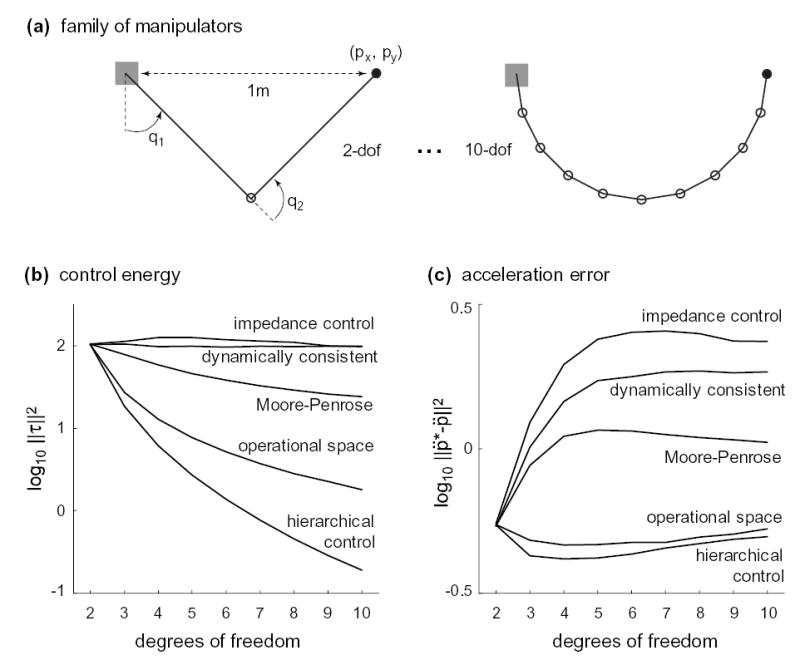
comparison of control methodologies on a family of robotic manipulators.

Note that the dynamically-consistent pseudo-inverse JM† also appears in the operational space formulation (despite the fact that the OS controller is driven by desired accelerations rather than desired velocities). Instead of JM†, our method as shown in (54) involves the pseudo-inverse JM2†. If one were to apply (55) using our pseudo-inverse, that would correspond to minimizing $\frac{1}{2}{\dot{\mathbf{q}}}^{\text{T}}M{(\mathbf{q})}^2\dot{\mathbf{q}}=\frac{1}{2}\parallel M(\mathbf{q})\dot{\mathbf{q}}{\parallel }^2$ – which is the vector norm of the generalized momentum. However we hesitate to propose this or any other method for kinematic redundancy elimination, because we do not believe that redundancy elimination during planning is a good idea in the first place.

Mapping desired end-effector velocities to joint velocities has traditionally been used for open-loop planning. In contrast, our method makes it possible to perform closed-loop control with end-effector velocity as the high-level control signal. All we have to do is redefine y as y = p, while the plant is still $\mathbf{x}=[\mathbf{q};\dot{\mathbf{q}}]$. Now h (x) = k (x) and so H (x) = [J (q), 0]. The prescribed high-level dynamics are f (y) = 0, G (y) = I, and the plant dynamics are the same as in (50). In this case we have a dynamic compatibility problem: H (x) B (x) = 0, and so in order to apply our method, the functions a, B have to be replaced with their predictive form $\tilde{\mathbf{a}},\tilde{B}$.

5 Numerical simulations

5.1 Comparison to robotic control methods

Our method was compared to existing methods in Robotics on a family of robotic manipulators (Fig 4a), which were simulated with the Matlab Robotics Toolbox [45]. The manipulators had between 2 and 10 hinge joints and moved in the plane.

The kinematics were scaled so that all links of a given manipulator were equal in length, and the end-effector (filled circle) was 1m away from the base in the shown configuration. The dynamics were also scaled, so that all links had the same mass and the sum of all link masses was 1kg. Material density was kept constant, and set so that a 1m cylindrical link with diameter 0.1m had mass 1kg. The link diameter for each manipulator was computed given the constraint on total mass and the fixed material density. Link inertia was then found assuming uniform density.

We compared the three kinematic methods given in (56) and the two dynamics methods given in (54), as follows. A database of joint positions q and joint velocities $\dot{\mathbf{q}}$, along with desired end-effector accelerations $\ddot{\mathbf{p}}\ast$, was generated randomly. For each manipulator, the database had 50,000 entries sampled uniformly from $q_i\in [–\pi ,\pi ],{\dot{q}}_i\in [–1,1],\hspace{0.17em}{\ddot{p}}_i^{\ast }\in [–10,10]$. Each method was used to compute a torque τ that yields end-effector acceleration $\ddot{\mathbf{p}}\ast$ when the plant is in state $[\mathbf{q};\dot{\mathbf{q}}]$. The dynamic methods (54) perform that computation directly. Using the kinematic methods (56) is more complicated, but possible. We first computed the current end-effector velocity $\dot{\mathbf{p}}$ from (47), and the desired velocity at a time Δ = 0.01s later as $\dot{\mathbf{p}}\ast (\mathrm{\Delta })=\dot{\mathbf{p}}+\mathrm{\Delta }\ddot{\mathbf{p}}\ast$. Then $\dot{\mathbf{p}}\ast (\mathrm{\Delta })$ was mapped to $\dot{\mathbf{q}}\ast (\mathrm{\Delta })$ using each kinematic method, the desired joint acceleration was computed as $\ddot{\mathbf{q}}\ast =(\dot{\mathbf{q}}\ast (\mathrm{\Delta })–\dot{\mathbf{q}})/\mathrm{\Delta }$, and used in the inverse dynamics (43) to obtain the torque τ. Despite this complication, both kinematic and dynamic methods achieved the desired end-effector acceleration in the absence of noise.

We compared two indices of performance, averaged over the entire database for each manipulator. The first index was control energy (Fig 4b). In the non-redundant case (dof=2) all methods are identical, but as redundancy increases we see clear differences. The dynamic methods outperform the kinematic ones, and in particular our method (hierarchical control) outperforms all others. The second index is the error in end-effector acceleration, caused by control-multiplicative noise injected in the computed torque: τ_i^actual = (1 + 0.1ε_i)τ_i^computed, where ε_i ~ N (0, 1). The results in Fig 4c are not identical to Fig 4b, despite the fact that noise is proportional to torque, because the nonlinear mapping from torques to end-effector accelerations makes a difference. But the rank order of the five methods remains unchanged.

The above simulations are encouraging – especially since they do not re‡ect the full power of our method. This is because the version (54) of the method was derived for trivial high-level dynamics (51), not adapted to the plant dynamics. The next example illustrates the advantage of such adaptation. We defined an optimal control problem with the following total cost:

$$\parallel \mathbf{p}(T)–\mathbf{p}\ast {\parallel ;}^2+w\mathrm{\Delta }\sum _{t=1}^{T–1}\parallel \tau (t){\parallel }^2$$ (57)

where p* is the target of a reaching movement executed with the 2-dof manipulator, T = 500 is the number of time steps, step duration is Δ = 0.001s (resulting in a 0.5s movement), and w = 0.0001 is the weight for the control cost. Targets were 0.3m away from the starting position, in eight equally spaced directions. This simulation also included gravity (downward direction in the figures).

We compared the performance of our method, with $\mathbf{y}=[\mathbf{p};\hspace{0.17em}\dot{\mathbf{p}}]$, applied to trivial high-level dynamics (51) versus high-level dynamics adapted to the plant. The latter were obtained by fitting a linear dynamical system model to data from the former set of simulations. The dataset contained entries of the form $(\mathbf{p},\dot{\mathbf{p}},\ddot{\mathbf{p}},\tilde{\mathbf{v}},r)$, where $\tilde{\mathbf{v}}$ is the end-effector force $\tilde{\mathbf{v}}=J{(\mathbf{q})}^{†}\tau$, and r is the control cost r = wΔ||τ||². There were 4,000 such entries.

The model fitting was based on the equations

$$\begin{array}{l}\ddot{\mathbf{p}}=F[\mathbf{p};\dot{\mathbf{p}}]+G\tilde{\mathbf{v}}\\ r={\tilde{\mathbf{v}}}^{\text{T}}R\tilde{\mathbf{v}}\end{array}$$ (58)

These equations are linear in the unknown matrices F, G, R, and therefore can be solved in a least squares sense via linear regression. The fit accounted for 87% of the variance in $\ddot{\mathbf{p}}$ and 95% of the variance in r, despite the nonlinear dynamics of the manipulator. Once F, G, R were computed, the adapted high-level dynamics could be defined as (58) by replacing $\tilde{\mathbf{v}}$ with v. The fit also yielded a control cost model v^TRv on the high level. In case of the trivial dynamics, that cost model was in the same form but with R = wΔI. Thus in both cases we have linear high-level dynamics, and quadratic cost

$$\parallel \mathbf{p}(T)–\mathbf{p}\ast {\parallel }^2+\sum _{t=1}^{T–1}\mathbf{v}{(t)}^{\text{T}}R\mathbf{v}(t)$$ (59)

which corresponds to a linear-quadratic optimal control problem. The optimal high-level controller in each case was found with standard LQR techniques, and the resulting two-level control scheme was applied to the manipulator.

Results are shown in Fig 5. For the trivial dynamics (before learning) the end-effector paths were straight as expected. For the adapted dynamics (after learning) the paths became systematically curved. As a result of this strategy, the total cost (57) was reduced by 23%. The improvement was largely due to the adapted controller’s ability to take advantage of gravity.

Figure 5.

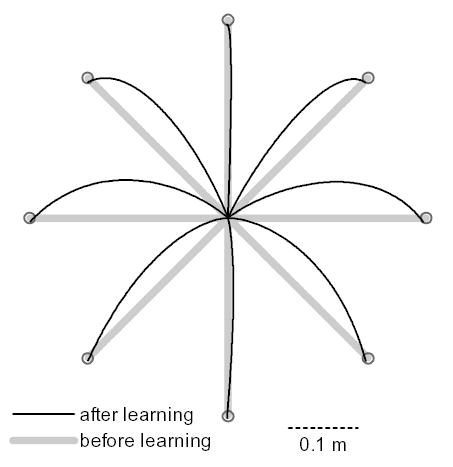
effects of adapting the high-level dynamics to the plant dynamics.

5.2 Application to arm movements, and comparison to optimal control

Here we apply our method to a model of the human arm (Fig 6a). The details of this model can be found elsewhere [46], so we will keep the description brief. The skeletal kinematics and dynamics are identical to the above 2-dof robotic manipulator (apart from parameter settings), but the muscle actuators make this model more complex: the dynamics become third-order, and the controls become constrained. The muscles acting on the human arm in the horizontal plane can be organized into six actuator groups: shoulder flexors (SF) and extensors (SX), elbow flexors (EF) and extensors (EX), bi-articular flexors (BF) and extensors (BX). The tension produced by muscle i depends on its physiological cross-sectional area PCSA_i and activation state a_i, as well as the muscle length and velocity. The substantial length-and-velocity dependence is illustrated in Fig 6a, for maximal activation a = 1. This surface is based on the Virtual Muscle model [47], which provides a state-of-the-art fit to a range of physiological data. Tensions are multiplied by moment arms to yield joint torques. Moment arms are posture-dependent (Fig 6a), in a way consistent with experimental data. They also determine the mapping from joint positions q and velocities $\dot{\mathbf{q}}$ to muscle lengths and velocities. Muscle activation states have first-order low-pass filter dynamics ${\dot{a}}_i=(u_i–a_i)/\tau$. The controls u_i are constrained to the range [0, 1]. The complete system has a 10D state vector $\mathbf{x}=[q_1;q_2;{\dot{q}}_1;{\dot{q}}_2;a_1;\cdots a_6]$ and a 6D control vector u = [u₁;···u₆].

Figure 6.

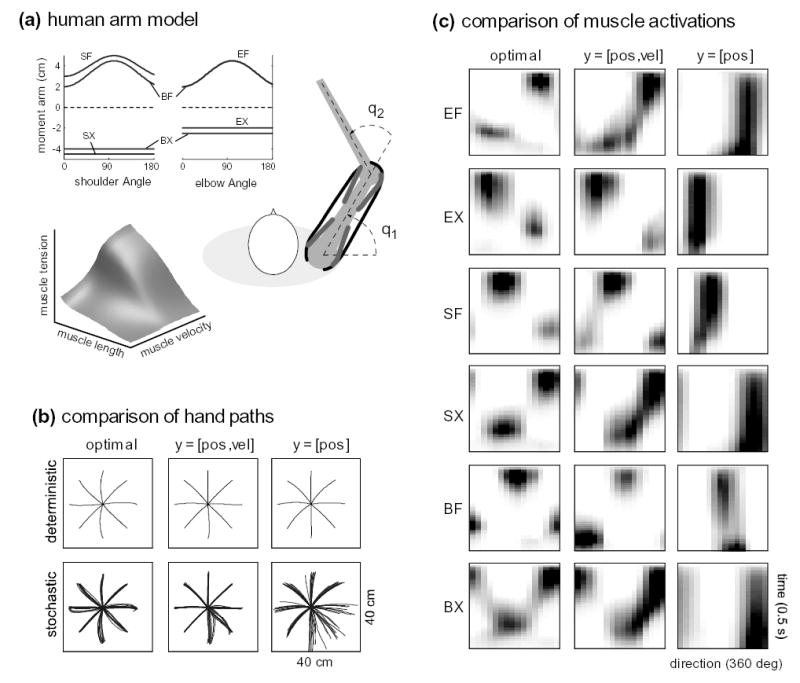
comparison to the optimal controller in human reaching.

The task is reaching: the arm starts from rest at (q₁ = π/4; q₂ = π/2), and has to reach a specified target in 0.5s, with minimal control energy. The cost-per-step is

$$s(t)\parallel \mathbf{p}(t)–\mathbf{p}\ast {\parallel }^2+\mathbf{u}{(t)}^{\text{T}}R\mathbf{u}(t)$$ (60)

where s(t) = 1 when t > 0.4s and 0 otherwise (we want the hand to remain stationary at the target for the last 0.1s). The diagonal matrix R has entries proportional to PCSA_i –because larger muscles generate more force per unit activation, and therefore consume more metabolic energy. Targets are arranged in a circle with 15cm radius around the start position.

We designed two hierarchical controllers, for y = p and $\mathbf{y}=[\mathbf{p};\dot{\mathbf{p}}]$ respectively. Because of the third-order dynamics, our method relied on the predictive functions $\tilde{\mathbf{a}},\tilde{B}$ in both cases. The control inequality constraints made the explicit solutions (11,33) inapplicable, and therefore the low-level controller used Quadratic Programming at each time step to compute u (v, x). Instead of modeling the high-level dynamics, here we used the implicit method described above (which yields a high-level feedback controller). In addition to the two hierarchical controllers, we also computed the optimal feedback controller in each case, using our iLQG method [38].

Fig 6b shows deterministic and stochastic hand paths for each controller. Stochastic trajectories were simulated by corrupting each control signal with 100% control-multiplicative noise. The differences on the level of kinematics are small, although they increase (especially for the y = p controller) when noise is added. Note that although the $\mathbf{y}=[\mathbf{p};\dot{\mathbf{p}}]$ controller appears to be more accurate than the optimal controller, that is not the case – the optimal controller allows more variability during the movement but reaches the target more accurately. Note also that the controllers can sustain such a large amount of noise because we are not modeling sensory delays and noise here. Fig 6c shows the (open-loop) muscle activations. Each subplot is one muscle-controller combination. The horizontal axis corresponds to movement direction, while the vertical axis is time during the movement (increasing downward). Dark means higher activation. We now see a much more clear distinction between the two hierarchical controllers. The muscle activations found by the $\mathbf{y}=[\mathbf{p};\dot{\mathbf{p}}]$ controller are quite similar to the optimal muscle activations, and furthermore resemble many features of experimentally observed muscle activations (but that is beyond the scope of the paper). On the other hand, the y = p controller misses the elaborate temporal pattern of muscle activation, although it still activates the appropriate muscles.

Apart from demonstrating the power and generality of the proposed method, these results are important with regard to prior models of end-effector arm movement control [29–34]. Our method completes these models by going all the way to muscle activations. It also reveals a problem. The relatively poor performance of the y = p controller suggests that controlling hand position through instantaneous velocity commands is not a good idea –because such commands are too far removed from the muscles that have to carry them out. In contrast, high-level commands related to hand force rather than velocity afford hierarchical control that is much closer to optimal.

5.3 Internal dynamics and sensorimotor synergies

Here we study a tracking task executed with a redundant linear plant. Linearity allows us to look more closely at the structure of the hierarchical controller, and compare it to the structure of the corresponding optimal controller. We also explore the behavior within the redundant subspace where the high-level controller cannot act.

The plant (Fig 7a) consists of two points (H,E) with mass 1, driven by three linear muscle-like actuators that can both push and pull. Actuator i has activation state ai and generates force $a_i–b{\dot{q}}_i–k(q_i–{\overline{q}}_i)$, where b = 10, k = 10 are intrinsic damping and stiffness, q_i is the length of the actuator, and ${\overline{q}}_i=0.3$ is the resting length of the spring. We can think of point H as the “hand”, and point E as the “elbow” of a telescopic linear “arm”. At each time step we are given a target position p*. The task is to track the target with the hand. The state vector is $\mathbf{x}=[q_1;q_2;{\dot{q}}_1;{\dot{q}}_2;a_1;a_2;a_3;1;p\ast ]$. The constant 1 is needed to implement the spring model, and p* is included in the state because it varies over time. Note that q₃ is not included in the state because q₃ = q₁ + q₂. The activation dynamics are ${\dot{a}}_i=(u_i–a_i)/\tau$ with time constant 40msec. The control vector is u = [u₁; u₂; u₃]. Tracking is formulated as an optimal control problem with cost-per-step x^TQx + u^TRu. We set R = 10⁻⁵, and Q = H^TH where H = [1, 1, 0, 0, 0, 0, 0, 0, −1]. This encodes the tracking error (q₁ + q₂ − p*)², where q₁ + q₂ is hand position. Representing p* (t) as Brownian motion, the problem becomes LQG and can be solved with standard methods.

Figure 7.

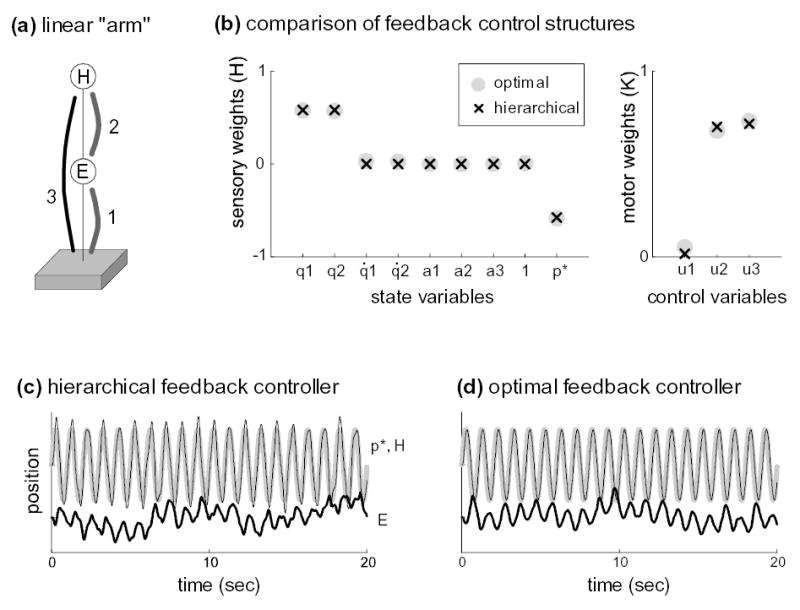
internal dynamics and sensorimotor synergies.

The optimal control law is u = L^ox, where L^o is a 3x9 matrix of optimal feedback gains.

The high-level state is defined as the instantaneous tracking error:

$$y=q_1+q_2–p\ast$$ (61)

Note that y = Hx, with H as defined above. The high-level dynamics and cost are $\dot{y}=v$ and y² respectively. Because of the linearity of the plant, the mapping from v to u is now linear: u = Kv, where K is computed from (11). The optimal high-level control law is also linear: v = gy, where the gain g is found via LQG techniques. Then the hierarchical controller is

$$\mathbf{u}=L\mathbf{x},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where\hspace{0.17em}}L=KgH$$ (62)

To compare the structure of the hierarchical and optimal controllers, we applied singular value decomposition to the optimal L^o and found that it has singular values (447.6, 1.9, 0) – which is essentially rank 1. So we can write the optimal controller as

$$\mathbf{u}=L^o\mathbf{x},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where\hspace{0.17em}}{L}^o\approx K^o{g}^o{H}^o$$ (63)

and K^o and H^o are the left and right singular vectors of L^o corresponding to the largest singular value. The elements of vectors H and H⁰ (normalized to unit length) are compared in Fig 7b (left), and K and K⁰ are compared in Fig 7b (right). The similarity in both cases is striking. Note that of these four vectors, the only one we set manually was H. Then K was computed automatically by our method, while K^o and H^o fell out of (non-hierarchical) optimal feedback control. In summary, the structure of the hierarchical and optimal feedback controllers can be is very similar.

This linear “arm” model is interesting because the augmented plant has internal dynamics: point E is free to move without affecting the task outcome. Of course it cannot move arbitrarily, since the actuators have stiffness and damping that couple points E and H. But the high-level controller has no means of monitoring and correcting the trajectory of E, because it sees only the trajectory of H. To explore the internal dynamics, we applied both the hierarchical and optimal control laws, with 100% control-multiplicative noise. Fig 7c,d show the trajectories of points H and E. While the “hand” H tracks the target reliably, the “elbow” E exhibits substantial variability for both controllers. The lack of control over E may seem undesirable, but in fact there is nothing undesirable about it –or else the optimal controller would not allow E to ‡uctuate. If we really want E to follow a certain trajectory, we should be honest about that fact and encode it in the performance criterion. Since the performance criterion for this task is not affected by E, we cannot blame our controller for failing to accomplish something we did not ask for. On the contrary, we should be pleased that it closely resembles the optimal controller.

6 Discussion

We presented a general framework for hierarchical feedback control of redundant systems. The design of the proposed control hierarchy involves: (i) specifying a set of high-level parameters and their desired dynamics; (ii) designing a low-level feedback controller which yields an augmented plant with the specified input-output behavior; (iii) designing a high-level feedback controller that solves the original control problem but operates on a simplified system. Our focus was on automating the design of the two feedback controllers, as well as the construction of high-level dynamics that mimic the plant dynamics. This provided a way of controlling the specified high-level parameters.

The choice of appropriate high-level parameters is presently an open question, although a few relevant comments can be made. One extreme case would be to use a scalar performance index as the only high-level parameter. Then the high-level commands will essentially say “perform better”, but will not contain information as to how to perform better. Clearly such commands are not useful to the low-level controller. The other extreme would be to include all the state information on the high level (perhaps transformed nonlinearly), but that would not in general lead to a simplification of the controller design problem. So we seek a middle ground, where the high level state contains task-related parameters that enter in the computation of the performance index, and perhaps other closely related parameters. The application to reaching movements, for example, revealed a benefit of including velocity as a high-level parameter, even though the state-dependent cost was only a function of position.

Another issue deserving closer examination is the internal dynamics. In the above numerical examples we did not attempt to shape that dynamics, although our framework provides a mechanism for doing so by specifying a potential function over the plant state. Yet we saw that both the structure and the behavior of the hierarchical controller can be very similar to the optimal controller. This issue is relevant not only in our framework, but in all methods for hierarchical control. Velocity control methods that yield integrable solutions [44,48] eliminate the internal dynamics altogether, by enforcing a one-to-one mapping from plant states to high-level (end-effector) states. However, such strategies are suboptimal and unlikely to be used by the nervous system. An alternative approach is to somehow choose high-level parameters that result in asymptotically stable internal dynamics (corresponding to the notion of “minimum phase” in feedback linearization). Asymptotic stability is of course appealing, but its relationship to optimal performance is unclear; how to achieve such stability without unnecessary waste of control energy is also unclear. Since we already know that optimal controllers for redundant tasks are in essence hierarchical, further analysis of their structure can illuminate the choice of both the high-level state and the potential function used to shape the internal dynamics.