The role of kinematic redundancy in adaptation of reaching

Abstract

Although important differences exist between learning a new motor skill and adapting a well-learned skill to new environmental constraints, studies of force field adaptation have been used frequently in recent years to identify processes underlying learning. Most of these studies have been of reaching tasks that were each hand position was specified by a unique combination of joint angles. At the same time, evidence has been provided from a variety of tasks that the central nervous system takes advantage of the redundancy available to it when planning and executing functional movements. The current study attempted to determine whether a change in the use of joint motion redundancy is associated with the adaptation process. Both experimental and control subjects performed 160 trials of reaching in each of four adaptation phases, while holding the handle of a robot manipulandum. During the first and last adaptation phases, the robot motors were turned off. During phases 2 and 3 the motors produced a velocity-dependent force field to which experimental subjects had to adapt to regain relatively straight line hand movements during reaching to a target, while the motors remained off for the control group. The uncontrolled manifold (UCM) method was used to partition the variance of planar clavicle–scapular, shoulder, elbow and wrist joint movements into two orthogonal components, one (V_UCM) that reflected combinations of joint angles that were equivalent with respect to achieving the average hand path and another (V_ORT) that took the hand away from its average path. There was no change in either variance component for the control group performing 640 non-perturbed reaches across four ‘pseudo-adaptation’ phases. The experimental group showed adaptation to reaching in the force field that was accompanied initially by an increase in both components of variance, followed by a smaller decrease of V_UCM than V_ORT during 320 practice reaches in the force field. After initial re-adaptation to reaching to the null field, V_UCM was higher in experimental than in control subjects after performing a comparable number of reaches. V_UCM was also larger in the experimental group after re-adaptation when compared to the 160 null field reaching trials performed prior to initial force field introduction. The results suggest that the central nervous system makes use of kinematic redundancy, or flexibility of motor patterns, to adapt reaching performance to unusual force fields, a fact that has implications for the hypothesis that motor adaptation requires learning of formal models of limb and environmental dynamics.

Introduction

Bernstein (1967) hypothesized that motor learning involved an initial ‘freezing’ or effective elimination of degrees of freedom (DOFs), followed by a release or ‘freeing’ of those DOFs with practice whereby they became incorporated into the movement. Although some evidence supporting this hypothesis is provided by a number of kinematic studies of learning tasks (McDonald et al. 1989; Smith et al. 2001; Vereijken et al. 1992), contradictory results have been reported (Caillou et al. 2002; Ko et al. 2003). Moreover, experimentally, the proposed “elimination of DOFs” has typically meant a reduction in the range of joint motion (Vereijken et al. 1992), in which case no DOFs are actually eliminated. Thus, evidence for the proposed ‘freezing–freeing’ hypothesis is weak at best.

An alternative proposal is that all motor elements or DOFs are used to accomplish a given task so that no DOFs are ever eliminated (Gelfand and Latash 1998; Gelfand and Tsetlin 1966). The DOFs (e.g., joint motions) are hypothesized to be organized into structural units (synergies) within which individual DOFs may show relatively large variability that may tend to destabilize the output of the unit (e.g., hand trajectory), while the outputs of other DOFs (e.g., joint motions) co-vary to ensure stable output of the unit. This principle emphasizes error compensation, or more generally, flexible solutions to the coordination of the motor elements underlying a motor task. Such flexibility may be the most important feature of a functional synergy (Latash et al. 2002b).

This hypothesis is supported by recent studies of finger force production tasks that report lower total force variance compared to the sum of variances of individual finger forces (Latash et al. 2002c, 2003). More extensive evidence comes from additional studies of finger force production tasks (Latash et al. 2001, 2002a; Scholz et al. 2002, 2003; Shinohara et al. 2004), of upper extremity targeting tasks (Scholz et al. 2000; Tseng et al. 2002, 2003; Tseng and Scholz 2005a, b) and of both kinematic (Krishnamoorthy et al. 2005; Reisman et al. 2002; Scholz et al. 2001) and muscular synergies (Krishnamoorthy et al. 2003, 2004) underlying postural control. These latter group of studies used the uncontrolled manifold (UCM) approach (Schöner 1995) to explore the phenomenon of motor redundancy quantitatively. The UCM is defined as a subspace within which all possible combinations of motor elements lead to a consistent value of a performance variable. In contrast, combinations of motor elements within a subspace orthogonal to a UCM lead to a change in the value of the performance variable. Quantitative comparisons of the extent to which combinations of motor elements lie within or orthogonal to the UCM have been performed using indices of variance across repetitive attempts at a task, V_UCM and V_ORT, respectively, estimated per dimension in each subspace. In the context of kinematic analyses, the motor elements refer to the joint motions. When a joint’s motion tends to take the hand away from its desired position, for example, other joints may compensate for that joint’s deviation to prevent or limit deviation of the hand trajectory. Across movement repetitions, the extent to which the motor system uses equivalent solutions (i.e., equivalent joint combinations) to generate a consistent hand position is represented by V_UCM. The extent to which the joints are not perfectly compensated so that the hand is deviated from the desired position is represented by V_ORT. The UCM theory hypothesizes that control of a particular performance-related variable is accomplished by restricting V_ORT while freely allowing or minimally restricting V_UCM. Thus, the amount of V_UCM relative to V_ORT indicates the degree to which the joint configuration variance is structured to stabilize a particular performance variable. Can motor learning be considered as a refinement of this process by which flexible combinations of motor elements are utilized to stabilize important performance variables?

Recent studies of motor learning using the UCM approach have produced ambiguous results. Most studies in adults revealed a decrease in both components of joint configuration variance (V_UCM and V_ORT) with practice. However, the decrease in V_UCM could be larger than (Domkin et al. 2002), equal to (Domkin et al. 2005), or smaller than (Kang et al. 2004; Yang and Scholz 2005) the decrease in V_ORT with practice. A related experiment using a slightly different approach to distinguish variance components revealed primarily decreases in V_ORT in an early stage of practice, leading to a higher ratio of the two components, while V_UCM decreased more than V_ORT at a later stage (Latash et al. 2003). In contrast, a study of adolescents with Down syndrome showed that V_UCM actually increased with practice while V_ORT decreased (Scholz et al. 2003). These differences may stem, in part, from differences in the novelty or the difficulty of the tasks that were studied.

All of the above studies examined the nature of changes in the coordination of DOFs when learning a relatively novel motor task. Motor adaptation is a similar phenomenon that has received much recent attention but has, to our knowledge, never been addressed from this perspective (Brashers-Krug et al. 1995; Buch et al. 2003; Malfait et al. 2005, 2002; Shadmehr et al. 1995; Shadmehr and Mussa-Ivaldi 1994; Wang and Sainburg 2004a, b). A common experimental paradigm used to study motor adaptation has been reaching in unusual force fields (Brashers-Krug et al. 1995; Shadmehr et al. 1995; Shadmehr and Mussa-Ivaldi 1994). These studies typically show that the hand’s path is distorted from its typical quasi straight-line movement when a force perpendicular to the movement path and proportional to the hand velocity is initially introduced (Brashers-Krug et al. 1995; Shadmehr et al. 1995; Shadmehr and Mussa-Ivaldi 1994). With extended practice the hand eventually recovers a quasi straight-line path. The presence of an after-effect when the force field is again turned off (i.e. null field), where the hand’s movement appears as a mirror image of the initially distorted hand path, is indicative of motor adaptation. A typical explanation is that this adaptation can be accounted for by the learning of a new internal model reflecting the interaction between the arm and the environment so that a new set of motor commands is generated to compensate for the predictable external force (Brashers-Krug et al. 1995; Shadmehr et al. 1995; Shadmehr and Mussa-Ivaldi 1994). Removal of the force field requires the internal model to be changed again. It has been suggested that the putative internal model is encoded in joint coordinates (Gandolfo et al. 1996; Shadmehr and Moussavi 2000; Shadmehr and Mussa-Ivaldi 1994).

The nature of changes in joint coordination during adaptation to unusual force fields has not been examined in detail, however, probably because studies using this paradigm have involved a non-redundant system of joints (although redundancy was present at the muscular level, this has not been examined in detail). Coordination of more joint motions is typically required to perform most functional tasks, possibly limiting the applicability of previous models and explanations of motor adaptation that have been proposed. For example, a stiffening strategy reported during the initial introduction of a novel force field (Takahashi et al. 2001) may be less important in a redundant motor system where deviation of the output at one joint’s motion can be compensated by changes in the trajectory of other joints to limit the effect of the perturbation on the hand’s path.

The method of the UCM approach was used in the current study to determine whether and how the use of multiple, equivalent solutions to configure the joints is modified during the process of motor adaptation. We hypothesized that during adaptation, changes would occur in the degree to which equivalent joint combinations are used to control the hand’s path. This was determined by examining changes in V_UCM and V_ORT, with the prediction that the relative amounts of V_UCM and V_ORT would differ between reaches produced prior to force field introduction and those occurring after re-adaptation to a null field. This prediction has implications for explanations of motor adaptation based on internal models. If internal models are created or optimized during learning (Davidson and Wolpert 2005; Hwang and Shadmehr 2005; Shadmehr and Mussa-Ivaldi 1994), then decreases in V_ORT with practice can be expected. However, changes in V_UCM would not be predicted because such changes, reflecting the use of many equivalent combinations of motor elements, are irrelevant to task success. The same may be argued for re-adaptation to the null field. Armed with an accurate internal model of the detailed dynamics of limb–environment interaction and consistent environmental and task constraints, the model should be able to define an optimal solution to coordinating the joints that achieves the desired goal. In contrast, if V_UCM were to show significant increases during motor adaptation, an argument can be made that this reflects an inherently flexible control system that allows for a set of solutions rather than resorting to a single, optimal solution. Such a solution might not require a detailed intrinsic model of the dynamics of the limb–environment interaction to solve the problem (Martin et al. 2004; see also Guenther and Barreca 1997; Todorov 2004).

Methods

Subjects

Twelve subjects constituted a ‘sample of convenience’ for the experiment, assigned in equal numbers to the experimental and control groups. All subjects were healthy and right handed by report, which was corroborated with the Edinburgh Handedness Questionnaire (Oldfield 1971). None of the subjects had previously participated in a similar experiment involving reaching in an artificial force field. The experimental group included five females and one male with the height and body mass 165.3 ± 9.4 cm and 67.1 ± 18.2 kg (mean ± SD), respectively. The control group included three females and three males with the height and body mass 169.5 ± 11.8 cm and 61.2 ± 13.7 kg (mean ± SD). All subjects gave their written informed consent as approved by the University’s Human Subjects Committee in accordance with the ethical standards laid down in the 1964 Declaration of Helsinki.

Experimental task

The task was to make reaching hand movements in the horizontal plane, with the right hand grasping the handle of a robot manipulandum (see Fig. 1). The robot was a two-link system allowing for two-dimensional movement. The manipulandum handle rotated freely in the horizontal plane and the handle was oriented horizontally so that the forearm was pronated and the hand faced palm down, allowing for unconstrained radial–ulnar deviation of the wrist. The hand/manipulandum position and the starting and target positions were represented by individual circular cursors on a computer monitor placed directly in front of the subject. Real-world coordinates of the starting and target positions differed by a distance of 25 cm. The global x and y axes were pointing towards the right and forward, respectively. Considering the hand’s starting position to be located at the origin, the target was located along the y-axis, directly forward from the origin. Thus, to reach the target directly, the handle had to be moved straight ahead from the starting position. The subjects sat in an adjustable height chair (adjusted to ensure that the shoulder was in the same plane as the manipulandum). The subject’s position was adjusted such that a line passing through the shoulder joint and pointing straight forward was parallel to the y-axis of the global coordinate system, along which the starting and target positions were also located. The starting position was located at a distance from the shoulder approximately equal to the length of the upper arm. After the subject was positioned, the chair was locked in place and the subject’s trunk was strapped to the chair back with a wide strap, just under the armpit, to prevent trunk motion. Before reaching, the subjects moved the robot manipulandum to align the manipulandum cursor with the starting cursor. The subjects were instructed to “After the ‘go’ signal, reach directly to the target on a subsequent metronome beat of your choosing while keeping your elbow horizontal”. It was emphasized that this was not a reaction time task. Although this instruction may imply a straight-line trajectory to the target, no additional instructions were given about the expected nature of subjects’ hand paths. The metronome was used in an attempt to ensure a relatively consistent movement time of approximately 600 ms to cover the 25 cm distance. Subjects were relatively successful at keeping the elbow horizontal as verified off-line by checking the position of a video marker placed on the elbow in relation to the hand marker. A short break was given in after each ten reaching movements. Subjects were told to inform the investigator if they were experiencing fatigue during the experiment and required additional rest. In addition, the experimenter asked the subject frequently during the experiment whether they were experiencing fatigue and needed additional rest. No subject reported a problem with fatigue.

Fig. 1.

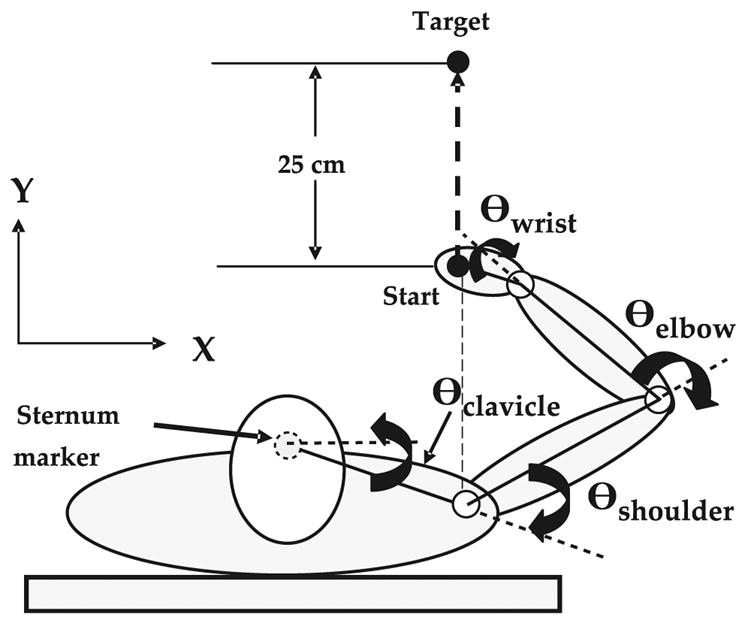
The relationship between the starting position, target, and subject is plotted to illustrate the experimental task. Joint angles are defined as outside angles formed with the previous segment except for the clavicle–scapula angle, which is formed with the horizontal

Experimental procedures

All subjects in the experimental group performed reaching movements to the target in four groups of trials, referred to here as “adaptation” phases. One hundred-sixty reaches were performed in four separate trial blocks of 40 trials each during each adaptation phase, for a total of 640 reaching movements. In the first and fourth adaptation phases, termed Null field I (NF1) and Null field II (NF2), reaches were performed without the application of an additional force field. The other two phases between null field I and null field II were true adaptation phases, termed the early force field (EFF) and late force field (LFF). They required subjects to reach while holding the robot handle while a velocity-dependent force field was applied to the manipulandum as described below.

The applied force was dependent on the damping matrix and the current hand velocity as

$$\left[\begin{array}{c}Fx\\ Fy\end{array}\right]=B\ast \left[\begin{array}{c}Vx\\ Vy\end{array}\right].$$ (1)

In this experiment, the damping matrix (B) was set to $\left[\begin{array}{cc}0& -15\\ 15& 0\end{array}\right]$ Ns/m. Subjects were instructed to compensate for the force field and try to continue to reach straight to the target from the starting position.

The subjects in the control group performed the reaching task over the same number of trials as the experimental group. However, an additional force field was not applied for any of the pseudo-adaptation phases. Even without the active force field, the inertial properties of the device and arm result in a reaching environment different than free-reaching movements. Thus, the control experiment was designed to determine if observed changes in the dependent variables (see below) for the experimental group were the result of the adaptation to the force field or simply due to practice of reaching in a different inertial environment.

Data collection

The arm motions of each reaching movement were recorded at 120 Hz by a 4-camera VICON motion measurement system. Prior to each experiment the cameras were calibrated to the spatial volume of the movement. A link-segment model was used to compute joint angular excursions based on the reconstructed two-dimensional motion of reflective markers placed on the arm at the approximate joint locations. Markers were placed at (1) the sternal notch, (2) immediately below the acromion process of the shoulder, (3) the lateral epicondyle of the elbow, (4) distal end of the radius, (5) the distal end of the third metacarpal bone, and (6–7) on each side of the manipulandum handle. The sternal marker served as a basis coordinate for the other markers.

Data processing

The coordinates of the reflective markers were reconstructed from the individual camera data using custom VICON software. Marker coordinates were then filtered using a second-order, 5 Hz zero-phase forward and reverse Butterworth filter. The resultant velocity of the hand marker was obtained after differentiation of its x and y coordinates. Movement onset was then determined using a custom MATLAB program, with onset determined as the time when the hand’s velocity exceeded 5% of its peak value. The same algorithm was used to determine movement termination. However, for movement termination, a criterion of 10% of the peak resultant velocity was used because terminal adjustments were often inconsistent from trial to trial and across subjects when reaching in the force field, creating problems when trying to time-normalize all trajectories to 100% for the analyses. Using a criterion of 10% peak velocity minimized this problem. Thus, the analysis is confined to the primary movement toward the target.

Four planar joint angles were calculated from the x to y coordinates of the reflective marker data. Abduction–adduction of the clavicle–scapula was calculated as the angle between a vector from the sternum marker to the acromion marker and a vector parallel to the global x-axis, with its origin at the sternum marker. Shoulder abduction–adduction was calculated as the angle between a vector from the sternum marker to the acromion marker and a vector from the acromion marker to the elbow marker. Elbow flexion–extension was calculated as the angle between a vector from the acromion marker to the elbow marker and a vector from the elbow marker to the wrist marker. Finally, the wrist joint angle was calculated as the angle between a vector from the elbow marker to the wrist marker and a vector from the wrist marker to the hand marker.

Dependent variables

Path length

Coordinates of the hand marker from movement onset to termination were time-normalized to 100 points using a cubic-spline fit in Matlab. The summed distance between the normalized data points was calculated as the path length for each movement trial. The path length was then averaged over every five trials. The averaged path lengths were plotted against practice sequence for the experimental group and the control group separately to determine if adaptation occurred for the experimental group during the force fields.

Joint configuration variance

The UCM approach hypothesizes that the control system selects a subspace (a UCM) within the state space of the motor elements (e.g. joint space in the current analysis) and then structures the variability of the motor elements such that it is mostly confined to the UCM (Scholz and Schöner 1999). The computed UCM represents a linear estimate of the space of all combinations of the motor elements that give rise to the same value of a particular performance variable, e.g. a particular 2D hand position at each point in the time-normalized movement trajectory in the current experiment. Thus, the synergy of joint motions, organized to produce a consistent trajectory of the hand, is expected to exhibit larger variability within the UCM at each position of the hand along its path to the target than variance orthogonal to the UCM (per dimension), which leads to an inconsistent hand position. The method of the UCM hypothesis allows partitioning of variance in the space of the motor elements (i.e. scapula, shoulder, elbow and wrist) across trials into variance that lies within the UCM (V_UCM) and variance in the space orthogonal to the UCM (V_ORT).

The question of whether many different combinations of joint angles that were equivalent with respect to the average hand path were used to adapt to the force field was quantified by the UCM analysis using the following procedures:

1. The joint angles were computed at each sample of each reaching trial and then time-normalized between movement onset and termination to 100 points using a cubic-spine algorithm.

2. The geometric model relating the two-dimensional hand position to the joint configuration was:

   $$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}{l}_1\cdot cos({\theta }_1)+l_2\cdot cos({\theta }_1+{\theta }_2)+l_3\cdot cos({\theta }_1+{\theta }_2+{\theta }_3)+l_4\cdot cos({\theta }_1+{\theta }_2+{\theta }_3+{\theta }_4)\\ l_1\cdot sin({\theta }_1)+l_2\cdot sin({\theta }_1+{\theta }_2)+l_3\cdot sin({\theta }_1+{\theta }_2+{\theta }_3)+l_4\cdot sin({\theta }_1+{\theta }_2+{\theta }_3+{\theta }_4)\end{array}\right],$$ (2)

3. where x: x coordinate of the end effector position; y: y coordinate of the end-effector position; l₁: length of the clavicle; l₂: length of the upper arm; l₃: length of the forearm; l₄: length of the hand; θ₁: abduction–adduction movement of the clavicle–scapula; θ₂: Shoulder joint horizontal abduction–adduction; θ₃: elbow flexion–extension; θ₄: Wrist medial–lateral deviation.

4. Based on the geometric model, the Jacobian matrix, relating changes in the joint angles to changes in the performance variable, was determined.

   $$\begin{array}{l}J=\left[\begin{array}{cccc}\frac{\partial x}{d{\theta }_1},& \frac{\partial x}{d{\theta }_2},& \frac{\partial x}{d{\theta }_3},& \frac{\partial x}{d{\theta }_4}\\ \frac{\partial y}{d{\theta }_1},& \frac{\partial y}{d{\theta }_2},& \frac{\partial y}{d{\theta }_3},& \frac{\partial y}{d{\theta }_4}\end{array}\right]\end{array}$$ (3)
5. The nullspace of the Jacobian matrix was then computed in Matlab, based on the mean joint configuration across trials at each normalized time point, to obtain a linear estimate of a subspace in joint space in which all joint combinations would be consistent with the 2D hand position corresponding to this mean joint configuration value. In this procedure, it is presumed that the CNS tries to achieve this mean value of the performance variable.

   $$0=J(\overline{\theta })\cdot \epsilon ,$$ (4)

6. where $\overline{\theta }$: Mean joint configuration, ε: Nullspace of Jacobian.

7. The mean joint configuration at each time point across trials was subtracted from the current configuration for each trial and then projected onto the nullspace and its complement, i.e. the orthogonal subspace:

   $${\theta }_{\parallel }=(\theta -\overline{\theta })\cdot {\epsilon }_i,$$ (5)

   $${\theta }_{\perp }=(\theta -\overline{\theta })-{\theta }_{\parallel },$$ (6)

8. where θ_∥: the vector of joint configuration projected to the nullspace of Jacobian, θ_⊥: the vector of joint configuration projected to the space orthogonal to the nullspace of Jacobian.

9. The variance of the magnitudes of the projections into each dimension of the two subspaces and the resultant across dimensions of each space were then computed and divided by the number of dimensions in each space.

   $${\sigma }_{\parallel }^2=\frac{{\sum }_{i=1}^{n-d}{\sum }_{j=1}^N{\theta }_{\parallel }^2}{(n-d)\cdot N},$$ (7)

   $${\sigma }_{\perp }^2=\frac{{\sum }_{i=1}^d{\sum }_{j=1}^N{\theta }_{\perp }^2}{d\cdot N},$$ (8)

10. where ${\sigma }_{\parallel }^2$ is variance within the UCM (V_UCM), ${\sigma }_{\perp }^2$ is variance in the joint space orthogonal to the UCM (V_ORT), N is the number of trials, n is the total number of DOFs or joint motions (n = 4), and d is the number of DOFs describing the task, i.e. 2 dimensional hand path.

We would emphasize that the nullspace is different at every point of time.

With two exceptions, trials were selected for analysis based on the relative time of occurrence of peak velocity as a percentage of movement time (i.e. trials within 1.75 standard deviations of mean relative time of peak velocity) in combination with targeting error (1.75 standard deviations of the mean end-effector position at movement termination) to try to ensure relative consistency of the movement across reaches used in the analysis, given that the value of the Jacobian was based on the mean trajectory. Application of these criteria resulted in approximately 25 trials for each block being used in the analyses. The exceptions were the initial block of trials in EFF and NF2. Here all trials were used because we wanted to capture the transient behavior upon experiencing the force field and during the subsequent return to the null field, which likely involves substantially inconsistent movement timing and accuracy from trial to trial.

The results of the variance decomposition performed at each percentage of the reaching movement were averaged over the period from 41 to 60% of normalized movement to address the effects occurring around the time of peak velocity, where the magnitude of the perturbation was maximal. We also analyzed the results at 100% of the time normalized trajectory, corresponding to when the hand had reached 10% of the peak velocity, near movement termination.

Statistical analysis

A univariate ANOVA was performed to compare the difference in path length between adaptation phases. The within-subjects factor was sequence of practice (Mean of every 5 path lengths, for a total of 32 measures for each adaptation phase) and the between-subjects factor was group (experiment and control).

A two-way mixed-design ANOVA was performed to confirm that there was no difference in joint configuration variance between the experimental and the control group in NF1. The within-subjects factors were practice block (I–IV) and variance component (V_UCM and V_ORT) and the between-subjects factor was group (experiment and control).

To compare the results of joint configuration variance between NF1 and EFF, and between NF1 and NF2, three-way mixed-design ANOVAs were performed. Each analysis included the within-subjects factors of adaptation phase, practice block (I–IV), and variance component (V_UCM and V_ORT) and between-subjects factor of group (experiment and control). These ANOVAs were performed separately to test for effects occurring around the time of peak velocity and at movement termination.

To assess the trends of changes in components of joint configuration variance within the force field adaptation phases (early and late) and separately during NF2, two 2-way mixed-design ANOVAs were performed. Each analysis included the within-subjects factors of practice block (eight blocks for the combined early and late force fields and four blocks for NF2) and variance component (V_UCM and V_ORT), and between-subjects factor of group (experiment and control).

Results

Path length

Figure 2 shows the path length for each adaptation phase, averaged for the experimental and control groups separately, indicating the distance traveled by the hand from the starting position to the target. The path length for the control group stayed relatively unchanged over the entire experiment. In contrast, the path length for the experimental group increased dramatically when the force field was turned on, decreasing to baseline levels across the early and late force fields. Another increase in path length occurred with the force field was turned off in NF2, returning again to baseline levels.

Fig. 2.

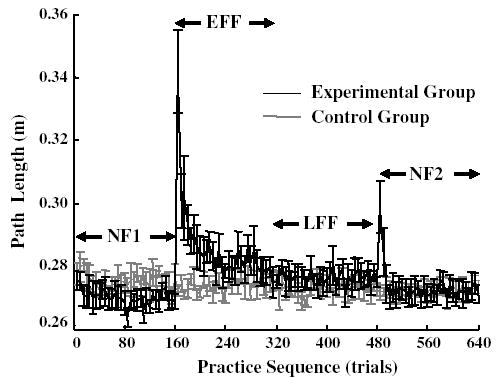
Path length (mean and standard error) is plotted against trial sequence. The black and gray lines represent the experimental and the control subjects, respectively. Each point represents the average of five consecutive trials per subject then averaged across subjects

In NF1, there was a small but significant difference in path length between the control (0.2755 ± 0.001) and experimental (0.2702 ± 0.001) groups (F_{1, 315} = 62.908, P < 0.001. The main effect for trial sequence (P > 0.5) and interaction of trial sequence by group (P > 0.5) were not significant, indicating a stable path length during this phase for both groups.

In the EFF, the experimental group showed an increase in path length followed by a rapid drop while the path length of the control group (not subjected to an additional external force field) was stable. The increases in the path length were due to a curved movement induced by the less than ideally compensated external force (Fig. 3). The difference between groups and the trend of change over practice sequence was supported by the significant main effect for group (F_{1, 315} = 125.702, P < 0.001), for sequence (F_{31, 315} = 4.391, P < 0.001), and for interaction of group by sequence (F_{31, 315} = 4.918, P < 0.001). In the LFF, there was a significant group effect (F_{1, 315} = 31.721, P < 0.001), indicating that the level of path length in the experimental group had not decreased to the same level as the control group. However, the path length was stable in both groups, corresponding to the non-significant sequence effect (P > 0.5) and interaction of group by sequence (P > 0.5).

Fig. 3.

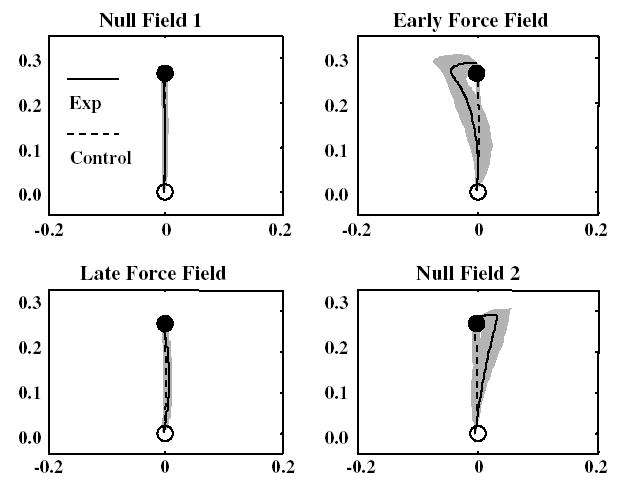
Average hand paths for a representative subject during reaches performed in the four adaptation phases. The dashed line represents the hand path of the control group during the same phase. Shaded area is one standard deviation

For NF2, the experimental group showed another increase in path length immediately after removal of the force field followed by a quick drop to the level similar to the control group. Therefore, the main effect for sequence (F_{31, 315} = 3.162, P < 0.001) and interaction of group by sequence (F_{31, 315} = 3.073, P < 0.001) were significant.

Overall, the results indicated that motor adaptation did occur during reaching in the force field for the subjects of the experimental group. The pattern of adaptation depicted by the average plot in Fig. 2 was qualitatively similar for all subjects in the corresponding groups.

Joint configuration variance

An example of the results of the analysis of joint configuration variance across the time-normalized reach is presented for one subject in Fig. 4. Figure 4a presents the variance components and average tangential hand velocity comparing reaching trials in NF1 (thin lines) to reaching trials during the last block of NF2 (thick lines), following re-adaptation to the null field. Figure 4b presents the same measures comparing the first reaches in the force field (thin lines) to reaches performed near the end of force field practice (thick lines). Reaches performed when the force field was just turned on (thin lines, Fig. 4b) resulted in an increase in both variance components that persisted throughout the reach when compared to reaching in NF1 (thin lines, Fig. 4a), despite similar tangential velocity profiles. Both V_UCM and V_ORT were substantially higher during early compared to later reaches in the force field (Fig. 4b), particularly during the middle of the movement, despite similar values of peak velocity. By late reaching trials in the force field, V_ORT had decreased to about the level found during NF1 reaches (compare thick dashed lines of Fig. 4b to thin dashed lines of Fig. 4a), while V_UCM continued to be higher for reaches in the late force field (solid thin line, Fig. 4a versus solid thick line, Fig. 4b). When comparing reaches in the early and late null fields (Fig. 4a) little difference was found between V_ORT (dashed lines). However, V_UCM was higher during the early and middle portions of the reach trajectory for NF2 reaches compared to NF1 reaches. Further statistical analyses were performed to evaluate the comparisons of primary interest for the entire group.

Fig. 4.

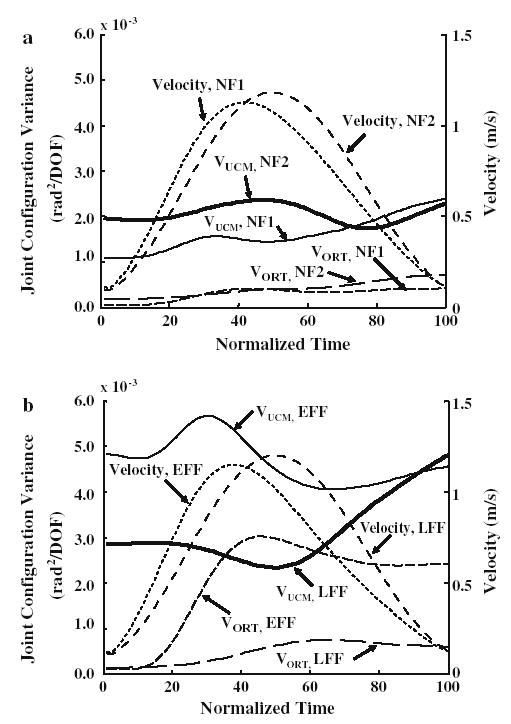
Time normalized velocity profiles and variance components (V_UCM and V_ORT) across the hand path for one subject a comparing null field 1 (NF1; light lines) and null field 2 (NF2; dark lines) and b comparing early (EFF; light lines) and late (LFF; dark lines) force field practice

A mixed-design ANOVA performed across groups, adaptation phases, and blocks of trials per phase and the two types of joint configuration variance revealed a significant four-way interaction (F_9,90 = 2.03, P < 0.05) when computed on data around the time of peak movement velocity. When performed on data from movement termination, there was a significant adaptation phase by block by group interaction (F_9,90 = 2.91, P < 0.01), but no interaction with the type of variance component (P > 0.1), although V_UCM was significantly higher than V_ORT when collapsed across other factors, both at the time of peak velocity (F_1,10 = 64.55, P < 0.0001) and at movement termination (F_1,10 = 64.07, P < 0.001).

Baseline performance in null field

We tested the hypothesis that the results from the baseline reaching trials (NF1) did not differ between experimental and control groups. This hypothesis was confirmed. The only significant effect was that V_UCM was greater than V_ORT, regardless of group, when measured both at the time of peak velocity (V_UCM: 0.00132 ± 0.00016 rad² per DOF; V_ORT: 0.00035 ± 0.00004 rad² per DOF; F_1,10 = 52.54, P < 0.0001) and at movement termination (V_UCM: 0.00219 ± 0.00027 rad² per DOF; V_ORT: 0.00062 ± 0.00010 rad² per DOF; F_1,10 = 68.94, P < 0.0001). There was no difference between the groups or any significant interactions with group (all P > 0.1).

Effect of early force field

The transition from NF1 to the EFF (i.e. the imposition of an actual force field for the experimental group and a comparable trial sequence for the control group without an additional force field) was marked by a substantial increase in both V_UCM and V_ORT for the experimental group but not for the control group (F_1,10 = 18.0, P < 0.01; Fig. 5a) when measured around the time of peak velocity. There were no significant interactions of the variance component with other factors because both V_UCM and V_ORT increased simultaneously.

Fig. 5.

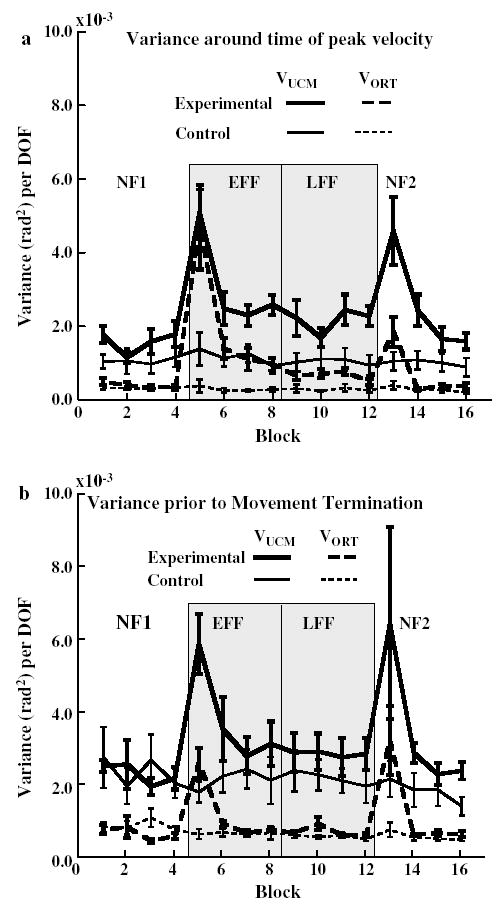
Components of joint configuration variance a around the time of peak velocity and b near movement termination, averaged (± SE) across subjects separately for each group for each block of trials (40 trials per block) of each adaptation phase (NF1, EFF, LFF and NF2)

The same analysis performed at movement termination revealed a significant interaction of adaptation phase by type of variance component by group (F_9.90 = 9.11, P < 0.05; Fig. 5b). While both V_UCM and V_ORT were higher at movement termination for the experimental group after transitioning to the force field, the increase in V_UCM was greater (F_1,5 = 9.03, P < 0.05). In contrast, the control group exhibited no significant changes in either variance component across the same adaptation phases.

Changes across learning to reach in the force field

The data of Fig. 5a, b within the gray region shows the trend of changes in variance components across the eight blocks of trials of combined EFF and LFF, measured at the times of peak velocity and at movement termination, respectively. At the time of peak velocity (Fig. 5a) the first block of trials in the force field for the experimental group resulted, on average, in nearly equal components of joint variance. Both V_UCM and V_ORT decreased precipitously by the second block of 160 trials and then more gradually thereafter, with the difference between the two components increasing gradually up to the end of the LFF. This change in joint variance over blocks of adaptation was reflected by a significant logarithmic fit to V_UCM (R² = 0.336, F_1,46 = 23.3, P < 0.0001) and to V_ORT (R² = 0.480, F_1,46 = 42.4, P < 0.001). In contrast, both components of variance for the control group remained constant during the reaching over the same number of trials. By the last block of trials, the difference of V_UCM between the groups was significantly greater than the difference in V_ORT (F_1,10 = 8.0, P < 0.05).

A similar, albeit weaker, effect was found when considering the variance components at the termination of reaching (Fig. 5b). As noted in the previous section, while both components of joint configuration variance increased when subjects first encountered the force field, the experimental group still exhibited higher V_UCM than V_ORT at movement termination. Thereafter, both variance components decreased logarithmically across trials (V_UCM: R² = 0.243, F_1,46 = 14.77, P < 0.001; V_ORT: R² = 0.484, F_1,46 = 43.17, P < 0.001). Once again, there was no change in either component of joint variance across the comparable trial sequence for the control group. Although V_UCM was quantitatively larger in the experimental group (0.0027 ± 0.0005 rad² per DOF) compared to the control group (0.0018 ± 0.00046 rad² per DOF) by the last block of LFF, this difference was not significant (P > 0.2). There was also no difference between the groups for V_ORT (Experimental: 0.00047 ± 0.0001 rad² per DOF; Control: 0.00036 ± 0.00007 rad² per DOF).

Changes in variance components during re-adaptation

Blocks 13–16 in Fig. 5a show the trend of variance component change around the time of peak velocity across the 4 blocks in NF2. The transition from the last block of trials in LFF to the first block of trials in NF2 led to a relatively proportional increase in both components of joint configuration variance for the experimental group while the variance components did not change for the control group (F_1,10 = 6.134, P < 0.05). Thereafter, V_ORT dropped to control group levels by the second block of trials, while V_UCM dropped more slowly before stabilizing by the third block of trials. Similar to the change in variance components across combined blocks of the EFF and LFF, both V_UCM (R² = 0.467, F_1,22 = 19.24, P < 0.001) and V_ORT (R² = 0.476, F_1,22 = 20.00, P < 0.001) showed a significant logarithmic decrease over trial blocks after returning to reaching in the null field. There were no significant trends, including linear changes, in the two components for the control group over blocks of NF2. Similar differences were not found when comparisons were made near movement termination (Fig. 5b, blocks 13–16).

Comparison between NF1 and NF2

Comparison of the last three blocks of NF1 with NF2 (eliminating the transient in the first block of re-adaptation) at the time around peak velocity revealed a significant group by adaptation phase by variance component interaction (F_1,10 = 5.51, P < 0.05). This interaction resulted from higher values of V_UCM for the experimental group in NF2 compared to NF1 and no difference in V_ORT, while both components of variance for the control group decreased slightly between NF1 and NF2. Thus, after training in the force field, the experimental group exhibited a small but significant increase in V_UCM compared to pre-training reaches that could not be attributed to practice of reaching alone.

A similar difference in the variance components for the two groups was present when measured at the time of movement termination, although the increase in V_UCM for the experimental group between NF1 (0.00209 ± 0.00043) and NF2 (0.00238 ± 0.00026) was smaller and the same interaction only approached significance (F_1,10 = 4.5, P = 0.059).

These effects are further illustrated in Fig. 6, where the average ratio of the variance components around the time of peak velocity is presented for the two groups for the four adaptation phases. An ANOVA comparing the groups across adaptation phases and blocks of trials within phases revealed only a significant group by adaptation phase interaction (F_3,30 = 7.3, P < 0.001) when measured at the time of peak velocity. Further analyses revealed that the ratio differed between the two groups only during EFF (F_1,10 = 13.7, P < 0.01), where the ratio was smaller for the experimental group, and NF2 (F_1,10 = 6.0, P < 0.05), where the ratio was higher for the experimental group.

Fig. 6.

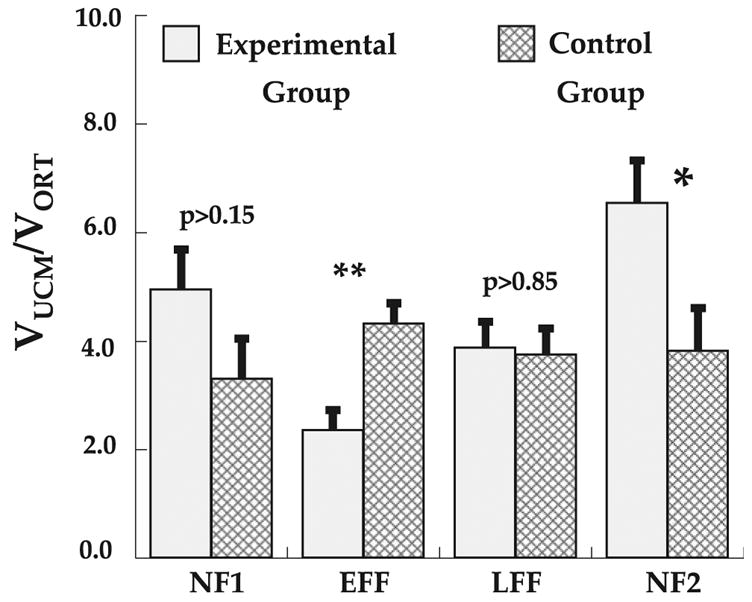
Variance ratio (V_UCM/V_ORT) for each phase of adaptation for the experimental and control groups. Ratio’s greater than 1 indicate V_UCM > V_ORT. **F_1,10 = 13.7, P < 0.01; *F_1,10 = 6.0, P < 0.05. Ratio is average of results around the time of peak velocity

Discussion

The current experiment explored the role of motor redundancy in motor adaptation by examining reaching with a kinematically redundant arm, i.e., an arm having more degrees than required to place the hand at a particular spatial location. Motor redundancy was addressed by performing an analysis that partitions joint variance into a component that represents different combinations of joints that lead to an equivalent hand position at a given point along the hand’s path (V_UCM) and a component that changes the hand path from trial to trial (V_ORT). Differential change in the two components of variance with practice was limited to the experimental group and supported the hypothesis that changes in the use of motor redundancy underlie the process of reaching adaptation. Although V_UCM and V_ORT changed proportionally upon initial introduction of the force field, suggesting a non-selective effect of the perturbation on joint variance, the only component that affected hand position, V_ORT, decreased more rapidly with practice while V_UCM remained elevated compared to the control group, even after re-adaptation to reaching in the null field, where V_ORT did not differ between the groups. These findings suggest, therefore, that variations of the joint configuration were structured by the controller to stabilize preferentially the path of the hand more than joint motions, and this effect was enhanced after the period of adaptation.

Goal-equivalent joint configuration variance increased in response to the changes in environmental dynamics

Results of a path length analysis indicated that the subjects who reached in the novel, velocity-dependent force field adapted in a manner similar to what has been reported in studies using a similar paradigm to study reaching adaptation (Brashers-Krug et al. 1995; Shadmehr et al. 1995; Shadmehr and Mussa-Ivaldi 1994). During the first block of reaching in the force field, the path length increased, decreasing thereafter with practice. Adaptation was evident by the presence of an after-effect, that is, an increase in path length due to an opposite direction hand deviation when subjects reached in the null field (NF2) after having practiced reaching in the force field.

In contrast to previous studies that examined reaching adaptation with kinematically non-redundant effector systems, subjects in the current experiment had the option of using available redundancy to adapt to the perturbing forces. With four available joint motions, the control system could flexibly assemble the joints to help compensate for the effect of the perturbing force on the hand’s path. That is, with only two joint motions allowed in previous studies, one unique combination of joint postures corresponds to a given hand position. In such cases, there are limited ways to resist a perturbing force. In contrast, with additional degrees of freedom available, alternative joint configurations can be used for a given desired hand position to optimize resistance to the perturbation, e.g. to increase hand stiffness in a given direction. Although we can provide no direct evidence from this report that different points within a UCM correspond to different values of directional stiffness, this seems to be a reasonable assumption given endpoint stiffness estimates reported in earlier studies (Shadmehr et al. 1993). The result is consistent with our view that variance in the values of movement components is not simply a reflection of noise (Latash et al. 2002b; Scholz and Schöner 1999).

Both components of joint configuration variance were found to decrease logarithmically during adaptation to the force field in the current study. However, an important finding was that this decrease was smaller for V_UCM than V_ORT (Figs. 5, 6, EFF through LFF). In contrast, neither component of variance changed for the control subjects despite producing the same number of reaches without an additional velocity-dependent force field. Thus, the increased joint variance reflecting equivalent joint configurations for a given hand position was not simply due to practice of reaching with the robot in general. It appears instead to reflect a strategy used by the control system to adapt reaching to the unusual environment. Using a broader range of solutions (within the UCM) allows the system to both perform the explicit task and handle possible task complications such as, for example, unexpected changes in the external force. The higher values of V_UCM and lower values of V_ORT found in the late phases of force field practice compared to early reaches in the force field indicate that this increased variance was functionally specific. Moreover, this flexibility appeared to carry over somewhat to reaches following re-adaptation to the null field. Note that a variety of joint configurations used to achieve a given hand position along its path toward the target was presumably not required, given that the starting joint configuration, the hand’s starting position and the target location were reproduced across trials. Only V_ORT needs to be reduced to produce a consistent hand path.

One mechanism that could explain the increase in both V_UCM and V_ORT during early adaptation is an increase in the gains of feedback loops. According to previous investigations, motor commands can be modified based on the motor output of the previous trial (Thoroughman and Shadmehr 1999). During adaptation, an increase of the feedback gains would amplify corrective action to minimize movement deviation across successive trials. Increased muscle contraction noise related to the high feedback gains might then be reflected in higher joint positional variance. However, high feedback gains alone cannot account for a differential effect of such ‘noise’ in joint space, i.e. a greater decrease in V_ORT compared to V_UCM with continued force-field practice and even after re-adaptation to the null field. The differential change of the two variance components suggests that the CNS creates a synergy allowing for selective variation of the movement components as long as they do not affect performance adversely. Variation captured by V_UCM reflects flexible solutions to combining instantaneous joint positions. A formal model of such a control strategy has recently been proposed by Martin et al. (2004, 2005; see also Latash et al. 2005) and used to account for experimental variance results of two-dimensional reaching tasks. The model, based on equilibrium-point control, feeds back the current joint configuration to the controller which leads to resistance to deviations from the planned configuration only if they lie in the range space of joint space, i.e. they lead to a change of the hand path (see also Guenther and Barreca 1997; Todorov 2004). Otherwise, deviations that lie in the null space (within the UCM) result in an updating of the plan so that a new sequence of joint configurations consistent with a transition from the current actual configuration to a target configuration is implemented. This effect of back-coupling from the physical plant to the planning level has been shown in simulations to be required to account for certain well-known phenomena such as motor equivalence (Martin et al. 2005).

Changes in the structure of joint configuration variance during motor adaptation were similar to those in studies of motor learning

Previous studies examining changes in coordination of multiple effectors during motor learning have led to inconsistent results. A relatively common thread of those studies which used the UCM approach to address changes in movement coordination has been a decrease in both components of variance with learning (Domkin et al. 2005, 2002; Yang and Scholz 2005). Depending on the study, the decrease in V_UCM could be smaller than (Yang and Scholz 2005), equal to (Domkin et al. 2005) or greater than (Domkin et al. 2002) the decrease in V_ORT. Based on the results of learning a challenging finger force production task, Latash et al. (2003) proposed two stages of motor learning. During the first stage, V_ORT decreases leading to improved task performance, with little or no change in V_UCM. At a later stage of practice, V_UCM decreases to varying extents, perhaps reflecting a refining of the coordination process. If this two-stage process is correct, the failure to find similar stages in the previous studies was presumably due to the tasks being inadequately novel and/or to an inadequate length of practice. In the present study, after initially increasing, both components of variance decreased during the early adaptation phase, although V_ORT decreased more than V_UCM. By the end of LFF, however, V_UCM did not differ compared to the late stages of the EFF and was still higher than reaching prior to introduction of the force field (i.e. NF1). Thus, the hypothesized two-stage process does not appear to be consistent with the current experimental results on motor adaptation, although it is conceivable that more practice could lead to a finding more consistent with that hypothesis.

In two recent studies, however, V_UCM was reported to actually increase with learning while V_ORT decreased (Kang et al. 2004; Scholz et al. 2003). The task being performed by the learners in these two studies was either significantly more difficult than in previous studies, or involved a special population of individuals who started training with diminished performance. The increase in V_UCM with learning in those studies is consistent with the results of the current study. V_UCM was significantly larger for the experimental than for the control group for reaches in the last three blocks of NF2, following re-adaptation, while the path length did not differ between the groups. Thus, results of these studies support the hypothesis that an increased use of equivalent solutions to coordinate the motor elements reflects a basic strategy used in both motor learning and adaptation if the task is sufficiently difficult.

The current results suggest that internal models may not involve a detailed model of the dynamics of joint motion

The presence of an after-effect following practice of reaching in a force field has led to the suggestion that learning a new model of the dynamics of the environment–limb interaction underlies reaching adaptation in such environments (Brashers-Krug et al. 1995; Shadmehr et al. 1995; Shadmehr and Mussa-Ivaldi 1994). Additional evidence comes from the relatively quick re-adaptation to a previously trained force field after a period of time from several hours to several months following initial learning (Shadmehr and Brashers-Krug 1997). The nature of the internal model is frequently assumed to be a formal detailed model of the arm’s dynamics (Shadmehr and Brashers-Krug 1997; Shadmehr and Mussa-Ivaldi 1994). The results of the current study raise questions about such an interpretation (Bagesteiro and Sainburg 2005, 2003; Feldman et al. 1998; Latash et al. 2003; Malfait et al. 2005).

Given an accurate internal model of the limb’s dynamics and a movement that is initiated from a controlled, initial hand position and joint configuration toward an identical target on each trial, one might expect an optimal trajectory of the joint configuration would be specified. As long as there is no unknown perturbation added to the reach, there is no reason to believe that multiple, equivalent solutions to the problem of joint coordination would be used across similar reaches. As discussed above, it is unlikely that noise due to high feedback gains could account for the differential changes in variance components with practice described in this study. In fact, even in NF1, where there was no significant difference between experimental and control subjects, control of the hand path was achieved in both groups by a significantly higher variance component that reflected equivalent joint configurations achieving the same hand path. Likewise, if reacquiring a straight hand path in late stages of practicing reaching in a force field results from the learning of a new internal model of the dynamics of limb–environment interaction, there is no reason to expect an increase of equivalent patterns of joint coordination in the later stages of adaptation, when the hand had reacquired a relatively straight path.

It could be argued that part of this difference results from the fact that all reaches do not achieve the identical hand velocity profile, leading to variations in the underlying joint configuration. We tried to control for this possibility by selecting trials for analysis that had a relatively consistent timing of peak velocity. However, this argument cannot be ruled out completely. One might expect, however, that such variations as introduced by variations in the hand’s velocity would tend to lead to higher V_ORT rather than V_UCM. This is because such differences would lead to a time distortion of different trials with respect to one another. To the extent that this is a problem, the same percent of the reach for different trials would actually reflect slightly different hand positions along its path. Given that the nullspace is estimated based on the mean joint configuration, the computation of joint variance components should lead to significantly higher V_ORT than would otherwise be the case if this were a problem. Certainly, this was not observed by the last blocks of practice in the force field.

Moreover, the increase in V_UCM during adaptation was maintained to an extent following re-adaptation to the null field (NF2), when the dynamics of the task was not different from reaching in the first null field (NF1). When measured at the time of peak movement velocity, there was a small but significant increase of V_UCM in NF2 compared to NF1 (after the transient in block I) for the experimental group while V_ORT did not differ. There was no difference in these components across a similar range of reaches for the control group. Although this result does not argue against the role of internal models in learning and adaptation in general, or for other functional tasks (Davidson and Wolpert 2005), it does raise questions about the nature of such models.

Results of the current experiment suggest that hypotheses that internal models represent a detailed, formal model of the limb and environmental dynamics may require reconsideration. We acknowledge, however, that direct comparisons of our results with those of previous experiments of reaching adaptation must be made with caution. Those studies were typically of center-out reaches of 10-cm extent to multiple target directions. In contrast, subjects in the current experiment reached to a 25-cm target distance. Because of the variance analysis, an adequate number of trials were needed, which limited our analysis to only one direction of reaching given the length of the experiment. Finally, previous studies largely limited analyses to the first 300 ms of the reach in an attempt to isolate the effect of feedforward processes. Because of the movement time in the present experiment, the analysis performed around the time of peak velocity was at the upper end of that range or slightly beyond. Thus, feedback processes certainly played more of a role in our results than in previous studies.

Recent evidence suggests that learning to perform even the simplest tasks involves the planning, execution and optimization of multiple performance features, of which hand path is just one important example. Factors such as joint torques (or muscle force; Scheidt et al. 2000), limb impedance (Takahashi et al. 2001; Burdet et al. 2001), and the relative contribution of feedforward and feedback mechanisms (Dizio and Lackner 1995; see also Bagesteiro and Sainburg 2005) likely play an important role in the adaptation process. Thus, our focus on the control of the hand trajectory will need to be extended in future work to account for the role of such factors in the adaptation process.

An alternative explanation to internal models has been recently proposed based on a generalized version of the equilibrium-point hypothesis. This model suggests that movements are planned using geometric variables ultimately related to muscle activation thresholds (Feldman 1986; Feldman et al. 1995, 1998). Planning an endpoint trajectory is assumed to be associated with specifying an equilibrium trajectory for the endpoint and then translating this equilibrium trajectory into control variables for individual joints and muscles. The process of mapping an equilibrium trajectory to muscle control signals has not been well developed (Feldman et al. 1995). We suggest that at this level of processing control signals, the muscle redundancy affords the controller a possibility to modify stability properties of the planned action. This may be reflected in changes in the structure of variability analyzed at the muscle or joint level. We propose, therefore, that adaptation is characterized by two processes. First, there is an attempt to generate a new equilibrium trajectory of the endpoint given the novel external conditions. Second, variability of joint configurations that do not affect the endpoint trajectory is allowed to increase to facilitate search for new optimal solutions. After practice, the system returns to a more limited set of solutions, but unlikely to a single optimal solution (based on the finding that there is always higher V_UCM than V_ORT). This can be understood by recognizing that a given UCM is specific to a particular controlled variable, e.g. hand position. All solutions within the UCM lead, in this case, to the same hand position. However, it is likely that the control of other variables (represented by a different UCM) is also important for optimal adaptation (see discussion above). Thus, certain regions of a UCM related to hand position control may not be ideal with respect to control of other important variables despite yielding an identical hand position. Extended practice, therefore, will likely lead to a reduction of both variance components, V_UCM and V_ORT, which in the present context may lead to a similar relationship as in the original null field condition.

In summary, the current study demonstrates that adaptation of reaching to a novel dynamic environment is associated with an increase in the use of equivalent joint combinations to achieve a stable hand path. Moreover, this increase tended to be maintained even after re-adaptation to the null field, at least for the number of trials studied in this experiment. Taken together, these results provide further evidence that the use of equivalent solutions to joint coordination, which reflects flexibility of coordination processes, is a typical feature of the control system and that this feature is enhanced when the system is forced to adapt to novel dynamics (compare these results, for example, with those of Scholz et al. 2002 for a very different task). These results would appear to be inconsistent with the likely predictions of an account of adaptation based on learning a detailed model of the dynamics of limb–environment interaction (Davidson and Wolpert 2005; Hwang and Shadmehr 2005). Future iterations of internal models of adaptation will need to account for the differential changes in joint variance, i.e. the use of flexible solutions to joint coordination by the control system, observed in this study.