Antifreeze Proteins at the Ice/Water Interface: Three Calculated Discriminating Properties for Orientation of Type I Proteins

Abstract

Antifreeze proteins (AFPs) protect many plants and organisms from freezing in low temperatures. Of the different AFPs, the most studied AFP Type I from winter flounder is used in the current computational studies to gain molecular insight into its adsorption at the ice/water interface. Employing molecular dynamics simulations, we calculate the free energy difference between the hydrophilic and hydrophobic faces of the protein interacting with ice. Furthermore, we identify three properties of Type I “antifreeze” proteins that discriminate among these two orientations of the protein at the ice/water interface. The three properties are: the “surface area” of the protein; a measure of the interaction of the protein with neighboring water molecules as determined by the number of hydrogen bond count, for example; and the side-chain orientation angles of the threonine residues. All three discriminants are consistent with our free energy results, which clearly show that the hydrophilic protein face orientations toward the ice/water interface, as hypothesized from experimental and ice/vacuum simulations, are incorrect and support the hypothesis that the hydrophobic face is oriented toward the ice/water interface. The adsorption free energy is calculated to be 2–3 kJ/mol.

INTRODUCTION

Molecular dynamics computer simulations of a Type I fish kinetic ice inhibitor protein (known as antifreeze protein (AFP)) at the ice/water interface are employed to provide new insight into the unique molecular properties that determine AFPs' ability to inhibit ice growth at the ice/water interface. Since their discovery 35 years ago (1), there has been a growing interest in the various families of AFPs, antifreeze glycoproteins (AFGP), and their mutants. They are structurally diverse families of proteins that protect polar fish, insects, and plants from freezing in cold environments, where the environmental temperature is below the freezing point of biological fluids. These proteins have the unique property of kinetically inhibiting ice growth by accumulating on the water side of the ice/water interface. The melting temperature of the ice crystal is unchanged at 0°C whereas the temperature for further ice growth is lowered. The resulting difference in temperature between the ice crystal growth and the normal melting point of the ice crystal in the presence of these biomolecules is referred to as thermal hysteresis (2). The presence of this hysteresis indicates that the mechanism is noncolligative. For some species, the observed temperature lowering can be as high as 500× that of a colligative salt on a molal basis. This unique noncolligative property of these biomolecules is used by nature to assist fish, insects, plants, and bacteria for cold environment survival.

To understand how antifreeze proteins interact with ice and thereby decipher the underlying molecular mechanism, various experimental approaches have been pursued. These include ice-etching studies (3), site-directed mutation studies (4–11), and structural studies including NMR (12–14), Fourier transform infrared spectroscopy (15), and x-ray (16,17). The NMR and x-ray experiments have provided three-dimensional structural details of these proteins in the solution phase. They show that AFP Type I from winter flounder (HPLC6), which is an alanine-rich (60%) 3–5 kDa protein with an 11 amino acid repeat (TA₂NA₇), has an amphipathic α-helical structure (16) in which all polar residues with the exception of one Glu-Lys salt bridge are located on one side of the helix. The residues at the i, i + 11 positions are collinear and spaced 16.5 Å apart. The ice etching studies (3) have demonstrated that this protein is located on the (2 0 1) ice plane along the [1 1 0 2] direction. The hypothesis was put forward that the repeat distance of the water molecules in the crystal lattice of ice along this direction is 16.7 Å would match the i, i + 11 spacing of the residues in the idealized α-helical protein. This distance match has been used to explain the interaction of the protein to the (2 0 1) ice plane. Site-directed mutagenesis studies have identified the face of the protein that faces the ice in the ice/water interfacial region. Although, initial studies (9) proposed that the protein face composed of Thr and Asx residues interacted with the ice, recent studies have shown that the protein face interacting with ice is composed instead of Thr and Ala residues (5,10) (see Fig. 1). These and related theoretical and structural studies have also shown that hydrophobic interaction between the protein and the ice/water interface is a more critical element of the mechanism of AFP than hydrogen bonding as was proposed previously (4–7). A detailed description of these approaches is available in a review by Yeh and Feeney (18). Although much has been learned from the different experimental studies, certain aspects of the molecular mechanism of the AFP-ice interaction are not directly accessible using experimental solution phase approaches. To better understand the molecular aspects of ice-protein interaction, a variety of research groups have performed molecular modeling and biomolecular simulation studies of the various interactions involved in the water/protein/ice system.

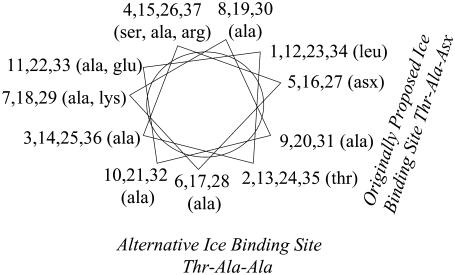
FIGURE 1.

Helical wheel representation of the protein. This representation shows the i, i + 11 repeat of the protein. The residue numbers are marked along with the residue composition. The originally proposed Thr-Ala-Asx “ice-binding” face is shown at right, whereas the newly proposed Thr-Ala-Ala face is shown at the bottom.

The first molecular dynamics studies were independently reported by two groups at CRYO92 (19,20). Haymet and Kay (19) simulated HPLC6 in a periodically replicated box of water using Biosym software and the cvff force field (21). In contrast, McDonald et al. (20,22) reported a similar simulation using the CHARMM19 force field (23). Their work was later extended to a simulation of the protein at the ice/water interface rather than the ice/vacuum interface (24). Additional molecular dynamics studies using the AMBER force field (25), which included solvent water at zero K, supported the separation distance of the threonine hydroxyls close to 16.7 Å and also indicated a number of other hydrogen bonding features involving Asp and Arg that assist in stabilization of the helical structure (26). Other molecular dynamics simulations examined HPLC6 (27,28) and mutants (28). Simulations of Type II (29) and III (30) AFP in water have been reported. In all the protein-in-water simulations to date, a clear understanding of the molecular mechanism by which these proteins operate has not emerged.

The first modeling study of HPLC6 (31) was an in vacuo energy optimization of the protein using the ECEPP/2 force field (32). Using the energy-minimized structure and the results from Knight's etching experiments, a mechanism was proposed wherein the polar residues of the protein form hydrogen bonds with the ice surface. Independently Lal et al. (33), using the COMMET software, proposed that the high affinity of the winter flounder protein for the (2 0 1) plane derives mainly from the steric compatibility between this plane and the protein molecule, giving rise to a manyfold increase in the van der Waals component of the surface/molecule interaction energy. Wen and Laursen (34), using the CHARMM19 force field (23), proposed that the face of the protein “binding” to the ice composed of asparagine, threonine, and leucine. Madura et al. (35) using CHARMM modeled the right-handed and left-handed helices on the (2 0 1) plane. On the basis of those calculations, it was shown that there are stereospecific sites that the protein can recognize on the ice surface. Combining ice-etching experimental results and modeling efforts, Wierzbicki et al. (36) reported on the interaction of shorthorn sculpin antifreeze protein to the (2 0) plane. They proposed that the helix backbone matches the ice corrugation and that the spacing of the lysine side chains match the channels on the (2 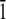0) plane. Recently, Dalal and Sönnichsen have reported upon a Monte Carlo rigid body docking study of HPLC6 on various ice planes (37). This study shows that although van der Waals interactions are a major source of ice-protein interactions, they cannot be used to completely explain the experimentally observed specificity.

Following the work on the Type I AFPs, further vacuum/ice modeling has been reported for the interaction of the Type II (29) and Type III (30) proteins on their respective ice planes. The conclusions from these simulations are that recognition relies upon the contoured fit of the protein backbone to the ice surface corrugation, whereas the interaction is through threonine/serine and lysine residues that create a hydrogen bond network between the protein and ice surface. Recently, Wathen et al. (38,39) employed a combination of molecular mechanics with statistical techniques to study large systems. Based on these studies, the authors proposed that the inhibitor effect of AFP depends upon the irreversibility of the protein attachment and on the ice-binding position rather than ice-binding strength (38,39). Although the results from these efforts have provided models and initial insight into the interactions between the AFP and ice (discussed in greater detail below), these models neglect the influence of explicit waters of solvation, which prohibits fully valid conclusions regarding the AFP mechanism.

Since 1987 (40), the nature of the ice/water interface has slowly been elucidated through experimental and computational efforts (41–46). Experimentally the ice/water interface has been examined using ellipsometry (47), dynamic light scattering (48), and second harmonic generation (49,50) methods. Computationally, several simulations have been done on the ice/water interface. In 1987, Karim and Haymet (40,42,51) published the first simulations of the basal ice plane/water interface, using the rigid molecule intermolecular water potential functions TIP4P (52) and SPC (53). These simulations yielded several important ideas. The most important finding was that the ice/water interface was a diffuse interface with a width of ∼10–15 Å thick (40,42). A second observation was that the different water models yielded different melting temperatures that are significantly different from the experimental melting temperature of 273 K. For example, the TIP4P model yielded a melting temperature of 240 K, whereas for the SPC model the melting temperature was 200 K (51).

Hayward and Haymet (43,54,55) have improved these ice/water interface calculations to four different interfaces of relevance to the Type I antifreeze proteins, for a modified flexible central force potential model. These simulations appear to place the melting temperature for the modified central force model around 280 K. More importantly, the interfacial region is observed to be dependent on a variety of order parameters such as average density, translation order, self-diffusion, and rotational orientation.

Recently Bryk and Haymet have studied the ice/water interface to understand the change in charge homogeneity at the interface for the SPC/E model (56). This study shows that the window average charge density has strong oscillations in the ice/water interface. The periodicity of these oscillations reflects the disordering of ice layers perpendicular to the interface. The authors proposed that these charge inhomogenities provide a mechanism for recognition of specific ice/water interfaces by solutes, provided they have appropriate charge distribution. Thus, different antifreeze proteins (with different charge distributions) would interact with different ice/water interfacial regions.

These findings pertaining to the ice/water interface clearly demonstrate that the realistic treatment of the process of adsorption of antifreeze molecules to ice cannot be done with the molecules in the ice confined to rigid lattice positions, since a rigid ice surface at the ice/water interface simply does not exist.

Three molecular dynamics studies of the ice/AFP Type I/water system have been reported to date. In the first, McDonald et al. (24) carried out 100 ps of molecular dynamics (MD) simulation. They concluded that there was significantly increased contact between the peptide and surrounding water molecules in comparison to the behavior of the AFP in bulk water due to the formation of strong ice/peptide hydrogen bonds. They also noticed a significant bend in the peptide's helical structure. Finally, in their simulation the four Thr side-chain hydroxyl groups faced away from the interfacial region, suggesting a mechanism other than interaction of the protein to the ice by the polar Thr groups. In another study, Cheng and Merz (28) also performed MD simulations on the ice/AFP/water system. In this study they reported 200 ps of MD simulation of the water/protein/ice system at 300 K and they demonstrated a relation among “binding energy”, the number of hydrogen bonds, and the activity. They observed that the higher number of hydrogen bonds leads to greater antifreeze activity. They did not report any bending of the peptide's helical structure. In both simulations (27,28) the ice molecules were kept fixed. Recently we have reported 500 ps of a MD simulation of the water/protein/ice system in which the molecules in the ice phase were not constrained (57). We observed that there was no difference in the number of hydrogen bonds when the protein was in water compared to when the protein was at the ice/water interface with the Thr-Ala-Asx face of the protein facing the ice, consistent with the hydrophobic mechanism.

In recent MM and MD studies (58) on Tenebrio molitor AFP (TmAFP), the authors have proposed that the regularly arrayed water molecules that remain associated with TmAFP facilitate initial stages of ice recognition and binding. Upon the final formation of the AFP-ice complex, the departure of the water molecules enables a better two-dimensional match between TmAFP and ice. However, in these studies the authors held the ice lattice rigid, creating a sharp, artificial ice/water interface.

Initially it was believed that the hydrogen bonding between the protein and ice drives the interaction between them. Consistent with this hypothesis, it was also proposed that the ice “binding” face of the protein consists of polar residues Thr and Asx. However mutation studies have shown that the hydrophobic interactions and not hydrogen bonds drive the interaction between protein and ice (4–7). Based on their mutation studies Baardsnes et al. (10) recently proposed that the “ice-binding” faces of the protein is not the previously thought Thr-Ala-Asx face but rather a more hydrophobic Thr-Ala-Ala face. The two ice “binding” faces of the protein are highlighted in the helical wheel representation of the protein shown in Fig. 1.

A study by Graether et al. (13) and other studies (59–61) suggest that the ice-protein complementarity is an important factor in determining the interaction between the ice and the protein. A recent review (62) depicts the AFPs “binding” to ice as a receptor-ligand interaction. They propose that the structural match is important and that the protein “binds” irreversibly to the ice. This hypothesis has been the predominant hypothesis in the field until recently. An alternate hypothesis originally proposed by Haymet (5) and reported by (57,63,64) suggests that the protein accumulates at the ice/water interfacial region and it is the protein that shapes the ice around it, rather than recognizing a distinct ice surface.

In summary and based on the available studies to date, a consistent hypothesis emerges that the Type I winter-flounder AFP is located at the (2 0 1) ice/water interfacial region primarily due to hydrophobic interactions between the hydrophobic face of the protein and ice. To obtain further molecular insight into the interactions of AFPs in the interfacial region, we have simulated an ice/water interface with: a), Thr-Ala-Asx face of the protein facing the ice and b), Thr-Ala-Ala face of the protein facing the ice. We have calculated the potential mean force (PMF) profile for moving these two faces of the protein from ice/water interface to bulk water. We also performed further equilibrium simulations of these faces of proteins near ice and compared those to the simulation of protein in bulk water and identified molecular properties that distinguish between the two faces of the ice. Calculations of water molecules organization at both Thr-Ala-Asx and Thr-Ala-Ala faces of AFP were also performed, and significantly different types of hydration of these faces were identified.

Computational methods

The system of two (2 0 1) ice/water interfaces (120 × 76.25 × 56.1 Å) was built with the ice slab of 5313 water molecules and two water boxes, each of 5646 water molecules. The TIP3P (52) water model was used for both phases of water. Electrostatics interactions were evaluated using the Ewald summation technique (65–67), while van der Waals interactions were smoothly switched off at a value of 11.0 Å. All bonds involving hydrogen were constrained using the SHAKE (68) algorithm. Periodic boundary conditions were used, and all atoms were free to move during the simulation. The system was initially thermalized to 165 K using the NVT (Berendsen temperature coupling algorithm) ensemble and then equilibrated for 500 ps using the NVE ensemble. 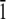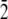At this point the winter flounder AFPs were placed within the (2 0 1) ice/water interfaces oriented in the[ 1 0 ] direction. The initial position along the [ 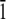1 0 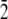] direction, for the Thr-Ala-Asx orientation, was taken to be where the threonine residues matched the lattice positions of ice water oxygen positions. For the Thr-Ala-Ala orientation, the helix was initially positioned along the [ 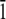1 0 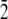] direction as in the Thr-Ala-Asx, except the helix was rotated about the helix axis so that the Thr-Ala-Ala face was oriented facing the ice. All water molecules within 2.5 Å of the protein were removed. A schematic of the system is shown in Fig. 2.

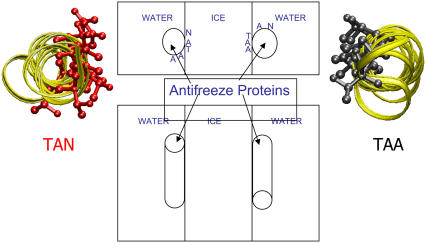
FIGURE 2.

Schematic of the model system. This figure shows the water/ice/water system with the antifreeze proteins. In the top view the positioning of the proteins can be observed. The protein placed in the left ice/water interfacial region has the Thr-Ala-Asx face of the protein facing the ice. The protein with the Thr-Ala-Ala side facing the ice is placed in the right ice/water interfacial region. The side view shows the antiparallel placement of the proteins relative to each other. For both the proteins the ribbon view is presented on the sides with the ice facing residues shown in stick representation.

The ice/AFP/water system was then minimized for 500 steps by steepest descent to relax any bad water-helix interactions. A 2-ns NVT (temperature = 165 K) simulation was run at this point using NAMD (69). Trajectory data were saved every 1 ps during these simulations. Data from the last 1 ns were used for analysis. Next the proteins were translated 0.25 Å along the z-direction, which is perpendicular to the ice, toward the bulk water. The simulation (minimization and NVT) was repeated for another 2 ns. This process was repeated until the proteins were 10 Å away from their original positions. For each simulation, the center of mass position for the proteins at each time step was calculated using CHARMM (23) and binned in 0.2 Å bins to generate a histogram. Overlapping histograms from these 41 simulations were matched, based on the procedure by Pangali et al. (70,71). The overlapped histograms were then used to calculate the PMF profile, i.e., free energy as a function of distance from the ice surface. Because the overlap between the histograms was not unique, histogram matching was performed in four unique ways to generate four PMF profiles. These profiles were averaged and then smoothed using splines to yield the final profile.

The PMF profiles yielded the difference in free energy between the two faces of the protein facing the ice. However, the molecular mechanism of this difference is not inherent in these profiles. To obtain a molecular picture, we ran equilibrium NVE molecular dynamics simulations in which the two faces of the protein were oriented toward the ice at a distance from the ice, which was the minimum in the PMF curves. The data collected from these simulations was used to compare the results from simulations of the protein in the bulk water. This system was equilibrated for 100 ps, and then simulated for 900 ps under NVE conditions. The molecular dynamics code used to run these simulations was DL_POLY 2.12 (72). The data were analyzed over the last 500 ps of the simulation. A snapshot of the system from the molecular dynamics simulation after 50 ps is shown in Fig. 3.

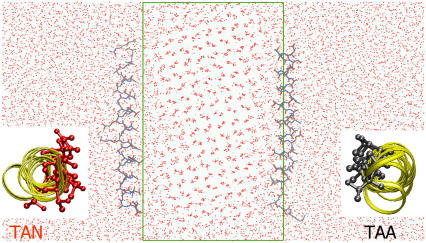
FIGURE 3.

Snapshot of the system. The red dots show the oxygen atoms of the water and ice molecules. The box shows the original dimensions of the ice slab. The proteins are shown in stick configuration. Inset pictures show the view of the protein from the terminus. The protein on the left is shown from N- to C-terminus, whereas the protein on the right is shown from C- to N-terminus. The residues facing the ice are highlighted in stick representation.

For the purpose of calculation of AFP hydration of the MD snapshots taken at 1 ps intervals from 500 ps ice/water interface simulations, the water oxygen atom positions were binned into a 100 × 100 × 100 grid with 0.5 Å grid spacing. For the Thr-Ala-Ala protein face, the reference frame for the grid was based on a root mean square (RMS) fit to residues 17, 21, and 24 (atoms C, CA, N). For the Thr-Ala-Asx protein face, the reference frame for the grid was based on a RMS fit to residues 20, 24, and 27 (atoms C, CA, N). This places the binding faces in the same frame of reference. In each case, the sequence of interest was centered and all solvent imaged appropriately (such that the Thr-Ala-Ala or Thr-Ala-Asx AFP orientations were placed at the center of the periodic box and fully solvated).

RESULTS

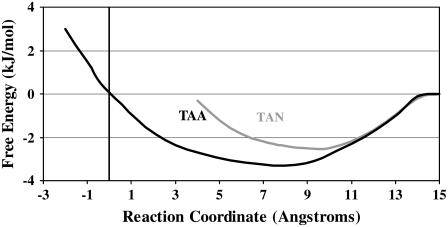
Fig. 4 shows the PMF profile of the AFP Type I moving through the ice/water interfacial region into the liquid water phase. In our previous simulation of the same system (57), we calculated the diffusion coefficient profile of the ice/water interface. We took the midpoint of such a profile to be our reference point, shown as zero on the x axis. The reaction coordinate is the distance of the protein's helix axis from this reference point. The y axis shows the PMF in kJ/mol. We have taken the free energy of the protein in bulk water as our reference (0.0 kJ/mol). The resulting PMFs (Fig. 4) show that the protein interacts more favorably within the ice/water interfacial region when the Thr-Ala-Ala face is oriented toward the ice, compared to the Thr-Ala-Asx face. Moreover, the free energy profiles show that the protein is closer to the “ice” in the ice/water interfacial region when the Thr-Ala-Ala face is oriented toward the ice as opposed to the Thr-Ala-Asx face.

FIGURE 4.

Potential of mean force profile. This figure shows the potential of mean force profile, i.e., free energy, of the proteins as a function of distance from the midpoint of the ice/water face. The x axis represents the distance between the center of the protein helix and the midpoint of the ice/water interfacial region. The midpoint of the interfacial region is defined by the inflection point of the diffusion coefficient profile (43). The y axis represents the free energy of interaction between the protein and the ice/water interfacial region in kJ/mol. The free energy of interaction between the protein and bulk water is set at the reference value of 0 kJ/mol.

Our results are consistent with the previous experimental results and indicate that the hydrophobic Thr-Ala-Ala face of the protein points toward the “ice” within the interfacial region. Comparison of the equilibrium NVE simulations for the two faces of the protein oriented toward the “ice” to those of the free protein in bulk water revealed three distinct molecular properties that discriminate between the two orientations.

Close contacts

To further analyze the environment around the protein, we have calculated the close contacts between the protein and any water molecule. Normally, we would denote this number the average number of “hydrogen bonds” between the protein and the surrounding water molecules in the ice/water interfacial region. However, in this field, the concept of hydrogen bond has been reserved for the calculation of contacts between the (unrelaxed) ice/vacuum interface and particular residues on one assumed face of the nonvibrating protein. Hence, to avoid confusion here we use the terminology “close contacts” to indicate that the interaction is occurring between every water molecule adjacent to protein, in the equilibrated simulation at the melting point of the model ice. Our calculations are averaged over 500 ps (Table 1). A close contact distance cutoff of 3.5 Å and an interaction angle cutoff of 120° were applied in examining the protein/surrounding water molecule interactions. These values are identical to those used by McDonald et al. (24) and therefore allow us to directly compare the results. From our previous simulations (57), we found that the average number of close contacts for the proteins to the water molecules in the interfacial region is 79 (Table 1). In that simulation, the Thr-Ala-Asx face of the protein was facing the ice. In our current simulations, we obtain the values of 81 ± 2.0 in similar conditions and 93 ± 1.8 when the Thr-Ala-Ala face of the protein is facing the ice in the interfacial region. Similar analysis shows that when the protein is solvated in bulk water, there are 79 ± 4.0 close contacts between protein and bulk water. Thus it appears that there is no significant increase in the total number of close contacts between the protein in water and the protein at ice/water interface when the Thr-Ala-Asx face of the protein is facing the ice. However, when the Thr-Ala-Ala face of the protein is facing the ice, we get a gain of 13 close contacts when the protein moves from the water into the interfacial region. Table 1 shows that the total number of hydrogen bonds in the interfacial region compare well with the obtained results by McDonald et al. for their protein in water (22) and the protein in ice/water interface (24) simulations, which are 81 and 75, respectively. We have also estimated similar numbers for other studies, based on the published plots (26,28). We obtained values of 77, Jorgensen et al. (26), and 75, Cheng and Merz (28), for the protein in water simulations and 78 for protein in ice/water interface (28).

TABLE 1.

Number of hydrogen bonds between AFP and water molecules in different systems and comparison with literature values

	Wat/AFP	Wat/AFP/Ice TAN	Wat/AFP/Ice TAA
New	79 ± 4.0	81 ± 2.0	93 ± 1.8
Previous	–	79*	–
McDonald	75†	–	81‡ (not TAN)
Jorgensen§	77	–	–
Cheng¶	75	78	–

^*Dalal et al. (57).

^†McDonald et al. (22).

^‡McDonald et al. (24).

^§Jorgensen et al. (26).

^¶Cheng and Merz (28).

We also calculated the contribution of different residues to the total number of close contacts. The majority of the difference in the number of contacts between the two faces arises from the fact that the polar residues form a greater number of contacts with the water molecules when the Thr-Ala-Ala face of the protein is facing the ice. The terminal residues account for the majority of the difference (6/13) in the close contacts.

Contact surface area

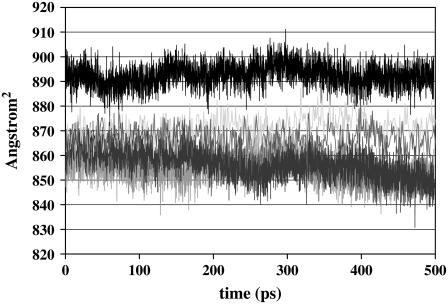
Fig. 5 shows the profile of the contact surface area of the protein. The contact surface area was calculated using Lee and Richards algorithm (73) implemented in CHARMM (23). In this algorithm a 1.6-Å sphere is rolled around the system defining a contact surface around the system. We observe that the contact surface area of the protein is the same when the protein is in water (857 ± 6.1 Ų) or when the Thr-Ala-Asx face of the protein is facing the ice in the ice/water interfacial region (854 ± 5.1 Ų). We also calculated a similar surface area from our previous protein/ice/water calculations (57) in which both the proteins had Thr-Ala-Asx face of the protein facing the ice. The calculated values (877 ± 6.3 Ų and 865 ± 5.7 Ų) are similar to those obtained from our current simulation when Thr-Ala-Asx face of the protein is facing the ice. However, there is a larger amount of protein contact surface area (892 ± 4.5 Ų) when the Thr-Ala-Ala face of the protein faces the ice.

FIGURE 5.

Surface area. The contact surface area of the protein in different environments as a function of simulation time (calculated using the Lee & Richards method using a 1.4-Å probe) is shown. The surface area of the protein solvated in water is shown in dark blue. The surface area of the protein in the ice/water interfacial region with Thr-Ala-Asx face of the protein facing the ice is shown in red, and with Thr-Ala-Ala face of the protein facing the ice is shown in black. The other two lines show the surface area of the protein from our previous simulations when Thr-Ala-Asx face of the protein is facing the ice.

Side-chain conformations

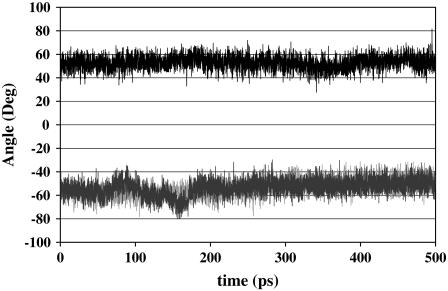
Analysis of the side-chain angles of Thr residues leads to further differences. For the Thr-2 residue near the N-terminus, when the Thr-Ala-Asx face of the protein is facing the ice in the interfacial region, the χ₁ dihedral is −50°. A similar value is observed when the protein is in water. However, when the Thr-Ala-Ala face of the protein is facing the ice then the χ₁ dihedral is +50° (Fig. 6). For the other Thr residues the χ₁ value is ∼180° for both the proteins (see Supplementary Material). An NMR study (12) has demonstrated that in solution near freezing temperature, for the Thr χ₁ dihedral there is a preference for −60° and +60° over 180°. Between −60° and +60°, there is a slight preference for −60°. One of the reasons for the discrepancy between our study and the NMR study could be the fact that in the NMR study the protein was in the solution, whereas in this study the protein is in the ice/water interfacial region. The aqueous environment is substantially different than that of ice/water interfacial region.

FIGURE 6.

χ₁ of Thr-2. The side-chain angle χ₁ of Thr at position 2 (Thr-2) is shown as a function of time. The χ₁ of Thr-2 when the protein is solvated in water is shown in blue, with Thr-Ala-Asx face of the protein facing the ice shown in red, and with Thr-Ala-Ala face of the protein facing the ice shown in black.

At this point we would like to point out that an earlier study (37) of the protein at the ice/vacuum interface did not find the interaction of the Thr-Ala-Ala face of the protein with the ice to be more favorable than the Thr-Ala-Asx face. In the ice/vacuum calculations the Thr-Ala-Asx face is more favorable. In comparison, the current results show that some of the properties of the interaction between the protein and the ice/water interfacial region are more favorable when the Thr-Ala-Ala face of the protein faces the ice as opposed to the Thr-Ala-Asx face. These results underscore the importance of performing full system, i.e., protein/ice/water simulations, and not generalizing the results from protein/ice simulations performed in vacuo.

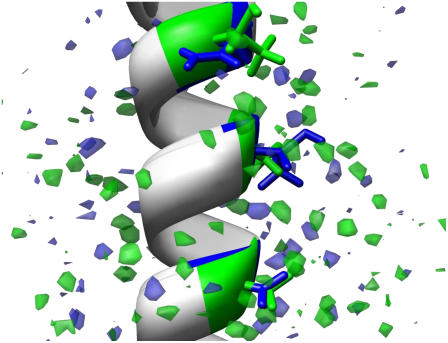
Fig. 7 shows a comparison, at an equivalent level of hydration, of the two superimposed ice-water interfaces containing the AFP with the Thr-Ala-Asx and Thr-Ala-Ala faces oriented toward ice, respectively. In other words, the Thr-Ala-Asx oriented interface and its hydration are in the same reference frame as the Thr-Ala-Ala interface and its hydration. The former is in blue and the latter is in green. Clearly more green is seen in Fig. 7, and from the picture, contoured at equivalent grid occupancies (occupancy 35 or greater), significantly more density and more ordered hydration is evident around the Thr-Ala-Ala orientation than the Thr-Ala-Asx.

FIGURE 7.

Protein hydration difference maps. A comparison at an equivalent level of hydration for the two interfaces superimposed. The TAA face (residues 17, 21, 24) and its hydration are in the same reference frame as TAN (residues 20, 24, 27). The former is in green, and the latter is in blue. The TAN interface shows much less ordered hydration than the TAA.

The results presented above are consistent with our calculation of water hydration around the APF positioned in two different orientations with respect to water/ice interface. Bulk water occupancy (at 300 K) corresponds to ∼2.1 water oxygens per grid element (over 500 frames). The contour levels in Fig. 7 show hydration at 35 or more hits per grid element over the 500 frames sampled (or ∼16× bulk water density). A direct comparison to bulk hydration is not fully relevant in this case as ice is more rigid and therefore will not show a complete smearing over all grid elements. However, motion of the water relative to the positions of the key residues is evident as none of the grid elements show complete occupancy. The highest occupied grid elements have occupancies of 134 or 26.8% for Thr-Ala-Ala and 119 or 23.8% for Thr-Ala-Asx.

DISCUSSION

The study by Graether et al. (13) and other studies (59–61) suggest that the ice-protein complementarity is an important factor in determining the interaction between the ice and the protein. A recent review (62) depicts the interaction between AFP and ice as a receptor-ligand interaction. They propose that the structural match is important and that the protein “binds” irreversibly to the ice. However, the free energy of binding for a receptor-ligand interaction is >9 kcal/mol (9 kcal ∼ nM). Currently, we do not have experimental data on free energy of interaction between AFP and ice/water region. We predict that the free energy of “binding” per face interaction is much smaller. Furthermore, the hypothesis of a structural match between the protein and ice neglects one of the most important factors—liquid water. We propose that the AFPs' interaction with ice cannot be simply construed as a ligand-receptor interaction since the ice phase presented to the AFP is not a solid ice surface but rather an ice/water interface; i.e., the “receptor” cannot be clearly distinguished from the solvent. There is phase equilibrium between the ice and water, and the protein is immersed in this semisolid-semiliquid phase of the ice/water interface. The properties of this region have been studied (43,47,54,55), and they are in between solid ice and bulk water. The numbers of hydrogen bonds and the diffusion coefficient of the water molecules in this region change slowly from ice to water as seen in these results. The thickness of this interfacial region is 10–20 Å, and there is no distinct ice surface for the protein to recognize. It is quite conceivable, as we mentioned earlier, that as proposed by Haymet (5) and reported by other literature (57,63,64), that as the AFP proteins accumulate at the ice/water interfacial region, they facilitate ordering of liquid water into a specific surface of ice at its hydrophobic face. This hypothesis is not only consistent with our results but also with the properties of the ice/water interfacial region. Furthermore, as mentioned by Bryk and Haymet (56), solutes such as AFPs based on their charge distribution may recognize the charge inhomogeneity in the interfacial region.

It is important to point out that, in all the previous modeling studies in which the ice has been modeled as a static surface, the Thr-Ala-Asx face of the protein has been proposed as the “ice-binding” side. In a previous study involving in vacuo simulations of ice and protein, the Thr-Ala-Ala face was shown to be less favorable compared to the Thr-Ala-Asx face on the (2 0 1) plane. This study is the first study in which the system has been modeled as the ice/water interfacial region and multiple faces binding to the protein are compared. The current results show that some of the properties of the interaction between the protein and the ice/water interfacial region are more favorable when the Thr-Ala-Ala face of the protein faces the ice as opposed to the Thr-Ala-Asx face. This strongly suggests that the protein interacts more favorably within the ice/water interfacial region when Thr-Ala-Ala face of the protein faces the “ice” as opposed to the Thr-Ala-Asx face.

CONCLUSIONS

In conclusion, the results from our simulations shed some light into why the protein interacts with the “ice surface” within the interfacial region via Thr-Ala-Ala face rather than the Thr-Ala-Asx face. The PMF profiles show that the protein adsorbs more favorably at the ice/water interfacial region with the Thr-Ala-Ala face oriented toward the ice, compared to the Thr-Ala-Asx face. The properties of this interaction such as number of protein/interfacial region hydrogen bonds and the protein surface area are more favorable with the Thr-Ala-Ala face of protein facing the ice compared to the Thr-Ala-Asx face. The Thr side-chain dihedrals also behave differently in both cases. This study is the first to show the difference between the two faces of the protein. Most importantly we would like to stress that the results from ice/protein studies are relevant as long as one understands that these calculations most closely represent a vacuum/ice interface, and hence it is important to perform protein/ice/water simulations to get a more thorough understanding of the mechanism. These studies are a step in that direction. We propose that the hypothesis involving lattice match between AFP and ice needs to be modified. We believe that the mechanism is closer to the one postulated in the field of biomineralization, i.e., poisoning of the interface. We propose that the protein, by interacting with the ice/water interfacial region, “poisons” it and thus stops the ice from growing. Almost from the very beginning the postulated mechanism of antifreeze action relied upon a kinetic effect (74). The most recently published mechanism of action of AFPs as demonstrated in an elegant work in Sander and Tkachenko (75), depends on the kinetic pinning mechanism that requires that the AFPs directly interfere with the growing surface of ice right at the water/ice interface. Thus for the antifreeze mechanism to be effective, the AFP molecules must be located within the ice/water interfacial region in a very close proximity of growing ice crystal. Based on this study we are beginning to see the emergence of the following molecular picture regarding the mechanism of AFPs.

The AFP does not “bind” to the ice directly, but rather accumulates at the ice/water interface. Such behavior is consistent with the hypothesis that the protein functions via its conserved hydrophobic face and that it induces water ordering within the interface (Fig. 7). Subsequent favorable adsorption in such an interfacial region may then occur by lowering the water/ice interfacial energy on the side of the protein that faces the ice. In this study, for the first time, we have demonstrated that the mechanism responsible for orientation of AFP molecules at the water/ice interface necessary for their antifreeze activity, occurs by means of a mechanism that in essence resembles the hydrophobic solvation effect (76) involving the hydrophobic face of antifreeze protein. Using the potential of mean force calculations, we have shown that the Type I antifreeze protein from winter flounder approaches the ice/water interface facing the ice surface with its hydrophobic side to minimize the interfacial energy of interaction with the ice surface. Although energetically this is a very subtle effect since the calculated difference of free energy between the orientation of Type I AFP when facing the ice with its hydrophobic side versus the hydrophilic side is not very large, from the location of the free energy minima however (Fig. 4) one can see that, in the hydrophobic orientation of AFP toward ice, the AFP helix can approach ice much closely and thus participate in the kinetic pinning leading to its antifreeze activity (75). The subtlety of this phenomenon is quite remarkable. The entropic and enthalpic contributions, although separately may be quite substantial, may nearly cancel each other, leaving only a small free energy excess sufficient to orient the AFP at the water/ice interface (77). A very similar effect was discussed recently for the water binding to calcite where large enthalpic and entropic free energy terms of water binding to stepped (104) calcite surface nearly cancelled each other, leaving only small negative contribution to the total free energy (78).

In a recent article by Jorov et al. (77) a hypothesis was put forward that hydrophobic interactions are responsible for the preferable interaction between the hydrophobic side of the AFP and ice. Quite interestingly, in a very recently published work using the CHARMM molecular dynamics (79), this hypothesis has been investigated by analyzing the structure of the first hydration shell of the wild-type winter flounder APF (TTTT) and its two antifreeze active (AAAA and VVVV) and one inactive (SSSS) mutants at the Thr residue positions. The analysis shown in this work revealed significant differences in the hydration structure for these four AFP I proteins. In this work it has been proposed that for the wild-type (TTTT) and both active (AAAA and VVVV) mutants, the polar groups on the ice binding side of the AFP have a very ice-like hydration, whereas for the inactive (SSSS) mutant, its polar groups exhibit standard polar-like hydration (79). According to Yang and Sharp (79) the more ice-like hydration structure of the binding side of the active types of winter flounder antifreeze protein promote binding with ice itself, and thus the hypothesis of the differences in the first hydration shell of the Type I antifreeze proteins from winter flounder could be used to explain the recognition and binding of these antifreeze proteins at the ice/water interface. In our work we show via the direct method of potential of mean force calculations that indeed the AFP would orient itself at the ice/water interface with its hydrophobic side facing the ice.

Finally, we would like to state that the in vacuo ice-protein models do not represent the full system, and it is important to perform full water/protein/ice simulations. With the recent advances in computational technology it is possible to perform such full system simulations.