Abstract
Recent experimental studies suggest that lactate dehydrogenase (LDH) binds its substrate via the formation of a LDH/NADH·substrate encounter complex through a select-fit mechanism, whereby only a minority population of LDH/NADH is binding-competent. In this study, we perform molecular dynamics calculations to explore the variations in structure accessible to the binary complex with a focus on identifying structures that seem likely to be binding-competent and which are in accord with the known experimental characterization of forming binding-competent species. We find that LDH/NADH samples quite a range of protein conformations within our 2.148 ns calculations, some of which yield quite facile access of solvent to the active site. The results suggest that the mobile loop of LDH is perhaps just partially open in these conformations and that multiple open conformations, yielding multiple binding pathways, are likely. These open conformations do not require large-scale unfolding/melting of the binary complex. Rather, open versus closed conformations are due to subtle protein and water rearrangements. Nevertheless, the large heat capacity change observed between binding-competent and binding-incompetent can be explained by changes in solvation and an internal rearrangement of hydrogen bonds. We speculate that such a strategy for binding may be necessary to get a ligand efficiently to a binding pocket that is located fairly deep within the protein's interior.
INTRODUCTION
Ligand binding is fundamental to many life processes. An enzyme has to bind its substrate to carry out chemistry. Hormones have to bind their cognate receptors to transmit a signal. Cofactors and allosteric effectors have to find the right binding site to modify function. Drug molecules have to bind to a target, and resistance to a drug is sometimes due to mutations that allow the target to not be bound as effectively to the drug (1–3). Clearly, viewed on a fundamental level, the process of ligand binding is as important as what happens after the ligand binds its receptor. Proteins are inherently flexible by virtue of the fact that the forces that hold together the tertiary structure are weak noncovalent forces. At physiological conditions, there is enough thermal energy available to cause the weak interactions to break and reform. The motions that are the consequence of such rearrangements are essential for function such as ligand binding and catalysis in enzymes (4). However, the dynamics of how a ligand actually moves from solution to its proper position within a protein remains a topic of active investigation.
We probe here the question of how an enzyme binds its substrate at the earliest stages of binding. We specifically examine the lactate dehydrogenase (LDH) system since recent experimental work (5–7) has provided some insight into the formation of the protein-ligand encounter complex. Lactate dehydrogenases catalyze the interconversion of lactate and pyruvate. Lactate formation is achieved in the enzyme by a direct transfer of a hydride ion from the pro-R face of the reduced nicotinamide group of NADH cofactor to the C2 carbon of pyruvate. LDH accelerates the pyruvate to lactate solution reaction by some 14 orders of magnitude (8,9).
Structures of LDH from a range of species are well represented in the Protein DataBank. A high level of structural similarity is apparent despite significant differences in primary structure between each of these enzymes. The biological unit is usually a tetramer with 222 symmetry. Each monomer forms a bilobal structure of two domains. The nucleotide-cofactor binding site is in the form of a Rossmann fold and consists of a pair of β-α-β-α-β motifs. Adjacent to the nicotinamide group of the cofactor is the substrate-binding pocket. It is formed at the interface with the adjoining mixed α/β substrate-binding domain (10). Experimental results indicate no cooperativity between/among the subunits of mammalian LDHs so each subunit structure is an independent snapshot of the enzyme in its various thermally accessible conformations.
The binding of substrate to LDH is obligatorily preceded by the formation of the LDH/NADH binary complex. The substrate is bound somewhat deep, ∼10 Å, into the LDH/NADH·substrate ternary complex. The active site contains a catalytically crucial His193 and Arg106 (numbering from the human heart enzyme), and the preformed pocket also “solvates” the carboxylate group of the substrate through the Arg169 side chain. The rate-limiting step in the turnover of LDH is not the chemical hydride transfer step but rather the final closure of a surface group of residues (98–110), often called the mobile loop over the substrate binding pocket, occurring in a timescale of 1–10 ms (5,11,12).
Recent experimental studies have been able to characterize the binding pathway of a substrate mimic to LDH/NADH utilizing temperature-jump relaxation methods (5–7,13) including rates, identification of specific structural changes, and thermodynamics. Of most interest for our study is the initial event: the formation of the LDH/NADH·substrate(mimic) encounter complex. These studies indicate that the LDH/NADH complex is populated in solution by a range of conformations such that some are binding-competent and some are not competent. The transition between the competent and noncompetent has the unusual thermodynamic properties suggestive of substantial heat capacity (5) ΔCp = 790 ± 116 cal/mol K. In transitions involving proteins, a positive ΔCp has been traditionally taken as a signature of exposure of hydrophobic residues to solvent (14,15) and/or changes in the hydrogen-bonding properties of water molecules (16).
A prominent difference between structures of the apo-enzyme and the LDH/NADH·substrate (ternary) complex from different species is the position of the mobile loop that extends into solution in experimental structures of the apoenzyme but is closed across the active center of the ternary complex in most species (17). An example of an open active site of a liganded form is that of ternary complex of human muscle LDH, wherein one of the monomers in the biological unit has a loop that extends into solvent (10). There is no consensus about the solution structure of the binary complex, although it has been suggested previously, based on the partially closed loop of an apo LDH, that the loop is in equilibrium between an open and a closed form when the enzyme is not bound to its ligand (18). It is generally believed that this loop opens to accept substrate for binding and closes to sequester the binding pocket from solvent and also introduce the key catalytic group, Arg106, into the active site in hydrogen-bonding contact with substrate.
Molecular dynamics simulation is a powerful tool for monitoring the structural evolution of biomolecules. Starting with a suitable model, one can obtain a time series of structures and the trajectory can be examined to look for interesting conformations that are not easily observed in solution experiments. In this article, we describe the computer simulation of the molecular dynamics of human heart LDH in the ternary and in the binary complex. The very high sequence similarity of this enzyme to pig heart LDH makes it a suitable model to understand the details that effect access to the active site. Such information is necessary to clarify the source of the anomalous heat capacity that was determined from ligand binding experiments that utilized pig heart LDH as reagent.
METHODS
Analysis of human muscle LDH structure in the Protein DataBank
From pure structural comparison, human muscle LDH is expected to share many common features with pig heart LDH since they are 74% identical (10). The structure of the ternary complex of human muscle LDH provides an instructive model to compare the loop-open and loop-closed conformation of a ternary complex. By deleting the coordinates of oxamate from the model, the structure is also an approximation of the open and closed form of the binary complex. The crystal structure (PDB entry 1I10) contains two biological units (two tetramers) in the crystallographic asymmetric unit. In each biological unit, there is a monomer (subunit) that has an active site that is open, its loop extending out to the solvent. The accessible surface area (ASA) of each subunit and the accessible surface area of individual residues in each subunit were calculated using a probe radius of 1.4 Å.
Preparation of simulated model from crystal structure
In amino-acid sequence, the human heart and pig heart isoforms of LDH are 97% identical so it is reasonable to assume conservation of both structure and mechanism in these enzymes. The structure of pig heart LDH bound to the coenzyme substrate analog (3S)-5-(3-carboxy-3-hydroxypropyl) NAD+ is available; however, this structure deviates the most in pairwise comparison of the known ternary complexes of pig and human LDH (10,19). It was decided to use the more recent and higher resolution structure, 2.1 Å, of the human heart isoform for further studies.
The binary complex of LDH with the cofactor NADH and the LDH/NADH·oxamate ternary complex were studied separately in this work. The initial coordinates of the biological unit of human heart LDH were obtained from Protein DataBank entry 1IOZ. This entry has coordinates for a tetramer of ternary complexes. To simulate the binary complex, the coordinates of oxamate were deleted from the structure file. What validates this approximation was the observed similarity in overall structure of the binary and ternary complex in the crystal structure of half binary-half ternary pig muscle LDH (11). It provides a useful comparison of stable structures of the same tissue isoform of LDH that have different active site occupancy, prepared using the same experimental condition and solved at the same resolution. The backbone RMSD of the two subunits for residues 20–331 was 0.566. The structures, however, show larger Debye-Waller factors in the binary complex for the loop residues and the domain it contacts in the closed loop form.
Hydrogens were added to the heavy atom coordinates using the HBUILD (20) command in the program CHARMM (21). The CHARMM all-atom parameter version 27 was used. The parameters for oxamate were determined by analogy to the closest templates in the topology file. Histidine-193 in the active site of human heart LDH was assigned a charge of +1, consistent with the known ionization state of this catalytic residue in the pyruvate to lactate direction. Waters in internal sites, in addition to the crystallographically resolved waters, were placed in the tetrameric assembly of the apo protein using the program Dowser (22). Any Dowser-assigned waters that overlap with the van der Waals sphere of crystal waters were deleted (i.e., when the distance between the oxygen atoms of two water molecules is closer than 2.8 Å).
Atomic clashes in the assembly were reduced, first by 50 steps of steepest-descent minimization while the heavy atoms were restrained with a harmonic force constant of 100 kcal/mol/Å2. This was followed by 500 steps of Adopted Basis Newton-Raphson (ABNR) minimization. The force constant was reduced to 50 kcal/mol/Å2 during the second ABNR minimization of 500 steps, and finally removed in the last 500 steps of ABNR minimization. This energy-minimized assembly was soaked in a cubic box of preequilibrated waters. To determine the cubic box dimension, the edge length was calculated by adding 16 Å to the longest dimension of the tetramer. This ensures that the solvent layer is at least 8 Å deep, when the center of the tetramer is placed in the center of the cubic box. Bulk waters that have oxygen atoms within 2.8 Å of the existing heavy atoms were deleted. The TIP3P model of water was used. To neutralize the system's charge, sodium ions were added to replace randomly selected bulk waters.
All covalent bonds with hydrogen were constrained to their parameter set values using SHAKE during all steps of the minimization and in all succeeding MD simulations. The long-range electrostatic interactions, computed with a dielectric constant equal to 1, and the van der Waals interaction, were handled with an atom-based shifting method to smoothly shift the force and the potential energy to zero at 12 Å. The nonbonded list was generated up to 14 Å and the list is updated whenever any atom moved >1 Å.
Simulation of molecular dynamics
Periodic boundary conditions were implemented in the simulation of the cubic box. The leap-frog algorithm was used in all simulations with a 2-fs integration timestep because high frequency X-H vibrations were constrained by SHAKE. The molecular dynamics of solvated ternary complex and binary complex were simulated separately; however, identical dynamics simulation protocols were implemented. The initial phase was heating for 20,000 steps of constant pressure MD. The temperature was increased from 200 K to 300 K by velocity scaling in increments of 10 K every 500 integration steps, with a constant pressure reference of 1 atm. After the last 10 K increment, the system temperature was checked every 2000 steps to ensure it is within 300 ± 5 K. The Langevin piston method (23) was used to maintain constant pressure using the following parameters for the algorithm: collision frequency = 20 ps−1, piston mass = 400 amu, and the piston was coupled to a temperature bath at 300 K. After additional 600 ps of CPT dynamics with velocity checking, the box dimensions were stable. The simulation box of binary complexes has equilibrated edge dimensions of (101.58 ± 0.04) Å and has a total of 107,110 atoms (28 Na+, 28,698 water molecules). The ternary system was a (101.5 ± 0.04) Å box that contained 106,846 atoms (32 Na+, 28,598 water molecules).
Analysis of trajectories obtained by MD simulation
The time-slice from 1.6 to 2.148 ns was analyzed to compare the average properties of the open and the closed subunit. By analyzing different subunits within the same time-slice, consistent length of equilibration was ensured. Hydrogen-bond occupancies within a trajectory slice were calculated using both distance and angle criteria. For each snapshot in the trajectory, a hydrogen bond was considered to exist between a donor hydrogen and an acceptor atom if the distance between them was ≤2.4 Å and the donor-hydrogen-acceptor angle was >130°. The number of solvent molecules within a certain radius was also calculated over a trajectory to report the average hydration. A similar calculation involving single snapshots was also carried out to report the instantaneous hydration number of the binary complex. Calculation of accessible surface area was carried out using a probe radius of 1.4 Å. Snapshots over a longer time window were used in the dataset for principal components analysis to capture all contributions to the structural transition during the duration of the simulated molecular dynamics. To implement principal components analysis of a subunit, the α-carbons of each frame of the subunit were least-squares-fitted to the starting structure. A snapshot was taken every 1 ps starting from 41 ps to 2.148 ns. The covariance matrix of the α-carbon atoms was then diagonalized.
RESULTS
Human muscle LDH structural data
The measured difference in accessible surface area between the open and closed conformation of human muscle LDH (Table 1) is used to estimate how much change in ASA is to be expected for the conformational change examined in this work. The human heart and human muscle LDH isoforms are of comparable size so this assumption is justified. By doing a residue-by-residue subtraction of the accessible surface area of two conformations of the same enzyme, ASAopen-ASAclosed, one can identify spots where solute/solvent rearrange during the conformational change. As shown in Fig. 1 derived from the structural model of human muscle LDH, the rearrangement is not local to the loop region (residues 98–110). Residues away from the loop become exposed and some are occluded from the solvent as a result of the conformational change.
TABLE 1.
Accessible surface area of each binary complex of human muscle LDH in the context of the tetrameric biological unit
| Subunit | Binary | Nonpolar | Backbone (N and O) |
|---|---|---|---|
| A | 9794 | 2190 | 884 |
| B | 9865 | 2272 | 894 |
| C | 9590 | 2228 | 911 |
| D | 10712 | 2483 | 938 |
The tetramer that was examined comprises LDH chains A, B, C, and D of PDB ID 1I10. The contribution from the nonpolar residues and the backbone N and O atoms were also calculated. ASA are reported in units of Å2. The most open and most tight binary complexes differ by 1122.53 Å2 in solvent exposure. For reference, the ASA of a solvent-exposed Ile is 80 Å2 and exposed Val has an ASA equal to 71 Å2 using a probe radius of 1.4 Å.
FIGURE 1.
Analysis of ASA in the crystal structure of human muscle LDH subunits. (A) Comparison of the residue-accessible surface area of the loop-open and loop-closed subunits. (B) Subtracting the loop-closed ASA from the loop-open ASA to identify hot spots of rearrangement. (C) Subtracting the ASA of residues in the loop-open ternary from the loop-open binary complex to highlight the residues that are shielded from the solvent as a result of ligand binding.
Molecular dynamics simulation of the binary and ternary complex
To augment the knowledge gained from static structure studies, a 2.148-ns molecular dynamics simulation of the solvated binary complex was performed to gain some understanding of the initial events that lead to the formation of a binding competent form of the binary complex. The structure of the binary complex that is obtained by deleting the coordinates of oxamate in the ternary complex is necessarily tight and the active site is not accessible to a ligand that is immersed in bulk solvent environment. Assuming that the initial structure of each of the four subunits is a physically realizable state of the binary complex in a biological milieu, molecular dynamics simulation of this system provides a time window to watch the evolution of the enzyme to a conformation that permits binding. A similar simulation of the ternary complex was carried out for comparison of the system's behavior in a different ligation state.
The active site loop fluctuates more in the binary complex
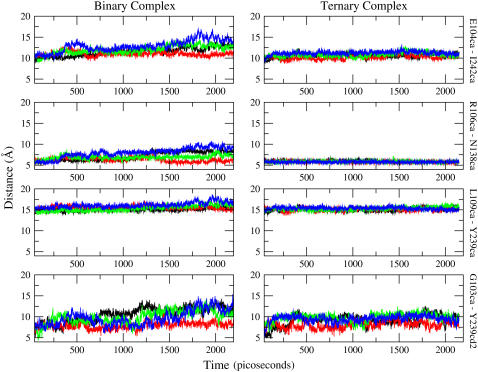
Many experiments clearly suggest that conformational fluctuation is necessary for the substrate to gain access into and out of the active site. What has not been known is how much the active site loop has to move to allow substrate binding. Convenient pairs of atoms from domains that contact each other in the closed active site were chosen to monitor the accessibility of the active site during the simulation. The distance between the following pairs of atoms, in CHARMM nomenclature, were monitored in each of the independent subunits of the binary and the ternary complex: Cα of Gly103 and CD2 of Tyr239; Cα of Glu104 and Cα of Ile242; Cα of Arg106 and Cα of Asn138; and Cα of Leu109 and Cα of Tyr239. The time-series data are plotted in Fig. 2.
FIGURE 2.
The time-series data from the binary complex are presented on the left panels, and those from the ternary complex are on the right. The vertical label on the right of each row indicates the pair that was monitored. The vertical axis (distance) of all panels are on the same scale for ease of comparison. Clearly, the binary complex is, on average, more open. Each color represents a different subunit and the scheme is consistent for both ternary and binary complex: black, subunit A; red, subunit B; green, subunit C; and blue, subunit D.
From the larger distance between the select pairs of atoms that were monitored and plotted in Fig. 2, it is very clear that the crevice lined by these pairs of residues is widening to a larger extent in the binary subunits. Calculating the average and the standard deviation of the measured distances over the entire trajectory further shows that fluctuations around the average value are larger in the binary complex, an indication that the loop is floppier and the active site is becoming more accessible (11). Moreover, the open and the closed binary subunits have clearly nonoverlapping statistical distributions of distances. This is a clear indication that different substates in the energy hypersurface are being sampled by the individual subunits.
By inspecting the time-series of distances in the binary complex in Fig. 2, from 1.6 ns onwards subunit D is on average more open compared to subunit B. We used the trajectory of subunit B in the binary complex to analyze the behavior of a closed binary complex and the trajectory of subunit D was processed for analyzing the open binary complex. The data in the trajectory from 1.6 ns to 2.148 ns (time zero is set at the initiation of heating) was used in data analysis, unless otherwise specified.
A useful measure of conformational change, one that has gained much emphasis in the traditional view of the source of anomalous heat capacities in proteins, is the change in accessible surface area (24). We obtained the time-series of the ASA of each subunit, using a probe radius of 1.4 Å, and from these, average values were obtained. A difference of 238 Å2 was observed between the two trajectories. This is not much, when compared to the result obtained from the static picture of human muscle LDH, but the change is in the correct direction that was expected in reference to the results of the muscle isoform. Other differences between the average properties were noted. We calculated the intramolecular hydrogen bonds of each binary complex and the number of hydrogen bonds that the binary complex makes with the solvent. To be more certain about the average number of waters that solvate the binary complex, the average hydration number within 3.0 Å was also calculated. The subunit that was, on average, open had fewer (5.3) intramolecular hydrogen bonds, three more hydrogen bonds with water, and had 7.8 more water molecules within 3.0 Å. The timescale covered by the molecular dynamics simulation is not sufficient to sample equilibrium structures that take longer timescales to interconvert. In addition, averaging over a trajectory may not be appropriate, because it is known from experiments that the species being sought after constitute only a tiny fraction of an equilibrium distribution. The focus is thus on the low probability conformations of widest variation rather than time-averaged values.
The time evolution of each subunit approximates an independent simulation
Searching for minor species in an equilibrium distribution is not trivial. Among the options are running the simulation for long enough time to carry out an extensive sampling or employing a biased search if a known order parameter characterizes the desired conformation. Caves et al. (25) made an interesting observation in a series of molecular dynamics simulations of the same system. Comparing the conformational distribution achieved from 10 independent 120-ps trajectories from that obtained with a single long trajectory (up to 5 ns), a wider distribution of structures was sampled by multiple short trajectories. In the case of the simulation of a tetramer of functionally independent subunits that is the subject of this report, the criteria of having different initial velocities is satisfied. By having initiated the dynamics of each subunit with different sets of velocities, the region of phase space that is explored is different in each subunit. In other words, the results of our simulation may be thought of as a search for separate regions of phase and conformational space.
A principal components analysis of the concatenated trajectories of the closed and open subunits was carried out to obtain eigenvectors that are common to both data sets. The eigenvectors constitute the set of orthogonal coordinates that can be used as a basis set to expand every snapshot in the dataset. The corresponding eigenvalue is the variance of the dataset along the eigenvector. When a large proportion of the total sample variance is captured by a few eigenvectors, the analysis can be focused on these so-called principal modes. Visualizing the projection of the dataset along these modes show clustering of very similar datapoints (26,27).
The eigenvectors were sorted based on the magnitude of the corresponding eigenvalues. The region of conformation space that is spanned by each trajectory was visualized by separately projecting each of the least-squares-fitted trajectories onto the first and second common eigenvectors, the modes that have the largest contribution to the overall variance of the dataset. In Fig. 3 , the trajectories of the open and closed subunits were plotted on the plane defined by the first and second common eigenvector. Each point on the plot corresponds to a unique snapshot. Treating the dataset this way allows clustering of similar structures to be visualized on a lower dimensional plane. The picture does seem to show that the open and closed trajectories occupy different regions of conformation space.
FIGURE 3.
Projection of trajectories onto the first and second common eigenvectors. Each point on the graph represents a conformational substate. The blue dots constitute the trajectory of the subunit that was closed in the time slice that was analyzed; the red dots are for the subunit that opened.
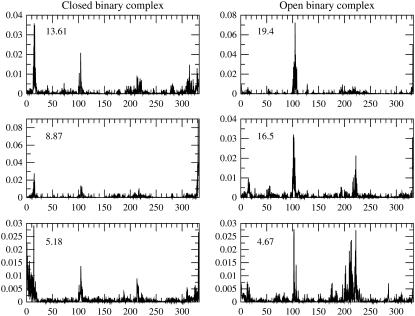
The time series shown in Fig. 2 already indicates a different behavior in each subunit. To study the fluctuation of each individual subunit, separate principal components analyses were done for the subunit that remained closed during the simulation time window and to the subunit that opened. Plots of the first three eigenvectors of the covariance matrices are presented in Fig. 4. Each eigenvector is labeled by its contribution to the total variance. The plots of the eigenvectors show that in the subunit that had an open conformation, the variance in the structures is largest along the modes that involve the loop region, residues 98–110, and the structure that it contacts in the reference crystal structure, residues 236–249. This is not surprising. However, from the plots of the same eigenvectors it is also revealed that residues apart from the loop region are involved in the correlated motions that effect opening of the active site. This points out that opening the access to the active site involves many residues adjusting to a new structure.
FIGURE 4.
Each column shows the first three eigenvectors of the covariance matrix. Every eigenvector is labeled by its percent contribution to the overall variance. The horizontal axis is the residue numbering in the linear polypeptide sequence. The loop region in human heart LDH spans residues 98–110. The structure that the loop contacts in the closed form include residues 236–249.
Interaction of the binary complex with water
It is known that rearrangement of hydrogen bonds in cooperatively bonded systems also manifests as change in the heat capacity. From the observed difference in trajectory-averaged properties of the open and closed binary subunits, we were able to say that the open binary subunit has fewer intramolecular hydrogen bonds than the closed binary subunit. In other words, the subunit that is open is melted compared to the subunit that remain closed in the time window that was examined. This is true for the overall hydrogen bonding in the apoprotein and for the LDH/NADH complex. This is similar to a solid-liquid transition, wherein the liquid state has a higher Cp because there are more degrees of freedom, translational and rotational in addition to the vibrational degrees of freedom that both the solid and liquid substance possess, that will soak up the added heat into the system. To relate this to the results of the principal components analysis, the more open subunit shows a larger degree of fluctuation. Presumably there are more isoenergetic states that it can populate when heat is injected into the system. That means it will require more input of heat to increase the temperature of the system. A related interpretation can be made for the binary complex-water hydrogen-bond accounting. Here we are looking at the number of hydrogen bonds that can soak up heat. The state that has more hydrogen bonds will require more input of heat, its latent heat, to melt (16).
The inventory above only takes into account hydrogen bonding. The energy that will be taken up by the translational and rotational degrees of freedom of the solvent that are liberated when the system is heated up also adds to the heat capacity.
Analysis of the extreme conformations
Different solution and crystallization conditions may selectively populate a different subset from the ensemble of possible structures of a condense phase system. This subset will then manifest as the dominant form in the experimentally determined structures (28). With this caveat, using the extreme value attained in the present simulation condition is tenable for qualitative purposes.
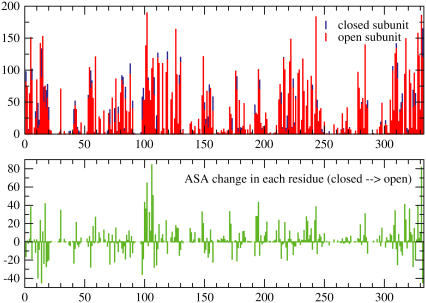
The ASA time series during the MD simulation of human heart LDH binary complex were obtained (not shown) for each subunit of the tetramer. We looked for the snapshot with largest ASA in the subunit that opened during the simulation and compared this number to the average ASA of the subunit that remained closed (Fig. 5). The difference was 538 Å2. This is approximately half of the difference in ASA between the open and closed subunit of the human muscle LDH crystal structure that is available in the PDB (see Table 1). The sampling achieved by the 2.148-ns simulation may not capture the full change that was observed in solution experiments. We note, once again, that in our molecular simulation we used the available crystal structure of the human heart LDH to derive structural and dynamic explanation for the anomalous heat capacity that was observed in ligand binding experiments using pig heart LDH. We also do not make any temporal connection between the states sampled by the different subunits. The two independent subunits, in this case, can only be linked in a stochastic sense because each subunit is tracking a different trajectory.
FIGURE 5.
The graph on top is an overlay of the ASA per residue of the most open snapshot and the average of the closed subunit. The lower graph shows the change in each residue from closed to open subunit. The rearrangement is clearly global, but it is clear that it is largest in the loop region. The largest change in ASA is that of Arg106.
What is also noteworthy in comparing the most open snapshot to the average of the closed subunit is the difference in hydration at 3.0 Å cutoff. There are 24 more waters that solvate the most open snapshot. The most open snapshot has 638 binary complex-water hydrogen bonds, and the average for the closed subunit is 612.4 hydrogen bonds, a difference of 26 hydrogen bonds. The agreement in these numbers justify the 3 Å cutoff that was used for accounting the relevant solvating water. Following Cooper (16), when comparing two states of the same system, any additional solvating water molecule contributes ∼75 J/mol K of heat capacity. The extra waters of solvation in the most open conformation contribute 1800 J/K−mol (430.2 cal/mol K) of heat capacity. This by itself is promising, coming close to reproducing the experimentally determined ΔCp. This estimation does not take into account the difference in intramolecular hydrogen bonds, which correlates with the fluidity of the cooperative unit. To avoid double-counting, the ΔCp that may be derived from the difference in ASA was not included in the estimate because the contribution from ΔASA and from change in solvation are not intuitively mutually exclusive effects. However all these highlight the possibly significant heat capacity contribution from intramolecular hydrogen bonding and solvation rearrangement.
Active site interactions in the ternary complex
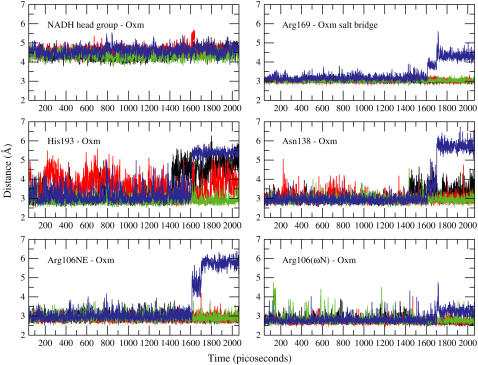
Key active site interactions observed in the crystal structure of hHLDH are shown in Fig. 6. A time-series of these distances obtained from the MD trajectory are shown in Fig. 7. The resolution of the data points is 1 ps. These interactions hold the ligand (oxamate) in a position that is believed to represent the catalytically competent configuration of the enzyme active site. The stable distance between the NADH headgroup and oxamate indicate that, within the time window that was sampled, oxamate did not migrate away from the immediate vicinity of the nicotinamide headgroup in all subunits of the tetramer. However, as shown in Fig. 7, there is a rearrangement of interactions in the active site that occurred at ∼1.6 ns from the initiation of the heating step. So even when the loop is closed over the active site, there remains some interesting changes in substrate-enzyme interactions (see right panel of Fig. 2).
FIGURE 6.
The following residues make close contact to oxamate in the crystal structure of hLDHA: Arg106, Asn138, Arg169, His193, and Thr248. This figure was generated from the coordinates of chain A of hHLDH (PDB ID 1I0Z).
FIGURE 7.
Distance time-series of several active site interacting pairs shown in Fig. 6. Each panel contains an overlay of time-series the specified pair in all four subunits. The coloring scheme is as follows: black, subunit A; red, subunit B; green, subunit C; and blue, subunit D. The distance between centers of mass were plotted for the following pairs: nicotinamide headgroup, oxamate; and guanidino group (starting from Cω) of Arg169, carboxylate group of oxamate. The rest are distances between heavy atoms of hydrogen-bond donor/acceptor. Arg106NE, His193, and Asn138 all approach the carbonyl oxygen of oxamate. Nω is a terminal nitrogen of the arginine side chain that interacts with one of the carboxylate oxygens of oxamate. All y axes units are distance in Ångstroms (Å) and x axes are time in picoseconds.
As shown in Fig. 7, a rearrangement of interactions in the active site occurred at ∼1.6 ns from the initiation of the heating step.
Arg169 provides the guanidinium moiety that solvates the carboxylate group of the ligand and is believed to steer the substrate into the active site (5). His193 is the catalytically important proton donor(acceptor) in the pyruvate-to-lactate (lactate-to-pyruvate) enzyme-catalyzed chemistry. In its protonated form, the nitrogen in the epsilon position shares its hydrogen with the carbonyl oxygen of the substrate. Arg106 interacts with the carbonyl oxygen in oxamate via the NE (δ-N) nitrogen and one of its ω-N donor nitrogen to the ligand's carboxylate oxygen.
Other groups found in close proximity, and presumably hydrogen-bonding, to oxamate in the crystal structure of hHLDH are Asn138 to the carbonyl oxygen and Thr248 (data not show) to the carboxylate oxygen.
The shift in the distances between interacting pairs in the active site of subunit D was abrupt and simultaneous. Furthermore, the critical salt-bridge between Arg169 and the carboxylate moiety was also disrupted while the ligand remains in close proximity to the cofactor headgroup. What managed to hold on to the ligand was the ω-N hydrogen-bond donor of Arg106. In the ternary complex, this charged side chain interacts tightly with the ligand. However, in the binary complex, the most open conformation that was achieved shows that Arg106 becomes exposed to bulk solvent (Fig. 8). The guanidinium moiety was displaced by 5.64 Å from deep in the active site toward the surface, exposed to bulk solvent.
FIGURE 8.
The channel to the active site in a the closed and open form. The coloring scheme is consistent to both pictures: white, Arg106; dark blue, loop residues except Arg106 (98:105 and 107:110); red, Asn138, Arg169, His193, and Thr248; and light blue, rest of the protein. Arg106 is displaced 5.64 Å from its position in the active site into the surface of the protein.
DISCUSSION
Our goal here is to gain insight into the earliest stages of substrate binding to lactate dehydrogenase, specifically to the binary LDH/NADH complex since substrate binding to LDH is ordered with the NADH cofactor binding first. Experiments suggest that the LDH/NADH exists in binding-competent and -incompetent conformations, with a substantial change in heat capacity between the two and the binding competent forms in the minority. The structural difference observed between the subunits of the ternary complex of muscle LDH formed with a substrate mimic (LDH/NADH·oxamate), determined in a crystallographic study (10), is suggestive of the endpoints of the opening up of the active site in human muscle LDH/NADH. One structure of the tetramer is substantially more open than the other three: the surface mobile loop extends out into solution, being closed in the other three subunits, and the open structure's solvent-accessible surface area differs considerably from the closed structures, by 1122 Å2. However, using the empirically derived relationship between ΔCp and ΔASA (29), the ΔASA difference accounts for a ΔCp of only 105 cal/mol K, which is substantially smaller than the 790 cal/mol K obtained from experiments (5). This discrepancy may be due to the obvious possibility that the crystallized open subunit does not represent the full extent of relaxation of the LDH/NADH binary complex to accommodate the substrate/ligand. On the other hand, if the experimental ΔCp is used to predict a ΔASA from the empirical relationship, an aggregate of ∼56 residues are expected to undergo significant solvent exposure (5). As an unfolding event, this is a large part of the 338-residue protein and seems unlikely.
To explore more fully conformational degrees of freedom accessible to the LDH/NADH binary complex and explore what structural factors can give rise to the substantial heat capacity observed in experiments, we performed molecular dynamics calculations. The results of the trajectory-averaged calculations for relatively open and closed binary complex subunit correlate with the known origin of the anomalous heat capacity in biomolecular processes (14,16,24). The open subunit has on average fewer intramolecular hydrogen bonds compared to the tighter/closed subunit. This is reminiscent of order-to-disorder transitions of hydrogen-bonded systems that are accompanied by an increase in the heat capacity of the more disordered phase. Hence, rather than the exposure of hydrophobic residues to solvent, the result of our simulation studies is more consistent with rearrangement in internal hydrogen bonding and an increase in solvation as the origin of the anomalous heat capacity of the binding competent LDH/NADH form. The change in solvation alone can account for ∼430 cal/mol K of heat capacity when the most open conformation that was sampled is compared with the average of the closed subunit. The number is reasonably close to that obtained in experiments, ΔCp = 790 cal/mol K. The conformational sampling achieved by the independent subunits of the tetramer in the simulation showed that, within 2.148 ns, an open conformation was achieved; and it seems poised to bind an incoming ligand. These results seem consistent with available structural data in the PDB for the half binary-half ternary pig muscle LDH. In preparing the half binary-half ternary crystal of pig muscle LDH, the single crystal of the ternary complex was washed with buffer containing NADH and ammonium sulfate (11). Within the confines of the crystal environment, half of the oxamate was washed off from the active sites. When the position of the loop residues and the critical active site side chains that make contact with oxamate in the ternary complex were examined, the change is not drastic. The average position of the loop residues remain in the closed form; however, larger B factors were reported for the loop residues. If ligand unbinding in this case did not cause a large displacement in the average loop position, it is possible to suggest that the loop opening, or full loop opening, is not an absolute requirement for ligand binding in LDH. By loop opening we mean a structural change to the same extent as that observed in crystallographic structures of the apo-forms of LDH. In these cases, the entire loop structure reaches out into the solvent causing a large scale opening and access into the active site.
So how does the ligand find its way into the catalytic vacuole that is shielded from bulk solvent? We speculate on the role of several structural changes we observed in our simulation. According to our calculations, the substrate binding site, normally buried 10 Å inside the protein, is substantially exposed to solvent, and hence ligand, in open conformations of the LDH/NADH complex (see Fig. 8). We did not observe the loop flap up or down over the active site opening. What was observed is more a sliding of the loop over the active site coincident with the exposure of possible acceptor moieties toward the surface. The obvious difference between the two motions is the friction that will be experienced by the mobile loop, which contributes to the free energy barrier to loop opening. Arg106 is the most likely, among the residues that interact with oxamate in the active site of the enzyme, to reach out of the catalytic vacuole. The bulk solvent accessibility of Arg106 in the snapshot of an open subunit may indicate an initiating role for this residue in productive ligand binding to the LDH and eventual uptake into the active site. While it is not the only Arginine side chain that is solvent-exposed (we note Arginines 99, 112, 157, and 298 in human heart LDH), it is provocatively positioned such that an incoming ligand that binds to it will likely be taken into the active site. Even with an active site that is wide open in the sense that we described earlier, this seems to be the active site side chain with which the ligand will first interact. However, based on our MD data and the observed ensemble and time-averaged crystal structure of the half binary-half ternary pig muscle LDH, we do not believe that a fully open loop for facile binding is needed. The observed large fluctuations in the loop region defined more globally than just the loop in the binary complex indicate a role for such structures in allowing the entry of the ligand into the active site. An incoming ligand will certainly find its optimum position in a wide open active site, whether or not the loop is fully open.
Furthermore, from our results, we suspect that ligand binding in LDH does not have one preferred path due to the ruggedness of the energy landscape. A transient breathing that exposes Arg106 may be sufficient to form an encounter complex with entering substrate. The presence of oxamate in the active site definitely stabilizes the loop-closed conformation, as seen in Fig. 7. It is not unreasonable to imagine the loop becoming largely exposed to bulk solvent during ligand binding because of its known orientation over the active site of the ternary complex. However, our result has so far detected only parts of the loop relaxing; the rest of the conformational adjustment is spread out in the entire structure (see Fig. 3).
In our simulation, one subunit of the LDH/NADH tetramer adopted an open conformation. In the subunit that was open, only few snapshots represent the structural features that explain the anomalous heat capacity of the binding-competent form as suggested by the experimental results. This seems consistent with the experimental finding that the binding-competent form(s) constitute a minority of the equilibrium population (7). Experiments also indicate that the formation of the encounter complex with the binding-competent form(s) is very close to the diffusion limit (on-rate of 108 M−1 s−1 or larger). It is interesting that nature will utilize a small population of species as the binding-competent forms. However, the active site of LDH lies fairly buried (10 Å) into the protein's interior. It may simply be a successful strategy to expose the binding pocket to solvent in some conformations, making those highly efficient toward the capture of ligand as opposed, in the more traditional view, to leading the ligand down a narrow channel in all of the protein populations. The latter mechanism requires some way to keep the mobile loop open in a majority of protein conformers and requires a delicate balancing of water release from within the channel in addition to the penetration of ligand. Also, we have seen in our simulation that the tetramer can sample a few of these conformations within nanoseconds, starting from a model of a closed binary complex. Presumably the tetramer of binary complexes is being hit from all directions by incoming ligand species at the diffusion limit. The interconversion of closed and open forms is therefore a process that limits the formation of the encounter complex. If it only takes a few nanoseconds, or even microseconds, to interconvert between closed and binding competent forms, there will be sufficient attempts for the ligand to find an open form and still have an on-rate rate that is only one order-of-magnitude below diffusion limit.
Acknowledgments
This work was supported by the National Institutes of Health grants No. GM41916 and No. GM068036, and by the Medical Scientist Training Program grant No. T32 GM07288 (to J.R.E.T.P.).
Editor: Ruth Nussinov.
References
- 1.Druker, B. 2006. Circumventing resistance to kinase-inhibitor therapy. N. Engl. J. Med. 354:2594–2596. [DOI] [PubMed] [Google Scholar]
- 2.Muzammil, S., P. Ross, and E. Freire. 2003. A major role for a set of non-active site mutations in the development of HIV-1 protease drug resistance. Biochemistry. 42:631–638. [DOI] [PubMed] [Google Scholar]
- 3.Rose, R., C. Craik, and R. Stroud. 1998. Domain flexibility in retroviral proteases: structural implications for drug resistant mutations. Biochemistry. 37:2607–2621. [DOI] [PubMed] [Google Scholar]
- 4.Petsko, G., and D. Ringe. 2004. Protein Structure and Function. New Science Press, London.
- 5.McClendon, S., N. Zhadin, and R. Callender. 2005. The approach to the Michaelis complex in lactate dehydrogenase: the substrate binding pathway. Biophys. J. 89:2024–2032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McClendon, S., D. Vu, K. Clinch, R. Callender, and R. Dyer. 2005. Structural transformations in the dynamics of Michaelis complex formation in lactate dehydrogenase. Biophys. J. 89:L7–L9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Qiu, L., M. Gulotta, and R. Callender. 2007. Lactate dehydrogenase undergoes a substantial structural change to bind its substrate. Biophys. J. 93:1677–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Basner, J. E., and S. D. Schwartz. 2004. Donor-acceptor distance and protein promoting vibration coupling to hydride transfer: a possible mechanism for kinetic control in isozymes of human lactate dehydrogenase. J. Phys. Chem. B. 108:444–451. [Google Scholar]
- 9.Burgner, J., and W. Ray. 1984. On the origin of lactate dehydrogenase induced rate effect. Biochemistry. 23:3636–3648. [DOI] [PubMed] [Google Scholar]
- 10.Read, J., V. Winter, C. Eszes, R. Sessions, and R. Brady. 2001. Structural basis for altered activity of M- and H-isozyme forms of human lactate dehydrogenase. Proteins: Struct. Funct. Gen. 43:175–185. [DOI] [PubMed] [Google Scholar]
- 11.Dunn, C., H. Wilks, D. Halsall, T. Atkinson, A. Clarke, H. Muirhead, and J. Holbrook. 1991. Design and synthesis of new enzyme based on the lactate dehydrogenase framework. Phil. Trans. R. Roc. Lond. B. 332:117–184. [DOI] [PubMed] [Google Scholar]
- 12.Clarke, A., D. Wigley, W. Chia, D. Barstow, T. Atkinson, and J. Holbrook. 1986. Site-directed mutagenesis reveals role of mobile arginine residue in lactate dehydrogenase catalysis. Nature. 324:699–702. [DOI] [PubMed] [Google Scholar]
- 13.Callender, R., and R. B. Dyer. 2002. Probing protein dynamics using temperature jump relaxation spectroscopy. Curr. Opin. Struct. Biol. 12:628–633. [DOI] [PubMed] [Google Scholar]
- 14.Sturtevant, J. 1977. Heat capacity and entropy changes in processes involving proteins. Proc. Natl. Acad. Sci. USA. 74:2236–2240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Prabhu, N., and K. Sharp. 2005. Heat capacity in proteins. Annu. Rev. Phys. Chem. 56:521–548. [DOI] [PubMed] [Google Scholar]
- 16.Cooper, A. 2005. Heat capacity effects in protein folding and ligand binding: a re-evaluation of the role of water in biomolecular thermodynamics. Biophys. Chem. 115:89–97. [DOI] [PubMed] [Google Scholar]
- 17.Waldman, A., K. Hart, A. Clarke, D. Wigley, D. Barstow, T. Atkinson, W. Chia, and J. Holbrook. 1988. The use of a genetically engineered tryptophan to identify the movement of a domain of B. stearothermophilus lactate dehydrogenase with the process that limits the steady-state turnover of the enzyme. Biochem. Biophys. Res. Commun. 150:752–759. [DOI] [PubMed] [Google Scholar]
- 18.Musick, W., and M. Rossmann. 1979. Structure of mouse testicular lactate dehydrogenase isoenzyme C4 at 2.9 Å resolution. J. Biol. Chem. 254:7611–7620. [DOI] [PubMed] [Google Scholar]
- 19.Grau, U., W. Trommer, and M. Rossmann. 1981. Structure of the active ternary complex of pig heart lactate dehydrogenase with S-lac-NAD at 2.7 Å resolution. J. Mol. Biol. 151:289–307. [DOI] [PubMed] [Google Scholar]
- 20.Brunger, A., and M. Karplus. 1988. Polar hydrogen positions in proteins: empirical energy placement and neutron diffraction comparison. Proteins. 4:148–156. [DOI] [PubMed] [Google Scholar]
- 21.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 22.Zhang, L., and J. Hermans. 1996. Hydrophilicity cavities in proteins. Proteins: Struct. Funct. Gen. 24:433–438. [DOI] [PubMed] [Google Scholar]
- 23.Feller, S., Y. Zhang, R. Pastor, and B. Brooks. 1995. Constant pressure molecular dynamics simulation: the Langevin piston method. J. Chem. Phys. 103:4613–4621. [Google Scholar]
- 24.Makhatadze, G., and P. Privalov. 1990. Heat capacity of proteins. I. Partial molar heat capacity of individual amino acid residues in aqueous solution: hydration effect. J. Mol. Biol. 213:375–384. [DOI] [PubMed] [Google Scholar]
- 25.Caves, L. S., J. D. Evanseck, and M. Karplus. 1998. Locally accessible conformations of proteins: multiple molecular dynamics simulations of crambin. Protein Sci. 7:649–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Amadei, A., A. B. M. Linssen, and H. J. C. Berendsen. 1993. Essential dynamics of proteins. Proteins. 17:412–425. [DOI] [PubMed] [Google Scholar]
- 27.Hess, B. 2000. Similarities between principal components of protein dynamics and random diffusion. Phys. Rev. E. 62:8438–8448. [DOI] [PubMed] [Google Scholar]
- 28.Ma, B., S. Kumar, C. Tsai, and R. Nussinov. 1999. Folding funnels and binding mechanisms. Protein Eng. Des. Sel. 9:713–720. [DOI] [PubMed] [Google Scholar]
- 29.Myers, J., C. Pace, and J. Scholtz. 1994. Denaturant m-values and heat capacity changes: relation to changes in accessible surface areas of protein unfolding. Protein Sci. 4:2138–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]