Theoretical Analysis of an Iron Mineral-Based Magnetoreceptor Model in Birds

Abstract

Sensing the magnetic field has been established as an essential part of navigation and orientation of various animals for many years. Only recently has the first detailed receptor concept for magnetoreception been published based on histological and physical results. The considered mechanism involves two types of iron minerals (magnetite and maghemite) that were found in subcellular compartments within sensory dendrites of the upper beak of several bird species. But so far a quantitative evaluation of the proposed receptor is missing. In this article, we develop a theoretical model to quantitatively and qualitatively describe the magnetic field effects among particles containing iron minerals. The analysis of forces acting between these subcellular compartments shows a particular dependence on the orientation of the external magnetic field. The iron minerals in the beak are found in the form of crystalline maghemite platelets and assemblies of magnetite nanoparticles. We demonstrate that the pull or push to the magnetite assemblies, which are connected to the cell membrane, may reach a value of 0.2 pN—sufficient to excite specific mechanoreceptive membrane channels in the nerve cell. The theoretical analysis of the assumed magnetoreceptor system in the avian beak skin clearly shows that it might indeed be a sensitive biological magnetometer providing an essential part of the magnetic map for navigation.

INTRODUCTION

Large varieties of animals possess a magnetic sense. Migratory birds use magnetic clues (in addition to light polarization, star signs, position of the sun) to find their way south in fall and north in spring (1–4). Salamanders, frogs, and sea turtles use the magnetic field for orientation when they have to find the direction of the nearest shore quickly, e.g., when they sense danger (5–8). Magnetoreception by honeybees (Apis mellifera) is demonstrated by such activities as comb building and homing orientation, which are affected by the geomagnetic field (9–13). Magnetotaxis was shown in bacteria (14–16), whose directional movement was oriented by the local geomagnetic field.

The best-studied example is the use of the geomagnetic field by migratory birds for orientation and navigation during migration. Reviews of these studies are given in the literature (4,17–21). Despite decades of research, the precise mechanism of avian magnetoreception is still not well understood. The two most likely candidates are a chemical reaction mechanism involving a specialized photoreceptor molecule called the radical pair model (21,22) and an iron-mineral-based model (23–33). Experimental evidence suggests that birds and turtles may use both types of magnetoreception simultaneously, using the iron-based mechanism to form a magnetic “map” while using a radical-pair mechanism as the basis of the orientational compass (25).

Ever since magnetite crystals of biogenic origin have been found in bacteria and higher organisms (9,34), it has been speculated that these particles are involved in magnetoreception (35,36). Subjecting birds to a brief high-intensity magnetic pulse, a treatment specifically designed to alter magnetization of a single-domain magnetite crystal, had a conspicuous effect on orientational behavior. It influenced the homeward orientation of displaced birds (37) and caused a shift of up to 90° from the seasonally appropriate migratory direction in three migrants (24,38,39).

Using various biophysical methods the presence of the small magnetic particles was demonstrated in the upper part of the beak of homing pigeons (Columba livia) (26,28,31) and later in several other birds species (40). With the use of different light and electron microscopic methods combined with x-ray analysis, Fleissner et al. concluded that there are two different types of iron compound in the beak. In the later articles (30,31,41), these compounds were identified using micro-synchrotron x-ray-absorption-near-edge-structure-spectroscopy as two ferrimagnetic materials: magnetite (Fe₃O₄) and maghemite (γ-Fe₂O₃). It was shown that magnetite forms micro clusters, attached to the cell membrane, while maghemite crystals have a plateletlike structure arranged in chains inside the dendrite.

Based on their experimental findings, Fleissner et al. (31,41) suggested a mechanism for iron-mineral based magnetoreception, namely that in an external magnetic field, the maghemite platelets become magnetized and enhance the local magnetic field in the cell by orders of magnitude. Thus the magnetite clusters will experience an attractive (repulsive) force inducing their displacement, what might induce primary receptor potential via strain-sensitive membrane channels leading to a certain orientation effect.

This mechanism is different from the magnetite-based magnetoreception mechanism suggested earlier because it involves two different types of iron-minerals (see, e.g., (27,29,35,42,43)). In these articles, only magnetite was considered and it was suggested that the magnetite clusters depending on the orientation of the external magnetic field will attract or repel each other, deforming the membrane and possibly opening (closing) the ion channels. This mechanism was suggested ∼15 years ago (44), long before the maghemite platelets were discovered in the beak of birds. Since maghemite has ferrimagnetic nature (45) and possesses pronounced magnetic properties the maghemite platelets should play an important role in the magnetoreception mechanism.

So far no direct experimental or theoretical verifications of the magnetoreception mechanism suggested in the literature (30,31,41) has been reported. In the present article, we address this problem from a theoretical point of view. Based on the known experimental observations, we develop a physical model that we use for the description of magnetoreception phenomena in birds. The magnetoreceptor mechanism, which we suggest in this article, is based on the magnetoreceptor model suggested in the literature (31,41), but is slightly different because in our mechanism the maghemite platelets have a static magnetic moment rather than an induced one. This assumption is motivated by the size of the platelets and their composition, which clearly show that maghemite platelets should behave like small permanent magnets. We calculate the forces acting on the magnetite particles and show that the suggested iron-mineral system can serve as a magnetoreceptor unit with distinct orientational properties. We demonstrate that, depending on the orientation of the external magnetic field, the pull or push exerted on the cell membrane can change significantly leading to different nerve signals. The nerve signals are delivered to the brain causing a certain orientational behavior of the bird. In this article, we suggest and analyze two transducer mechanisms of the geomagnetic field that are based on opening/closing of mechanosensitive ion channels. Based on the analysis of forces exerted on the membrane, we calculate the probability of the channel opening.

THE PROPOSED MAGNETORECEPTOR SYSTEM

Based on the histology studies of the upper beak of homing pigeons, it was shown (28,30,31,41) that there are six patches in the beak where iron minerals are concentrated. The iron minerals were found in symmetrical spots near the lateral margin of the skin of the upper beak inside the dendrites of nerve cells. The size of the iron mineral patches in dendrites was found to be always about the same, being 350-μm long and 200 μm in diameter (28,30,31,41). In every patch the iron-minerals were found parallel to the axon bundles with a certain spatial orientation. It was shown (31) that the dendrites in the frontal, middle, and caudal parts of the beak are aligned in three perpendicular directions: the frontal have a preferred dorsal-to-ventral direction; the middle ones median-to-lateral direction; and the caudal ones caudal-to-rostral direction.

In addition, it was demonstrated that dendrites containing iron also form regular pattern. Several of them may align side by side but longitudinally the distance between them is ∼100 μm. This fact was independently confirmed in the μ-SXRF-measurements of histologically undisturbed and unstrained material (31).

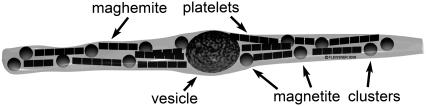
The construction of a primary magnetoreceptor unit discussed in this article is motivated by experimental findings of Fleissner et al. (28,30,31,41). To explain the choice of our model in Fig. 1, we show schematically the structure of a single dendrite containing iron-minerals. The figure is based on the experimental results discussed in the literature (28,30,31). Within the dendrite there are three different subcellular compartments containing iron-minerals: several magnetite clusters, an iron-coated vesicle, and many maghemite platelets. Each dendrite contains 10–15 clusters of magnetite nanocrystals of average size 5 nm (31–33). The clusters have an average diameter of 1 μm (28,30,31,41) and adhere to the cell membrane. The maghemite platelets form bands, which extend through the entire dendrite. The magnetite clusters were usually found at the edges of maghemite bands that include ∼10 platelets. Each platelet was found to be 1-μm wide and long and <0.1-μm thick (28,30,31,41). The vesicle is most often located in the center of the dendrite and its composition is still not well understood. In the literature (28,30,31,40), it was demonstrated that the vesicle is covered by some noncrystalline iron-substance and has a diameter of ∼5 μm.

FIGURE 1.

Experimental findings of Fleissner et al. (31) showing the characterization and subcellular localization of iron minerals within a dendrite. The drawing shows schematically the structure of a single dendrite as derived from serial ultrathin sections with the three subcellular components containing iron: chains of maghemite crystals (1 × 0.1 × 1 μm) magnetite clusters (diameter ∼1 μm), and the iron-coated vesicle (diameter 3–5 μm). Figure presented by the courtesy of Gerta and Günther Fleissner, Universität Frankfurt am Main.

Note that the particle arrangement in the dendrite presented in Fig. 1 is different from what was published in Fleissner et al. (28). This happens because the interpretation of experimental data in Fleissner et al. (28) was based on low-resolution measurements while the quality of experiments has been significantly improved in Fleissner et al. (31) and Stahl et al. (41). Thus the spatial orientation of iron-mineral particles in the dendrite has been determined more accurately and differs from the structure presented Fleissner et al. (28). Fig. 1 was obtained in the latest experiments by Fleissner et al. and has not been published elsewhere. The position of the large vesicle in the middle of the dendrite is also more reasonable than at the edge, as published in Fleissner et al. (28) due to the symmetry reasons. Later in the article we present two hypotheses explaining the possible roles of the vesicle.

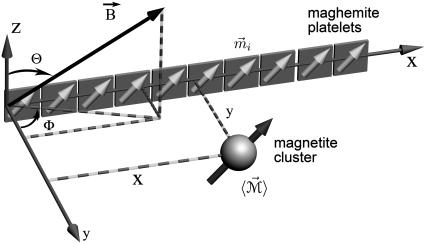
We define the magnetoreceptor unit as the smallest structure possessing the magnetoreception properties of the whole dendrite. Thus, the magnetoreceptor unit consists of 10 maghemite platelets and one magnetite cluster, as shown in Fig. 2. It was chosen to study the forces acting on a single magnetite cluster. In a dendrite there are ∼10–15 of such units (see Fig. 1).

FIGURE 2.

Smallest magnetoreceptor unit consisting of 10 maghemite platelets (boxes) and a magnetite cluster (sphere). The coordinate frame shown in the figure is used in the computations throughout the article. The direction of the external magnetic induction vector 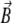is characterized by the polar angle Θ and the azimuthal angle Φ as shown. The magnetic moments of the i^th maghemite platelet and of the magnetite cluster are shown with 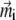and 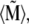respectively.

The geometry of the magnetoreceptor unit is determined from the experimental observations (31). Thus, the maghemite platelets have the dimensions 1 × 0.1 × 1 μm and the magnetite cluster has the diameter of 1 μm. To study the behavior of the magnetoreceptor unit at different orientations of the external magnetic field, it should be considered in a certain coordinate frame. In this article, the maghemite platelets are put in the (x,z)-plane being aligned along the x axis (see Fig. 2). The distance between two neighboring platelets is equal to 0.1 μm. The platelets are numbered in the positive direction of the x axis, with the first plate having its origin at (0.5,0,0) μm. The position of the magnetite cluster is defined by the vector 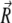= (x,y,z) (see Fig. 2).

The vector of the external magnetic induction, 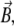is also shown in Fig. 2. It is described by an absolute value, B, polar angle Θ, and azimuthal angle Φ:

(1)

THEORETICAL MODEL

At room temperature, magnetite and maghemite are ferrimagnetic minerals. Magnetite has the chemical formula Fe₃O₄, being one of several iron oxides and a member of the spinel group. Maghemite (Fe₂O₃, γ-Fe₂O₃) can be considered as a Fe^II-deficient magnetite with formul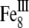a ()_A[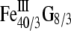]_BO₃₂, where G represents a vacancy, A indicates tetrahedral positioning, and B octahedral (46).

The magnetoreceptor unit includes 10 maghemite platelets and a magnetite cluster (see Fig. 2) that consist of ferrimagnetic minerals and thus should have magnetic moments. The magnetic moments of the platelets and the cluster have different natures: the platelets behave like small permanent magnets while the cluster has an induced magnetic moment. In Magnetic Moment of the Maghemite Platelet, and Magnetic Moment of the Maghemite Cluster, the expressions for magnetic moments of maghemite platelets and magnetite clusters were derived, respectively, and in Model of Interacting Pointlike Dipoles, and Model of Interacting Dipoles of Finite Size, two theoretical models for calculating the potential energy of the magnetite cluster and the forces acting on it were suggested.

The magnetization of a ferrimagnet determines its magnetic properties. The magnetization of magnetite and maghemite has a hysteresis shape (see Fig. 3) if considered as a function of external magnetic induction (47,48). The hysteresis loop is characterized by the remanent magnetization M, saturation magnetization M_sat, and coercive force B_cf (see Fig. 3). The hysteresis parameters depend on the temperature and on the size of the particle. The hysteresis parameters for 1 μm maghemite particles at room temperature are M = 50 emu/cm³ (47), M_sat = 377 emu/cm³ (48), and B_cf = 233 G (48). For magnetite nanoparticles (1–10 nm) the hysteresis parameters are M ≈ M_sat = 480 emu/cm³ (13,48), while B_cf = 180–295 G.

FIGURE 3.

Hysteresis profile of a ferrimagnet. The remanent magnetization M, saturation magnetization M_sat, and coercive force B_cf are indicated. The typical parameters of the hysteresis plot for maghemite are M = 50 emu/cm³ (47), M_sat = 377 emu/cm³ (48), and B_cf = 233 G (48). For magnetite, M_sat = 480 emu/cm³ (47) and B_cf = 180–300 G (48).

The Earth magnetic field has the induction of ∼0.5 G, while the typical magnetic field created by the chain of maghemite platelets is 10 G, as follows from our calculations. Note, that the chainlike assembly of the maghemite platelets is energetically the most favorable, because in that case the magnetic moments of the platelets are aligned one after another. The resulting magnetic field in this case is maximal. The magnetite cluster interacts with the external magnetic field and with the magnetic field created by the platelets. If all maghemite platelets would bundle together, then the magnetic moments of individual platelets would be stochastically distributed, leading to lower magnetic field than in the case of an ordered chain. Since for maghemite and for magnetite 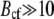G, only a narrow region of the magnetization plot in Fig. 3 corresponding to the field strengths <10 G is used in the system, and the magnetization of magnetite and maghemite is almost constant equal to the remanent saturation magnetization.

Magnetic moment of the maghemite platelet

Magnetic properties of a ferrimagnetic material vary with size and shape of the particle (32,33,35). In the problem considered here, the size of a single maghemite platelet is 1 × 0.1 × 1 μm (see discussion in The Proposed Magnetoreceptor System) which is sufficient for the formation of a multidomain structure in the (x,z)-plane (35) (see Fig. 2). Since maghemite is a ferrimagnetic mineral, the maghemite platelets have a non-zero magnetic moment in this plane even in the absence of the external magnetic field. The magnetic moment of a platelet with index i, 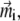is proportional to its volume and, therefore, is given by

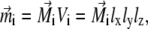(2)

where 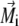is the volume magnetization of the i^th platelet, V_i is its volume, and l_x, l_y, and l_z are its dimensions along the x, y, and z axes, respectively.

The direction of the magnetic moment of a platelet is governed by the projection of the total magnetic field on the (x,z)-plane. The total magnetic field at the site of the platelet with index i, 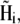is the sum of the external magnetic field, the magnetic field created by other platelets and by the magnetic field created by the magnetite cluster. It reads as

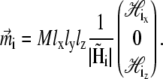(3)

The expression for the magnetic field strength is discussed in Model of Interacting Pointlike Dipoles in detail.

With M = 50 emu/cm³ (48), l_x = l_z = 1 μm, and l_y = 0.1 μm, one obtains m_i ≈ 3.121 eV/G, being a typical value of the magnetic moment of a maghemite platelet.

Magnetic moment of the magnetite cluster

The magnetite cluster consists of magnetite nanomagnets, which are ∼5 nm in diameter (31–33), and thus the magnetic properties of the cluster are significantly different from the magnetic properties of bulk magnetite. The nanomagnets behave like dipoles that can rotate freely inside the cluster. Thus the magnetite cluster behaves like a superparamagnet, i.e., if it is subject to an external magnetic field, then the nanomagnets try to align in the direction of the field, so that the potential energy of each nanomagnet is minimal. In this case all magnetic moments of the nanomagnets add to a total magnetic moment 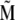of the cluster. On the other hand, at a given temperature the statistical motion of the nanomagnets counteracts the alignment. In the limit of a very high temperature, therefore, all nanomagnets are statistically distributed, and their magnetic moments cancel each other, so that the total moment 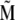vanishes. In the case of a finite temperature and a finite magnetic field, the mean total moment 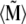is somewhere between these two extreme cases.

In the latest transmission electron view of the nanomagnets inside the magnetite cluster (40), it was demonstrated that the nanomagnets often assemble in short chains of ∼5–10 elements. In this article, this fact is neglected and therefore a lower estimate for the magnetic moment of the magnetite cluster is obtained. The fact that the nanomagnets form chains inside the cluster will enhance the magnetic properties of the cluster, leading to an increase of its magnetic moment.

As a model of a superparamagnetic cluster we consider a system of n freely revolvable nanomagnets, the translational motion of which we neglect. The total number of nanomagnets within a cluster can be estimated from the relation

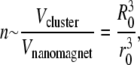(4)

where V_cluster and V_nanomagnet are the volumes of the cluster and the nanomagnet, respectively, and R₀ and r₀ are their radii. With R₀ = 0.5 μm and r₀ = 2.5 nm, one obtains n ≈ 8 × 10⁶.

To calculate the mean total moment of the magnetite cluster, one needs to calculate the partition function of a system with energy

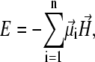(5)

where 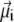is the magnetic moment of the i^th nanomagnet and 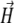is the magnetic field strength. Since we want to estimate the magnetic moment of the cluster we assume that the magnetic field at its site is homogeneous, equal to 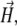and all nanomagnets have magnetic moments of equal magnitude, μ. Let us introduce a coordinate system associated with the field vector We will denote it as (x₁, y₁, z₁) and assume that the field vector points in the z₁-direction. Then the orientation of each dipole can be expressed by the polar angles θ_i and ϕ_i.

Each microstate of the system corresponds to a set {θ_i;ϕ_i} of orientations of all dipoles. The partition function over all microstates depends on the temperature of the system T, magnetic field strength H, and the number of nanomagnets n

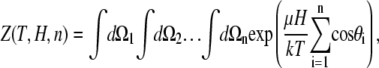(6)

where k is the Boltzmann factor. The integrals 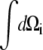extend over all spatial angles. The partition function factors, since the individual nanomagnets are assumed noninteracting, are therefore

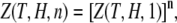(7)

where

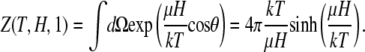(8)

The probability for a nanomagnet to assume an orientation between θ, θ + dθ and ϕ, ϕ + dϕ is given by

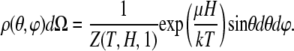(9)

With the aid of Eq. 9, the mean magnetic moment of a nanomagnet can be calculated:

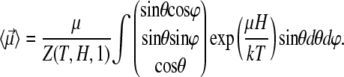(10)

From Eq. 10 follows that 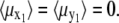The reason is that all orientations of the nanomagnet perpendicular to the z₁ axis are equally probable. Thus

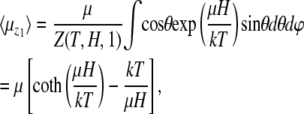(11)

and the total mean dipole moment of the magnetite cluster in the z₁ direction becomes

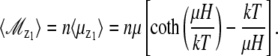(12)

If 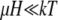the expression in the square brackets of Eq. 12 can be expanded, and the expression for the average total magnetic moment of the magnetite cluster is given by

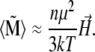(13)

From Eq. 13 it is clear that the total magnetic moment of the magnetite cluster is proportional to the field strength. The proportionality constant is called the magnetic susceptibility, which is defined as

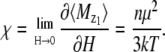(14)

The magnetic moment of a nanomagnet reads as

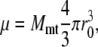(15)

where M_mt is the saturation magnetization of magnetite (see Fig. 3). With M_mt = 480 emu/cm³ (13,48) and r₀ = 2.5 nm (13,32,33,45), one obtains μ ≈ 19.61 μeV/G. Substituting this value into Eq. 14 and dividing it by the volume of the magnetite cluster, one obtains the volume susceptibility of the cluster χ_v, which at 300 K is equal to χ_v = 0.12 CGS units. (The volume susceptibility is a dimensionless quantity. It can be measured in the CGS and SI systems of units: 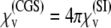units.) Note that this value is in very good agreement with the value used in an earlier investigation (27), and is typical for ferrofluids based on magnetite (χ_v = 0.1 CGS units). With H = 10 Oe as the typical value of the local field at the site of the magnetite cluster—Oersted (Oe) is the unit of magnetic field strength in the CGS electromagnetic system; 1 Oe equals 1000/4π ampere-turns per meter (49)—one obtains ≈ 0.392 eV/G. Note that this value is approximately an order-of-magnitude smaller than the magnetic moment of a single maghemite platelet (see estimates in Magnetic Moment of the Maghemite Platelet).

Model of interacting pointlike dipoles

Let us now consider the potential energy of the magnetite cluster. In this section we discuss a model that neglects the size of the maghemite platelets and of the magnetite cluster and treats them as pointlike dipoles.

The potential energy of the magnetite cluster reads

(16)

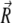where is defined in Eq. 13, describes the position of the magnetite cluster (see Fig. 2), and 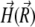is the magnetic field vector at the site of the cluster, which is given by

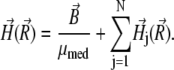(17)

Here is the induction vector of the external magnetic field, μ_med ≈ 1 is the permeability of the medium, N is the number of platelets, 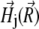is the magnetic field created by the j^th platelet at the site of the magnetite cluster, which is known to be (50,51)

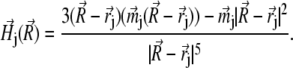(18)

Here 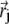describes the position of the j^th platelet and 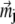is its magnetic moment defined in Eq. 3. To calculate the magnetic moment of a platelet, one needs to know the local magnetic field at its site. The local magnetic field at the site of the i^th platelet consists of three terms:

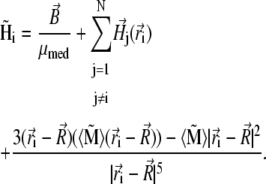(19)

The first term describes the external magnetic field, the second term describes the magnetic field created by all platelets except the i^th one, and the third term describes the field created by the magnetite cluster. The third term in Eq. 19 can be neglected because 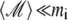(see estimates in Magnetic Moment of the Maghemite Platelet, and Magnetic Moment of the Maghemite Cluster).

It follows from Eq. 19 that the local magnetic field 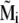is determined by the magnetic moments of the platelets. Thus Eqs. 3 and 19 have to be treated iteratively. In the 0^th order of approximation, 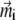values are assumed to be aligned along the x axis, which corresponds to the energetically most favorable configuration. The expression for the magnetic moment of a platelet is then given by

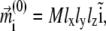(20)

where 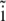is the basis vector of the x axis. Substituting Eq. 20 into Eq. 19 one obtains the first-order approximation of the local magnetic field at the site of the i^th platelet

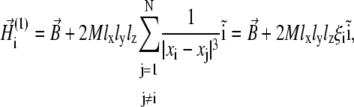(21)

where x_i is the x-coordinate of the i^th platelet and 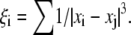Substituting Eq. 21 into Eq. 3, one yields the first-order approximation for :

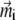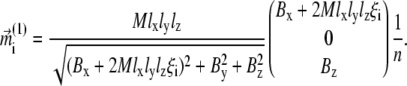(22)

Here B_x, B_y, and B_z are the x, y, and z components of the external magnetic induction vector, respectively. The iterative procedure should be continued until 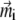and 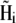do not change more than a given threshold value. Then the potential energy 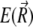of the magnetite cluster reads as

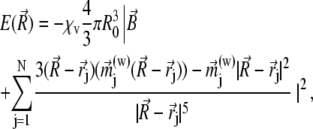(23)

where (w) is the approximation-order of the magnetic moment of a platelet. If w = 1, then the expression for 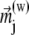is given in Eq. 22. From Eq. 23, one calculates the force acting on the magnetite cluster according to

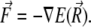(24)

Model of interacting dipoles of finite size

In this subsection we extend our model and account for the finite size of the maghemite platelets and of the magnetite cluster. We will consider these particles as bodies with homogeneous magnetic moments.

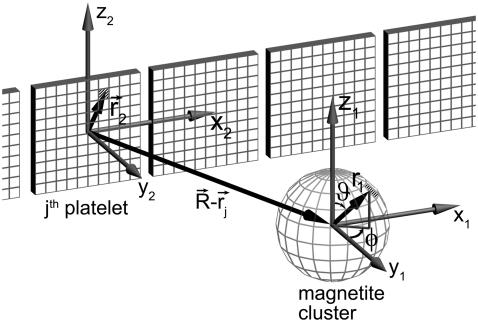
By splitting the platelets and the cluster into infinitesimal parts and integrating over their volumes it is possible to calculate the interaction energy of a magnetite cluster with the platelets and with the external field (see Fig. 4). The magnetic field created by an infinitesimal part of the maghemite platelet is given by

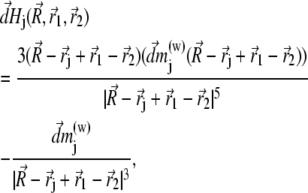(25)

where 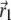is the vector from the center of the magnetite cluster to a point inside its volume, 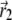is the vector from the center of the platelet to a point inside its volume, 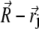is the vector from the center of the j^th platelet to the center of the cluster (see Fig. 4), and is

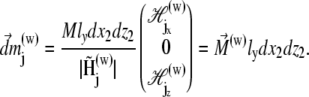(26)

FIGURE 4.

Illustration of the integration scheme used in the model of interacting dipoles of finite size. Coordinate frames used for the integration over the volume of the magnetite cluster (x₁, y₁, z₁) and over the maghemite platelets (x₂, y₂, z₂) are indicated. The splitting of the platelets and of the cluster into infinitesimal parts is schematically shown. The infinitesimal part inside the cluster is characterized by the vector 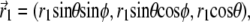while the infinitesimal part inside a platelet is characterized by the vector 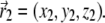The vector 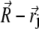connects the center of the j^th platelet with the center of the cluster.

Substituting Eq. 26 into Eq. 25 and integrating over dx₂ and dz₂, one obtains the field created by a platelet:

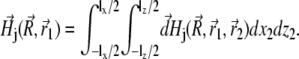(27)

The integration of Eq. 27 in its general form is not trivial. Therefore, we will use reasonable simplifications allowing the analytical solution of Eq. 27. We assume

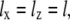(28)

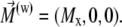(29)

Equation 29 will be discussed in the next section in more detail. With these assumptions the expression for the magnetic field components created by the platelet with index j at the point defined by the vector 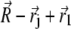is given by

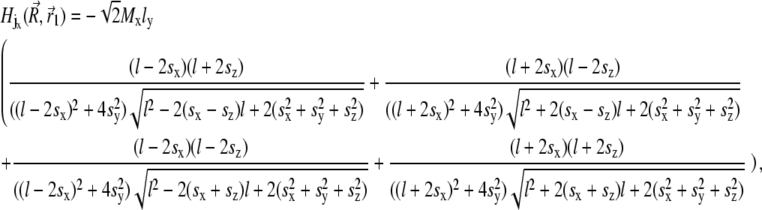(30)

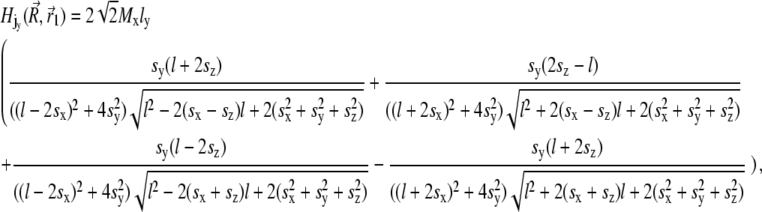(31)

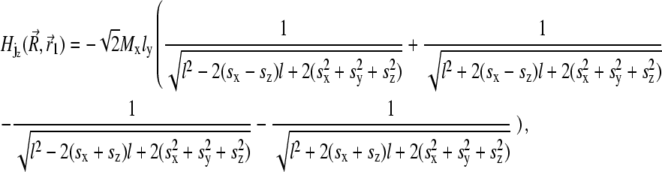(32)

where s_x = x − x_j + x₁, s_y = y − y₁, and s_z = z − z₁. Thus, the potential energy of the magnetite cluster follows as

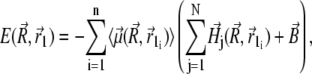(33)

where i specifies a certain nanomagnet within the magnetite cluster. Here n denotes the total number of nanomagnets and 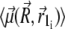is the average magnetic moment of the i^th nanomagnet defined by vectors and 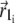(see Fig. 4). The sum in Eq. 33 can be replaced by an integration over the volume of the cluster

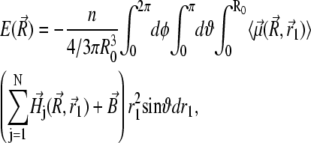(34)

where r₁, ϑ, and φ represent in spherical coordinates (see Fig. 4). The average magnetic moment of a nanomagnet is defined as (see Eq. 13)

(35)

Substituting Eq. 35 into Eq. 34 yields

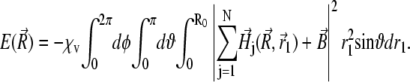(36)

The force that acts on the cluster can be calculated according to the general relation equation (Eq. 24).

RESULTS AND DISCUSSION

In this section the magnetoreception mechanism is discussed in detail. First, we present the potential energy surfaces of the magnetite cluster calculated at different orientation of the external magnetic field and discuss the differences. From the potential energy surfaces, we calculate the forces that act on the magnetite cluster and show the differences arising at different orientations of the external magnetic field. In Pointlike Dipoles, we assume all particles in the system to behave like pointlike dipoles, while in Dipoles of Finite Size we account for their size. In Model for a Transducer Mechanism, the transducer mechanism of the geomagnetic field is discussed. In Role of the Nonmagnetic Vesicle, we suggest several possible roles of the nonmagnetic vesicle, which might play an important role in the magnetoreception process. Experimental confirmations of the suggestions are necessary.

Pointlike dipoles

Fig. 5 shows the potential energy of the magnetite cluster as a function of coordinates x and y, while z = 0 μm (see Fig. 2), calculated at different orientations of the external magnetic field vector. Fig. 2, a–c, shows the potential energy surfaces calculated for three different orientations of the external magnetic field vector corresponding to alignment along the x, y, and z axes of the considered coordinate frame, respectively. In this calculation, the maghemite platelets and the magnetite cluster are considered as pointlike dipoles. However, because of their real dimensions, an excluded region exists on the potential energy surface, where the magnetite cluster cannot be placed. The maghemite platelets in Fig. 5 are shown with solid rectangles. The shaded rectangle in the center of the potential energy surfaces defines the excluded region for the magnetite cluster.

FIGURE 5.

Potential energy surfaces of the magnetite cluster calculated in the case when the maghemite platelets and the magnetite cluster are assumed pointlike dipoles. The potential energy surfaces are shown as a function of its x and y coordinates, while z = 0 μm (see Fig. 2) calculated at different orientations of the external magnetic field vector: magnetic field vector aligned along the x axis (a); magnetic field vector aligned along the y axis (b); and magnetic field vector aligned along the z axis (c). The maghemite platelets are shown with solid rectangles. The shaded rectangle in the center of the potential energy surfaces shows the region where the magnetite cluster can not be placed due to the finite size of the particles in the system. The energy scale is given in eV to the right of the contour plots. The equipotential lines are shown for the energies −0.03, −0.06, −0.12, −0.24, −0.48, and −0.96 eV. The region of the potential energy surface near the maghemite platelets chain tip is shown to the left of the corresponding surface with greater resolution. The equipotential lines in these contour plots are shown for the energies −1, −2, −3, −4, −5, −6, −7, −8, and −9 eV.

In the calculations, the external magnetic field strength was assumed 0.5 G, being a typical value of the earth magnetic field strength. The potential energy surfaces shown in Fig. 5 were calculated using Eq. 23 with w = 1, corresponding to the first order of approximation of the magnetic moments of the platelets.

To study the accuracy of the first-order approximation in Fig. 6, we plot the difference between the potential energy surface of the magnetite cluster calculated with w = 1 and with w = 4, assuming that the external magnetic field is oriented along the z axis (see Fig. 2). Fig. 6 shows that the energy difference between the two approximations is <3 meV, being maximal when the energy of the magnetite cluster is <−1 eV (see Fig. 5). Therefore we conclude that with w = 1 it is possible to calculate the potential energy surface of the magnetite cluster with an error of <1%.

FIGURE 6.

The difference between the potential energy of the magnetite cluster calculated in the first and in the fourth orders of approximation using Eq. 23. The energy scale is given in meV. The equipotential lines are shown for the energies −0.2, −0.5, −1.0, −1.5, −2.0, −2.5, and −3.0 meV. The external magnetic field is directed along the z axis.

The reason why corrections of higher order do not influence the potential energy surface of the magnetite cluster significantly can be understood if one considers the magnetic moment of the platelets calculated at different orders of successive approximation. The x and z components of the magnetic moments of the 10 platelets obtained with w = 0, 1, 2, 4, and 10 are compiled in Table 1, with the external magnetic field oriented along the z axis. Since the magnetic moment of a platelet rotate only in the (x,z)-plane, its y component is zero. From Table 1 it is clear that accounting for approximations of higher orders does not change the direction of the magnetic moments significantly. The reason for that is that the external magnetic field is of the order of 0.5 G, being significantly lower than the magnetic field created locally by the platelets. Therefore the magnetic moments of the platelets are aligned along the x axis with only a small deviation in the z direction (see Table 1). Comparing the magnetic moments obtained with w = 1 and w = 10, one concludes that the first-order approximation describes the magnetic moments of the platelets with a reasonable accuracy (deviation ≈ 10⁻³). In further considerations, the first-order approximation will be used, since it describes the essential physics of the system and provides a relatively simple analytical expression for the potential energy.

TABLE 1.

Magnetic moments of the maghemite platelets of the magnetoreceptor unit (see Fig. 2) calculated at different orders of successive approximation, w

	Magnetic moment of a platelet () eV/G
N	w = 0	w = 1	w = 2	w = 4	w = 10
1	(3.212, 0)	(3.116, 0.173)	(3.119, 0.127)	(3.118, 0.145)	(3.117, 0.150)
2	(3.212, 0)	(3.120, 0.095)	(3.121, 0.031)	(3.121, 0.040)	(3.121, 0.044)
3	(3.212, 0)	(3.120, 0.090)	(3.121, 0.042)	(3.121, 0.056)	(3.121, 0.061)
4	(3.212, 0)	(3.120, 0.088)	(3.121, 0.043)	(3.121, 0.054)	(3.121, 0.058)
5	(3.212, 0)	(3.120, 0.088)	(3.121, 0.043)	(3.121, 0.054)	(3.121, 0.058)
6	(3.212, 0)	(3.120, 0.088)	(3.121, 0.043)	(3.121, 0.054)	(3.121, 0.058)
7	(3.212, 0)	(3.120, 0.088)	(3.121, 0.043)	(3.121, 0.054)	(3.121, 0.058)
8	(3.212, 0)	(3.120, 0.090)	(3.121, 0.042)	(3.121, 0.056)	(3.121, 0.061)
9	(3.212, 0)	(3.120, 0.095)	(3.121, 0.031)	(3.121, 0.040)	(3.121, 0.044)
10	(3.212, 0)	(3.116, 0.173)	(3.119, 0.127)	(3.118, 0.145)	(3.117, 0.150)

The values in the table correspond to the x and z components of the magnetic moments are indicated as 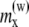and 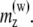The y component of the magnetic moments is 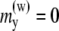eV/G. The external magnetic field is aligned along the z axis.

The potential energy surfaces calculated for the x, y, and z orientations of the external magnetic field are shown in Fig. 5, a–c, respectively. The potential energy surfaces for these three cases are similar, although some differences can be observed. For instance, the potential energy surfaces corresponding to the x and z orientations of the external magnetic field have axial symmetry along the y = 0 μm, z = 0 μm axis, while the potential energy surface corresponding to the y orientation of the external magnetic field has point symmetry with respect to the point (5.45,0) μm. At y ≈ ± 0.7 μm, z = 0 μm, there are two valleys with several minima whose steepness is determined by the external magnetic field.

Additionally, there are two strong minima at the tips of the platelet chain with the energy of ∼−8.5 eV. This is significantly lower than the energy of minima in the valleys at y ≈ ± 0.7 μm, which is −2.8 eV (see plots in Fig. 5, left). This fact leads to a conclusion that the spots of most energetically favorable attachment of the magnetite cluster are at the tips of the maghemite chain. This fact is in agreement with experimental observations (28,30,31,41).

From the potential energy surface of the magnetite cluster, it is possible to calculate the force acting on it. In Fig. 7 we show three force components as a function of the x coordinate of the magnetite cluster while y = 0.8 μm and z = 0 μm (see Fig. 2). The force components were calculated with Eq. 24 for three perpendicular orientations of the external magnetic field. Fig. 7, a–c, corresponds to the magnetic field orientation along the x, y, and z axes, respectively. Solid-thin, dotted, and dashed lines in Fig. 7 correspond to the x, y, and z components of the force vector, respectively. Thick lines show the dependence of the force vector magnitude on x coordinate of the magnetite cluster.

FIGURE 7.

Force components acting on the magnetite cluster as a function of the x coordinate of the magnetite cluster, while the y and z coordinates are 0.8 μm and 0 μm, respectively (see Fig. 2), calculated at different orientations of the external magnetic field vector: plots a–c correspond to the alignment of the magnetic field vector along the x, y, and z axes, respectively. The x, y, and z components of the force vector are shown with thin-solid, dotted, and dashed lines, respectively. Thick lines show the dependence of the force vector magnitude on the x coordinate of the magnetite cluster.

From Fig. 7 it is clear that the largest force acts on the magnetite cluster at the tips of the maghemite platelet chain. Note that the z component of the force vector is zero if the external magnetic field is directed along the x and y axes. In these cases, the magnetic moments of the platelets and of the cluster are found in the (x,y)-plane, and therefore the force acting on the cluster in the z direction is zero. If the external field is directed along the z axis, then the magnetic moments of the platelets and of the cluster have a z component (see Table 1), and a z component of the force vector exists. This fact is illustrated in Fig. 7.

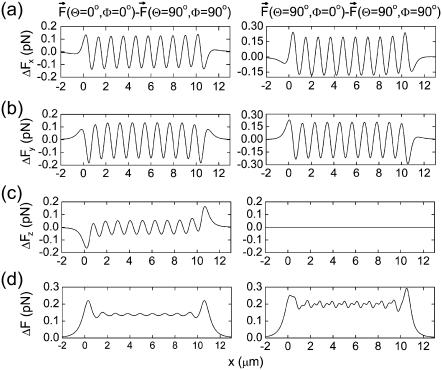
The effect of the external magnetic field on the forces acting on the magnetite cluster can be seen if one considers the differences between the forces at different orientations of the external magnetic field vector. The plots in the left part of Fig. 8 show the difference between the force components corresponding to the change of external magnetic field orientation from x to z, while the plots in the right part of the figure show the differences between the force components corresponding to the change from x to y orientation. Fig. 8, a–c, shows the differences arising in the x, y, and z components of the force vector as a function of the x coordinate of the magnetite cluster. The x dependence of the magnitude of the force difference vector is shown in Fig. 8 d. Fig. 8 shows that the 90° change in the direction of the external magnetic field changes the force acting on the magnetite cluster by 0.1–0.2 pN (see Fig. 8 d). In the next subsection we show how this force change influences the probability of opening the mechanosensitive ion channels.

FIGURE 8.

Difference in force components acting on the magnetite cluster at different orientations of the external magnetic field vector. The plots in the left part of the figure show the difference between the force components corresponding to the change of external magnetic field orientation from x to z, while plots in the right part of the figure show the differences between the force components corresponding to the change from x to y orientation are shown. Plots a–c show the differences arising in the x, y, and z components of the force vector as a function of the x coordinate of the magnetite cluster. The x dependence of the magnitude of the force difference vector is shown in plot d of the figure. The y and z coordinates of the magnetite cluster are 0.8 μm and 0 μm, respectively.

Model for a transducer mechanism of the geomagnetic field

In this subsection a model for a transducer mechanism of the geomagnetic field based on the magnetite clusters interacting with maghemite platelets and the external field is discussed. The suggested model is based on the magnetic interactions that arise between the magnetite clusters and the chain of maghemite platelets. We present two possible transducer mechanisms as the connection between the cluster and the membrane is not fully understood.

The magnetite-containing endings are embedded in the layers of adipose tissue, which apparently function as shock-absorbers, while the whole assembly is supported by the bone adding to its stability. It would be impossible to make the system work if it was embedded in muscle or other soft tissue. It should be technically feasible to remove the layer of skin with the sensory endings still attached to the afferent nerves and perform gentle distortions that may mimic effects of magnetic fields. This kind of data may hint to the preferential direction and magnitude of the expected dendrite deformations.

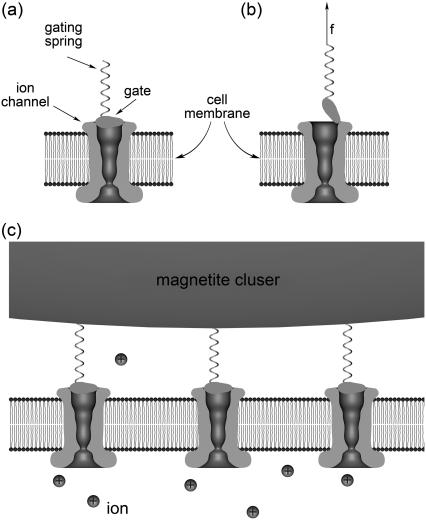
Depending on the magnetic field strength the magnetite cluster can exert forces on the membrane and activate certain mechanosensitive ion channels increasing the flux of ions into the cell. Gating these channels will alter the membrane potential and produce a receptor potential that can be transmitted to other cells and thus influence the behavior of the bird. A typical example of a mechanosensitive ion channel is the transduction channel of a hair cell (for review, see (52–56)). A schematic illustration of an ion channel gated by mechanical force is shown in Fig. 9. The channel is assumed to have two conformations, closed (see Fig. 9 a) and open (see Fig. 9 b). Because the gate swings through a distance λ upon opening, an external force f changes the energy difference between open and closed states and can bias the channel to spend more time in its open state. The gating springs are connected to the magnetite cluster (see Fig. 9 c) that produces an external pull on the gates. The magnitude of the external force can be estimated. Consider an animal rotating by 90°. The direction of the earth's magnetic field lines through the sensor changes, causing a force difference of ∼0.2 pN (see Pointlike Dipoles), which is transmitted to the membrane.

FIGURE 9.

Schematic illustration of the gating-spring transducer mechanism of the geomagnetic field. The opening/closing of the mechanosensitive ion channel is regulated by the gate, which is connected to an elastic element, the gating spring. The channel has two conformations, closed (a) and open (b), being in thermal equilibrium. The gating springs are connected to the magnetite cluster (c), which produces an external pull on the gates.

If the work done in gating the channel is ΔE and the equilibrium probability of the open state is p_O, then, according to the statistical physics,

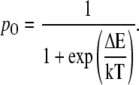(37)

Assuming that the magnetite cluster exerts a pull on the gate, then the expression for ΔE reads as (57,58)

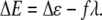(38)

Here the first term represents the change of the intrinsic energy between the open and the closed states of the channel and the second term shows the work of the external force required for opening the channel. The value λ is the displacement value of the gate. For the mechanosensitive ion channels in hair cells, λ ≈ 4 nm (53,57). Substituting Eq. 38 into Eq. 37, one obtains the probability for the channel to be open in the presence of external force:

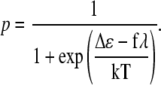(39)

Thus, the change of channel opening probability due to the applied force is

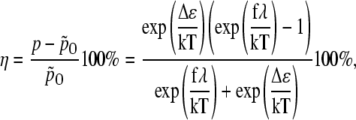(40)

where is the probability for the channel to be open if no external force is applied (i.e., f = 0). Usually (57) it is assumed that Δɛ = 0, but in general it is not because the gate can build hydrogen bonds with the membrane, which become broken when the gate is opened. Thus, Δɛ > 0.

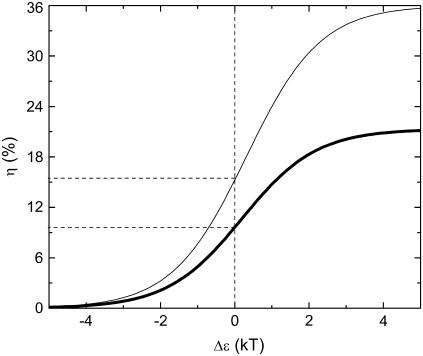
In Fig. 10 we show the dependence of the change of channel opening probability, η on Δɛ (thick line). This curve was obtained for f = 0.2 pN. From Fig. 10 and from Eq. 40 follows that the change of channel opening probability saturates at large values of Δɛ. The limiting value is 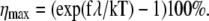For the given f, Δx, and T, η_max = 21%, being the maximal change of channel opening probability possible in the suggested mechanism. If Δɛ = 0, then η₀ = 9.6%. If Δɛ is positive, then η is somewhere between η₀ and η_max.

FIGURE 10.

Change of the mechanosensitive ion channel opening probability calculated as the function of the intrinsic energy between the open and the closed states of the channel. Thick line corresponds to the gating-spring transducer mechanism and thin line corresponds to the mechanism based on the elastic deformation of the membrane (thin line). The change of channel opening probability for the gating-spring transducer mechanism and for the mechanism based on the elastic deformation of the membrane were calculated using Eqs. 40 and 50, respectively.

Another possible transducer mechanism of the geomagnetic field is based on the elastic deformation of the membrane. The deformation mechanism might arise in addition to the gating mechanism or be an alternative to it. It is difficult to specify the precise transducer mechanism, because little information is available on the structure that connects the magnetite clusters with the cell membrane.

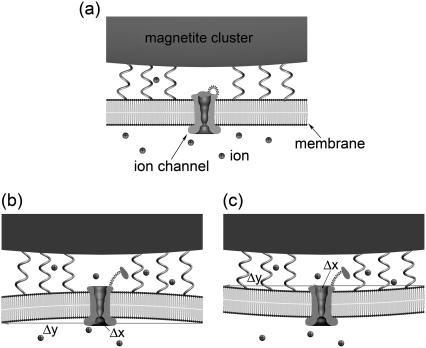
Let us discuss the deformation mechanism of the channel opening. Fig. 11 a shows the nondeformed membrane, while Fig. 11, b and c, shows the possible membrane deformation caused be either pull (see Fig. 11 b) or push (see Fig. 11 c) of the magnetite cluster on the membrane. Both deformation cases are physically identical, since the work needed to deform the membrane in both cases is equal. The connections of the magnetite cluster with the membrane are shown schematically with the springs. Note that the ion channel, the membrane and the magnetite cluster in Fig. 11 are drawn approximately in the correct scale, while the ions are shown schematically. The nondeformed membrane corresponds to the case of low magnetic field acting on the magnetite cluster (see Fig. 11 a), while an increase in the magnetic field strength creates a stress situation (see Fig. 11, b and c).

FIGURE 11.

Schematic illustration of the transducer mechanism of the geomagnetic field based on the elastic deformation of the membrane. The external magnetic field causes the change in the pressure that the magnetite cluster puts on the cell membrane, causing its deformation. The nondeformed membrane corresponding to the case of low magnetic field is shown in part a of the figure. The increase of the magnetic field creates a stress situation leading to the membrane deformation caused by either pull (b) or push (c) of the magnetite cluster on the membrane. The magnetite cluster is shown schematically atop the membrane. The connections of the magnetite cluster with the membrane is shown with the springs. Note that the ion channel, the membrane, and the magnetite cluster are drawn approximately in the correct scale, while the ions are shown schematically.

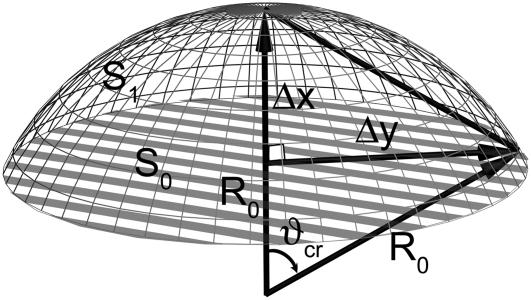
With f being the force difference and γ being the membrane surface tension coefficient, the deformation criteria is given by

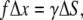(41)

where Δx is the displacement of the cluster and ΔS is the change of the membrane surface area. Assuming that the membrane deformation has a spherical profile with the same radius as the magnetite cluster one can introduce two deformation increments, Δx and Δy, which describe the deformation region (see Fig. 11 b and Fig. 12). The assumption on the deformation radius of the membrane is correct near the point where the force is applied (59). This is a well-known fact from mathematical physics of elastic membrane deformation (59). From simple geometrical considerations (see Fig. 12) follows

(42)

where R₀ is the radius of the magnetite cluster and Δy is the radius of the deformation zone (see Fig. 11 b). The magnetite cluster deforms a certain area of the membrane. Let S₀ and S₁ be this area in the normal and stress cases, respectively (see Fig. 12),

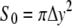(43)

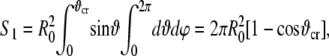(44)

where ϑ_cr is defined in Fig. 12 as

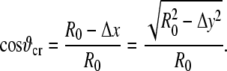(45)

Substituting Eq. 45 into Eq. 44, one obtains the final expression for S₁. The change of membrane area of deformation is then given by

(46)

Substituting Eq. 46 into Eq. 41, one obtains

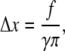(47)

with Δx being the characteristic value of membrane deformation. Finally, substituting Eq. 47 into Eq. 46, one obtains

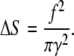(48)

Note that Δx and ΔS do not depend on the radius of membrane deformation. The work, A, on membrane deformation is given by

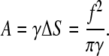(49)

Thus the change in channel opening probability caused by the membrane deformation is

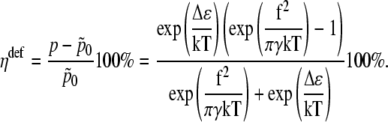(50)

FIGURE 12.

Schematic illustration of the membrane deformation caused by the external magnetic field. The values Δx and Δy are the deformation increments describing the membrane deformation, R₀ is the radius of the deformation, and S₀ and S₁ are the areas of the membrane deformation region corresponding to the nondeformed and stress cases, respectively.

In Fig. 10 we show the dependence of the change of channel opening probability caused by the membrane deformation, on Δɛ (thin line). This curve was obtained for f = 0.2 pN and γ = 0.01 dyn/cm = 10⁻⁵ N/m, which is the typical surface tension coefficient of a membrane (60–68). The tension of membranes has been extensively studied during the last decades. For review, we refer to the literature (65–73). The resting tension of chicken neurons was estimated 3 × 10⁻⁶ N/m (66). The tension in normal molluscan neuron is 4 × 10⁻⁵ N/m (67). The elastic shear modulus of a red blood cell was measured as 6.6 × 10⁻⁶ N/m (68). In this article, we do not discuss the differences in different tension coefficients published earlier. This question will be considered in the future. Therefore we use a characteristic value of membrane tension equal to 10⁻⁵ N/m. The maximal value of η^def is 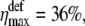being 1.7 times greater than in the case of the gate-spring mechanism discussed above. If Δɛ = 0, then Since Δɛ is expected to be positive, then 15% < η^def < 36%.

We have shown that in both of the considered transducer mechanisms, the forces the magnetite cluster exerts on the membrane are sufficient to influence the probability of the mechanosensitive ion channel opening. From the performed analysis it follows that the change of magnetic force caused by a 90° change of the external geomagnetic field produce a change in channel opening probability in the range of 15–30%. Semm and Beason (74) have suggested that the bird's magnetoreceptory system can respond to a 1% change of the normal geomagnetic field. The change of the geomagnetic field on 0.01 G changes the forces acting on the magnetite cluster on ∼0.004 pN. This leads to the change of channel opening probability of ∼0.5%.

Another important feature of the suggested magnetoreception mechanism, which is worth noting, is the so-called safety principle. Experiments of Fleissner et al. show that the dendrite contains ∼10–15 magnetoreceptor units, which have a similar behavior in the external magnetic field. When the dendrite is subject to the external field, the repetition of the magnetoreceptor units increases the functional safety of the whole dendrite magnetoreception process.

Dipoles of finite size

To account more precisely for the interaction of the magnetite cluster with the chain of maghemite platelets, in this section we account for their sizes. The aim of this discussion is to strengthen the suggested magnetoreception mechanism that was shown to be feasible in the model case of interacting pointlike dipoles.

The potential energy surface of the magnetite cluster is shown in Fig. 13 as a function of coordinates x and y, while z = 0 μm (see Fig. 2). The surfaces shown in Fig. 13, a–c, were calculated for the external magnetic field vector oriented along the x, y, and z axis, respectively. Similar to Fig. 5 the excluded region on the potential energy surfaces in Fig. 13 is shown with the shaded rectangle in the center of the potential energy surfaces. The maghemite platelets are shown in Fig. 12 with solid rectangles.

FIGURE 13.

Potential energy surfaces of the magnetite cluster calculated in the case when the integration over the volume of the maghemite platelets and of the magnetite cluster is performed. The potential energy of the magnetite cluster is plotted as a function of x and y coordinates of the magnetite cluster, while z = 0 μm (see Fig. 2). The energy is calculated at different orientations of the external magnetic field vector. Plots a–c correspond to the alignment of the external magnetic field along the x, y, and z axes, respectively. The maghemite platelets are shown with solid rectangles. The shaded rectangle in the center of the potential energy surfaces shows the region where the magnetite cluster cannot be placed due to its finite size. The energy scale is given in eV. The equipotential lines are shown for the energies −0.03, −0.06, −0.12, −0.24, −0.48, and −0.96 eV.

The potential energy surfaces in Fig. 13 were calculated with the use of Eq. 36 (see Model of Interacting Dipoles of Finite Size for details) and are topologically close to the corresponding potential energy surfaces obtained for the pointlike dipoles shown in Fig. 5. The potential energy surfaces shown in Fig. 13 have two strong minima at the tips of the maghemite platelets chain, which are also found in the pointlike dipole model (see Fig. 5). The energies of these minima in Fig. 13 are −15.6 eV, being 7.1 eV lower than the corresponding value for the pointlike dipoles. The fact that the minima are found in both models proves that the energetically most favorable attachment of the magnetite cluster occurs at the tip of the maghemite platelets chain.

Another significant difference between the potential energy surface for the pointlike dipoles and dipoles of finite size concerns the valleys at y ≈ ± 0.7 μm, z = 0 μm, which are found for the pointlike dipoles and are absent for the dipoles of finite size (see Figs. 5 and 13). The reason why the valleys vanish is a simple one. The distance between the maghemite platelets is 0.1 μm, while the size of a platelet is 1 μm. The direction of magnetic moments of the platelets does not change much if the direction of the external magnetic field changes (see discussion in Pointlike Dipoles) and therefore the chain of platelets behaves like a solid magnetic bar, which attracts magnetic particles only at its tips.

In Pointlike Dipoles it was shown that an important characteristic, which determines the feasibility of the magnetoreception mechanism, is the difference between the forces acting on the magnetite cluster at different orientations of the external magnetic field vector. The force differences calculated for the dipoles of finite size are shown in Fig. 14. The plots in the left part of Fig. 14 show the differences between the force components arising due to the x → z change of the direction of the external magnetic field vector, while plots in the right part of the figure show the differences between force components arising due to the x → y change. Fig. 14, a–c, show the differences arising in the x, y, and z components of the force vector as a function of the x coordinate of the magnetite cluster. The x dependence of the magnitude of the force difference vector is shown in Fig. 14 d. In the case of dipoles of finite size, the characteristic change in force caused by the external field of 0.5 G is 0.05–0.1 pN (see Fig. 14 d), which is ∼2–3 times lower than the value obtained for the case of pointlike dipoles (see Fig. 8).

FIGURE 14.

Difference in forces acting on the magnetite cluster at different orientations of the external magnetic field vector calculated in the case when the integration over the volume of the maghemite platelets and of the magnetite cluster is performed. Plots in the left part of the figure show the difference between the force components arising due to the x → z change of the direction of the external magnetic field vector, while plots in the right part of the figure show the differences between force components arising due to the x → y change. Plots a–c show the differences arising in the x, y, and z components of the force vector as a function of the x coordinate of the magnetite cluster. The x dependence of the magnitude of the force difference vector is shown in plot d of the figure. The y and z coordinates of the magnetite cluster are 0.8 μm and 0 μm, respectively.

Thus, substituting ΔF = 0.1 pN in Eqs. 40 and 50 one obtains the change in channel opening probability in the gating-spring transducer mechanism, η, and in the mechanism based on the elastic deformation of the membrane, η^def. Thus, η₀ = 5%, η_max = 10% and Note that the values of η^def are smaller than the values of η. This happens because the work performed in the gating-spring transducer mechanism is linearly proportional to the force (see Eq. 38), while the work performed on the membrane deformation is proportional to its second power (see Eq. 49). Therefore the channel opening probability in the mechanism based on the elastic deformation of the membrane decreases faster with decrease of the applied force.

Fig. 14 shows that, away from the tips of the maghemite chain, the force differences are significantly smaller than the force differences at the tips (see Fig. 14 d). Note that this is different from the case of pointlike dipoles, where the force differences were of approximately the same order of magnitude along the whole chain of maghemite platelets (see Fig. 8 d). This happens because in the case of dipoles of finite size there are no valleys on the potential energy surface at y ≈ ± 0.7 μm, z = 0 μm, which are present for the pointlike dipoles, causing additional forces on the magnetite cluster in this region.

Role of the nonmagnetic vesicle

As discussed in the Introduction, dendrites contain maghemite platelets, magnetite clusters, and the nonmagnetic vesicle. In the previous sections it was shown that the maghemite platelets and the magnetite clusters play a very important role in the magnetoreception mechanism. However, the role of the nonmagnetic vesicle is still a matter of discussion since little experimental information is presently available.

In the latest experiment by Fleissner et al. (40), it was demonstrated that the vesicle might be located in the center of the dendrite and is probably covered by some noncrystalline iron-substance. The diameter of the vesicle was estimated to be ∼3–5 μm (28,30,31,40).

We believe that since the vesicle is found in the dendrite it should play a certain role in the magnetoreception process of birds and therefore we suggest two hypotheses that might explain how the vesicle is involved in this phenomenon.

The first possible function of the vesicle is the divider-function. Indeed, from the potential energy surfaces in Figs. 5 and 13, it follows that the force acting on the magnetite clusters rapidly increases if the distance between the platelets and the cluster decreases. Hence, without the nonmagnetic vesicle the magnetite clusters is free to stick anywhere to the chain of maghemite platelets, in which case no further magnetic field effects will be possible. Therefore, one possible role of the vesicle might be to prevent the clusters from getting close to the chain of maghemite platelets. With the size of ∼5 μm it keeps the walls of the cell membrane far apart, acting as a divider and protecting the dendrite from collapse.

In addition to the divider-function the vesicle might be a sort of iron-reservoir, which provides iron for the maghemite platelets and magnetite cluster formation. This idea is inspired by experimental findings (28,30,31,40), showing that the vesicle seems to be covered with some nonmagnetic iron material. However, at present it is still not clear how the magnetite clusters and the maghemite platelets emerge in the beak of birds and how the size of the magnetoreceptor unit evolves with the age of the animal. The young bird dendrite might have no magnetic platelets or clusters, which might appear only at a later age, crystallizing from the iron contained in the vesicle. To verify this assumption, one has to perform experiments on birds of different age and determine how the vesicle, maghemite platelets, and magnetite clusters change/grow with the age of an animal.

CONCLUSION

In this article, a possible mechanism of avian orientation in a magnetic field is discussed. The mechanism is based on the experimental findings of Fleissner et al. (31,41), which proved the existence of two types of magnetic minerals in the beak of birds, namely the maghemite platelets and magnetite clusters.

It was shown that, in the external magnetic field, the magnetite clusters will experience an attractive (repulsive) force leading to their displacement, which induces a primary receptor potential via strain-sensitive membrane channels leading to a certain orientation effect of a bird. Note that the discussed mechanism is very different from the magnetite-based magnetoreception mechanism suggested by other authors (27,29,35,42–44) because it involves two different types of iron minerals.

Based on the analysis of forces acting on the magnetite particles we showed that the considered iron-mineral system can deal as a magnetoreceptor unit with distinct orientational properties. We demonstrated that—depending on the orientation of the external magnetic field—the pressure on the cell membrane can change significantly leading to different nerve signals. The nerve signals are thought to be delivered to the brain causing a certain orientational behavior of the bird. We suggested and analyzed two transducer mechanisms of the geomagnetic field based on opening/closing of mechanosensitive ion channels. Based on the analysis of forces exerted on the membrane, we calculated the probability of the channel opening.

In this article, we show qualitatively and quantitatively the possibility of the iron-mineral based magnetoreception mechanism. However, many questions remain open and need further investigation. For example, the role of the big nonmagnetic vesicle found in the dendrite is still not clear and needs further experimental investigation. To answer this question, one should perform experiments on birds of different age and determine how the vesicle, maghemite platelets, and magnetite clusters change/grow with the age of an animal. The precise spatial structure of the dendrite is also an open question. It would be interesting to perform experiments similar to the literature (31,41) but without disturbing the dendrite (e.g., by computer tomography or x-ray analysis) to confirm the spatial location of the maghemite platelets and the magnetite clusters precisely. The connection of the magnetite clusters to the cell membrane should also be studied in a more careful systematic way.

Another problem concerns the analysis of influence of oscillating magnetic (and electrical) fields on the magnetoreception mechanism. The analysis of field frequencies at which the magnetoreception is violated can be used to suggest certain experimental conditions for probing the magnetoreception mechanism in birds.

We believe that the suggested magnetoreception mechanism is a realistic candidate for the magnetoreception mechanism in birds, which might also be responsible for magnetosensation in other animals like fishes (32), salamanders (5–8), bees (9–13), and others. Unfortunately, lack of sufficient information about magnetic particles in these species hinders us to draw conclusions about their precise magnetoreception mechanism. However, we believe, that the magnetoreception mechanism should be general for all kinds of animals with, probably, minor alternations. Therefore, when more experimental data regarding the magnetic particles in animals become available, the present investigation can be extended to a more general description.