The Extent of Cooperativity of Protein Motions Observed with Elastic Network Models Is Similar for Atomic and Coarser-Grained Models

Abstract

Coarse-grained elastic network models have been successful in determining functionally relevant collective motions. The level of coarse-graining, however, has usually focused on the level of one point per residue. In this work, we compare the applicability of elastic network models over a broader range of representational scales. We apply normal mode analysis for multiple scales on a high-resolution protein data set using various cutoff radii to define the residues considered to be interacting, or the extent of cooperativity of their motions. These scales include the residue-, atomic-, proton-, and explicit solvent-levels. Interestingly, atomic, proton, and explicit solvent level calculations all provide similar results at the same cutoff value, with the computed mean-square fluctuations showing only a slightly higher correlation (0.61) with the experimental temperature factors from crystallography than the results of the residue-level coarse-graining. The qualitative behavior of each level of coarse graining is similar at different cutoff values. The correlations between these fluctuations and the number of internal contacts improve with increased cutoff values. Our results demonstrate that atomic level elastic network models provide an improved representation for the collective motions of proteins compared to the coarse-grained models.

Introduction

Elastic Network Models^1–3 have been quite successful in predicting the large-scale motions of proteins and other biological structures, even for such large complexes as the ribosome^4–6. These models originated from the theory of polymer networks^7,8 using the pioneering idea of Tirion³, who proposed a single uniform spring constant parameter for all atom-atom contacts used in a normal mode analysis. Elastic Network applications have usually focused on coarse-grained representations of proteins, using mostly C^α-atoms and relying upon C^α-C^α proximity for placement of springs. The predicted position fluctuations of amino acids in proteins obtained from Elastic Network Models usually give quite good agreement with experimental B-factors measured by crystallographers, but as we will see here more detailed atomic models yield similar, if slightly better results. This is an important finding that may be particularly important for developing mixed coarse-grained models wherein the functionally important part of the protein is represented by atoms and the remainder of the structure is rendered in lesser detail. The only information utilized in Elastic Network Models is the structure of the protein, from the Protein Data Bank (PDB)⁹, but this approach can also be applied to hypothetical protein models based on sequence similarities or other techniques. The essential aspect of these models is a representation of proteins as highly interconnected structures, which represents well their cohesive and cooperative nature. It has been shown that fluctuations of residues in proteins depend mostly on the packing density and that the slowest modes corresponding to the motions of large domains depend essentially on the protein shape^10,11. Elastic Network Models have been useful in studies of protein binding¹² and the analysis of the binding pocket flexibility¹³.

One of the strengths of the Gaussian Network Model is its success in the determination of functionally significant collective motions in proteins with an extremely simple model based only on packing density and geometry. However, does such a simple model, which does not differentiate between various bonded and non-bonded interactions (such as covalent and hydrogen bonds), produce physically meaningful results? There is strong evidence that it actually does. First, the accumulated normal mode analysis results demonstrate clearly that GNM produces experimentally-verifiable results, e.g. for X—ray analysis^2,14, NMR¹⁵, hydrogen-exchange¹⁶, and cryo-EM^4,17,18 experiments. Second, the normal mode results correlate well with results of molecular dynamics (MD) simulations¹⁹ based on detailed atomistic force fields. These studies have proven that the normal mode analysis using coarse-grained models is extremely useful, and that collective motions derived from the equilibrium structure depend largely on the shape of the protein, rather than on particular types of interactions^10,11. A lack of any dependence on discriminating between bonded and non-bonded interactions is most likely due to the large number of interactions inside compact structures of biomolecules that leads to their cohesiveness and cooperativity. Essentially for large compact structures the number of covalent bonds is small compared to the number of non-bonded interactions. Note that this conclusion does not negate the differential importance of certain types of interactions for protein stability or for the folding process.

Although elastic network models have proven to provide a good description of protein collective motions, the effect of coarse-graining over the full range of scales has not been thoroughly explored. Jernigan and co-workers have mostly analyzed one end of the spectrum - coarser-grained models of proteins - and have observed that even when 40 residues of hemagglutinin A, are represented by a single node, the global motions are only slightly affected^20,21 in comparison to more detailed models. Here we will explore the other end of the spectrum, and study the effect of more detailed representations of proteins for the elastic network models. We will analyze the effect of scaling in elastic network models by comparing results obtained at varying levels of coarse-graining. These levels will include one point per residue, one point per atom for heavy atoms alone, and the case when protons are also included. Additionally we will investigate the effect of explicit inclusion of solvent molecules insofar as they are reported for high-resolution protein structures. For the residue-level coarse-graining, a single node (located at C^α) is assigned to each residue. For the atomic-level representation, each heavy atom in the protein is assigned a node, and hydrogen atoms are neglected. For the proton-level additional nodes for each hydrogen atom in the protein are included. Finally, in the explicit solvent-level representation oxygen and hydrogen atoms of the water molecules reported in the crystallographic data are also taken into account and each of these atoms is represented by a node. Our study will allow us to analyze the effects of scaling at various levels of accuracy and present a multi-scale picture of the normal mode of protein dynamics.

Previously²² we had observed a strong correlation between the entropies computed from the elastic network models with the number of internal contacts in the given protein. This corresponds to a simple view of protein stabilities, in which the number of contacts (stabilizing energy) compensates directly for the extent of motions within the structure (motional entropy). Conceivably such a simple relationship could also depend upon the level of cooperativity in the model, i.e. the cutoff distance defining both the number of contacts and their restraining effects on the motions of the protein. We have investigated this correlation for the same set of proteins and at different levels of coarse-graining with the same elastic network models.

Although normal mode analyses provide a remarkable tool for probing protein dynamics, they have some limitations: every interaction is treated identically for all contacts regardless of the contact distance or type of interaction. We have observed however that the results obtained by using residue-type specific potentials^23,24 at the residue-level coarse-graining (unpublished results) or adjusted springs based on number of contacts²⁵ are not substantially different from those obtained by using a harmonic potential with a single uniform spring constant. Furthermore, elastic network model results are comparable to those of molecular dynamics based on AMBER potential¹⁹. Here, we take a different route and explore the effect of assigning a harmonic potential with a single uniform spring constant for each pair of nodes being in contact regardless of the type of the interaction, at all of the different scales of coarse-graining.

There are other important reasons to introduce more detailed atomic level elastic network models. For other types of studies such as enzyme mechanisms²⁶, unraveling the details of molecular hinges or detailed investigations of residue conservation around hinges, further detail is likely to be important. One potential outcome from the atomic elastic networks could be the identification of specific conserved atomic groups, in more detail than residue conservation, relating to critical functional motions and flexibility, within molecular hinges, enzyme active sites or other functional loci. This could be information of importance for protein design. One of the appealing aspects of the atomic models is that they can be conveniently combined with other more coarsely grained parts of the structure (mixed coarse-graining), as has been demonstrated previously^20,21,27.

Methods

Dataset

We used search tools available on the PDB web site to find proteins with resolution better than 0.8 Å and with less than 50% sequence similarity to one another. We narrowed our list for this initial study to only eight mostly single chain proteins whose lengths range from 64 to 158 amino acids. These proteins, listed in order by their increasing size are: Type III antifreeze protein rd1 (pdb id: 1ucs) (64 residues), syntenin Pdz2 domain (1r6j) (82 residues), high-potential iron-sulfur protein (1iua) (83 residues), Lys-49 phospholipase A2 homologue (lysine 49 PLA2) (1mc2) (122 residues), cobratoxin (1v6p) (2 chains 62 residues each), bacterial photoreceptor pyp (1nwz) (125 residues), carbohydrate Binding Domain Cbm36 (1w0n) (131 residues), and E. Coli pyrophosphokinase HPPK (1f9y) (158 residues).

Multi-scale representations

Our defined models are: “Residue-level models” include only C^α atoms; “Atomic-level models” include every atom in a protein except hydrogen atoms; “Proton-level models” include every atom in a protein including hydrogen atoms; and finally, “explicit solvent-level models” include every protein atom and also every oxygen and hydrogen atom of water molecules in the crystallographic data provided in the protein PDB. If the positions of hydrogen atoms are not found in the pdb file, Accelrys DS ViewerPro is used to generate locations of missing hydrogen atoms. Ligands are removed from the protein structures and are not included in the present analyses.

Gaussian network models

The details of the Gaussian Network Model² (GNM) and its extension considering the directionalities of fluctuations - the Anisotropic Network Model¹ can be found elsewhere. The GNM originates from the theory of rubber-like elasticity^7,8 and Tirion's approach of using a uniform spring constant parameter in the harmonic analysis of protein motions³. The cohesiveness of the protein structure in the elastic network model is represented by assuming that all pairs of nodes separated by less than a certain cutoff distance are connected by uniform springs. In the standard coarse-grained version, each residue is represented by a single point ( node) positioned at its C^α atom, but we will also use an atomic version here where the points represent atoms. There are two parameters in the model: the cutoff distance R_c and the spring constant γ. The cutoff distance R_c determines whether two residues are connected by a spring, i.e. are in contact, without differentiating between bonded and non-bonded interactions. These contacts are mathematically expressed as the contact (Kirchhoff) matrix, Γ, where the ij-the element of the matrix is −1 if nodes i and j are connected by a spring, and zero otherwise, and the diagonal elements are the sums of non-diagonal elements in a given row (or column) taken with the negative sign. Because of this definition the matrix Γ is singular (its determinant is zero) and only the pseudoinverse of Γ can by calculated by using the singular value decomposition (SVD) method. It can be shown that the zero eigenvalues of Γ that are eliminated by using SVD correspond to the six external rigid body degrees of freedom. The equilibrium correlations < ΔR_i · ΔR_j> between fluctuations of residues i and j are proportional to the ij-th element of the inverse of Γ,

$$<\text{Δ}{R}_i\cdot \text{Δ}{R}_j>=\frac{3k_{B}T}{2\gamma }{({\Gamma }^{-1})}_{ij}$$ (1)

where ΔR_i and ΔR_j are the vectors representing the instantaneous displacements of the i^th and the j^th nodes from their mean positions. Here k_B is Boltzmann's constant, T is temperature and γ is is the spring constant. The mean square fluctuation < (ΔR_i)² > of the i-th node is then given by the i-th diagonal element [Γ⁻¹]_ii of the matrix Γ⁻¹. The mean square fluctuations may be compared directly with the experimental crystallographic Debye-Waller temperature factors (B-factors) usually available in the pdb files by the equation:

$$B_i=8{\pi }^2<{(\text{Δ}{R}_i)}^2>/3$$ (2)

The pseudoinverse matrix Γ⁻¹ can be expanded in the series of eigenvalues λ_k and eigenvectors u_k of the contact matrix Γ as follows:

$${\Gamma }^{-1}=\sum _k{\lambda }_k^{-1}{u}_k{u}_k^T$$ (3)

where zero eigenvalues (that physically correspond to motions of the center of mass of the system) are excluded from the summation. This eigen-expansion has a direct physical meaning by showing contributions from individual modes associated with the eigenvalues of Γ.²⁸ The i^th component of the eigenvector u_k (corresponding to the k^th normal mode) specifies the magnitude of the mean square fluctuations of the i^th node in the k^th mode. It can also be shown that all eigenvalues of Γ are non-negative. If we order eigenvalues according to their ascending values starting from zero, then the most important contributions in Eq. 3 are given by the smallest non-zero eigenvalues λ_k, that correspond to the large-scale, slow, collective modes. Slowest modes play a dominant role in the fluctuational dynamics of protein structures, because their contributions to the mean-square fluctuations scale with λ_k⁻¹. It has been shown that the most important motions of proteins^29–31 or large biological structures (such as the ribosome)^4–6,32,33 that are associated with their biological function can be clearly identified with a few slowest modes of GNM. The large-scale changes of protein conformations between ‘open’ and ‘closed’ forms, or domain swapping in proteins can be also well represented with elastic network models³⁴. Reviews of elastic network applications can be found in References 16,35.

Correlation coefficients

The usual criterion for choosing parameters is based upon achieving the best agreement between the computed fluctuations and the experimental B-factors. For this purpose, here we use the linear correlation coefficient:

$$C=\frac{{\displaystyle \sum _{i=1}^N}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{{\displaystyle \sum _{i=1}^N}{(x_i-\overline{x})}^2.{\displaystyle \sum _{i=1}^N}{(y_i-\overline{y})}^2}}$$ (4)

In this equation, N is the number of nodes, x_i and x̄ are the mean-square fluctuations of the i^th node calculated by GNM and their mean over all nodes, respectively. Similarly, y_i and ȳ are the experimentally determined B-factor for the i^th node and the mean over all nodes. The linear correlation coefficient is a straightforward way to analyze the extent of linear dependence between any two quantities. Its value can range between 1 and −1, where the limiting values 1 and −1 correspond to perfect correlation and perfect anti-correlation.

Overlaps

Absolute overlap between two eigenvectors, each representing specific motions, is defined as

$$|cos\theta |=\frac{|{\displaystyle \sum _i^n}{x}_i{y}_i|}{|\text{x}|\cdot |\text{y}|}$$ (5)

In this equation, x and y are two eigenvectors, x_i and y_i denote their i^th components and θ is the angle between x and y. If two eigenvectors are exactly collinear, then their absolute overlap equals 1. If they are orthogonal to each other, than the absolute overlap is zero, and the angle between the two eigenvectors is 90°. This provides a measure of the extent of similarity in the directions of motions for different modes.

Entropy

In the Gaussian Network Model fluctuations of residues about their mean positions obey the Gaussian distribution

$$W(\text{Δ}{R}_{\text{i}})=Aexp\{-3{(\text{Δ}{R}_i)}^2/2<{(\text{Δ}{R}_i)}^2>\}$$ (6)

The conformational entropy change ΔS_i resulting from fluctuations in the position of the i^th residue can be obtained from the equation

$$\text{Δ}{S}_i=k_{B}lnW(\text{Δ}{R}_i)=-\gamma {(\text{Δ}{R}_i)}^2/(2T{[{\Gamma }^{-1}]}_{ii})$$ (7)

Eq. 1 for the case i=j was applied in the above derivation. Equation 7 can be used to calculate the free energy increase of entropic origin contributed by the i^th residue, upon distortion ΔR_i of its coordinates

$$\text{Δ}{G}_i=-T\text{Δ}{S}_i=\frac{\gamma }{2}{(\text{Δ}{R}_i)}^2/{[{\Gamma }^{-1}]}_{ii}$$ (8)

This free energy change is inversely proportional to < (ΔR_i)² >. Physically, this signifies a stronger resistance to deformation, including unfolding, of residues subject to smaller amplitude fluctuations in the folded state.¹⁶

Results and Discussion

Choosing spring constants for different resolution scales

The Gaussian Network Model requires specification of two parameters: the spring constant that defines the strength of interactions and the cutoff distance that defines whether two given nodes are in contact or not. The spring constant ultimately scales the amplitudes of motions calculated from the contact matrix. When comparing results obtained at different scales, the spring constant should be adjusted to reflect the scale at which the protein is modeled²⁷. Here, the spring constants at each scale are calculated for each protein by comparing fluctuations predicted by GNM with experimentally determined B-factors, as this method has proven to be generally successful in the past.

Choosing cutoff radii for different resolution scales

Correlations between the GNM-derived mean-square fluctuations and crystallographic B-factors calculated from Eq. 4 clearly show the extent to which GNM results represent actual protein motions. Phillips and co-workers¹⁴ showed that GNM coarse-grained at the residue-level has a correlation of about 0.6 with these experimental data, depending on the cutoff radius and on the extent of inclusion of neighboring molecules packed in the crystal. Although 60% correlation at the residue-level is rather impressive, here we are studying the effect of including other atoms together with solvent molecules in the crystal on these correlations. Table 1 shows the correlation coefficients for C^α-atoms calculated at the residue, atomic, proton, and the explicit solvent levels for various cutoffs.

Table 1. The average correlation coefficients between computed mean square fluctuations and experimental B-factors for four different resolution levels of coarse-graining as a function of the cutoff distance.

A correlation of 1 shows perfect correlation and 0 the lack of correlation (maxima are indicated in bold).

Cutoff (Å)	Residue Level	Atomic Level	Proton Level	Solvent Level
1	--	--	--	--
2	--	0.17	0.37	0.27
3	--	0.46	0.59	0.51
4	0.17	0.61	0.58	0.42
5	0.38	0.59	0.59	0.48
6	0.38	0.57	0.59	0.52
7	0.51	0.60	0.60	0.56
8	0.55	0.60	0.61	0.56
9	0.52	0.60	0.61	0.57
10	0.56	0.60	0.60	0.58
11	0.56	0.61	0.60	0.59
12	0.54	0.60	0.60	0.59
13	0.55	0.59	0.59	0.59
14	0.55	0.58	0.59	0.60
15	0.54	0.57	0.58	0.59

The results in Table 1 show that at the residue level, the correlation increases with increasing cutoff radius reaching a peak around 11 Å as shown in Figure 1. However, the average correlation coefficient never exceeds 0.56. Although the value of this correlation is close to the result (∼0.6) obtained by Phillips¹⁴, the optimum cutoff radius (11 Å ) found here is much larger than the Phillips' optimum cutoff of 7.3 Å. One major difference is that we have neglected intermolecular contacts due to packing in crystal. It is also important to note that the number of proteins in our data set is quite limited (8 proteins only). For further comparison with the Phillips group's results¹⁴, we repeated the average correlation coefficient calculations as a function of cutoff distance with their data set of 113 proteins. These results shown in Fig. 1 indicate that for the 113-protein data set, another peak around 11.1 Å is also clearly visible. Figure 1 also demonstrates that although the 8-protein set consistently exhibits lower correlations than the 113-protein set, the average correlation coefficients of both sets have similar patterns; thus the 8-protein set seems to be sufficiently representative to make comparisons at various radii.

Figure 1. Average correlation coefficients as a function of the cutoff radius for the 8-protein set used in this study and the 113-protein set used by Phillips¹⁴.

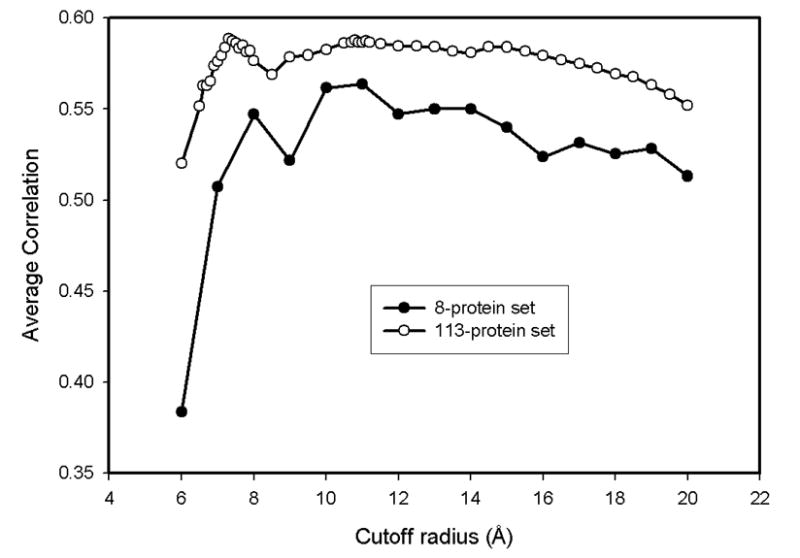
The correlation coefficients between the results of residue-level coarse-grained model and experimental B-factors for both data sets suggest two optimal cutoff radii around 7.3 Å and 11.1 Å.

Table 2 lists the optimum cutoff distances for all eight proteins for each of the four different resolution level models studied here. The correlation coefficients are also given in Table 2 in parentheses. A real surprise comes upon examination of average correlation coefficients obtained at better resolution with more detailed scales. The inclusion of other atoms in the normal mode analysis increases the average correlation coefficient for the fluctuations of the C^α-atoms by 0.05 to 0.61. This is highly interesting, because although all interactions are treated similarly, a better correlation is obtained. The inclusion of all heavy atoms clearly provides a superior representation of protein structure and protein dynamics. Interestingly, the further inclusion of protons or even atoms of the solvent does not enhance these correlations, and only shifts the optimum cutoff radius. The optimum cutoffs for various scales differ: for atomic and proton-level calculations, the optimum cutoff values are 4 Å and 9 Å, respectively, and for the explicit solvent level the optimum cutoff is 14 Å. It is worth emphasizing that the inclusion of atoms redefines the packing density critical for protein dynamics. While the consideration of protons in protein structure is associated with small uncertainties such as the ionization state of histidine, the inclusion of atoms of the explicit solvent is much more uncertain. At least it is encouraging that there is no visible loss of correlation when these possibly incomplete sets of solvent atoms are included.

Table 2. The optimum cutoff radii (Å) for eight proteins in the data set for four different resolution level models.

The correlation coefficients are given in parentheses.

	1ucs	1iua	1r6j	1w0n	1mc2	1nwz	1v6p	1f9y
Residue	8 (0.65)	13 (0.54)	14 (0.76)	12 (0.48)	7 (0.60)	10 (0.54)	6 (0.63)	19 (0.78)
Atom	4 (0.67)	5 (0.56)	14 (0.72)	8 (0.58)	5 (0.73)	4 (0.67)	7 (0.64)	22 (0.78)
Proton	3 (0.66)	5 (0.54)	15 (0.71)	8 (0.59)	5 (0.68)	3 (0.63)	7 (0.67)	23 (0.78)
Solvent	15 (0.59)	15 (0.53)	18 (0.69)	9 (0.51)	5 (0.62)	10 (0.66)	7 (0.64)	23 (0.78)

Atomic and proton resolution level models give better results than the residue-level models

To analyze the effect of the resolution scale of the model, we have chosen one of the proteins from the data set lysine 49 PLA2 (pdb code: 1mc2) for a more detailed presentation of the results. A schematic representation of the protein backbone colored according to the magnitude of mean-square fluctuations of residues derived from the experimental data, and from residue-level, and explicit solvent-level models is shown in Figures 2a–c, respectively. The residue-level model computations were performed with the cutoff radius 7 Å, and the atomic-level calculations with the cutoff 5 Å. Figure 3 shows the computed mean-square fluctuations of C^α-atoms for the residue-level and the atomic-level models. B-factors are also provided for comparison. The predicted fluctuations are calculated by summing over all internal normal modes. The mean square fluctuations obtained for the residue-level model have a correlation of 0.60 with B-factors, whereas the atomic-level model calculations with 5 Å cutoff give a correlation 0.73 with the experimental data. Figure 3 shows that mean square fluctuations predicted from the atomic-level model are significantly closer to the experimental B-factors, both qualitatively and quantitatively.

Figure 2. The schematic picture of lysine 49 PLA2.

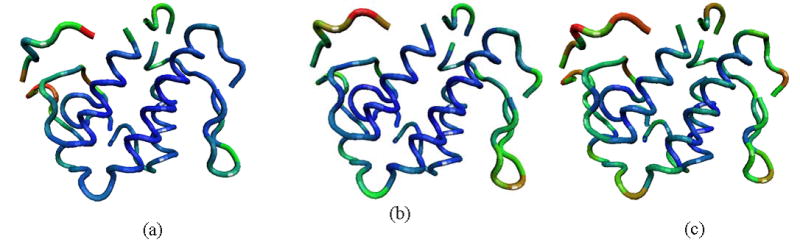
(PDB id: 1mc2). The backbone is colored according to the magnitude of mean-square fluctuations obtained (a) experimentally, (b) computed from the residue-level GNM, and (c) calculated from the atomic-level GNM. Most mobile regions are colored with red, less mobile regions with green, and finally, almost immobile regions with blue.

Figure 3. The mean-square fluctuations for lysine 49 PLA2 computed from the residue-level and the atomic-level models using optimal cutoffs.

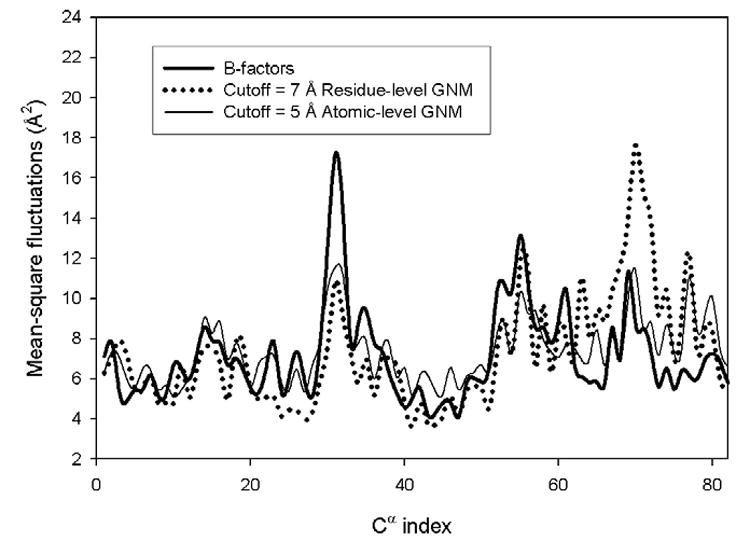
Results are shown for C^α atoms only.

What is the source of the discrepancy between theoretical predictions and the experimental data? For further analysis, we focus on the PDZ2 domain of syntenin (1r6j). PDZ domains are mainly involved in the regulation of intracellular signaling and in the assembly of large protein complexes³⁶. The structure of the PDZ2 domain of syntenin was resolved with a resolution 0.73 Å, allowing determination of coordinates of the hydrogen atoms in the crystal³⁷. The PDZ2 domain contains 82 residues and 1867 atoms (including solvent atoms and hydrogen atoms). Figure 4 shows the dependence of the absolute value of the difference between predicted mean square fluctuations and experimental B-factors as a function of the number of contacts in the protein structure. An inverse relationship can clearly be seen between this difference and the number of neighbors (contacts). Since nodes inside the protein core have more contacts, Figure 4 shows that the GNM predictions are generally less accurate on the protein surface. This implies that atoms on the protein surface should perhaps be treated in a more cooperative way than atoms of residues inside the core.

Figure 4. The absolute differences between atomic-level model predictions and experimental B-factors for the PDZ2 domain.

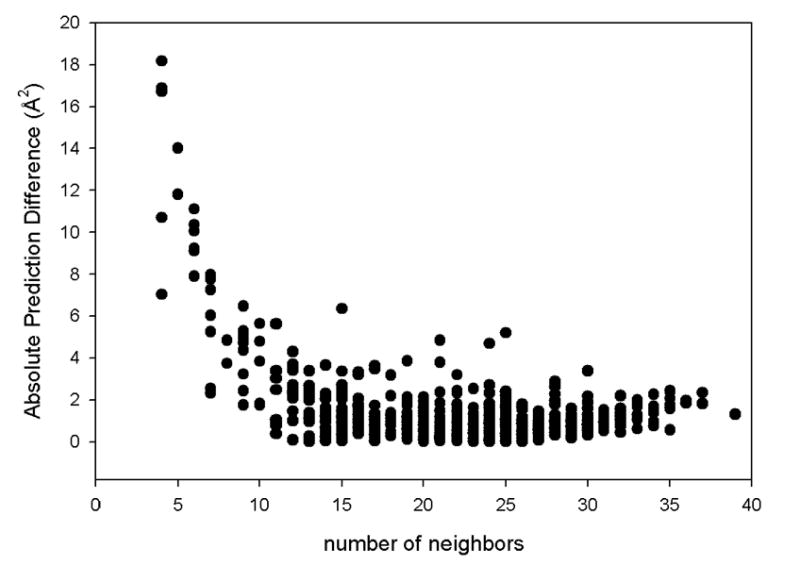
The calculations are performed at the cutoff 5 Å as a function of the number of contacts (neighbors).

Since the GNM is mainly used to analyze cooperative global motions with functional relevance, a detailed analysis of slowest normal modes is of critical importance. For this purpose, we show in Figure 5 the overlaps of the eigenvectors computed for the residue-level and proton-level models. The overlap is defined by Eq. 5 as the absolute value of the cosine of the angle between these two eigenvectors. The absolute value of the overlap is used because the term u_ku^T_k in Eq. 3 does not depend on the direction of the eigenvector u_k, and the use of absolute cosine ensures that a the 180° rotation still specifies the same type of motion. The overlap is calculated only for the eigenvector components corresponding to the C^α-atoms. Figures 5a to 5d illustrate these overlaps for four different proteins: (5a) 1ucs, (5b) 1r6j, (5c) 1w0n, and (5d) 1f9y.

Figure 5. The absolute overlaps, |cosθ|, between eigenvectors obtained for the residue-level and the proton-level models for (a) Type III antifreeze protein rd1 (1ucs), (b) syntenin Pdz2 domain (1r6j), (c) carbohydrate Binding Domain Cbm36 (1w0n), and (d) E. Coli pyrophosphokinase HPPK (1f9y).

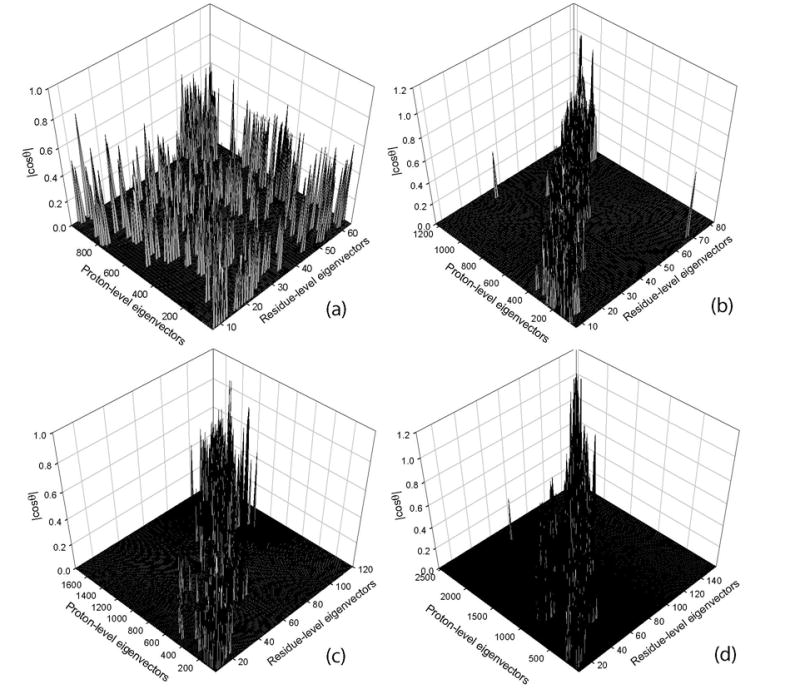
The calculations were performed by using optimum cutoffs for each protein for a given model. Proteins are arranged from (a) to (d) according to increasing protein size.

Each point in Figures 5a–d shows a pair of eigenvectors, one computed from the residue-level model and the other from the proton-level model that have an absolute overlap of at least 0.4. The results were obtained by using optimum cutoff radii for each level of resolution for various proteins according to Table 2. For the case of syntenin, the eigenvectors corresponding to the first 10 slowest modes in both the residue-level and proton-level models have overlap higher than 0.4. However, this correspondence does not always hold, for example, for the case of pyrophosphokinase HPPK, this overlap is less good. More detailed studies are needed to conclude whether there may be certain regularities in the overlaps of modes in protein multi-scale models.

Figure 5 shows scattered, sporadic, rather weak overlaps for 1ucs (5a) but not for other proteins (5b–d): The small (64 residues) Type III antifreeze protein rd1 (pdb id: 1ucs) indeed shows very scattered overlaps, but for the larger proteins, there is a strong overlap between corresponding eigenvectors (around the diagonal of the plot), and very weak overlap between dissimilar eigenvectors (far from the diagonal). This high overlaps between these two different scales can be due to the protein size, which is indirectly related to packing density (the larger the protein, then the larger is its core having high packing density). Since the successes of Elastic Network Models depend on having an adequate representation of protein packing, larger proteins in general might be expected to exhibit better multi-scale overlaps.

The effect of fluctuations in elastic network models on protein entropy

We have calculated the correlation coefficient (defined by Equation 4) between the free energy change of entropic origin given by Equation 8 and the numbers of contacts for alpha-carbons of each residue at four different levels of coarse graining. The results have been averaged over the set of eight proteins and are shown in Table 3 as the function of the cutoff distance used for defining contacts. It is interesting that Table 3 strongly resembles Table 1. This resemblance originates from the fluctuational nature of these free energy changes.

Table 3. The average correlation coefficients between the free energy change due to fluctuations (entropy) and the contact number (energy) as a function of the cutoff distance for four different resolution level models.

Correlation coefficients have been averaged over the set of eight proteins. High values are achieved for the three more detailed models at lower cutoff values, as is also seen in Table 1.

Cutoff (Å)	Residue Level	Atomic Level	Proton Level	Solvent Level
1	--	--	--	--
2	--	−0.32	−0.03	0.01
3	--	0.15	0.50	0.50
4	0.19	0.76	0.91	0.89
5	0.61	0.95	0.99	0.97
6	0.73	0.99	1.00	0.99
7	0.89	1.00	1.00	1.00
8	0.95	1.00	1.00	1.00
9	0.98	1.00	1.00	1.00
10	0.99	1.00	1.00	1.00

Figure 6 shows plots of the absolute value of the entropy of fluctuations as a function of the total number of contacts for 3 different proteins: 1f9y, 1iua and 1mc2. The calculations have been performed for the standard residue-level coarse-grained GNM. We used six different values of the cutoff radius defining contacts, ranging from 5Å to 10Å with increments of 1Å. Each of these six cutoffs is represented by a marked point in Fig. 6 starting from 5Å on the left to 10Å on the right. The linearity of the plots in Figure 6 reemphasizes the dependence of entropy on packing density. A related study was also done by us³⁸ and by Halle³⁹, where an inverse relationship between mean-square fluctuations and contact densities can be seen. It is also worth noting that entropy depends on the size of the protein. The largest of the three proteins 1f9y (158 residues) has the smallest entropies, and the smallest one 1iua (83 residues) has also the largest entropies for the same number of contacts, as seen in Fig. 6. This means that the fluctuation entropy per contact is smaller for larger proteins, i.e., large proteins exhibit more cooperative motions.

Figure 6. The absolute value of the entropy of fluctuations as a function of the total number of contacts for 3 different proteins.

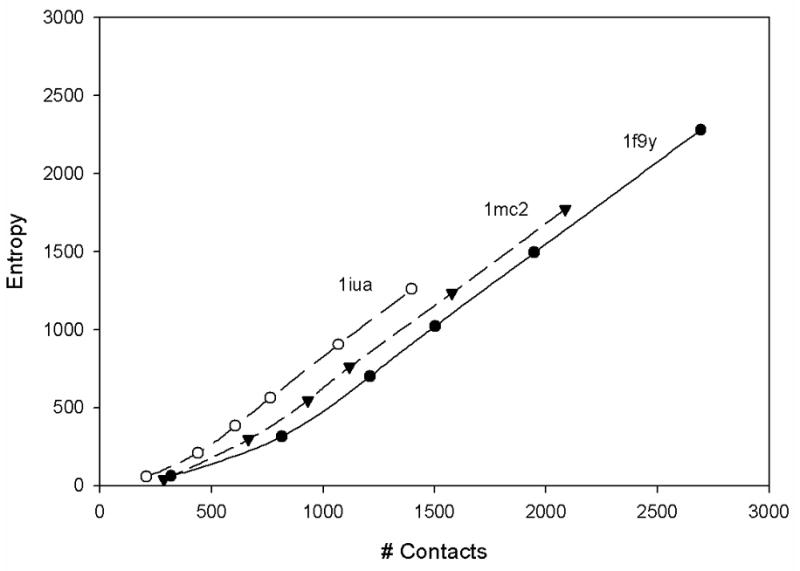
The residue-level coarse-grained model was used. For each protein, there are 6 points corresponding to 6 different cutoffs varying from 5Å on the left to 10Å on the right in increments of 1Å.

Conclusions

We have applied normal mode analysis with multi-scale coarse-graining to high-resolution protein structures. The atomic, proton, and explicit solvent level models all provide quite similar results, showing significantly higher correlations of the predicted fluctuations of C^α-atoms with the experimental B-factors, than the residue level GNM. At the residue-level coarse-graining, the optimum cutoff radius is ∼11 Å, which is significantly larger than the value 7.3 Å obtained by Phillips and coworkers¹⁴. This suggests that the optimum cutoff radius may depend on the specific protein structure, and the inclusion of intermolecular contacts in the crystal seems to be necessary at the residue level resolution. The absence of these intermolecular contacts in our model must be compensated by an increased cutoff that increases the number of springs and leads to better agreement with experimental data. The inclusion of atoms in our models significantly improves predictions of fluctuations of C^α-atoms and gives better correlations with experimental B-factors. Additionally better resolution atomic scale models require small cutoff radius (4 Å). However, there is a second maximum in the correlation values appearing at 11 Å, notably the same cutoff distance where the maximum occurs for the residue-level models. More detailed atomic resolution level elastic network models are likely to provide a better representation of motions in proteins. Our results also show that small proteins may require atomic scale resolution models to achieve a good representation of their dynamics. However, the atomic level GNM computations for larger proteins require significantly larger computer resources than those for the residue-level GNM. An alternative that offers a compromise might be mixed coarse-grained modeling of proteins proposed by Doruker and Jernigan^20,21,27 - to include a high level of detail for the most important parts of the protein structure and less detail for other parts. Our analysis shows that the multi-scale normal mode analysis can be useful for understanding and predicting the collective motions in proteins.