Re-establishment of local populations of vectors of Chagas disease after insecticide spraying

Summary

1. Prevention of Chagas disease is mainly dependent on control of the insect vectors that transmit infection. Unfortunately, this control is not wholly successful and the vectors have been resurgent in some areas. Where re-infestation has occurred, it is important to understand the dynamics of the process. We investigated how a metapopulation framework can elucidate key aspects of re-infestation and thereby contribute to more efficient disease control.

2. Triatoma infestans, the main vector of Chagas disease, re-infested sites in three villages in north-west Argentina after community-wide insecticide spraying in October 1992. Ten surveys were carried out at 6-monthly intervals from November 1994 to May 1999.

3. Comparisons were made of different methods of estimating the sources of dispersal and the number of sites in which bug infestations became established.

4. The results indicated that (i) the number of dispersing Triatoma infestans from a given site was proportional to the number of bugs found at the site; (ii) there was a 6-month time lag between detection of a new infestation and dispersal events; (iii) the relationship between infestations and new establishments varied by season.

5. Three of 156 sites at which bugs were found were estimated to be the source of more than 50% of establishment events. These three sites were the only ones with large, persistent bug populations.

6. Synthesis and applications. To reduce the risk of human Chagas disease, identifying those few sites infested with large, persistent bug populations and targeting control measures at those sites should greatly improve the efficiency of vector control. The appropriate seasonal timing of vector control could also greatly increase its efficiency. Specific recommendations for the timing of insecticide spraying require further research to establish how the observed temporal pattern of bug establishment is associated with the seasonality of bug dispersal.

Introduction

Trypanosoma cruzi is the causative agent of Chagas disease in the Americas, and between 10% and 40% of approximately 17 million people infected develop a clinically overt disease, affecting heart, digestive and neurological functions (World Health Organization 2002). Trypanosoma cruzi is transmitted in wide areas of South America by Triatoma infestans (Klug), a blood-sucking reduviid bug. Interrupting the transmission cycle by control of the vector is currently the major control strategy for Chagas disease (World Health Organization 2002).

Triatoma infestans occurs mainly in rural areas in and around houses, where humans and domestic animals such as chickens, dogs and goats are its principal hosts (Gürtler et al. 1996; Cecere et al. 1997). The population of Triatoma infestans within our study area (northwest Argentina) was structured as a metapopulation (defined by Hanski & Simberloff 1997). The bugs occurred mainly in discrete sites such as goat corrals, chicken coops and houses and there was evidence of a limited exchange of bugs between sites (Cecere et al. 2004).

The key problem in long-term vector control is preventing re-establishment of vector populations at sites where the vector has been eliminated by insecticide application. Understanding re-establishment is crucial for effective elimination of the vector. This problem precludes standard methods of analysis for metapopulation data, such as incidence functions (Hanski 1994a,b; Wahlberg, Moilanen & Hanski 1996) because the vector metapopulation is not in statistical equilibrium during re-establishment.

An alternative approach is to use metapopulation data of Triatoma infestans to estimate the rate of re-establishment as a function of current infestation. From long-term studies of the biology of Triatoma infestans, we developed competing hypotheses about the mechanisms of spatial population dynamics. We compared the predictions with data on the size of hundreds of subpopulations of Triatoma infestans that were surveyed semi-annually in three villages in Argentina over 10 years.

We assumed that sites that changed from uninfested to infested between two consecutive surveys received bugs, at least in part, from already infested source sites. Hence there should be a correlation across the surveys between an appropriately chosen summary indicator of the number of dispersers from source sites (the explanatory variable in our models) and an appropriately chosen summary indicator of the number of bug establishment events (the response variable).

We selected regression models that produced the closest association between the number of dispersers at each survey and the number of sites making the transition from uninfested to infested between each survey and the next to draw inferences about the underlying establishment process. We investigated the time lag between the establishment of a new bug population and its detection, the time lag between establishment and dispersal, the timing of dispersal within a time interval, and differences between seasons, villages and ecotypes. The overall goals of our analyses were to (i) give an overview of all a priori plausible regression models for the relationship between the number of bugs on source sites and new bug establishments; (ii) devise a coherent procedure for comparing the fit of different regression models; and (iii) determine the contribution of individual sites to overall bug establishment based on the best fitting regression model.

We used this observational and analytical approach because dispersal behaviour of Triatoma infestans is difficult to investigate experimentally and demographic parameters (including migration rates) measured in a laboratory may differ in the field. This study complemented previous work that predicted the establishment on new sites based on assumptions about details of dispersal behaviour (Schofield & Matthews 1985).

Materials and methods

Triatoma infestans density data were collected in three villages in rural north-west Argentina (Amamá, Mercedes and Trinidad, 27·1°S, 63·0°W, province of Santiago del Estero) after the villages were subjected to a blanket insecticide spraying in October 1992. Data were collected in October 1993 and then twice a year for the following 6 years (November 1994–May 1999). From November 1995 individual sites were sprayed irregularly with insecticide by householders or professionals but no blanket spraying was conducted.

Two methods were used to estimate densities. The first method, flushing-out, involved spraying the irritant 0·2% tetramethrin into all potential hiding spaces that could contain bugs and collecting all emerging individuals (Gürtler et al. 1995, 1999). This method detects 77–89% of infestations and the number of bugs remaining at a site afterwards is proportional to the number of bugs collected (Gürtler et al. 1993, 1995). For the second method, sensor boxes were placed in domestic areas as artificial hiding places for the bugs (Gürtler et al. 1999). During each survey, bugs, exuviae and eggs were collected and triatomine faeces were counted. For both sampling methods, the number of Triatoma infestans bugs within the nymphal (instars 1–5) and adult (males and females) life-stage categories was recorded.

A flushing-out survey of the Triatoma infestans density at the majority of the peri-domiciliary sites (i.e. sites surrounding houses) that potentially harbour triatomine bugs (such as corrals and chicken coops) was performed in each village in October 1993 and from November 1994 onwards twice a year (November and May, 10 surveys). Domiciliary sites (i.e. living room and bedroom) were surveyed with sensor boxes during each survey and by flushing-out only once a year (November).

During flushing-out at domestic sites, one person hour was spent per household. During each survey, half a person hour was spent for all peri-domiciliary sites within one household regardless of the number of sites per household. Unless stated otherwise, only data from the flushing-out collections of peri-domiciliary sites were used in the regressions because that was the most consistent and exhaustive sampling method. The data used for modelling are given in Table S1 (see the supplementary material).

We treated two adjacent villages (Mercedes and Trinidad) as one site because the smallest distance between houses from these two different villages is 144 m, a distance bugs can cover by flight dispersal (Schofield et al. 1992). Hence bugs might disperse between these two villages. This reduced the number of independent village locations to two and produced 18 data points in total (nine half-year intervals between successive surveys times two village locations).

In addition, each survey noted when each site was last sprayed and whether the site existed (some sites were constructed or demolished during the years of observation). The ecotype (chicken coop, goat corral, bedroom, etc.) of each site (1212 in total) was also recorded. Following Cecere et al. (2004), we excluded from the analysis all sites that were never infested in any of the surveys. This reduced the number of sites to 81 peri-domiciliary and 21 domestic sites for the first village location (Amamá) and 75 peri-domiciliary sites and 10 domestic sites for the second village location (Mercedes–Trinidad).

A site was termed ‘infested at t’ if one or more Triatoma infestans bugs (nymphs or adults) was collected at this site at survey t, and ‘uninfested at t’ otherwise. We distinguished between sites that were ‘truly’ uninfested and sites that were ‘observed’ uninfested to account for the possibility that bugs were present but not detected at a site that was surveyed. An observed infested site was always truly infested but an observed uninfested site could be truly uninfested or truly infested but undetected.

A site could change from truly uninfested to infested between two consecutive surveys (denoted as survey t and t + 1) only if at least one bug arrived at this site from somewhere else between survey t and t + 1 (called an arrival event) and it or its descendants persisted to survey t + 1. We called the combination of arrival and persistence to the next survey an establishment event. Only establishment events on observed uninfested sites were observable. We compared different ways of estimating the number of establishment events and the number of dispersers between t and t + 1 for models derived from possible underlying dispersal processes.

A site that was observed uninfested at survey t − 1 and at survey t was more likely to be truly uninfested at t than a site uninfested at t without additional restrictions (see Appendix S1 in the supplementary material). We therefore only considered a transition of a site uninfested at t − 1 and t to infested at t + 1 as an observed establishment event. We called a site that was observed uninfested at t − 1 and t a ‘target site’ at t. Dispersers might not emigrate from all sites infested at t but only from a subset that we called ‘source sites’ at t. Using regression analysis, we sought to determine which source sites predicted establishment.

GENERAL REGRESSION MODEL

We used all pairs of consecutive surveys (survey t and t + 1) to fit different alternatives of the following general regression model: bug establishment between t and t + 1 = (bugs at t across all source sites) × (season) × (village location) × (type of target site). Different hypotheses about dispersal produced alternative methods of estimating the response and explanatory variables. We assessed which hypotheses were supported by the data by performing a separate regression for each combination of response and explanatory variables and factor level combination. For each response variable we compared the fit produced among all alternative models with the respective response variable using the bias-corrected Akaike information criterion (AIC_c).

We used the proportion p of target sites at t becoming infested at t + 1 as the response variable and estimated the regression coefficients a and b of the equation p = 1 − exp(a + bx), where x is some measure of bug abundance on source sites. This equation was derived from assumptions about the dispersal process (see Appendix S2 in the supplementary material) and fitted as a generalized linear model (McCullagh & Nelder 1989) with link ln(1 − p) and binomial error variance p(1 − p)/n, where n is the number of target sites. The fitting procedure was programmed in Mathematica 4·2. We had no estimate of how spraying between t and t + 1 might interfere with the probability of establishment between t and t + 1 and therefore calculated two different response variables using either all or only unsprayed target sites.

The regression model was calculated separately for all combinations of the two alternative response variables described above and 36 alternative explanatory variables. These alternative explanatory variables arose from combining all the alternatives listed in Table 1. A detailed derivation of these alternative explanatory variables from vector biology is provided in Appendix S2 in the supplementary material.

Table 1.

Alternatives for calculating the explanatory variable derived from proposed mechanisms. The alternatives within each component were combined with the alternatives from all other components

Proposed mechanism
Component	Alternatives	Resulting explanatory variable
I Time lag	Because of development time Because of population dynamics No time lag	Source sites = sites infested at t and t − 1, or uninfested at t − 1 but with nymphs at t Source sites = only sites infested at t and t − 1 Source sites = all sites infested at t
II Timing of establishment	Shortly after t Shortly before t + 1 Continuous	Source sites = all sites infested at t Source sites = only sites infested at t and t + 1 Source sites = sites infested at t and t + 1, multiplied by the proportion of time infested during t and t + 1
III Number of bugs per site was a reliable indicator for number of dispersers	No Yes	Number of source sites at t Number of bugs on source sites at t
IV Difference between source ecotypes	No Yes	Single explanatory variable Separate explanatory variables for different ecotypes

For each regression model we explored the effect of the categorical variables season, village location and ecotype of target sites. A hypothesis-testing approach to multiple categorical variables in regression poses the problem of multiple comparisons (Burnham & Anderson 2002). We therefore used the AIC_c to compare the fit produced by a single regression line with the fit obtained by estimating a separate regression line per factor level of the categorical variable (for details see Appendix S2 in the supplementary material).

MODEL COMPARISONS

We determined for each response variable the best-fitting model using the bias-adjusted Akaike information criterion AIC_c (Burnham & Anderson 2002). For both best models we estimated the relative importance of each model component by summing the Akaike weights (Burnham & Anderson 2002) of all models containing the respective model component. The Akaike weight of a model is its relative likelihood, i.e. its likelihood divided by the sum of all model likelihoods. The sum of the Akaike weights of all models containing a certain model component is therefore close to 1 if the model component is part of all models with a high relative likelihood. These sums can be interpreted as the posterior probability (given the data set and the set of a priori models) that the respective model component is part of the best model (Burnham & Anderson 2002).

DETECTING MAJOR SOURCE SITES

We used the best model to identify sites that acted as important sources for dispersing vectors. A given definition of the explanatory variable provided, for each site at any given survey, a source value indicating how important that particular site was as a source for dispersers at that survey. Depending on the explanatory variable, this value was either a weight between 0 and 1 or the weight multiplied by the number of bugs found at the site. We used the explanatory variable of the best model to estimate the relative contribution of any given site to overall bug establishment events as follows.

We calculated for each survey the relative contribution of each site to bug establishment at the respective time interval by dividing the source value of a site by the sum of all source values at the respective survey. Then we estimated the number of bug establishments from internal sources as the number of bug establishments minus the intercept of the regression line of the best model. We estimated the overall relative contribution of a site by averaging the relative contribution of a site per time interval over all time intervals, weighted by the number of bug establishments per time interval attributed to internal sources. We compared the relative contribution of different sites to overall bug establishment as estimated here with the results of a previous attempt to identify source sites based on local spatial clustering of bug abundance (Cecere et al. 2004).

We also estimated the proportion of bug establishment events that could not be attributed to the source sites determined by the regression results. We summed the estimated number of establishment events for the observations with no internal source (explanatory variable equals zero) and the intercept values for the observations with non-zero values for the explanatory variable. This sum was divided by the total number of estimated establishment events.

HETEROGENEITY AMONG TARGET SITES

We tested for evidence that some sites were more likely to experience establishment events than others. For both villages we counted how often establishment events were observed at sites that had already experienced establishment in a previous time step and compared this number with numbers obtained through Monte Carlo simulations. In our simulations we selected for each survey t from the set of target sites at t, randomly and without replacement a number of sites equal to the number of establishment events observed during t and t + 1. If some sites were more likely to experience establishment than others, we would expect the observed count of repeated establishments on the same site to be significantly higher than the average count obtained in simulations.

ALTERNATIVE REGRESSION ANALYSIS

We also used a standard linear regression, with the number of target sites at t becoming infested at t + 1 as the response variable, to compare different model alternatives. The main results of this analysis were qualitatively the same as the results of the general model. However, a priori considerations of the dispersal mechanism suggested that standard linear regression's assumptions of linearity and homogeneity of variances were violated. Because probabilistic inference from standard linear regression is based on these doubtful assumptions, we have not shown the details of these results.

Results

For both response variables (the proportion of all or of unsprayed target sites only becoming infested between t and t + 1) the best explanatory variable was the number of bugs found at t on a site, multiplied by the estimated fraction of the time interval between t and t + 1 during which that site was infested and summed over all sites that were infested at t and t − 1 (i.e. a combination of components Ib, IIc, IIIb and IVa; Table 1). For both response variables, the best model allowed for differences among seasons, but not among village locations nor among ecotypes, as target or source, and in both cases the best model produced a satisfactory fit (both P-values > 0·3, chi-squared test of goodness-of-fit, d.f. = 13; see Fig. S1 in the supplementary material). Standard likelihood ratio tests led to the same conclusion, namely a significant effect of season (P-values < 0·001 for both response variables) and no significant effects of village location (P-values > 0·16 for both response variables) and source ecotype (P-values > 0·13 for both response variables). However, the P-values for each explanatory variable were contingent on all other components of the best model and their probabilistic interpretation was unclear because the best model had been selected from the full set of a priori models (Burnham & Anderson 2002). There was no evidence for overdispersion of the best model (deviance < n − p for both response variables).

As the graphs of the best model looked very similar for both response variables, we only show one here (Fig. 1), comparing the best model (Fig. 1a; AIC_c = 78·4) with a null model where all infested sites were counted as source sites (Fig. 1b; AIC_c = 93·2). One limitation of these results is that, for some models that distinguished among target ecotypes, the parameter estimation algorithm failed to converge within 30 iterations. For all other model classes the parameter estimates converged. The AIC_c values of the best model and deviations from the best model are shown in Table 2.

Fig. 1.

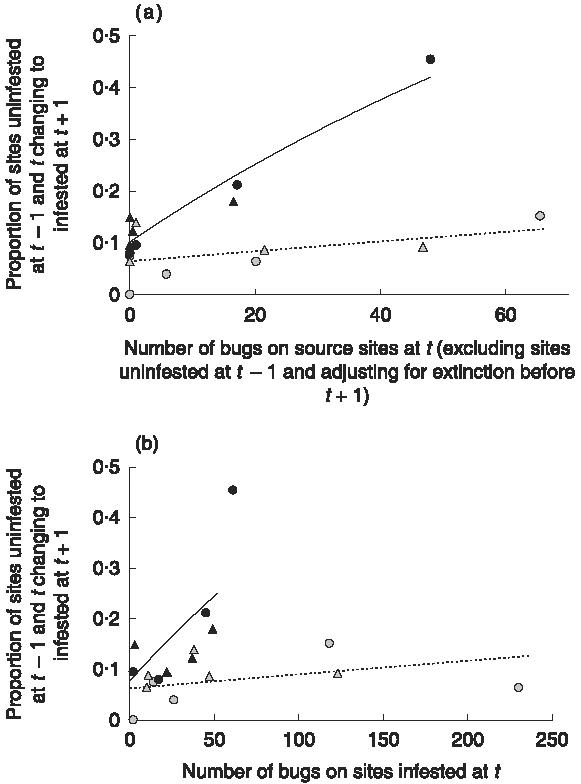
Estimated proportion of all target sites changing to infested, plotted against the explanatory variable of the best fitting model (a) and a null model (b). The explanatory variable of the best fitting model was calculated as the number of bugs found at t on sites that were infested at t − 1 and t, multiplied by the proportion of the time interval between t and t + 1 during which these sites were infested. The grey symbols show time intervals from November to May and the black symbols from May to November. Circles depict data points from Amamá, and triangles from Mercedes–Trinidad. Each village location had four data points for the season May–November and five for November–May [one grey triangle is hidden by overlapping points around (0,0·7)]. The regression equations (with 95% confidence intervals) of the best model were for November–May y = 1 − exp(−0·067 (± 0·03) − 0·001 (± 0·0014) (x), and for May–November y = 1 − exp(−0·11(± 0·04) − 0·0091(± 0·0042) (x).

Table 2.

AIC_c for both response variables of the respective best model and all perturbations from the best model. For each possible perturbation from the best model, the corresponding best model was selected and AIC_c was calculated

	Response variable (AICc)
Perturbation from best model	Proportion of all target sites	Proportion of unsprayed target sites
No perturbation (best model)	78·4	79·8
Sites uninfested at t − 1 but with nymphs at t included as source sites	86·3	83·3
Sites uninfested at t − 1 included as source sites	86·6	85·2
Sites uninfested at t + 1 included as source sites	78·5	80·0
Number of infested sites instead of number of bugs	86·7	88·2
Regression coefficients vary by ecotype	80·8	82·9
No effect of season	87·6	83·3
Effect of village location	80·4	81·5
Effect of target ecotype	87·6	83·3

More establishment events per bug found on a source site at t happened between May (t) and November (t + 1) than between November (t) and May (t + 1) (Fig. 1a). The difference between the seasons depended strongly on a single data point with a high number of establishment events (Fig. 1a). However, even when this point was removed, including a seasonal difference led to lower AIC_c values regardless of whether the response variable was measured in numbers or proportions.

As the results were similar irrespective of whether all or only unsprayed sites were included, we concentrated on the response variable that included sprayed and unsprayed sites. Table 3 shows the Akaike weights (w_i) of all components of the best model. These weights can be interpreted as a posteriori probability of the respective component being part of the best model. Three model elements linked to the bugs' dispersal biology were likely to be part of the best model: measuring the explanatory variable in number of bugs (w_i = 0·99), allowing for seasonality (w_i = 0·99), and excluding sites uninfested at t − 1 as source sites (w_i = 0·97).

Table 3.

For each component of the best model (with response variable taken as the proportion of all target sites changing to infested), the sum of relative likelihoods (Akaike weights, w_i) of all models with the respective component is shown. The third column gives the proportion of all models that have the respective component

Component of best model	Akaike weight (wi)	Proportion of models with respective component
No distinctions between target ecotypes	1	1/2
Explanatory variable calculated by summing number of bugs on source sites at t	0·99	1/2
Distinction between seasons	0·99	1/2
Source sites = only sites infested at t and t − 1	0·97	1/3
One explanatory variable per ecotype	0·84	4/7
No distinction between village locations	0·73	1/2
Source sites = sites infested at t and t + 1, multiplied by the proportion of time infested during t and t + 1	0·45	1/3

During the period of observation, 64% of all establishment events could not be attributed to source sites in Amamá and 89% in Mercedes–Trinidad. Graphically (Fig. 1a), many points were on the y-axis (i.e. had zero internal sources). Very few sites were responsible for the majority of establishment events attributed to internal sources. In Mercedes–Trinidad, two source sites accounted for roughly equal shares of 61% of all establishment events attributed to internal sources. In Amamá, a single source site accounted for about 48% of all establishments from internal sources, about three times more than the next most important source. This site, a pig corral, was identified as a major source for establishment by analysing spatial clustering of bug abundance (Cecere et al. 2004). The number of times an establishment event happened on a site that experienced establishment before was significantly lower than observed in Monte Carlo simulations (P-value = 0·017 for Amamá and 0·001 for Mercedes–Trinidad).

Discussion

The model of the relationship between potential sources of dispersing bugs and the establishment of bug infestations in peri-domestic sites in three rural villages in north-west Argentina did not depend on alternative possible specifications of the response variable, and identified the same major source of dispersers as a method based on spatial clustering of bug abundance (Cecere et al. 2004). Three major model elements were strongly supported by the analyses. (i) The relationship between infestation at t and establishment between t and t + 1 varied by season, as indicated by the different slopes of the regression lines in Fig. 1a. (ii) The number of bugs on source sites at t was a better predictor of establishment events during t and t + 1 than the number of source sites. (iii) Excluding sites that were not infested at t − 1 as source sites improved the fit.

In addition to these three major results, the analyses yielded two further findings. First, bug establishment did not differ markedly between sprayed and unsprayed sites. This result is consistent with an earlier study that showed limited residual effects of insecticides in peridomiciliary sites (Gürtler et al. 2004). Secondly, the results did not differ detectably among village locations or ecotypes. While the results for Amamá alone were more or less the same as for both village locations combined, the results for Mercedes–Trinidad alone depended on the choice of response variable and yielded low R² values (around 0·2) in general.

We view the best model as a hypothesis for future explorations of similar data sets and subsequent spatial analysis of the same data. The fit of a regression model cannot prove causal links. However, as a causal link between the number of dispersers and number of establishment events can be postulated a priori, a good fit should be expected from a regression model that correctly identifies sources of dispersers and establishment events. We therefore interpret the model fit as guidance for evaluating hypotheses about bug dispersal.

The first major result (i) can be explained either by higher bug establishment between May and November or by a lower sensitivity of the flushing-out method in May as a result of lower temperatures. At this point both explanations seem possible and a planned spatial analysis might shed some light on this question.

Seasonal variation in bug dispersal is important for the timing of vector control. A full analysis of the optimal time for spraying also has to consider seasonal variation in the effectiveness of spraying and the risk of transmission, as well as economic and operational constraints on the fraction of sites monitored. A previous study (Gürtler et al. 2004) determined September–November as an optimal spraying time, based on seasonal variation of insecticide effectiveness. We suggest well-monitored spraying experiments at different times of year (maybe November and April) in otherwise matching villages to explore this further.

The second major result (ii) was tested experimentally. Vazquez-Prokopec et al. (2004) light-trapped dispersing Triatoma infestans and found a positive correlation between the number of dispersing Triatoma infestans caught in a given light trap and the total number of adult Triatoma infestans collected by flushing-out at the sites within 200 m of the trap. The high-density sites were apparently producing more dispersers. A local emigration of dispersers proportional to local population size has been observed in other systems ( Hanski, Kuussaari & Nieminen 1994; Thomas & Hanski 1997; Gaggiotti et al. 2002). However, the best models excluded all sites that were uninfested at t − 1 as sources of bug establishment from t to t + 1 (result iii), suggesting that bug population size alone could not explain the number of dispersers per infested site. The precise reason for this time lag is unclear but the AIC_c values suggest it was not because of development time. A possible reason could be an increasing proportion of dispersers with increasing population density, as observed in other organisms (Olivieri & Gouyon 1997).

As a consequence of results (ii) and (iii), not all infested sites contribute equally to establishment. Because a site has to harbour a bug population for at least a year to become a source site, internal sources are lacking in many surveys, as indicated by the data points clustered around the y-axis in Fig. 1a. Observed establishment events that could not be attributed to source sites might either not be true establishment events or establishment events by dispersers from sources that were not considered in the analysis.

The remaining establishment events could be attributed to very few sources. According to our analyses, only nine sites (four in Mercedes–Trinidad and five in Amamá) were source sites during the 5 years after blanket spraying and, of these nine sites, three were responsible for more than 50% of all establishment events attributed to internal sources. Targeting these few source sites after blanket spraying should severely reduce re-establishment and is important for vector control programmes.

No heterogeneity among sites in their propensity to experience bug establishment was detected. However, such heterogeneity might exist among villages because the attractants for dispersing bugs (such as artificial light sources) as well as the bug habitat surrounding villages could vary among villages. The villages investigated in this analysis have no electric lights, which is typical for rural areas in the Grand Chaco region.

Our analyses indicate that the major sources are sites with large numbers of bugs found by flushing-out and with bug populations that tend to persist for more than a year. Further research into what properties of a site allow a persistent high-density bug population can lead to more targeted control in areas where no flushing-out monitoring is performed and might help to prevent the creation of such sites in the first place.

Our analyses move us towards a better understanding of the process of bug dispersal and population establishment. Understanding this process is important because re-establishment of populations on sprayed sites prevents complete elimination of the vector, and bug dispersal creates possibilities for disease transmission contacts between hosts at different sites. An improved knowledge of the seasonality of bug dispersal as well as which sites act as the main sources for dispersers therefore leads to improved estimates of the temporal and spatial properties of the contact network created by bugs among their hosts. The properties of disease transmission contact networks affect efficient disease control (Keeling 1999; Newman 2003; Eubank et al. 2004).

Our analyses of the connection between the number of bugs found on source sites and new bug establishment took the course of infestation on source sites (persistence or extinction) into account without assumptions about the mechanisms driving the course of infestation. As long as the mechanisms of bug establishment stay the same, our results should be generalizable to other villages regardless of whether extinction of local sites is caused by ‘natural’ extinction or different methods of vector control.

CONCLUSION

This work is the first attempt to identify the link between infestation and bug establishment from data on Triatoma infestans, which are unique in their temporal and spatial scope. The results show a close link between the number of bugs found at infested sites and the number of sites where bugs established subsequently, once the right sites were identified as source sites. The identification of the source sites suggested a half-year time lag between sites becoming infested and the beginning of bug dispersal from such sites. There might be a dispersal season but more research into the seasonal variation of the sensitivity of the sampling method is required to confirm this hypothesis. Our results suggest that targeting a few major source sites could greatly increase the efficiency of control.