Accumulation of slightly deleterious mutations in mitochondrial protein-coding genes of large versus small mammals

Abstract

After the effective size of a population, N_e, declines, some slightly deleterious amino acid replacements which were initially suppressed by purifying selection become effectively neutral and can reach fixation. Here we investigate this phenomenon for a set of all 13 mitochondrial protein-coding genes from 110 mammalian species. By using body mass as a proxy for N_e, we show that large mammals (i.e., those with low N_e) as compared with small ones (in our sample these are, on average, 369.5 kg and 275 g, respectively) have a 43% higher rate of accumulation of nonsynonymous nucleotide substitutions relative to synonymous substitutions, and an 8–40% higher rate of accumulation of radical amino acid substitutions relative to conservative substitutions, depending on the type of amino acid classification. These higher rates result in a 6% greater amino acid dissimilarity between modern species and their most recent reconstructed ancestors in large versus small mammals. Because nonsynonymous substitutions are likely to be more harmful than synonymous substitutions, and radical amino acid substitutions are likely to be more harmful than conservative ones, our results suggest that large mammals experience less efficient purifying selection than small mammals. Furthermore, because in the course of mammalian evolution body size tends to increase and, consequently, N_e tends to decline, evolution of mammals toward large body size may involve accumulation of slightly deleterious mutations in mitochondrial protein-coding genes, which may contribute to decline or extinction of large mammals.

Natural selection is more efficient in large populations. In a population of effective size N_e, mutations with selection coefficient s such that |s| < 1/N_e are effectively neutral, in the sense that their dynamics are affected mostly by random drift (1, 2). Effectively neutral nucleotide substitutions, both slightly deleterious and slightly beneficial, play a major role in evolution at the molecular level (3). Provided that the distribution of selection coefficient is independent of N_e, the fraction of mutations which are effectively neutral must be higher in populations with smaller N_e. Because selection is mostly purifying, in species with low N_e a larger fraction of slightly deleterious mutations can reach fixation.

Purifying selection affects nonsynonymous substitutions much stronger than synonymous substitutions (4–6). Indeed, when the ratio of the rate of nonsynonymous (amino acid changing) substitutions over the rate of synonymous (silent) substitutions, K_a/K_s, is <1, it is indicative of purifying selection on nonsynonymous substitutions and reflects its strength: the closer the K_a/K_s to 1, the weaker is the purifying selection (3). Another measure of the strength of purifying selection is the ratio of the rate of radical (presumably more harmful) over the rate of conservative (less harmful) amino acid substitutions, K_r/K_c (7, 8). Furthermore, because species with reduced population sizes experience less efficient purifying selection, they are expected to accumulate more deleterious mutations and thus to show a greater amino acid dissimilarity to its most recent ancestor. One measure of such dissimilarity is Grantham's distance (9), which is often used in the context of protein comparisons (10).

In this study, we analyze six molecular traits: K_a/K_s, four K_r/K_c ratios under various types of amino acid classification (based on volume, charge, polarity, and both polarity and volume), and Grantham's distance, all of which characterize, in a variety of ways, the efficiency of purifying selection. Our hypothesis is that at least some of these traits would increase with decreasing N_e, as a response to less efficient purifying selection in small populations. To test this hypothesis, we take advantage of an extensive set of complete mammalian mitochondrial genomes not available in the previous studies (8, 11–15). The choice of mitochondrial genome is motivated by its having a low effective population size due to uniparental inheritance, effective haploidy, and the absence of recombination. In addition, the probability of fixation of a slightly deleterious mutation with a given selection coefficient is so structured that it is particularly sensitive to changes in N_e when N_e is low (16). These features make the mitochondrial genome particularly suitable to study the rate of deleterious-mutation accumulation in relation to N_e (17, 18), although recurrent events of positive selection in mitochondrial DNA, as may be the case in invertebrates (19) but less likely in mammals (20), may hamper this dependence.

Because for most mammalian species no direct estimates of N_e are presently available, we use body mass W as a proxy for N_e, based on the nearly universal inverse relationship between body mass and population size (21–24). Thus, this study aims to determine the rate of accumulation of slightly deleterious mutations (expressed through K_a/K_s and K_r/K_c) and the resulting amino acid dissimilarity between modern species and their most recent reconstructed ancestors (measured as Grantham's distance) in large versus small-bodied mammals and, by implication, in small versus large populations.

Results

Average Values of Nonsynonymous to Synonymous Nucleotide Substitutions, K_a/K_s, and of Radical to Conservative Amino Acid Substitutions, K_r/K_c.

All species-specific values of K_a/K_s are well below 1 (typically 0.03–0.06, Table 1). These values indicate that most nonsynonymous substitutions (at least 94–97%) produced by mutation process are subject to purifying selection and thus are deleterious. The majority of our K_r/K_c values are also <1, and none is considerably larger than 1 (Table 1), which indicates stronger purifying selection against radical substitutions.

Table 1.

Averages, standard errors, and parameters of ordinary linear and mixed-effects regressions on log_e body mass along with associated P values for each trait under study

Trait	Average (SE)	Ordinary linear models			Mixed-effects models
		Intercept	Slope	P	Intercept	Slope	P
Ka/Ks	0.046 (0.002)	0.028	0.0020	<0.001	0.023	0.0024	0.010
Polarity-based Kr/Kc	0.846 (0.028)	0.525	0.0348	<0.001	0.475	0.0369	0.002
Volume-based Kr/Kc	0.872 (0.027)	0.528	0.0373	<0.001	0.547	0.0337	0.001
Polarity-volume-based Kr/Kc	0.504 (0.012)	0.443	0.0066	0.013	0.449	0.0057	0.061
Charge-based Kr/Kc	0.420 (0.016)	0.330	0.0097	0.007	0.353	0.0066	0.157
Grantham distance	56.940 (0.462)	52.614	0.4692	<0.001	52.314	0.4784	0.001

Calculations are based on 110 mammalian species. SE, standard error.

Comparison of Large Versus Small Mammals.

We divided the whole sample into two groups, 55 species each, with small mammals having ln W < 9.04 and large mammals having ln W > 9.04, where 9.04 (or ≈8,400 g) is the median of log_e transformed body mass W (in grams).

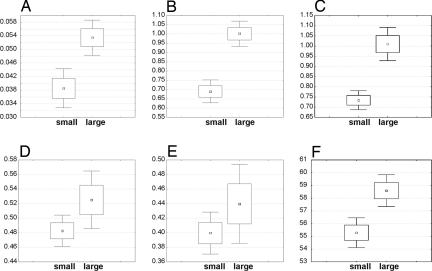
Three substitution rate ratios (K_a/K_s, polarity-based K_r/K_c, and volume-based K_r/K_c) are found to be smaller in small than in large mammals, polarity–volume-based K_r/K_c is marginally significantly smaller (P = 0.07), and charge-based K_r/K_c shows no significant difference at a 5% significance level (t test, Fig. 1 A–E).

Fig. 1.

Comparison of averages of six molecular traits for 55 small (ln W < 9.04) and 55 large (ln W > 9.04) mammals where 9.04 is the median of log_e transformed body mass W (in grams). (A) K_a/K_s, P < 0.001. (B) Polarity-based K_r/K_c, P < 0.001. (C) Volume-based K_r/K_c, P < 0.001. (D) Polarity–volume-based K_r/K_c, P = 0.069. (E) Charge-based K_r/K_c, P = 0.20. (F) Grantham distance, P < 0.001 (t test). Small squares represent mean; rectangles are ±1 SE; and whiskers are 0.95 confidence interval.

Ordinary Linear Models.

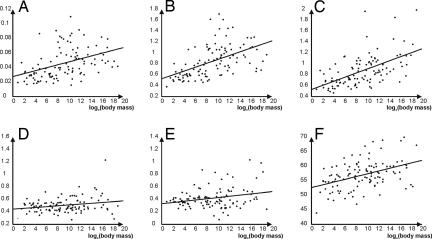
In terms of ordinary linear regressions, all of the rates of nonsynonymous over synonymous, and of radical over conservative, substitutions show a statistically significant (at a 5% level) positive relationship with body mass (Table 1), albeit with considerable scatter (r² = 0.16, 0.28, 0.32, 0.06, and 0.07 for Fig. 2 A–E, respectively). Although such a scatter implies the influence of multiple factors on the traits under study, the increasing trend with increasing body mass is clearly corroborated.

Fig. 2.

The ordinary linear regressions of molecular traits on log_e body mass W for 110 mammalian species. (A) K_a/K_s. (B) Polarity-based K_r/K_c. (C) Volume-based K_r/K_c. (D) Polarity–volume-based K_r/K_c. (E) Charge-based K_r/K_c. (F) Grantham distance. For regression parameters see Table 1.

Data Nonindependence and Mixed-Effects Models.

The linear mixed-effects models, which account for nonindependence of the individual-species data due to the effect of shared ancestry, differ only slightly from the ordinary linear models in terms of slopes and intercepts, except for the slope of charge-based K_r/K_c (Table 1). However, mixed-effects models all show larger P, indicating that taking species nonindependence into account makes the relationships of molecular traits on body mass generally less reliable than implied by ordinary regressions (Table 1). This result is probably because of a lower number of the effective degrees of freedom left after accounting for nonindependence. A bigger discrepancy in terms of statistical significance occurs for charge-based K_r/K_c and for polarity–volume-based K_r/K_c, which yield significant, at a 5% level, relationships with body mass based on ordinary models but either nonsignificant (charge-based K_r/K_c) or marginally significant (polarity–volume-based K_r/K_c) relationships with body mass based on mixed-effects models (Table 1). All of the other relationships are significant according to either type of models.

The Relative Efficiency of Purifying Selection.

As a measure of the relative efficiency of purifying selection in large versus small mammals, we compared K_a/K_s and K_r/K_c ratios for different-sized animals. The log_e body mass for a typical small mammal is taken to be 5.62 (which corresponds to 275 g) and that for a typical large mammal to be 12.82 (which corresponds to 369,500 g), these values being the averages of log_e body mass over 55 smaller and 55 larger species in our sample. K_a/K_s is found to be ≈43% higher in large than in small mammals, whereas K_r/K_c is 8–40% higher, depending on the type of amino acid classification used (Table 2). These estimates are very similar for ordinary linear and mixed-effects models (Table 2).

Table 2.

Ratios of nonsynonymous to synonymous (K_a/K_s) and of radical to conservative (K_r/K_c) substitution rates, and amino acid dissimilarity between modern species and their most recent reconstructed ancestors measured in terms of Grantham's distance for large versus small mammals

Model	Ka/Ks	Kr/Kc based on				Grantham distance
		Polarity	Volume	Polarity–volume	Charge
OLM	0.054/0.039	0.97/0.72	1.01/0.74	0.53/0.48	0.45/0.38	58.63/55.25
MEM	0.054/0.036	0.95/0.68	0.98/0.74	0.52/0.48	0.44/0.39	58.45/55.00

The values refer to typical large (369.5 kg, left number) versus small (275 g, right number) mammals in our sample. The values are calculated from ordinary linear models (OLM) and mixed-effects models (MEM).

The Amino Acid Dissimilarity Between Modern Species and Their Most Recent Reconstructed Ancestors in Large Versus Small Mammals.

Because, as shown above, purifying selection acts on most amino acid changing substitutions versus silent substitutions and is less efficient in large than in small species, we expect that large mammals, as compared with small ones, accumulate more harmful mutations and thus evolve farther away from their most recent ancestors. The Grantham distance supports this prediction: it is larger in large animals in terms of averages (Fig. 1F), ordinary linear models (Fig. 2F), and mixed-effects models (Table 1). Quantitatively, the amino acid dissimilarity between modern and ancestral sequences is 6% greater in large than in small mammals (Table 2).

Discussion

Most of our analyses show that mitochondrial protein-coding genes of large mammals have a higher rate of accumulation of nonsynonymous substitutions relative to synonymous substitutions and, among nonsynonymous substitutions, a higher rate of accumulation of radical substitutions relative to conservative substitutions. Because nonsynonymous substitutions must be more harmful than synonymous substitutions, and radical amino acid substitutions must be more harmful than conservative ones, this implies that large mammals experience less efficient purifying selection than small mammals. Consequently, large mammals appear to accept more harmful mutations, leading to a higher level of amino acid dissimilarity between modern species and their most recent reconstructed ancestors, as observed in this study.

Charge-based K_r/K_c is the only molecular trait that does not significantly differ in large versus small mammals both in terms of averages and mixed-effects models (although it does differ on the basis of ordinary linear models.) To understand this finding, we note that among four K_r/K_c ratios, the charge-based K_r/K_c has the lowest average (Table 1), which indicates a strong purifying selection against changes in amino acid charge for the proteins under study. The selection coefficient s < 0 is then so large by absolute value that not only small mammals (with high N_e) but also large mammals (with low N_e) experience strong purifying selection, s < −1/N_{e,large mammals} < −1/N_{e,small mammals}, and get rid of such mutations. In contrast, purifying selection against changes in amino acid polarity and volume is relatively weak (corresponding K_r/K_c values are the largest, Table 1), and selection coefficient is intermediate in the sense that it falls in an effectively neutral zone for large mammals but beyond it for small mammals, i.e., −1/N_{e,large mammals} < s < −1/N_{e,small mammals}. Consequently, radical substitutions in regard to these traits are fixed in large species as if conservative (note that for large mammals polarity-based K_r/K_c and volume-based K_r/K_c lie almost precisely at 1; Fig. 1 B and C), but tend to be eliminated in small species. The slightly deleterious mutations with such an intermediate s will accumulate predominantly in large mammals.

Only slightly deleterious mutations that are fixed in populations are considered in the previous paragraph. However, in this paper we are dealing not only with mutations that are fixed in populations and thus associated with interspecific divergence, but also with mutations that are not fixed and thus associated with the amount of intraspecific polymorphism, because our K_a/K_s and other molecular traits represent external-branch estimates to which both components of genetic variation contribute. K_a/K_s representing internal-branch estimates to which only fixed mutations would contribute are of little interest here because body mass on internal nodes is unavailable. The problem with these two classes of mutations is that polymorphism often dominates fixed mutations (25–28) but it is only the latter that are thought to have a long-term evolutionary effect (e.g., ref. 29). Our data do not allow us to distinguish between these classes, so the question arises whether our K_a/K_s and other molecular traits reflect the behavior of either, or perhaps both, of them. Clearly, both classes are closely interrelated because currently fixed mutations were part of the past polymorphism, and the current polymorphism may harbor mutations that will become fixed in the future. Moreover, it seems likely that both classes will change in the same direction: as long as body mass increases, the effective population size tends to decrease, which results in an elevated fixation probability and in enhanced polymorphism due to less efficient purifying selection against deleterious mutations in small populations (2). Because less efficient selection drives both components of genetic variation, they go in the same direction, so that fixed mutations will most likely show the same positive trend with increasing body mass as K_a/K_s does. This reasoning suggests an accumulation of slightly deleterious mutations in large mammals, which might incur a threat to species persistence.

Indirectly, we can assess the impact of polymorphic mutations on K_a/K_s by computing the product S = s N_e from our estimates of K_a/K_s. This assessment can be done through the well known equation for the probability of fixation of a new mutation (2, 16). Assuming that silent sites evolve neutrally, the ratio of the fixation probability for a mutation with selection coefficient s ≠ 0 to the fixation probability for a neutral mutation with s = 0 can be equated with K_a/K_s ratio (30)

By using function uniroot in R package (31), we computed S from Eq. 1 for every of 110 mammalian species. All of the values of S turn out to be negative, which once again (see Results) is indicative of the preponderance of purifying selection. They lie in a rather narrow range from −2.97 to −1.69, with mean S being −2.38 (SE = 0.03, n = 110). Clearly, our estimates of |S| > 1 reflect the effect of polymorphic mutations on K_a/K_s, with some of them being deleterious with |s| > 1/N_e. This effect, however, does not seem to be too strong because the estimates of |S| are closer to the lower boundary of the range for |S|, 1 < |S| < 10, characteristic for polymorphic mutations (2, 25, 32). This allows for the effect of fixed mutations on K_a/K_s to appear, and is another reason why K_a/K_s would follow the behavior of fixed mutations with regard to body mass.

Mitochondrial genes are highly predisposed to mutation accumulation. Because mitochondria have a low effective population size, molecular evolution of mitochondrial DNA genes should be associated with a high rate of accumulation of slightly deleterious mutations as compared with nuclear genes (17). The absence of recombination can additionally increase the rate of degradation of mitochondrial DNA due to Muller's ratchet (33). A number of comparative-species studies have corroborated these theoretical expectations (34, 35). It is less clear whether a higher rate of deterioration of mitochondrial genes can actually lead to a faster rate of extinction (36), but recent research (37) lends support to this possibility.

The contrast between small and large modern mammals examined in this study can be turned to the past and thus viewed from a long-term evolutionary perspective by taking into account the general evolutionary trend toward larger body size, known as Cope's rule. Although there are some exceptions, this trend is common among mammals (38, 39); suffice it to mention, by way of example, that their ancestral forms were small, shrew-sized creatures (40), whereas modern mammals include such giants as blue whales and African elephants. We suggest, on the basis of present findings, that evolution of mammals toward large body size is accompanied by increasing width of the selective sieve (manifested by increased K_a/K_s and other molecular traits, and caused by less efficient purifying selection; see ref. 36), which leads to the deterioration of mitochondrially encoded proteins, and may contribute to decline or extinction of large species. Two additional lines of evidence are in favor of this hypothesis. First, many theoretical studies (41–43) conclude that small populations (that is, those typical of large-bodied species) can go extinct because of accumulation of slightly deleterious mutations and resulting mutational meltdown (42, 44). Second, large animals (45), including mammals (46–48), are more prone to extinction. However, additional analyses are needed to evaluate directly the role of less efficient purifying selection in elevated extinction risks in large mammals.

Materials and Methods

Source Data and Initial Treatment.

The fully sequenced mitochondrial genomes from all of the 138 mammalian species available at early summer 2005 were downloaded from the National Center for Biotechnology Information database (http://www.ncbi.nlm.nih.gov/genomes/ORGANELLES/animalabout.html, downloaded June 5, 2005). All 13 protein-coding mitochondrial genes were extracted from each genome and translated into amino acid sequences. Alignments of the amino acid sequences for each gene were performed by using Clustal X (49) with default settings and then reverse transcribed to get nucleotide alignments. The aligned 13 amino acids and 13 corresponding nucleotide sequences without stop codons were concatenated into a single amino acid and a single nucleotide sequence for each species. The concatenated amino acid sequences were used to reconstruct a mammalian phylogenetic tree by using PHYML (50). The concatenated nucleotide sequences were used to analyze the pattern of nucleotide substitutions.

Ratio of Nonsynonymous to Synonymous Nucleotide Substitutions (K_a/K_s).

The ratio of the rates of nonsynonymous over synonymous substitutions (K_a/K_s) was estimated for each branch of the mammalian phylogenetic tree by using the program codeml from PAML package (51). Because an independent estimate of K_a/K_s for each branch of the whole tree would have taken too much time, the tree was divided into 11 monophyletic (52) subtrees, each of which was treated separately. 16 species with an uncertain position on the whole tree (i.e., with a low bootstrap value) were omitted from further analyses. The 122 remaining species were distributed over 11 groups (subtrees) as follows: Afrotheria (13 species), Artiodactyla (9 species), Carnivora (12 species), Cetacea (22 species), Chiroptera (8 species), core insectivores (hedgehogs, shrews, and moles) (6 species), Rodentia (7 species), Lagomorpha (4 species), Metatheria (19 species), Perissodactyla (5 species), and Primates and Dermoptera (17 species). For each subtree, two evolutionary models were implemented: model 0 with K_a/K_s held constant over the whole subtree and model 1 with free K_a/K_s estimated separately for each branch (the models' designation as in PAML). Model 1 was run twice: under transition/transversion parameter [k in Kimura's notation (53)] set at 3 across all subtrees (8), and under transition/transversion parameter estimated for each subtree individually. Only K_a/K_s values associated with external branches were used to describe relationships with species body mass.

Ratio of Radical to Conservative Amino Acid Substitutions (K_r/K_c).

The ratio of the rates of radical over conservative substitutions (K_r/K_c) was estimated by comparison of the nucleotide sequences of modern animals with the nucleotide sequences of their most recent reconstructed ancestors through Zhang's algorithm (7). The ancestral nucleotide sequences were reconstructed by using the method implemented by Yang et al. (54) in PAML. Because K_r and K_c values were small enough (<0.3), the Jukes–Cantor formula was used to correct for multiple hits; that is, our K_r/K_c ratio is identical to d_R/d_C ratio in Zhang's notation (7).

The 20 amino acids were classified into groups in four different ways according to their volume (55), charge, polarity, and both polarity and volume (7). Amino acid substitutions within groups (i.e., when ancestral and modern amino acids in homologous sites belong to the same group) were regarded as conservative, and those between groups as radical.

Comparison of Evolutionary Models.

Our analyses of alternative evolutionary models (free, branch-specific K_a/K_s values versus constant K_a/K_s across all branches of a subtree and the transition/transversion parameter k specific to each subtree versus k fixed at 3 across all subtrees) provide reason to compute K_a/K_s and K_r/K_c on the basis of branch-specific K_a/K_s values (that is, through PAML model 1) and subtree-specific estimates of k [see A Check for Alternative Parameter Estimates in supporting information (SI) Text for more detail]. The K_a/K_s and K_r/K_c obtained in this manner are used throughout this paper.

In total, 110 of 122 mammal species were each characterized by K_a/K_s and K_r/K_c values. Twelve species were deleted from further analyses because of too few (<20) nonsynonymous substitutions per 13 protein-coding genes, having occurred since the most recent ancestor.

Average Grantham Distance.

To measure amino acid dissimilarity, we computed an average physicochemical distance between modern species and their most recent reconstructed ancestors. The distance between each ancestral (if substituted) and descendant amino acid was taken from Grantham's matrix (9), and averaged over all pairs of substitutions for a given external branch.

Body Mass.

The body mass of adult individuals for the majority of analyzed species was obtained from a database compiled by Smith et al. (56). In the case of different body masses for the same species on different continents being reported, body mass was averaged. A few missing data were taken from other sources. All of the data are available upon request.

Statistical Treatment.

A number of statistical analyses were performed. First, we compared the average values of the investigated molecular traits which belong to small versus large mammals (with body mass below and above the median, respectively). Then we performed the ordinary linear regressions of molecular traits on body mass. However, the characters we are dealing with may not be independent among species due to the effect of phylogenetic inertia, which might compromise comparative-species analyses (57, 58). The standard way around this problem is a method of phylogenetically independent contrasts (59). It is based on a Brownian motion model of character evolution, which assumes that increases and decreases in the character of interest are equally likely, so that the character's average does not change over time (60). Changes in body mass may not always agree with the Brownian motion model, because according to Cope's rule, which is justified for mammals (38, 39), body mass tends to increase over evolutionary time, and thus exhibits a largely directional change. There are more complex evolutionary models, which allow for a directional shift in character evolution and are used in the context of phylogenetically independent contrasts (61). A bigger problem is that molecular traits such as branch-specific K_a/K_s are already contrasts (because they are based on a sequence difference between two nodes of the branch), whereas phenotypic traits such as body mass are of course not contrasts and possess some phylogenetic inertia. Furthermore, if we were to try to associate K_a/K_s with contrasts based on body mass we would find them to be incongruent: the former are due to differences between the present and the past (present and past nucleotide sequences), whereas the latter are due to differences pertinent entirely to the present (that is, to modern species). These considerations seem to preclude a simultaneous use of molecular and body-mass traits in an analysis of phylogenetically independent contrasts.

To control for the effect of data nonindependence, we carried out a regression analysis using the linear mixed-effects model, which does not require an a priori model of character evolution, nor does it rely on contrasts. Instead, it explicitly takes into account a hierarchical (nested), and therefore correlated, structure of comparative-species data (ref. 62 and J. Fox, personal communication). This method has been widely used in social and medical sciences (see ref. 63 for review) and recently in comparative-species research (64, 65). Here, it was implemented using function lme in nlme package (66) of R language (31). Our data are nested into the following levels: species within genera within families within orders. We used a mixed-effect model which included both random intercept and random slope.

Check for Saturation Effect.

An additional check for saturation effect was performed. After omitting species which tipped the relatively long branches of ≥1 nucleotide substitution per codon, and examining the remaining data set (n = 89), the pattern of the relationships between molecular traits and body mass remains largely unchanged (see A Check for Saturation Effect in SI Text).