Chemotaxis of sperm cells

Abstract

We develop a theoretical description of sperm chemotaxis. Sperm cells of many species are guided to the egg by chemoattractants, a process called chemotaxis. Motor proteins in the flagellum of the sperm generate a regular beat of the flagellum, which propels the sperm in a fluid. In the absence of a chemoattractant, sperm swim in circles in two dimensions and along helical paths in three dimensions. Chemoattractants stimulate a signaling system in the flagellum, which regulates the motors to control sperm swimming. Our theoretical description of sperm chemotaxis in two and three dimensions is based on a generic signaling module that regulates the curvature and torsion of the swimming path. In the presence of a chemoattractant, swimming paths are drifting circles in two dimensions and deformed helices in three dimensions. The swimming paths can be described by a dynamical system that exhibits different dynamic regimes, which correspond to different chemotactic behaviours. We conclude that sampling a concentration field of chemoattractant along circular and helical swimming paths is a robust strategy for chemotaxis that works reliably for a vast range of parameters.

Sperm chemotaxis plays an important role for fertilization. It implies that a swimming sperm cell steers upwards a gradient of a chemoattractant that is released by the egg. Sperm chemotaxis is well established in marine invertebrates with external fertilization (e.g., sea urchins) (1) and has been demonstrated in mammals (e.g., humans) (2).

In bacteria, chemotaxis is well understood both experimentally and theoretically. It has been shown that bacteria undergo a biased random walk toward the source of a chemoattractant. This is achieved by stochastic switching between running and tumbling modes of motion which is controlled by a chemotactic signaling system in a way that depends on the history of the chemotactic stimulus (3–5). This chemotactic system provides a general mechanism for chemotaxis of microorganisms (3, 5).

The swimming of sperm is very different from bacterial swimming. Sperm possess a single eukaryotic flagellum of ≈50 μm length. Dynein motors in the microtubule based axonem of this flagellum generate a bending wave with a frequency of ≈50 Hz that propels the sperm forward at a speed of ≈200 μm/s (6, 7). Sperm of many species do not swim on straight trajectories but instead move in circles or helical paths (1, 6, 8–10). The differences of the swimming motion of sperm cells as compared to bacteria suggest that fundamentally different principles of chemotaxis are at work in sperm.

Here, we will focus on the chemotaxis of sea urchin sperm because of the large amount of experimental data available for this system. Chemotaxis of sea urchin sperm is usually observed under experimental conditions where sperm swim in a small observation chamber under the microscope. In this situation, sperm become localized near the surfaces of the chamber where they swim on circular paths (1, 10–12). The curvature of their swimming path is a consequence of the asymmetry of the flagellar beat (9). In a concentration gradient of a chemoattractant, the circular swimming path drifts toward positions with higher concentration (1, 10). It has also been possible to track sperm swimming far from surfaces in three-dimensional space. In this case, sperm swim on helical paths. In the presence of a chemoattractant concentration gradient, the helices bend, eventually leading to alignment of the helix axis with the gradient (8).

Chemotaxis is mediated by a signaling system that is located in the sperm flagellum (10). Specific receptors in the flagellar membrane are activated upon binding of chemoattractant molecules and start the production of cyclic guanine monophosphate (cGMP). A rise in cGMP gates the opening of potassium channels and causes a hyperpolarization of the flagellar membrane. This hyperpolarization triggers the opening of voltage-gated calcium channels and the membrane depolarizes again. The overall effect of this signaling cascade is the generation of a transient increase of the internal calcium concentration along the flagellar length (9, 10, 13). This calcium signal is thought to regulate the activity of dynein motor proteins in the flagellum, thus affecting the geometry of the swimming path (14). Interestingly, this signaling system operates over a vast range of chemoattractant concentrations ranging from picomolar to micromolar concentrations (13). This observation suggests that adaptation plays an important role in sperm chemotactic signaling.

In this article, we develop a theoretical description of sperm chemotaxis. We characterize a simple and general mechanism for chemotaxis in two dimensions that is motivated by recent experiments (9–11, 13). Sperm swimming on circular paths in a concentration gradient of a chemoattractant sample a periodic concentration stimulus. The signaling system transfers this stimulus into a periodic modulation of the curvature of the swimming path. As a result, the circular path drifts in a direction that depends on the internal dynamics of the signaling system. We show that this principle is more general and also works for helical trajectories in three dimensions. We discuss conditions under which a swimming sperm reaches the egg, in both two and three dimensions. Our work characterizes a principle for the chemotaxis of microorganisms that is based on the idea of helical klinotaxis introduced by the earlier work of Crenshaw (15–17).

Theoretical Description of Sperm Chemotaxis

Chemotaxis in a Plane.

Chemotaxis can be studied in two dimensions for sperm swimming near a surface along a path r(t). The swimming path is defined as the position of the head averaged over one cycle of the flagellar beat as a function of time. This average eliminates rapid periodic movements of the head at the frequency of the flagellar beat. The swimming velocity is characterized by the speed v = |ṙ| and the tangent vector t = ṙ/v of the swimming path. Dots denote time derivatives. The geometry of the swimming path is described by the Frenet–Serret equations in two dimensions

where the normal n is orthogonal to t, and κ is the local curvature of the swimming path. If the curvature is constant, κ = κ₀, the swimming path is a circle with radius r₀ = 1/κ₀. The angular frequency of swimming in circles is ω₀ = v₀κ₀ if the speed v = v₀ is constant.

We consider a swimming path in a concentration field c(x) of chemoattractant, where x = (x, y) denotes a position in two-dimensional space. The swimming sperm perceives a temporal concentration stimulus s(t)

This stimulus s(t) triggers a response of the chemotactic signaling network. In general, the signaling network is a dynamic system that generates a time-dependent output that depends on the history of the stimulus. We characterize this response by a dimensionless output variable a(t) with a = 1 in steady state. We assume that this output variable directly affects the curvature κ of the swimming path by

The variable a(t) plays a similar role as the internal calcium concentration within the flagellum. The calcium concentration is controlled by the chemotactic signaling network and influences the activity of dynein motors, thereby modulating the flagellar beat pattern and the curvature of the swimming path. For simplicity, we assume that the swimming speed is constant v = v₀ and not affected by chemotactic signaling.

We can capture the essential properties of the chemotactic signaling network, namely its ability to adapt and its relaxation dynamics by a simple dynamical system (18, 19)

Here, p(t) is an internal variable that governs adaptation, σ is a relaxation time, and μ has units of time per volume. For a time-independent stimulus s(t) = s₀, the system reaches a steady state with a = 1 and p = 1/s₀. The system is adaptive because the steady-state output is independent of the stimulus level s₀. Eqs. 1–4 determine a unique swimming path r(t) in a self-consistent manner for given initial conditions and the concentration field. Examples of swimming paths for linear and radial concentration fields are shown in Fig. 1. These paths can be described as circles whose centers drift along well defined trajectories.

Fig. 1.

Swimming paths r(t) in two dimensions for two different chemoattractant concentration fields. (a) In a linear concentration field c(x) = c₀ + c₁ · x with constant gradient vector (blue arrow), the swimming path (black line) is a drifting circle. This drift can be described by the motion of the center of the circle R(t) (red line). This centerline encloses an angle of α with the gradient direction. (b) In a radial concentration field c(x) = c₀/|x|, the swimming path is a circle that drifts along a spiral to the center of the radial distribution (blue dot). The paths shown are numerical solutions to Eqs. 1–4 with parameters in (a) |c₁| = 0.1 c₀/r₀, κ₁ = 1/r₀, μ=5 c₀/σ, v₀ = 0.5 r₀/σ, and in (b) κ₁ = 1/r₀, μ = 0.5 c₀/σ, v₀ = 0.5 r₀/σ, where c₀, r₀, σ set the concentration, length and time scales of the problem, respectively. In both cases, initial conditions were r(0) = (10, −1) r₀, a(0) = 1, and p(0) = 1/c(r(0)).

Small periodic variations of the stimulus s(t) = s₀ + s₁ cos ω₀t evoke a periodic response of the curvature κ(t) = κ₀ + ρ_κs₁ cos (ω₀t + φ_κ) + 𝒪(s₁²) with amplitude gain ρ_κ and phase shift φ_κ. For the signaling system (Eq. 4), the linear response coefficient χ_κ = ρ_κexp(iφ_κ) reads

This linear response will play a key role to characterize swimming paths.

Chemotaxis in Three-Dimensional Space.

Far from any surface, sperm cells swim along helical paths if no chemoattractant is present (8). The geometry of the swimming path r(t) is characterized by the tangent t = ṙ/v, the normal n = ṫ/|ṫ| and the binormal b = t × n. The time evolution of these vectors is given by the Frenet–Serret equations in three dimensions

For constant curvature κ(t) = κ₀ and torsion τ(t) = τ₀, the swimming path is a perfect helix with radius r₀ = κ₀/(κ₀² + τ₀²) and pitch 2πh₀ = 2π τ₀/(κ₀² + τ₀²). The angular frequency of helical swimming is ω₀ = v₀ (κ₀² + τ₀²)^1/2.

Swimming along such a helical path in a chemoattractant concentration field leads again to a time-dependent stimulus s(t) of the signaling system as in the two-dimensional case. In our three-dimensional description, we assume that the output variable a(t) of this system modulates both the curvature κ(t) and the torsion τ(t) of the swimming path

The system of Eqs. 2, 4, 6, and 7 uniquely determines the swimming path r(t) for given concentration field and initial conditions. Fig. 2ashows an example of a swimming path in a radial concentration field, which leads toward the origin of the concentration field. The swimming path r(t) is superhelical: It is a perturbed helix that winds around a curved centerline R(t) (see Fig. 2b).

Fig. 2.

Three-dimensional swimming path of a sperm cell in a radial concentration field c(x) = c₀ /|x|. (a) The swimming path r(t) is superhelical and leads to the chemoattractant source (blue dot). (b) The centerline R(t) of the full swimming path. (c) Dynamics of the coarse-grained quantities R = |R| and alignment angle ψ between helix vector and gradient direction (red curve). Temporal information is provided by dot marks along the (R, ψ)-trajectory, which are seperated by a time interval of 100 σ. For comparison, the (R, ψ)-trajectory as obtained by our perturbation calculation for the small pertubation parameter υ (see Eq. 12) is shown in black. Although the value of the perturbation parameter υ rises from 0.1 to 1 along the trajectories, qualitative agreement between both trajectories persists. Numerical integration of Eqs. 2, 4, 6, and 7 was done for κ₁ = −0.1/r₀, τ₀ = 0.2/r₀, τ₁ = 1/r₀, μ = 10 c₀ /σ, v₀ = r₀ /σ, and initial conditions r (0) = (15, 25,−10)r₀, t(0)=(1,0,0), n(0)=(0,1,0), b(0) = (0,0,1), a(0) = 1, and p(0) = 1/c(r(0)). The size of the box in (a) and (b) is approximately 25r₀ × 40r₀ × 40r₀.

The response of the torsion to weak stimuli is characterized by a linear response coefficient χ_τ = ρ_τ exp(iφ_τ), which is defined analogously to the linear response coefficient χ_κ of the curvature (Eq. 5).

Properties of Swimming Paths

Motion in a Plane.

Eqs. 1–4 for the swimming path r(t) can be solved numerically. For a linear concentration field c(x) = c₀ + c₁ · x, the swimming paths are drifting circles. The overall motion of these circling paths is captured by the trajectory of the circle centers, which defines the centerline R(t). The centerline R(t) is oriented approximately at constant angle α with respect to the direction of the concentration gradient c₁ (see Fig. 1a). In a radial concentration field with c(x) = c₀ /|x|, the centerline R(t) is a spiral that circles toward the origin at x = (0, 0) (see Fig. 1b). This choice of the radial decay is is motivated by the steady-state concentration field established in three dimensions by diffusion from a source. Note that the spiral shape of the centerline does not depend on the precise form of the radial decay.

To understand these results, we consider the limit of weak gradients. We determine the swimming path in a linear concentration field c(x, y) = c₀ + c₁ x by a perturbation calculation in the small parameter υ = ρ_κr₀²c₁, which describes the strength of the perturbation of the swimming path by chemotactic signaling. Here we explain the logic of the calculation, a detailed deviation is provided in supporting information (SI) Text. When swimming along a perturbed circular path, the sperm cell perceives a concentration stimulus that is periodically modulated. This periodic stimulus elicits periodic modulations of the curvature of the swimming path. The resulting swimming path is thus a drifting circle with corresponding centerline

and drift velocity v_d = δ_κ ρ_κ c₁ + 𝒪(υ²) where δ_κ = 1/2 v₀r₀². For the angle with respect to the gradient, we obtain

These results can be generalized to a nonlinear concentration field provided that the gradient is weak, υ ≪ 1, and the nonlinearities are small on the length-scale r₀, |∇²c| ≪ |∇c|/r₀. Eq. 8 for the centerline can then be generalized as

where the operator M(α) rotates the vector ∇c in the plane by the angle α in a counterclockwise sense. Eq. 10 represents a differential equation for the centerline R(t) if the gradient ∇c of the concentration field is evaluated at any time at position R(t).

This equation for the centerline can be illustrated for the case of a radial concentration field c(x) = C(|x|). In this case, according to Eq. 10, the centerline R(t) winds around the origin in a logarithmic spiral, R(θ) = R₀ exp(−cot(α)θ), where θ is the polar angle and R = |R| (see Fig. 3).It spirals inwards for −π/2 < α < π/2, which corresponds to a phase shift of the signaling system of π < φ < 2π. Otherwise, it spirals outwards.

Fig. 3.

Schematic representation of a swimming path in two dimensions in a radial concentration field of chemoattractant. The swimming path r(t) (black line) is a drifting circle whose center moves along the centerline R(t) (red line). In the limit of weak concentration gradients with the parameter υ small (see text) this centerline is a logarithmic spiral whose tangent encloses a constant angle of α with the gradient direction at every point. The distance R=|R| of the centerline to the source and the polar angle θ are used in the formula of the logarithmic spiral (see text).

We have compared solutions to the dynamic equations (Eqs. 1–4) for the swimming path to solutions of Eq. 10 for the center line in our perturbation calculation and found good quantitative agreement for υ ≲ 0.1. Furthermore, Eq. 10 could predict perfectly whether the path reached the egg.

Motion in Three-Dimensional Space.

Our numerical solutions for swimming paths in three dimensions shown in Fig. 2a demonstrate that the modulation of curvature and torsion of the path by the signaling system lead to chemotactic behavior. In the absence of a gradient, the swimming path is a perfect helix with a straight centerline. If this trajectory encounters a linear concentration field, the helix bends until its axis is parallel or antiparallel to the concentration gradient. In a radial concentration field, swimming paths are deformed helices that wind toward the origin of the concentration field. To understand these numerical observations, we generalize the ideas developed in the previous section to three dimensions.

The net motion resulting from swimming along a deformed helical path r(t) is captured by the trajectory of the centerline R(t). For given centerline, the helical path can be described by tracing the trajectory of a point on the circumference of an imagined solid disk with radius r₀, rotating in its plane with a rotation rate Ω₃ and with its center moving along R(t). The orientation of the disk is characterized by the unit vector h normal to the disk, which we call the helix vector (see Fig. 4). For a comparison of the full swimming path r(t) and its centerline R(t), see Fig. 2 a and b.

Fig. 4.

A deformed helical path r(t) can be generated by the motion of a point on an imagined solid disk that spins around the helix axis given by the vector h normal to the disk. The center of the disk moves along a curved centerline R(t) with tangent Ṙ. The gradient direction ∇c and the helix vector h enclose an angle ψ.

As in the planar case, the chemotactic feedback loop for three space dimensions (Eqs. 2, 4, 6, and 7) can be studied in the limit of weak gradients by a perturbation calculation in the small parameter υ = (ρ_κ/κ₀+ρ_τ/τ₀) r₀ |∇c|, see SI Text for details. In the limit of a weak gradient, the swimming path is a perturbed helix. In a concentration field, this helical swimming path samples a time-dependent chemotactic stimulus that has a periodic component that is governed by the projection ∇_⊥c = (1 − h h·) ∇c of the three-dimensional gradient on the plane of the disk. This periodic component of the stimulus generates an output signal that periodically modulates both curvature and torsion of the path with phase shift φ_κ and φ_τ, respectively. These fast modulations result in slow variations of Ṙ and h. Also, helix frequency ω = ω ₀ + 𝒪(υ) and helix pitch 2πh = 2πh₀ + 𝒪(υ) are shifted to first order in υ.

In a linear concentration field, we obtain a dynamic equation for the alignment angle ψ between h and the gradient vector ∇c (see Fig. 5) which reads

where β = |∇c| (ε_τ Re χ_τ − ε_κ Re χ_κ) with ε_κ = ω ₀r₀ h ₀/2, ε_τ = ω₀ r₀²/2. This equation has two fixed points at ψ = 0 and ψ = π, which correspond to helical paths whose helix vectors are parallel and antiparallel to the gradient vector, respectively. The sign of β determines which of the fixed points is stable. The rate at which the helix aligns with the gradient direction is |β|. Therefore, for almost all initial conditions, the system exhibits chemotaxis upwards the gradient if β > 0. This behavior is therefore robust and does not depend on fine-tuning of parameters.

Fig. 5.

In a linear concentration field c(x) = c₀+c₁ · x with constant gradient vector (blue arrow), the swimming path is a deformed helix (black line), which bends and eventually aligns with the gradient: The angle ψ between the the gradient direction ∇c and the helix vector h decreases monotonically, see Eq. 11. The path shown is a numerical solution to Eqs. 2, 4, 6, and 7 with parameters κ₁ = −0.5/r₀, τ₀ = 0.1/r₀, τ₁ = 0.5/r₀, μ=c₀ /σ, v₀ = r₀ /σ, and initial conditions r(0) = (15,25,−10)r₀, t(0) = (1,0,0), n(0) = (0,10), b(0) = (0,0,1), a(0) = 1, and p(0) = 1/c(r(0)). The size of the box is approximately 45r₀ × 20r₀ × 25r₀.

Consider the case of a radial concentration field c(x) = C(|x|). The five degrees of freedom represented by R and h can be expressed by the distance to the origin R = |R|, the alignment angle ψ between helix vector and radial concentration gradient, as well as three Euler angles θ, ξ, and η (see SI Text). Because of rotational symmetry, the variables R and ψ decouple from the other three variables and obey the dynamic equations

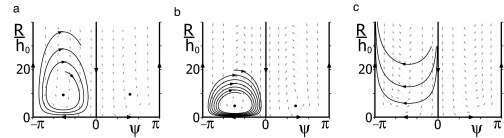
where β is as above and γ = |∇c|(δ_τ Im χ_τ − δ_κ Im χ_κ) with δ_κ = ω₀ r₀ (2r ₀² + 3h₀²)/4, δ_τ = ω₀ r₀² h₀ /4 (see SI Text). As in the case of a linear concentration field, we can analyze under what conditions swimming paths find an egg of radius R_egg at the origin by discussing phase space trajectories of this dynamical system. We restrict ourselves to the case |γ| < ω₀ h₀ relevant to our perturbation calculation and assume for simplicity constant values of β and γ, as well as ω = ω₀, h = h₀. These assumptions correspond to a signaling network that has constant linear response coefficients χ_κ, χ_τ, independent of the average stimulus level, and perfectly adapts to ramp stimuli. However, the following analysis will not change qualitatively if these assumptions are not imposed, provided that β and γ do not switch sign. Depending on the two parameters β and γ, the flow of the dynamical system can exhibit three different regimes: Regime A for β > 0, γ > 0, B for β > 0, γ < 0, and C for β < 0 (see Fig. 6). In regime A and B with β > 0, two symmetric fixed points (R₀, ψ₀) exist, where R₀ = ω ₀ h₀ /β + 𝒪(υ), ψ₀ = ±π/2 + 𝒪(υ), which correspond to swimming paths for which the centerline circles around the origin and R is constant. Linear stability analysis reveals that for regime A, these fixed points are repulsive while for regime B they are attractive (see Fig. 6 a and b). In both regimes, (R, ψ)-trajectories of the dynamical system are spirals near the fixed points which correspond to swimming paths that repeatedly (i) align with the gradient vector, (ii) approach the origin, (iii) loose alignment when they come near the origin, and (iv) move away again. As a consequence, R subsequently decreases and increases, with an increasing amplitude of R changes in regime A and a decreasing amplitude in regime B. For regime C with β < 0, no fixed points exist, the trajectories are U-shaped and move toward large R at long times (see Fig. 6c).

Fig. 6.

Flow field and typical trajectories in the (R, ψ)-phase space for the dynamic system given by Eq. 12, which describes chemotaxis in three dimensions in a radial concentration field. Here R is the distance of the centerline to the chemoattractant source, and ψ is the angle between the helix vector and the gradient direction. Distance R is shown relative to h₀ where 2πh₀ is the pitch of the unperturbed helix. (a), (b), and (c) are examples for the three regimes A, B, and C, respectively (see text for details). Typical (R, ψ)-trajectories (black lines) as well as the gradient vector field (gray arrows) are shown. (a) In regime A, the system possesses two repulsive fixed points (black dots). The (R, ψ)-trajectories are spirals which spiral away from the fixed points. (b) In regime B, the fixed points are attractive and (R, ψ)-trajectories spiral toward the fixed points. (c) In regime C, no fixed points exist, the (R, ψ)-trajectories are U-shaped and eventually move away from the chemoattractant source. The parameter values used were β = 0.1 ω ₀, γ = 0.1 ω ₀ h₀ (a); β = 0.2 ω ₀, γ = −0.05 ω ₀ h₀ (b); and β = −0.1 ω ₀, γ = −0.1 ω ₀ h₀ (c).

In the presence of an egg with radius R_egg, the centerline of swimming paths reaches the egg for almost all initial conditions in case A (see Fig. 7a). For case B, (R, ψ)-trajectories starting in a finite neighborhood of the fixed points (R₀, ψ₀) correspond to swimming paths that do not reach the egg. Further away from this neighborhood, trajectories can reach the egg before they spiral to the fixed point (see Fig. 7b). In case C, swimming paths are repelled from the egg and chemotaxis acts down the gradient (see Fig. 7c). Therefore, we find again that chemotaxis is a robust property that does not require fine-tuning of parameters. It is most reliably in case A for which a sufficient condition is given by π < φ_κ < 3π/2, 0 < φ_τ < π/2.

Fig. 7.

Chemotactic success as a function of initial conditions of swimming paths according to the dynamic system given by Eq. 12. The initial condition of a path is characterized by the initial distance R(0) of the centerline to the chemoattractant source and the initial angle ψ (0) between the helix axis and the gradient direction. Distance R is shown relative to h₀ where 2πh₀ is the pitch of the unperturbed helix. For a given initial condition, chemotaxis is unsuccessful if the correspondent swimming path has a distance R(t) to the chemoattractant source which is always greater than an egg radius R_egg, R(t) > R_egg. Initial conditions with unsuccessful chemotaxis are shown as blue dots, blue lines, and blue hatched regions. The radius of the egg R_egg is indicated by a dashed line. (a), (b), and (c) are examples for the three regimes A, B, and C, respectively (see text for details). (a) In regime A, where repulsive fixed points exist (see Fig. 6a), chemotaxis is robust and fails only at the fixed points and the marginal case ψ (0) = ±π. (b) In regime B, fixed points are attractive (see Fig. 6b). Chemotaxis is successful in a large range of initial conditions and fails only in a neighborhood of the fixed points as well as in the marginal case ψ (0) = ± π. (c) In regime C, no fixed points exist and chemotaxis is repulsive with respect to the chemoattractant source (see Fig. 6c). Chemotaxis is unsuccessful except for those initial conditions where the initial distance to the source is already small and the helix axis is nearly aligned with the gradient direction. The parameter values used were R_egg = h₀ and β = 0.1 ω ₀, γ = 0.1 ω ₀h₀ (a); β = 0.2 ω ₀, γ = −0.05 ω ₀ h₀ (b); and β = −0.1 ω ₀, γ = −0.1 ω ₀h₀ (c).

Discussion

We have presented a theoretical description of sperm swimming paths, taking into account chemotactic signaling. Our main assumptions are (i) that the curvature and torsion of the swimming path are modulated by the signaling system, and (ii) that the signaling system receives a temporal chemoattractant concentration stimulus implying that concentration differences along the length of the flagellum are irrelevant. We study swimming paths both in two and three dimensions and for linear and radial concentration fields. In all cases, periodic components occur in the stimulus that elicit periodic variations of curvature and torsion of the path. Using both numerical and analytical methods, we show that the resulting swimming paths are drifting circles in two dimensions and helices that are bent and tilted in three dimensions. We discuss the geometry of these paths and determine the conditions under which the system moves to regions of high chemoattractant concentration. We find that key parameters for chemotactic success are the phase shifts φ_κ and φ_τ between stimulus and modulations of curvature and torsion, respectively. In both two and three dimensions, there exist large ranges of these parameters for which chemotaxis is reliable. There is an extensive overlap of those ranges where chemotaxis works for the same parameters in two and three dimensions. Therefore, chemotaxis is a robust property of the system that does not require fine-tuning of parameters if the signaling system is adaptive. Our work is related to earlier work by Crenshaw, who suggested that chemotaxis could be realized for helical paths by periodically modulating rates of translation and rotation of swimming sperm (15–17). Several works have studied chemotaxis for helical paths using computer simulations (20) or by experiments with robots (21).

Our results are consistent with experimental observations both in two and three dimensions. When sperm swims close to a surface, observed swimming paths in a concentration gradient resembled drifting circles (1, 10). Recent experiments have shown that, upon periodic stimulation, the signaling network generates calcium spikes which are phase-locked to the stimulus with a phase shift of about −0.4 × 2π (11). This value is in the range where chemotaxis is successful in two dimensions. Note, however, that between the calcium spike and the curvature modulation, there could be an additional phase shift stemming from the dynamic dependence of the curvature on the flagellar beat pattern. In three dimensions, tracking experiments showed that sperm swim along helices (8) as had been suggested earlier (6, 22). Furthermore, it was observed that in a concentration gradient the helix axis aligned with the gradient vector (8).

From experiments, we can estimate parameter values which are relevant to our description. Typical values for the swimming speed, average curvature and torsion are v₀ ≈ 200 μm s⁻¹, κ₀ ≈ 0.025−0.05 μm⁻¹, and τ₀ ≈ −0.025 μm⁻¹, respectively (7, 8, 10). The radius of the egg is R_egg ≈ 100 μm (23). From the drift speed v_d ≈ 25–50 μm s⁻¹ of swimming circles reported in ref. 11, we estimate the perturbation parameter υ = v_dr₀² /δ_κ = 2v_d/v₀ ≈ 0.25−0.5. In an early experiment with bracken fern spermatozoids, Brokaw measured the bending rate of the helix as a function of the concentration gradient. He suggested Eq. 11 as a phenomenological description of his observations and could estimate βc/|∇c| ≈ 350 μm s⁻¹ (22). Furthermore, he observed that bending of the helix occurred in the plane spanned by the helix vector and the gradient, which suggests that β′ = |∇c|(ε_κImχ_κ−ε_τ Im χ_τ) ≈ 0 (see Eq. S14 in SI Text).

We used a simplified description of the signaling network which captures essential properties such as adaptation and a simple relaxation dynamics that generates a phase shift between stimulus and output. Experimental studies of the signaling system revealed that the flagellar membrane potential exhibits spikes on a 100-ms time scale with an amplitude that increases from 2 to 45 mV when stimulus concentration is varied over 5 orders of magnitude from 250 fM to 25 nM. The spike amplitude saturates for stimulus concentrations as low as ≈25 pM (13). This nonlinear response suggests a more complex dynamics than the simple system described by Eq. 4. If the signaling network generated spikes of constant amplitude that are phase-locked to a periodic stimulus, the perturbation parameter υ would be independent of concentration. We speculate that an adaptation mechanism ensures that υ does not change significantly over a large range of concentrations.

Helical swimming paths are ubiquitous in nature and are a direct result of an asymmetric propulsion mechanism. In addition to sperm, it has been observed for ascidian larvae, eukaryotic flagellates such as Chlamydomonas, flagellated plant spermatozoids, and even some bacteria such as Thiovulum majus (24–27). In the case of ascidian larvae, both positive and negative phototaxis have been observed in different developmental stages. Such a change in phototactic behavior can be accounted for by our theory by a simple change of the phase shift between the stimulus and the response (24).

In summary, we have shown that temporal sampling of a concentration field along a helical path provides a robust strategy for chemotaxis if curvature and torsion are modulated in response to the stimulus. This mechanism can work reliably over a large concentration range, does not require fine-tuning of parameters, and depends only on a few generic properties of the signaling network.