Replication Fork Velocities at Adjacent Replication Origins Are Coordinately Modified during DNA Replication in Human Cells

Abstract

The spatial organization of replicons into clusters is believed to be of critical importance for genome duplication in higher eukaryotes, but its functional organization still remains to be fully clarified. The coordinated activation of origins is insufficient on its own to account for a timely completion of genome duplication when interorigin distances vary significantly and fork velocities are constant. Mechanisms coordinating origin distribution with fork progression are still poorly elucidated, because of technical difficulties of visualizing the process. Taking advantage of a single molecule approach, we delineated and compared the DNA replication kinetics at the genome level in human normal primary and malignant cells. Our results show that replication forks moving from one origin, as well as from neighboring origins, tend to exhibit the same velocity, although the plasticity of the replication program allows for their adaptation to variable interorigin distances. We also found that forks that emanated from closely spaced origins tended to move slower than those associated with long replicons. Taken together, our results indicate a functional role for origin clustering in the dynamic regulation of genome duplication.

INTRODUCTION

The complete and correct duplication of the genome once and only once per cell cycle is one of the most challenging cellular tasks. In metazoan cells, DNA replication initiates at multiple sites, called origins of replication, from which two forks emanate and progress bidirectionally. The efficient duplication of the eukaryotic genome depends on the orderly activation of those origins, estimated to be several tens of thousands, and on the proper progression of their forks. In spite of its importance in the transmission of genetic information, the regulation of origin distribution and fork progression and the coordination of these two processes still remain to be fully elucidated in human cells. In metazoans, origins of replication are generally not encoded by specific sequences (DePamphilis, 1999; Todorovic et al., 1999; Gilbert, 2001; Mechali, 2001). Origins are dynamically regulated by a number of cis-acting, metabolic and epigenetic factors depending on the transcriptional and developmental programs (Maric et al., 1999; Sasaki et al., 1999; Aladjem and Fanning, 2004; Danis et al., 2004).

In early Xenopus embryos, transcription is repressed and DNA replication starts at nonspecific sites every 5–15 kb. The exit from midblastula and the beginning of transcription reorganizes the spatio-temporal pattern of origin firing, with replication occurring at specific sites every 150–300 kb (Hyrien et al., 1995). In spite of this flexibility in the distribution of active origins along the genome, the total number of origins is a crucial parameter for the efficient duplication of the genome (Machida et al., 2005; Shechter and Gautier, 2005). Initiation of DNA replication from a reduced number of origins is associated with gross chromosomal abnormalities in Saccharomyces cerevisiae Sic1 mutants (Lengronne and Schwob, 2002). The number of origins and their initiation timing are also checkpoint-restricted in unstressed Xenopus extracts, perhaps in order to limit fork density and fork arrest (Marheineke and Hyrien, 2004; Shechter et al., 2004), which are potential sources of genomic instability (Rothstein et al., 2000; McGlynn and Lloyd, 2002; Nyberg et al., 2002; Cleary and Pearson, 2005).

Efficient duplication of large genomes requires the coordinated activities of several proteins, including not only replication factors, but also cell cycle regulators (Cardoso et al., 1993), base excision repair enzymes (Otterlei et al., 1999), and DNA methyltransferases (Leonhardt et al., 1992; Feng et al., 2006). Chromatin modifications, namely methylation and acetylation, are coordinated with DNA replication (Feng et al., 2006; Ozdemir et al., 2006). In the cell nucleus, proteins bound to the DNA are spatially organized into microscopically visible functional structures, which are referred to as replication factories, or replication foci (Leonhardt and Cardoso, 1995; Newport and Yan, 1996; Cook, 1999). In those replication foci, newly synthesized DNA can be detectred by pulse-labeling with nucleotide analogues that can be detected by immunofluorescence (Cook, 1999).

Characteristic replication patterns have been described for different stages of the S-phase (Dimitrova and Gilbert, 1999; Dimitrova and Berezney, 2002). It has been also observed that these replication foci display a typical nuclear distribution and timing, which are maintained at subsequent cell cycles (Leonhardt et al., 2000; Sadoni et al., 2004). Therefore, these stable replication structures likely represent a fundamental unit of chromatin organization, where replicons are thought to cluster into functional domains formed by chromatin loops. This spatial organization of replicons into clusters seems to be of critical importance for the timely completion of replication in higher eukaryotes. According to the classical view of replicon clustering in mammalian nuclei, each focus consists of 2–9 replicons of relatively small size (100–200 kbp), which are equally spaced and simultaneously duplicated in 45–60 min (Huberman and Riggs, 1968; Jackson and Pombo, 1998; Berezney et al., 2000).

The corresponding average fork movement rate can be estimated at ∼1–3 kbp/min, depending on species, cell type, and stage within the S-phase. It is becoming increasingly evident that the size and number of replicons per focus can be extremely heterogeneous and that a large fraction of the foci may contain only one single large replicon (Mbp-long; Berezney et al., 2000). Previous studies have already raised questions about the mechanistic role of origin clustering in the regulation of genome duplication (Sadoni et al., 2004); that is, how origin firing is defined in space and time and how replication fork progression is coordinated with other processes, such as transcription. It appears that interorigin distances can vary significantly, either between adjacent origins or between different regions of the genome (Berezney et al., 2000). Therefore, the coordination and compensation between origin spacing and fork progression may be one mechanism for the complete duplication of the genome in the limited amount of time of S-phase. Elucidation of the relationship between origin spacing and fork velocity and its role in the control of the replication kinetics requires the simultaneous analysis of multiple, adjacent origins and of individual replication forks emanating from those origins.

As presented in this study, we used a single-molecule approach based on molecular combing (Bensimon et al., 1994; Herrick and Bensimon, 1999; Lebofsky and Bensimon, 2005; Conti et al., 2007) to measure interorigin distances and replication fork velocities over extensive regions of the genome in both primary keratinocytes and cancer cells. Because molecular combing stretches individual DNA molecules with a constant stretching factor (1 μm = 2 kb; Bensimon, 1994), quantification of interorigin distance and fork speed can be performed without the use of an internal control. While being in agreement with previous reports using prior techniques (Edenberg and Huberman, 1975; Hand, 1978; Berezney et al., 2000), our study provides evidence suggesting a novel replicon cluster model for the regulation of origin activation, with replicon clusters playing a direct role in adapting the velocities of adjacent replication forks to the interorigin distance. The data therefore provide the first molecular evidence for a functional role of origin clustering in the dynamic regulation of genome duplication in somatic cells.

MATERIALS AND METHODS

Cells Cultures

Primary normal keratinocytes were derived from skin biopsies carried out on three different donors and cells were grown in different media as follows: donor 1, grown in SFM medium (serum and growth factors), in presence and absence of feeders; donor 2, grown in SFM medium without feeders; and donor 3, grown in green medium (growth factors only) with feeders and in SFM medium with and without feeders (Supplementary Table 1). IC1 keratinocyte cells (Sastre-Garau et al., 2000) were derived from a cervical cancer naturally infected and established by HPV18 and cells were grown in RPMI with 5% fetal calf serum.

Cell Labeling

Two independent sequential labelings, with iodo-deoxyuridine (IdU) and chloro-deoxyuridine (CldU), were performed for both the normal and cancer cell samples. A subconfluent asynchronous population of cells was first labeled for 20 min with 100 μM IdU, washed with 1× phosphate-buffered saline (PBS) and then labeled for another 20 min with 100 μM CIdU. For the total labeling, cells were pulsed for 24 h with 100 μM bromo-deoxyuridine (BrdU). PBS solution and dNTP containing media were heated at 37°C before labeling. Cells were trypsinized, pooled, and resuspended in a suitable volume of 1× PBS and low-melting point agarose 1%, to a final cell concentration of 1 × 10⁵cells/100 μl. The solution was then aliquoted in pulse-field gel electrophoresis molds and kept at +4°C for 30 min.

Digestion and Removal of Proteins

Agarose plugs were resuspended in a suitable volume of EDTA and treated overnight at 50°C with 1% N-lauryl sarcosyl and 1 mg/ml proteinase K. Complete removal of digested proteins and other degradation products was performed by several gentle washings in TE (10 mm Tris, pH 8, 1 mM EDTA). Protein-free DNA plugs were then stored in EDTA at 4°C or immediately used for combing.

DNA Molecular Combing

An agarose plug was melted at 70°C for 20 min with 100 mM 4-morpholinepropanesulfonic acid (pH 6.5). The solution was maintained at 42°C for 15 min and treated overnight with 2 μl β-agarose (New England Biolabs, Beverly, MA). The solution was dropped into a Teflon reservoir and DNA was combed on silanized cover slips as previously described (Michalet et al., 1997).

Detection of IdU and CldU, Image Scanning, and Signal Measurement

Combed DNA was denatured in 0.5 M NaOH for 20 min with gentle shaking, washed several times in 1× PBS, and incubated with the primary antibodies. All antibodies were diluted in a 1% blocking solution (Boehringer-Mannheim, Indianapolis, IN) in 1× PBS, incubated in a humid chamber, and washed three times for 3 min with 1× PBS, as follows: First step, 2/5 mouse anti-BrdU-FITC (Becton Dickinson, Lincoln Park, NJ) + 2/5 rat anti-CldU (SeraLab, Loughborough, Leicestershire, United Kingdom), incubated 1 h at room temperature; Second step, 1/25 donkey anti-mouse FITC (Jackson ImmunoResearch Laboratories, West Grove, PA) + 1/25 donkey anti-rat-594 (Molecular Probes, Eugene, OR), incubated 20 min at 37°C. Mounting in Vectashield was as follows: to detect BrdU into fully labeled DNA, the previous protocol was used, with the following modifications: First step, 2/5 mouse anti-BrdU (Becton Dickinson); Second step, 1/10 goat anti-mouse-594 (Molecular Probes). The slides were scanned with an epifluorescent microscope (Axioplan, Zeiss, Thornwood, NY) using a 40× objective. Images were recorded by Smartcapture 2 (Digital Scientific, Cambridge, United Kingdom), and fluorescent signals were measured using the homemade software CartographiX. The length of the signals, measured in micrometers, was converted to kilobases according to a constant and sequence-independent stretching factor (1 μm = 2 kb), as previously reported (Bensimon et al., 1994). Removal of the background was performed in order to distinguish better the fluorescent signals.

Statistical Analysis

Data were inserted in an Excel spread sheet (Microsoft, Redmond, WA) and analyzed by KyPlot (KyensLab, 2-1-4-412 Sotokanda, Tokyo 101-0021, Japan) and SigmaPlot (Stystat, San Jose, CA). For the calculation of the fork velocity, we did not use: 1) the red segments from merged forks; 2) the green segments from type 2 signals (see Figure 1A), and 3) the red segments from type 3 signals (Figure 1A). The values of fork velocity and interorigin distance were calculated for each single molecule and plotted as a frequency distribution. Statistical values of mean and median (as the most representative value for our non-Gaussian distributions) were obtained from a large set of sample data and are therefore representative of the corresponding cell population. Right versus left fork rates (both for outgoing and incoming forks) were determined for each single replication bubble, and their value is represented by a dot in the scatter diagrams. Extension to a large set of data permitted reliable calculation for both their linear correlation (R) and linear regression (b) coefficients, as well as the statistical parameters of their ratio distribution, both reported in Table 1. Envelopes were arbitrarily drawn in order to define a pair of coordinated forks when the deviation of their ratio from the theoretical value 1 is <33% (0.75 < right/left fork speed < 1.33). Therefore, the points lying inside this envelope indicate the pairs of coordinated forks. Such a preset threshold will allow for future comparative studies with different cell lines and growth conditions. Comparison between the values obtained for normal and cancer cells was performed by a two-sided t test or a Wilcoxon U test for unpaired data, depending on the normality of the distribution, and using a significance level of α = 0.05.

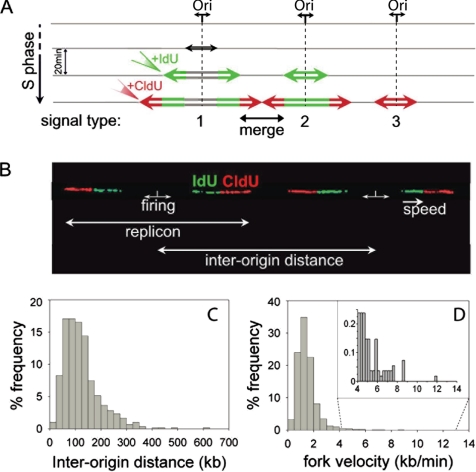
Figure 1.

Interorigin distances and total fork velocities. (A) Schematic representation of signals deriving from equal pulse-labeling with iodo-deoxyuridine (IdU) and chloro-deoxyuridine (CldU). Replication forks progress bidirectionally at the same rate from the origin and incorporate the analogues forming a symmetrical replication bubble. On detection of IdU and CldU, three types of signals may be obtained: a green and red signal with a gap between the green segments, corresponding to initiations that occurred before the beginning of the pulse (1); a dual-color signal with a continuous green segment corresponding to origins that fired during the first pulse (2); and a single isolated red signal corresponding to origins that fired during the second pulse (3). A continuous red signal flanked by two green ones is formed by the merging of two forks from adjacent origins. (B) Two adjacent replication bubbles are visualized on a combed DNA molecule (type 1 signal). The replication origins are assumed to be located in the midpoints of the unlabeled segments (see text). The distance between adjacent replication origins represents the interorigin distance. Fork speed is calculated by dividing the length of each fluorescent signal by the time of the pulse. (C) Histogram of the interorigin distances (median = 111; N = 606). (D) Histogram of the total fork velocities (mean = 1.46; N = 5460) for the human primary normal keratinocytes. In the panel, an enlarged view of the higher fork velocities (4–12 kb/min) is shown.

Table 1.

Statistical analysis of the kinetics of DNA replication for both the normal and cancer keratinocyte populations

	Primary normal	Cancer IC1	Two-sided t test t(0.05) = 1.96
Fork velocity (kb/min)
Mean	1.46	1.67	t(calc) = −7.07
SEM	0.01	0.03
SD	0.81	0.72
Median	1.30	1.54
N	5460	657
Inter-origin distance (kb)
Mean	124	120	t(calc) = 0.70
SEM	3	7
SD	73	71
Median	111	104
N	606	111
Outgoing fork velocity (kb/min)
R	0.53; p < 0.001	0.86; p < 0.001	r = 2.5
R2	0.29	0.74
Corr. forks (%)	63	83
b	0.87	0.97
Mean	1.08	1.04	t(calc) = 1.93
SEM	0.02	0.02
SD	0.64	0.27
Median	0.98	1.01
N	1518	247
Incoming fork velocity (kb/min)			r = 1.8
R	0.50; p < 0.001	0.68; p < 0.001
R2	0.25	0.46
Corr. forks (%)	63	65
b	0.93	0.97
Mean	1.11	1.14	t(calc) = 0.52
SEM	0.02	0.06
SD	0.65	0.41
Median	1.00	1.03
N	1172	49
Inter-origin distance vs. average incoming fork velocity
R	0.54; p < 0.001	0.65; p < 0.01	r = 1.4
R2	0.30	0.42
N	219	15

N, total number of measurements; b, linear regression coefficient; R, linear correlation coefficient; R², coefficient of determination (percentage of the total variation due to the relationship between the two fork velocities); r = R_cancer²/R_normal² (difference in relative strength of the two correlation coefficients); correlated forks (corr. forks) are defined for 0.75 < right/left fork speed < 1.33. A two-sided t test or a Wilcoxon (Mann-Withney) U test for unpaired data was used for normal or nonnormal distributions, respectively. Values −1.96 < t(calc) < 1.96 indicate no significant difference between the two populations (significance level: α = 0.05).

RESULTS

Experimental Design

We examined human primary keratinocytes obtained from skin biopsies carried out on three different donors and grown with three different media conditions (see Materials and Methods). For each of the donor samples, we analyzed two kinetic parameters of DNA replication, fork speed, and interorigin distance. We also investigated the relationship between the right and the left forks emanating from the same origin (outgoing forks) or from adjacent origins (incoming forks). Our analyses showed no appreciable differences between the donor samples (Supplementary Materials). Therefore, the data were pooled together in order to define a reference pattern for the DNA replication parameters in normal keratinocytes, independent of the genetic background and culture medium of the cells. Comparison with the replication pattern obtained from tumor-derived transformed keratinocytes allowed us to evaluate the effect of malignant transformation on genome duplication. For each donor sample, an asynchronous population of cells was sequentially pulse-labeled with IdU and CldU, for an equal time of 20 min each. Cells were immediately harvested and embedded in agarose plugs to prepare a protein-free solution of high-molecular-weight genomic DNA. DNA fibers were then prepared by molecular combing with a constant and sequence-independent stretching factor (Bensimon, 1994). The high performance of the combing technique allows for a precise investigation of single events, which may be hardly unraveled by other methods. Newly synthesized DNA, labeled with IdU and CldU, was detected by fluorescent antibodies (green and red, respectively) resulting in three major patterns of signals (Figure 1A). Images were acquired with an epifluorescence microscope and, because of the constant stretching factor obtained on silanized surfaces, reproducible measurements were obtained. The use of an asynchronous population of cells avoided any artifacts introduced by synchronization procedures, but required the collection of a large number of signals for a reliable representation of the S-phase. Additionally, the sequential incorporation of two nucleotide analogues rather than one (Lebofsky and Bensimon, 2005) permitted unambiguous determination of the progression and direction of the replication forks, of the replication fork speeds, and of the sites of firing. Figure 1B shows a representative example for two adjacent replication bubbles on the same DNA molecule. In this case, both origins fired before addition of the IdU and CldU nucleotides and therefore are placed at the midpoint of the unlabeled segments. The distance covered by the two ongoing forks emanating from the same origin of replication is defined as the replicon size, and the interorigin distance is defined as the length between adjacent initiation sites (Figure 1B).

Origin Spacing Is Variable and Correlates with Chromatin Loop Size

To study the origin distribution and clustering, we focused on the interorigin distance. In normal keratinocytes, we measured and plotted more than 600 interorigin distances, resulting in a median value of 111 kb (Figure 1C), which is shorter than previous estimates (150–300 kb; Yurov, 1980; Berezney et al., 2000). A model has been proposed predicting that a cluster of replicons, within a replication focus, is composed of a series of chromatin loops of 120 kb each, anchored to the nuclear matrix in a rosette-like arrangement (Berezney et al., 1995). The close correlation between the observed interorigin spacing (Figure 1C), and the predicted length of chromatin loops (Berezney et al., 1995) strongly supports a role for chromatin organization in origin specification and selection (Sadoni et al., 2004) and leads to a good estimate of the average origin spacing within a cluster. Despite the combing of long DNA molecules (900 kb in average, up to several megabases, measured after staining with the fluorescent intercalator YOYO-1), two or more adjacent clusters could not be detected. Distantly spaced and isolated origins (200–600 kb) were indeed observed, conferring a tail-shape distribution to the histogram of interorigin distances (Figure 1C).

Replication Fork Progression Rate Is Highly Variable

The molecular combing of pulse-labeled DNA enabled us to investigate whether replication factories adapt to the widely varying replicon sizes of somatic cells, given that the replication program is believed to be fixed before S-phase. For example, if replication fork velocity is ∼1 kb/min, a 1-Mb replicon would take over 8 h to replicate compared with 70 min for a 140-kb replicon. Moreover, individual replication foci, where DNA is synthesized, last for a period of ∼60 min (Leonhardt et al., 2000). This suggests that the coordinated activation of replication origins alone cannot account for genome duplication in the limited and defined time of the S-phase when interorigin distances may vary either between adjacent origins or between different regions of the genome. Thus, in addition to the interorigin distance, the rate of replication fork progression is also crucial for the complete duplication of the genome in pace with the cell cycle. We therefore performed a detailed analysis of individual replication fork velocities that, together with interorigin distance data, are necessary to elucidate the dynamics of DNA replication within a focus. Fork speed was calculated by dividing the length of each fluorescent signal by the time of the pulse (Figure 1B). As shown in Figure 1D, measurements of IdU and CldU signals revealed a mean fork velocity of 1.46 ± 0.01 kb/min (Table 1), in agreement with previous reports (Yurov, 1980; Jackson and Pombo, 1998). Noticeably, a large heterogeneity in fork velocity was also observed, with values ranging from 0.14 to 11.8 kb/min (panel in Figure 1D).

Forks Emanating From One Origin Tend To Proceed with the Same Velocity and Their Velocities Change Simultaneously

During DNA synthesis, the replisome or the protein complexes at the fork may encounter obstacles that can perturb or block fork progression. Obstacles may result from secondary DNA structures, DNA lesions, or large protein complexes bound to the DNA. Assuming that DNA synthesis is not disturbed by fork arrest or pausing and that the two forks emanating from a single origin (referred to in the text as “outgoing forks”) move bidirectionally with the same speed, the expected outcome would be a symmetric replication bubble (Figure 1A). Accordingly, this would result in a positive linear correlation (R) between the two fork velocities, with a theoretical maximum value of one. Replication fork arrest, on the other hand, will result in asymmetric fork progression, with little or no correlation between the two fork rates (Figure 2A).

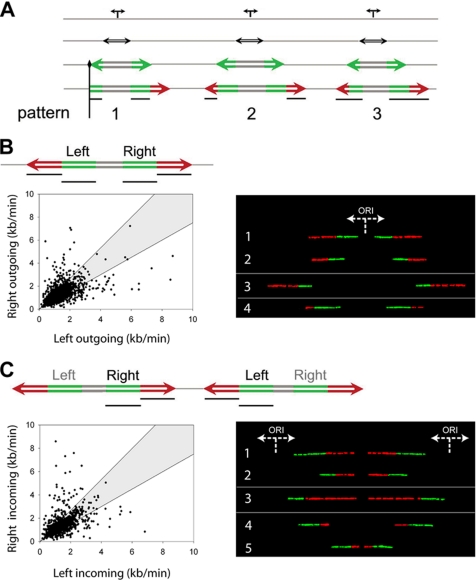
Figure 2.

Correlated changes in fork velocities. (A) Schematic representation of asymmetric replication bubbles resulting either from blocked forks (type 1 signal) or from changes in fork velocity (type 2 and 3 signals). Vertical black line, a permanent replication fork barrier; horizontal black lines, the segments that were measured and compared in order to examine fork speed correlations. (B) Coregulation of forks moving from a single origin (outgoing forks). Left, a scheme of the signals used in the analysis is represented at the top, with black lines indicating the segments that were measured and plotted against each other. In the scatter diagram, each dot corresponds to the ratio between the right and the left fork velocities of a pair of outgoing forks belonging to the same replication bubble. The shaded area includes all points whose ratios deviate from the expected theoretical value of 1 for <33%. The significant positive correlation of the outgoing forks (R = 0.53; p < 0.001; N = 1518) and the value of their linear regression coefficient (b = 0.87) indicate that they move bidirectionally at nearly the same rate. Right, examples of correlations between corresponding outgoing forks on individual DNA molecules. Generally, forks tend to maintain a constant speed between the first (green) and the second (red) pulse (see molecules 1 and 2). However, when this condition is not satisfied (see molecules 3 and 4), the symmetry between corresponding outgoing forks is still maintained, indicating a simultaneous change of their velocities. (C) Coregulation of forks moving from adjacent origins (incoming forks). Left, as in B, a scheme of the signals used for the analysis is shown at the top of the diagram. The black lines indicate the pair of segments measured and plotted against each other and are represented in the scatter graph with the same delimiting envelope. The significant positive correlation of the incoming forks (R = 0.50; p < 0.001; N = 1172) and the value of their linear regression coefficient (b = 0.93) indicate that they move at nearly the same rate. Right, examples of correlations between corresponding incoming forks on individual DNA molecules. As in B, right panel, forks tend to keep a constant speed between the first and the second pulse (see molecules 1 and 2). However, when this condition is not fulfilled (see molecules 3–5), the symmetry between corresponding incoming forks is still maintained, indicating a simultaneous change of their velocities.

To measure the progression of outgoing forks and to quantify the frequency of replication fork arrests in the genome, we performed a molecule-by-molecule analysis of individual replication bubbles. The velocity of the right fork during the first and second pulse was compared with the velocity of the left fork (Figure 2B, left panel). To assess the frequency of asymmetric replication bubbles, we defined an envelope (shaded area in the scatter diagram) to discriminate between coordinated and noncoordinated fork pairs (Materials and Methods). Figure 2B shows that two thirds (63%) of the data points lay inside the envelope. The data points outside of the envelope (37%) indicated a difference of up to fivefold between the left and right fork and correspond to asymmetric replication bubbles where one of the two forks experienced an arrest and/or differential velocity. In all the samples investigated, independently of the donor and medium condition, we always observed more than 60% (even more than 80% in the transformed cells) of coordinated fork speeds, indicating a tendency that cannot be simply attributed to chance (p < 0.001, Table 1). Therefore, we conclude that the majority of outgoing forks proceed bidirectionally at nearly the same speed, as demonstrated by the significant linear correlation and the good linear regression in the scatter diagram (Table 1). This conclusion is not only consistent with earlier reports (Hand, 1975; Dubey and Raman, 1987), but it also point out a novel feature of fork velocities: their dynamic correlation. In other words, fork speeds change simultaneously in both directions while the forks are moving. In fact, measurements of the green and red segments belonging to the same fork mostly showed a continuous and constant fork movement (Supplementary Materials). However, differences could be observed between the first and second pulse, indicating fork velocity may change during DNA strand elongation (up to about sixfold). Because those results were independent of the type and labeling order of the nucleotide analogues (Supplementary Materials), variations in fork speed appear to be intrinsic to the replication program, thus demonstrating the existence of an intrafork regulation mechanism. Interestingly, fork velocity changes within a DNA fiber were observed to occur simultaneously for both outgoing forks (Figure 2B, right panel), indicating a coordinated regulation of velocities for forks emanating from a common origin. This interfork correlation demonstrates that outgoing forks are able to coordinate each other's progression, implying spatial proximity within the same chromatin environment or simultaneous regulation by the same protein complex.

These findings support the factory model of DNA replication within a replication focus, according to which the DNA polymerases for a given replicon are held close to each other, while replicating DNA is extruded in loops through the polymerase complexes (Cook, 1999). The consequent colocalization of the two replication forks would allow for an easier coordination of their velocities. Our results favor the hypothesis of a coupled replisome model, rather then the independent replisome model recently proposed for Escherichia coli (Breier et al., 2005) and suggest a possible evolutionary difference in the regulation of DNA replication between prokaryotes and eukaryotes. Forks moving from neighboring origins display nearly the same progression rate and undergo simultaneous changes in velocities. The model of coupled replisomes raised the possibility that several origins grouped within a given discrete replication factory may be coordinated and that neighboring origins may harmonize the progression of their forks for successful strand duplication. To investigate this issue, we examined the velocity of forks originating from adjacent origins (referred to as “incoming forks”). As shown in Figure 2C (left panel), the velocity of the right fork during the first and second pulse was compared with the velocity of the corresponding incoming left fork. The results show a significant positive linear correlation (Table 1) and a linear regression, revealing that the majority of the incoming forks (63%) moved at comparable speed. Moreover, changes of fork speed occurred simultaneously at both incoming forks (Figure 2C, right panel), implying that the replication velocity of neighboring replicons tends to be coregulated to coordinate their velocities.

Origin Spacing Is Linearly Correlated with Fork Progression Rate

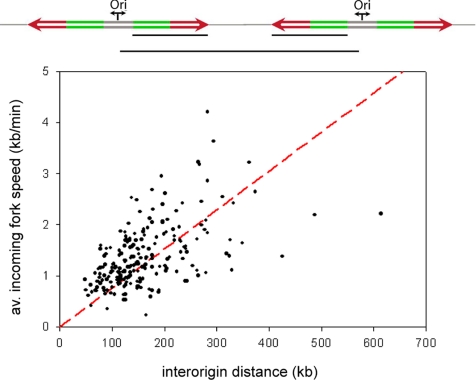
Our observation of variable origin spacing and variable fork progression reveals a certain plasticity in the replication program. Therefore, in order to complete the duplication of the genome within the S-phase, we tested the existence of a correlation between fork velocities and interorigin distances. This hypothesis is supported by the consistency between the observed sixfold maximum difference in fork speeds and the sixfold variation in interorigin distances (140 kb to 1 Mb), previously reported in higher eukaryotes (Berezney et al., 2000). To clarify this relationship, average incoming fork speeds were measured and plotted against the distance of their respective neighboring origins. As shown in Figure 3 and Table 1, the two parameters displayed a significant linear correlation, suggesting the presence of a biological mechanism that coordinates replication fork progression with interorigin distance. Two representative long molecules with multiple replication bubbles are shown in Figure 4 to exemplify this relationship. This homeostatic regulation explains how the replication program compensates for widely varying replicon sizes or for replication errors, such as the unexpected silencing of an origin or the unscheduled arrest of a replication fork.

Figure 3.

Positive linear correlation between interorigin distance and average incoming fork velocity. At the top is a scheme of two replication eyes and, as indicated by the black lines, the parameters that were measured and plotted against each other, which is the distance between two adjacent origins and the average value of their corresponding incoming fork speeds. The graph shows a positive linear correlation between the two parameters (R = 0.54; p < = 0.001; N = 219), indicating that the average value of the incoming fork speeds increases linearly with the interorigin distance. In red the regression line is represented. This homeostatic mechanism of coregulation between replication fork progression and origin spacing ensures the complete duplication of the genome while keeping pace with the cell cycle.

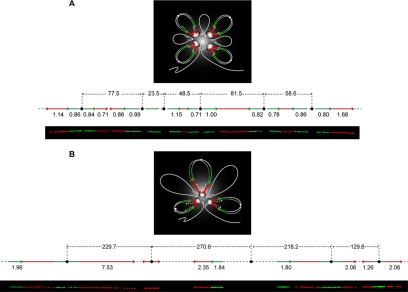
Figure 4.

Model for DNA replication within a replicon cluster. In the figure, the diffuse gray color indicates the mass of the focus, where the replisomes are represented by white ovals. At the top of the loops, the small circles indicate the origins. During DNA replication in S-phase, replicons remain associated with the replisome forming the foci. Newly synthesized DNA (daughter duplexes labeled in green and red) is extruded in loops while the parental duplex (single white line) slides through the fixed sites. During this process, parental loops shrink and daughter loops grow (as indicated by the white arrows). The green and red segments refer to the first and second pulse labels, respectively, with the arrows indicating the direction of their progression. Stripping the looped DNA from the factory and spreading it as a linear fiber, produces a pattern as the one visualized by molecular combing and schematically represented on the bottom of each model. (A) For relatively shortly and regularly spaced origins, the correlations between the replication forks emanating from a same origin (outgoing forks) or from contiguous origins (incoming forks) are generally maintained. A representative molecule is shown in the picture and schematically depicted above with the corresponding values of fork velocities (kb/min) and interorigin distances (kb). (B) In the case of largely and irregularly spaced origins, instead, the symmetry between outgoing forks is preferentially maintained over that of the incoming forks, suggesting a higher control of the replication program at the level of the single replicons. However, the plasticity of the replication program allows for compensation of wide replicon sizes with increasing average incoming fork speed, thus ensuring the timely completion of genome duplication. A representative example is shown in the picture together with its schematic depiction.

The Parameters Governing Replication Kinetics Are Conserved in Cancer Cells

Several studies have been performed to evaluate differences between normal proliferating cells and transformed cells. However, limited and controversial data are available about differences in the spatio-temporal regulation of DNA replication between normal and transformed cells (Kennedy et al., 2000; Dimitrova and Berezney, 2002). For this reason, we analyzed an asynchronous population of human keratinocyte-derived cancer cells (IC1; Sastre-Garau et al., 2000). Following the same procedure described for the normal keratinocytes, we investigated the effect of malignant transformation on the kinetics of DNA duplication. The results obtained from the normal and cancer cells are summarized in Table 1. The linear correlations (R) between the left and right forks, both outgoing and incoming, were maintained, although their values in cancer cells were higher than in the normal ones, thus indicating a stronger coordination between forks (Table 1, third and forth section). This tighter regulation of the replication process in the IC1 cells, which are deficient in pRb and display very low levels of p53 (data not shown), may be due to a clonal expansion from a single starting cell or to less sensitivity to DNA damage or fork arrest, as suggested by the faster fork velocity. Despite small differences, the comparative analysis between normal and transformed cells (at least for this particular cancer derived cell line) clearly shows that, in both cases, the parameters governing the kinetics of DNA replication are conserved.

DISCUSSION

Previously reports in metazoan cells indicated a weak, but significant, correlation between the activation of adjacent replication origins and suggested that initiations occur in clusters in several cell types (Blumenthal et al., 1974; Hyrien and Mechali, 1993; Jackson and Pombo, 1998; Berezney et al., 2000; Herrick et al., 2000; Blow et al., 2001). However, the role of clustering in regulating DNA replication was unclear. Questions remained as to whether origin clustering plays a necessary regulatory role or whether it is a fortuitous consequence of genome structure and organization. In this study, we present molecular evidence for a functional role of replicon clustering in the regulation of DNA replication and propose a model of fork coordination for its dynamic control. We have investigated and compared the kinetics of DNA replication in human normal primary keratinocytes and in keratinocytes-derived cancer cells.

Origin spacing and fork progression were studied using individual DNA molecules stretched by molecular combing, which allows for quantitative measurements of the interorigin distance and fork velocity. A good agreement was observed between the interorigin spacing and the predicted length of chromatin loops, thus supporting a role for chromatin organization in origin specification and selection (Sadoni et al., 2004). Measurements of interorigin distances also provided additional molecular evidence for the existence of large replicons in mammalian cells and suggested a more heterogeneous arrangement of replicons with respect to size. The apparent size heterogeneity within clusters (Berezney et al., 2000) was confirmed by the large variability of experimentally measured sizes of replication bubbles (ranging from a median value of ∼195 kb to a maximum value of ∼480 kb, data not shown). The approach used here allows for the examination of how clusters are topologically ordered, meaning if there exist constraints on origin activation.

Lebofsky et al. (2006) recently showed the presence of the origin interference effect in human primary keratynocytes. Given the event of an origin firing, the closest suppressed zone was located at 7 kb, whereas the highest probability of a second origin firing was at ∼25 kb from the neighbor. In the experiments reported here, we observed clusters with both regularly spaced origins (mostly composed of closely situated and synchronously activated origins) and with variable interorigin distances. Clusters of up to six origins with short interorigin distances (ranging from 20 to 80 kb) were observed, as well as clusters of up to five origins with long interorigin distances (120–330 kb). The majority of clusters, however, included only three origins spaced at an intermediate distance (around 100 kb). Large interorigin distances (hundreds of kilobases) were mainly found at the extremities of the cluster. In those cases, it is not clear whether the external origin is still part of the cluster or, rather, whether it is an isolated replicon.

Because we are analyzing the origin distribution in a limited window of time, we are not measuring the absolute distance between all origins that will be activated by the end of the S-phase. Therefore, we cannot exclude that an additional origin might fire later, thus shortening that interorigin distance. Although a small tendency for intermediate values of interorigin distances is apparent, the number of suitable multiorigin molecules is too limited for a reliable conclusion on this point. The timing and regulation of origin firing can also explain observations made on the regulation of fork progression. Our analysis reveals that fork progression is dynamically regulated, with fork movement being adjusted in relation to adjacent forks and initiation events. As a consequence, we observed that fork velocities tended to be higher when interorigin distances were longer. However, some long distances between two origins were not compensated by a proportionally higher fork velocity (Figure 4B). This might be due to the presence of an additional origin that might fire later between the two origins and that is not visible in the time window we analyzed. The capability of replication forks to adjust their speed indicates the existence of a yet unknown molecular mechanism that intervenes directly to modify fork rates during the S-phase.

We observed that the forks are mainly coordinated; nevertheless a certain plasticity is still permitted, in particular at the level of the incoming forks (Figure 4). One putative feedback mechanism may be based on the accumulation of torsional strain as incoming forks approach each other and therefore as replicon size decreases. However, a mechanism based only on mechanical stress would strongly limit the possibility of modification and adaptation of the fork rates, in particular for closely spaced replicons. Thus, it is likely that additional mechanisms control the dynamic regulation of fork progression that we observed. For relatively short and regularly spaced interorigin distances, the correlation of velocities between the replication forks emanating from one origin (outgoing) or from contiguous origins (incoming) is generally maintained (Figure 4A). On the other hand, in the case of large and irregularly spaced origins (Figure 4B), the correlation of velocities between outgoing forks is preferentially respected over that of the incoming forks, which suggests a higher control of the replication process locally confined to the individual replication bubble. On the other hand, to ensure complete duplication of the genome within a limited time, an interreplicon mechanism is present that allows for the compensation of large origin spacing with increasing average incoming fork speeds.

It is now evident that only a small fraction of the genome is replicated by clustered origins (Berezney et al., 2000), underscoring the relevance of large individual replicons in coordinating genome duplication with cell cycle progression. Because the influence of neighboring origins could be lost beyond a certain high interorigin distance, we believe, based on our observations, that a preferential coregulation of outgoing forks is the preferred mechanism of regulation also for individual larger replicons. Taken together, these data indicate the importance of origin clustering in coordinating and regulating the two major parameters of the DNA replication program, i.e., origin spacing and replication fork velocity, thus ensuring the complete duplication of the genome in pace with the cell cycle. Figure 4 shows a schematic representation of our replicon cluster model. A replication bubble spans ∼120 kb (data not shown), and in a replication factory the bubble is folded in order to occupy a small volume (see Figure 4). In the microenvironment of a replication bubble, it is reasonable to assume a homogenous and constant concentration of dNTPs. The observation made here, of dynamically regulated adjacent forks, supports the idea that dNTP pool sizes alone are not implicated in the observed changes in fork velocity. However, it remains to be clearly demonstrated how local concentrations of dNTPs at individual replication forks affect polymerase activity and fork processivity. Also, intracellular dNTP pool sizes are expected to increase, rather than decrease, during S-phase (Malinsky et al., 2001). Consequently, the average speed of a replication fork during S-phase would always increase if dNTP pool sizes were the key factor regulating fork velocities, in contrast to the dynamic changes in the fork rate observed here. Therefore, although the dNTP concentrations probably regulate bulk global fork velocity, as demonstrated in CHO cells, our results suggest that the local control and dynamic correlation between adjacent forks is not directly affected by the dNTP pool sizes but must involve other factors, for example, the processivity of DNA helicases and topoisomerases.

Analyses carried out in several human and hamster cell types show that the mechanism coordinating fork velocity with replicon size is conserved among different cell types (data not shown). Subtle variations in the pattern of DNA replication (for example, in the strength of fork correlations) may be indicative of different genetic backgrounds or epigenetic modifications, permitting investigation of the effects of internal and external stimuli on the kinetics of DNA replication and leading to a better understanding of the mechanisms governing the regulation of the replication program. In conclusion, our studies demonstrate a tight correlation between origin spacing and fork progression, while providing the first evidence that replication fork velocities at adjacent origins change simultaneously during S-phase and are dynamically regulated. It is worth pointing out that in Xenopus extracts, the activation of ATM and ATR kinases in response to fork stalling and DNA damage has been shown to be feedback-controlled by active replicons in unstressed conditions, perhaps to regulate origin spacing and timing (Marheineke and Hyrien, 2004; Shechter et al., 2004; Sorensen et al., 2004). We also recently found that the checkpoint kinase Chk1 kinase regulates fork velocity (Seiler et al., 2007). Therefore, proteins belonging to the ATM/ATR-Chk1 checkpoints could be the transducers controlling the coordination shown here between origin spacing and fork velocity. However, further studies will be necessary to determine whether origin spacing is dictating changes in fork velocity or vice versa.