Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Jul 1.
Published in final edited form as: Clin Biomech (Bristol, Avon). 2007 Mar 28;22(6):639–644. doi: 10.1016/j.clinbiomech.2007.02.001

Comparison of model-predicted and measured moment arms for the rotator cuff muscles

Christopher J Gatti a, Clark Dickerson c, Edward K Chadwick d, Amy G Mell b, Richard E Hughes a,b
PMCID: PMC1950345  NIHMSID: NIHMS25746  PMID: 17395346

Abstract

Background

The ability of mathematical models of the shoulder to accurately replicate physiological muscle moment arms is unknown. The purpose of this study was to compare model-predicted and experimentally measured moment arms for the rotator cuff muscles during arm elevation.

Methods

Moment arms obtained from 6 mathematical models and 7 experimental studies were compared for the supraspinatus, infraspinatus, teres minor, and subscapularis for elevation in the scapular plane.

Results

All of the included models generated moment arms that generally fell within the range of experimentally measured data.

Interpretation

The quantitative agreement between model-predicted and experimentally measured moment arms supports the use of the included models for biomechanical shoulder analyses.

Keywords: shoulder, moment arms, computational model

INTRODUCTION

Mathematical models of shoulder and upper extremity muscles are useful for many applications, including analysis of tendon transfers (Magermans et al., 2004), rehabilitation (Labriola et al., 2005), finite element modeling of prosthesis components (Stone et al., 1999), and ergonomics (Laursen et al., 2003). EMG-driven (Laursen et al., 1998) and optimization-based models (Hogfors et al., 1987, 1991, 1995; van der Helm, 1994a, 1994b) have been developed for estimating muscle forces around the shoulder. A critical component of optimization-based methods is the accurate determination of muscle moment arms as muscle force predictions have been shown to be highly sensitive to these parameters (Raikova and Prilutsky, 2001).

There have been several experimental investigations of elevation moment arms for the rotator cuff muscles (Graichen et al., 2001; Howell et al., 1986; Kuechle et al., 1997; Liu et al., 1997; Nyffeler et al., 2004; Otis et al., 1994; Poppen and Walker, 1978), as these muscles are critical for normal shoulder function. Although some models have used empirical measurements of muscle moment arms (Hughes and An, 1996, 1997, 1999; Langenderfer et al., 2006; Poppen and Walker, 1978), many modern shoulder models apply mathematical representations of musculoskeletal geometry (Dickerson et al., 2005, 2006; van der Helm, 1994a, 1994b). One advantage of this approach is that the models can analyze arm positions other than those for which moment arm data were experimentally collected. However, the resulting accuracy of the models to predict muscle moment arms is unclear.

The objective of this paper was to compare model predicted moment arms of the rotator cuff muscles to experimentally measured moment arms reported in the literature. Our comparison was limited to elevation in the scapular plane because of the availability of experimental data.

METHODS

A structured literature review process, which is standard practice when conducting a meta-analysis (Petitti, 2000), was followed to identify published experimental data on rotator cuff muscle moment arms. Four inclusion criteria were defined: (1) experimental measurement of moment arms of either the supraspinatus, infraspinatus, teres minor, or subscapularis, muscles in vivo or in cadavera; (2) moment arm data presented for abduction in the plane of the scapula; (3) data presented in text, tabular, or graphical format; and (4) clearly described experimental method. A protocol was developed for selecting papers, which included searching Medline and PubMed using keywords rotator cuff, shoulder, moment arm, lever arm, mechanical advantage, and muscle line of action. Book chapters were also consulted for references to primary sources of moment arm data. References in all documents were scrutinized for additional data sources. Forty-two papers were identified and each full paper was checked for inclusion criteria by two authors (AGM and CJG). Ten papers met the inclusion criteria; however, only seven were used because some data sets from independent studies were published in multiple manuscripts.

The moment arms included in the comparison were for arm elevation in the scapular plane at glenohumeral angles (GHAs) of 30° and 60° with 0° of humeral axial rotation for the supraspinatus, infraspinatus, teres minor, and the subscapularis. Experimentally measured moment arm data were obtained from studies by Graichen et al. (Graichen et al., 2001), Howell et al. (Howell et al., 1986), Kuechle et al. (Kuechle et al., 1997), Liu et al. (Liu et al., 1997), Nyffeler et al. (Nyffeler et al., 2004), Otis et al. (Otis et al., 1994), and Poppen and Walker (Poppen and Walker, 1978). The methods used in these studies are presented in Table 1. Model-predicted moment arm data were obtained from the use of the Dickerson model (Dickerson et al, 2005, 2006), Holzbaur model (Holzbaur et al., 2005), and Delft Shoulder and Elbow Model (DSEM) (van der Helm, 1994a, 1994b); these models are available to the biomechanics community. It should be noted that the Dickerson model is an implementation of the model developed by Hogfors and co-workers (Hogfors et al., 1987, 1991, 1995). For the other included models, moment arm data were extracted from published or dissertation data from the Favre model (Favre et al., 2005), Garner model (Garner and Pandy, 2001), and Newcastle model (Charlton, 2003); the availability of these models is not known.

Table 1.

Moment arm measurement method used in each study

Study Method
Graichen et al., 2001 3-D measurement using reconstruction from MRI
Howell et al., 1986 Roentgenographic measurement
Kuechle et al., 1997 Tendon excursion/joint displacement method
Liu et al., 1997 Tendon excursion/joint displacement method
Nyffeler et al., 2004 Tendon excursion/joint displacement method
Otis et al., 1994 Tendon excursion/joint displacement method
Poppen and Walker, 1978 Radiographic measurement
Open in a new tab

Moment arms were extracted from published figures for the studies performed by Graichen et al., Kuechle et al., Liu et al., Nyffeler et al., Otis et al., and Poppen and Walker as well as for the Garner and Newcastle models. For the study by Howell et al. and for the Favre model, moment arms were taken from the published article text and tables, respectively.

Graichen et al., Howell et al., and Poppen and Walker reported moment arms with respect to arm elevation angle, whereas the current study compares moment arms with respect to GHA. The arm positions of these studies were converted using a 2:1 ratio of arm elevation angle to glenohumeral angle as reported by Inman et al. (Inman et al., 1944). Thus, GHAs of 30° and 60° correspond to arm elevation angles of 45° and 90°, respectively. The experimentally measured moment arms are presented in Tables 2 and 3 for 30° and 60° GHA, respectively. Two studies divided each rotator cuff muscle into multiple muscle elements and measured each muscle element moment arm (Nyffeler et al. and Otis et al.). Thus, ranges of values were obtained and are presented for each individual muscle element in the tables.

Table 2.

Experimentally measured rotator cuff abduction moment arms at 30° glenohumeral abduction in the scapular plane

Study Supraspinatus Infraspinatus Teres minor Subscapularis
Graichen et al.
Howell et al. 25.0 0.0
Kuechle et al. 16.0 4.0 −5.0 3.0
Liu et al. 29.0 11.0 6.0
Nyffeler et al. 27.5 8.5, 15.5, 21.5† −9.0 0.0, 10.0, 16.0†
Otis et al.
Poppen and Walker
Range 16.0 to 29.0 0.0 to 21.5 −9.5 to −5.0 0.0 to 16.0
Open in a new tab
*

moment arms measurements in mm;

†

inferior, middle, superior muscle elements, respectively

Table 3.

Experimentally measured rotator cuff abduction moment arms at 60° glenohumeral abduction in the scapular plane

Study Supraspinatus Infraspinatus Teres minor Subscapularis
Graichen et al. 21.0
Howell et al. 25.0 0.0
Kuechle et al. 7.0 2.0 −13.0 11.0
Liu et al. 23.0 10.0 1.0
Nyffeler et al. 22.5 13.0, 18.0, 22.0† −4.0 −1.0, 8.0, 11.0†
Otis et al. 25.1, 27.0‡ 5.4, 8.4, 16.9† −2.2 4.3, 7.3, 13.6†
Poppen and Walker 21.0 −1.0
Range 7.0 to 27.0 0.0 to 22.0 −13.0 to −2.2 −1.0 to 13.6
Open in a new tab
*

moment arms measurements in mm;

†

inferior, middle, superior muscle elements, respectively

‡

anterior, posterior muscle elements, respectively

Moment arms from the Holzbaur and Dickerson models and the DSEM were computed directly with the respective models. The Holzbaur model output moment arms with respect to arm elevation angles that were converted to GHAs using the calculated scapulohumeral rhythm of the model. A superior-inferior vector was aligned and attached to the medial border of the scapula; the GHA was defined to be the angle between said vector and the long axis of the humerus. The scapulohumeral rhythm was calculated and the moment arms at the GHAs of interest were computed. For the Dickerson model, the position of the humerus was defined with respect to the torso. Arm position was defined relative to a starting position extracted from the geometric model of Hogfors et al. (Hogfors et al., 1987) (humerus abducted to 90°, with epicondyles parallel to the gravity vector, the thumb pointed up and elbow range of motion in the horizontal plane). Three sequential Euler rotations (3, −2, 1) defined humeral position relative to the scapula in order to ensure consistency with the shoulder rhythm formulation used (Hogfors et al., 1991). Glenohumeral angles were confirmed following humeral positioning as matching those of the empirical data used. For the DSEM, the humerus was positioned in 30° and 60° elevation with respect to the scapular vector in the scapular plane, with zero degrees axial rotation. Moment arms were extracted in the local humeral system of the model.

RESULTS

In general, all of the models evaluated generated moment arms that fell within the range of experimentally measured data for the muscles reported by each. The moment arms predicted by each model are shown together with the range of experimentally measured moment arms in Figure 1 (a–h) for each rotator muscle at 30° and 60° GHA. The Favre, Dickerson, Holzbaur models and the DSEM contained muscle elements for all four rotator cuff muscles. The Favre model predicted both the infraspinatus and supraspinatus abduction moment arms within the experimental range. However, for the subscapularis and teres minor, the predicted moment arms tend towards a greater adduction function than that of the experimental data. The Dickerson model produced moment arms in the experimental data range for all postures and muscles except for supraspinatus at 60° GHA (over prediction by 0.05 mm) and the teres minor at 30° GHA. Predictions from the Holzbaur model wholly agreed with the empirical data except for underpredicting the teres minor adduction moment arm at 60° GHA. The DSEM has high anatomical fidelity with multiple muscle elements for each muscle, and therefore produces a range of predicted moment arms for each muscle. In several situations, some muscle elements agree with experimental ranges, while others do not. For example, approximately half of the muscle elements for the subscapularis are within the range. Moreover, substantial adduction function was predicted for some muscle elements, while a substantial abduction function was predicted for others. The Garner model predicted moment arms within the experimental range for the supraspinatus and subscapularis, although data was unavailable for the infraspinatus and teres minor. The Newcastle model accurately predicted subscapularis moments arms, however, at 60° GHA it predicted higher abduction moment arms for both the supraspinatus and infraspinatus. No data were available for the teres minor in the Newcastle model.

Figure 1. Model predicted rotator cuff moment arms.

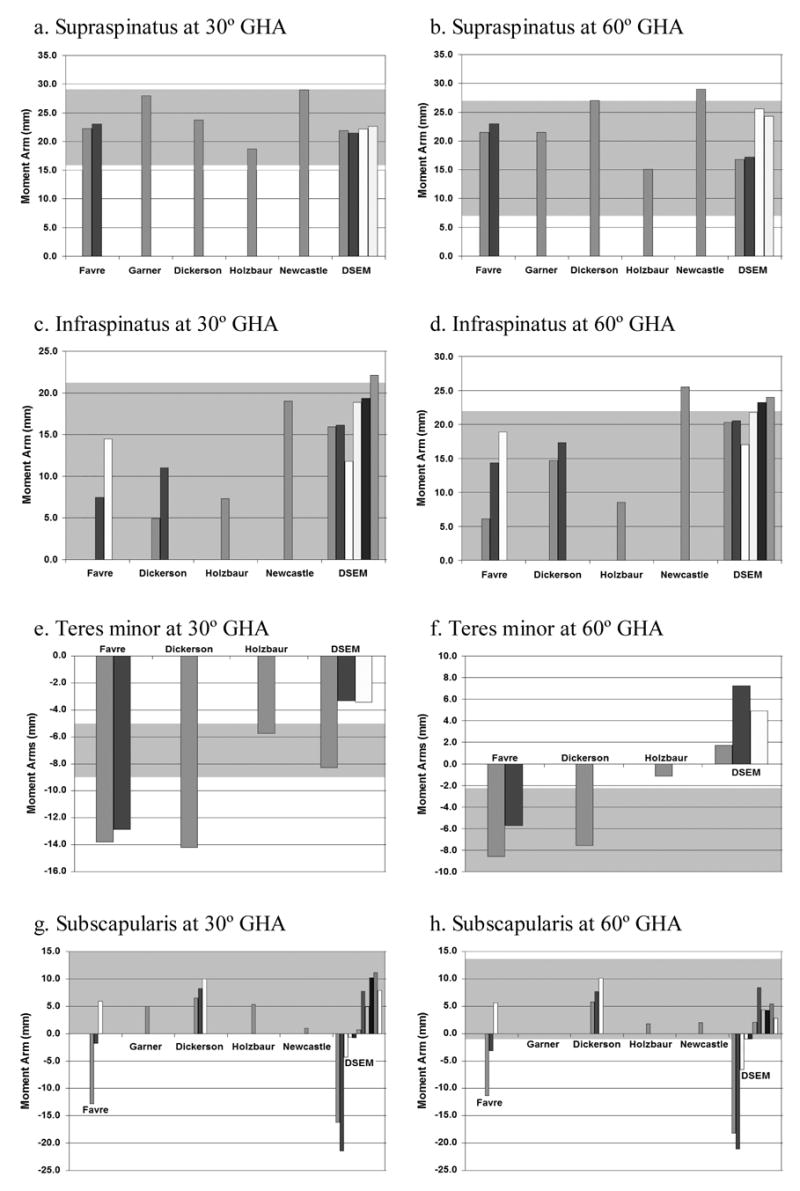
Figure 1

Open in a new tab

Model predicted muscle (or muscle element if applicable) moment arms for the supraspinatus (a,b), infraspinatus (c,d), teres minor (e,f), and subscapularis (g,h) at 30° and 60° GHA compared to the range of experimentally measured moment arms (shaded area). For models which have multiple muscle elements, the moment arms are presented (left to right) using the following conventions: supraspinatus – anterior to posterior muscle elements; infraspinatus, teres minor, and subscapularis – inferior to superior muscle elements.

DISCUSSION

This study compared rotator cuff moment arms obtained from multiple shoulder models to those reported in several sets of experimental data. The moment arms from the models showed overall agreement and were within the range defined by the empirically measured data. The experimental data included represent the body of literature concerning moment arms for the arm positions of interest, as these two arm positions are clinically relevant.

The Garner and Newcastle models did not publish moment arm data for all muscles at both arm positions considered. Further, published data concerning experimentally measured moment arms did not always include data on all muscles in both positions. Discrete positions were selected due to the limited literature concerning experimental studies. The experimental studies were performed independently; thus, variations in methodology and in the arm positions at which moment arms were measured are possible. Some studies (Graichen et al., 2001; Howell et al., 1986; Poppen and Walker, 1978) reported measured moment arms with respect to arm elevation angle, whereas the current comparison uses glenohumeral angle. Conversion of these angles is subject to variations in subject-specific scapulohumeral rhythm. The model moment arms were either computed (Dickerson and Holzbaur models and DSEM) or extracted (Garner, Favre, and Newcastle models) from published or dissertation data, and some variation in the arm positions of the models is possible. The included studies did not report anthropometric specimen data, and, with the exception of the Dickerson model, the models either did not report or do not allow for subject scaling. Therefore, this comparison does not account for potential anthropometric variation, which may alter the results. Finally, the method of subdivision of muscles into functional mechanical elements differed across models and experiments and this may have resulted in discontinuities between the data sets. These limitations should be considered as they can influence experimental and model-predicted moment arms. It should also be noted that variation in moment arm values would cause large variation in torque calculations. Despite these limitations, however, the performance of the models in predicting the empirical data confirms the robustness of the modeling approaches used and informs users of the models as to their utility.

The quantitative agreement between model-predicted and experimentally measured moment arms supports use of the included models for biomechanical analyses of the rotator cuff muscles of the shoulder. The comparison between computational models and published empirical data is important because moment arms are a critical factor in the outputs of muscle force prediction models.

Acknowledgments

We thank the National Institute of Health for financial support via grant AR048540.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Charlton IW, Johnson GR. Application of spherical and cylindrical wrapping algorithms in a musculoskeletal model of the upper limb. J Biomech. 2001a;34(9):1209–16. doi: 10.1016/s0021-9290(01)00074-4. [DOI] [PubMed] [Google Scholar]
  2. Charlton IW, Johnson GR. An interactive biomechanical model of the shoulder. Proceedings: “Comrades in Arms”, Conference of Biomechanics of the Upper Limb. Institution of Mechanical Engineers; London. April 2001; 2001b. pp. 16–22. [Google Scholar]
  3. Charlton IW. A model for the prediction of the forces at the glenohumeral joint. Dissertation, University of Newcastle; United Kingdom: 2003. [Google Scholar]
  4. Dickerson CR, Chaffin DB, Hughes RH. A mathematical musculoskeletal shoulder model for proactive ergonomic analysis. Submitted to: Computer Methods in Biomechanics and Biomedical Engineering. 2005 December 19; doi: 10.1080/10255840701592727. 2005 identifier C0356. [DOI] [PubMed] [Google Scholar]
  5. Dickerson CR, Martin BJ, Chaffin DB. The relationship between shoulder torques and the perception of muscular effort in load reaches. Ergonomics. 2006;49(11):1036–51. doi: 10.1080/00140130600730960. [DOI] [PubMed] [Google Scholar]
  6. Dul J. A biomechanical model to quantify shoulder load at the workplace. Clin Biomech. 1988;3:124–128. doi: 10.1016/0268-0033(88)90057-5. [DOI] [PubMed] [Google Scholar]
  7. Favre P, Sheikh R, Fucentese SF, Jacob HAC. An algorithm for estimation of shoulder muscle forces for clinical use. Clin Biomech. 2005;20:822–833. doi: 10.1016/j.clinbiomech.2005.04.007. [DOI] [PubMed] [Google Scholar]
  8. Garner BA, Pandy MG. Musculoskeletal model of the upper limb based on the visible human male dataset. Comp Meth Biomech Biomed Eng. 2001;4:93–126. doi: 10.1080/10255840008908000. [DOI] [PubMed] [Google Scholar]
  9. Graichen H, Englmeier KH, Reiser M, Eckstein H. An in vivo technique for determining 3D muscular moment arms in different joint positions and during muscular activation. Clin Biomech. 2001;16:389–94. doi: 10.1016/s0268-0033(01)00027-4. [DOI] [PubMed] [Google Scholar]
  10. Hogfors C, Sigholm G, Herberts P. Biomechanical model of the human shoulder – I. Elements. J Biomech. 1987;20:157–166. doi: 10.1016/0021-9290(87)90307-1. [DOI] [PubMed] [Google Scholar]
  11. Hogfors C, Peterson B, Sigholm G, Herberts P. Biomechanical model of the human shoulder joint – II. The shoulder rhythm J Biomech. 1991;24:699–709. doi: 10.1016/0021-9290(91)90334-j. [DOI] [PubMed] [Google Scholar]
  12. Hogfors C, Karlsson D, Peterson B. Structure and internal consistency of a shoulder model. J Biomech. 1995;28:767–777. doi: 10.1016/0021-9290(94)00134-p. [DOI] [PubMed] [Google Scholar]
  13. Holzbaur KRS, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann Biomed Eng. 2005;33(6):829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
  14. Howell SM, Imobersteg AM, Seger DH, Marone PJ. Clarification of the role of the supraspinatus muscle in shoulder function. J Bone Joint Surg Am. 1986;68A:398–404. [PubMed] [Google Scholar]
  15. Hughes RE, An KN. Force analysis of rotator cuff muscles. Clin Orthop Rel Res. 1996;330:75–83. doi: 10.1097/00003086-199609000-00010. [DOI] [PubMed] [Google Scholar]
  16. Hughes RE, An KN. Monte Carlo simulation of a planar shoulder model. Med Biol Eng Comp. 1997;35:544–548. doi: 10.1007/BF02525538. [DOI] [PubMed] [Google Scholar]
  17. Hughes RE, An KN. Identification of optimal strategies for increasing whole arm strength using Karush-Kuhn-Tucker multipliers. Clin Biomech. 1999;14:628–634. doi: 10.1016/s0268-0033(99)00022-4. [DOI] [PubMed] [Google Scholar]
  18. Inman VT, Saunders JBDM, Abbot LC. Observations on the function of the shoulder joint. J Bone Joint Surg Am. 1944;26A:1–30. [Google Scholar]
  19. Karlsson D, Peterson B. Towards a model for force predictions in the human shoulder. J Biomech. 1993;25:189–199. doi: 10.1016/0021-9290(92)90275-6. [DOI] [PubMed] [Google Scholar]
  20. Kuechle DK, Newman SR, Itoi E, Morrey BF, An KN. Shoulder muscle moment arms during horizontal flexion and elevation. J Should Elb Surg. 1997;6:429–439. doi: 10.1016/s1058-2746(97)70049-1. [DOI] [PubMed] [Google Scholar]
  21. Labriola JE, Lee TQ, Debski RE, McMahon PJ. Stability and instability of the glenohumeral joint: the role of shoulder muscles. J Should Elb Surg. 2005;14(1S):32S–38S. doi: 10.1016/j.jse.2004.09.014. [DOI] [PubMed] [Google Scholar]
  22. Langenderfer JE, Carpenter JE, Johnson ME, An KN, Hughes RE. A probabilistic model of glenohumeral external rotation strength for healthy normals and rotator cuff tear cases. Ann Biomed Eng. 2006;34(3):465–476. doi: 10.1007/s10439-005-9045-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Laursen B, Jensen BR, Nemeth G, Sjogaard G. A model predicting individual shoulder muscle forces based on relationship between electromyographic and 3D external forces in static position. J Biomech. 1998;31:731–739. doi: 10.1016/s0021-9290(98)00091-8. [DOI] [PubMed] [Google Scholar]
  24. Laursen B, Sogaard K, Sjogaard G. Biomechanical model predicting electromyographic activity in three shoulder muscles from 3D kinematics and external forces during cleaning work. Clin Biomech. 2003;18(4):287–295. doi: 10.1016/s0268-0033(03)00004-4. [DOI] [PubMed] [Google Scholar]
  25. Liu J, Hughes RE, Smutz WP, Niebur G, An KN. Roles of deltoid and rotator cuff muscles in shoulder elevation. Clin Biomech. 1997;12:32–38. doi: 10.1016/s0268-0033(96)00047-2. [DOI] [PubMed] [Google Scholar]
  26. Magermans DJ, Chadwick EK, Veeger HE, van der Helm FCT, Rozing PM. Biomechanical analysis of tendon transfers for massive rotator cuff tears. Clin Biomech. 2004;19(4):350–357. doi: 10.1016/j.clinbiomech.2003.11.013. [DOI] [PubMed] [Google Scholar]
  27. Nyffeler RW, Sheik R, Jacob HA, Gerber C. Influence of humeral prosthesis height on biomechanics of glenohumeral abduction. J Bone Joint Surg Am. 2004;86A:575–580. doi: 10.2106/00004623-200403000-00017. [DOI] [PubMed] [Google Scholar]
  28. Otis JC, Jiang CC, Wickiewicz TL, Peterson MGE, Warren RF, Santner TJ. Changes in the moment arms of the rotator cuff and deltoid muscles with abduction and rotation. J Bone Joint Surg Am. 1994;76A:667–676. doi: 10.2106/00004623-199405000-00007. [DOI] [PubMed] [Google Scholar]
  29. Petitti DB. Meta-analysis, decision analysis, and cost-effectiveness analysis: Methods for quantitative synthesis in medicine. 2. Oxford University Press; New York: 2000. [Google Scholar]
  30. Poppen NK, Walker PS. Forces at the glenohumeral joint in abduction. Clin Orthop Rel Res. 1978;135:165–170. [PubMed] [Google Scholar]
  31. Raikova RT, Prilutsky BI. Sensitivity of predicted muscle forces to parameters of optimization-based human leg model revealed by analytical and numerical analyses. J Biomech. 2001;34:1243–1255. doi: 10.1016/s0021-9290(01)00097-5. [DOI] [PubMed] [Google Scholar]
  32. Stone KD, Grabowski JJ, Cofield RH, Morrey BF, An KN. Stress analyses of glenoid components in total shoulder arthroplasty. J Should Elb Surg. 1999;8(2):151–158. doi: 10.1016/s1058-2746(99)90009-5. [DOI] [PubMed] [Google Scholar]
  33. van der Helm FCT. Analysis of the kinematic and dynamic behavior of the shoulder mechanism. J Biomech. 1994a;27:527–550. doi: 10.1016/0021-9290(94)90064-7. [DOI] [PubMed] [Google Scholar]
  34. van der Helm FCT. A finite element musculoskeletal model of the human shoulder mechanism. J Biomech. 1994b;24:615–629. doi: 10.1016/0021-9290(94)90065-5. [DOI] [PubMed] [Google Scholar]

RESOURCES