Abstract
Most parametric methods for detecting foreign genes in bacterial genomes use a scoring function that measures the atypicality of a gene with respect to the bulk of the genome. Genes whose features are sufficiently atypical—lying beyond a threshold value—are deemed foreign. Yet these methods fail when the range of features of donor genomes overlaps with that of the recipient genome, leading to misclassification of foreign and native genes; existing parametric methods choose threshold parameters to balance these error rates. To circumvent this problem, we have developed a two-pronged approach to minimize the misclassification of genes. First, beyond classifying genes as merely atypical, a gene clustering method based on Jensen–Shannon entropic divergence identifies classes of foreign genes that are also similar to each other. Second, genome position is used to reassign genes among classes whose composition features overlap. This process minimizes the misclassification of either native or foreign genes that are weakly atypical. The performance of this approach was assessed using artificial chimeric genomes and then applied to the well-characterized Escherichia coli K12 genome. Not only were foreign genes identified with a high degree of accuracy, but genes originating from the same donor organism were effectively grouped.
INTRODUCTION
One lesson of comparative genomics has been that numerous intricate and interdependent processes underlie organismal evolution. Even attempts to obtain an unambiguous picture of bacterial evolutionary relationships—organisms which reproduce in the absence of genetic exchange—have often been confounded with the emergence of the data that contradict accepted beliefs. For example, while bacterial phylogenies have historically used the highly conserved sequences of the small subunit ribosomal RNA, more complete genome sequence data has documented significant levels of gene transfer between the distantly related organisms, a strongly confounding influence on the elucidation of taxonomic relationships (1). Beyond obfuscating the tree form of life, lateral gene transfer (LGT) mobilizes ecologically important genes among taxa, making it a potent force in the diversification and speciation of prokaryotes (2,3).
Change in gene inventory is a historical process. In the absence of experimental means to determine the evolutionary history of a gene, several complementary methods have been developed to infer the occurrence of gene transfer events, categorized as phylogenetic incongruency tests and parametric methods. The former identifies single gene topologies that deviate significantly from consensus relationships; aberrant phylogenies are considered to be the most reliable indicator of ancestral gene transfer events. Caveats for their use include biased mutation rates, improper clade selection, gene loss, segregation of paralogs and long branch length attraction (4). More importantly, the success of phylogenetic methods depends entirely on the breadth and depth of the sequence database, which is especially evident in the inability to use these approaches to identify orphan genes of foreign origin. Lastly, phylogenetic studies may yield ambiguous results. For example, a recent survey of 13 species of γ-proteobacteria concluded that few LGT events took place among them, since organismal relationships inferred from the sequences of most genes failed to reject the consensus topology (5); however, it was later reported that these same data failed to reject any topology, not only the consensus one (6), suggesting that the phylogenetic signal was insufficiently robust to either accept or reject hypotheses regarding gene transfer.
In contrast, parametric approaches are based on the hypothesis that sequence features are similar within a genome but differ significantly between genomes. Genes which share a common set of features —that is, typical genes—are classified as native. In contrast, putatively foreign genes have atypical features inconsistent with the patterns reflected by the bulk of the genome; the features of these genes are posited to reflect the mutational proclivities of their donor organisms. While ancient gene transfer events would be difficult to detect as their atypical features ameliorate (7,8), genes of recent foreign origin are of special interest to microbiologists due to their role in recent changes in their ecological niche and/or metabolic repertoire. However, the sets of foreign genes detected by parametric approaches often differ significantly (4); this may result from the different metrics being utilized, or different thresholds used to discriminate between ‘typical’ and ‘atypical’ genes. Such conflicts between methods have not been easy to resolve; until recently, the efficacy of parametric methods had been difficult to assess due to the lack of benchmark protocols (9).
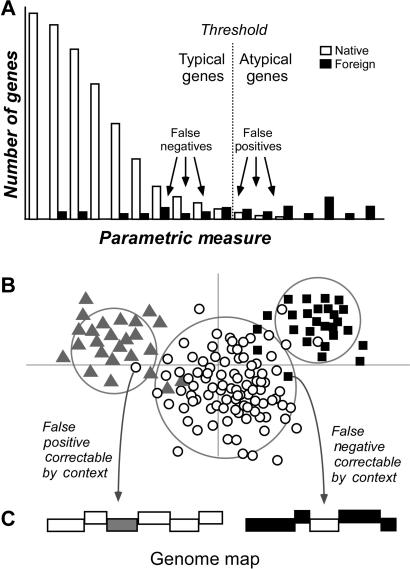
Yet these caveats are somewhat minor compared to an intrinsic weakness shared by nearly all parametric methods. Rather than falling into totally discrete groups corresponding to typical and atypical genes, compositional features of genes lie along a continuum (Figure 1A). That is, there is no easily defined threshold beyond which atypical genes are clearly of foreign origin. Native genes may also be strongly atypical; for example, highly expressed genes have codon usage bias patterns that distinguish them from the majority of chromosomal genes (10). As a result, arbitrary thresholds must be employed for declaring atypical genes to be of likely foreign origin, where choice of threshold balances Type I and Type II errors (9). Conservative thresholds lead to rare misclassification of native genes as foreign, at the expense of more falsely declared native genes. Liberal thresholds detect more foreign genes, but also incur more false predictions (i.e. native genes misclassified as foreign). Advances in the efficacy of parametric methods critically depend upon a decoupling of Type I and Type II errors, so that genes that lie in the twilight zone (the somewhat atypical native genes or weakly atypical foreign genes) may be robustly classified as either native or foreign. To accomplish this goal, we use two features of gene transfer in bacterial genomes. First, many alien genes are introduced in genomic islands; here, large number of genes arrive from a single donor genome and are physically adjacent. Second, the non-random distribution of donor genomes for any one recipient (11) increases the likelihood that foreign genes may resemble each other even if they arrived in separate transfer events.
Figure 1.
(A) Foreign gene identification by common threshold approaches; native and foreign genes overlap in sequence features. (B) Foreign genes detecting using a clustering approach. Genes from a single source may have features that overlap with features of genes from other sources, making unambiguous delineation difficult. (C) Positional information may be used to accurately classify weakly atypical genes. Misclassified genes may be correctly identified using positional information.
Using this information, we have implemented here a 2-fold approach for foreign gene identification. First, we employ a novel gene clustering method based on Jensen–Shannon (JS) divergence measure. Contrary to the arbitrary thresholds used by existing parametric methods, this approach segregates genes into distinct classes within a hypothesis testing framework. In this way, we identify foreign genes not solely by their incongruence with the majority of genes in the genome but also by their similarity to each other (Figure 1B). Yet even here, we would expect that somewhat atypical native genes may be misclassified as alien, and vice versa. To escape the limitations imposed by any single threshold in classifying genes with ambiguous features, we use genome position information to reassign genes between native and foreign classes based on the characteristics of physically adjacent genes (Figure 1C). The performance of this approach was assessed on a test platform of artificial chimeric genomes (9) and then applied to well-understood Escherichia coli K12 genome.
MATERIALS AND METHODS
DNA sequences
The complete genome sequences of the prokaryotes Archaeoglobus fulgidus DSM4304, Bacillus subtilis 168, Deinococcus radiodurans R1 chromosome I, Erwinia carotovora SCRI1043, E. coli K12, Haemophilus influenzae Rd KW20, Methanocaldococcus jannaschii DSM2661, Neisseria gonorrheae FA1090, Ralstonia solanacearum GMI1000, Salmonella enterica serovar Paratyphi A str. ATCC 9150, Sinorhizobium meliloti 1021, Synechocystis sp. PCC6803 and Thermotoga maritima MSB8, Vibrio cholerae O1 biovar eltor str. N16961 chromosome I, and Yersinia pestis KIM were obtained from GenBank. Protein-coding genes were extracted using the coordinates provided in the annotation.
The entropic gene clustering method
The JS divergence between two probability distributions P1 and P2 of a discrete random variable is defined as (12),
| 1 |
where π1 and π2 are weight factors, with π1 + π2 = 1. H(.) is the Shannon information entropy defined as
| 2 |
where P(i) is the probability of the ith element of distribution P.
DNA sequences are represented by alphabet  = (A,C,G.T). To measure the compositional difference between two DNA sequences S1 and S2 of length L1 and L2, respectively, the probability distribution Pk (k = 1, 2) is represented by the relative frequency vector {fk(i), i∈ A}, fk(i) = Ck(i)/Lk, Ck(i) is the count of nucleotide i in sequence Sk. Assigning weight factors to be proportional to the lengths of the sequences, π1 = L1/L and π1 = L2/L, L = L1 + L2, the JS divergence between two sequences S1 and S2 is expressed as,
= (A,C,G.T). To measure the compositional difference between two DNA sequences S1 and S2 of length L1 and L2, respectively, the probability distribution Pk (k = 1, 2) is represented by the relative frequency vector {fk(i), i∈ A}, fk(i) = Ck(i)/Lk, Ck(i) is the count of nucleotide i in sequence Sk. Assigning weight factors to be proportional to the lengths of the sequences, π1 = L1/L and π1 = L2/L, L = L1 + L2, the JS divergence between two sequences S1 and S2 is expressed as,
| 3 |
where 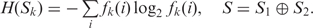 .
.
To assess the statistical significance of this measure under the null hypothesis that sequences S1 and S2 are similar, that is, both sequences are generated from the same probability distribution, we use the analytical approximation of the probability distribution of JS that was shown to follow a χ2 distribution function [Arvey,A., Raval,A., Azad,R.K. and Lawrence,J.G., unpublished data; (see also Section IV(C) in (13)]. For asymptotically large values of L,
| 4 |
where Fν (.) is the chi-square distribution function for ν degrees of freedom (ν = |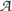 |−1); γ(.) and Γ(.) represent the incomplete and complete gamma functions, respectively. The P-value for the test is thus obtained as 1-Pr{JS ≤ x}.
|−1); γ(.) and Γ(.) represent the incomplete and complete gamma functions, respectively. The P-value for the test is thus obtained as 1-Pr{JS ≤ x}.
We employed the JS divergence in an agglomerative hierarchical clustering method to measure the dissimilarity (or similarity) between genes or gene classes. The clustering algorithm begins with N single gene classes. For each iteration, each pair of classes is considered and the JS distance between classes is measured. If the P-value computed for the JS distance between closest classes is less than pre-set significance threshold, the distinction between the two classes is deemed statistically significant precluding the merger of these classes; otherwise the classes are merged. The algorithm is repeated recursively until the distinction between all classes is statistically significant, preventing any further class merger. The frequency vector for multigene classes is the mean frequency vector of the constituent genes and its size is the mean size.
To quantify the compositional difference between genes, the DNA sequence of a gene is represented by a 12-symbol alphabet 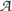 = {Ai, Ti, Ci, Gi, i = 1–3} accounting for nucleotide identity and the three codon positions. A 48-symbol alphabet representation of DNA sequence accounting for the dinucleotide identity and the codon positions was also used. We termed the respective JS(S1, S2) as JS-N and JS-DN. To measure the difference in codon usage bias between genes, each of the synonymous codon group was considered separately; the Shannon entropy, H(Sk), is thus defined as,
= {Ai, Ti, Ci, Gi, i = 1–3} accounting for nucleotide identity and the three codon positions. A 48-symbol alphabet representation of DNA sequence accounting for the dinucleotide identity and the codon positions was also used. We termed the respective JS(S1, S2) as JS-N and JS-DN. To measure the difference in codon usage bias between genes, each of the synonymous codon group was considered separately; the Shannon entropy, H(Sk), is thus defined as,
| 5 |
where fk(a) denotes the relative frequency of synonymous codon group a and fk(c | a) is the frequency of codon c normalized in the synonymous codon group a. The JS(S1,S2) for codon usage bias is termed JS-CB.
Construction of artificial chimeric genomes
To evaluate the performance of our proposed method, we constructed artificial genomes using generalized hidden Markov models (HMMs) (9). Briefly, genes making the core of a genuine genome—those representing the spectrum of mutational signatures native to that genome—are obtained by a gene clustering algorithm based on Akaike information criterion [AIC (14–16)]. These genes are segregated into distinct classes using a k-means clustering algorithm employing relative entropy as distance measure to decide the algorithm convergence. Multiple gene models trained on these gene classes are then used in the framework of a generalized HMM to generate an artificial genome representing the variability found among genuine core genes. A chimeric artificial genome is obtained as the mosaic collection of genes sampled from different artificial genomes. To a chosen recipient artificial genome, we inserted at a random position one or more contiguous genes selected randomly from a sample of donor artificial genomes. Insertion is carried out recursively until a chimeric genome of a desired composition is obtained. Because the evolutionary histories of genes are known precisely in these genomes, and because the genes fairly represent the variability seen in genuine genomes, chimeric artificial genomes serve as valid test beds for assessing the parametric methods of gene transfer detection (9).
Two sets of 4000-gene artificial genomes were created. Artificial Genome I had a core of 3000 genes (75%) representing an artificial E. coli genome; the remaining genes were acquired from five different donors—A. fulgidus (7%), B. subtilis (5%), H. influenzae Rd (3%), M. jannaschii (6%), R. solanacearum (4%). Artificial Genome II had a core of 3400 genes (85%) representing an artificial E. coli genome with the remainder acquired from 10 donors—A. fulgidus (1%), B. subtilis (1%), D. radiodurans (2%), H. influenzae Rd (2%), M. jannaschii (1%), N. gonorrhoeae (1%), R. solanacearum (2%), S. meliloti (2%), Synechocystis PCC6803 (1%) and T. maritima (2%).
Class reassignment and refinement
Compositional properties of genes rarely lie as points about a single defining set of parameters; rather, they fall along a range of parameters (for example, of codon usage bias). At high stringency (significance threshold), the JS clustering algorithm may cause native genes, or the genes from a donor organism, to be sorted into more than one class representing this spectrum; relaxing the stringency may raise the misclassification error and lead to the undesirable merger of classes of genes. Gene-context information can be used to identify classes of genes that may have originated from the same source organism. If a gene belongs to class ci whereas the two flanking genes are grouped in class cj, we define this adjacency as a link between classes ci and cj. To quantify the significance of this link, we define P(ci↔cj) as,
| 6 |
where N(ci→cj) is the total number of connections from class ci to cj and L(cx) is the number of genes in class cx. If P(ci↔cj) exceeds an established threshold, the genes comprising the two classes are physically associated within the genome, perhaps due to common origin; the genes from these two entropic classes are assigned to a single logical class.
In the next post-processing step, we again use the genome context information of genes to refine the composition of gene classes. Here, a gene is reassigned to the class of its neighbors only if it plausibly lies within that class. Specifically, if a gene belongs to logical class ci whereas the immediate neighbors of this gene are grouped in logical class cj, this gene is reassigned to class cj, if and only if it is either not atypical or only slightly atypical with respect to class cj (determined by slightly relaxing the stringency) as inferred within a hypothesis testing framework.
Existing parametric methods for alien gene identification
Other parametric methods for foreign gene detection were coded as follows. Karlin (17) suggested dinucleotide bias as a genome signature, ρXY = fXY/fXfY, assessed through the odds ratio, fXY is the frequency of the dinucleotide XY and fX is the frequency of the nucleotide X. If the dinucleotide average relative abundance difference between gene g and genome G (average over all genes) defined as 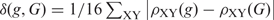 exceeds an established threshold, the gene is classified as foreign. The Karlin's Codon Usage Difference (18) between gene g and genome G was quantified as
exceeds an established threshold, the gene is classified as foreign. The Karlin's Codon Usage Difference (18) between gene g and genome G was quantified as 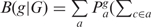
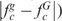 , fc is the frequency of codon c normalized in the respective synonymous codon group a, Pa is the normalized frequency of amino acid a. If B(g|G) exceeds an established threshold, g is classified as a foreign gene.
, fc is the frequency of codon c normalized in the respective synonymous codon group a, Pa is the normalized frequency of amino acid a. If B(g|G) exceeds an established threshold, g is classified as a foreign gene.
Hayes and Borodovsky (19) developed a k-means gene clustering algorithm using Kullback–Leibler distance, 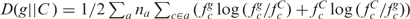 , as a measure of codon usage difference between gene g and cluster C to decide the algorithm convergence (na is the size of the ath group of synonymous codons, fc denotes the normalized frequency of codon c as described above). Initial seeds for typical and atypical clusters were obtained from GeneMark predictions, each gene was reassigned to the cluster with the closest cluster center determined through D, cluster centers were recomputed and this process was repeated until convergence. Our recently developed AIC-based gene clustering algorithm is similar in spirit to our proposed JS divergence based gene clustering method, gene classes are populated in a hierarchical agglomerative clustering fashion, however, here clustering is decided in a model selection framework. We used a generalized version of AIC,
, as a measure of codon usage difference between gene g and cluster C to decide the algorithm convergence (na is the size of the ath group of synonymous codons, fc denotes the normalized frequency of codon c as described above). Initial seeds for typical and atypical clusters were obtained from GeneMark predictions, each gene was reassigned to the cluster with the closest cluster center determined through D, cluster centers were recomputed and this process was repeated until convergence. Our recently developed AIC-based gene clustering algorithm is similar in spirit to our proposed JS divergence based gene clustering method, gene classes are populated in a hierarchical agglomerative clustering fashion, however, here clustering is decided in a model selection framework. We used a generalized version of AIC, 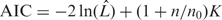 , as a stopping criterion for clustering [
, as a stopping criterion for clustering [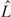 is the maximum likelihood, K is the number of free parameters, n is the sample size and n0 is the tuning parameter (16)]. Garcia-Vallve et al. (20) used multiple metrics, namely G+C content, codon and amino acid usage to compile putative horizontally transferred genes in their HGT-DB database. The machine-learning method Wn-SVM uses a one-class support vector machine for identifying alien genes (21). Alien-Hunter detects putative alien genes using variable order motif distributions (22).
is the maximum likelihood, K is the number of free parameters, n is the sample size and n0 is the tuning parameter (16)]. Garcia-Vallve et al. (20) used multiple metrics, namely G+C content, codon and amino acid usage to compile putative horizontally transferred genes in their HGT-DB database. The machine-learning method Wn-SVM uses a one-class support vector machine for identifying alien genes (21). Alien-Hunter detects putative alien genes using variable order motif distributions (22).
Assessment parameters for evaluating the parametric methods
For assessing the performance of the parametric methods in identifying the foreign genes, we obtain the misclassification error rates as Type I error = FN/(TP + FN) and Type II error = FP/(TP + FP), where TP = true positives, FN = false negatives and FP = false positives (note that conventionally TP, FN and FP are interpreted in accordance with a null hypothesis testing, here without loss of generality, positives and negatives respectively mean the genes declared as foreign and native by a method). Type I error is the percentage of foreign genes that were misclassified as native, whereas Type II error is the percentage of predicted foreign genes that were actually native. The average value of Type I error and Type II error was used as a single error rate parameter. JS- or AIC-based clustering methods yield one class comprising the majority (60–95%) of genes in the genome; the remaining genes are distributed among several smaller classes. Native genes are represented by the largest class while the foreign genes are, by definition, identified as the residents of all other classes. Artificial genomes contain ‘foreign’ gene with known sources; donor-specific misclassification error rate is defined as the percentage of genes from a donor organism misclassified as native genes. Classes generated by the clustering methods were assessed using two parameters: class abundance and class purity. Class abundance is the percentage of genes from a source organism identified correctly in a respective class (the sensitivity with respect to the class). Class purity is the percentage of genes in the class correctly assigned to that class (the specificity with respect to the class).
RESULTS
Using entropic divergence to classify genes
We posit that both native and foreign genes in bacterial genomes will fall into multiple classes. That is, foreign genes will not only be atypical, but they may also be segregated into groups of similar genes (Figure 1). As a result, the identification of atypical genes can rely both on their dissimilarity to native genes as well as on their shared characteristics. These features may help delimit the boundaries between typical genes and sets of atypical genes. We employed our proposed JS gene clustering methods to segregate genes in bacterial genomes into classes. As described in the Materials and Methods section, all genes from a genome were initially assigned to N single-gene classes (Table 1, row 1). The most similar classes merged recursively until the classes were distinct from each other at a given significance threshold. A trade-off between Type I and Type II errors is evident by changing the stringency used to discriminate the gene classes. As the number of classes decrease, more native genes are identified correctly, but more foreign genes are incorrectly deemed native (Table 1). Clustering stops prematurely at high significance thresholds, generating numerous potentially similar classes; at low significance thresholds the distinction between classes is high, however, the likelihood of undesirable merger of classes increases. Optimum performance is defined as the threshold setting which minimizes the mean error.
Table 1.
Grouping genes in Artificial Genome I using JS entropic divergence, with codon usage bias as the discriminant criterion; values are averages of 10 trials
| Significance threshold | Number of classes | Number of genes in largest class | Percent of genes in largest class | Type I error (%) | Type II error (%) | Mean error (%) |
|---|---|---|---|---|---|---|
| 1 | 4000 | 1 | 0.025 | |||
| 0.99 | 446.7 | 69 ± 9 | 1.7 ± 0.2 | naa | na | na |
| 0.95 | 258.8 | 234 ± 26 | 5.8 ± 0.6 | 0.01 ± 0.02 | 73.5 ± 1.0 | 36.7 ± 0.5 |
| 0.9 | 185.4 ± 6.0 | 452 ± 35 | 11.3 ± 0.8 | 0.01 ± 0.03 | 71.9 ± 0.9 | 35.9 ± 0.4 |
| 0.8 | 123.1 ± 5.6 | 782 ± 39 | 19.5 ± 0.9 | 0.07 ± 0.06 | 69.1 ± 1.0 | 34.5 ± 0.5 |
| 0.7 | 90.5 ± 3.4 | 1203 ± 34 | 30.0 ± 0.8 | 0.2 ± 0.1 | 64.5 ± 1.1 | 32.3 ± 0.6 |
| 0.6 | 69.8 ± 4.5 | 1473 ± 34 | 36.8 ± 0.8 | 0.3 ± 0.2 | 60.7 ± 1.3 | 30.5 ± 0.7 |
| 0.5 | 56.0 ± 3.6 | 1712 ± 41 | 42.8 ± 1.0 | 0.5 ± 0.2 | 56.7 ± 1.1 | 28.6 ± 0.5 |
| 0.4 | 44.3 ± 3.3 | 1912 ± 37 | 47.8 ± 0.9 | 0.7 ± 0.2 | 52.6 ± 1.1 | 26.7 ± 0.5 |
| 0.3 | 35.2 ± 2.0 | 2114 ± 35 | 52.8 ± 0.8 | 1.0 ± 0.2 | 47.7 ± 1.2 | 24.4 ± 0.6 |
| 0.2 | 27.4 ± 2.2 | 2290 ± 36 | 57.2 ± 0.9 | 1.3 ± 0.2 | 42.6 ± 1.2 | 21.9 ± 0.6 |
| 0.1 | 22.0 ± 1.5 | 2462 ± 33 | 61.5 ± 0.8 | 2.0 ± 0.3 | 36.6 ± 1.4 | 19.3 ± 0.8 |
| 10−2 | 15.4 ± 1.5 | 2724 ± 43 | 68.1 ± 1.0 | 4.2 ± 0.7 | 25.3 ± 1.4 | 14.8 ± 0.9 |
| 10−3 | 12.8 ± 1.2 | 2848 ± 34 | 71.2 ± 0.8 | 6.2 ± 1.4 | 19.0 ± 1.8 | 12.6 ± 0.9 |
| 10−4 | 11.6 ± 1.2 | 2934 ± 33 | 73.3 ± 0.8 | 8.2 ± 1.7 | 14.4 ± 0.8 | 11.3 ± 0.9 |
| 10−5 | 10.9 ± 1.1 | 2986 ± 35 | 74.6 ± 0.8 | 10.3 ± 2.2 | 12.0 ± 0.9 | 11.1 ± 1.2 |
| 10−6 | 11.0 ± 1.1 | 3020 ± 35 | 75.5 ± 0.8 | 12.2 ± 2.5 | 10.9 ± 0.9 | 11.6 ± 1.5 |
| 10−7 | 10.6 ± 1.0 | 3049 ± 39 | 76.2 ± 0.9 | 13.9 ± 3.0 | 9.9 ± 1.1 | 11.9 ± 1.7 |
| 10−8 | 10.0 ± 1.3 | 3079 ± 45 | 76.9 ± 1.1 | 16.3 ± 3.5 | 9.5 ± 1.3 | 12.9 ± 2.1 |
| 10−9 | 9.4 ± 0.9 | 3117 ± 52 | 77.9 ± 1.3 | 18.1 ± 3.7 | 7.7 ± 1.1 | 12.9 ± 2.0 |
| 10−11 | 9.0 ± 0.7 | 3160 ± 54 | 79.0 ± 1.3 | 21.4 ± 4.1 | 6.9 ± 1.2 | 14.2 ± 2.1 |
| 0 | 1 | 4000 | 100 |
aNot applicable; the largest clusters did not correspond to native genes.
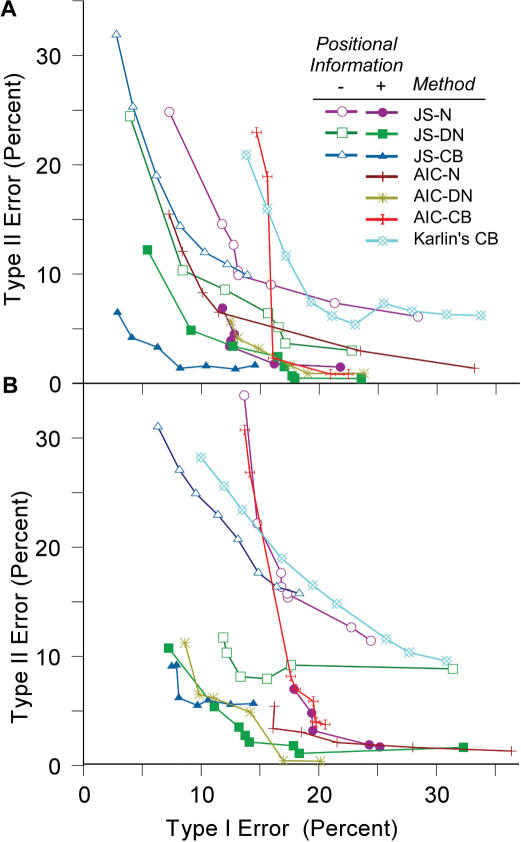
We used three criteria for class merger: codon position specific nucleotide composition (JS-N) and dinucleotide composition (JS-DN) as well as codon usage bias (JS-CB); their relative performance is shown in Table 2. Depending on genome composition and the threshold parameters, between 6 and 11 major classes were typically obtained; additional classes contained very few genes. For all methods, decrease in Type I error caused an increase in Type II error and vice versa (Figure 2). JS-based clustering methods, which form many atypical gene classes, generally outperform other methods which sort genes into a single foreign gene class (Table 2; Figure 2), including Karlin's dinucleotide (17) and codon usage bias methods (18), and Hayes and Borodovsky's k-means method (19). Gene classification methods based on the AIC, which also allow for the assignment of atypical genes to more than one class (9), also performed well.
Table 2.
Error rates of the methods for foreign gene detection
| Classification methoda | Artificial Genome I | Artificial Genome II | ||||||
|---|---|---|---|---|---|---|---|---|
| Threshold | Type I error (%) | Type II error (%) | Mean error (%) | Threshold | Type I error (%) | Type II error (%) | Mean error (%) | |
| JS-N | 0.25 | 13.1 ± 4.0 | 9.9 ± 2.6 | 11.5 ± 1.9 | 0.2 | 17.3 ± 4.6 | 15.7 ± 3.2 | 16.5 ± 1.9 |
| JS-N pos | 0.25 | 12.4 ± 4.3 | 3.4 ± 1.2 | 7.9 ± 2.0 | 0.2 | 18.9 ± 4.9 | 2.4 ± 1.1 | 10.6 ± 2.1 |
| JS-DN | 0.4 | 8.4 ± 7.7 | 10.3 ± 1.8 | 9.3 ± 3.1 | 0.2 | 13.2 ± 3.9 | 8.1 ± 1.1 | 10.6 ± 2.0 |
| JS-DN pos | 0.4 | 9.1 ± 8.6 | 4.8 ± 1.9 | 7.0 ± 3.5 | 0.4 | 11.1 ± 3.6 | 5.4 ± 2.1 | 8.2 ± 2.5 |
| JS-CB | 10−5 | 10.3 ± 2.2 | 12.0 ± 0.9 | 11.1 ± 1.2 | 10−8 | 14.8 ± 2.5 | 17.6 ± 1.8 | 16.2 ± 1.6 |
| JS-CB pos | 10−2 | 4.1 ± 0.6 | 4.2 ± 1.5 | 4.1 ± 0.9 | 10−3 | 8.1 ± 2.4 | 6.2 ± 2.0 | 7.1 ± 1.4 |
| AIC-N | 0.5 | 12.5 ± 6.1 | 10.8 ± 6.9 | 11.6 ± 2.6 | 0.4 | 15.9 ± 3.4 | 9.6 ± 2.3 | 12.8 ± 2.1 |
| AIC-N pos | 0.5 | 11.4 ± 6.5 | 6.5 ± 5.6 | 8.9 ± 2.3 | 0.4 | 16.1 ± 3.0 | 3.4 ± 1.3 | 9.7 ± 1.8 |
| AIC-DN | 1.9 | 16.3 ± 6.7 | 5.7 ± 6.1 | 11.0 ± 2.4 | 1.8 | 14.4 ± 4.0 | 5.6 ± 4.4 | 10.0 ± 2.5 |
| AIC-DN pos | 1.4 | 13.0 ± 6.5 | 4.1 ± 4.2 | 8.6 ± 2.3 | 1.2 | 9.8 ± 5.8 | 6.4 ± 11.2 | 8.1 ± 5.2 |
| AIC-CB | 1.5 | 19.4 ± 5.0 | 4.7 ± 4.0 | 12.0 ± 2.9 | 1.8 | 16.9 ± 6.4 | 13.4 ± 10.8 | 15.2 ± 5.5 |
| AIC-CB pos | 1.1 | 16.0 ± 2.0 | 2.3 ± 1.9 | 9.2 ± 1.4 | 1.6 | 19.6 ± 6.8 | 4.0 ± 4.1 | 11.8 ± 3.5 |
| Karlin's dinuc | 0.15 | 34.2 ± 3.5 | 28.6 ± 0.8 | 31.4 ± 2.0 | 0.12 | 17.3 ± 2.3 | 56.4 ± 1.5 | 36.9 ± 1.7 |
| Karlin's dinuc pos | 0.15 | 40.6 ± 4.0 | 9.6 ± 0.8 | 25.1 ± 2.2 | 0.13 | 31.3 ± 4.0 | 25.8 ± 2.0 | 28.6 ± 2.9 |
| Karlin's codon | 0.49 | 18.9 ± 4.4 | 16.1 ± 0.8 | 17.5 ± 2.5 | 0.48 | 20.7 ± 2.8 | 29.8 ± 1.5 | 25.3 ± 2.0 |
| Karlin's codon pos | 0.47 | 19.3 ± 5.1 | 7.4 ± 0.7 | 13.3 ± 2.7 | 0.43 | 14.7 ± 3.4 | 21.0 ± 1.4 | 17.8 ± 2.2 |
| k-means | N/A | 23.2 ± 4.0 | 4.4 ± 1.5 | 13.8 ± 2.4 | N/A | 41.2 ± 6.4 | 42.6 ± 27.7 | 41.9 ± 16.2 |
| k-means pos | N/A | 21.7 ± 4.4 | 4.5 ± 1.6 | 13.1 ± 2.6 | N/A | 44.0 ± 6.4 | 28.6 ± 19.6 | 36.3 ± 12.4 |
The methods were applied to identify atypical genes in an artificial E. coli genome with foreign genes from five or ten donor organisms (see text for detail) aJS-N, JS-DN and JS-CB denote Jensen–Shannon-divergence-based gene clustering method using respectively the nucleotide composition, dinucleotide composition and codon usage bias as the discriminant criterion. Similarly for AIC-based gene clustering method. ‘pos’ denotes the use of positional information.
Figure 2.
Trade-offs in error rates of foreign gene identification in artificial genomes. JS-N, JS-DN and JS-CB denote Jensen–Shannon divergence-based gene clustering method using respectively the nucleotide composition, dinucleotide composition and codon usage bias as the discriminant criterion. AIC stands for AIC-based gene-clustering methods. (A) Artificial Genome I, with 5 donors. (B) Artificial Genome II with 10 donors.
Because native genes show a spectrum of compositional properties, we must decrease the significance threshold to allow them to join the large class of native genes (Table 1). Yet this simple change in threshold may also allow foreign genes to be included, leading to increased Type I error. This coupling of Type I and Type II errors can only be circumvented if other information is used to perform class merger. That is, we must only merge classes of weakly atypical native genes to the largest class, while leaving classes of weakly atypical foreign genes separate. To do this, we rely on gene position to perform a differential class merger, termed class reassignment.
Differential class merger and refinement using positional information
For reassigning foreign genes misclassified as native and native genes misclassified as foreign, we used genome context information, a technique developed by Lawrence and Ochman (7,8). There, reassignment of native or foreign genes was performed through human intervention by examining the class identity of genes flanking ambiguously assigned, weakly atypical genes. If a small number of genes from an otherwise contiguous set of foreign genes were identified as native, they were reassigned into the foreign class by invoking the rule of adjacency. In our case, positional information can be used to map the JS methods’ generated gene classes originating from the same source organism and vet the incorrect assignments of genes to the classes. We used the class linking measure P(ci↔cj) to merge classes obtained at strict stringency on the basis of relative positions of their constituent genes and not on their entropic divergence. If P(ci↔cj) exceeded an established threshold, the classes ci and cj were merged; this process was iterated until the merger of any two classes was not legitimate. The threshold was set to 0.3 after testing on a number of data sets.
The composition of classes was also refined using gene context information. We examined genes that were flanked by genes both belonging to a different class (Figure 1B); if such a gene was reasonable member of that different class—that is, if it had sufficient affinity for that class inferred within a hypothesis testing framework—the gene was reassigned to that class. We repeated this process until no gene reassignment was significant. This process would serve to purify classes, enabling them to add members that were sufficiently different so that they were misclassified, an inevitable result of classes of genes which overlap in sequence features (Figure 1B). For Karlin's methods, the refinement of the predictions using positional information was done in a multi-threshold approach, where genes whose features lay between the ‘clearly typical’ and ‘clearly atypical’ boundaries were reclassified in this way. Although Hayes and Borodovsky's clustering method does not use a threshold to discriminate between typical and atypical genes, we used the distance from class center to discriminate between genes which are strongly associated with the class and those which are weakly associated.
The use of gene context information reduced remarkably both the Type I and Type II errors for all three JS methods, visualized in Figure 2 as curves that approach the intersection of the axes; the JS-CB algorithm showed the most improvement. The JS-CB method also balanced the Type I and Type II errors better than other methods at the optimal thresholds, and the variances in the errors generated by JS-CB were much lower compared to other clustering methods (Table 2). Note that the inclusion of positional information makes the JS-CB method more efficient than the JS-DN approach which had earlier yielded consistently lower misclassification error rates; the decrease in the misclassification error rates of the JS-CB method is nearly 3-fold on Artificial Genome I and 2-fold on Artificial Genome II. Results were not improved if class refinement preceded class reassignment (data not shown).
Using positional information, we also see that the margin of improvement in JS-based classification methods was higher than in AIC-based gene classification methods. The variances in error rates of both AIC-CB and AIC-DN methods were also much higher. The AIC methods are thus sensitive to the thresholds used; as a result, an optimal threshold, one which minimizes the error values with significantly low variances, is difficult to realize. The use of positional information also increased the accuracy of Karlin's, and Hayes and Borodovsky's methods, although not to the same degree as gene-clustering algorithms (Table 2). That is, positional information became more useful when atypical genes were assorted into multiple classes.
Effect of donor genome identity
We would anticipate that genes with markedly different compositional properties would be the easiest to detect as foreign. We examined the performance of JS methods as a function of donor genome and found that all three discriminant criteria served well in detecting gene transfer from four of the donors in Artificial Genome I, where the misclassification error rate (percent of genes from a donor genome misclassified as native) was less than 5% (Table 3). Genes from the artificial B. subtilis genome were misclassified at much higher rates by all methods, with the JS-CB method performing best. These results show that the error rates are also functions of the discriminant criterion and the gene number. We anticipate that combining the methods using more than one discriminant criterion may compensate for any one metric weaknesses, as was seen for AIC-based methods (9).
Table 3.
Misclassification error rates of Jensen–Shannon-divergence-based clustering methods in detecting foreign genes in artificial E. coli genomes
| Artificial Gene Donor | Artificial Genome I | Artificial Genome II | ||||||
|---|---|---|---|---|---|---|---|---|
| Percent contribution | Classification method | Percent contribution | Classification method | |||||
| JS-N | JS-DN | JS-CB | JS-N | JS-DN | JS-CB | |||
| A. fulgidus | 7.0 | 5.7 ± 2.7 | 0.1 ± 0.1 | 0.3 ± 0.3 | 1.0 | 32.0 ± 19.8 | 1.3 ± 3.3 | 0.6 ± 1.8 |
| M. jannaschii | 6.0 | 0.0 ± 0.1 | 1.1 ± 0.7 | 0.2 ± 0.3 | 1.0 | 1.0 ± 1.6 | 2.0 ± 2.1 | 0.8 ± 1.2 |
| B. subtilis | 5.0 | 56.0 ± 18.8 | 38.3 ± 32.3 | 18.1 ± 6.4 | 1.0 | 66.2 ± 21.0 | 77.5 ± 27.0 | 60.8 ± 38.0 |
| R. solanacearum | 4.0 | 3.5 ± 3.5 | 3.4 ± 3.0 | 3.3 ± 1.0 | 2.0 | 1.0 ± 1.1 | 2.8 ± 3.3 | 3.1 ± 2.0 |
| H. influenzae | 3.0 | 1.4 ± 1.9 | 2.1 ± 2.2 | 3.3 ± 2.2 | 2.0 | 1.9 ± 2.0 | 3.0 ± 2.0 | 4.4 ± 3.9 |
| D. radiodurans | 2.0 | 4.4 ± 3.6 | 4.8 ± 4.6 | 2.1 ± 2.2 | ||||
| N. gonorrheae | 1.0 | 66.7 ± 31.6 | 58.2 ± 31.2 | 36.4 ± 13.0 | ||||
| S. meliloti | 2.0 | 5.3 ± 4.5 | 3.8 ± 2.3 | 1.8 ± 2.1 | ||||
| Synechocystis | 1.0 | 99.6 ± 0.8 | 3.3 ± 4.9 | 12.5 ± 8.7 | ||||
| T. maritima | 2.0 | 8.2 ± 3.9 | 1.1 ± 0.9 | 0.8 ± 0.9 | ||||
| Type I error (100-sensitivity) | 12.4 ± 4.3 | 9.1 ± 8.6 | 4.1 ± 0.6 | 18.9 ± 4.9 | 11.1 ± 3.6 | 8.1 ± 2.4 | ||
| Type II error (100-specficity) | 3.4 ± 1.2 | 4.8 ± 1.9 | 4.2 ± 1.5 | 2.4 ± 1.1 | 5.4 ± 2.1 | 6.2 ± 2.0 | ||
| Mean error | 7.9 ± 2.0 | 7.0 ± 3.5 | 4.1 ± 0.9 | 10.6 ± 2.1 | 8.2 ± 2.5 | 7.1 ± 1.4 | ||
The positional information of a gene was used to further minimize the classification errors.
By their very nature, the accuracy of JS methods in detecting classes of atypical genes increases as the number of genes in each class increases. To determine if the strong performance of the JS methods in detecting most atypical genes was a result of gene numbers, we compared results for Artificial Genome I to those for Artificial Genome II, wherein fewer genes were selected from each of a greater number of donor genomes. Here, all JS methods performed well (<10% misclassification error) in discriminating foreign genes from six donors; only JS-CB was most consistent in classifying correctly genes from A. fulgidus, N. gonorrhoeae and Synechocystis and none of the methods performed well on genes from B. subtilis (Table 3). In most cases, the methods generated higher misclassification error rates than those for Artificial Genome I. The performance of the AIC gene clustering methods in classifying the genes of donor genomes is shown in Supplementary Table 1. While AIC-DN performed better than AIC-N and AIC-CB, it could not classify the majority of the B. subtilis and N. gonorrhoeae genes correctly. Overall, JS-CB emerged as the most effective method in classifying the genes as foreign or native, being least affected by the identity of the donor genome.
Identification of distinct atypical gene classes in a genome
To assess the efficiency of JS methods in grouping genes contributed by different donor organisms, we examined two accuracy parameters—class abundance and purity—after the gene classes were refined using positional information (Table 4). While all the JS methods grouped the genes that have arrived from 4 donors in the Artificial Genome I into distinct classes, JS-CB performed the best as measured by both accuracy parameters. For the most part, all JS methods generated classes with a very high degree of purity (>90%); class purity was highest where genes arrived from compositionally distinct donors. Only JS-CB could group well the B. subtilis genes (class abundance and purity were both greater than 80%). Even when Type II error was relatively high—for example, when many B. subtilis genes were misclassified as ‘native’ by JS-N and JS-DN—those genes that were identified as ‘foreign’ were placed into a relatively pure class (∼80% B. subtilis genes). With Artificial Genome II, the performance of JS-N dropped significantly, with only three gene classes having class abundance and purity above 70%. The JS-N method grouped R. solanacaerum and S. meliloti genes (class abundance and purity in the range of 60–70%), but it failed to cluster genes originating from five genomes, even if they were identified as foreign (Tables 3 and 4). JS-DN performed better, grouping genes from seven donor genomes. The JS-CB method performed even better, classing the genes of eight donors very well (class abundance and purity both exceeded 70%), N. gonorrhoeae less efficiently, and B. subtilis genes poorly. These results show that the JS methods, particularly the JS-CB, can be powerful tools for identifying genes that originate from the same donor organism.
Table 4.
Assessment of the ability of Jensen–Shannon-based gene clustering methods in identifying the genes from a donor organism in the artificial E. coli genomes as a distinct group
| Artificial gene donor | JS-N | JS-DN | JS-CB | |||
|---|---|---|---|---|---|---|
| Class abundancea | Class purityb | Class abundance | Class purity | Class abundance | Class purity | |
| Artificial Genome I: 5 donors | ||||||
| A. fulgidus | 92.9 ± 2.8 | 92.2 ± 2.9 | 93.4 ± 2.1 | 99.8 ± 0.2 | 99.4 ± 0.5 | 99.6 ± 0.2 |
| M. jannaschii | 96.0 ± 2.2 | 99.5 ± 0.3 | 88.0 ± 3.5 | 99.8 ± 0.1 | 97.8 ± 1.5 | 99.6 ± 0.3 |
| B. subtilis | 33.5 ± 16.8 | 81.0 ± 5.9 | 55.2 ± 31.0 | 75.0 ± 7.2 | 80.0 ± 7.0 | 84.5 ± 9.9 |
| R. solanacearum | 92.8 ± 4.4 | 98.9 ± 1.5 | 86.1 ± 3.2 | 98.4 ± 2.1 | 94.8 ± 3.8 | 98.2 ± 1.6 |
| H. influenzae | 92.8 ± 2.1 | 90.7 ± 6.4 | 82.2 ± 5.2 | 96.8 ± 2.8 | 91.1 ± 4.7 | 97.5 ± 1.5 |
| Artificial Genome II: 10 donors | ||||||
| A. fulgidus | 8.7 ± 26.2 | 56.5 ± 0.0 | 80.3 ± 8.1 | 98.8 ± 2.2 | 86.1 ± 9.9 | 93.7 ± 6.7 |
| M. jannaschii | 84.7 ± 14.3 | 98.3 ± 2.8 | 77.0 ± 8.9 | 99.5 ± 1.4 | 94.3 ± 5.7 | 98.3 ± 2.3 |
| B. subtilis | 0.0 ± 0.0 | – | 11.4 ± 23.1 | 63.2 ± 6.4 | 17.3 ± 30.2 | – |
| R. solanacearum | 69.2 ± 28.5 | 61.2 ± 10.8 | 66.9 ± 23.4 | 77.4 ± 18.1 | 79.1 ± 14.8 | 83.5 ± 15.1 |
| H. influenzae | 93.2 ± 5.4 | 95.1 ± 3.6 | 77.3 ± 6.8 | 89.8 ± 6.1 | 88.8 ± 5.6 | 97.2 ± 2.3 |
| D. radiodurans | 15.1 ± 28.3 | 63.1 ± 17.8 | 36.4 ± 34.0 | 80.2 ± 20.2 | 72.3 ± 20.1 | 89.6 ± 11.0 |
| N. gonorrheae | 22.0 ± 29.2 | 67.7 ± 15.4 | 28.6 ± 29.8 | 78.8 ± 11.7 | 58.2 ± 13.5 | 72.7 ± 6.5 |
| S. meliloti | 62.1 ± 40.7 | 67.1 ± 13.0 | 77.8 ± 11.2 | 85.4 ± 9.8 | 85.7 ± 23.6 | 84.1 ± 7.2 |
| Synechocystis | 0.0 ± 0.0 | – | 87.2 ± 6.6 | 89.1 ± 5.9 | 88.3 ± 6.1 | 88.6 ± 10.9 |
| T. maritima | 81.1 ± 27.5 | 71.5 ± 9.6 | 89.8 ± 4.0 | 97.1 ± 4.0 | 96.6 ± 1.7 | 94.1 ± 4.1 |
aThe percentage of total contributory genes from a source organism identified correctly in a respective class.
bThe percentage of genes in a class correctly assigned to that class.
The performance of the AIC gene clustering method in classing the genes from donor genomes is shown in Supplementary Table 2. None of the AIC methods seemed proficient in grouping the B. subtilis genes from Artificial E. coli I. On Artificial E. coli II, the performance went worse with AIC-DN grouping together majority of the genes of only four genomes. The performance of AIC-CB was no better; AIC-N, however, performed comparably with JS-N. Overall our analysis shows that JS methods are most consistent and efficient in classing the genes in genomes.
Phylogenetic breadth of potential donor classes
As expected, classification accuracy increases with the number of genes in each class. In artificial genomes, classes are represented by genes from a single donor species. Yet genuine genomes will likely not receive multiple transfer from any single donor, although it may experience multiple events from related donors. Because LGT is believed to occur more frequently among evolutionary closely related organisms (11,23), the array of donor genomes may indeed be non-random. More importantly, differences in genome composition increase as a function of the evolutionary distance between species, and related genomes are compositionally similar. As a result, JS methods should sort genes from related donors into one or few classes.
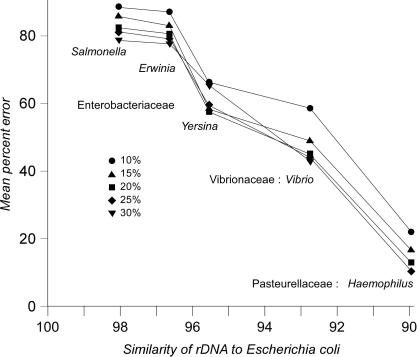
To assess how the effectiveness of the JS entropy clustering depends on the evolutionary distance between donor and recipient genomes, we performed simulated gene transfers into an artificial E. coli genome using genes from genomes modeled after the related γ-proteobacteria as donors (Figure 3). Salmonella enterica, being the closest to the E. coli among the five donors, had most of its genes (∼80%) misclassified by JS-CB. That is, JS methods could not distinguish E. coli genes from S. enterica genes, so that these genes would form a single class if they were both introduced into a foreign genome. Genes from artificial genomes constructed from other members of the Enterobacteriaceae were also found to be compositionally similar to E. coli genes (Figure 3), while genes from more distantly related γ-proteobacteria were distinguished more efficiently. Thus, JS methods do not form species-specific classes; rather, genes from any member of a bacterial family would be placed into a single compositional class.
Figure 3.
Performance of the Jensen–Shannon divergence-based gene clustering method in identifying the foreign genes introduced from artificial γ-proteobacterial genomes into an artificial E. coli genome. The percentage of the acquired genes was varied from 10 to 30% of the genome.
Application of entropic clustering to genuine genomes
Although artificial genomes mimic the genic complexity of genuine genomes, it is difficult to model the positional distribution of foreign genes. Therefore, it is unclear if the advantages of using positional information will be seen in genuine genomes. To examine this, we applied the best performing method, JS-CB, to the well-characterized E. coli K12 genome. A set of putative horizontally transferred genes (‘HT’ genes henceforth) was defined as those present in the E. coli K12 genome but absent from the S. enterica LT2 genome. This yielded 891 HT genes (very short genes, those with length <300 nt, were not considered). Given the vagaries of genuine data, this set is known to be imperfect in two ways. First, foreign genes acquired before the divergence of E. coli and S. enterica will be excluded, leading to some foreign genes being mislabeled native. Second, homologs of native genes lost from the S. enterica genome will be included in our test set.
Using this set of HT genes as a guide, we observed that the JS-CB method performed well (Table 5). At a baseline significance threshold of 0.05 (Supplementary Table 3), the number of false predictions was high due to several small classes of native genes misclassified as foreign (mean error ∼49%). Class reassignment caused a significant drop in the number of false predictions at the cost of fewer true predictions (mean error 42%). Upon class refinement, the mean error decreased further to 39.6%. An equivalent number of predicted foreign genes was obtained at a significance level of 10−6 without using positional information, but the mean error was 59.5%. Thus the use of positional information results in remarkable improvement in the HT gene detection in genuine genomes, as predicted from the artificial genome simulations.
Table 5.
Performance of the methods for lateral gene transfer detection in identifying the putative horizontally transferred genes in the E. coli K12 genome
| Parameter | Karlin's codon usage (18) | HGT-DB (20) | Wn-SVM (21) | Alien Hunter (22) | AIC-DN. (9) | JS-CB |
|---|---|---|---|---|---|---|
| Number of predicted HT genes | 50 (>600 nt) | 306 | 490 | 1239 | 464 | 639 |
| True positives | 45 | 223 | 302 | 504 | 306 | 449 |
| False positives | 5 | 83 | 188 | 735 | 158 | 190 |
| False negatives | 577 | 668 | 589 | 387 | 585 | 442 |
| Type I error (%) | 92.76 | 74.97 | 66.10 | 43.43 | 65.65 | 49.60 |
| Type II error (%) | 10.0 | 27.12 | 38.36 | 59.32 | 34.05 | 29.73 |
| Mean error (%) | 51.38 | 51.04 | 52.23 | 51.37 | 49.85 | 39.66 |
The ‘positives’ and ‘negatives’ respectively mean the genes declared as foreign and native by a method.
Using this benchmark set of putative foreign genes, the JS-CB method also outperformed other parametric methods for foreign gene detection (Table 5). Karlin's codon usage method (18) identified only 50 genes (>600 nt) as the laterally transferred candidates; while specificity was high, sensitivity was very low. Garcia-Vallve et al. (20) have compiled 306 putative HT genes of E. coli K12 in their HGT-DB database, their method was also not found to be sensitive. We also tested two recently proposed parametric methods for LGT detection, Wn-SVM (21) and Alien-Hunter (22). Alien-Hunter had a comparatively lower Type I error as it identified highest number of foreign genes among all methods but this came at the cost of very high number of false predictions. Wn-SVM generated less false predictions but could identify fewer foreign genes We also tested the best performing method among the AIC methods (AIC-DN) which performed slightly better than Wn-SVM, generating less of false predictions at equivalent number of true predictions. JS-CB achieved much better accuracy than other methods, identifying correctly 449 HT genes at the cost of 190 false predictions. While the mean errors of other methods were close to 50%, it was remarkably less by more than 10% for JS-CB. While these numbers are a function of the data set analyzed, they suggest that the JS-CB method is a promising approach when compared to other commonly used approaches.
DISCUSSION
Statistical significance of atypical gene identification
Current parametric methods select a threshold to discriminate between foreign and native genes. While these thresholds are often arbitrary, our proposed entropic clustering method discriminates between the gene classes in the framework of statistical significance. As a caveat, there are multiple hypothesis testing problems involved, namely the repetition of the test in each iteration step and over the hierarchy. Therefore, appropriately stringent thresholds must be chosen to compensate for multiple tests. Although sporadic rejection of the null hypothesis when using multiple tests results in failure to merge classes, these classes may be merged in subsequent steps using positional information. Although the AIC-based approach we introduced earlier (9) also has a strong theoretical underpinning, the thresholds in the generalized AIC cannot be rigorously described. Among the parametric methods of foreign gene detection, to our knowledge, the JS clustering methods are the only methods that classify atypical genes in the framework of statistical significance.
Use of genome position information decreases remarkably both Type I and Type II errors
A shortcoming of parametric methods is their difficulty in identifying weakly atypical genes. The trade-off is clear: classifying only strongly atypical genes as foreign decreases false predictions, however, this comes at the expense of many foreign genes misclassified as native, a more relaxed criteria increases the sensitivity of a method at the expense of false predictions. This inherent weakness limits the abilities of this class of methods. Through this study, we propose gene context information as a means to address this issue. The utility of positional information increases when the confidence of typical and atypical gene classes increases. That is, optimal assignment occurs at higher stringencies ensuring the purity of both typical and atypical gene classes, at the expense of creating a larger number of classes. In a two pronged approach (class reassignment followed by class refinement), the misclassification of foreign genes was reduced by allowing weakly atypical native genes to join the native gene class by virtue of their positions, not by relaxing the criteria for class merger. This also serves to reduce the misclassification of native genes as weakly atypical foreign genes join their classes in a similar fashion (Supplementary Table 4).
Grouping similar genes improves foreign gene identification
We also observed that positional information works synergistically with gene clustering methods reducing the classification errors better than for methods which classify the genes only as native and foreign (Table 2). To examine this further, we carried out numerical experiments where genes from all the small classes generated by JS-CB were pooled as a single foreign class and the largest class represented native genes. Class refinement was then done using the positional information of genes. By minimizing the mean error over the parameter space of the method, comparison was made with cases when class refinement was done for all method-generated classes and also when full power of positional information (both class reassignment and refinement) was used for these classes (Supplementary Table 5). The Type II error decreased significantly causing a decrease in mean error when class refinement was performed on all method- generated classes as opposed to two classes (typical and atypical). Both Type I error and Type II error decreased remarkably when class reassignment followed by class refinement was done at strict stringencies. In addition, since JS methods effectively group genes from common donors (Figure 3), they may be useful in helping identify potential donors for foreign genes in bacterial genomes.
Implications in gene identification
Hayes and Borodovsky (19) developed a k-means algorithm for partitioning a gene-set into primarily two classes (k = 2). The gene models trained on these classes were then incorporated in a prokaryotic gene finder, GeneMark-genesis, where the use of two gene classes improved considerably the identification of genes, particularly those with atypical composition. The success of such prediction algorithms critically depends on the purity of the gene classes. The value of ‘k’ is not known a priori and k = 2 may not be best option to model genic complexity, as shown by our experiments on chimeric artificial as well as genuine genomes. Our hierarchical agglomerative gene-clustering algorithm provides a solution: gene classes grow logically starting with single genes and the process is halted when the distinction between the gene classes is deemed statistically significant. Native genes are identified as belonging to the single largest class that has typically ∼60–95% of the total genes, and foreign genes are divided into several small classes. It should be possible to build a gene model for each gene class, which will likely improve the accuracy of gene identification.
CONCLUSIONS
In comparison to the frequently used parametric methods for foreign gene detection, as well as our previously devised AIC-based methods, our proposed JS gene clustering methods were found to be much robust and consistent in classifying foreign genes in artificial as well as genuine genomes. Among the three JS methods, JS-CB proved to be most efficient not only in identifying foreign genes, but also in grouping genes contributed by distinct donor organisms as distinct classes. In pursuance of our long- term goal of quantification of lateral gene transfer in prokaryotes, we intend to exploit this ability of the JS methods in identifying the sources of gene transfer in prokaryotes. Development of the highly accurate gene classification methods has brought us closer to realizing the genome scale quantization and characterization of lateral gene transfer events in prokaryotes.
SUPPLEMENTARY DATA
Supplementary Data is available at NAR Online.
ACKNOWLEDGEMENTS
This work was supported by grants from the National Institutes of Health, the National Science Foundation and from the David and Lucile Packard Foundation. Discussions with Pedro Bernaola-Galvan, Ram Ramaswamy and Wentian Li are gratefully acknowledged. Funding to pay the Open Access publication charges for this article was provided by the Natoinal Institutes of Health.
Conflict of interest statement. None declared.
REFERENCES
- 1.Doolittle WF. Phylogenetic classification and the universal tree. Science. 1999;284:2124–2129. doi: 10.1126/science.284.5423.2124. [DOI] [PubMed] [Google Scholar]
- 2.Lawrence JG. Gene transfer, speciation, and the evolution of bacterial genomes. Curr. Opin. Microbiol. 1999;2:519–523. doi: 10.1016/s1369-5274(99)00010-7. [DOI] [PubMed] [Google Scholar]
- 3.Ochman H, Lawrence JG, Groisman E. Lateral gene transfer and the nature of bacterial innovation. Nature. 2000;405:299–304. doi: 10.1038/35012500. [DOI] [PubMed] [Google Scholar]
- 4.Ragan MA. On surrogate methods for detecting lateral gene transfer. FEMS Microbiol. Lett. 2001;201:187–191. doi: 10.1111/j.1574-6968.2001.tb10755.x. [DOI] [PubMed] [Google Scholar]
- 5.Lerat E, Daubin V, Moran NA. From gene trees to organismal phylogeny in prokaryotes: the case of the γ-proteobacteria. PLoS Biol. 2003;1:E19. doi: 10.1371/journal.pbio.0000019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bapteste E, Susko E, Leigh J, MacLeod D, Charlebois RL, Doolittle WF. Do orthologous gene phylogenies really support tree-thinking? BMC Evol. Biol. 2005;5:33. doi: 10.1186/1471-2148-5-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lawrence JG, Ochman H. Amelioration of bacterial genomes: rates of change and exchange. J. Mol. Evol. 1997;44:383–397. doi: 10.1007/pl00006158. [DOI] [PubMed] [Google Scholar]
- 8.Lawrence JG, Ochman H. Molecular archaeology of the Escherichia coli genome. Proc. Natl Acad. Sci. USA. 1998;95:9413–9417. doi: 10.1073/pnas.95.16.9413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Azad RK, Lawrence JG. Use of artificial genomes in assessing methods for atypical gene detection. PLoS Comput. Biol. 2005;1:E56. doi: 10.1371/journal.pcbi.0010056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Médigue C, Rouxel T, Vigier P, Hénaut A, Danchin A. Evidence of horizontal gene transfer in Escherichia coli speciation. J. Mol. Biol. 1991;222:851–856. doi: 10.1016/0022-2836(91)90575-q. [DOI] [PubMed] [Google Scholar]
- 11.Beiko RG, Harlow TJ, Ragan MA. Highways of gene sharing in prokaryotes. Proc. Natl. Acad. Sci. USA. 2005;102:14332–14337. doi: 10.1073/pnas.0504068102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lin J. Divergence measures based on the Shannon entropy. IEEE Trans. Inform. Theory. 1991;37:145–151. [Google Scholar]
- 13.Grosse I, Bernaola-Galvan P, Carpena P, Roman-Roldan R, Oliver J, Stanley HE. Analysis of symbolic sequences using the Jensen-Shannon divergence. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:041905. doi: 10.1103/PhysRevE.65.041905. [DOI] [PubMed] [Google Scholar]
- 14.Sakamoto Y, Ishiguro M, Kitagawa G. Akaike Information Criterion Statistics. Berlin: Springer; 1999. [Google Scholar]
- 15.Akaike H. A new look at the statistical model identification. IEEE Trans. Automat. Control. 1974;AC-19:716–723. [Google Scholar]
- 16.Kuha J. AIC and BIC: Comparisons of assumptions and performance. Sociol. Methods Res. 2004;33:188–229. [Google Scholar]
- 17.Karlin S. Global dinucleotide signatures and analysis of genomic heterogeneity. Curr. Opin. Microbiol. 1998;1:598–610. doi: 10.1016/s1369-5274(98)80095-7. [DOI] [PubMed] [Google Scholar]
- 18.Karlin S, Mrazek J, Campbell AM. Codon usages in different gene classes of the Escherichia coli genome. Mol. Microbiol. 1998;29:1341–1355. doi: 10.1046/j.1365-2958.1998.01008.x. [DOI] [PubMed] [Google Scholar]
- 19.Hayes WS, Borodovsky M. How to interpret an anonymous bacterial genome: machine learning approach to gene identification. Genome Res. 1998;8:1154–1171. doi: 10.1101/gr.8.11.1154. [DOI] [PubMed] [Google Scholar]
- 20.Garcia-Vallve S, Guzman E, Montero MA, Romeu A. HGT-DB: a database of putative horizontally transferred genes in prokaryotic complete genomes. Nucleic Acids Res. 2003;31:187–189. doi: 10.1093/nar/gkg004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tsirigos A, Rigoutsos I. A sensitive, support-vector-machine method for the detection of horizontal gene transfers in viral, archaeal and bacterial genomes. Nucleic Acids Res. 2005;33:3699–3707. doi: 10.1093/nar/gki660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vernikos GS, Parkhill J. Interpolated variable order motifs for identification of horizontally acquired DNA: revisiting the Salmonella pathogenicity islands. Bioinformatics. 2006;22:2196–2203. doi: 10.1093/bioinformatics/btl369. [DOI] [PubMed] [Google Scholar]
- 23.Gogarten JP, Doolittle WF, Lawrence JG. Prokaryotic evolution in light of gene transfer. Mol. Biol. Evol. 2002;19:2226–2238. doi: 10.1093/oxfordjournals.molbev.a004046. [DOI] [PubMed] [Google Scholar]