Predicting the Size of the Progeny Mapping Population Required to Positionally Clone a Gene

Abstract

A key frustration during positional gene cloning (map-based cloning) is that the size of the progeny mapping population is difficult to predict, because the meiotic recombination frequency varies along chromosomes. We describe a detailed methodology to improve this prediction using rice (Oryza sativa L.) as a model system. We derived and/or validated, then fine-tuned, equations that estimate the mapping population size by comparing these theoretical estimates to 41 successful positional cloning attempts. We then used each validated equation to test whether neighborhood meiotic recombination frequencies extracted from a reference RFLP map can help researchers predict the mapping population size. We developed a meiotic recombination frequency map (MRFM) for ∼1400 marker intervals in rice and anchored each published allele onto an interval on this map. We show that neighborhood recombination frequencies (R-map, >280-kb segments) extracted from the MRFM, in conjunction with the validated formulas, better predicted the mapping population size than the genome-wide average recombination frequency (R-avg), with improved results whether the recombination frequency was calculated as genes/cM or kb/cM. Our results offer a detailed road map for better predicting mapping population size in diverse eukaryotes, but useful predictions will require robust recombination frequency maps based on sampling more progeny.

A limited number of forward genetics techniques exist to isolate an allele that underlies a mutant or polymorphic phenotype and that require no prior knowledge of the gene product. These include protocols to isolate host DNA flanking insertional mutagens (e.g., transposons) (Ballinger and Benzer 1989; Raizada 2003) and positional gene cloning techniques (Botstein et al. 1980; Paterson et al. 1988; Tanksley et al. 1995) that permit the discovery of alleles created by chemical mutagens, radiation, or natural genetic variation. Positional gene cloning is feasible when the following conditions are met: (1) two parents exist that differ in a trait of interest; (2) the parents can be distinguished at the chromosome level by polymorphic DNA markers (e.g., RFLP); and (3) in a population of progeny, the underlying gene can be mapped relative to nearby DNA segments that have previously been cloned (Botstein et al. 1980; Tanksley et al. 1995). Unfortunately, positional gene cloning suffers from unpredictability in terms of the number of post-meiotic progeny that a researcher can expect to genotype to narrow a candidate chromosomal region to a small number of candidate genes (Dinka and Raizada 2006). For example, in rice (Oryza sativa L.), only 1160 gametes were genotyped to narrow the Pi36(t) allele to a resolution of 17 kb (Liu et al. 2005), whereas 18,944 gametes were genotyped to map the Bph15 allele to a lower resolution of 47 kb (Yang et al. 2004). During fine mapping, the physical distance between a known physical location on a chromosome (i.e., the molecular marker) and the target allele is inferred by the frequency of meiotic recombinants that can break cosegregation of the phenotype encoded by the target allele with physically anchored molecular markers (Botstein et al. 1980; Paterson et al. 1988). Ideally, a gene hunt ends once a molecular marker is found that always cosegregates with the target phenotype in a large population of genotyped and phenotyped F₂ (or post-F₂) progeny. Therefore, the frequency of meiotic recombination in the vicinity of the target locus (defined as R = kilobase/cM), along with the local density of molecular markers, determines the size of the mapping population. We are interested in helping researchers predict mapping population size. As initial analysis assigns a target allele to a 1–5-cM map interval, the goal of this study is to determine whether the recombination frequency at this interval size, obtained from a high-density molecular marker map, can be used to predict the number of progeny required for subsequent sub-centimorgan mapping in combination with user-friendly mathematical formulas.

Durrett et al. (2002) used the kb/cM ratio (R) as the basis of an equation (which we will refer to as the Durrett–Tanksley equation) to predict genotyping requirements during positional cloning, the only such equation we could find in the literature. Durrett et al. compared the results of their equation to empirical evidence from 12 published positional cloning successes in Arabidopsis thaliana; the model often appeared to overestimate the number of progeny required to be genotyped. However, the accuracy of the model was difficult to assess, because only the genome-wide recombination frequency was employed, rather than local rates of recombination. Perhaps as a result, it was simply concluded that some researchers were lucky or unlucky (Durrett et al. 2002).

Building upon the work of Durrett et al., we have tried to understand and predict when a researcher will be lucky or unlucky during positional gene cloning by accounting for: (1) over-genotyping (resulting in redundant crossovers between the target locus and the closest molecular markers); (2) a low density of available molecular markers in the target interval (causing some crossovers to be missed); and most important, (3) high or low local rates of local recombination (R) compared to the genome-wide average (Nachman 2002). We have compared the predictions of the Durrett–Tanksley equation to empirical data obtained from 41 positional cloning studies in rice (O. sativa L.), which is a model system for the world's most important crops, the cereals (Paterson et al. 2005). Specifically, we have measured the predictability of the Durrett–Tanksley equation and then focused on whether “neighborhood” (<2 cM) recombination values obtained from a reference genetic map (Harushima et al. 1998) further improve the accuracy of the model compared to using the genome-wide average recombination rate (R-avg). In addition, we have derived and tested a simpler equation that predicts progeny mapping size. Finally, we have measured the utility of employing R-values calculated as genes/cM rather than kb/cM to predict mapping population size, as the former allows the candidate gene number to be estimated, which is of greater interest to researchers targeting sequenced, annotated genomes.

MATERIALS AND METHODS

Use and modification of the Durrett–Tanksley equation:

First, we used the Durrett–Tanksley equation (Durrett et al. 2002) which estimates the number of F₂/post-F₂ meiotic gametes required to positionally clone an allele as derived from an F₁ heterozygote, based on the following probability:

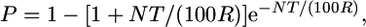where P is probability (P) that if a (proximal) crossover occurs in the vicinity of a target allele that a second (distal) crossover will be carried by a sibling gamete; N is number of genotyped chromosomes (informative gametes) required; T is map resolution, the candidate kilobase or gene block distance between the closest two molecular markers containing the target allele; and R is recombination frequency (kb/cM or genes/cM).

As the equation is dependent only on the value NT/100R, then if the probability is set at 0.95, NT/100R = 4.744, which may be rewritten as N = (4.744 × 100R)/T.

To adjust for the target number of gametes containing an informative crossover (λ_T), which we assume may decrease T (better map resolution), we introduced the empirically-derived T modifier, 4.744/λ_T (see results); the resulting modified Durrett–Tanksley equation is as follows:

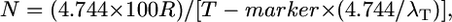or simplified,

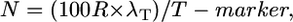where N is total number of informative chromosomes (gametes) that must be genotyped with the probability of success set at P = 0.95, R is the local recombination frequency (R-local) (kb/cM or genes/cM), T-marker is distance between the closest two molecular markers (in which crossovers are detected relative to the target allele) (kilobases or gene block), and λ_T is number of crossovers between the closest two molecular markers (≥2).

The Durrett–Tanksley equation assumes that the recombination frequency (R) is constant in the vicinity T of the target allele. This equation also requires that the genotype of the target allele (a) in F₂/post-F₂ progeny can be assigned. Thus, in the case of a recessive target allele, N equals the number of F₂ testcross progeny. Alternatively, where F₂ progeny are the product of selfing F₁ heterozygotes (such as in plants), then since each F₂ progeny is derived from two meioses, N equals two times the number of F₂ progeny genotyped; this is only true, however, when the F₂ progeny genotype AA can be distinguished from the genotype Aa since this is required to determine whether a crossover occurred on the proximal or distal side of the target allele. Such a determination requires testing progeny for segregation of phenotypes in the F₃ generation (progeny testing).

Derivation of a simplified equation based on single-crossover probability:

We developed the following user-friendly equation to estimate the fine-mapping population size, an estimate of the number of F₂ testcross progeny required to be genotyped to detect sufficient crossovers to achieve a desired kilobase or gene block resolution:

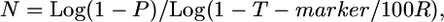where N is the number of meiotic gametes (chromosomes) that must be genotyped in which it can be determined whether a crossover is located proximal or distal to the target allele, P is threshold probability of success (e.g., 0.95), T-marker is expected distance between flanking molecular markers (kilobases or candidate genes), and R is local or genome-wide average recombination frequency (kb/cM or genes/cM).

This equation was based on the assumption that if a crossover occurs in a segment (with length T) on the proximal side of a target allele in a large population of F₂ progeny (N), then there is an equal chance that a recombination event will be carried by a sibling F₂ gamete on the distal side within a distance of <T from the target allele as shown in Figure 1B. Hence, because the probability of only a single recombination event occurring within the mapping population must be calculated, the equation is simplified. However, it is recognized that the distance between the two crossovers will range from zero to 2T; on average, however, the distance will be T, and likely <T when there are more than two informative crossovers and/or when the molecular marker resolution is limiting. However, since the majority of positional cloning studies report more than two informative crossovers (λ) (see Table 2), and since the minimum distance between flanking molecular markers (T-marker) is often limiting, then the probability is high that the distance between the closest two crossovers will be <T-marker.

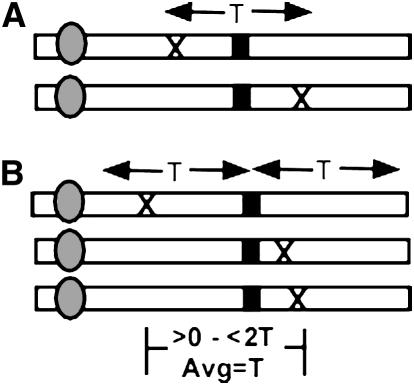
Figure 1.—

An explanation of how the map resolution (T) was calculated for the equations used in this study. (A) The Durrett–Tanksley equation calculates the probability that two sibling post-meiotic (F₂) gametes will carry informative crossovers: a proximal crossover occurring (X) flanking the target allele (solid line) and a second, distal crossover occurring at a distance <T from the first crossover. (B) The simplified, single crossover equation divides the flanking region of the target allele into T segments, and calculates the probability that a crossover will occur in any T segment. Thus, on average, within the F₂ gamete population, the average distance between flanking crossovers will be T (range >0 to <2T).

TABLE 2.

Calculation of local recombination frequencies (R-local) in chromosome intervals containing target loci

	R(Local) as defined by positional cloning studies				Regional R(map) as determined by anchoring locus to the rice RGP 1391-marker mapa
Target allele	Proximal (λ1) crossovers	Distal (λ2) crossovers	R(local)b (kb/cM)	R(local)b (genes/cM)	Chromosome	Physical interval (bp)c	Proximal marker	Distal marker	R(map)d (kb/cM)	R(map)d (genes/cM)
bc1	5	2	66.6	20.2	3	17215334–17217366	C12819	E61171	403.6	46.8
bel	1	2	169.4	27.7	3	31379697–31385021	C0012	S2722	140.2	21.4
Bph15	2	3	1,780.7	416.8	4	6882835–7231621	C0708	R0288	1460.4	125.4
chl1	1	2	227.7	28.6	3	33894227–33900896	E50580	C1484	369.9	53.8
chl9	2	3	14,718.0	1344.2	3	20204631–20202305	E61340	S2992	6028.8	512.0
cpt1	3	10	700.0	49.5	2	21602296–1927256	E3634	E50850	175.3	20.7
d11	5	7	493.3	95.6	4	23252491–23248070	S10702	R0278	272.7	36.3
d2	1	1	1,800.0	300.0	1	5233425–5241321	E60110	C12072	250.7	31.3
dbs	2	5	761.7	132.9	1	18477785–18484690	C0585	E60808A	2944.1	316.7
dgl1	1	3	255.9	28.8	1	28463215–28470187	R1012	C0922	169.3	21.3
eui	1	2	224.0	9.3	5	23645362–23655166	S14889	E30003	127.0	18.7
eui1	1	2	524.6	52.5	5	23645362–23655166	S14889	E30003	127.0	18.7
f5-DU	13	2	93.0	12.0	5	1278649–1379421	R0830	S16113	106.7	11.9
fon1	3	2	725.7	48.4	6	30473475–30469084	R1479	E10139	185.5	26.3
fon4	1	10	1,718.2	316.9	11	22163672–22162134	E4336	C0050	2171.6	236.7
gh2	1e	1e	976.7	97.7	2	4874079–4870146	S1511	S13446	177.5	23.9
gid1	1	1	684.0	72.0	5	19785334–19788132	S2689	C1268	252.2	28.3
gl-3	3	3	145.5	16.6	3	16469400–16556900	E0323	C60318A	128.5	12.5
Gn1a	1	1	819.0	130.0	1	5272324–5267274	E60110	C12072	250.7	31.3
hd1	1	2	120.4	20.1	6	9335377–9337570	C0235	R10069	257.9	22.4
Hd6	4	3	211.7	8.0	3	31453402–31447755	C0012	S2722	140.2	21.4
htd1	1	1	1,380.0	276.0	4	27348729–27351393	C11378	E51196	283.7	40.7
moc1	2	2	201.0	20.1	6	24310311–24315385	S10324	R1559	151.8	18.7
Pi36(t)	2	5	28.2	3.3	8	2762977–2888909	S4144B	C60293	139.4	12.5
Pib	1	3	1,322.0	198.3	2	35112900–35107768	C0379	S10020	98.3	12.9
Pi-d2	1	3	3,600.0	660.0	6	17159337–17163823	C0058	S20510	9503.8	840.0
Pi-kh	6	4	59.7	7.5	11	24761902–24762922	R10829	S5730	198.6	22.3
pla1	1e	1e	427.7	17.3	10	13329113–13327360	C0961	R1738A	135.1	13.7
Psr1	2	1	321.7	25.3	1	14429394–14435943	R2501	C0045	428.0	39.1
qSh1	1	2	42.4	69.2	1	36776800–36772211	R0578	E20351	1145.6	131.3
qUvr10	2	1	333.0	74.0	10	4433064–4429249	E30589B	E1064	291.7	28.2
Rf-1	2	1	1,303.4	68.6	10	18606065–18624126	S11841	S21174	318.5	48.2
S32(t)	4	2	224.0	24.5	2	2109653–2227836	S20351	R10479	201.1	22.6
S5n	1	2	1,066.7	133.3	6	5606631–5758152	R1954	R2349	70.7	10.0
Skc1	1	1	220.0	29.7	1	11460220–11455734	E4175	E10119	190.4	18.9
spl11	2	1	138.3	15.4	12	23439842–23434652	E61976	S5375	95.2	13.3
spl7	1	1	29.4	29.4	5	26261154–26263625	C0466	C11368	222.2	43.6
Xa1	3	2	96.5	27.0	4	31419036–31425732	C52068	S1544	298.3	45.0
xa13	3	2	439.3	59.4	8	26595951–26593109	R3961A	R0639	109.1	16.0
Xa26	2	14	40.1	7.2	11	27688448–27692198	R1506	R3342	383.4	32.5
Xa5	1	1	194.0	47.9	5	323538–325468	C12015	C0568	111.9	13.1

For comparison, the genome-wide average R (avg) = 277 kb/cM or 28.0 genes/cM.

^aRice Genome Project (RGP) RFLP map based on an F₂ population between Nipponbare and Kasalath (http://rgp.dna.affrc.go.jp/) (Harushima et al. 1998).

^bThe local recombination frequency was calculated as follows: R-local = T(local)/m(local), where T(local) is number of kilobases or genes between the closest flanking molecular markers with at least one crossover between each marker and the target locus, and m(local) is genetic distance between these two markers in centimorgans. The value for T(local) is reported in Table 1. The genetic map distance, m(local) = 100 × (λ₁ + λ₂)/N, where λ₁ is number of proximal crossovers (Table 2), λ₂ is number of distal crossovers (Table 2), and N is total number of informative chromosomes genotyped (Table 1). In a testcross, m = 100 × λ/progeny (hence m = 100 × recombinants/progeny), whereas in a selfed cross with progeny testing, m = 100 × (λ/2 × progeny) since genotyping permits both chromosomes to contribute to the mapping population.

^cThis is the precise chromosome physical location of the target locus or candidate region on the rice physical map (Version 4.0 TIGR rice pseudomolecules).

^dR(map) = T(map)/m(map), where T(map) is number of kilobases or genes between the RGP proximal and distal markers containing the target locus as listed in Table 2, and m(map) is genetic map distance between these two RGP markers in centimorgans. These values can be found in supplemental Table 1 at http://www.genetics.org/supplemental/.

^eNumber of recombinants not reported, so set at λ₁ = 1 and λ₂ = 1.

The detailed derivation of this equation is as follows:

1. P(failure) of a crossover in the target interval (T) per gamete = (total genome crossovers − target interval crossovers)/total genome crossovers.

2. Alternatively, P(failure) per gamete = 1 − (fraction of genome × number of crossovers in whole genome).

3. Thus, P(failure) per gamete = 1 − [(kb resolution/kb genome size × (genome map in cM/100)] or P(failure) per gamete = 1 − [(gene block resolution/genome-wide gene number × (genome map in cM/100)].

4. Since P(failure) = (Pfailure per gamete)^N, where N is number of informative gametes, then

   

   and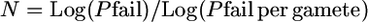

   

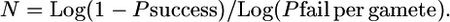
5. Therefore, N = Log (1 − Psuccess)/Log [1 − (gene block/genome gene number × genome map cM/100)] or N = Log (1 − Psuccess)/Log [1 − (kb target/genome kb × genome map cM/100)].

6. Simplified, the above equation can be rewritten as:

   

   or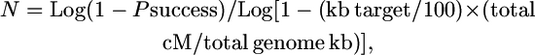

   

   whereR is local or genome-wide recombination frequency.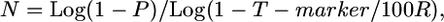

Additional assumptions of this model are as follows:

1. The equation assumes that the phenotype of the trait of interest can be readily scored to determine if a crossover occurred proximal or distal to the target allele; hence N is equivalent to the number of testcross progeny, 0.5 × the number of F₂ (selfed) progeny (if no progeny testing performed), or 2 × the number of F₂ (selfed) progeny (if F₃ progeny testing is performed).

2. The equation assumes that the frequency of double-recombinants in a small interval is negligible due to crossover interference.

3. The equation assumes that the crossover may occur anywhere in the defined interval T such that the distance between each informative crossover and the target locus is <T.

4. The recombination frequency is assumed to be constant in the region <2T.

Modified single crossover equation:

Based on empirical data, we then modified this equation by adjusting the genetic map resolution T by the number of crossovers (see results), resulting in the equation:

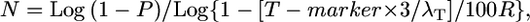where N is total number of informative chromosomes that must be genotyped with the probability of success, P = 0.95, R is the local recombination frequency (R-local) (kb/cM or genes/cM), T-marker is distance (kb or candidate gene block) between the closest two molecular markers (in which crossovers are detected relative to the target allele), and λ_T is number of crossovers between the closest two molecular markers (≥2).

Analysis of published positional cloning studies:

We analyzed 41 published positional cloning/fine-mapping studies in rice to extract or calculate the three variables, N, T, and R (Table 1). The candidate gene resolution (T) [in kb or gene number, T(kb) or T(gene)] was either reported in each study or obtained by personal communication with the authors. In the latter case, these were confirmed by corroborating the kilobase resolution with the gene resolution using the TIGR Pseudomolecules Release 4.0 database (Yuan et al. 2005); retroelements, transposons, and transposases were excluded for gene resolution. The calculation of N gametes genotyped was more complex; it required us to distinguish the actual number of progeny genotyped (g) from the number of informative chromosomes (N), defined as chromosomes that had the potential of having a crossover between the target allele and a flanking molecular marker, and where the location of that crossover (proximal or distal to the target) was distinguished (e.g., using progeny testing). To convert g to N, we multiplied g by a meiosis factor (f) as shown in Table 1 (also see footnotes to Table 1). This required us to classify the mapping strategy used and note whether the target trait was dominant, recessive, or was expressed in the haploid generation (gamete or gametophyte). For example, for the cloning of the recessive bc1 allele (Y. Li et al. 2003), since only F₂ recessive progeny were genotyped (7068 recessives genotyped out of 30,000 F₂ progeny) and hence the genotype of the target allele was non-ambiguous, the total number of informative chromosomes genotyped was 2 × 7068 (i.e., f = 2, hence N = 2 × g). In contrast, for the fine mapping of the dominant Psr1 allele (Nishimura et al. 2005), since 3800 (Backcross 3, BC3) F₁ progeny were genotyped, and thus only 50% of the target chromosomes underwent informative meioses, then f = 0.5, and N = 1900 informative chromosomes. For rice, it was assumed that males and females had equal rates of recombination, but in many species, such as zebrafish, this is not true (Singer et al. 2002; Lenormand and Dutheil 2005) and must be accounted for in the meiosis factor. Finally, to calculate the local recombination frequency (R-local) (Table 2), we used the following equation:

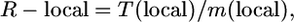where R is local recombination frequency (kilobases/cM), T(kb) is distance in kilobases between the closest two crossovers, m is genetic map distance between the two crossovers in centimorgans, and m = 100 × (λ₁ + λ₂)/N, where λ₁ is number of closest, proximal crossovers (Table 2), λ₂ is number of closest, distal crossovers (Table 2), and N is total number of informative gametes (chromosomes) genotyped (Table 1). In a testcross, m = 100 × λ/progeny, whereas in a selfed cross with progeny testing, m = 100 × (λ/2 × progeny) since genotyping permits both chromosomes to contribute to the mapping population.

TABLE 1.

Analysis of published positional cloning and fine-mapping studies in rice (Oryza sativa)

Target allele	TIGR annotation	Inheritance		Mapping strategya	Total progeny	Progeny genotyped (g)	Meiosis factor (f)b	Informative gametes (N)c genotyped	Candidate resolution (T)d
									Type	Trait						kb	Genese	Reference
bc1	LOC_Os03g30250	Simple	Rec	F2-Rec	∼30,000	7,068	2	14,136	3.3	1	Y. Li et al. (2003)
bel	LOC_Os03g55240	Simple	Rec	F2-Rec	987	231	2	462	110	18	Pan et al. (2006)
Bph15f	BAC20M14/BAC64O9	Simple	Dom	RIL F2-All + PT	9,472	9,472	2	18,944	47	11	Yang et al. (2004)
chl1	LOC_Os03g59640	Simple	Rec	F2-All + PT	∼2,000	477	2	954	71.6	9	H. T. Zhang et al. (2006)
chl9	LOC_Os03g36540	Simple	Rec	F2-All + PT	∼10,000	2,458	2	4,906	1500	137	H. T. Zhang et al. (2006)
cpt1	LOC_Os02g35970	Simple	Rec	F2-Rec	5,000	1,400	2	2,800	325	23	Haga et al. (2005)
d11	LOC_Os04g39430	Simple	Rec	SSL F2-Rec	∼15,000	3,020	2	6,040	98	19	Tanabe et al. (2005)
d2	LOC_Os01g10040	Simple	Rec	SSL F2-All + PT	3,000	3,000	2	6,000	60	10	Hong et al. (2003)
Dbs	LOC_Os01g33040	Simple	Rec	F2-Rec	∼12,400	3,100	2	6,200	86	15	Sazuka et al. (2005)
dgl1	LOC_Os01g49000	Simple	Rec	F2-Rec	∼4,600	1,150	2	2,300	44.5	5	Komorisono et al. (2005)
Eui	LOC_Os05g40384	Simple	Rec	NIL F2-Rec	5,500	1,400	2	2,800	24	1	Zhu et al. (2006)
eui1	LOC_Os05g40384	Simple	Rec	F2-Rec	∼10,000	2,623	2	5,246	30	3	Luo et al. (2006)
f5-DUf	PAC P0008A07	QTL	Gameteg	NIL hybrid testcross	1,993	1,993	1	1,993	70	9	Wang et al. (2006)
fon1	LOC_Os06g50340	Simple	Rec	F2-All	2,419	2,419	1	2,419	150	10	Suzaki et al. (2004)
fon4	LOC_Os11g38270	Simple	Rec	F2-Rec	∼8,400	2,100	2	4,200	450	83	H. W. Chu et al. (2006)
gh2	LOC_Os02g09490	Simple	Rec	F2-Rec	13,000	3,256	2	6,511	30	3	K. W. Zhang et al. (2006)
gid1	LOC_Os05g33730	Simple	Rec	F2-Rec	∼7,200	1,800	1	3,600	38	4	Ueguchi-Tanaka et al. (2005)
gl-3f	BAC OSJN3b0074M06	QTL	Rec	SSL BC4F2 Rec	2,068	499	2	998	87.5	10	Wan et al. (2006)
Gn1a	LOC_Os01g10110	QTL	Additive	NIL BCF2-All + PT	∼13,000	13,000	2	26,000	6.3	1	Ashikari et al. (2005)
Hd1	LOC_Os06g16370	QTL	Dom	BC3 F3-Rec	9,000	1,505	2	3,010	12	2	Yano et al. (2000)
Hd6	LOC_Os03g55389	QTL	Dom	NIL BC3F2 PT	2,807	2,807	2	5,614	26.4	1	Takahashi et al. (2001)
Htd1	LOC_Os04g46470	Simple	Rec	F2-Rec	20,000	4,600	2	9,200	30	6	Zou et al. (2005, 2006)
Moc1	LOC_Os06g40780	Simple	Rec	F2-Rec	2,010	2,010	2	4,020	20	2	X. Li et al. (2003)
Pi36(t)f	PAC P0443G08	Simple	Dom	F2-Rec	4,884	580	2	1,160	17	2	Liu et al. (2005)
Pib	LOC_Os02g57310	Simple	Dom	BC2F3/F4-Rec + PT	∼13,000	3,305	2	6,610	80	12	Wang et al. (1999)
Pi-d2	LOC_Os06g29810	Simple	Dom	F2-Rec	20,000	4,000	2	8,000	180	33	Chen et al. (2006)
Pi-kh	LOC_Os11g42010	Simple	Dom	F2-All + PT	208	208	2	416	143.5	18	Sharma et al. (2005)
pla1	LOC_Os10g26340	Simple	Rec	F2-Rec	2,312	578	2	1,156	74	3	Miyoshi et al. (2004)
Psr1	LOC_Os01g25484	QTL	Dom	NIL BC3F2	3,800	3,800	0.5	1,900	50.8	4	Nishimura et al. (2005)
qSh1	LOC_Os01g62920	QTL	Dom	SSL BC4F2 + PT	10,388	10,388	2	20,766	0.612	1	Konishi et al. (2006)
qUvr10	LOC_Os10g08580	QTL	Additive	NIL F2-All + PT	1,850	1,850	2	3,700	27	6	Ueda et al. (2005)
Rf-1	LOC_Os10g35436	Simple	Gameteg	NIL CMS testcross	5,145	5,145	1	5,145	76	4	Komori et al. (2004)
S32(t)f	PAC AP005294	QTL	Gameteg	Het BC4F2 gametes	1,050	1,050	2	2,100	64	7	Li et al. (2007)
S5nf	PAC P0021C04	QTL	Gameteg	NIL hybrid outcross	8,000	8,000	1	8,000	40	5	Qiu et al. (2005)
Skc1	LOC_Os1g20160	QTL	Dom	BC3F2-All + PT	2,973	2,973	2	5,946	7.4	1	Ren et al. (2005)
spl11	LOC_Os12g38210	Simple	Rec	F2-Rec; F3-All	∼3,000	2,143	2/0.5h	1,537	27	3	Zeng et al. (2004)
spl7	LOC_Os05g45410	Simple	Rec	SSL F2-All + PT	2,944	2,944	2	5,888	1	1	Yamanouchi et al. (2002)
Xa1	LOC_Os04g53120	Simple	Dom	F3-Rec	4,225	965	2	1,930	25	7	Yoshimura et al. (1998)
xa13	LOC_Os08g42350	Simple	Rec	F2-All + PT	∼8,000	7,972	2	14,842	14.8	2	Z. H. Chu et al. (2006)
Xa26	LOC_Os11g47000	Simple	Dom	F2/NIL-Rec	∼1,908	477	2	954	67.2	12	Yang et al. (2003); Sun et al. (2004)
xa5	LOC_Os05g01580	Simple	Rec	F2-All + PT	2,345	2,345	2	4,790	8.1	2	Iyer and McCouch (2004)
Median					∼4,884	2,419		4,200	44.5	5

QTL, quantitative trait locus; Rec, recessive; Dom, dominant; Gamete, gametophytic; RIL, recombinant inbred line; PT, progeny tested; SSL, chromosome/segment substitution line; het, heterozygous.

^aTo distinguish whether a crossover occurred between the target allele and the proximal vs. distal molecular marker, the post-meiotic genotype of the target locus (AA, Aa, aa) must be discernible, as this determines the number of effective meioses that contributes to the final mapping of the target locus. For example, for a recessive trait, in the F₂ generation, whereas a crossover can be detected by genotyping flanking molecular markers, because AA vs. Aa alleles cannot be distinguished, the proximal vs. distal location of the crossover cannot be assigned without phenotyping segregants (PT, progeny testing) in the F₃ generation; without progeny testing, only ∼1/4 (aa class) of recombinant progeny contribute to the final map assignment of the allele. The following genotyping and phenotyping strategies were employed: F₂-Rec, only F₂ recessive progeny genotyped; F₂-All, all F₂ progeny genotyped randomly; F₂-All + PT, all F₂ progeny genotyped, then F₃ progeny phenotyped to distinguish AA from Aa alleles at the target locus in the F₂ generation; RIL/NIL/SSL/BC, used backcrossing and/or recombinant inbred lines, near-isogenic lines, and/or segment substitution lines to distinguish the target QTL phenotype or to introgress the target allele into an appropriate chromosome background suitable for mapping; F₁ or F₂ gametes, since the target gene product is expressed in the haploid gametophyte (pollen or embryo sac), used the ratio of gametophyte phenotypes (e.g., pollen germination) of the spikelet, in combination with genotyping the plants carrying the spikelets, to distinguish AA/Aa/aa genotypes of the target allele.

^bThe meiosis factor (f) is multiplied by the number of post-meiotic progeny genotyped to give the number of meioses that contributed to the final mapping resolution of the target allele. For example, if the F₂ population was derived from selfing F₁ parents, then each F₂ plant represents two meioses (f = 2) when the precise F₂ genotype was discerned by progeny testing (phenotyping segregants in the F₃ generation). Without progeny testing, then only 1/4 recessive (aa) F₂ progeny were considered to be useful, but since two meioses contributed to this class, f = (1/4) × 2 = 0.5.

^cNumber of chromosomes or effective post-meiotic products that were genotyped (N), where N = g × f.

^dThe final map resolution (T) is defined as the number of kilobases or genes in the interval between the most proximal and distal molecular marker flanking the target allele, in which at least one crossover was found. When this value was not published, it was estimated using the Version 4 TIGR rice pseudomolecules genome browser, and when possible confirmed by personal communication with the study authors.

^eOnly non-transposon, non-retroelement gene models are included as defined by the Version 4 TIGR rice pseudomolecules annotation database.

^fGene not yet isolated.

^gThe allele acts in the haploid gamete-derived generation, either pollen or embryo sac. See results for details.

^hTwo progeny populations, with two genotyping strategies, were used.

The only crossovers (λ_T) in the calculation were those that were in between the two molecular markers used to define T. For each of the 41 studies, we applied the values for R(local), T(kb) and set P at 0.95, to the Durrett–Tanksley equation and compared the number of informative gametes (N) required by this equation to the empirical numbers shown in Table 1. We performed both nonparametric correlation analysis (Spearman coefficient) and linear regression analysis using the software program Instat 3 (GraphPad Software).

Generation of a reference meiotic recombination frequency map (MRFM) for rice:

To determine whether recombination frequencies derived from a reference genetic map could be used to predict progeny sampling requirements using the Durrett–Tanksley equation, we first assembled such a map, inspired by a previous report (Wu et al. 2003), to generate two types of recombination values: R(gene), in genes/cM; and R(kb), in kilobases/cM (see supplemental Table 1 at http://www.genetics.org/supplemental/). The names and GenBank accession numbers of RFLP markers genetically mapped in an F₂ population between Nipponbare and Kasalath were obtained from the Rice Genome Project (RGP: http://rgp.dna.affrc.go.jp/) (Harushima et al. 1998). FASTA sequence files for the markers were obtained from NCBI. The RFLP marker sequences from the RGP map were physically mapped onto the version 4 TIGR rice pseudomolecules map (http://www.rice.tigr.org) using the Genomic Mapping and Alignment Program (GMAP) (Wu and Watanabe 2005). The physical map position of each marker was derived from the top hit that exceeded a threshold of 95% identity over 90% of the length. After physically positioning the RFLP markers onto the pseudomolecules, Perl scripts and manual inspection were used to remove all markers showing map incongruency (where the physical and genetic position of the markers were at odds). We obtained 1391 congruent markers for the RGP map. This established both physical and genetic locations and hence interval distances for each RFLP marker; from these values, the kb/cM recombination frequency was calculated for each marker pair. To generate the corresponding genes/cM frequencies, we queried the Osa1 database at TIGR: the coordinates of all 42,535 non-transposable element-related transcription units were obtained (Yuan et al. 2005). Custom Perl scripts were written to bin these transcription units between each RFLP marker pair. This established the number of non-transposable element candidate genes for each interval along with the genetic locations of these markers, and hence the following parameters were calculated for each RFLP marker pair: the genetic distance between each marker and the corresponding genes/cM recombination rate.

Testing the predictive value of the Modified Durrett–Tanksley equation using R-map recombination frequencies:

Next we assigned each target allele to a physical location on the RGP physical map, which contains 1400 marker intervals. To accomplish this, each target allele was assigned a TIGR locus number (if cloned) onto a BAC/PAC clone (if not cloned; TIGR Pseudomolecules Release 4.0); sometimes this information was published. In remaining examples, the GenBank gene sequence or molecular marker information was used to screen the TIGR rice sequence database; the genetic map position, marker data, and BAC/PAC assignment helped to verify the physical assignment. The locus or BAC/PAC name and sequence was then used to assign each allele to an interval between two mapped markers on the RGP MRFM of rice (Table 2; supplemental Table 1 at http://www.genetics.org/supplemental/). The recombination frequency of the corresponding marker interval (R-map) was then employed; because we feared that chance crossovers might distort the recombination frequency in small intervals (<277 kb, 1-cM average) on this map, adjacent segments were sometimes added together (to achieve a >280-kb interval) before calculating an average R-map value with the goal of situating the target allele at the physical center of the larger interval. In rare situations, an R-map value for an interval of <280 kb was accepted because adjacent intervals were unusually large. The choice to add or not add marker intervals was done blindly from the R-local values in order to not bias R-map values. The R-map values were then applied to each equation.

Calculation of R-avg values:

The genome-wide average recombination frequency in kilobases/cM was calculated by dividing the total genome size (∼430 Mb) (IRGSP 2005) by the total genetic map length (∼1521 cM) (Harushima et al. 1998); the average recombination frequency in genes/cM was calculated by dividing the total number of non-transposable element-encoded transcription units (∼42,535) (Yuan et al. 2005) by the map length. The resulting genome-wide recombination frequency (R-avg) in rice is 277 kb/cM and 28 genes/cM.

RESULTS

Initial equations to predict mapping population size:

Initially, we employed two equations to predict the size of the fine-mapping population, one of which is developed here. First, we used the Durrett–Tanksley equation (Durrett et al. 2002), which estimates the number of F₂/post-F₂ meiotic gametes required to positionally clone an allele as generated from an F₁ heterozygote; it calculates the probability (P) that if a (proximal) crossover occurs in the vicinity of a target allele that a second (distal) crossover will be carried by a sibling gamete, such that the distance between the two crossovers will be the kilobase distance T (Figure 1A), for a prescribed number of genotyped gametes (N) (informative chromosomes) and for a given recombination frequency (R), according to the following equation:

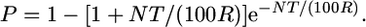The primary assumption of the equation is that the progeny number will vary with the recombination frequency: the higher the frequency of recombination, the fewer progeny will be required to detect a crossover between the target allele and flanking molecular markers. See materials and methods for additional details.

We then derived a second equation with the goal of making it more user-friendly for researchers. This equation was based on the following premise: if a crossover occurs in a segment (with length T) on the proximal side of a target allele in a large population of F₂ progeny (N), then there is an equal probability that a sibling gamete will carry a crossover on the distal side within a distance of <T from the target allele as shown in Figure 1B. This simplifies the equation by only having to calculate the probability of a single crossover within the population, noting, however, that although on average any two crossovers will be distance T apart, they may range from zero to 2T (see materials and methods for further details). The number of F₂ testcross progeny required to be genotyped to detect sufficient crossovers to achieve a desired kilobase or gene block resolution is thus as follows:

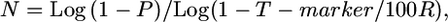where N is the number of meiotic gametes (chromosomes) that must be genotyped in which it can be determined whether a crossover is located proximal or distal to the target allele, P is threshold probability of success (e.g., 0.95), T-marker is expected distance between flanking molecular markers (kilobases or candidate genes), and R is local or genome-wide average recombination frequency (kb/cM or genes/cM).

Similar to the Durrett–Tanksley equation, this model assumes that the phenotype of the trait of interest can be readily scored to determine if a crossover occurred proximal or distal to the target allele; hence N is equivalent to the number of testcross progeny, 0.5 times the number of F₂ (selfed) progeny (if no progeny testing performed), or two times the number of F₂ (selfed) progeny (if F₃ progeny testing is performed). The derivation of this equation is in the materials and methods section.

Empirical gamete number, mapping resolution, and lessons from published studies in rice:

To validate the equations noted above, we first analyzed 41 published positional cloning/fine-mapping studies in rice, to extract or calculate N and T (Table 1) (see materials and methods). We made several observations that might be useful to future research groups who wish to undertake positional cloning in rice. First, as in other species, in rice there was a wide range in the number of informative gametes (N) (potential recombinant chromosomes) that were genotyped to positionally clone target alleles: this ranged from only 416 gametes for the Pi-kh allele (Sharma et al. 2005) to ∼20,000 gametes for the alleles Gn1a (Ashikari et al. 2005), qSH1 (Konishi et al. 2006), and Bph15 (Yang et al. 2004), an ∼25-fold range. The average number of informative gametes genotyped was 5686; the median was 4200. The median target resolution (T) achieved was 44.5 kb or five genes. There were seven examples of single-gene resolution mapping (Table 1), and to achieve this resolution, the number of informative gametes employed ranged from 2800 to 26,000 (∼10-fold range); the average was 11,593 gametes. Single gene resolution mapping in a smaller genome, A. thaliana, has been much rarer (Dinka and Raizada 2006).

Several fine-mapping strategies were used successfully:

1. Of 41 studies, 11 groups reported isolation of a quantitative trait locus (QTL); to reduce the effects of minor QTL and/or to be able to employ a background with well-characterized molecular markers, the target QTL was isolated by limited backcrossing (BC) or full introgression (near isogenic line, NIL) into a new genetic background. In other examples (e.g., qSH1) (Konishi et al. 2006), the original QTL genome was used for mapping such that all but the target QTL was fixed (not segregating); to create heterozygosity in the region containing the target allele for mapping, a corresponding chromosome segment from a polymorphic genotype was crossed in [segment substitution line (SSL)] (Table 1).

2. Because outcrosses/testcrosses are challenging in rice, most studies involved selfing progeny, which has the potential of carrying informative crossover events on both diploid chromosomes, thus potentially doubling the effective number of informative gametes (N). One of the challenges created by selfing, however, for recessive alleles, is that it is not possible to determine whether a crossover occurred proximal or distal to the target without checking for the segregation pattern (progeny testing, PT) in the subsequent generation (e.g., F₃) to distinguish all genotype combinations (aa, Aa, AA) at the target locus. Six groups progeny-tested to check the recessive genotype (e.g., chl1) (H. T. Zhang et al. 2006). Alternatively, to avoid F₃ generation phenotyping, 15 groups (e.g., bc1) (Y. Li et al. 2003) preselected recessive (mutant) progeny by phenotyping and then only genotyped this subset, thus discarding 75% of all progeny.

3. There were 12 fully dominant alleles targeted; in these cases, as in recessive alleles, because the proximal vs. distal location of flanking crossovers could not be distinguished without distinguishing AA from Aa genotypes, researchers either progeny-tested in the subsequent generation (e.g., Pi-kh) (Sharma et al. 2005) or, cleverly, preselected only the recessive progeny class for genotyping (e.g., Xa1) (Yoshimura et al. 1998).

4. Finally, there were four examples [f5-DU, Rf-1, S32(t), S5ⁿ] where the target alleles were expressed in the haploid generation (e.g., pollen grain, embryo sac) and where the nature of the gene products often required generating outcross/testcross progeny for mapping. In the case of f5-DU (Wang et al. 2006), an allele that boosts pollen viability in specific hybrid genotypes, testcross progeny were used for mapping, since phenotyping required a hybrid background to check for segregation of viable pollen grains (either high or low). Similarly, to fine map the S5ⁿ locus (Qiu et al. 2005), which confers embryo sac viability to wide-cross hybrids, 8000 hybrids were generated by outcrossing a heterozygous NIL S5ⁿ/− parent (NIL F₁) to a wide-cross tester; phenotyping was performed by measuring segregation of fertility of F₂ embryo sacs on hybrid rice spikelets. In the case of S32(t) (Li et al. 2007), which also confers (post-meiotic, haploid) embryo sac viability, the segregation of embryo sac viability was measured in the spikelets of selfed F₂ plants. Finally, in the case of Rf-1, a nuclear locus that restores male gamete (pollen) fertility by overcoming the effects of a mitochondrial [cytoplasmic male sterility (CMS)] gene, 5145 testcross F₂ progeny (three-way cross: heterozygote restorer × non-restorer tester) were generated for mapping and the segregation of pollen viability scored (Komori et al. 2003, 2004).

Lessons from calculating empirical local recombination frequencies (R-local) and their use in validating predictive equations:

To both validate the equations noted in this study and later understand any discrepancies between the experimental data and predictions based on the molecular marker map, we then calculated the experimental (local) recombination frequency (R-local) for each of the 41 successful fine-mapping studies in rice (see materials and methods) (Table 2). From each study, we counted the number of crossovers located between the closest two markers used to define the final map resolution (T); these are the first recombinants used to define the edges of the candidate target region. Although we expected to find only 1 crossover on each distal or proximal flank (2 total), in 32 of 41 examples we found between 3 and 16 total crossovers, due to hotspots of recombination and/or poor marker density; such redundant crossover targets suggested that an excess number of progeny were genotyped given the available marker density in the majority of rice positional cloning attempts, an important observation.

Since a high density of molecular markers and large progeny numbers are used in positional cloning, the R-local values provide an interesting snapshot into the variation in recombination frequency in the rice genome: we found that though the genome-wide average R was 277 kb/cM or 28.0 genes/cM in rice, locally, R-values ranged from 3.3 to 1344.2 genes/cM or 28.2 to 14,718 kb/M, an ∼400-fold and ∼500-fold range, respectively. Strongly influenced by chance, such a wide range in recombination frequencies would largely explain the wide range in the number of progeny that were genotyped in rice (Table 1). The most hyper-recombinogenic region (3.3 genes/cM, 28.2 kb/cM) flanked the Pi36(t) allele (Liu et al. 2005), which required only 1160 informative gametes to achieve a map resolution of 17 kb or two candidate genes. The region with the least amount of recombination (1344.2 genes/cM or 14,718 kb/cM) encompassed the chl9 allele; in this study, although 4906 informative chromosomes were genotyped, the map resolution was 1500 kb or 137 genes (H. T. Zhang et al. 2006). These two groups define the extremes of good and bad “luck,” respectively, in rice, and as such may set upper and lower map-population-size boundaries for future positional cloning attempts in this important species.

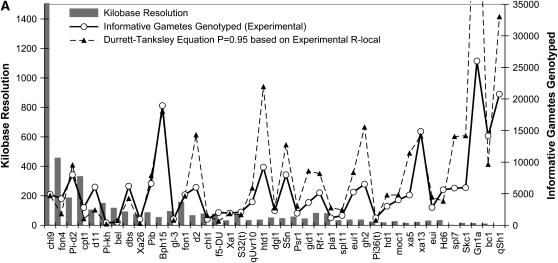
We then compared the empirical number of gametes that were genotyped (N) in each study to the number predicted by both equations (see above) given only the variables T and R-local; this allowed us to first test the validity of the equations in rice and to modify the equations if necessary. The size of the mapping population (informative chromosomes) (N) predicted by the Durrett–Tanksley equation compared to the empirical data, for given T and R-local values (in kb/cM), is shown in Figure 2A; we found a strong positive correlation between the mapping size predicted by the Durrett–Tanksley equation and the experimental results (Spearman r = 0.85, P < 0.0001, n = 41). In at least 10 examples (10/41), however, in spite of using the actual recombination frequencies, we found that the Durrett–Tanksley equation overestimated the mapping population by at least twofold, which would have caused researchers to unnecessarily genotype thousands of extra progeny. The simpler, Single Crossover model appeared to be a slightly better predictor of the progeny mapping population size as shown in Figure 2B. Although this second equation predicted the mapping population N with a near-equivalent correlation as the Durrett–Tanksley equation (Spearman r = 0.86; P < 0.0001; n = 41), linear regression analysis of the two models (Figure 3, A and B) demonstrated that the single crossover equation came closer to a linear slope of m = 1 on an x–y scatter plot of predicted vs. experimental N values; in the case of the Durrett–Tanksley model, the best-fit line followed the equation y = 1.70x − 1323 (goodness of fit r² = 0.76, Sy.x = 5456), whereas for the single crossover equation, the best-fit line was y = 1.07x − 833 (r² = 0.76, Sy.x = 3426). Although one equation was slightly better than the other, these results demonstrate for the first time that (both) simple formulas, if based on accurate local recombination frequency values, can provide significant guidance in predicting the mapping population size in the majority of alleles targeted for positional cloning.

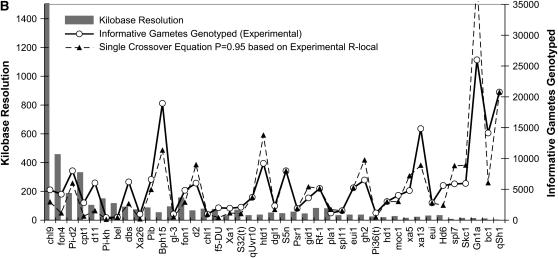
Figure 2.—

Testing the validity of two mathematical equations as predictors of the size of the progeny mapping population (N) required to positionally clone target alleles using rice as a model system. We compared N values predicted by the Durrett–Tanksley equation (A) and the Single Crossover model equation (B) to 41 published, empirical studies (shown in Table 1). In both graphs, the target alleles are shown on the x-axis; solid histograms denote the kilobase map resolution achieved, and the solid graphed line is the number of informative post-meiotic gametes (N) genotyped, as calculated in Table 1; the spotted line is the number of informative gametes predicted. When the probability of success is set at 95%, then the Durrett–Tanksley equation is simplified such that N = (4.744 × 100R)/T, where R is relevant meiotic recombination frequency and T is final map resolution achieved, notably the distance between the closest distal and proximal molecular markers that are subject to at least one crossover between the marker and the target trait in the progeny population. The single crossover model predicts that N = Log (1 − P)/Log (1 − T/100R). For both equations, we employed the published, empirical local recombination frequency (R-local) as shown in Table 2, and hence these graphs represent the upper limit of prediction possible by the equations. For the graphs above, we set the probability of success at 95% (P = 0.95).

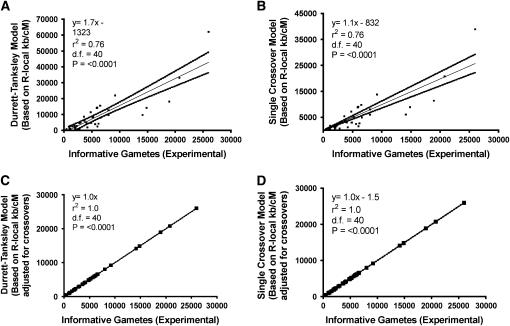
Figure 3.—

Linear regression analysis to validate and determine which mathematical models predict mapping population size during positional cloning attempts in rice. In each case, the y-axis is the number of gametes predicted by each model, and the x-axis is the published, empirical number of informative gametes genotyped. (A) Linear regression analysis of the Durrett–Tanksley equation, based on the calculation P = 1 − [1 + NT/(100R)] e^−NT/(100R), where P is threshold probability of success, N is the number of meiotic gametes (chromosomes) that must be genotyped in which it can be determined whether a crossover is located proximal or distal to the target allele, T is expected distance between flanking molecular markers (kilobases or candidate genes), and R is local recombination frequency (kb/cM or genes/cM). The equation was simplified by setting the probability of success at P = 0.95, resulting in N = (4.744 × 100R)/T. (B) Linear regression analysis of the Single Crossover equation, where N = Log (1 − P)/Log (1 − T-marker/100R). (C) Linear regression analysis of the modified Durrett–Tanksley equation, calculated as N = (100R × λ_T)/T-marker, where λ_T is number of crossovers between the closest two molecular markers (≥2). (D) Linear regression analysis of the modified Single Crossover equation, calculated as N = Log (1 − P)/Log {1 − [T-marker(3/λ_T)]/100R}. For each model, experimentally-derived R-local values were used from Table 2, and hence these graphs represent the upper accuracy limit of the equations as typically such high resolution frequencies are not available before a positional cloning experiment. The results demonstrate that the Single Crossover model is moderately better predictive of the mapping population size compared to the Durrett–Tanksley equation, but both models become accurate when the equations are adjusted for the number of gametes carrying crossovers immediately flanking the target locus.

Fine-tuning of the equations based on empirical studies:

We then wondered if we could fine-tune both predictive models. We noticed that the Durrett–Tanksley equation overestimated the number of progeny needed when the experimental number of crossovers found in distance T was low (<5 total); when the number of crossovers found was high (>5), this equation underestimated the number of progeny required (Figure 2A; Table 2). In the latter cases, it appeared as if T was limited by the local density of molecular markers; given this low density, the published studies appear to have “over-genotyped” the progeny population. Restated, when many crossovers were found within the interval T (final map resolution), then the actual candidate distance (in kilobases) might have been smaller (higher map resolution) had more molecular markers been available in the vicinity. By plotting the ratio N^model/N^empirical relative to the number of crossovers (λ_T) (where λ = λ₁ + λ₂) (Table 2) on a scatter plot, we found that there was an inverse Power relationship between the two variables such that N^model/N^empirical = 4.744/λ_T. Therefore, we adjusted T by multiplying it by 4.744/λ_T, where λ_T is the total number of crossovers in this region. Accordingly, we also redefined T as T-marker to note that marker density often rate-limits the physical resolution. The resulting modified Durrett–Tanksley equation is

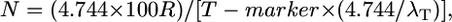or simplified,

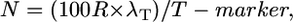where N is total number of informative chromosomes that must be genotyped with the probability of success set at P = 0.95, R is the local recombination frequency (R-local), T-marker is distance between the closest two molecular markers (in which crossovers are detected relative to the target allele), and λ_T is number of crossovers between the closest two molecular markers (≥2). This is a rewritten version of the standard map distance calculation: m = 100 × recombinants/progeny for a testcross, assuming no double crossovers (Haldane 1919).

We then compared the predictions of the modified Durrett–Tanksley equation, using R-local values (Table 2), to the published mapping size population values (N); as shown in Figure 3C, the modified equation was 100% predictive (y = 1.0x, r² = 1.0, F = 0). Using a similar approach, we also modified the Single Crossover equation. By plotting the ratio N^model/N^empirical relative to the number of crossovers (λ_T) (where λ_T = λ₁ + λ₂) (Table 2) on a scatter plot, we found that there was an inverse Power relationship between the two variables such that N^model/N^empirical ∼ 3/λ_T. Therefore, we modified the genetic map resolution T by the number of crossovers, resulting in the following modified Single Crossover equation:

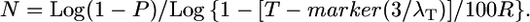As shown in Figure 3D, again the modified equation was close to 100% predictive of the empirical results (y = 1.0x − 1.5, r² = 1.0).

These modified equations offer some advantages for researchers: these equations define probability explicitly as the number of crossovers (informative gametes) that a researchers can expect to achieve for a given progeny population. A researcher is taking more of a risk if the goal is to achieve only two informative gametes, each carrying a crossover on either side of the target allele (λ_T = 2), compared to if the target is five informative gametes. These equations also make it explicit that the density of available molecular markers in the target region is critical: if there are few available molecular markers, a researcher does not achieve better resolution by increasing the number of progeny genotyped (N) beyond a certain threshold. We suggest that users of this equation who wish to predict N should select T based on a realistic density of achievable molecular markers in the vicinity of the target allele, and adjust λ_T according to their own risk assessment. For example, if obtaining only two informative recombinant gametes is too risky, N should be increased.

Predictive value of the equations using recombination frequencies derived from a MRFM:

In the analysis above, we validated both Durrett–Tanksley equations and the Single Crossover equations using published high-resolution, local recombination frequencies (R-local) derived from already fine-mapped alleles. Our goal was to predict the progeny mapping population (N informative gametes) in advance, however, whereas R-local data is not available until the conclusion of a positional cloning attempt. Previous a priori mapping population estimates only used the genome-wide average recombination frequency (R-avg) (Durrett et al. 2002), but as we have confirmed (Table 2) and as many others have noted (Wu et al. 2003; Crawford et al. 2004; McVean et al. 2004), recombination frequencies vary tremendously along any chromosome. Therefore, we wondered if we could more accurately predict N in advance by employing regional meiotic recombination frequencies from a high-density molecular marker map (R-map). To accomplish this, we first developed a MRFM for 1400 marker intervals in rice, based on the Rice Genome Project (RGP) F₂ [Nipponbare (Japonica) × Kasalath (Indica)] RFLP map (Harushima et al. 1998). Mean R-map values were 33.5 genes/cM and 294 kb/cM, similar to calculations of the whole-genome average recombination frequency (R-avg) for rice (28 genes/cM and 277 kb/cM). The entire R-map data set is located in supplemental Table 1 (http://www.genetics.org/supplemental/) and it should serve as a useful reference for future positional cloning studies in rice.

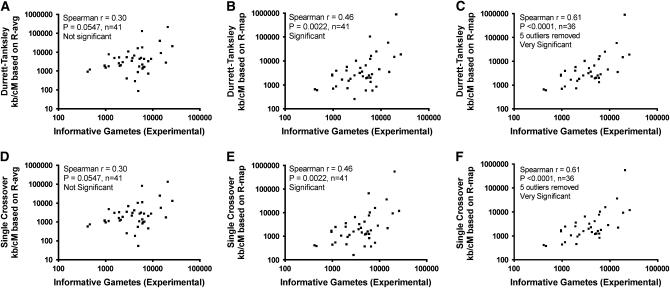
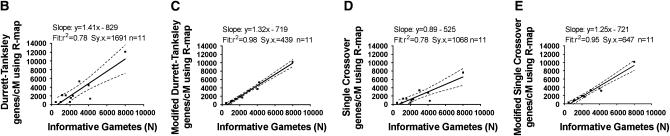
Next, in silico, we mapped each cloned allele onto a physical and genetic interval on this map as shown in Table 2 (see materials and methods). We then used the corresponding “neighborhood” recombination frequencies (R-map) to calculate mapping population sizes (N). As shown in Figure 4, we found that there was a modest but significant improvement in predicting the number of informative gametes (N) required to be genotyped when recombination frequencies (calculated as kilobases/cM) were based on rice RGP R-map values; as we suspected, we found that there was not a significant correlation between the empirical mapping size (N) vs. mapping sizes predicted by either of the two (unmodified) equations when the R-avg value was used (Spearman r = 0.30, P = 0.0547, n = 41) (Figure 4, A and D). In contrast, the correlation was significant when R-map values were used (Spearman r = 0.46, P = 0.0022, n = 41) (Figure 4, B and E) and this correlation increased even further when several outliers were removed (Spearman r = 0.61, P < 0.0001, n = 36) (Figure 4, C and F). Surprisingly, however, the correlation did not improve even further when the modified equations were used that took into account the number of immediate crossovers (λ_T) (for R-map, Spearman r = 0.35, P = 0.0232, considered significant); however, the correlation was still a significant improvement over when the R-avg value was used in conjunction with the modified equations (Spearman r = 0.21, P = 0.19, n = 41, not significant; data not shown). We conclude that mapping size predictions based on neighborhood (>280-kb segments) recombination frequencies (in kilobases/cM) better predict the number of progeny required to be genotyped to positionally clone a gene than predictions based on using the genome-wide average recombination frequency.

Figure 4.—

Modest improvement in predicting the size of the progeny mapping population (informative gametes) required to be genotyped during positional cloning when using neighborhood recombination frequencies extracted from a reference genetic map (R-map) compared to the whole genome average (R-avg) using R-values based on kilobase/cM calculations. On the x-axis is the mapping population size from published positional cloning studies in rice (see Table 1). On the y-axis is the prediction. (A–C) Models based on the Durrett–Tanksley equation (unmodified). (D–F) Models based on the Single Crossover equation (unmodified). R-map values were calculated from the 1400-marker Rice Genome Project (RGP) RFLP map (F₂ of Nipponbare × Kasalath cross) (see materials and methods). In C and F, five outliers were removed in comparison to B and E, respectively. Both equations set the probability of success at 95%.

The effect of using R-map recombination frequencies calculated as kb/cM vs. genes/cM:

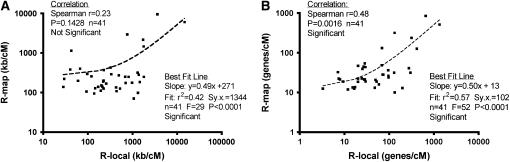
Although use of R-map values better predicted the size of the progeny mapping population compared to the genome-wide average recombination frequency, we were disappointed that the improvement was not more significant. In order to understand the reason, we asked to what extent R-map values calculated as kilobases/cM (from the rice RGP 1400-marker map) in fact correlated with the R-local values that we extracted from the 41 published studies. As shown in Figure 5A, the correlation was in fact poor (Spearman r = 0.23, P = 0.1428, considered not significant); of course, there was no correlation when R-local was compared to R-avg, so the R-map (kb/cM) values were still useful.

Figure 5.—

Meiotic recombination frequencies (R-map) extracted from the Rice Genome Project (RGP) RFLP map better correlate with local frequencies (R-local) from published positional cloning studies when calculated as genes/cM rather than kilobases/cM. (A) Linear regression analysis of R-map vs. R-local values using kilobase/cM ratios. (B) Linear regression analysis using genes/cM ratios. The correlation between R-map vs. R-local will have to be calculated empirically for each map and each species to determine if the methodology described in this study can be employed.

However, we then asked whether the correlation improved when R-map was calculated as genes/cM instead of kb/cM. Limited evidence (Fu et al. 2001) suggested that the crossovers contributing to R-map values might primarily be occurring in and around genes. In fact, as shown in Figure 5B, we found a significantly improved correlation between R-map values calculated as genes/cM to R-local values also calculated as genes/cM (Spearman r = 0.48, P = 0.0016).

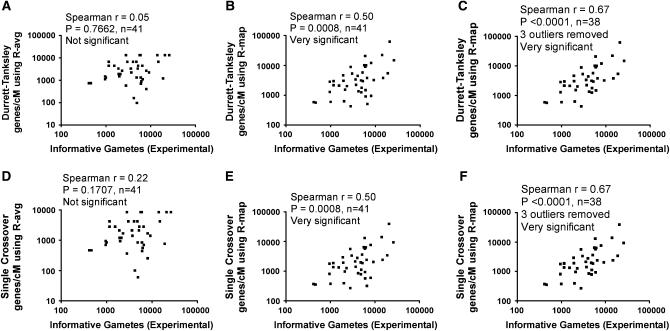
Therefore, we retested whether we could better predict progeny mapping population sizes (N) when using rice RGP R-map values calculated as genes/cM rather than kilobases/cM. Using R-map (genes/cM) calculations shown in Table 2, Figure 6 demonstrates that indeed the map population (N) predicted by both the (unmodified) Durrett–Tanksley equation and the (unmodified) Single-Crossover equation based on R-map (genes/cM) values better predicted the published results over the genome-wide R-avg (28 genes/cM) or R-map values based on kb/cM (Figure 6 vs. Figure 4). In fact, with three outliers removed, the correlation between the progeny size predictions based on R-map vs. the published data was extremely significant (Spearman r = 0.67, P < 0.0001, n = 38) (Figure 6, C and F). Although the predictions did not improve further when the modified equations were used (for R-map, Spearman r = 0.38, P = 0.0151, considered significant), the predictions were significantly better than when the R-avg value was used in conjunction with the modified equations (Spearman r = 0.05, P = 0.7662, n = 41, not significant; data not shown). We conclude that mapping size predictions based on neighborhood (>280-kb segments) recombination frequencies (R-map) better predict the number of progeny required to be genotyped for positional gene cloning in rice when R-values are calculated as genes/cM rather than kilobases/cM, and both are significant improvements over calculations based on the genome-wide R-avg.

Figure 6.—

More significant improvement in predicting the size of the progeny mapping population (informative gametes) required to be genotyped during positional cloning in rice when employing neighborhood recombination frequencies (R-map) from the RGP map calculated as genes/cM rather than kb/cM. On the x-axis is the mapping population size from published positional cloning studies in rice (see Table 1). On the y-axis is the prediction. (A–C) Models based on the Durrett–Tanksley equation (unmodified). (D–F) Models based on the Single Crossover equation (unmodified). R-map values were calculated from the 1400-marker Rice Genome Project (RGP) RFLP map (F₂ of Nipponbare × Kasalath cross) (see materials and methods). In C and F, three outliers were removed in comparison to B and E, respectively. Both equations set the probability of success at 95%. A significant improvement over use of the R-avg frequency (A and D) is demonstrated.

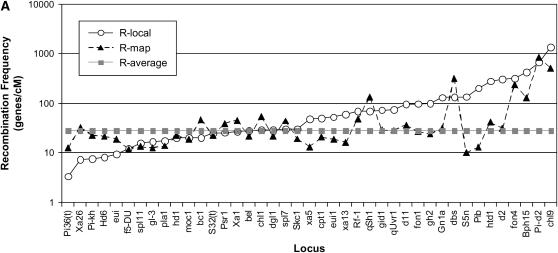
The limiting factor is that R-map values often do not reflect R-local frequencies, but when they do the progeny mapping size can be accurately predicted:

As calculated in Table 2 and shown in Figure 7A, the limiting factor is that the neighborhood recombination frequency often does not reflect the local recombination frequency, even though it is more reflective of local rates of recombination than the genome-wide average. The situation may or may not be better for other maps in other species, particularly as more robust, higher-resolution maps are constructed. Indeed, the rice map gave us hope for the future; in spite of the problems with our use of this map (see discussion) as shown in Figure 7A, we found 11 examples where the R-map values (calculated as genes/cM) were only <30% different than the corresponding R-local value. These corresponded to the following loci: f5-DU, spl11, gl-3, pla1, hd1, moc1, S32(t), bel, dl1, fon4, and Pi-d2. When the mapping population size (N) was calculated for only these 11 alleles, shown in Figure 7, B–E, linear regression analysis showed that both the modified Durrett–Tanksley equation as well as the modified Single Crossover equation very accurately predicted the mapping population size (N) using recombination frequency (R-map) values from the RGP map: the best fit lines were linear (m = 1.2) and the predictions matched the best-fit lines with very high r² values (0.95–0.98). Similar results were obtained for 10 examples where R-map values, calculated as kb/cM, were used; in that case, the predictions matched the best-fit line also with r² value of 0.98 (slope y = 0.8x − 590; data not shown).

Figure 7.—

The underlying limiting factor is that the neighborhood (>280 kb) recombination frequency R-map often does not reflect the recombination frequency in the vicinity (<50 kb) of the target locus (R-local), but when the values do match, then the progeny mapping size can be accurately predicted. (A) Comparison of recombination frequencies in the vicinity of the target gene (R-local) compared to neighborhood recombination frequencies (R-map) derived from the Rice Genome Project (RGP) RFLP map. The graph shows at which loci R-map reflects R-local and where it does not. In the vicinity of the qSh1, dbs, fon4, chl-9, and Pi-d2 loci, R-map accurately predicted a low recombination frequency, unlike R-avg, and thus predicted that large numbers of progeny would need to be genotyped. (B–E) Linear regression analysis demonstrating that when R-map values were within 30% of R-local values, including several high or low recombination intervals shown in A, then the modified Durrett–Tanksley equation and modified Single Crossover equation could accurately predict the final outcome, namely large or small mapping populations, respectively. The modified equations (C and E), which took into account the number of gametes carrying crossovers immediately flanking each target locus, were more accurate than the original equations (B and D).

The utility of our approach was best demonstrated by comparing the data for bel (Pan et al. 2006) vs. Pi-d2 (Chen et al. 2006); empirically, only 462 informative gametes (N) were genotyped to fine map bel to a map resolution (T) of 18 genes; in contrast, 8000 informative gametes were required to fine map Pi-d2 to a map resolution of 33 genes. The RGP map correctly predicted that the recombination frequency (R-local) flanking Pi-d2 was ∼20-fold lower than that flanking bel. As a result, both modified equations would have predicted in advance that mapping bel to this resolution would require ∼360 gametes, and that Pi-d2 would require ∼10,000 gametes. If such accurate predictions could be made across the majority of target loci in the future, then researchers will be able generate appropriately sized map populations and properly allocate human, growth room, and financial resources.

DISCUSSION

A key frustration during positional gene cloning, also known as map-based cloning, has been that the size of the mapping population has been found to vary >25-fold within a species (Dinka and Raizada 2006) (Table 1) depending on the target locus, and that this final size has been difficult to predict. As a result, researchers often undertake positional cloning attempts with some fear. More importantly, it has been difficult to estimate the time, resources, growth space, and personnel required to generate, propagate, genotype, and phenotype an appropriately sized progeny population. The goal of this research was to create a detailed methodology to improve mapping size predictability across eukaryotic species once researchers have initially mapped a target locus to a small interval (1–2 cM). As a side benefit, we have provided a detailed review of positional cloning strategies and results in rice, which should be useful information for the research community studying rice, the world's most important crop. Building upon the work of Durrett et al. (2002), we have demonstrated the utility of a formula (the Durrett–Tanksley equation) that predicts progeny population size N (Figure 2). By further fine-tuning the Durrett–Tanksley equation, taking into account how many (redundant) crossovers defined the map resolution T (a measure of the local marker density), we were able predict the size of the mapping population with 100% accuracy when provided with local, high-resolution recombination frequencies (Figure 3). We also derived and tested a simpler, more user-friendly equation, based on the probability of achieving only one crossover within the progeny population, instead of the two calculated by the Durrett–Tanksley equation. We found that the Single Crossover model was as predictive as the Durrett–Tanksley equation, and that the number of crossovers (λ) was again a useful equation modifier (Figures 2 and 3). With validated equations, and researchers not having the luxury of having access to robust recombination frequencies in the vicinity of their target allele, we measured whether recombination frequencies derived from a 1400-marker reference genetic map (supplemental Table 1 at http://www.genetics.org/supplemental/) could be useful, and indeed the map population size was more accurately predicted when these values were used instead of the genome-wide average recombination frequency (Figures 4 and 6). Since researchers targeting a fully sequenced genome care more about how many candidate genes they must distinguish, not the number of kilobases per se, we also determined that the models could predict gene resolution as well as or better than the kilobase resolution (Figures 5 and 6). Although the rice map, in conjunction with our formulas, could have accurately predicted several unusually large or small mapping population-requiring target alleles, including alleles located near centromeres suffering from suppressed meiotic recombination (e.g., chl9, Pi-d2, and Bph15), we found that the limiting factor was the correlation between R-map vs. R-local recombination frequencies (Table 2, Figure 7).

Understanding R-map vs. R-local discrepancies:

There are likely several reasons for why recombination frequencies from a reference genetic map (R-map) in rice often did not match the frequency in the vicinity of target alleles (R-local), and these are important lessons for future attempts to predict mapping population size. First and most obvious, even within a >280-kb interval (∼1 cM average), the rice RGP map demonstrated that the meiotic recombination frequency could vary significantly (Wu et al. 2003) (supplemental Table 1 at http://www.genetics.org/supplemental/). Second, as is the case with many whole-genome genetic maps, only small numbers of progeny (typically 100–200) were genotyped to generate the RGP map (Harushima et al. 1998); as a result, the location of rare crossovers was more subject to chance. In other words, had the RGP map been generated multiple times using independent populations, the recombination frequencies would likely have varied significantly within 1–2-cM intervals. Third, whereas the RGP map was based on two parental genotypes, the rice Indica variety (Kasalath) and the Japonica variety (Nipponbare) (Harushima et al. 1998), only 8 of 41 of the studies that we compared our models to also used these genotypes to generate their mapping populations. Differences between genotypes, such as the density of repetitive DNA or local cytogenetic rearrangements as seen in maize (Bennetzen and Ramakrishna 2002; Wang and Dooner 2006), might have caused R-map values from the RGP map to differ from the published studies. Indeed, it has been shown that domesticated rice cultivars have an unusually high rate of ongoing gene duplications, vary considerably in the location and density of repetitive DNA (e.g., retroelements), and have very high rates of intergenic nucleotide polymorphisms (SNPs, indels), perhaps in part due to human selection in geographically isolated locations (Garris et al. 2005; Yu et al. 2005; Tang et al. 2006). Finally, the RGP map was generated using F₂ selfed progeny, whereas the mapping populations used in the 41 published studies were generated by diverse methods, including the use of NILs, chromosome SSLs, and recombinant inbred lines (RILs), and in at least at one locus with low recombination rates, fon4-1, an ∼200-kb chromosome deletion was involved (H. W. Chu et al. 2006). It has been shown that when two chromatids differ in their relatedness to one another, as in RILs vs. NILs, the local recombination frequency may be affected (Burr and Burr 1991; Lukacsovich and Waldman 1999; Li et al. 2006); in the most extreme case, unequal deletions between chromatids, suppression of meiotic recombination has long been observed (Rieseberg 2001). All of these factors might have contributed to our observation that R-map values from the rice RGP map often did not match recombination frequencies in the vicinity of target alleles.

Applying these results:

As for our recommendations to researchers undertaking positional cloning, we recommend that the R-map strategy should only be relied upon when they have access to a reference genetic map that has been demonstrated to have a strong correlation between R-map values and R-local values. To make this possible, higher resolution maps, with more markers, must be generated and/or employed to account for sub-centimorgan R variation. In potato, a genetic map with 10,000 markers was recently constructed (van Os et al. 2006), demonstrating progress in this area. Such high-resolution maps will provide researchers with a range of recombination frequencies across a 1–2-cM interval, and thus, at best, researchers could expect to predict an upper and lower range of N, not the precise number. To improve the robustness (reproducibility) of R-map frequencies, genetic maps must be generated based on sampling hundreds to thousands of progeny rather than only 100–200 individuals (Ferreira et al. 2006). To make reference map frequencies relevant to the genotypic targets of positional cloning, maps must be constructed from more parental genotype pairs. In addition, for some species, the number of informative gametes (N) might need to be adjusted to account for male vs. female differences in recombination frequency (Lenormand and Dutheil 2005) by adjusting the meiosis factor (f) (see materials and methods). As to whether R-map values based on genes/cM or kilobases/cM should be used, we had assumed, given that meiotic recombination in plant genomes has been shown to be highly biased to gene regions, rather than flanking heterochromatin (Fu et al. 2001), that if we ascribed most recombination as occurring within or flanking genes, then the genes/cM ratio would be less variable than the kb/cM ratio; in other words, as the number of genes increased in an interval, the frequency of crossovers would also increase in proportion, keeping the genes/cM ratio constant. However, in retrospect, two pieces of data now suggest that this assumption was incorrect. First, in the meiotic recombination frequency calculations we made on the RGP rice map, we found that the genes/cM ratio varied within the genome nearly as much as the kb/cM ratio; the coefficient of variation for R (genes/cM) was 98% across the rice genome (n = 971) compared to 113% for R (kb/cM) (n = 952). Second, if recombination was biased to within or near genes, then the recombination frequencies from positional cloning studies (R-local) would be predicted to be higher than the genome-wide average for rice (R-avg = 277 kb/cM); in fact, out of the 41 published studies, 20 studies had a R-local value below R-avg with 20 above the R-avg, suggesting no bias in recombination near genes (Table 2). It is therefore possible that the stronger correlation we found for the RGP map between R-map vs. R-local, when calculated as genes/cM, was random, but this should be tested for more maps and for more species. Indeed, it will be interesting to test the predictions of this paper in both larger and more compact genomes.

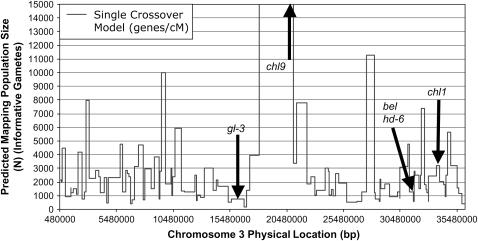
As more robust, higher-resolution maps across more parental genotypes become available, our hope is that the methodology we have described here will generate accurate mapping population size graphs that predict a range of N-values for a given target allele. We conclude by showing an example of such a map in Figure 8, representing our predictions for rice chromosome 3. In spite of the challenges noted, this map did accurately predict the very different mapping population sizes required for the five alleles shown.

Figure 8.—

The final goal of this research: a mapping population size prediction graph. Shown are the predictions for rice chromosome 3 of the number of progeny (informative gametes, N) required to positionally clone a target allele to achieve a five-candidate gene map resolution (T) based on the Single Crossover equation (unmodified) with a 95% probability of success. The x-axis denotes the physical base pair location along the sequenced chromosome. Arrows point to previously isolated alleles in rice; the model was effective in predicting the relative mapping population size for these alleles (see results text). For example, the graph accurately predicted that 20-fold more progeny would be required to positionally clone the chl9 locus compared to the nearby gl-3 locus. The model is based on meiotic recombination frequencies (R-map in genes/cM) as calculated from the Rice Genome Project (RGP) map (see supplemental Table 1 at http://www.genetics.org/supplemental/).