Linkage Disequilibrium and Recombination Rate Estimates in the Self-Incompatibility Region of Arabidopsis lyrata

Abstract

Genetic diversity is unusually high at loci in the S-locus region of the self-incompatible species of the flowering plant, Arabidopsis lyrata, not just in the S loci themselves, but also at two nearby loci. In a previous study of a single natural population from Iceland, we attributed this elevated polymorphism to linkage disequilibrium (LD) between variants at loci close to the S locus and the S alleles, which are maintained in the population by balancing selection. With the four S-flanking loci whose diversity we previously studied, we could not determine the extent of the region linked to the S loci in which neutral sites are affected. We also could not exclude the possibility of a population bottleneck, or of admixture, as causes of the LD. We have now studied four more distant loci flanking the S-locus region, and more populations, and we analyze the results using a theoretical model of the effect of balancing selection on diversity at linked neutral sites within and between different functional S-allelic classes. In the model, diversity is a function of the number of selectively maintained alleles and the recombination distances from the selectively maintained sites. We use the model to estimate the number of different functional S alleles, their turnover rate, and recombination rates between the S-locus region and other loci. Our estimates suggest that there is a small region of very low recombination surrounding the S-locus region.

IN the sporophytic self-incompatibility system found in Brassica species and in Arabidopsis lyrata, two closely linked genes are involved in the recognition reactions. SRK encodes the receptor kinase responsible for the recognition responses of stigmas to incompatible and compatible pollen, whose incompatibility types are specified by the SCR gene, located a few kilobases away from SRK (reviewed in Kusaba et al. 2001). The S-locus region is thought to have evolved low crossing over, since recombination between SRK and SCR would generate self-compatible, presumably maladaptive, genotypes (Casselman et al. 2000), but it is difficult to test whether recombination is really lower than that in other genome regions. In Ipomoea trifida, a diploid relative of sweet potato with a sporophytic self-incompatibility system, recombination is estimated to be suppressed in the S-locus region, although the incompatibility loci have not yet been identified. A recombination distance of ∼0.11 cM was estimated over a completely sequenced region whose physical distance is 250 kb (i.e., ∼2.3 Mb/cM; Tomita et al. 2004); this was estimated to be about one-tenth of the recombination rate of the immediately flanking region.

To test whether recombination is detectable in the A. lyrata S-locus region, we have been using population genetic approaches. We previously studied DNA sequence diversity of four loci located in the genome region containing the self-incompatibility loci and closely linked to the S loci (Kawabe et al. 2006), but not involved in the incompatibility reaction. In the Icelandic population surveyed, two loci, B80 and B120, had extremely high diversity; since our tests did not detect any evidence for balancing selection at these loci, we concluded that the high diversity was due to linkage disequilibrium (LD) with the S loci (Kamau and Charlesworth 2005), as predicted for sites close to a locus under balancing selection (Hudson and Kaplan 1988; Charlesworth et al. 1997). The boundary of the region over which the influence of balancing selection at the A. lyrata S loci extends was not defined. Two other nearby loci had lower diversity, but the difference was not statistically significant, so data from further loci linked to the S loci are needed.

Ideally, the diversity data should be analyzed in relation to the theory of how the balanced polymorphism affects linked sites at different distances away. Diversity is expected to be higher, the higher the number of alleles that are maintained (Takahata and Satta 1998; Navarro and Barton 2002). Because we initially surveyed only one population, it was also possible that the high diversity observed is due to linkage disequilibrium within this population (Wakeley and Aliacar 2001) and might not necessarily imply very infrequent recombination with the S loci. For instance, some of our sampled individuals might recently have immigrated from a genetically different population. This can be tested using data from reference loci, together with data from further populations. The ideal sample for testing for LD is to include one individual from each of multiple different populations, to minimize LD due to recent common ancestry within populations (Wakeley and Aliacar 2001).

Here, we extend the survey of diversity at the B80 and B120 loci to eight more Icelandic populations (of which seven proved to have S haplotypes that allowed comparisons between populations), plus additional samples from other European populations, and we add four more loci at increasing distances from the S-locus region. If the flanking loci have high nucleotide diversity because of linkage disequilibrium with the S loci, we expect to detect associations between the flanking locus sequences and the S-locus sequences of different incompatibility alleles; i.e., we expect S haplotypes carrying a given sequence at an S locus to be characterized by defined alleles at the flanking loci across independent families and populations. Our tests give evidence for associations at the flanking loci closest to the S locus, but not at the more distant ones, since the former had much lower diversity within S haplotypes (defined by their SRK sequences), compared with between haplotypes, whereas the latter had similar diversity regardless of haplotype.

Using approximate expressions for diversity within and between S haplotypes as functions of the genetic recombination rate, in an explicit population genetics model, we show how it is possible to estimate the allele numbers and turnover times of S alleles and to use these to estimate the rates of crossing over between the S loci and the flanking loci at different probable physical distances away. This approach of using diversity values (which are directly related to LD near a site under balancing selection; Charlesworth et al. 1997) should be preferable to estimating recombination using standard analyses of linkage disequilibrium; therefore we did not attempt to infer the phase of our haplotypes and quantify linkage disequilibrium. Our data suggest that recombination is unusually infrequent in the region close to the S loci, but do not suggest a very extensive region of suppressed crossing over. Despite some uncertainty in our estimates, the approach is the first simple method for estimating recombination in the S-locus region, and the results are consistent with direct estimates of recombination by genetic mapping (Kawabe et al. 2006). Genetic mapping cannot, however, exclude some recombination within the region.

MATERIALS AND METHODS

Plant samples and loci studied:

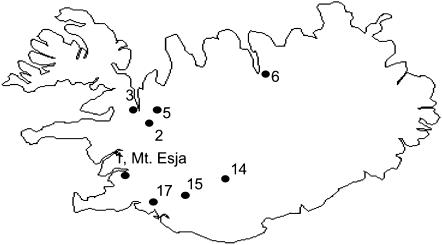
Our study concentrates on a sample consisting of plants from several Icelandic populations (Figure 1), provided by J. Bechsgaard (University of Aarhus). As many plants as possible were members of full-sib families, so that we could often infer the phase of different loci in the parental haplotypes of the region of interest (see below). The S1 haplotype (i.e., haplotypes carrying the S₁ allele of SRK) is the commonest in most populations (Mable et al. 2003; Bechsgaard et al. 2004) and was present in the samples from nine populations. Moreover, because S₁ is the most recessive S allele (Mable et al. 2004), it is found in homozygotes, making haplotypes immediately evident. Our sample thus contains many more sequences of this haplotype than of any other. A set of seven more SRK alleles was present in plants studied from two or more populations (S₁₁, S₁₂, S₁₄, S₁₆, S₂₂, and S₂₅ from two populations each and S₁₅ from three populations, but sequences of the genes studied here were not always obtained from all of these). Plants from these populations were used in previous studies of polymorphism in the Aly8 gene, which is also physically close to SRK (Kusaba et al. 2001; Hagenblad et al. 2006).

Figure 1.—

Location of the nine A. lyrata populations in Iceland (the Mt. Esja population is close to population 1, and only one symbol is shown). For further description, see Bechsgaard (2002).

Sequences were obtained for six loci, three on either side of the S-locus region. Table 1 lists the genes chosen, with their putative functions and GenBank accession numbers in A. thaliana. All the loci studied are linked to the SRK locus in A. lyrata (Kawabe et al. 2006). Primers (Table 1) were designed using the published sequence of the A. thaliana genome. Physical distances between the six loci and SRK are not known for A. lyrata haplotypes in Iceland; thus in what follows we use the distances from SRK determined for the sequenced genome of the A. thaliana Columbia strain (Table 1). BLAST searches of the A. thaliana genome (http://www.arabidopsis.org) were done to choose single-copy loci in the A. thaliana genome, and all primer sequences were checked by BLAST searches of the A. thaliana genome to ensure that each primer combination was unique to the region of interest. PCR amplification conditions were as follows: 94° for 3 min followed by 30 cycles of 94° for 30 sec, 55° for 30 sec (annealing), and 72° for 60 sec followed by a 10-min extension at 72°.

TABLE 1.

Loci studied, distances from the S loci in A. thaliana, and primers used for the PCR amplifications in A. lyrata

	Data from A. thaliana Columbia strain
Locus name	Position on chromosome 4	Distance from SRK (kb)	3′ or 5′ of SRK	Primers	Putative function
S2	At4G20130	504	3′	F: tcacttctggcggctctatg	Ribulose-1,5 bisphosphate carboxylase/oxygenase large subunit N-methyltransferase related
				R: tctttaggacgccaatgtag
S4	At4G20760	255	3′	F: gatgcttgcttacgaggtta	Short-chain dehydrogenase/reductase (SDR) family protein
				R: gccgctgtcttgtttcttag
B80	At4G21350	27	3′	F: gaatcagcagcttcaaccaaa	U-box domain-containing protein
				R: gttatcctccaatcgggtcatac
B120	At4G21390	10	5′	F: gat cttaggatccacaagctcctc	S-locus lectin protein kinase family protein
				R: ctcgaagatggacgtgagatag
S8	At4G21800	189	5′	F: accttccccactgttgtcac	ATP-binding family protein
				R: aaagtcctcatcatcctcctc
S12	At4G22720	554	5′	F: acaccgccaactatcaaaac	Glycoprotease M22 family protein
				R: tttcagccattgttgttagag

DNA sequencing:

DNA was extracted from leaves of A. lyrata plants using the FastDNA kit (BIO 101, Vista, CA). PCR products from all the loci were sequenced directly using both forward and reverse primers. Sequences were obtained directly from PCR products where the base calls were unambiguous and only one allele was found in the individual. Otherwise, when heterozygous insertion and deletion (indel) polymorphisms were found, the PCR products were cloned using TOPO TA (Invitrogen, San Diego) and purified using either the QIAquick PCR purification kit (QIAGEN, Valencia, CA) or an “ExoSAP” protocol (ExoSAP-IT; Amersham Biosciences, Arlington Heights, IL) before performing the sequencing PCR reaction.

All sequencing was performed on an ABI 377 automatic sequencing machine using Dyenamic (Amersham Biosciences). Sequences were verified manually using Sequencher version 4.2.2 (Gene Codes, Ann Arbor, MI). At least five clones were sequenced from each plant: the base assigned at each position for each clone was that found in all or most of the sequences. The GenBank accession numbers for the new sequences obtained are as follows: locus B80, EF599769–EF599795; B120, EF599796–EF599820; S2, EF599821–EF599861; S4, EF599862–EF599882; S8, EF599883–EF599905; and S12, EF599906–EF599946.

Associations between loci:

To test for associations, we used plants in which at least one of the SRK alleles was known from previous work, and we defined haplotypes according to the SRK allele carried, determined as follows. For as many haplotypes as possible, we established the phase between the alleles at each S-linked locus and the individual's known A. lyrata S alleles, using full-sib families made by crossing plants from different Icelandic populations, in which the SRK haplotypes for at least one of the parents, and several progeny, had been established in a previous study (Bechsgaard et al. 2004). We sequenced portions of the loci of interest in both parents of the families and at least two offspring, to distinguish the parental alleles; at least three clones per allele in all samples were sequenced to verify the sequences of the four alleles. We could then infer the linkage phase of the parental haplotypes for the set of linked loci studied, as described in Hagenblad et al. (2006). When only one allele was identified, the individual was treated as a homozygote in our analyses.

Polymorphism and divergence analysis:

For each of the six loci, sequences from our natural population samples (including the sequences of alleles identified from the families) were aligned using Clustal X v. 1.81 using the default conditions, and further modifications to the alignment were done manually in BioEdit. Intron–exon boundaries were determined after alignment with the cDNA sequences of the A. thaliana orthologs of all genes. Nucleotide diversity among the A. lyrata alleles and divergence from their A. thaliana orthologs were estimated with the software DNAsp v. 4.0 (Rozas and Rozas 1999), using Nei and Gojobori's (1986) method. Diversity values per synonymous or nonsynonymous site were estimated for the coding regions of the six loci, as well for the intron sites when present, using similar samples of plants (PCR amplification was unsuccessful for one or two individuals at each of the loci).

HKA tests were used to compare polymorphism within A. lyrata with divergence from the orthologous A. thaliana sequences. Multilocus tests were conducted using the HKA program distributed by J. Hey (http://lifesci.rutgers.edu/heylab). Nested HKA tests within a maximum-likelihood framework were implemented in MLHKA (Wright and Charlesworth 2004) for an A. lyrata data set that included the 6 flanking loci and 12 other loci studied in European populations, all on the same arm of the A. lyrata chromosome 7 as the S loci (Kuittinen et al. 2004; Kawabe et al. 2006). We refer to these as reference loci. The general model that assumes no selection at any of the loci was compared to one in which selection was assumed to be acting at one or more loci. Loci with no variants within A. lyrata were assigned a low diversity.

Except for locus S8, for which we observed only two haplotypes, neighbor-joining trees were estimated on the basis of pairwise divergence of all sites (with pairwise deletion and Jukes–Cantor correction), using MEGA version 3 (Kumar et al. 2004). The significance of clusters was assessed by bootstrapping (1000 permutations).

Estimating recombination for flanking genes:

Below, we derive the expected coalescence times for alleles from the same functional allelic class and alleles from different classes, respectively T_within and T_between, as functions of three parameters, the number of selectively maintained alleles, n, the turnover rate of these alleles (i.e., the rate at which new functional S alleles arise), c, and the recombination rate, r. Under the infinite-sites model, and assuming no mutation rate differences, these are proportional to the expected nucleotide diversity values in samples of the sequences of the two respective kinds (Hudson 1990). The estimates make use of π, the estimated reference locus diversity; i.e., we compare our results with the predicted relative values from the equations: T_within/2N_e = π_within/π and T_between/2N_e = π_between/π. We used observed values of silent- or synonymous-site diversity measures from samples of these two kinds based on sequence data from the SRK locus kinase domain (Charlesworth et al. 2003b), and from the other loci in the S-locus region, to estimate the quantities in the equations. The reference loci for the π-estimate were 12 loci from the same chromosome arm as the S loci, the A. lyrata chromosome 7 (Kawabe et al. 2006); these loci were surveyed for sequence diversity in natural populations of A. lyrata (A. Kawabe, A. Forrest, S. I. Wright and D. Charlesworth, unpublished data) and have diversity similar to that of other loci in the species (Wright et al. 2003, 2006).

The SRK locus data allow us to estimate the two quantities describing the selected locus itself (the S locus in the present study), n and 2N_ec, assuming that sites within the SRK kinase domain do not recombine with the selected sites in the S domain (i.e., r = 0). Estimating c requires knowing the N_e value. We estimated N_e using nucleotide diversity estimates from reference loci, since π estimates 4N_eμ, where μ is the neutral mutation rate. We used two different μ-estimates based on synonymous- or silent-site divergence from A. thaliana orthologs, one value at the high end of the likely range and a more moderate one (Wright et al. 2002).

Given these estimates, we then applied the equation for a neutral site recombining with a self-incompatibility locus (Equation A3 in the appendix) to synonymous- or silent-site diversity data from loci at different physical distances from the S locus, to estimate the recombination rates, r (in crossovers). These estimates were then converted into values per megabase, using physical distance estimates. To estimate π_within, we used S haplotypes, defined as haplotypes with the same SRK sequence, whose sequences at a flanking locus were determined from two or more plants; the mean over all such haplotypes was used in the calculations, similarly to estimating within-deme diversity for a subdivided population (for example, see Hudson et al. 1992); we used the unweighted mean, since the sample size for most haplotypes was two (although larger numbers were studied for S₁ haplotypes, as explained above). π_between for each flanking locus was estimated as the mean of the nucleotide diversity values between different S haplotypes; we estimated this by subtracting the π_within values either from the diversity in the whole sample or conservatively from the diversity estimated using one sequence randomly chosen from each S haplotype from the Mt. Esja population. The results were very similar, and results from the first method are used below.

These diversity estimates were obtained using DNAsp (Rozas and Rozas 1999). The two diversity values were used to describe subdivision into allelic classes with respect to the SRK locus, using estimates of the proportion of variability that is between classes, analogous to F_ST values for quantifying how much variability is between, as opposed to within, demes in a subdivided population (the F_AT statistic of Charlesworth et al. 1997; see also Takahata and Satta 1998). The F_AT values estimate a quantity 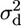(Charlesworth et al. 1997) that is closely similar to the LD measure ρ² (McVean 2002). To estimate F_AT values, we treated alleles from different S haplotypes, defined by their SRK alleles (see above), as “populations” and used the measure K_ST that takes the sequence differences of alleles into account (Hudson et al. 1992), and we tested the significance of the “subdivision” using K* (Hudson et al. 1992), by permutation tests in DNAsp; we refer to this below as K_AT. To compare with subdivision between the populations sampled, we also estimate K_ST values between the populations. In both the between-population and the between-haplotype analyses, we included indel variants in the subdivision estimates.

Although the principle of our approach is based on the existence of LD, LD estimation is not required. The approach relies purely on diversity values; however, it is necessary to have reliable information about the phase of variants in the flanking loci. We did not attempt to analyze haplotypes in which phase was inferred from unphased sequences, because the frequency of heterozygotes at the SRK locus and the flanking genes (see below) is very high and there is therefore little information from which to infer the phases of variants; such inferences will thus be very unreliable.

RESULTS

Theory:

It is possible to derive the mean coalescence times for alleles from the same functional allelic class, and for alleles from different classes, following Takahata's work on MHC alleles (Takahata and Satta 1998). We denote these by T_within and T_between. The equations were derived using the analogy with population subdivision, with recombination between S-allele haplotypes replacing migration between demes (Maruyama and Kimura 1980; reviewed by Takahata 1995; Charlesworth et al. 1997, 2003). To obtain analytical results, we have assumed that all alleles are present at equal frequencies, as is reasonable for gametophytic but not sporophytic self-incompatibility. The consequences of this assumption are examined in the discussion.

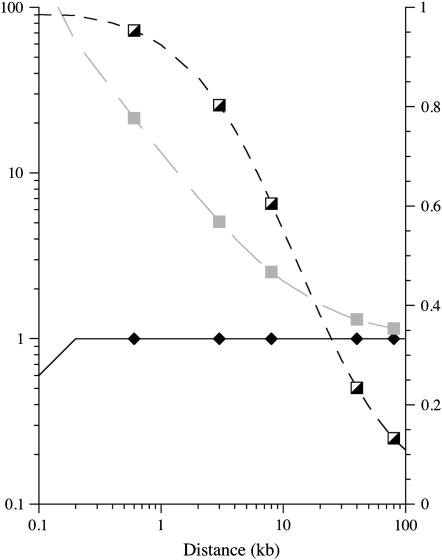
The case in which diversity is observed at sites that recombine with the selected locus is given in the appendix, and Figure 2 illustrates some results from the model. The diversity between haplotypes carrying different functional alleles at the selected site (π_between) can be extremely high relative to that at reference loci not close to the selected locus, as noted by Takahata and Satta (1998). A crucial result is that π_within and π_between for sequences linked to a locus under balancing selection are expected to be similar unless recombination is extremely infrequent. F_AT (the proportion of variability that is between classes or its value estimated as K_AT) will thus be close to zero if recombination occurs, and very high values suggest low recombination.

Figure 2.—

Example showing the predicted values of three observable quantities. The number of alleles at the selected locus (n) in this example was assumed to be 50, and the recombination rate in the region was 0.1 cM/Mb. An effective population size of N_e = 10,000 was assumed. The coalescence times are shown relative to those for loci unlinked to the S locus (predicting the relative nucleotide diversity values). The left y-axis shows both the scaled within- and between-allele values T_within and T_between (solid line and solid diamonds and shaded dashed line and shaded squares, respectively), and the right y-axis shows the predicted values of F_AT (equivalent to the estimated K_AT between alleles in different S haplotypes, shown as solid/open squares and a solid dashed line).

Using the approach explained in the appendix, we obtain two equations for the situation when there is no recombination:

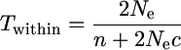(1a)

and

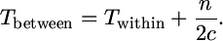(1b)

These two equations are applied below to sequence data on the SRK locus kinase domain (Charlesworth et al. 2003a), along with data from reference loci to provide an N_e estimate (see materials and methods, and below), to estimate two quantities: n, the number of alleles at the selected locus itself (the S locus in the present study), and c, the turnover rate of these alleles. Data on diversity at the flanking loci are then used with Equations A1 and A2 to estimate recombination rates.

Observed polymorphism at flanking loci:

The loci studied are shown in Table 1. The two loci closest to the S loci, B80 and B120, were included in a previous diversity survey of a sample from a single natural population of A. lyrata from Iceland (Mt. Esja, also referred to as 99R, Kamau and Charlesworth 2005), and the sequences obtained previously were included in the present analyses. Diversity has not previously been studied at the four other loci, S2, S4, S8, and S12, which are more distant from the S loci. The physical distances in A. thaliana from the ortholog of the SRK locus are shown in Table 1, and in that species the pollen incompatibility gene (SCR) is close to SRK. The corresponding physical distances in A. lyrata are known only for two haplotypes (Sa and Sb of Kusaba et al. 2001), respectively equivalent to S₁₃ and S₂₀ of Schierup et al. (2001), neither of which has been found in European populations (Charlesworth et al. 2003a; Mable et al. 2003; Bechsgaard et al. 2004). Since these two well-studied haplotypes differ considerably in gene arrangement and intergene distances, the distances in other haplotypes, including those studied here, may also differ. However, the flanking gene orders are the same in haplotypes Sa and Sb and in A. thaliana (Kusaba et al. 2001). The higher total DNA content of A. lyrata (Bennett et al. 2003) suggests that using A. thaliana distances should be conservative in evaluating the extent of recombination suppression in the S-locus region.

Pooling the sequences from all populations, regardless of their S haplotypes, nucleotide diversity (π) is highest for the two closest S-flanking genes, B80 and B120, and lower for the distant flanking loci (Table 2). B80 and B120 were heterozygous in all individuals. No plants were heterozygous at the S8 locus, which has very low diversity; we observed only two haplotypes at this locus. Haplotype numbers were higher for S2, S4, and S12, and heterozygotes were common (Table 2).

TABLE 2.

Polymorphism in Icelandic populations of A. lyrata in six S-locus region genes and divergence from the A. thaliana orthologs

						Diversity		Divergence from A. thaliana
Locus name	No. of sequences	Length of sequence	No. of haplotypes	Site type	Nos. of sites	Nos. of polymorphic sites (Sn)	π	JC DXYa	KA/KS
S2	42	632	9	Noncoding	287	3	0.0039	0.177	0.191
				Synonymous	66	1	0.00044	0.096
				Nonsynonymous	242	2	0.0023	0.018
S4	20	597	9	Noncoding	233	3	0.0023	0.094	0.223
				Synonymous	78	2	0.0049	0.114
				Nonsynonymous	225	6	0.0032	0.025
B80b	40	669	26	Synonymous	173	63	0.09384	0.155	0.163
				Nonsynonymous	497	26	0.00982	0.0253
B120	54	803	24	Noncoding	221	42	0.06473	0.165	0.006
				Synonymous	116	22	0.06602	0.120
				Nonsynonymous	402	3	0.00126	0.0008
S8	44	661	2	Noncoding	160	0	0	0.0930
				Synonymous	111	0	0	0.1768	0.084
				Nonsynonymous	377	1	0.00024	0.0148
S12	40	689	14	Noncoding	177	10	0.01647	0.0495
				Synonymous	115	7	0.01533	0.1389	0.012
				Nonsynonymous	376	2	0.00233	0.0017

^aDivergence with Jukes–Cantor correction for saturation.

^bThere are no noncoding sequence data for the B80 locus, as the gene has no introns.

Our previous results (Kamau and Charlesworth 2005) did not find a significant diversity difference between the B80 and B120 loci and two slightly more distant flanking loci, B70 and B160, so more, slightly more distant, flanking loci were needed to test the extent of the region of high diversity around the S loci. Using the four new more distant flanking loci, HKA tests confirm the previous conclusion that the B80 and B120 genes have unusually high diversity. The null hypothesis that all loci have similar polymorphism levels had a significantly lower (P < 0.0023) likelihood than that of a nested model where B80 and B120 were allowed to have a different level of polymorphism from the other loci. On both sides of the S loci, the region of unusually high diversity therefore does not extend as far as the location of the four new flanking loci.

The diversity differences do not result from differences in the mutation rates of the loci, since silent-site divergence between A. lyrata and A. thaliana ranges from 0.09 to 0.17, within the normal range for these two species. Raw silent-site divergence varies, but few genes sequenced in both species have K_s > 0.2 or < 0.05 (Wright et al. 2002; Barrier et al. 2003; Ramos-Onsins et al. 2004); the mean K_s and K_a for these species are 0.119 ± 0.004 and 0.025 ± 0.002, respectively, based on 304 ESTs from A. lyrata and their A. thaliana putative orthologs (Barrier et al. 2003). All six S-flanking loci had low K_a/K_s values (Table 2), indicating that they are functional genes in both species.

Associations between S alleles and loci flanking the S-locus region:

Using full-sib families to establish the phase of the haplotypes (see materials and methods), we identified haplotypes from different populations carrying a number of different SRK alleles. To denote the sequences at flanking loci, we use a notation that gives the locus in question, with a subscript giving the SRK allele (e.g., B80_S1). Of the B80 sequences from known S haplotypes, five sets have identical sequences, although they originated from different populations (S₁₂, S₁₄, S₂₂, and S₂₅); S₆, S₉, and S₁₈ alleles were each studied from only one population, and the S₁₈ alleles (all from population 5) were identical in sequence. However, although most of the B80_S1 alleles cluster together, one is very different, and the B80_S15 and B80_S27 sequences were also variable (not shown). These results are similar to those previously found for B80 (Kamau and Charlesworth 2005) and for another nearby locus, Aly8 (Hagenblad et al. 2006).

For the B120 locus, diversity is again high (Table 2), but associations with SRK are less clear than for B80, and B120 alleles from several S haplotypes are found in disparate parts of the tree, as was previously found within the Mt. Esja population (Kamau and Charlesworth 2005). Again, S₆ and S₉ haplotypes were studied only from the Mt. Esja population, and again the B120_S6 and B120_S9 sequences included a few variants. The B120_S1 alleles are found in three groups, with very different sequences, and B120_S15, B120_S16, B120_S25, and B120_S27 alleles are also scattered across the tree, suggesting some recombination between the S locus and the B120 locus. Some of these results could arise if a plant is heterozygous for two haplotypes, but only one SRK allele was detected, which is not the one from which our B120 allele was sequenced, so that a haplotype is then misclassified; thus our results are likely to underestimate associations with SRK alleles. Nevertheless, as is seen below, there is clear evidence of associations.

A. lyrata S alleles can be divided into four dominance levels, and alleles within the same dominance class are most similar in sequence (Prigoda et al. 2005). A flanking locus that is in linkage disequilibrium with SRK will have the same evolutionary history as that of the S alleles and might thus be associated with the dominance classes. Our sequences of alleles at the B80 and B120 loci do not, however, show clustering that is congruent with these allele classes. Finally, consistent with their low diversity, the gene trees for the four distant loci show no evident associations with the S haplotypes or with S-allele dominance classes.

Diversity within and between different S haplotypes or natural populations:

To quantify the proportion of variability that is between S-allele classes, we estimated nucleotide diversity within and between the haplotype classes defined by their SRK sequences and used these to calculate the measure K_AT explained above, which is analogous to K_ST for quantifying how much variability is between, as opposed to within, demes in a subdivided population.

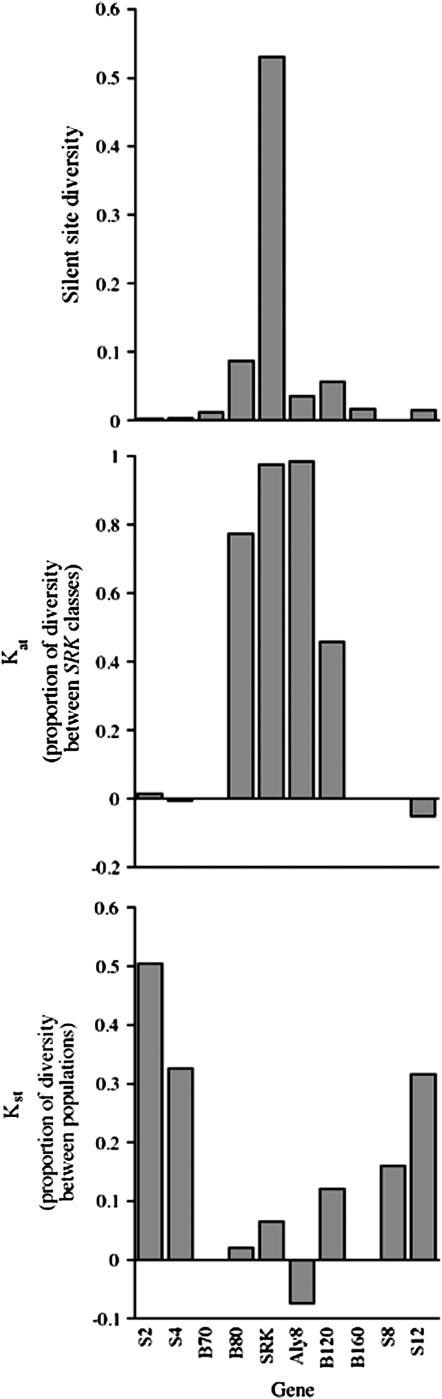
The results for silent sites are shown in Table 3 and Figure 3. Consistent with its high diversity (Kamau and Charlesworth 2005), the B80 gene has a high F_AT value (estimated as K_AT, see materials and methods), which is highly significant using the K* test (P < 0.0001), suggesting strong isolation between the B80 sequences in haplotypes with different SRK alleles and high similarity among the sequences when the SRK allele is the same. The B120 sequences also show significant associations with SRK alleles (P < 0.0001), as does Aly8, the A. lyrata ortholog of the A. thaliana ARK3 gene, which is also in the region flanking the S loci (Hagenblad et al. 2006). For the close flanking loci, the high diversity is thus evidently due to high proportions of sites differing between S haplotypes. For the four more distant flanking loci, samples of different compositions with respect to the S haplotype yield similar diversity, and K_AT values are low (Table 3) and not significantly different from zero (P = 0.21 for S2, 0.51 for S4, and 0.9 for S12).

TABLE 3.

Estimates of the recombination rates at different distances from the S loci, assuming n = 25 S alleles

Gene	Estimated distances from SRK (kb)	πwithin	πtotal	Estimated recombination rates (cM/Mb)
ARK3	−20	0.0017	0.0353	0.056
B120	−28.05	0.013	0.0554	0.050
B80	+ 39.6	0.016	0.0821	0.018
S8	−189	0	0	Cannot be estimated
S4	+ 225	0.0037	0.0036	Cannot be estimated (πbetween negative)
S2	+ 504	0.0013	0.0024	Cannot be estimated (πwithin > πbetween)
S12	−554	0.019	0.015	Cannot be estimated (πbetween negative)

The values of silent-site diversity π_within and the estimate from all sequences from haplotypes with known SRK sequences (π_total) are shown; the diversity between allelic classes is the difference between the total values and within values. The estimated distances are from the S domain of SRK, which are values in the sequenced A. thaliana Col-0 strain and thus probably underestimates for A. lyrata (see text); the + or − symbols in the distance column indicate genes on the two sides of the SRK locus.

Figure 3.—

Estimated nucleotide diversities, π (top), and values of K_AT (between alleles in different haplotypes defined by their SRK alleles, middle) and K_ST (between alleles from different natural populations, bottom) at loci in and close to the S-locus region.

Between the different populations, however, it is expected that F_ST values will be low for the locus under balancing selection and for very closely linked loci; for loci that recombine with them, however, the values should be similar to those for unlinked or distant loci (Schierup et al. 2000a,b). This expectation is borne out by the results (Figure 3). K_ST values are unusually low for the SRK, B80, and B120 genes (0.065, 0.02, and 0.018, respectively) and mostly do not differ significantly from zero for any of these loci (although P = 0.03 for B80) or for Aly8 (Hagenblad et al. 2006), whereas for all the more distant flanking loci the values indicate significant population subdivision. K_ST values for the 3 loci that have variants, S2, S4, and S12, respectively, are 0.50, 0.33, and 0.32 (P-values are 0.004 for S2 and <0.001 for the other two loci). These are similar to the high values observed for different European A. lyrata populations for the 12 chromosome 7 reference loci (0.52 for all sites; A. Kawabe, A. Forrest, S. I. Wright and D. Charlesworth, unpublished results; Figure 3). A rather lower value might be expected for our data, which are mostly from Icelandic populations.

Estimates of SRK allele numbers and turnover rates and recombination rates with flanking loci:

We used the equations in the appendix to analyze jointly diversity results from SRK and from flanking loci, including the four new genes whose sequence diversity was described above and also Aly8. We first estimated the number of functional classes of alleles, n, on the basis of polymorphisms in the kinase domain of the SRK gene. This locus has very high diversity, which cannot be estimated accurately, but silent-site diversity is at least 0.6, whereas within allelic classes it is much lower (estimated π_within = 0.00052, on the basis of the data reported in Charlesworth et al. 2003a). The n estimates vary, depending on the set of reference loci used, since the diversity estimates differ significantly between different A. lyrata chromosomes (A. Kawabe, A. Forrest, S. I. Wright and D. Charlesworth, unpublished data). The lowest estimated n value is 8, on the basis of a silent-site diversity of 0.0097 for 12 loci from the chromosome arm AL7 on which the S loci are located (these loci have unusually low diversity), and the highest is 39, on the basis of the mean synonymous-site diversity value of 0.027 from AL7 plus 24 AL1 loci. The higher the number of alleles maintained at the selected locus, the less recombination is required to maintain diversity at linked loci (see Equation 3). Since we wish to test whether recombination may be restricted in the S-locus region, it is conservative to assume large n. We therefore used values of 25 and 50 in our calculations.

For the turnover rate of S alleles, c, we require an estimate of 4N_e, and we estimated this using either of two mutation rates (see materials and methods) and using either silent or synonymous sites; there are thus four c estimates for each value of the reference locus diversity. All values are similar, and all are very low, so we do not show the values here. The highest value, 1.14 × 10⁻⁶, assumes the low mutation rate and the high reference locus diversity above. We discuss below the inaccuracy caused by applying a model of a gametophytic system to a species with a sporophytic incompatibility system.

Given these estimates, we then applied the equation for a site recombining with a self-incompatibility locus (Equation A3) to synonymous- or silent-site diversity data from loci at different physical distances from the S locus, to estimate the recombination rates. The highest estimates (based on the high mutation rate) are shown in Table 3. The estimates are low for the three loci close to SRK. For the more distant loci, the values of π_within are similar to the diversity from this set of sequences estimated without taking account of the haplotype's SRK sequence (π_total); thus π_between is either small or negative, suggesting that recombination is frequent enough at this distance to break down linkage disequilibrium. For two loci, π_within > π_between, while the S8 gene has only a single (nonsynonymous) SNP variant. The results therefore suggest sufficient recombination that the balancing selection at the S loci has not led to reduced diversity within allelic classes; thus the recombination rate cannot be estimated.

DISCUSSION

The results show clearly that the major reason for high diversity at the loci closest to the S loci is sequence differences between allelic classes at the S locus, not between populations. This is predicted by theoretical models of balancing selection (reviewed in Charlesworth et al. 2003). It is well known that functionally different alleles at a locus under balancing selection acting within demes in a species with subdivided populations are expected to show less population structure than neutral variants (Schierup et al. 2000b; Muirhead 2001). It has also been shown in such models, including the cases of both gametophytic and sporophytic self-incompatibility, that closely linked neutral sites are affected similarly to the selected site (Charlesworth et al. 1997; Schierup et al. 2000a).

Neither the allele number estimates nor the estimates of recombination rates are highly accurate. The equations we have used are expected to be accurate only for gametophytic self-incompatibility and do not take into account the differences in allele frequencies that occur with sporophytic self-incompatibility (Schierup et al. 1998; Uyenoyama 2000). A minor inaccuracy arises because the model ignores the effects of allelic turnover, which involves a selective sweep when a new S allele arises and spreads in a population, so that the diversity within this haplotype will initially be low. This was modeled by Takahata and Satta (1998) and Takebayashi et al. (2004), but the effect is generally small, particularly when the turnover rate is low, as seems to be the case for the SRK alleles (see above).

More serious difficulties come from unequal S-allele frequencies. Using the n-island model of migration to model the n-allele case of self-incompatibility loci is appropriate only if allelic classes are interchangeable. This should be correct for alleles in a gametophytic incompatibility system, unless there is some “extra effect” of selection acting on different alleles (Lawrence and Franklin-Tong 1994), but it is not true for sporophytic incompatibility, because dominance means that certain allele classes are expected to be consistently more frequent than others (reviewed in Schierup 1998; Uyenoyama 2000). A. lyrata populations have large numbers of alleles, in at least four dominance classes (Mable et al. 2004; Schierup et al. 2006), and the predicted higher frequencies are indeed estimated for the more recessive alleles (Schierup et al. 2006). We also cannot assume that no extra effect of selection acts on A. lyrata alleles, since segregation anomalies have been observed for these alleles in plants from our study populations (Bechsgaard et al. 2004).

With unequal allele frequencies, the probability that a neutral variant recombines onto a given allelic type from a different one, r′, is affected, since, rather than being exclusively homozygotes (at a frequency determined strictly by the number of alleles), or else heterozygous for two different S-allele classes, plants can carry two members of the same high-frequency allelic class, and between-class recombination cannot then occur. For our species' self-incompatibility system, a single n value is therefore incorrect for the equations in the appendix that take account of the chance that an allele is present heterozygous with one of a different allelic class with which it could recombine (see Equation A3 and the expression for r′). With a large number of alleles, however, most individuals will be heterozygous, and so the effective recombination rate between different alleles in our equations is close to the true recombination rate, r. If there are many alleles, r′ is approximately equal to the product of r and the sum of the squared allele frequencies, which is greater than r/n, implying that the true value of r is less than nr′ in Equation A6, so that our method overestimates r. As we are testing the possibility of low recombination in the S-locus region, this is conservative, and we can thus use this approach to obtain rough parameter estimates for A. lyrata, which has large numbers of alleles, in at least four dominance classes (Mable et al. 2004; Schierup et al. 2006).

Even for gametophytic incompatibility systems, and even when there is no recombination, the equation for T_within is only approximate (Vekemans and Slatkin 1994), because the effective size of allelic classes in a finite population is affected by fluctuations in the number of copies of an allele over the generations, and it is not the arithmetic mean, but the harmonic mean number that determines this effective size (Vekemans and Slatkin 1994).

Although our estimates are therefore rough, they clearly indicate a very low turnover rate. The effect of fluctuations in an allele's number of copies is to lower T_within, which will lead to overestimation of the number of alleles. An effect in the opposite direction, leading to an overestimate of n by our approach, arises due to the differences in allele longevity expected in sporophytic incompatibility systems. There is thus no single coalescence time, and no single turnover rate, for all alleles. Diversity may evolve within old S alleles, due to mutation as well as to recombination between different S haplotypes, and such variants lead to an inference that recombination is occurring, but in reality this reflects the age of these particular alleles, not the recombination rate.

The turnover rate and allele number estimates assume no recombination, and both yield plausible values. The per locus mutation rate to new functional S alleles must be lower than the turnover rate. Given that two loci are involved in self-incompatibility, and that suitable changes must occur in both to generate a new functional S allele (Schopfer et al. 1999; Charlesworth 2000; Takayama et al. 2000; Kusaba et al. 2001; Chookajorn et al. 2003; Charlesworth et al. 2005), it has long been realized that this mutation rate should be very low; thus the very low value estimated here seems plausible.

The highest estimated recombination rate in Table 3 corresponds to a value of almost 18 Mb/cM, a very large physical distance per map unit. The average physical distance per centimorgan is ∼1 Mb in maize (Dooner 1996), barley (Künzel et al. 2000), Medicago truncatula (Choi et al. 2004), and Allium (Khrustaleva et al. 2005). In A. lyrata AL7, the estimated value is 205 kb/cM (Kawabe et al. 2006). King et al. (2002) review the wide range of values estimated for different regions of the same species' genome for the few plants where data are available. In chromosome arms (i.e., not including centromeric regions, which have much lower rates of crossing over), the highest values are ∼550 kb/cM in A. thaliana chromosome IV (Drouaud et al. 2005), ∼1 Mb in rice (Zhang and Wing 1997), and 22 Mb in wheat (Gill et al. 1996), and in poplar, with an average of ∼200 kb/cM, a region with 25 times less recombination was found near a rust resistance gene (Stirling et al. 2001).

The main factor causing our r estimates to be misleading will be an incorrect n estimate. Our estimates of S-allele numbers based on silent or on synonymous sites are lower than the numbers of SRK alleles directly observed (and sequenced) in A. lyrata (Charlesworth et al. 2003a; Bechsgaard et al. 2004; Mable et al. 2004). Even assuming n = 50, however, only doubles the estimated recombination rates in Table 3. Our estimates are also probably conservative because we used physical distances for A. thaliana, whose genome is smaller than that of A. lyrata. Unless the A. lyrata physical distances are considerably smaller than those in A. thaliana, our results suggest that there is a region of suppressed crossing over, which may not extend as far as the distant flanking genes we have studied, since none of these four loci has high diversity and two of them yielded similar estimated diversity within S haplotypes and between different haplotypes. Since diversity estimates have high variance, and our sample of haplotypes whose phase could be established is small, the extent of the region remains uncertain. Balancing selection at the S loci may be affecting the polymorphism of a large set of loci in this region. Although the apparently nonrecombining region is thus probably small, the homologous region in A. thaliana (i.e., between the same loci that delimit the mapped region in A. lyrata) contains >200 genes.

Other systems with long-term balancing selection:

The approach used here should be applicable to other systems with long-term balancing selection, including MHC and the honeybee sex-determining system (Hasselmann and Beye 2004; Cho et al. 2006), and it should be possible to estimate the numbers of functionally different alleles. A difficulty, however, is that the sequences that have been determined for these systems are not assigned to different functional classes of alleles. Such assignment is feasible for the honeybee sex-determining system, though it is laborious, but for MHC alleles it is very difficult, because the functions of these loci are unknown, so that alleles are classified and named according to sequence similarity; thus one cannot estimate diversity within and between classes, other than dividing the sequences arbitrarily. For instance, a study of HLA-DPB1 sequences in human populations (Bergström et al. 1998) found much lower nucleotide diversity within 13 such “lineages” than between them. The within-lineage diversity estimates range from 0.0007 for introns 1 and 2 and 0.0006 for nonantigen recognition sites in exon 2 (both ∼100 times less than the values between the lineages) to 0.087 for sites encoding the amino acids in exon 2 involved in antigen recognition (more than half the between-lineage estimate of 0.139). The exon 2 antigen recognition sites are thought to be directly involved in the protein's function, and there is evidence that they are under balancing selection (Hughes et al. 1990), so these are sites in the gene corresponding to r = 0, or close to zero, and they should thus have the highest ratio of diversity between vs. within lineages. This suggests that the lineages may not correspond to functionally distinct alleles. Another possibility is that different allelic types can recombine without losing their functional distinctiveness, but this cannot account for the low ratio for the nonantigen recognition sites (non-ARS) in exon 2. Although much more data are needed for this kind of estimate, we used the equation appropriate for MHC (see appendix); the ARS yield a surprisingly high estimate of 97 functional allelic classes, while the non-ARS in exon 2 yield a value of 8, and an implausibly high estimated r value of 19.6 cM/Mb.

The “subdivision theory” developed here and by Takahata and Satta (1998) should nevertheless help toward understanding the high diversity in MHC regions in a quantitative manner, by making it possible to use recombination rate data to ask whether high diversity in any given region can be explained by linkage to regions under balancing selection or whether it requires selection acting within the region (Grimsley et al. 1998). It has been suggested that the higher than usual polymorphism of loci in the region of the genome surrounding the MHC loci is due to “hitchhiking” by the selected loci (Shiina et al. 2006). A better characterization of the situation would be in terms of the subdivision due to balancing selection at loci in the region, since the term hitchhiking refers to a situation in which allele frequencies are being altered by directional selection. If there are enough functionally different alleles (high n in the model), and low enough recombination, this may even be capable of accounting for the functional variants in the 5′ cis-regulatory region of the MHC-DQA1 gene, ∼4 kb from the gene's coding region (Loisel et al. 2006).

Conclusions:

Since diversity data have high variances, accurate estimates using this approach will require large samples of alleles of many functional classes. Such samples are not easy to obtain for self-incompatibility, even though functional classes can, in principle, be determined, and our recombination rate estimates are clearly rough (and were impossible for some of the S-flanking loci, due to higher diversity estimates within haplotypes with the same SRK alleles than between them). They will be even more difficult to obtain for MHC loci. In both cases, however, the theory shows clearly that sets of very similar sequences may represent alleles of the same functional class, and this may help determine the number of such classes, given estimates of the recombination rate, even without knowing the actual nature of the function.

APPENDIX: DERIVATION OF EXPRESSIONS FOR NUCLEOTIDE DIVERSITIES AT SITES CLOSELY LINKED TO A LOCUS UNDER BALANCING SELECTION

We wish to find the coalescence times of sites at a genetic distance r from the selected locus, where r is the recombination rate per nucleotide between the site and the selected locus. This can be done using the approach previously developed for a population subdivided into demes, as suggested by Takahata (1995). There are two expected pairwise coalescence times, one for pairs of different allelic classes, and one for two members of the same allelic class, T_between and T_within, respectively. We assume that the allelic classes are exchangeable (Wakeley 1999), i.e., all allelic classes are at the same frequency.

Using the approach of Nagylaki (1998), Equation 6, the fundamental expression for T_within is

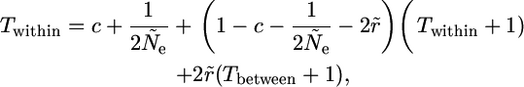(A1)

where N_e is the effective size of the population, and

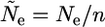(A2)

is the effective population size within an allelic class.

In addition, n is the number of alleles at the selected locus, and c is the “turnover rate,” i.e., the probability that an allele in a given generation originated from a different allele. The first two terms in the fundamental equation for T_within describe coalescences in the preceding generation within a new allele and within existing alleles, respectively. The remaining terms represent cases when no coalescence has occurred in the previous generation, so that there is a delay of one generation in the time to coalescence. The third term describes the case when turnover has not occurred, nor has there been recombination. The final term takes account of recombination with other allelic classes.

In the terms on the right-hand side of Equation A1, r is modified according to the number of different functional types of alleles with which recombination of a given allele type can occur, as indicated by a tilde. Assuming equal frequencies of all functional types of allele, if the form of selection is such that homozygous genotypes can occur, as in MHC systems, the frequency with which a given functional type of allele encounters an allele of a different class (i.e., is heterozygous for two functional classes or types of allele) is (n − 1)/n. The chance that, in such a heterozygote, a neutral variant switches to a given allele by recombination from another allele is r. Thus the per generation probability of such a switching event is

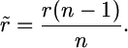(A3)

In the case of gametophytic self-incompatibility, where homozygotes for alleles of the same functional class cannot occur, functionally different alleles are always present in the heterozygous state, and so the frequency of such a switching event is simply r.

For determining T_between, we have

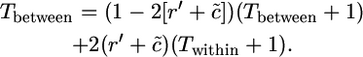(A4)

In this case, we again have to consider whether or not homozygous genotypes can occur. In Equation A4, we use r′ = r/n when homozygous genotypes can occur, as can be seen as follows. If we consider a randomly chosen pair of alleles, one from each of two distinct allelic classes, the frequency with which one member of the pair is present in combination with the other, among all members of the population that contain the other allele, is 1/n. The chance that a recombination event allows a neutral variant to switch from one functional type to the other is thus r/n. In the case of gametophytic self-incompatibility, however, r′ = r/(n − 1), since alleles are always present in the heterozygous state, and the chance that one of a given pair of distinct alleles is present in heterozygotes that contain the other allele is 1/(n − 1). We also have to take account of the number of alleles that can lead to turnover events, and so c is divided by n (indicated by a tilde in Equation A4).

These expressions simplify to the following, using the same notation as defined above:

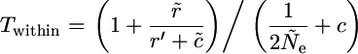(A5)

and

(A6)

When there is no recombination, we can simplify further, to Equations 1a and 1b in the results section above. The first expression is the same as in Takahata and Satta (1998), but the second differs slightly, because we have used c/n, rather than c/(n − 1), as just explained. When there are many alleles, the differences become very small.

Finally, for the case of a site recombining with a gametophytic self-incompatibility locus, we have, from Equation A2,

(A7)