Metastable Polymerization of Sickle Hemoglobin in Droplets

Abstract

Sickle cell disease arises from a genetic mutation of one amino acid in each of the two hemoglobin β chains, leading to the polymerization of hemoglobin in the red cell upon deoxygenation, and is characterized by vascular crises and tissue damage due to the obstruction of small vessels by sickled cells. It has been an untested assumption that, in red cells that sickle, the growing polymer mass would consume monomers until the thermodynamically well-described monomer solubility was reached. By photolyzing droplets of sickle hemoglobin suspended in oil we find that polymerization does not exhaust the available store of monomers, but stops prematurely, leaving the solutions in a supersaturated, metastable state typically 20% above solubility at 37°C, though the particular values depend on the details of the experiment. We propose that polymer growth stops because the growing ends reach the droplet edge, whereas new polymer formation is thwarted by long nucleation times, since the hemoglobin concentration is lowered by depletion of monomers into the polymers that have formed. This finding suggests a new aspect to the pathophysiology of sickle cell disease, namely, that cells deoxygenated in the microcirculation are not merely undeformable, but will actively wedge themselves tightly against the walls of the microvasculature by a ratchet-like mechanism driven by the supersaturated solution.

Sickle cell disease is pathogenic because of the microvascular obstruction that occurs when the intracellular sickle hemoglobin polymerizes into long rod-like fibers which have been found to form a rigid gel ^{1; 2}. While other non-pathological polymers, especially those formed by actin or tubulin, are well known to exert forces that have important functions ^{3; 4; 5; 6; 7}, polymers of HbS have been viewed as constituents of a pathological but passive gel. Here we show that growing HbS gels can generate forces and pressures that are pathologically relevant, and that the effects of gelation cannot be reduced to passive resistance by a solid body.

These results follow upon the simple attempt to resolve a remarkable gap in describing the process of polymerization. Despite the recognition of sickle hemoglobin polymerization as the underlying cause of sickle cell disease for over a half century ⁸, no non-invasive means has been known by which the net mass of polymerized monomers in solutions or cells can be measured. Light scattering becomes nonlinear in mass ⁹ as the reaction proceeds and is uncalibrated even in the linear regime. Birefringence or linear dichroism only reveals aligned polymers ¹⁰. Calorimetry, while promising in principle, cannot be used for microscopic samples such as cells, and even in solutions, questions remain about the interpretation of the measurements. ¹¹ No other spectroscopic “tags” have been discovered, such as fluorescent labels, mainly due to the difficulty posed by the ability of hemes to quench nearby fluorophores. Although sedimentation can be used robustly to determine solubility, it is not suited to small samples such as cells. It has therefore been assumed without proof that the cessation of polymerization only occurred when the monomer concentration reached solubility ¹².

The importance of knowing the extent of polymerization derives from the fact that incomplete polymerization would leave the solution in a metastable state of supersaturation, capable of exerting an outward pressure against the cell wall. If the cell is within a confining capillary, this pressure would be exerted against the capillary walls, and would revise a dominant paradigm of sickle hemoglobin pathophysiology, namely that vascular problems simply arise from the incompressibility of the gel^{2; 13}.

Our solution to the problem of measuring reaction extent uses an emulsion of sickle hemoglobin droplets in oil. Polymerization is induced in most but not all of a droplet by laser photolysis. Continuous intense illumination of COHbS (which will not itself polymerize) reversibly creates deoxyHbS which is equivalent to chemically deoxygenated HbS, and thus forms polymers while illuminated.¹⁴ Complete photolysis is assured by measurement of the change in absorption spectrum. Temperature increase due to photolysis under such conditions has been established to be no more than a few °C.^{14; 15; 16} The emulsion is sealed between coverslips, and microscope optics are used to view the droplets, which range from 20 μm to 300 μm diameter (in all cases larger than red cells which have diameters of 7–8 μm) with thickness fixed by the slide, between 3 and 6 μm. An optical mask keeps a part of the observed droplet from being illuminated by the laser. This mask is placed at a point in the laser path conjugate to the sample plane, so that the masked area can be observed, even though the laser is blocked from hitting it. Figure 1 shows such a droplet with an edge mask. As monomers in the photolyzed portion are consumed in making polymers, the unphotolyzed segment becomes a finite reservoir for their replenishment. The optical properties of this segment are still those of a simple solution with constant path length, and so permit accurate concentration measurement there (in contrast to polymerized regions which contain fibers with strong optical anisotropy.) It was our expectation that the concentration of Hb in this reservoir would diminish until it reached solubility. This did occur if the final mass of polymers was small, such as polymerization in high phosphate buffers or in the presence of dextran which crowds the solution and assists polymerization¹⁷. For example, in 1.0 M phosphate buffer at 30°C, conventional methods measured a solubility of 32 mg/ml ¹⁸ and 33 mg/ml ¹⁹ , while our method found 29 ± 1 mg/ml. In the presence of 12 mg/ml dextran (work to be published), agreement is better than 4% between sedimentation methods and this approach. However, in low phosphate buffers that are close to physiological the polymerization stopped well short of solubility. (See Figure 2)

Figure 1.

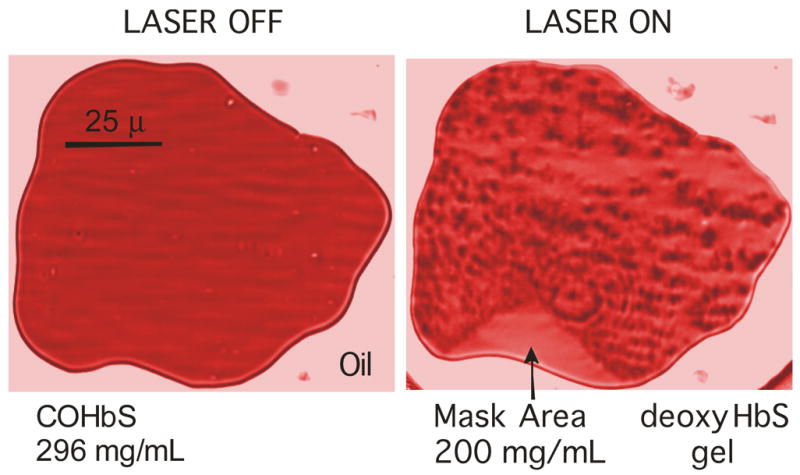
A droplet of sickle hemoglobin in castor oil is shown before and after photolysis. The sample of chromatogrpahically purified Hb (in 0.15 M phosphate buffer at pH 7.35; 0.55 M sodium dithionite) has a thickness of 3.7 μm and is observed using a Leitz 32×LWD microscope objective; images are shown at 426 nm in the intensely absorbing Soret band. (Color has been introduced to help distinguish the regions). Laser photolysis by the 488 nm line of an Argon ion laser deoxygenates the COHb, which forms polymers. The rough texture is the result of the combination of turbidity, linear dichroism and non-uniformity of the polymer mass. On the perimeter of the droplet a triangular region has been masked from laser illumination, and remains HbCO, retaining the good optical characteristics of the unpolymerized Hb. Monomers diffuse from that region into the polymerized region as polymerization proceeds, until the final concentration is reached, as shown.

Figure 2.

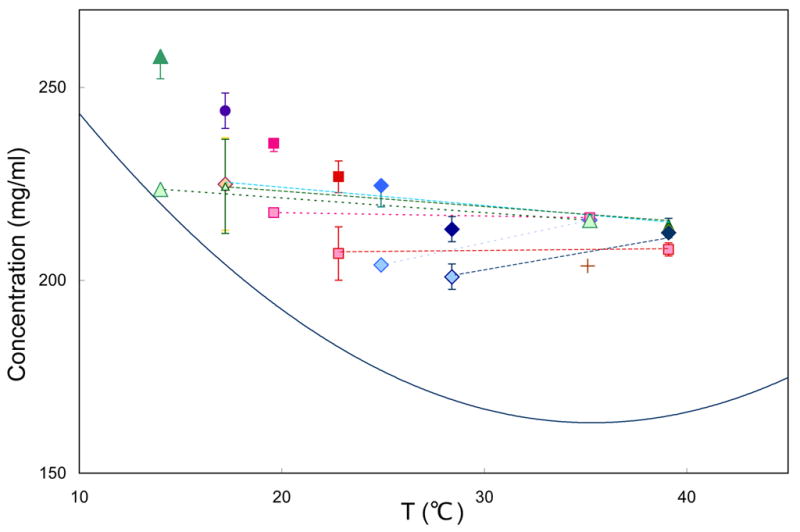
Final concentration as a function of temperature. The solid curve is the solubility of HbS ¹². All samples are in 200–300 μm droplets, in which the masked area is 4–5% of the total, and is placed at the center of the Hb drop. Points connected by dashed lines were polymerized at the higher temperature of the pair, and the temperature then was changed to the lower temperature. At the high temperatures, some symbols occlude others because the concentrations achieved were the same. All temperature-shift experiments involved polymerization at the high temperature, followed by shifting to a lower temperature, and then finally depolymerization. Solo points (all in darker colors) have been polymerized directly to the final temperature. The cross shows a concentration achieved by pressing on the slide, initially gelled at 35°C. Temperatures were regulated by a thermoelectric stage. Samples were observed by an Ealing 15×reflecting objective; spectra were recorded in the Soret region using an Ocean optics 2000 spectrometer. Photolysis was by a Lambda-Pro diode-pumped 532 nm solid state laser.

This shortfall occurred regardless of the geometry of the masked area, which was variously tried at the center, as a cut-in at the edge, or as an annulus around the photolyzed spot. The final concentration was dependent on its history. Photolysis and observation at 20 °C gave a different final concentration than that obtained by photolysis at 35 °C, followed by lowering the sample temperature to 20°C without intermediate depolymerization. This can be seen in Figure 2.

An explanation for these results is that the growing polymer ends encounter the boundary of the droplet or internal obstructions such as other polymers causing the cessation of growth. This is not compensated by the formation of new polymers because of the long time required for their nucleation once much of the hemoglobin is consumed. In sickle hemoglobin, two types of nucleation generate polymers. Homogeneous nucleation generates polymers by random coalescence of monomers in solution; heterogeneous nucleation creates new polymers on the surface of other polymers that are already present, generating attached polymer arrays, called domains²⁰. Both pathways are extraordinarily concentration dependent: as concentration drops from 300 mg/ml to 210 mg/ml, for example, the heterogeneous nucleation rate drops by 10 orders of magnitude ²⁰ even though 210 mg/ml is well above solubility. Generation of additional polymers at the final concentration seen here is thus hindered by the lowered rate of heterogeneous nucleation at these concentrations.

We reasoned that if fibers could be broken, additional ends would be generated that would permit lower final monomer concentrations to be achieved. To test our hypothesis, therefore, we tried the simple expedient of pressing on the thin slides in which the polymers were formed. In almost all cases this resulted in a decrease of the final monomer concentration, as we expected, though not generally to the solubility measured in sedimentation experiments. (See Figure 2 for one example.) In no case was a concentration ever achieved below the solubility. The variability is most likely because domains grow in different orientations relative to the slides, and some orientations are more conducive to breakage.

Striking support comes from an experiment in which we used a triangular mask at one edge of a droplet as shown in Figure 3. Some 71 minutes after a final value had been achieved in the masked region, an abrupt flow of hemoglobin shrunk the masked area and redistributed the hemoglobin to the droplet perimeter. We interpret this as due to the outward force of the polymer mass exceeding the surface tension of the droplet with the glass, and causing substantial and sudden mass flow. Such behavior was regularly observed in experiments of similar duration, and was one of the motivations for using geometries with a fully interior mask (e.g. Figure 2).

Figure 3.

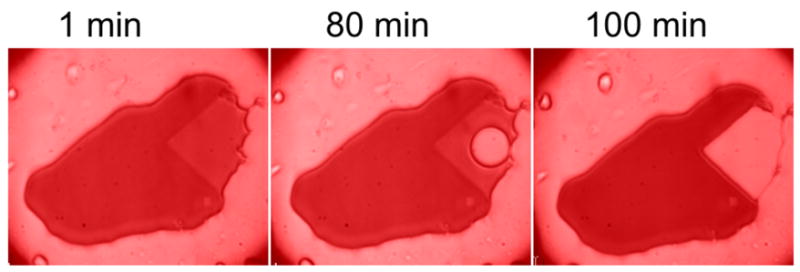
A droplet shown during collapse of the masked area. As in Figure 1, a triangular edge mask kept an unphotolyzed reservoir of COHbS adjacent to a region polymerized by photolysis. After 71 minutes, the hemoglobin in the reservoir flowed to the perimeter, and we interpret this as due to the outward pressure of the fibers against the surface. A bubble forms first because the edge of the droplet is pinned. Conditions otherwise are as in Figure 1.

Alternate hypotheses were tested. We considered the possibility that an oil-hemoglobin interaction might inactivate some molecules. Because nucleation rates are exquisitely sensitive to concentration, we measured nucleation rates in paired samples with and without oil, using stochastic nucleation methods described elsewhere ²¹. The measured rates translated into concentrations that differed by less than 3%, far less than the observed final concentration differences. We also speculated that a polymer barrier might have been formed in the thin slide to dam the motion of monomers. We tested this hypothesis by creating a sample with masked areas simultaneously on left and right sides of a droplet. After a final concentration was achieved, we abruptly increased the mask size on one side, allowing some of the Hb to depolymerize. This caused the reservoir concentration to rise immediately on that side (as nearby depolymerized monomers spilled back in) followed by a slower decay to a new final concentration, higher than that present when both masks were initially set. Meanwhile, the concentration in the opposite side reservoir also rose as monomers leaked through the gel. The monomer concentration on the opposite side ultimately reached the same final concentration as on the side with the mask that had been moved, and hence excluded the monomer-barrier hypothesis.

These results suggest a new aspect to the pathophysiology of sickle cell disease. Hitherto it has been assumed that the rigidity of the polymerized red cell is responsible for any mechanical occlusion. From the results seen here, we see that in a red cell there can be an outward pressure of the polymer mass against the confining boundary of the capillaries, which have a diameter that is smaller than that of the resting red cell, mandating erythrocyte deformability as a condition of successful circulation. Such a pressure would not exist if polymer length had reached equilibrium.

Indeed, single polymer experiments have been performed that illustrate the ratchet-like behavior that can generate such pressures. In those experiments, a polymer growing within a red cell first deforms the cell and finally buckles as the force generated by the fiber can no longer stretch the cell membrane ²². The reason such growth leads to pressure is that random fluctuations of the boundary permit growth, which in turn lowers the free energy of the system. The fluctuations allow growth by a Brownian-type motion, and the lowering of the energy of the system represents a kind of ratchet. This behavior, known as a Brownian ratchet, has been characterized theoretically ^{22; 23}, and the force on a fiber when its growth stalls is given by f = (kT/δ) ln S where S is the supersaturation of the solution, δis the length of elongation per added monomer, k is Boltzmann’s constant, and T the absolute temperature. When solutions stop polymerization with S > 1, as reported here, this supersaturation provides a source of free energy to press the cell into the surrounding vascular tissue. More than passive obstruction, this envisions active wedging of the cell against its surroundings. We can use typical values of polymerization rates and parameters ^{21; 24} to infer how many polymers will be impinging on the surface per unit area. Coupled with the Brownian ratchet approach that provides the force per polymer, it is possible to compute the total force per area, viz. the outward pressure. We predict an average added pressure of 0.1 atm (76 mm Hg). This pressure is a direct consequence of the supersaturation of the solution, and is exerted against the walls of the microcirculation.

This gives rise to a plethora of other possibilities which must be explored, including damage to the cytoskeleton, and a response from the cells against which the pressure is exerted. While not all cells will deoxygenate within constraining vessels, very few cells need actually sickle to generate problems; it has been estimated that, on average, one in 60,000 trips of a sickle red cell lead to destructive vasooclusion ¹. The work here illustrates a previously unknown way in which that might occur.