A Bayesian Measure of the Probability of False Discovery in Genetic Epidemiology Studies

Abstract

In light of the vast amounts of genomic data that are now being generated, we propose a new measure, the Bayesian false-discovery probability (BFDP), for assessing the noteworthiness of an observed association. BFDP shares the ease of calculation of the recently proposed false-positive report probability (FPRP) but uses more information, has a noteworthy threshold defined naturally in terms of the costs of false discovery and nondiscovery, and has a sound methodological foundation. In addition, in a multiple-testing situation, it is straightforward to estimate the expected numbers of false discoveries and false nondiscoveries. We provide an in-depth discussion of FPRP, including a comparison with the q value, and examine the empirical behavior of these measures, along with BFDP, via simulation. Finally, we use BFDP to assess the association between 131 single-nucleotide polymorphisms and lung cancer in a case-control study.

With the advent of new genotyping and other molecular biology technologies, there has been a huge increase in the quantities of data that are available for analysis; this has focused attention on the manner by which associations are reported in the epidemiology literature^1–3 and, in particular, on methods by which the number of false positives can be controlled without missing too many scientifically interesting associations. Motivated by candidate-gene and genomewide association studies,^4–7 we consider here the reporting of associations and the problem of multiple-hypothesis testing.

Despite numerous protestations to the contrary (for a particularly clear exposition, see the work of Goodman⁸), a common error is to view P values as the probability of the null hypothesis given the observed statistic, when, in fact, they give the probability of the statistic given the hypothesis. To assess the probability of the hypothesis given the data, a Bayesian approach is needed, and this requires the specification of the prior probability of the hypothesis and the probability of the data under specified alternatives.² This motivates a move away from P values, and here we suggest an approach based on an approximate Bayes factor that we call the “Bayesian false-discovery probability” (BFDP). Recently, Wacholder et al.² introduced the false-positive reporting probability (FPRP) as a means to assess whether the strength of an association was “noteworthy,” a terminology we use here interchangeably with “discovery,” the latter term being common in the literature on multiple-hypothesis testing.^9,10 FPRP was introduced as a criteria, “to help investigators, editors, and readers of research articles to protect themselves from overinterpreting statistically significant findings that are not likely to signify a true association”^2(p434); this endeavor seems extremely useful, and we introduce BFDP to satisfy the same objective. FPRP has generated a lot of interest, and we discuss its relationship to BFDP and to the related but subtly different q value.¹⁰ The difference is that FPRP uses the observed significance region, whereas the q value has a fixed region, which allows the false-discovery rate (FDR) to be controlled, a property not inherited by FPRP, making it difficult to calibrate. We outline how BFDP may be used for design and, in a multiple-hypothesis–testing context, how BFDP provides the expected numbers of false and missed discoveries.

Methods

Reporting a Hypothesis as Noteworthy via Bayesian Decision Theory

Under frequentist inference, the null hypothesis H₀ is viewed as nonrandom; so, to calculate the probability of H₀, one must take a Bayesian standpoint; alternatives to H₀ must also be considered, to define the sample space of hypotheses. Let y=(y₁,…,y_n) denote the observed data and H₁ the alternative hypothesis. The application of Bayes's theorem gives the probability of the hypothesis H₀ given data y as

where

is the probability of the data averaged over H₀ and H₁, Pr(H₀|H₀∪H₁) is the prior probability that H₀ is true (given that one of H₀ and H₁ is true), and Pr(H₁|H₀∪H₁)=1-Pr(H₀|H₀∪H₁) is the prior on the alternative hypothesis. It is clear from equation (1) that we are calculating the probability of the null given that either H₀ or H₁ is true. Hence, we are calculating the “relative truth”; H₀ may provide a poor fit to the data, but so may H₁.

Although recognizing that we are conditioning on either H₀ or H₁ being true is of crucial importance, we now suppress this in our notation, for brevity, and write:

where π₀=Pr(H₀) is the prior on the null. We rewrite equation (2) as

where

is the Bayes factor and

is the prior odds of no association. The use of the Bayes factors as a summary of the evidence contained in the observed data has been advocated in both a medical context¹¹ and a genetic epidemiology context.¹² Often, the alternative hypothesis will be indexed by a continuous parameter. For example, for the case of H₀:θ=0 versus H₁:θ≠0, we have 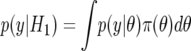, where π(θ) is the prior on -∞<θ<∞.

In terms of making a decision as to which one of H₀ and H₁ to report (given that we will report one of them), the Bayesian decision theoretic solution is to assign costs to the consequences of making a decision, given the truth of H₀ or H₁. Specifically, let C(δ,H) be the cost associated with decision δ, when the truth is H. Table 1 gives the four costs, two of which are zero; C_α is the cost of a false discovery (we decide to report an association as noteworthy when, in fact, the null is true), and C_β is the cost of a false nondiscovery (we decide to call an association nonnoteworthy when, in fact, an association exists). Appendix A shows that, to minimize the posterior expected cost, we should report an association as noteworthy according to the intuitive condition:

which is equivalent to

Hence, we need to consider only the ratio of costs, C_β/C_α.

Table 1. .

Costs Corresponding to Decision δ^[Note]

	C(δ,H) for Decision
Truth	δ=0 (Nonnoteworthy)	δ=1 (Noteworthy)
H=H0	0	Cα
H=H1	Cβ	0

Note.— C_α is the cost of a false discovery, and C_β is the cost of a false nondiscovery.

To implement this approach, one must recognize that π₀ and C_β/C_α are playing quite different roles. The prior probability of no association, π₀, is based on the totality of evidence available before analysis of the data from the current study. The quantity C_β/C_α corresponds to the ratio of costs of false nondiscovery and false discovery. If, for example, missing a true association is four times more costly than falsely reporting an association, so that C_β/C_α=4, we should report H₁ if Pr(H₁|y) is at least 0.2 or, equivalently, if Pr(H₀|y) is <0.8. In a multiple-hypothesis–testing context, the choice of π₀ will strongly influence the total number of associations called noteworthy, whereas C_β/C_α will determine the expected number of these that are false discoveries and false nondiscoveries. The ratio of costs, C_β/C_α, for candidate-gene studies is likely to be lower than that for genomewide association studies, since, in the latter, we wish to produce a “long list” of candidates for future investigation, whereas, in the former, the follow-up of noteworthy candidates is more expensive. If a large study attempts to be definitive, then the cost of a false discovery will be greater, and a more stringent (i.e., lower) threshold for Pr(H₀|y) will result. Wacholder et al.² provide an excellent discussion of issues regarding the decision process in a variety of contexts.

Simple Null Hypothesis with Composite Alternative and Adjustment for Confounding

We now consider a specific situation in which disease risk, p, is modeled via the logistic regression

with γ, a c×1 vector of log relative risks corresponding to confounders, and θ, the log relative risk of interest; x is a c×1 vector of confounders, and z is the value of an “exposure.” The null and alternative hypotheses are H₀:θ=0 and H₁:θ≠0, with γ unspecified under each. For concreteness, suppose that the association between risk and a particular SNP is of interest and assume a dominant model, so that z is an indicator of being heterozygous or homozygous for the mutant allele and e^θ is the associated relative risk.

The calculation of the Bayes factor in equation (3) requires the complete specification of both the data-generating mechanism (the likelihood), the prior distribution for all parameters of the model, and the calculation of multidimensional integrals. In general, each of these steps is difficult (appendix B contains details of these specifications). Instead, suppose a logistic regression produces an estimate, 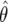, with associated standard error 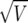. We then (i) summarize the information in the likelihood concerning the parameter of interest θ, using 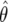and its asymptotic distribution N(θ,V), and (ii) consider a prior for θ only, rather than a joint specification for θ and γ. We assume this prior is θ∼N(0,W); it is natural to assume that the prior is centered at 0, corresponding to the null of no association (the probability of any specific value, in particular the null value θ=0, is zero, and the prior on the null value is π₀). Whereas π₁=1-π₀ is the prior probability on the existence of an association, W describes the size of the strength of the association, conditional on the existence of one.

Appendix B shows that, with (i) and (ii), the Bayes factor p(y|H₀)/p(y|H₁) is replaced by , and we obtain the approximate Bayes factor

where 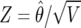is the usual Z statistic and the shrinkage factor

is the ratio of the prior variance to the total variance. It is important to note that the Bayes factor depends not only on Z but also on the power through V, which itself depends on the minor-allele frequency (MAF) and on the size of the effect. We define the BFDP as follows:

The name “BFDP” reflects the fact that, if we report an association as noteworthy, this is the probability of the null, and, therefore, the probability of a false discovery. The “Bayesian” label emphasizes that we are taking a model-based approach, so the probability is conditional on the model and, in particular, on the assumed π₀. Given that BFDP is an approximation of Pr(H₀|y), we should report the association as noteworthy if expression (4) is satisfied.

In addition to reporting BFDP, it is also informative to give point and interval estimates for θ. Under the model given above, and given an association, the approximate posterior for the relative risk is given by

so that the posterior median is 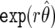. Hence, the maximum-likelihood estimator (MLE) 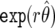undergoes shrinkage toward the prior mean of 1, with the amount of shrinkage given by equation (6). As the sample size increases, V→0 and r→1, so that the posterior concentrates around the MLE. Shrinkage is desirable in situations in which the power is low (i.e., V is large), since it reduces the reporting of chance associations based on few data. Hierarchical models also produce this behavior and have been advocated in an epidemiological context.^13,14 Under expression (7), a 100(1-α)% credible interval for the relative risk is given by , where Φ(·) is the distribution function of a standard normal random variable.

Prior Choice

Recall that we assume the prior θ∼N(0,W). It is relatively straightforward to pick the prior variance W under the alternative by specifying that the relative risk e^θ lies in with probability 1-ε. This leads to

For example, we might assume that, with probability 0.95, the relative risk lies between 2/3 and 3/2; this corresponds to the choices ε=0.05 and θ_p=log(1.5), which give, via equation (8), W=0.21². In practice, we can examine the sensitivity to W by considering a range of values. We should be wary of setting W to be very large, however, since BF→∞ as W→∞, so that the null is chosen for very large values of the prior variance.¹⁵ In practice, this is not an issue in the context considered here, since one can choose sensible values as an upper bound for the relative risk a priori.

In the context of a genomewide association study, we may wish to specify the prior variance (and hence the expected effect size) conditional on the MAF associated with the SNP whose relative risk we are estimating, although we do not pursue such a specification here. The allelic spectrum has been discussed by a number of authors.⁶

A graphical representation of BFDP is provided in figure 1a. In this hypothetical situation, we suppose that a logistic regression has produced an estimate of 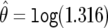, along with associated SE of 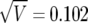(the latter depending on the estimate and on the MAF), and we assume a prior variance of W=[log(2)/1.96]²=0.35². 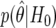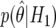These values result in the two normal curves in figure 1, N(0,0.10²) under H₀ and N(0,0.10²+0.35²) under H₁; and are indicated, and the ratio of these values provides an approximate Bayes factor of 0.11, so is 1/0.11=9 times more likely under H₁ than under H₀.

Figure 1. .

Graphical representation of BFDP (a) and FPRP (b). For BFDP, the approximate Bayes factor is the ratio of indicated densities, whereas, for FPRP, the dark- and light-shaded areas represent and 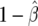, respectively.

Design by Use of BFDP

We now describe how BFDP may be used to assess whether a study is likely to provide a noteworthy association. Recall that the data are entered into the BFDP via the approximate Bayes factor, which is a simple function of 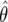and V, so we need only these quantities to calculate BFDP, along with the prior specifications W and π₁. For illustration, we consider a dominant model with h, the probability of being heterozygous or homozygous for the mutant allele (we refer to this as “exposed”); g₀, the probability of disease given two copies of the wild-type (referred to as “unexposed”); and g₁=g₀×e^θ, the probability of disease given one or two mutant alleles. Under this scenario, the expected frequencies by exposure and disease status are

and

and, asymptotically, we have

where n₀ and n₁ are the numbers of controls and cases. For any particular set of design parameters, there is a distribution of BFDP, since the observed numbers of exposed and unexposed in the case and control groups vary across simulations. To illustrate, figure 2 shows the distribution of BFDP for data simulated with π₀=0.99, θ=log(1.5), n₀=n₁=1,000, g₀=0.001, and W=[log(2)/1.96]², for h of 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, and 0.5. For these frequencies, the Bayesian “powers” of achieving a noteworthy BFDP at a level of 0.8 (which corresponds to a false nondiscovery being four times as costly as a false discovery) are 0%, 13%, 42%, 76%, 88%, 92%, and 92%, respectively.

Figure 2. .

Distribution of BFDP by allele frequency for 1,000 cases and 1,000 controls with a relative risk of 1.5 and with π₀=0.99. The solid line connects the median BFDP at each frequency. The dotted line corresponds to a noteworthy threshold of 0.8; the powers to achieve this level (i.e., for the BFDP to fall below this threshold) at the given frequencies are 0%, 13%, 42%, 76%, 88%, 92%, and 92%.

We next calculate the sample size required to obtain a BFDP <0.8, with probability 0.8 (the Bayesian power)—that is,

Figure 3 shows the sample size required to satisfy expression (9) as a function of the frequency of one or two copies of the mutant allele (across the range 0.05–0.50) and π₁. We see that, for rare alleles and unlikely alternatives, very large sample sizes are required. We emphasize that these calculations were performed assuming that the SNP was causative; if the SNP is only in linkage disequilibrium with the true causal SNP, then the sample sizes will increase further.

Figure 3. .

Number of cases required to obtain a BFDP of <0.8 with probability 0.8, as a function of the frequency of one or two mutant allele copies and π₁, with a relative risk of 1.5 (under the assumption of an equal number of cases and controls).

FPRP

Since its introduction in 2004, FPRP has been the subject of great interest, as evidenced by the >200 references to the article by Wacholder et al.,² according to a Web of Science citation search performed in March 2007, with the article discussed in both applied^16–20 and methodological^7,21,22 contexts.

FPRP is defined as follows:

where is the observed significance level of a statistic (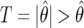 in the logistic regression context); π₀ is the prior probability that H₀ is true; and 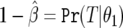is the “power” evaluated at θ₁. It is not the conventional power, since it is evaluated at the observed 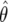and hence does not have the usual frequentist properties (being based on the observed P value, a data-defined threshold).

For examination of an association between a SNP and a disease, Wacholder et al.² recommend the following steps:

• 1. Preset a noteworthy FPRP for each hypothesis; 0.2 and 0.5 are given as examples.
• 2. Determine the prior probability of the alternative hypothesis, π₁=1-π₀.
• 3. Specify the parameter value, θ₁, at which the power is to be evaluated; the value θ₁=log(1.5) is suggested by Wacholder et al.² for a detrimental SNP, and θ₁=log(2/3) for a protective SNP.
• 4. Calculate FPRP by use of equation (10), and report the association as noteworthy or not by comparing the value with the cutoff specified in step 1.

Insight into FPRP may be gained by considering a formal Bayesian approach. Assume that the “data” consist of T as defined above, and consider the point null and alternative hypotheses H₀:θ=0 and H₁:θ=θ₁. Then,

is equal to equation (10). Writing

we see that the “frequentist factor” is taking the role of the Bayes factor. An alternative derivation of FPRP occurs if we take H₀:θ=0 versus H₁:θ≠0 but assume a point mass prior at θ=θ₁. In this case, Pr(T|H₁)=Pr(T|θ₁), and we again obtain equation (10).

Figure 1b graphically illustrates the calculation of FPRP for the same 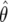and V used for the calculation of the approximate Bayes factor. The power is calculated at θ₁=log(1.5), and and 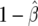are shown as the dark- and light-shaded areas, respectively. In this example, 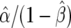, so that the data, T, are 150 times more likely under the alternative than under the null, a much stronger conclusion than that reached using the approximate Bayes factor.

Although FPRP is a Bayesian procedure, when compared with BFDP, it differs in each of the likelihood, prior, and decision-rule choices.

The likelihood

Information is being lost by considering 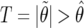(a censored observation), rather than 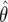itself. Given that we are using the observed P value, this does not seem appropriate, since the observation is not larger than a particular value, it is exactly that value. An intermediary approach between FPRP and BFDP, which considers only a single alternative but does not censor the observation, would be to use

where

is the likelihood ratio and φ(·) is the density function of a standard normal random variable. Note that

so that taking the censored observation gives a lower bound on the posterior probability of the null associated with the observed value of the estimate. In their appendix, Wacholder et al. state, “the FPRP value is the lowest FPRP value at which a test would yield a noteworthy finding.”^2(p441) Although expression (11) would suggest that FPRP<BFDP, the inequality in (11) is for a fixed prior, and it is possible for FPRP to be larger than BFDP if θ₁ is close to 1 (since, then, the power is low and FPRP is relatively larger). Finally, the use of a two-sided P value is not consistent with the evaluation of power at a point (one-sided) alternative.

The prior

Assuming that θ=θ₁ as a prior is overly restrictive, BFDP averages over all alternatives θ≠0.

The decision rule

The earlier discussion of decision theory reveals that it is helpful to base the definition of “noteworthiness” on the costs of false discovery and nondiscovery. For FPRP, the decision is with respect to the specific alternative, θ₁, which is more difficult to assess than the cost for the general alternative. One of the values suggested by Wacholder et al.² is 0.2, which corresponds to the belief that the cost of a false declaration that θ=θ₁ is four times larger than the cost of calling nonnoteworthy a true association of strength θ=θ₁. This will often not reflect the aims of a genomewide association study, because, as noted, we would rather have a longer list than a shorter list of SNPs. For a candidate-gene study, a lower threshold is more plausible.

Multiple-Hypothesis Testing

We now consider how BFRP may be used for multiple-hypothesis testing, a situation not explicitly considered by Wacholder et al.²³ Table 2 gives the possible outcomes when m tests are performed; m₀ is the true number of null hypotheses, and k the number of tests that are classified as noteworthy. There is now a large body of literature on how to perform multiple tests.^9,10,24–28 It has been recognized that estimating and characterizing procedures according to the expected numbers of false discoveries and nondiscoveries (given by E[V] and E[T] in table 2) or their rates (E[V/k] and E[T/(m-k)]) is far more relevant than controlling familywise error rates, as is done, for example, by the Bonferroni method (which controls the probability that V⩾1). The latter produces a relatively small k and is therefore conservative, which can lead to substantial power loss and the missing of many true associations.

Table 2. .

The Four Possibilities When m Tests Are Performed and k Tests Are Called Noteworthy^[Note]

Hypothesis	Nonnoteworthy Tests (m-k)	Noteworthy Tests (k)	All Tests (m)
H0	U	V	m0
H1	T	S	m-m0

Note.— V is the number of false discoveries, and T is the number of false nondiscoveries.

Appendix C shows that, if C_β/C_α describes the common ratio of costs of false nondiscovery to costs of false discovery across tests, then we should report associations for which

so that, as with a single test, we have an intuitive rule that is defined in terms of the posterior probability of the null. Let k be the number of such associations. We rank the associations in order of increasing BFDP, 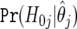, j=1,…,m, so that j=1,…,k represent the noteworthy tests. The expected numbers of true nonnoteworthy, false noteworthy, false nonnoteworthy, and true noteworthy tests are given in table 3. The expected number of false discoveries is the sum of the null probabilities over those hypotheses we report, whereas the expected number of false nondiscoveries is the sum of the probabilities on the alternative over the nonnoteworthy tests. The expected number of false noteworthy tests divided by the number of noteworthy tests has been proposed²² in conjunction with FPRP, to “control the Bayes FDR”; one can evaluate this quantity with any Bayesian approach, however, not just with the specific likelihood and prior setup considered in FPRP.

Table 3. .

Expected Numbers of Tests That Are True or False and Nonnoteworthy or Noteworthy When m Tests Are Performed and k Tests Are Called Noteworthy

Hypothesis	Nonnoteworthy (m-k)	Noteworthy (k)	Total (m)
H0	Expected True	Expected False	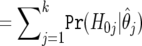m0
H1	Expected False	Expected True	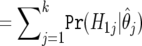m-m0

q Values

Recently, there has been a great deal of interest in the q-value method,¹⁰ which, in a setting of multiple-hypothesis testing and for a fixed critical region, Γ, provides an estimate of the FDR (or, more precisely, the positive FDR, which is the FDR conditioned on at least one noteworthy test). The q value corresponding to Γ is

with the term 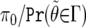estimated from the totality of P values. If all hypotheses are null, then the distribution of P values is uniform, so departures from uniformity informs on the fraction of nulls, π₀, whereas the complete distribution gives an estimate of the denominator in (12).

For a given region, Γ, the average FDR is controlled at level . Suppose a SNP has a q value of q₀; this does not mean that this SNP is false positive with probability q₀. The false-positive probability for this SNP could be much higher, because q₀ is the average proportion of false-positive SNPs that would occur if we call the SNP noteworthy, and this collection contains SNPs that are more noteworthy. The ranking of P and q values is identical, since the denominators of all tests are equal (unlike BFDP and FPRP, which explicitly use the powers of each test in the calculation of their respective denominators).

In microarray experiments (to which q values have been extensively applied), the empirical estimation of π₀ is reliable because a large number of tests are nonnull. Estimation is more difficult in genomewide association studies because the true number of associations is a tiny fraction of the total number of tests performed. It may also be argued that the false-nondiscovery rate is more relevant for genomewide association studies, since missing a true association is more costly than making a false discovery; however, the false-nondiscovery rate still requires an estimate of π₀.

Summary of FPRP

FPRP is a Bayesian procedure that takes as data the observed tail area and assumes a point prior under the alternative. FPRP ignores information by conditioning on a tail area and is difficult to calibrate from a Bayesian perspective, because the ratio of costs is with respect to a specific alternative. Because FPRP uses critical regions defined by the observed P values, the regions are not constant across tests, so frequentist FDR is not controlled; such control is provided by the q-value method.

Results

Empirical Comparison of FPRP and BFRP

We consider a hypothetical, genomewide association case-control study in which the association between disease and m=100,000 SNPs, with alleles A and a at each candidate marker, is evaluated for 3,000 cases and 3,000 controls. To simulate data, we assume that the disease risk, p, is given by the logistic regression model

where e^α=0.002 is the baseline risk and z=0, 0.5, and 1 corresponds to 0, 1, and 2 copies of the mutant allele, respectively. Hence, we assume an additive genetic model,²⁹ with e^θ corresponding to the relative risk associated with two copies of the mutant allele. We take penetrances, from equation (13), to be given by

and then evaluate the probabilities of aa, Aa, and AA, given case and control status, by use of Bayes's theorem. Across all m SNPs, we randomly generate the MAF from a uniform distribution on [0.05, 0.50]. We assume that m-m₀=100 SNPs are associated with disease and generate the log relative risks from a beta distribution with parameters 1 and 3, scaled to lie between log(1.1) and log(1.5); hence, we have an L-shaped distribution of effect sizes, with the relative risks more likely to be closer to 1.1 than to 1.5. The remaining m₀=99,900 SNPs are not associated with disease. We take θ₁=log(1.5) for FPRP and W=[log(1.5)/1.96]² for BFDP.

A major conclusion from this simulation is that, even with 3,000 cases and 3,000 controls, there is very low power for detection of SNPs with low MAFs and/or log relative risks close to 0. With ratios of cost of false nondiscovery to cost of false discovery of 4:1, 10:1, 20:1, and 50:1, the BFDP thresholds of noteworthiness are 0.80, 0.91, 0.95, and 0.98 and yield only 9, 11, 15, and 20 true associations, respectively. Figure 4 plots θ against MAF for the 100 true associations for these four thresholds and indicates the noteworthy and nonnoteworthy SNPs (blackened and nonblackened circles, respectively). The inability to detect SNPs with low MAF and/or relative risks close to 1 is apparent.

Figure 4. .

Log relative risk versus MAF for the 100 nonnull SNPs in the simulated data. Blackened and nonblackened circles represent SNPs called noteworthy and nonnoteworthy, respectively, by BFDP at the stated threshold.

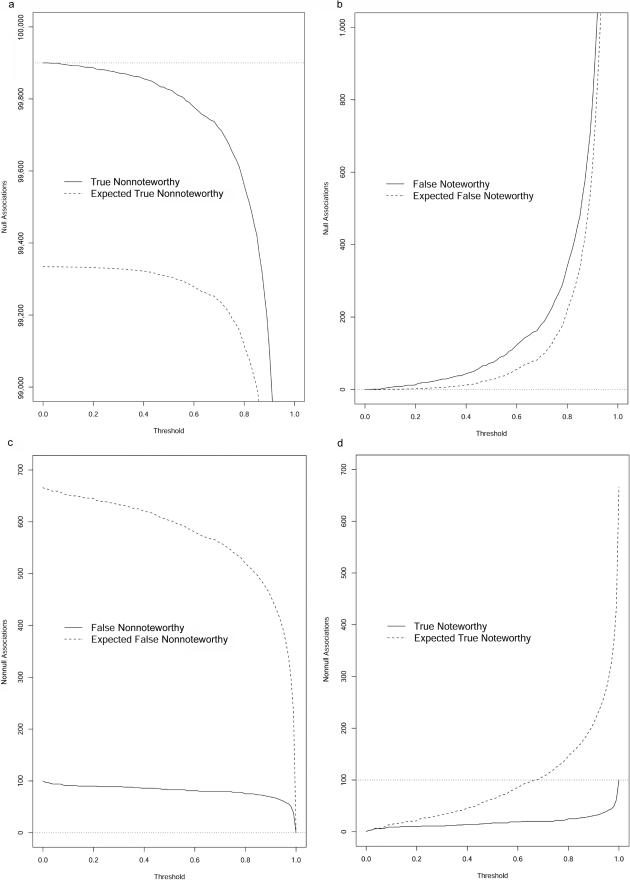
As discussed above, FPRP and BFDP are not directly comparable; so, rather than present side-by-side results, we discuss each in turn. Figure 5 gives the numbers of true nonnoteworthy, false noteworthy, false nonnoteworthy, and true noteworthy tests (i.e., the quantities U, V, T, and S in table 2) for BFDP as a function of the chosen threshold. The expected posterior estimates of each of these quantities (calculated using the formulas in table 3) are displayed as dashed lines, and the true numbers of null and nonnull associations appear as dotted lines. The problem with nondiscoveries is apparent in figure 5d—even for thresholds very close to 1, the majority of true nonnull associations go undetected. Figure 5b shows that the number of false discoveries increases dramatically as the threshold approaches 1. The only comfort from this simulation is that the expected numbers of true and false noteworthy and nonnoteworthy tests are very accurate, so at least we have some indication of the reliability of the results. A caveat, however, is that these numbers were calculated using the true π₀ and are highly sensitive to this value. The prior on θ was N(0,W), however, which is quite different from the distribution from which the effects of the nonnull SNPs were generated.

Figure 5. .

Operating characteristics of BFDP. Panels a, b, c, and d correspond to possibilities U, V, T, and S in table 2, respectively. In each panel, the solid lines represent the numbers of true nonnoteworthy, false nonnoteworthy, false nonnoteworthy, and true noteworthy tests at each threshold for BFDP. The dashed lines are the posterior expected numbers of tests that are true nonnoteworthy, false nonnoteworthy, false nonnoteworthy, and true noteworthy. The dotted lines represent the ideal outcome that a perfect test would achieve.

The results for FPRP are displayed in figure 6, on the same scale as figure 5. The overall behavior of BFDP and FPRP is the same, as can be seen in figure 7a, in which we see that the rankings are generally quite similar (with a few exceptions), but FPRP produces posterior null estimates that are much smaller than those produced by BFDP. This is because, from expression (11), FPRP is a lower bound on the posterior probability corresponding to the observed estimates. This inequality is for a fixed prior, and the priors for FPRP and BFDP are different, but the dominant difference between the two approaches for the priors chosen here is because of conditioning on point estimates (for BFDP) versus conditioning on tail areas (for FPRP). The estimates of the expected numbers of true and false noteworthy and nonnoteworthy tests under FPRP (the dashed lines) are not useful. In the first row of figure 6, the posterior probabilities of H₀ are summarized, and FPRP gives a lower bound on these probabilities; hence, the dashed lines fall beneath the solid lines. Similarly, in the second row, the probabilities of H₁ are bounded above. In each case, the bounds are not tight and so are not practically useful.

Figure 6. .

Operating characteristics of FPRP. Panels a, b, c, and d correspond to possibilities U, V, T, and S in table 2, respectively. In each panel, the solid lines represent the numbers of true nonnoteworthy, false nonnoteworthy, false nonnoteworthy, and true noteworthy tests at each threshold for FPRP. The dashed lines are the posterior expected numbers of tests that are true nonnoteworthy, false nonnoteworthy, false nonnoteworthy, and true noteworthy. The dotted lines represent the ideal outcome that a perfect test would achieve.

Figure 7. .

Comparison between BFDP, FPRP, P, and q for the 5,000 SNPs with the lowest values of BFDP. a, BFDP versus FPRP. b, P values versus FPRP. c, q values versus FPRP. d, q values versus BFDP.

Using the P values from the m=100,000 tests, we implement the q-value approach that controls FDR; π₀ was estimated as 1, reflecting the difficulty in estimating a proportion very close to 1. Table 4 gives the numbers of true and false nonnoteworthy and noteworthy results as a function of the selected FDR level. The final column shows that the procedure does control FDR, although, as with BFDP and FPRP, the number of missed true associations is large. Figure 7d plots the q values versus BFDP; the latter are always larger, which reflects expression (11) to a large extent. q values are a lower bound because they are evaluated by conditioning on a tail area. Table 5 provides a tabulation of BFDP values, although we stress that BFDP and q values are not directly comparable because they are packaging the information in the totality of tests in a different manner. BFDP does control FDR here, however.

Table 4. .

Summary of q Values for Simulated Data^[Note]

q	k	True and Nonnoteworthy	False and Noteworthy	False and Nonnoteworthy	True and Noteworthy	Empirical FDR
.05	2	99,900	0	98	2	.00
.10	4	99,900	0	96	4	.00
.20	4	99,900	0	96	4	.00
.30	8	99,898	2	94	6	.25
.40	8	99,898	2	94	6	.25
.50	8	99,898	2	94	6	.25
.60	23	99,886	14	91	9	.61
.70	28	99,882	18	90	10	.64
.80	37	99,874	26	89	11	.70
.90	160	99,760	140	80	20	.88
.95	199	99,721	179	80	20	.90

Note.— Columns 3, 4, 5, and 6 correspond to possibilities U, V, T, and S, in table 2, respectively.

Table 5. .

Summary of BFDP Values for Simulated Data^[Note]

BFDP	k	True and Nonnoteworthy	False and Noteworthy	False and Nonnoteworthy	True and Noteworthy	Empirical FDR
.05	2	99,900	0	98	2	.00
.10	2	99,900	0	98	2	.00
.20	3	99,900	0	97	3	.00
.30	3	99,900	0	97	3	.00
.40	4	99,900	0	96	4	.00
.50	7	99,899	1	94	6	.14
.60	7	99,899	1	94	6	.14
.70	8	99,898	2	94	6	.25
.80	16	99,893	7	91	9	.44
.90	32	99,879	21	89	11	.67
.95	66	99,848	52	86	14	.79

Note.— Columns 3, 4, 5, and 6 correspond to possibilities U, V, T, and S, in table 2, respectively.

Figure 7c and 7d plots the q values (which have the same rankings as the P values) against FPRP and BFDP, respectively, and we see that the rankings can be different because the power of each test is not used in the q-value calculation. For example, in figure 7c, there are two SNPs (highlighted with boxes) with q values of 0.26 but with quite different FPRP values of 0.02 and 0.21, corresponding to powers of 0.90 and 0.07, respectively. A striking example of this phenomenon in a candidate-gene study is presented in the next section.

Lung Cancer Association Study

We now present an illustration of the calculation of BFDP in the context of a multicenter, case-control study with 2,250 lung cancer cases and 2,899 controls and examine the association with 131 SNPs. This study is described more fully by Hung et al.¹⁷; the results for the study are not yet published, so we do not reveal the SNP names here. To calculate BFDP, we take W=[log(1.5)/1.96]² and, for FPRP, θ₁=1.5, with π₀=0.98 for both BFDP and FPRP, reflecting that, in this candidate-gene study, we believe that two or three SNPs might be associated with lung cancer. Under both BFDP and FPRP, the priors are such that we are implicitly assuming that the SNPs are independent (and, in particular, are not in linkage disequilibrium). In practice, the effect of ignoring the dependence will be a loss of efficiency in estimation. One approach to overcoming this problem is to specify a hierarchical model³⁰, although this causes loss of the ease of implementation of BFDP.

We assume an additive genetic model; it would be straightforward to repeat this experiment with dominant or recessive genetic models or with a nonadditive model. Appendix D gives details of how BFDP may be calculated in the situation in which there are two or more relative risks. We fit 131 logistic-regression models, controlling for age, sex, cigarette-pack years, and country, and retain for the calculation of BFDP the estimates and SEs, 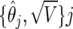, j=1,…,131.

We assume that the cost of a false nondiscovery is three times as great as the cost of a nondiscovery, which gives a cutoff value for BFDP of 3/4=0.75. We list the six most likely SNP associations under BFDP in table 6, along with a number of additional summaries. Use of the 0.75 cutoff gives one noteworthy SNP under BFDP, with 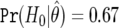, so that the null is more likely than the alternative. Notice that SNP D has the smallest P value, but the power is very low (MAF is 0.02, with power at θ₁ of just 0.0006), and it is the fourth most noteworthy SNP under FPRP and BFDP. The noteworthiness of SNP D is reduced because the observed data are incompatible with the alternative as well as the null, and the latter is considered only by the P value. This shows that ranking on the basis of P values can be misleading because the power associated with each test is not considered.

Table 6. .

Six Most Likely SNP Associations under BFDP (the Posterior Probability of the Null)^[Note]

SNP		Z Statistic	P	FPRP	BFDP
A	−.31	−3.15	.0016	.087	.67
B	−.34	−2.96	.0031	.17	.78
C	.27	2.76	.0057	.23	.83
D	−1.61	−4.34	.000014	.55	.86
E	.63	2.73	.0063	.65	.93
F	.21	2.17	.030	.60	.94

Note.— With false nondiscovery three times as costly as false discovery, a cutoff value of 0.75 provides the decision threshold; under this threshold, only the top SNP is deemed noteworthy.

For k=0, which corresponds to not reporting any SNPs, the expected number of false discoveries is obviously zero, increasing to 128.0 (the sum of across all tests) if we choose to report all 131 SNPs as noteworthy. For k=0, the expected number of false nondiscoveries is 2.96, which decreases to zero if we choose to report all 131 SNPs (k=131). The weighted combinations of costs is minimized at k=1—as it has to be, because our cutoff minimizes this quantity—at which point, we have 2.63 expected false nondiscoveries, and 0.67 is the probability that SNP A is a false discovery; the latter is the BFDP value in table 6.

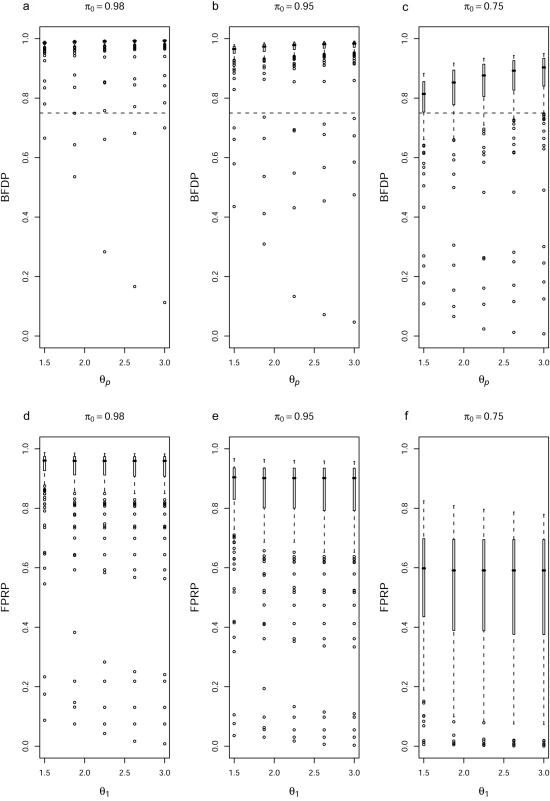
In figure 8, we examine the sensitivity to the prior by examining the effect of varying π₀, θ_p, the 97.5% point of the prior for θ under BFDP, and θ₁, the value at which the power is evaluated for FPRP. Boxplots of BFDP (fig. 8a–8c) and FPRP (fig. 8d–8f) are shown with π₀=0.98, 0.95, and 0.75. Within each plot, we have θ₁=θ_p=1.50, 1.88, 2.25, 2.63, and 3.00. The largest sensitivity is seen when we assume π₀=0.75; under this choice, there are 31, 26, 22, 21, and 18 noteworthy SNPs under BFDP for the five values of θ_p. Within each choice of π₀, there is relatively little sensitivity to θ_p—for example, with π₀=0.98, there are 1, 3, 2, 2, and 2 noteworthy SNPs under the five choices for θ_p. The ranking of SNPs is unchanged as π₀ varies. Sensitivity to the ratio of costs is revealed by moving the dashed line vertically—upwards if missing associations are thought to be more costly, and downwards if false discoveries are more costly.

Figure 8. .

Boxplots of BFDP (a–c) and FPRP (d–f). π₀ values are shown above each panel. For panels a–c, each set of boxplots corresponds to θ_p=1.50, 1.88, 2.25, 2.63, and 3.00 (the 97.5% point of the prior); for panels d–f, we evaluate the power at θ₁=1.50, 1.88, 2.25, 2.63, and 3.00. The dashed lines in panels a–c denote the thresholds that correspond to false nondiscovery being three times as costly as false discovery, so that SNPs with BFDP values below the line are noteworthy.

We calculate q values for these data, using the default choice of the smoothing parameter, to give 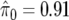. With control at an FDR level of 0.05, there is one noteworthy test, corresponding to SNP D in table 6. At level 0.10, there are two noteworthy tests, corresponding to SNPs D and A, and, at levels 0.20–0.50, there are five in total, with SNPs B, C, and E additionally flagged as noteworthy.

Discussion

In this article, we have suggested a new measure for identifying noteworthy associations, BFDP, keeping the objectives of but refining the criteria for FPRP in the work of Wacholder et al.² Specifically, we advocate BFDP for reducing the number of “discoveries” that are reported but not replicated in subsequent investigations. Whereas FPRP is difficult to calibrate, a threshold for BFDP may be chosen that explicitly considers the costs of false discovery and false nondiscovery.

BFDP can be applied using an estimate and SE or with a confidence interval. Published articles that report such summaries can therefore be critically interpreted. An Excel spreadsheet and an R function for calculation of BFDP are available online at J.W.'s Web site.

We have developed BFDP, using the model-based asymptotic distribution of the MLE, but we can replace V with any estimate that is thought to be appropriate—for example, a sandwich estimator or one that allows for overdispersion to account for population heterogeneity.²⁹ Within a logistic-regression framework, observed race/ethnicity may be explicitly modeled with additional parameters to control for heterogeneity; simulations have demonstrated that logistic regression can control population substructure.³¹ We have concentrated on SNPs, but BFDP may also be applied to insertions/deletions or copy-number changes.

Different studies that report the required summaries can be combined to produce the totality of evidence of a particular association. For example, for two studies with estimates and :

where ,

and 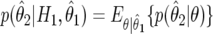is the density for 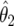averaged over the posterior for θ given 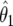(and is available in closed form). Expression (14) may be used for replication studies. In such a context, even if two studies provide small Bayes factors (and therefore strong evidence of an association), this must still be combined with the prior odds on the null, π₀/(1-π₀); if the latter is large, then the overall evidence may still be inconclusive.

It is becoming increasingly common to perform genomewide scans in multiple stages.³² When specifying the ratio of costs, to determine a cutoff point for BFDP, these costs may change across stages, since, early on, we do not wish to lose SNPs that might be associated with disease, whereas, in the final stage, a more stringent cutoff is desirable. It is straightforward to perform such a procedure with BFDP. Currently, it is common to rank P values and then select a set of SNPs for the next phase on the basis of the smallest P values. We would advocate ranking via the approximate Bayes factor instead. This will, in general, provide a different ordering, since the powers are not constant across SNPs (because they depend on the allele frequencies and the strength of the association), which is not accounted for by the P value. In the lung cancer example, we saw a situation in which the smallest P value did not correspond to a noteworthy SNP.

If one is willing to relax ease of computation in the multiple-testing scenario, then one may model the totality of estimates 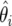, i=1,…,m, as arising from a mixture of two distributions. The proportion of null tests, π₀, may be estimated from the data, as may the densities of null and nonnull estimates, although, with a small expected number of nonnull associations, estimation is likely to be sensitive to the prior for π₀. A number of models and implementation strategies have been suggested for simultaneous inference using data from multiple tests. Two of the easiest to implement are empirical Bayes³³ and full Bayes with importance sampling.³⁴ Each of these procedures may be used in the context considered here, by replacing the likelihood with the asymptotic distribution of the MLE. A great advantage in using the asymptotic distribution is that it results in a model that is very conducive to analytic examination and provides straightforward computation. In the lung cancer example, we did not attempt hierarchical modeling because the number of SNPs was relatively small and the a priori fraction of nonnull associations was also small, so that reliable estimation of the nonnull density would not be feasible.

Appendix A: Minimizing Expected Loss

With respect to table 1, the posterior expected cost associated with decision δ is

so that, for the two possible decisions (nonnoteworthy or noteworthy), the expected costs are

and we should choose δ=1 if C_β×Pr(H₁|y)⩾C_α×Pr(H₀|y)—that is, if

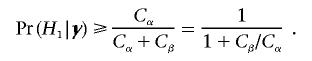Appendix B: The Approximate Bayes Factor

We derive an approximation of the Bayes factor Pr(y|H₀)/Pr(y|H₁) for logistic-regression model (5) and n individuals. The likelihood under H₁ is given by

whereas, under H₀, we set θ=0. We have

and

where π(γ,θ) is the prior. The integrals in (B1) and (B2) are analytically intractable; thus, some form of approximation or simulation technique is required.

To calculate an approximation of the Bayes factor, we first replace the likelihood Pr(y|γ,θ) by the asymptotic distribution 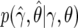, where 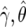is the MLE. This approximation will be accurate given the sample sizes in typical genomewide-association and candidate-gene studies, unless the MAF is very small. We write β=(γ,θ) and assume normal priors for γ and θ:

Straightforward algebra yields the predictive distribution 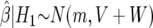. A similar derivation is available under H₀, allowing a closed form for the Bayes factor. This approach requires specification of the joint prior π(γ,θ); we adopt a simpler strategy here.

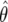Suppose that and are independent—that is,

where I_γ is the c×c expected information associated with γ, I_θ is the expected information associated with θ, and 0 is a c×1 vector containing zeros. Further, suppose that the prior factorizes as π(γ,θ)=π(γ)×π(θ). Under these circumstances, it is straightforward to show that, under H₁,

where 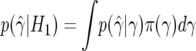and, under H₀,

An approximate Bayes factor is given by the ratio of these quantities and depends on only θ:

In genome association studies, the independence assumption in (B3) is likely to be reasonable, since genetic information will often be at least approximately independent of environmental information.

The above derivation means that, effectively, we need to consider only the sampling distribution of the MLE, 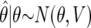, and the prior for θ∼N(0,W), where we have assumed the prior mean is zero. These choices result in the approximate Bayes factor (B4) being the ratio of the prior predictive densities:

to give

where 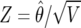is the usual Z statistic and r=W/(V+W) is a shrinkage factor. This form is used within BFDP throughout this article.

To investigate the accuracy of the approximation, we simulated case-control data with varying numbers of cases and controls, MAFs, and relative risks. In all cases, we placed an N(0,1) prior on the intercept. The exact Bayes factor was calculated using both a rejection algorithm and importance sampling.³⁵ Figure B1 displays the approximate Bayes factors plotted against the exact Bayes factors for a subset of the simulations. In each of the scenarios, 50 data sets were generated, and, in all cases, the approximation is accurate.

Figure B1. .

Approximate Bayes factor versus exact Bayes factor as a function of the number of controls, n₀; the number of cases, n₁; and the log relative risk, θ. The MAF is 0.05, and there are 50 simulated data sets in each plot. In panel a, n₀=n₁=250 and θ=log(1.0). In panel b, n₀=n₁=250 and θ=log(1.3). In panel c, n₀=n₁=500 and θ=log(1.0). In panel d, n₀=n₁=500 and θ=log(1.3).

Appendix C: Multiple Testing

Suppose we wish to perform m tests with common costs C_β and C_α for each test. The aim is to define a rule for deciding which of the m null hypotheses we will flag as noteworthy and to determine the operating characteristics, in terms of false discovery and false nondiscovery, for this rule. The cost associated with a particular set of decisions δ₁,…,δ_m is

where δ_j=0 or 1, according to whether we call test j nonnoteworthy or noteworthy. In this case, Muller et al.²⁷ show that we should report association j as noteworthy if

Without loss of generality, assume the tests are ranked from smallest to largest in terms of Pr(H_0j|y_j), j=1,…,m, and that the first k tests, 0⩽k⩽m, are deemed worthy of reporting as noteworthy according to rule (C1). The posterior expected numbers of true and false nonnoteworthy tests are given in table 3; note that the sum of these two quantities is m-k, the number of tests not deemed noteworthy. Similarly, the expected numbers of false and true noteworthy tests are given in table 3, and the sum of these two quantities is k, the number of tests called noteworthy.

Appendix D: General BFDP

Suppose we have the logistic regression model

where, for example, z₁ and z₂ may be indicators of one or two copies of a mutant allele, with e^θ₁ and e^θ₂ representing the associated relative risks. A classical testing procedure would compare H₀:θ₁=θ₂=0 and H₁:θ₁≠0, θ₂≠0, by use of a likelihood-ratio statistic with 2 df. The approximate Bayes factor is only slightly more complicated than in the single exposure case and is based on

where θ=(θ₁,θ₂), V is the asymptotic variance-covariance matrix of the estimate 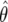, and W is the 2×2 variance-covariance matrix of the prior. This leads to

to give the approximate Bayes factor

In specifying

it is sensible to choose W₁₁⩽W₂₂, since we expect the effect of a single copy of the mutant allele to be no greater than the effect of two copies: 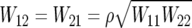 , and ρ may be specified on the basis of linkage-disequilibrium information.