Correlation of Intergenerational Family Sizes Suggests a Genetic Component of Reproductive Fitness

Abstract

Reproductive fitness is a complex phenotype that is a direct measure of Darwinian selection. Estimation of the genetic contribution to this phenotype in human populations is confounded by within-family correlations of sociocultural, economic, and other nongenetic factors that influence family sizes. Here, we report an intergenerational correlation in reproductive success in the Hutterites, a human population that is relatively homogeneous with respect to sociocultural factors that influence fertility. We introduce an estimator of this correlation that takes into account the presence of multiple parent-offspring pairs from the same nuclear family. Statistical significance of the estimated correlation is assessed by a permutation test that maintains the overall structure of the pedigree. Further, temporal trends in fertility within this population are accounted for. Applying these methods to the S-Leut Hutterites yields a correlation in effective family size of 0.29 between couples and their sons and 0.18 between couples and their daughters, with empirical P<1×10^-6 and P=.0041, respectively. Similar results were obtained for completed families (0.31 between couples and their sons and 0.23 between couples and their daughters; empirical P<1×10^-6 and P=.00059, respectively). We interpret these results as indicating a significant genetic component to reproductive fitness in the Hutterites.

Reproductive fitness is the relative proportion of genes that one contributes to subsequent generations. Formally, it is a measure of both fertility (the ability to reproduce) and mortality (the survival of children to reproductive age). Both components of fitness and the ability to reproduce and to have children that also reproduce are complex phenotypes, influenced by genetic and environmental factors. Studies of model organisms suggest that hundreds of genes directly influence fertility,^1,2 and thousands of human genetic disorders that influence the ability to reproduce have been described (OMIM). Although it is relatively straightforward to study the second component of fitness in humans, fertility potential is difficult to assess, because human family sizes are often deliberately limited for a variety of reasons, and few populations reach their true reproductive potential, because of sociocultural or economic reasons. Thus, although a handful of genes have been identified that cause infertility in humans (reviewed by Layman³), it has been difficult to assess genetic contributions to fertility. For example, parent-child correlations in family sizes have been reported in many populations (table 1); however, in each study, the contribution of nongenetic factors to the correlation could not be excluded, and, in all cases, the correlation was attributed to social or cultural phenomena.^4–9 Thus, the relative contribution of genes to fertility differences between couples in human populations is currently not known.

Table 1. .

Correlations in Family Size in Different Populations^[Note]

	Correlation in Family Size
Population and Measure of Family Size	Couple-Children	Father-Sons	Mother-Daughters
British4:
CFS	NR	.066a	.21a
Japanese5:
CFS	NR	−.031	.014
French Canadians6:
EFS	.16	.14	.17
Icelanders7:
CFS	NR	.041	.079
Irish8:
CFS	NR	NR	∼.17b
Hutterites:
rreg:
EFS	NR	.29c	.18d
CFS	NR	.31c	.23d
Pearson’s r:
EFS	NR	.34c	.19d
CFS	NR	.34c	.24d

Note.— All correlations are estimated by Pearson’s r except where noted. NR=not reported.

^aCorrelation not confirmed in a subsequent study that accounted for time trend in data.

^bEstimated from reported heritability of .34.

^cCouple-son correlation.

^dCouple-daughter correlation.

The Hutterites are a founder population of European descent that offers the opportunity to study human fertility potential.^10,11 The Hutterites traditionally proscribe contraception, and, as a result, median completed sibship sizes among the S-Leut Hutterites are large (median sibship size was >10 in the 1960s¹²), and interbirth intervals are small (mean interval was <2 years between births through the 10th birth during this same time period¹⁰). Moreover, the Hutterite communal lifestyle assures that sociocultural factors known to influence family size, including wealth, access to medical care, age at marriage, desire for large families, and nursing practices, are remarkably uniform in the population.¹³ The naturally high fertility rate coupled with their communal lifestyle makes them ideally suited for genetic studies of fertility, as noted elsewhere.^10,11

As a first step in assessing genetic contributions to fertility, we sought to determine whether intergenerational correlations in family size were present in the Hutterites, as they are in other populations.^4–9 However, because of the general absence of variation in nongenetic factors that are known to influence family sizes, parent-children correlations in Hutterite family sizes would indicate a genetic component (i.e., heritability) to this complex trait. Two measures of family size have been used in previous studies. The first, census family size (CFS), is defined as the total number of children born to a couple, whereas the second, effective family size (EFS), is defined as the number of children who reproduce in the population per reproducing individual.⁶ Differences in CFS and EFS could reflect differences in out-migration or marriage rates between families or in children’s mortality rates prior to reproductive age. Whereas the former is not likely to be genetic in origin, the latter could include genetic causes.

For these studies, we used demographic data for the S-Leut Hutterites that are part of the database originally collected by Dr. A. G. Steinberg nearly 50 years ago¹¹ and maintained and updated at the University of Chicago by C.O.¹⁴ For this study, the 13,165-person S-Leut genealogy was divided into 1,037 3-generation subpedigrees. We constructed 3-generation subpedigrees, beginning with the founders, and moved down through the pedigree (a top-down approach), in contrast to a coalescent (or bottom-up) approach in which pedigrees are constructed backward in time from current descendants, as was used for the older periods (18th century) in one study.⁶ In the coalescent approach, only ancestors with descendants in the current population are represented in the sample; therefore, no couples with EFS values of zero would be included. With the top-down approach, couples with an EFS of zero are included as long as they do not prevent the formation of a 3-generation pedigree. Therefore, couples with EFS of zero would not be included in the grandparental (top) generation but would be included in the second (middle) generation if at least one of the children in that generation has a nonzero EFS. In the third (bottom) generation, it is possible for all values to be zero.

To ensure that only completed families were included in our sample, we considered 3-generation pedigrees in which the grandmother (top generation) was born in or before 1860. We assumed that nearly all women born in 1940 or earlier would have completed their families by 1980 (the date of the most recent complete update of our database), since relatively few Hutterite women have children after age 40 years. Thus, by setting the upper limit at 1860, we ensure that the children in the 3rd generation would have reached age 40 years and likely completed their families by 1980. Of the 1,037 subpedigrees, 235 met this criterion. We excluded an additional 75 couples because one spouse from each couple died before reaching age 40 years. In the remaining 160 3-generation pedigrees, one male had a marriage and remarriage, both of which met the above criteria and were therefore included as two separate families in our analysis. Our final sample included 161 3-generation pedigrees.

Previous studies of CFS or EFS used the standard estimator of correlation (Pearson’s r), which assumes that the data are in the form of independent pairs (consisting of a couple’s EFS or CFS and an offspring’s EFS or CFS). However, for each Hutterite couple, we generally have information about all couples' reproducing offsprings’ EFS or CFS values, rather than for a single reproducing offspring. Therefore, to allow for the fact that a couple’s EFS or CFS would be compared with multiple offsprings’ EFSs or CFSs, we developed a regression-based estimator of the correlation in EFS and CFS, which we refer to as “r_reg.” Our estimator of correlation was derived as follows. For j=1,…,m, where m is the number of 3-generation pedigrees, let M_j be the jth couple’s EFS or CFS—that is, the number of reproducing children. Given M_j, for i=1,…,M_j, let Y_ji be the EFS or CFS of the ith reproducing child of the jth couple. We assume that E(M_j)=μ_M, Var(M_j)=σ²_M, E(Y_ji|M_j)=α+βM_j, and Var(Y_ji|M_j)=σ²_Y. The ordinary least-squares estimators of the parameters, obtained from simple linear regression of Y on M (see, e.g., chapter 1 in the work of Weisberg¹⁵), would then be

and

where

and

(We actually use m and 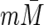in the denominators of and , respectively, which give asymptotically equivalent estimators.) This leads to the following estimator of the correlation, r_reg, between M and Y

Although we are not aware of any sociocultural factors that could influence interindividual differences in Hutterite family sizes, it remained possible that a time trend in the data, or temporal heterogeneity, was present that could affect a correlation in family size.⁷ To explore this possibility, we examined the relationship between family size and generation number for the 161 pedigrees. Because the S-Leut pedigree contains overlapping generations and the founders (ordinarily generation 0) entered at different time points over ∼100 years, we scored generations in a way that related generation number to absolute time by first assigning the founder couples born between 1700 and 1800 to generation 0. We then incremented the generation number of their children by one. When we assigned generation number to children of nonfounders, the highest generation of either parent was incremented by one. When a founder married a nonfounder, we used the nonfounder generation to determine the generation number of their children. Because ages of Hutterite spouses are highly correlated (r=0.955), this latter step aligned generation number with absolute time. EFS values plotted by generation revealed temporal heterogeneity (fig. 1). The two most recent generations (6 and 7) had higher mean EFS values than did generations 0–5, which were all similar. Interestingly, generations 6 and 7 correspond to the period following the Hutterite migration to North America in the late 1870s, which was associated with an exponential increase in population size.¹³ We corrected for temporal trends by subtracting the mean EFS (or CFS) value for each generation from the EFS (or CFS) value for each individual within that same generation. This created an approximately normal distribution of EFS and CFS values, centered at zero. These “corrected” values were used in our analyses. With use of the regression-based estimator, the correlation between the EFS of couples and the EFS of their sons was r_reg=0.29 and between the EFS of couples and the EFS of their daughters was r_reg=0.18, which were high compared with estimates of correlations in family sizes in other populations (table 1 also shows the uncorrected values for comparison with previous studies). The correlations in the EFS values with sons and with daughters are illustrated in figure 2.

Figure 1. .

EFS values by generation. Data are shown for the 161 3-generation subpedigrees, where g is the number of individuals within each generation and horizontal bars indicate the variance. Outliers are shown as unblackened circles, and the mean EFS is represented by a horizontal line within each rectangle.

Figure 2. .

Scatterplots showing correlation in EFS values for couples and sons (A) and couples and daughters (B). EFS values are adjusted for generation.

To assess the significance of these correlations, we used a permutation test that both accounted for the lack of independence among the couple-child pairs and maintained the overall structure of the pedigree. To maintain the shape of the pedigrees, individuals in the 3-generation subpedigrees were separated by their generation number, and EFS and CFS values were randomly permuted among couples within each generation (i.e., horizontally in the pedigree). This process was repeated for the entire pedigree 1,000,000 times, and, each time, the estimator of correlation, r_reg, was determined for correlations with sons and for correlations with daughters. The value of r_reg from the data was then compared with the null distribution of the correlations from 1,000,000 repeated permutation processes, to obtain an empirical P value. This strategy of permuting only the EFS (or CFS) values of contemporaneous individuals has the added benefit of maintaining any time trends that may exist in the data that are not otherwise accounted for. With use of this approach, the likelihood of observing a correlation in EFS between a couple and their sons of at least 0.29 is <1×10^-6 and of observing a correlation in EFS between a couple and their daughters of at least 0.18 is .0041. The corresponding values for CFS were 0.31 (P<1×10^-6) for sons and 0.23 (P=.00059) for daughters. These highly significant correlations in parent-child EFS and CFS suggest a heritable (i.e., genetic) component to reproductive fitness in the S-Leut Hutterites.

Only one previous study, of the population of Sauguenay-Lac Saint Jean (Quebec), considered correlations in EFS between generations.⁶ Although EFS was correlated between generations (table 1), CFS was not. Those authors interpreted this difference as reflecting the greater out-migration among some families and concluded, therefore, that the correlations in EFS were due to sociocultural factors. In the Hutterites, correlations in CFS and EFS were both significant, further supporting the role of genetic differences between families that underlie these correlations. Other nongenetic factors that have explained correlations in CFS are social transmission of reproductive behavior in Iceland,⁷ differential access to resources (including ability to acquire a mate) in western Ireland,⁸ socioeconomic class in 19th-century England,⁴ the introduction of birth-control use in Japan,⁵ wealth (most importantly, its effect on number of wives) in South American Indian tribes,⁹ and cultural factors (such as cooperation based on kinship) in hunter-gather populations.¹⁶

In these regards, the Hutterites are remarkable in a number of ways. First, they are strictly monogamous, and only 2% of Hutterite couples are childless, compared with 10% of the general population.¹⁷ Second, there is a very small variance in the wife’s age at marriage, with most women marrying at age 20–24 years and few (∼10%) after age 24 years.¹⁰ Third, their communal lifestyle guarantees equal access to education, income, food, health care, and housing.¹³ Fourth, their religion proscribes contraception; even today, birth-control use is minimal and family sizes are large.¹⁸ Lastly, the lengths of time that women nurse their infants are relatively uniform among Hutterites, although nursing length for daughters is longer than that for sons.¹⁹

Because of the absence of any known sociocultural factor that could influence differences in family sizes among Hutterite families, we interpret the results of our study as indicating that genetic differences among couples influence reproductive fitness in this population. This conclusion is supported by previous studies of the Hutterites that showed decreased fertility among the most inbred women²⁰ and genomewide transmission distortion among sibships.²¹ Those studies suggested that genetic variation segregating in the population influences reproductive success or fetal survival, respectively. Because most genetic variation that is present in the Hutterites is also present in outbred European populations,^22,23 it is likely that common variation influencing fertility in the Hutterites is also present in outbred populations. On the other hand, the reduced environmental heterogeneity may enhance the effects of genetic variation on complex phenotypes in this population, making them easier to detect in the Hutterites compared with more-heterogeneous populations, as discussed elsewhere.²⁴

To our knowledge, this is the first report of correlations in human family size that cannot be explained by sociocultural or other nongenetic differences between families. Although we cannot exclude the possibility that unknown differences exist, we think it most likely that the observed differences reflect genetic differences between couples. In this context, two observations are noteworthy. First, there is stronger correlation for CFS than for EFS between couples and their daughters, but that is not the case between couples and their sons. This likely reflects the fact that, because of the excess number of adult women compared with adult men, nearly all Hutterite men but not all Hutterite women marry. Because the probability of marriage (and subsequent reproduction) is not genetic, there would be more nongenetic variation influencing EFS, compared with CFS, among Hutterite women. Second, there is a stronger correlation in both EFS and CFS between couples and their sons than between couples and their daughters. This difference could reflect, at least in part, the influence of both Y-chromosome and mitochondrial genes on male reproduction, since mutations in both have been associated with male infertility.^25,26 However, this difference may also reflect the overall larger number of genes involved in male compared with female reproductive processes.² Nonetheless, the highly significant correlations in family sizes in the Hutterites suggest that genes influencing reproductive fitness are segregating in the population, making this complex phenotype amenable to mapping studies for the identification of human fertility genes.