Interactions between two divalent ion binding sites in N-methyl-d-aspartate receptor channels

Abstract

N-methyl-d-aspartate receptor channels exhibit a high permeability for calcium ions. In this report, we confirm that calcium ions permeate effectively through the wild-type channels, and find that their presence within the pore blocks the flux of sodium and other ions. Further proof for this ionic block comes from the analysis of the ɛ1(N614Q) mutation where the high permeability of calcium is unchanged but the block by calcium ions is increased twofold. In both the wild-type and mutant channels, calcium ion block is independent of membrane voltage; therefore, the calcium binding site is outside the voltage gradient through the pore and must be close to the extracellular mouth of the ion conductance pathway. This calcium site is distinct from the magnesium binding site, which lies 80% into the pore’s electrostatic field and thus exhibits a marked voltage dependence of binding. The ɛ1(N614Q) mutation reduces the affinity of magnesium ion for its binding site but increases the affinity of calcium ion for its binding site. Since a single mutation perturbs two distinct binding sites in opposite ways, we postulate that binding of divalent ions at the two sites interact.

N-methyl-d-aspartate (NMDA) receptors are cation selective ion channels with unusual permeability properties that set them apart from other ligand-gated ion channels: they are very effectively blocked by magnesium ions in a voltage-dependent way (1, 2, 3, 4) but are, at the same time, highly permeable to calcium ions. Calcium flux through the NMDA receptor channels has a number of important functional consequences (5, 6, 7, 8, 9, 10)

The high permeability of NMDA receptor channels for calcium ions has been determined by direct measurements of calcium entry using calcium-sensitive dyes (11, 12, 13, 14) and by the reversal potential (15, 16, 17, 18, 19) method. Calcium ions not only readily pass through the channel but also markedly reduce the single channel conductance (17, 20). Models proposed to account for these apparently contradictory effects of calcium ions assume either the presence of significant negative surface charges or the existence of one or more cation binding sites in the ion conduction pathway (the “pore”) (20, 21, 22, 23). The location at which calcium ions most strongly bind within the channel pore is, however, still unclear. Competition experiments indicate that calcium ions may bind to the same site as magnesium (16); however, since the binding of calcium ions exhibits very little voltage dependence in other experiments, the calcium binding site has been placed close to the mouth of the channel by other workers (20, 24, 25).

Mutation of a single asparagine residue in the region of the protein termed TM2 has been shown to alter both the permeability to calcium ions and the block of the recombinant NMDA channel by magnesium ions (26, 27, 28). Substitution of Asp-614 with glutamine in the ɛ1 subunit (29, 30) has no effect on calcium permeability but strongly reduces the affinity of magnesium ion for its binding site due to an increase in the rate of unbinding. The same mutation in the ζ1 subunit (31, 32), on the other hand, reduces both the permeability of the channel for calcium ions and its block by magnesium (33, 34). This asparagine is at a position homologous to the N/Q/R site that is conserved in ionotropic glutamate receptors. The amino acid at this site is determined by RNA editing and has been shown to control the divalent cation permeability of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and kainate receptors (35, 36, 37, 38). In a previous study (39), we have demonstrated that the asparagine at position 614 in the ɛ1 subunit is likely to be involved in coordinating magnesium ions. Here we examine the effects of this mutation on the flux of ions through the pore in the presence of extracellular calcium ions.

We use the theoretical approach taken by Jahr and Stevens (20) and treat calcium as a permeant but also blocking ion for NMDA receptor channels; the idea is that, during the passage of each calcium ion through the pore, the calcium ion transiently binds to a site that prevents all ionic flux as long as the calcium ion resides at that site. Our data indicate that the ɛ1(N614Q) mutation studied earlier (39) does not change the permeability of calcium ions but leads to a twofold increase in the calcium block. Further, this block by extracellular calcium ions is largely independent of membrane voltage in both wild-type and mutant channels. The calcium binding site responsible for block therefore must be outside the electrostatic field gradient across the pore. In contrast, the same mutation causes magnesium ions to bind less tightly to a site estimated to be more than halfway through the pore’s voltage gradient in both wild-type and mutant NMDA receptor channels (39). Thus, our data provide direct evidence that the two binding sites are located in spatially separate parts of the pore. Since a single mutation perturbs two distinct binding sites and produces effects in opposite directions (tighter calcium binding and less tight magnesium binding), we propose that calcium ions bind to both sites and interact electrostatically to alter binding stability.

METHODS

The methods used here are the same as those described earlier by Sharma and Stevens (39).

RESULTS

We have investigated the effects of extracellular calcium ion concentration on the ionic flux through wild-type ζ1/ɛ1 and mutant ζ1/ɛ1(N614Q) NMDA receptor channels expressed transiently in HEK-293 cells. Fig. 1 illustrates the two principal effects of increased extracellular calcium concentration on the behavior of NMDA receptors. First, the current–voltage curves are shifted toward more positive potentials; this observation shows that calcium ions are quite permeable. Second, the amplitude of the whole cell response to transient glutamate application is reduced; this observation means that calcium ions block the pore. In the data from the wild-type cell illustrated in Fig. 1, the presence of 10 mM calcium decreases the amplitude of the response to glutamate at −80 mV by 54% (as compared with that obtained in 0.1 mM calcium) and shifts the reversal potential by +4 mV. A qualitatively similar effect is seen in the mutant cell where 10 mM calcium reduces the amplitude of whole cell response at −80mV by 75% and shifts the reversal potential by +4 mV. We have quantified the calcium ion block by measuring the reduction in whole cell response to glutamate with increasing external calcium ion concentrations and have estimated the permeability of the channel for calcium ions by examining shifts in reversal potential that result from the various concentrations of extracellular calcium.

Figure 1.

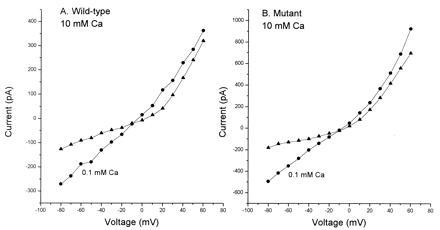
Current–voltage relationship of wild-type and mutant NMDA receptors depends on extracellular calcium concentration. (A) Wild-type channels typically show reduced amplitude of whole cell response in high external calcium concentrations. Responses obtained in 0.1 mM calcium are represented by triangles and circles represent responses in 10 mM calcium. (B) Representative current–voltage relationship of mutant channels. Circles represent data from whole cells in 0.1 mM calcium and triangles from cells in 10 mM calcium. In both wild-type and mutant increasing extracellular calcium concentrations lead to a shift in the reversal potential toward more positive potentials.

Block of the Channel by Extracellular Calcium Ions: Theory.

The goal of this section is to establish a simple relationship between whole cell conductance of NMDA receptors and extracellular calcium ion concentration. According to the model proposed by Jahr and Stevens (20), whenever calcium ions are present in the extracellular solution, they occupy the NMDA receptor channel in a manner that excludes all other ions for a fraction of the time during which the occupancy occurs. During each brief occupancy of the channel by a calcium ion, the channel is effectively “turned off” so that the average flux of ions is reduced and the average channel conductance is decreased. Single channel conductance γ is, according to this picture, given by (20)

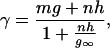1

where m and n are the movalent cation and calcium ion activities, and g, h, and g_∞ are constants. The term mg is experimentally determined as the conductance, γ₀, of the channel in the presence of isotonic sodium solution (no calcium block). If the total number of channels present on the cell is N and p is the probability that a channel is open, the whole cell conductance, G(V), is related to the single channel conductance by the equation

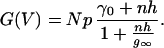2

This equation relates the measured agonist induced conductance change to the extracellular concentration of sodium and calcium ions.

We define a blocking function, B(C), as the whole cell conductance of NMDA receptor channels in presence of high extracellular calcium concentration, G(V), relative to the conductance in minimal calcium concentration G₀(V) by the equation

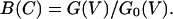3a

This blocking function specifies the fraction of the time the channel is free to conduct current [note that B(C) = 1 when there is no block and B(C) = 0 when there is full time block of the channel]. If we assume that calcium ions do not effect the probability of opening of the channel, then from Eqs. 2 and 3a the blocking function B(C) is a function of voltage and calcium concentration and has the following form:

3b

where c is the standard minimal calcium (100 μM) concentration, C is a higher concentration of external calcium, and α is the appropriate activity coefficient for calcium. We have used this equation to quantify the calcium block in wild-type and mutant channels.

Conductance Versus Voltage Relationships.

Current–voltage relationships, like the ones illustrated in Fig. 1, were obtained in the presence of six different extracellular calcium concentrations ranging from 100 μM to 100 mM for 20 wild-type and 17 mutant cells. At least two current–voltage plots were obtained from each cell: one in the standard minimal (100 μM) calcium and a second one in a higher concentration of calcium ions. To quantify the decrease in the amplitude of whole cell response, we constructed conductance–voltage plots from these data. Current in the presence of high external calcium can be expressed as a combination of a conductance function, G₀(V), in minimal calcium and a blocking function, B(C), such that

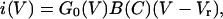4a

B(C) is the conductance remaining after block by calcium ions and is a function of voltage and calcium concentration, C. G₀(V) can be calculated from the current–voltage relationship in minimal calcium when B(C) = 1 according to

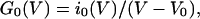4b

where i₀ is the current and V₀ is the equilibrium potential in 100 μM calcium.

Calcium Block Is Increased in Mutant Channels.

The fraction of whole cell conductance remaining after block by calcium ions, B(C), was estimated experimentally at a fixed voltage (the resting potential). Data from 15 wild-type cells, plotted as a function of external calcium concentration, are presented in Fig. 2. These data are normalized for the conductance at 0.1 mM extracellular calcium as earlier work (39) showed that the single channel conductance is the same for mutant and wild-type channels at this concentration. As is clear from Fig. 2, block by calcium ions increases with calcium concentration and then reaches a maximum value for high concentrations. Eq. 3a was used to calculate the smooth curve that specifies the theoretical B(C) as a function of calcium concentration. Using the least squares criterion, we found a best fit was achieved for the values of the h = 9 pS/mM and g_∞ = 14 pS. These values differ slightly from the ones obtained earlier for native NMDA receptors in cultured hippocampal neurons (20) where h = 11.3 pS/mM and g_∞ = 15.2 pS. Some variation might be expected since the present measurements on wild-type cells used whole cell recordings, whereas constants for native hippocampal channels were determined from single channel data. Our observations do, however, provide evidence that the main characteristics of calcium block of wild-type channels are essentially the same as those of native NMDA receptor channels.

Figure 2.

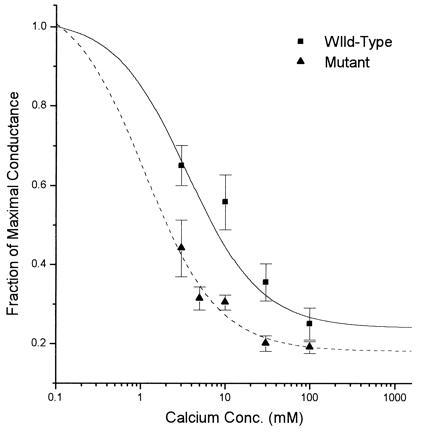
ɛ1(N568 → Q) mutation increases inhibition of NMDA responses by extracellular calcium. Block of conductance by calcium ions was quantified using Eq. 3b, as described in the text. Inhibition is twofold greater in mutants (▴) as compared with wild-type (▪).

Extension of this analysis to the mutant channels shows that the block by calcium ions is increased by the mutation. Data from 13 mutant cells have been fitted to Eq. 3b with the values of h and g_∞ estimated by least squares as above. The constant h, the conductance per mole of calcium, is a measure of the decrease in conductance with increasing calcium concentration. In mutant channels, the value of h is 19.5 pS/mM as compared with 9 pS/mM in the wild-type channels. This finding implies that, for a given concentration of calcium ions, mutant channels are blocked about twice as much of the time as wild-type channels. Thus, the conductance of mutant channels declines faster with increasing calcium concentrations. The limiting conductance g_∞ attains a lower value of 10.9 pS in isotonic solutions containing only calcium cations as compared with the wild-type value of 14 pS.

Voltage Dependence of Calcium Block.

We next examined the location of the calcium binding site in the electrostatic field across the channel pore. Voltage dependence of the binding of calcium ions is used to define the distance down the electrostatic field gradient traveled by a calcium ion to reach its binding site. A high voltage dependence would imply that, if ionic movements are not coupled, the binding site is deep within the voltage gradient through the pore, whereas a low dependence on voltage would place the site closer to the mouth of the channel.

The fraction of response blocked by high calcium concentrations, B(C), was determined in 20 wild type and 17 mutant cells for voltages ranging from −80 mV to +60 mV for six concentrations of extracellular calcium (0.1 to 100 mM). The relative conductance (the degree of block) as a function of membrane potential is illustrated in Fig. 3A for typical wild-type and in Fig. 3B for typical mutant channels. For comparison, we include (Fig. 3 C and D) comparable data for magnesium block where the blocking site is situated more than halfway through the pore’s electrostatic field.

Figure 3.

Voltage dependence of divalent ion effects for representative cells. (A) Relative conductance (extent of calcium ion block) as a function of voltage for wild-type channels with 30 mM calcium ion concentration. (B) The same plot for mutant channels. (C) Relative conductance (extent of magnesium in block) as a function of voltage for wilt-type channel with 10 mM magnesium. (D) A similar plot for the mutant channels with 30 mM magnesium.

The voltage dependence for divalent ion block like that shown in Fig. 3 can be characterized by computing a “slope factor”: this slope factor is the constant k that appears in equation 1a of Sharma and Stevens (39), and is the growth rate (units: mV⁻¹) of an exponential fitted to data like those illustrated in Fig. 3. A slope factor not significantly different from zero is found for both wild-type and mutant channels over the range of calcium concentrations investigated, as illustrated in Fig. 4; for comparison, Fig. 4 also includes the slope factor that describes magnesium block for wild-type and mutant channels as a function of magnesium concentration.

Figure 4.

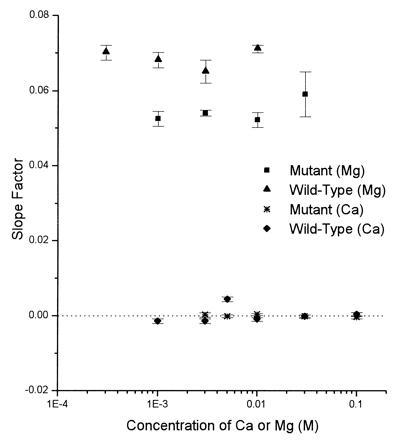
Voltage dependence of divalent ion block, characterized by the “slope factor” as a function of calcium magnesium concentration for wild-type and mutant channels. The slope factor is the rate of increase of an exponential fitted to the fraction of blocked channels [B(C)] as a function of voltage over the range of negative voltages as illustrated in Fig. 3.

The lack of voltage dependence exhibited by calcium block indicates that these ions bind to a site that is outside the voltage gradient through the pore, that is, near the extracellular mouth of the pore. Magnesium binding is highly voltage-dependent and its binding site lies deep in the pore as the magnesium ions travel a large electrical distance to reach their binding site (39). Thus, our data provide direct evidence that the calcium and magnesium binding sites are distinct and are in separate regions of the pore. The lack of voltage dependence of calcium binding also indicates that the change in calcium block is not because the magnesium site is altered in a way that it binds divalent cations nonselectively.

The ɛ1(N614Q) mutation increases the affinity of calcium for its binding site but decreases the affinity of magnesium for its binding site as we have shown in a previous study (39). The calcium and magnesium binding sites, however, are distinct and in separate parts of the channel. Thus, a single mutation has opposite effects on divalent ion binding at two separate molecular locations, a point to which we return in the discussion.

Relative Permeability of Calcium.

We define permeability ratios in terms of reversal potential, V_r, using a theory developed directly from the Nernst relation and without assuming a specific barrier model for the pore (20) to obtain the equation

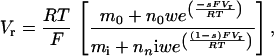5

where m_j is the activity of monovalent ion and n_j is the activity of divalent ion; j = o for extracellular and j = i for intracellular ions. Permeability of calcium is defined by the constant w relative to sodium where w is defined to be one. The constant s corresponds to the position of the barrier in the more conventional Goldman–Hodgkin–Katz (GHK) model (40) and has a value of 0.8 determined in earlier work.

To measure the permeability of calcium we obtained current–voltage plots in six different extracellular calcium concentrations for wild-type and mutant cells. Reversal potential was determined from such plots obtained from 20 wild-type and 17 mutant cells. Fig. 5 presents reversal potential plotted as a function of extracellular calcium concentration. Eq. 5 provided a smooth fit of the data points. From this fit, the value of w was calculated to be 11. An indistinguishable fit was obtained for both mutant and wild-type data. Calcium ions are, by this measure, 11 times more permeable than sodium ions and ɛ1(N614Q) mutation does not change the permeability of calcium through the NMDA channels.

Figure 5.

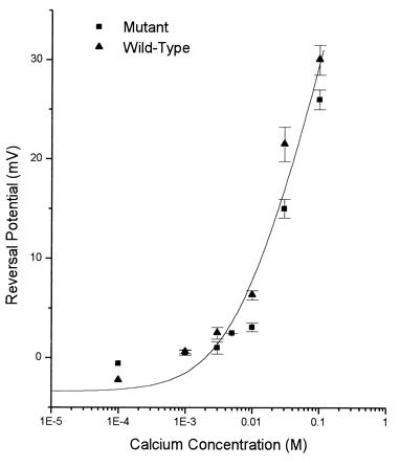
Permeability of calcium through wild-type and mutant NMDA channels. Reversal potential is plotted as a function of extracellular calcium concentration. Triangles are data from wild-type channels and circles from mutant channels. Permeability ratio PCa/PNa was calculated to be 11 for wild type and mutant using Eq. 9, which provides a smooth fit of the data.

DISCUSSION

In an earlier study (39), we showed that the magnesium block in wild-type ζ1/ɛ1 receptor channel is quantitatively like that in native hippocampal receptors and found that the magnesium ions bind to a site that is situated about 80% into the voltage field of the pore. The ɛ1(N614Q) mutation has only a small effect (17%) on the voltage dependence but reduces the affinity of magnesium for its site 10-fold. In this study, we have examined the effects of extracellular calcium ions on the ionic flux through the wild-type and mutant channels in an effort to further our understanding of the biophysical basis for the movement of divalent cations through the NMDA receptor pore. We find that calcium permeability is unaffected by the mutation but that the affinity of calcium for its superficial binding site is about doubled.

Theory.

We have used the theory described by Jahr and Stevens (20) to study the flux of calcium ions through the native NMDA channels. According to this theory, NMDA receptor channels are highly permeable to calcium, but calcium ions also block the channels as they permeate. Jahr and Stevens (20) demonstrated that this model provides a satisfactory description for the behavior of NMDA receptors over a wide range of extracellular calcium concentrations. Here we find this to be true for recombinant heteromeric ζ1/ɛ1 NMDARs as well. Our data indicate that the behavior of wild-type channels in the presence of extracellular calcium is like that of native NMDA channels: block of the channel by calcium ions and the calcium permeability of wild-type channels is quantitatively similar to that of the NMDA channels found on the hippocampal neurons in culture. The model we have used has two advantages over alternative ones: First, our model can account for all our results without assuming the presence of a large negative surface charge. This is in agreement with the observations of Zarei and Dani (22) who found experimentally that 0.02 charges per nm² were present at the mouth of the pore and had an effect on permeation only in low ionic strength solutions. Second, it allows us to directly determine the voltage dependence of calcium binding. By assuming that calcium ions block the channel pore as they permeate, we can study the effect of calcium ions in the absence of other divalent cations and identify the position of the calcium binding site based upon voltage dependence of binding.

Separate Calcium and Magnesium Binding Sites.

Our data indicate that calcium ions block ionic flux through wild-type channels in a mostly voltage-independent fashion. This lack of voltage dependence of calcium binding is similar to that observed in the native channels and implies that calcium ions bind to a site close to the mouth of the pore, outside the voltage gradient through the pore. Since the magnesium-binding site is deep within the voltage field gradient through the pore (magnesium blocking is very voltage dependent), the two divalent binding sites must be physically separate. This conclusion has been reached previously for wild-type channels (20, 24), and has recently been confirmed for wild-type and a mutant channel similar to the one studied here (25). Unfortunately, a comparison of the present data with that presented by Premkumar and Auerbach (25) is difficult because the two studies examined somewhat different mutant channels with different expression systems (oocyte versus the mammalian cells used here). The comparison is further complicated by the fact that Premkumar and Auerbach (25) interpreted their data in terms of a model that supposed the existence of two distinct conductance pathways through the channel: one pathway that feels the influence of a bound calcium ion and a second independent pathway that does not. Here we suppose that all permeant ions pass through the same physical pore and that all ionic permeation is greatly diminished whenever a calcium ion occupies its blocking site.

Since the data require the existence of two separate binding sites, one for magnesium part way through the conduction pathway (the “deep” site) and another for calcium near the pore’s outer mouth (the superficial site), how can a single point mutation affect the binding to both sites, and in opposite directions (increased calcium binding and decreased magnesium binding)? Although one can envision complicated schemes that require substantial reorganization of the channel structure, the simplest idea is that the main mutational effect is on the magnesium site, and that the altered binding to the calcium site is a consequence of this main effect. Although the deep site has the highest affinity for magnesium, there is evidence that calcium can also briefly occupy this site (16), probably as one of the permeation steps. If the two sites were electrostatically fairly close, then the occupancy of the deep site by calcium would raise the energy for calcium binding to the superficial site. Of course, magnesium bound to the deep site would also diminish the binding of calcium to the superficial site, but one would never measure this effect because the ion conduction through the channel is blocked whenever magnesium occupies the deep site. If the affinity of magnesium for the deep site is decreased in the mutant channels, one would certainly expect that the affinity of calcium would similarly be decreased. This would mean that the fraction of the time the deep site is occupied by calcium would be decreased and that the effect on the superficial site of a calcium ion bound to the deep site would be decreased. With less occupancy of the deep site, the superficial site would be more fully occupied, as we have observed.

Structure of the Calcium Binding Site.

Calcium and magnesium ions, although very similar, differ in a number of ways. First, calcium ions have a bigger Pauling radius (0.99 Å) than magnesium ions (0.65 Å). Second, the preferred coordination number for calcium ions is 8 as opposed to 6 for magnesium ions. Third, as a consequence of their larger crystal radius, calcium ions exhibit lower hydration energy than magnesium ions, which require a large amount of energy to for the removal of their hydration shells. Weakly acidic and neutral groups such as amines bind to magnesium much more strongly than to calcium. Further, calcium is bound preferentially by strongly acidic anions and sites showing preference for this cation could include phosphate, carboxylate, or sulfonate groups and no nitrogen bases. Thus, a protein site that binds magnesium need not bind calcium so strongly or alternatively a calcium binding site may be a very poor site for magnesium (41).

Our results provide direct evidence that the calcium and magnesium ions bind to different sites in the pore. We postulate that Asp-614 of the epsilon subunit forms a part of the magnesium coordinating site. Substitution of asparagine with a larger amino acid like glutamine decreases the affinity of the deep site for divalent ions (both calcium and magnesium) and the consequent altered occupancy, in turn, produces a smaller (twofold) but significant secondary effect on the binding of calcium ions at the superficial site.