Abstract
With computer simulations of >100,000 atoms, the mechanism for the hydrophobic collapse of an idealized hydrated chain was obtained by tiling space with (0.2 nm)3 cubes and projecting the atomistic water molecule positions onto this grid. With the coarse-grained field thus defined, the string method in collective variables was used to compute a minimum free-energy pathway (MFEP) for the collapsing chain. These calculations provide a proof of principle for a coarse-grained description of water solvent. Furthermore, the calculated MFEP characterizes the mechanism for the collapse of the hydrated chain by providing a path of maximum likelihood for dynamical trajectories. The reliability of the calculated MFEP was confirmed with the use of conventional molecular dynamics trajectories. Analysis of the MFEP provides atomistic confirmation for the mechanism of hydrophobic collapse proposed by ten Wolde and Chandler. In particular, we show that length-scale-dependent hydrophobic dewetting is the rate-limiting step in the hydrophobic collapse of the considered chain.
Keywords: rare-event dynamics, water
This paper applies the string method (1–3) to the phenomenon of hydrophobic collapse. We show that the method can describe complex dynamics in large atomistic systems, ones for which other currently available rare-event methods would seem intractable. Furthermore, we use the string method to demonstrate that atomistic dynamics can be usefully projected onto that of a coarse-grained field. The specific application of the string method considered herein finds results that are consistent with the mechanism of hydrophobic collapse put forward by ten Wolde and Chandler (tWC) (4).
The hydrophobic effect, or the tendency of oil and water to separate on mesoscopic length scales, has long been recognized as an important driving force in molecular assembly (5). Recent theoretical developments have helped establish a quantitative understanding of the thermodynamics of hydrophobicity (6, 7), but the dynamics of hydrophobic collapse remain poorly understood because it couples a large range of length and time scales. Relevant processes include the atomic-scale motions of individual water molecules, collective solvent density fluctuations, and the nanometer-scale movements of the hydrophobic solutes. Bridging these dynamical hierarchies and addressing the problem of complex dynamics in large systems are fundamental challenges for computational methods.
We address this challenge by using the string method in collective variables (1–3). We consider the collapse of a chain composed of 12 spherical hydrophobes in an explicit solvent of ≈34,000 water molecules. We studied the system by coarse-graining the water molecule positions onto a set of 129,000 collective variables that represent the solvent density field and then using the string method in these variables to compute the minimum free-energy path (MFEP) for the hydrophobic collapse of the chain. Conventional molecular dynamics (MD) simulations were subsequently performed to confirm that this coarse-grained description adequately describes the mechanism of hydrophobic collapse.
tWC have previously reported simulations of an idealized hydrophobic chain solvated by a coarse-grained model of liquid water (4). For this model, they found that the key step in the collapse dynamics is a collective solvent density fluctuation that is nucleated at the hydrophobic surface of the chain. However, it was not clear whether this mechanism was an artifact of their coarse-grained model of water. Atomistic simulations are needed to resolve the issue.
Previous efforts to characterize the mechanism of hydrophobic collapse using atomistic computer simulations neither confirm nor disprove the mechanism proposed by tWC. In recent work, for example, MD simulations showed that dewetting accompanies the collapse of hydrophobes in water (8–11). However, the rate-limiting step and, thus, the mechanism for hydrophobic collapse were not characterized. Specifically, in ref. 10, MD trajectories were initiated at various separation distances for a pair of melettin protein dimers. Collapse dynamics were observed only when the initial dimer configuration was on the product side of the free-energy barrier, but the actual nature of that barrier and the dynamics of crossing it were not studied. In ref. 11, the thermodynamics and solvation of a hydrophobic chain were studied as a function of its radius of gyration, but, again, the dynamics of collapse was not characterized.
Our atomistic simulations explicitly confirm the mechanism of hydrophobic collapse put forward by tWC (4). In particular, we show that the rate-limiting step in the collapse of their hydrophobic chain coincides with a collective solvent motion and that performing the rate-limiting step involves performing work almost exclusively in the solvent coordinates. We further show that the solvation free energy along the MFEP can be decomposed into small- and large-length-scale contributions. This analysis demonstrates that atomistic solvent energetics can be quantitatively modeled by using a grid-based solvent density field, and it suggests that the rate-limiting step for hydrophobic collapse coincides with length-scale-dependent hydrophobic dewetting.
Atomistic Model, Coarse-Graining, and the String Method
The System.
As indicated, we considered the atomistic version of the hydrated hydrophobic chain studied by tWC (4), a model that exhibits the length-scale-dependent hydrophobic effect (6). More complicated models can be considered, but we limited this study to this particular chain. The chain is composed of 12 spherical hydrophobes, each with a diameter of 7.2 Å and a mass of 71 atomic mass units. These are ideal hydrophobes, because they exert purely repulsive interactions with water that expel the centers of the oxygen atoms from the volume within 0.5 nm of the center of the hydrophobe. The volume and mass are typical of amino acid residues (12, 13). Consecutive hydrophobes in the unbranched chain interact via harmonic bonds, and the chain is made semirigid by a potential energy term that penalizes its curvature. The rigidity is chosen so that the extended configurations of the chain are dominant in vacuum. It is only solvent (and thus the hydrophobic interaction) that stabilizes the collapsed globule configurations. The chain is hydrated with 33,912 rigid water molecules interacting with the SPC/E (simple point charges/extended model) potential (14) in an orthorhombic simulation box with periodic boundary conditions. Electrostatic interactions were included by using the smoothed particle mesh Ewald method (15), and all simulations were performed at 300 K. Full details of the simulation protocol are provided in supporting information (SI) Text: “Details of the System.”
To describe hydrophobic collapse, it is necessary to choose an appropriate thermodynamic ensemble for the simulations. Nanometer-scale fluctuations in solvent density are suspected to play a key role in these dynamics. Use of the NVT ensemble (with a 1-g/cm3 density of water) might suppress these density fluctuations and bias the calculated mechanism. We avoided this problem with a simple technique that is based on the fact that, under ambient conditions, liquid water is close to phase coexistence. Indeed, it is this proximity that leads to the possibility of large-length-scale hydrophobicity (6, 16). By placing a fixed number of water molecules at 300 K in a volume that corresponds to an average density of <1 g/cm3, we obtained a fraction of the system at the density of water vapor and the majority at a density of bulk water. Because we are not concerned with solvent fluctuations on macroscopic length scales, the difference between simulating bulk water at its own vapor pressure compared with atmospheric pressure is completely negligible. This strategy has been used to study the dewetting transition between solvophobic surfaces (17, 18). To ensure that the liquid–vapor interface remains both flat and well distanced from the location of the chain, we repelled particles from a thin layer at the top edge of the simulation box, as is discussed in SI Text: “Details of the System.”
Coarse-Graining of Solvent.
Throughout this study, we simulated water and the hydrated chain by using atomistic MD. To apply the string method to the dynamics of this system, we employed a choice of collective variables that describe the density field of water. In particular, a coarse-graining algorithm was developed to connect the atomistic and collective variable representations of the solvent. By following tWC (4), the simulation box was partitioned into a three-dimensional lattice (48 × 48 × 56) of cubic cells with a side length of l = 2.1 Å. We labeled the cells with the vector k = (kx, ky, kz), where each kζ takes on integer values bounded as follows: 1 ≤ kx ≤ 48, 1 ≤ ky ≤ 48, and 1 ≤ kz ≤ 56. On this grid, the molecular density ρ(r), as determined by the positions of the water oxygen atoms, is coarse-grained into the field Pk, where
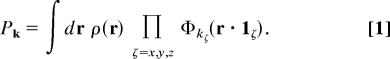 |
Here, the integral extends over the volume of the system, and 1ζ denotes the unit vector in the ζth Cartesian direction. The coarse-graining function, Φkζ(x), is normalized, ensuring that ΣkPk = N is the total number of water molecules. The particular function that we have chosen to use is
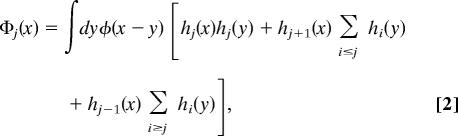 |
where φ(x) = (2πσ2)−1/2 exp(−x2/2σ2), σ = 1 Å, and hj(x) is unity when x is in the jth interval and zero otherwise. In effect, this choice spreads the atomistic density field ρ(r) over the length scale σ and bins it into a grid of length scale l in such a way as to preserve normalization. While we have found this choice of coarse-graining function to be convenient, others are possible.
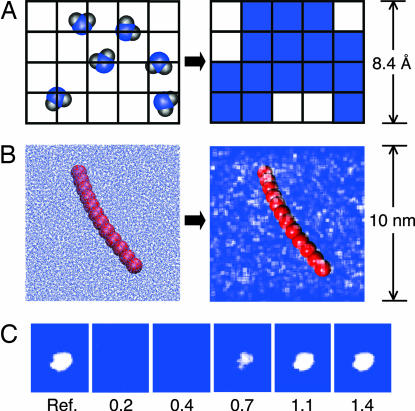
Fig. 1 A and B illustrates the coarse-graining procedure. In Fig. 1A, the solvent is schematically shown before and after coarse-graining. Fig 1B, the same mapping is shown for the actual system considered here. Cells are shaded white when their solvent occupation, Pk, is less than half of the bulk average value of 〈P〉bulk ≡ c = 0.3 molecules. Small local density fluctuations are seen throughout the simulation box, as is expected for an instantaneous solvent configuration.
Fig. 1.
Solvent coarse graining. (A) The coarse-graining procedure is schematically shown to project the atomistic solvent density onto a discrete grid. (B) The same procedure is shown for an instantaneous solvent configuration of the actual system. Grid cells containing less solvent density than c/2 are colored white; the remaining cells are left transparent against the blue background. The hydrophobic chain is shown in red. (C) Atomistic solvent density is restrained to the reference distribution at the far left. With larger restraint force constant κ reported numerically in units of 2 kBT/c2, the average atomic solvent density reproduces the reference distribution in detail (see text for notation).
In addition to visualizing solvent density, the coarse-graining algorithm is useful for controlling the solvent density in MD simulations. For example, if it is desired that a particular cell k exhibit a solvent occupation P∗k, the potential energy term κ(Pk − P∗k)2/2 can be used to derive the appropriate forces on the atoms in the simulation, where κ is a force constant. This technique is illustrated in Fig. 1C. The leftmost image shows a density distribution that is exceedingly unlikely for a simulation of ambient liquid water. Images to the right show the average solvent density distribution from MD simulations that are restrained to this unlikely reference distribution with increasing κ. Force constant values of >2 kBT/c2, in which the simulation incurs an energetic penalty of at least kBT for placing the average bulk density in a cell that is restrained to be empty, ensure that the reference distribution is recovered in detail. Here, kBT denotes Boltzmann's constant times temperature T.
Defining the MFEP.
We used the coarse-graining procedure to obtain collective variables that describe the position of the hydrophobic chain and the water density field. Specifically, let x = (xc, w) be the position vector of length n = 3 × 12 + 3 × 3× N for the atomistic representation of the entire system, where xc is the position vector for the hydrophobes in the chain and w is the position vector for the atoms in the water molecules. Then, z(x) = (xc, P) is the vector of length 𝒩 = 3 × 12 + 48 × 48 × 56 for the collective variable representation of the system, where the elements of P are defined in Eq. 1.
The MFEP is a curve in the space of collective variables. It is represented by z*(α), where α = 0 corresponds to the collapsed chain and α = 1 corresponds to the extended chain. For intermediate values α ∈ (0, 1), the MFEP obeys the condition
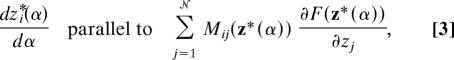 |
where F(z) = −β−1ln〈Π𝒩i=1δ(zi − zi(x))〉 is the free-energy surface defined in the collective variables, and
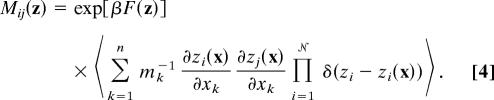 |
Here, angle brackets indicate equilibrium expectation values, β−1 = kBT, and mk is the mass of the atom corresponding to coordinate xk. The matrix Mij(z), which arises from projecting the dynamics of the atomistic coordinates onto the collective variables (and, thus, in general, curving the coordinate space) (3, 19), ensures that the various collective variables evolve on a consistent time scale. As is seen in Eq. 10, the matrix scales the relative diffusion coefficients for the collective variables.
If the used collective variables are adequate to describe the mechanism of the reaction (here, the hydrophobic collapse), then it can be shown that the MFEP is the path of maximum likelihood for reactive MD trajectories that are monitored in the collective variables (3). For the current application, we checked the adequacy of the collective variables a posteriori by running MD trajectories that are initiated from the presumed rate-limiting step along the MFEP (i.e., the configuration of maximum free energy) and verified that these trajectories led with approximately equal probability to either the collapsed or extended configurations of the chain (see Hydrophobic Collapse of a Hydrated Chain: “The Committor Function and a Proof of Principle for Course-Graining”).
String Method in Collective Variables.
The string method yields the MFEP by evolving a parameterized curve (i.e., a string) according to the dynamics (3, 20)
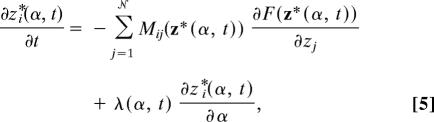 |
where the term λ(α, t)∂z∗i(α, t)/∂α enforces the constraint that the string remain parameterized by normalized arc length. The endpoints of the string evolve by steepest descent on the free-energy surface,
for α = 0 and α = 1. These artificial dynamics of the string yield the MFEP, which satisfies Eq. 3.
In practice, the string is discretized by using Nd configurations of the system in the collective variable representation. The dynamics in Eqs. 5 and 6 are then accomplished in a three-step cycle, where (i) the endpoint configurations of the string are evolved according to Eq. 6 and the rest of the configurations are evolved according to the first term in Eq. 5, (ii) the string is (optionally) smoothed, and (iii) the string is reparameterized to maintain equidistance of the configurations in the discretization. This cycle is repeated until the discretized version of Eq. 3 is satisfied. Step i requires evaluation of the mean force elements ∂F(z)/∂zi and the tensor elements Mij(z) at each configuration. These terms are obtained by using restrained atomistic MD simulations of the sort illustrated for the solvent degrees of freedom in Fig. 1C. The details of the string calculation are provided in SI Text: “String Method in Collective Variables.”
Hydrophobic Collapse of a Hydrated Chain
MFEP.
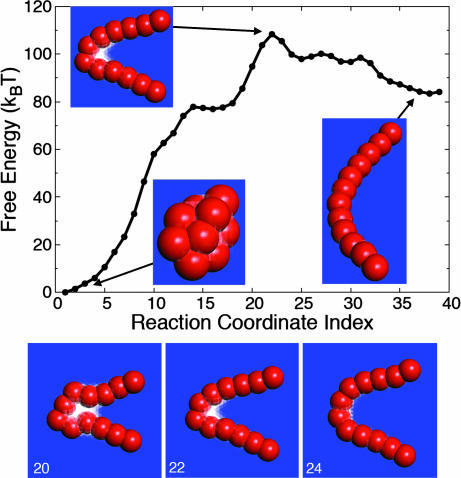
Fig. 2 shows the MFEP for the hydrophobic collapse of the hydrated chain. It was obtained by using the string method in the collective variables for the chain atom positions and the grid-based solvent density field. The converged MFEP was discretized by using Nd = 40 configurations of the system, and we shall hereafter refer to these configurations by their index number, s = 1, …, Nd. The free-energy profile was obtained by integrating the projection of the mean force along the MFEP, using
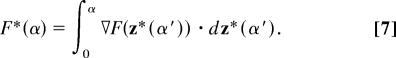 |
The resolution of F*(α) in Fig. 2 could be improved by employing a larger Nd but at larger computational cost.
Fig. 2.
The minimum free-energy path obtained by using the string method. (Upper) The free-energy profile exhibits a single peak at configuration 22. (Lower) The configurations of the path in the vicinity of the free-energy peak are shown with configuration numbers indicated in white text.
The statistical errors in the free-energy profile between consecutive configurations are approximately the size of the plotted circles, and the small features in the profile at configurations 27 and 31 are due to noise in the convergence of the string calculation. Further discussion of the statistical error in the string calculation is provided in SI Text: “String Method in Collective Variables.” Fig. 2 Lower presents configurations along the MFEP in the region of the free-energy barrier. As in Fig. 1, lattice cells with less than half of the bulk solvent occupation number fade to white.
The free-energy profile in Fig. 2 is dominated by a single barrier at configuration 22, where a liquid–vapor interface is formed at a bend in the hydrophobic chain. The sharply curved chain geometry presents an extended hydrophobic surface to molecules located in the crook of the bend, an environment that is analogous to that experienced by water trapped between hydrophobic plates and known to stabilize large-length-scale solvent density fluctuations (16, 21, 22). The barrier in the calculated free-energy profile clearly coincides with a collective motion in the solvent variables.
The string method characterizes the most likely member among a local channel of reactive trajectories. A reasonable concern, however, is the extent to which other channels (such as those that might correspond to forming bends at other points along the hydrophobic chain) are accessible and important. However, if other bends in the chain did correspond to well separated transition channels, then it seems unlikely, given the arbitrary manner in which the string was initialized, that we could locate a MFEP that exhibits a totally symmetric bend in the chain. Furthermore, an estimate for the energetic cost of translating the bend along the chain, which is described in SI Text: “Estimation of the Barrier Between Reactive Barriers,” suggests that trajectories that collapse by forming asymmetric bends in the chain do not belong to a distinct reactive channel from those that form a symmetric bend. That said, the less symmetric transition state configuration illustrated in figure 2 of ref. 4 is but one member of the transition-state ensemble, the most likely of which is pictured here in Fig. 2.
Solvation Free Energy.
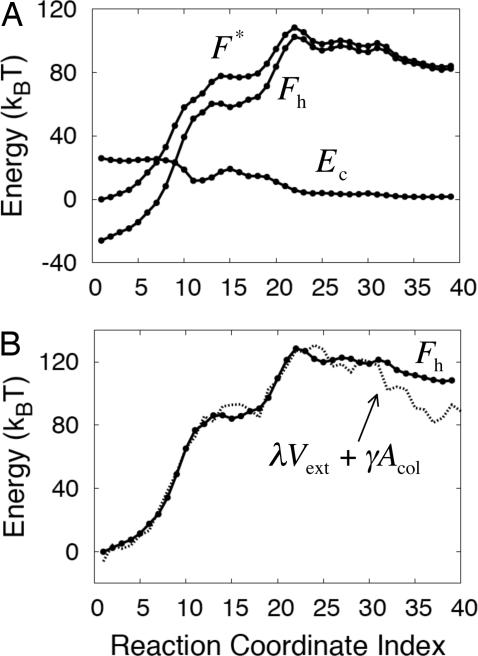
A simple theory was constructed to understand the contributions to the free-energy profile in Fig. 2 and to test the validity of coarse-graining solvent interactions. Noting that our choice of collective variables for the string calculation neglects the configurational entropy of the chain, the free-energy profile F(α) can be decomposed into the configurational potential energy of the chain Ec(α) and the free energy of hydrating the chain, Fh(α).
The term Ec(α) is easily evaluated from the chain potential energy term, yielding the components of the free-energy profile shown in Fig. 3A.
Fig. 3.
A simple theory describes the solvation free energy of irregular hydrophobic solute geometries. (A) The free-energy profile F* from simulation, decomposed into contributions from the chain configurational potential energy Ec and the free energy of solvation Fh. (B) The free energy of solvation obtained from Eq. 9 (dotted line) and from simulation (solid line).
Now we will focus our attention on Fh. The solvation free energy for hydrophobes of idealized geometry is well understood. For small-length-scale hydrophobes (<1 nm), this energy scales linearly with the solute volume, whereas, for large-length-scale hydrophobes, it scales linearly with the solute surface area (16, 23). However, theoretical prediction of the solvation free energy for more complicated solute geometries is not necessarily trivial. For example, depending on its configuration, some parts of the chain considered here might be solvated like a large-length-scale hydrophobe, whereas other parts might behave like a small-length-scale hydrophobe.
Here, we present a technique for separating a general hydrophobic solute into components that belong to either the small-length-scale or large-length-scale regimes. We define the solvent-depleted volume as the continuous set of lattice cells that are, on average, occupied by <50% of the average bulk solvent value (this set includes both the volume that is excluded by the hard-sphere-like interactions between the solute and solvent interactions and any additional volume in the vicinity of the solute that is not substantially occupied by the solvent). We also introduce a probe volume that is a cubic 4 × 4× 4 set of cells, which is approximately the size at which the water solvation structure changes from the small-length-scale to the large-length-scale regime.
The probe volume is used to determine whether a given section of the solvent-depleted volume is in the small- or large-length-scale regime. This is done by moving the probe volume throughout the simulation box and determining whether it can be fit into different portions of the solvent-depleted volume. If at a given position the vast majority of this probe volume (specifically, 59 of 64 cells) fits within the solvent-depleted volume, then the cells in that portion of the solvent-depleted volume are included in the large-length-scale component, Vcol. Portions of the solvent-depleted volume that do not meet this criterion for any position of the probe volume are included in the small-length-scale component, Vext. The volumes Vcol and Vext, which are plotted in SI Fig. 8A, primarily include contributions from the collapsed portions and extended portions of the chain, respectively. The total volume Vtot is obtained by counting the total number of cells in the solvent-depleted volume, such that Vtot = Vext + Vcol.
The total surface area, Atot, and its large-length-scale component, Acol, were obtained by counting the number of external faces on the cells that comprise Vtot and Vcol, respectively. The surface area of the small-length-scale component was obtained by using Aext = Atot − Acol. To account for the fact that we are calculating the area of a smooth surface by projecting it onto a cubic lattice, each surface area term also is multiplied by a 2/3, a correction factor that is exact for an infinitely large sphere. The surface area components are plotted in SI Fig. 8A.
We use the separated components of the solute volume and surface area to estimate the solvation free energy for the chain along the minimum free-energy path with the relationship.
The coefficients λ and γ are, respectively, the prefactors for the linear scaling of the solvation free energy in the small-length-scale and large-length-scale regimes, as obtained by calculations on a spherical hydrophobic solute (23). Their values are taken to be λ = 8 mJ/(m2Å) and γ = 45 mJ/m2.
The results of this calculation are presented in Fig. 3B. The dotted line indicates our theoretical estimate of the solvation free energy using Eq. 9, and the solid line indicates the data from the atomistic simulations (from Fig. 3A). The agreement is very good, and, as is shown in SI Text: “Alternate Models for the Solvation Free Energy,” it is better than can be obtained from solvation free-energy estimates that exclusively consider either the solute volume or the solute surface area. This result demonstrates that atomistic solvent energetics can be quantitatively modeled by using a grid-based solvent density field. Furthermore, note in SI Fig. 8 that the collapsing chain first develops large-length-scale components in the vicinity of configuration 22, which suggests that both the peak in the free energy profile in Fig. 2 and the corresponding collective solvent density motion coincide with the crossover from small- to large-length-scale solvation (i.e., dewetting).
The Committor Function and a Proof of Principle for Coarse-Graining.
The various assumptions that are used in our implementation of the string method, including our choice of collective variables and the corresponding neglect of the chain configurational entropy, raise the possibility that the barrier in the free-energy profile in Fig. 2 does not correspond to the dynamical bottleneck for hydrophobic collapse. This is a general concern in trying to relate free-energy calculations to dynamical quantities, such as the reaction mechanism and the reaction rate. To confirm that the calculated free-energy profile is dynamically relevant, we evaluated the committor function at several configurations along the MFEP. The committor function reports the relative probability that MD trajectories that are initialized from a particular collective variable configuration first proceed to the extended configurations of the chain, as opposed to the collapsed configurations. For initial collective variable configurations that coincide with the true dynamical bottleneck, the committor function assumes a value of exactly 0.5.
We first evaluated the committor function at configuration 22, which corresponds to the peak in the calculated free energy profile in Fig. 2. The committor function is obtained by performing straightforward MD trajectories from initial conditions that are consistent with this collective variable configuration and then tallying the fraction of those trajectories whose endpoints are “extended,” as opposed to “collapsed.” The initial conditions for these trajectories are obtained from a 20-ps MD trajectory that is restrained to the collective variables for configuration 22; the atomistic coordinates of the restrained trajectory are recorded every picosecond. From each set of atomistic coordinates, an unrestrained trajectory was run for 150 ps forwards and backwards in time with the initial atomistic velocity vector drawn from the Maxwell–Boltzmann distribution at 300 K. To decide whether a given unrestrained trajectory terminates in either an extended or collapsed configuration of the chain, we employed an order parameter based on the number of chain atoms that are within d = 1.25 Å of another chain atom to which it is not directly bonded, where d refers to the separation between the surfaces of spheres with 3.6-Å radii surrounding the chain atoms. If the number of nonbonded contacts exceeds three, the chain is considered to be in a collapsed configuration; otherwise it is considered extended. This order parameter need only distinguish between collapsed and extended configurations of the chain; it need not be (and in fact is not) a good reaction coordinate. Fig. 4 illustrates representative forward and backwards unrestrained MD trajectories. Fig. 4B reminds the reader of the atomistic basis for the coarse-grained field.
Fig. 4.
Snapshots from unrestrained MD trajectories that are initiated from the calculated free-energy barrier at configuration 22. (A) The instantaneous configurations are visualized in the collective variable representation by using the same technique that was introduced in Fig. 1. (B) The boxed area from the 0-ps snapshot in A, with a planar cross-section of water with a thickness of 7.2 Å, is shown in atomistic detail.
The committor function at configuration 22 is 0.3 ± 0.1, suggesting that the calculated free-energy barrier is slightly biased toward the basin of stability for the collapse chain. However, this deviation from the ideal value of 0.5 is only marginally statistically significant, and we emphasize that the committor function is exponentially sensitive in the region of the dynamical bottleneck. To illustrate this point, we repeat the evaluation of the committor function at configuration 20, which is seen in Fig. 2 to be near the barrier peak but slightly closer to the collapsed configurations of the chain, as well as at configuration 24, which is slightly closer to the extended configurations. We found the committor function at configuration 20 to be 0.00 ± 0.05 and the value at configuration 24 to be 0.90 ± 0.05. Only very minor shifts along the MFEP dramatically change the value of the committor function.
Given the extreme sensitivity of the committor function near the dynamical bottleneck, the fact that configuration 22 gives rise to a significant fraction of trajectories that proceed to both the collapsed and extended basins is very significant. Furthermore, the direction in which the committor function changes as a function of the configuration number is as is expected in the vicinity of the dynamical bottleneck. We conclude that the barrier in the calculated free-energy profile correctly characterizes the true free-energy barrier, thus identifying the rate-limiting step for the collapse dynamics.
The committor function calculations, which are based on straightforward MD simulations, indicate that our choice of collective variables provides a reasonable description of the mechanism of hydrophobic collapse. This result yields atomistic support for the strategy of coarse-graining solvent dynamics. Because it is straightforward (3) to obtain the stochastic dynamics in the collective variables for which the most likely reaction pathway is the same as the mechanism obtained by using the string method, and further, because the mechanism for hydrophobic collapse obtained in the used collective variables agrees with the mechanism obtained by using atomistic dynamics, we obtain a proof of principle that atomistic solvent dynamics can be usefully projected onto a coarse-grained field. The Langevin equation for the collective variables in this description is (3)
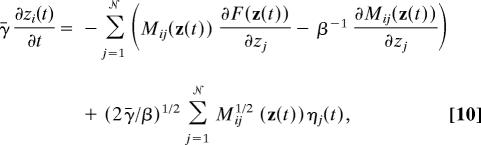 |
where ηi(t) is a white noise satisfying 〈ηi(t)ηj(t′)〉 = δijδ(t − t′) and t is an artificial time that is scaled by the friction coefficient γ̄.
The computational feasibility of directly integrating these coarse-grained dynamics, however, hinges on the cost of calculating the mean force elements ∂F(z)/∂zj and the tensor elements Mij(z) and ∂Mij(z)/∂zj, because these terms are required at every coarse-grained time step. It is therefore encouraging that the free-energy surface in the collective variables can be quantitatively modeled in lieu of atomistic simulations, by using Eqs. 8 and 9. Similar approximations for the tensor elements might also be possible.
The Rate-Limiting Step.
Using the calculated MFEP and committor function values, we established that the rate-limiting step for the hydrophobic collapse of the hydrated chain coincides with a collective solvent motion. Using a simple analysis of the solvation free energy, we found that this collective solvent motion is consistent with length-scale-dependent dewetting. However, it remains to be shown whether the rate-limiting step involves performing work in the solvent or chain degrees of freedom. This is an important distinction. If the latter case is true, then dewetting merely accompanies hydrophobic collapse as a spectator, but, if the former case is true, then dewetting is the rate-limiting step to hydrophobic collapse.
To address this issue, we again decomposed the free-energy profile, this time into contributions from work performed along the solvent and the chain collective variables. The definition of the free-energy profile in Eq. 7 can be written more explicitly as
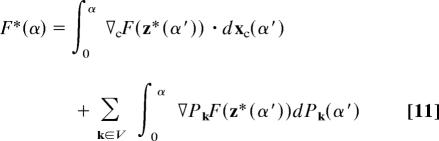 |
where ∇cF(z*(α′)) is the vector of mean forces acting on the chain atom positions at configuration s = Nd × α along the MFEP, and ∇PkF(z*(α′)) is the corresponding mean force on the solvent collective variable Pk. The full free-energy profile is obtained by setting the volume V equal to the entire simulation box. To understand the role of solvent in hydrophobic collapse, however, it is informative to calculate the free-energy profile by using various smaller solvent volumes.
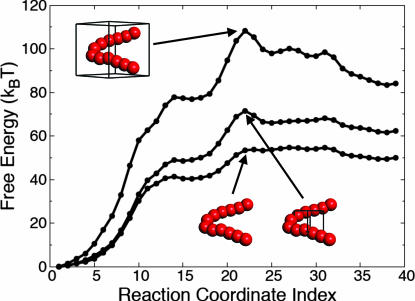
The bottom curve in Fig. 5 is obtained from Eq. 11 by letting V be the empty set, thus eliminating the second term. The middle curve is obtained by letting V be the set of 8 × 8 × 8 lattice cells at the middle of the simulation box, as is indicated in the corresponding image, and the top curve is obtained by letting V be the middle set of 20 × 20 × 20 lattice cells. Consideration of larger sets of lattice cells does not further alter the free-energy profile, as is shown in SI Text: “Convergence of the Free-Energy Profile with Increasing Solvent Box Sizes.” The solvent variables for regions of space that are distant from the collapsing chain remain constant along the path and do not contribute to the free-energy profile.
Fig. 5.
The free-energy profile from Fig. 2 is separated into contributions from the chain and solvent coordinates. In the bottom curve, only the first term in Eq. 11, which corresponds to work performed in the chain coordinates, is included in the free-energy profile. Solvent contributions additionally are included in the middle and top curves. The solvent volume included for each curve is indicated with a wire box. Inclusion of larger solvent volumes does not substantially change the profile.
The bottom curve in Fig. 5 shows only the work performed on the chain atom positions during hydrophobic collapse. Remarkably, it lacks almost any free-energy barrier, indicating that essentially no work is performed in the chain degrees of freedom in crossing the dynamical bottleneck. Instead, we see that the barrier emerges only upon inclusion of the work performed in the solvent collective variables. Performing the hydrophobic collapse involves traversing a free-energy barrier that exists only in the solvent coordinates. Fig. 5 shows that the dewetting transition not only accompanies the rate-limiting step for hydrophobic collapse, but that it is the rate-limiting step.
Supplementary Material
Acknowledgments
We thank Giovanni Ciccotti, Mauro Ferrario, Ray Kapral, and Luca Maragliano for useful discussions and the National Energy Research Scientific Computing Center for computing resources. T.F.M. was supported by Department of Energy Grants CHE-0345280 and DE-FG03–87ER13793. E.V.-E. was supported by the Miller Institute at University of California (Berkeley, CA), Office of Naval Research Grant N00014-04-1-0565, and National Science Foundation Grants DMS02-09959 and DMS02-39625. D.C. was supported by National Science Foundation Grant CHE-0543158.
Abbreviations
- tWC
ten Wolde and Chandler
- MFEP
minimum free-energy path
- MD
molecular dynamics.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0705830104/DC1.
References
- 1.E W, Ren W, Vanden-Eijnden E. Phys Rev B. 2002;66:52301. [Google Scholar]
- 2.E W, Ren W, Vanden-Eijnden E. J Phys Chem B. 2005;109:6688–6693. doi: 10.1021/jp0455430. [DOI] [PubMed] [Google Scholar]
- 3.Maragliano L, Fischer A, Vanden-Eijnden E, Ciccotti G. J Chem Phys. 2006;125:024106. doi: 10.1063/1.2212942. [DOI] [PubMed] [Google Scholar]
- 4.ten Wolde PR, Chandler D. Proc Natl Acad Sci USA. 2002;99:6539–6543. doi: 10.1073/pnas.052153299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kauzmann W. Adv Prot Chem. 1959;14:1–63. doi: 10.1016/s0065-3233(08)60608-7. [DOI] [PubMed] [Google Scholar]
- 6.Chandler D. Nature. 2005;437:640–647. doi: 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- 7.Hummer G, Garde S, Garcia AE, Pratt LR. Chem Phys. 2000;258:349–370. [Google Scholar]
- 8.Huang X, Margulis CJ, Berne BJ. Proc Natl Acad Sci USA. 2003;100:11953–11958. doi: 10.1073/pnas.1934837100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Huang Q, Ding S, Hua C-Y, Yang H-C, Chen C-L. J Chem Phys. 2004;121:1969–1977. doi: 10.1063/1.1766017. [DOI] [PubMed] [Google Scholar]
- 10.Liu P, Huang X, Zhou R, Berne BJ. Nature. 2005;437:159–162. doi: 10.1038/nature03926. [DOI] [PubMed] [Google Scholar]
- 11.Athawale MV, Goel G, Ghosh T, Truskett TM, Garde S. Proc Natl Acad Sci USA. 2007;104:733–738. doi: 10.1073/pnas.0605139104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang DM, Chandler D. Proc Natl Acad Sci USA. 2000;97:8324–8327. doi: 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mishra AK, Ahluwalia JC. J Phys Chem. 1984;88:86–92. [Google Scholar]
- 14.Berendsen HJC, Grigera JR, Straatsma TP. J Chem Phys. 1987;91:6269–6271. [Google Scholar]
- 15.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 16.Lum K, Chandler D, Weeks JD. J Phys Chem B. 1999;103:4570–4577. [Google Scholar]
- 17.Bolhuis PG, Chandler D. J Chem Phys. 2000;113:8154–8160. [Google Scholar]
- 18.Huang X, Zhou R, Berne BJ. J Phys Chem B. 2005;109:3546–3552. doi: 10.1021/jp045520l. [DOI] [PubMed] [Google Scholar]
- 19.Fukui K. Acc Chem Res. 1981;14:363–368. [Google Scholar]
- 20.E W, Ren W, Vanden-Eijnden E. J Chem Phys. 2007;126:164103. doi: 10.1063/1.2720838. [DOI] [PubMed] [Google Scholar]
- 21.Luzar A, Leung K. J Chem Phys. 2000;113:5836–5844. [Google Scholar]
- 22.Leung K, Luzar A. J Chem Phys. 2000;113:5845–5852. [Google Scholar]
- 23.Huang DM, Geissler PL, Chandler D. J Phys Chem B. 2001;105:6704–6709. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.