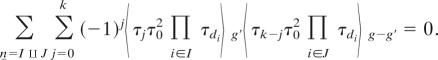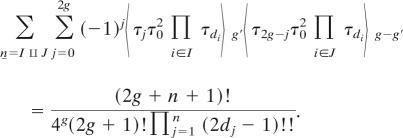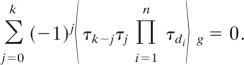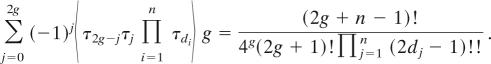New results of intersection numbers on moduli spaces of curves

Abstract

We present a series of results we obtained recently about the intersection numbers of tautological classes on moduli spaces of curves, including a simple formula of the n-point functions for Witten's τ classes, an effective recursion formula to compute higher Weil–Petersson volumes, several new recursion formulae of intersection numbers and our proof of a conjecture of Itzykson and Zuber concerning denominators of intersection numbers. We also present Virasoro and KdV properties of generating functions of general mixed κ and ψ intersections.

Let 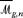denote the Deligne–Mumford moduli stack of stable curves of genus g with n marked points. Let ψ_i be the first Chern class of the line bundle 𝔼, whose fiber over each pointed stable curve is the cotangent line at the ith marked point. Let λ_i be the ith Chern class of the Hodge bundle 𝔼, whose fiber over each pointed stable curves is H⁰ (C, ω_c).

We also have the κ classes originally defined by Mumford (1), Morita (2), and Miller (3). A more natural variation was later given by Arbarello–Cornalba (4). It is known that the κ and ψ classes generate the tautological cohomology ring of the moduli spaces, and most of the known cohomology classes are tautological.

The following intersection numbers

are called the higher Weil–Petersson volumes (5). These are important invariants of moduli spaces of curves.

In 1990, Witten (6) made the remarkable conjecture that the generating function of intersection numbers of ψ classes on moduli spaces are governed by KdV hierarchy. Witten's conjecture (first proved by Kontsevich; ref. 7) is among the deepest known properties of moduli spaces of curves and motivated a surge of subsequent developments.

The intersection theory of tautological classes on the moduli space of curves is a very important subject and has close connections to string theory, quantum gravity and many branches of mathematics.

The n-Point Functions for Intersection Numbers

Definition 1:

We call the following generating function

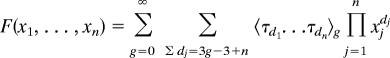the n-point function.

Consider the following “normalized” n-point function

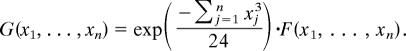Starting from 1-point function G(x) = 1/x², we can obtain any n-point function recursively by the following theorem.

Theorem 1 (8).

For n ≥ 2,

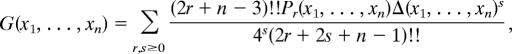where P_r and Δ are homogeneous symmetric polynomials defined by

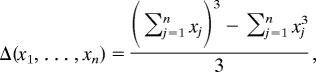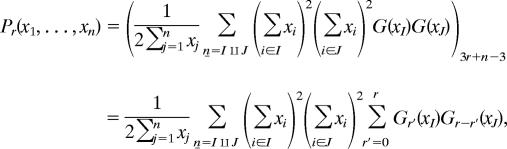where I, J ≠ θ, ṉ = {1, 2, …, n}, and G_g (x_I) denotes the degree 3g + |I| − 3 homogeneous component of the normalized |I|-point function G(x_k1, …, x_k|I|), where k_j ∈ I.

Thus, we have an elementary and more efficient algorithm to calculate all intersection numbers of ψ classes other than the celebrated Witten–Kontsevich theorem.

Because 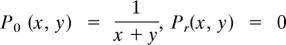for r > 0 and

we recover Dijkgraaf's 2-point function and Zagier's 3-point function obtained years ago.

There is another slightly different formula of the n-point functions. When n = 3, this has also been obtained by Zagier.

Theorem 2 (8).

For n ≥ 2,

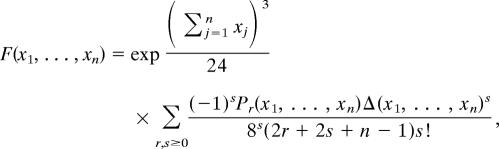where P_r and Δ are the same polynomials as defined in Theorem 2.

Okounkov (9) obtained an analytic expression of the n-point functions using n-dimensional error-function-type integrals. Brézin and Hikami (10) use correlation functions of GUE ensemble to find explicit formulae of n-point functions.

Higher Weil–Petersson Volumes

We have discovered a general recursion formula of higher Weil– Petersson volumes (11), which is a vast generalization of the Mirzakhani's recursion formula (12).

First we fix notations as in ref. 5. Consider the semigroup N^∞ of sequences m = (m₁, m₂, …), where m_i are nonnegative integers and m_i = 0 for sufficiently large i.

Let m, t, a₁, …, a_n ∈ N^∞ and s := (s₁, s₂, …) be a family of independent formal variables.

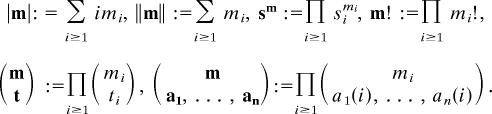Let b ∈ N^∞, we denote a formal monomial of κ classes by

Theorem 3 (11).

Let b ∈ N^∞ and d_j ≥ 0.

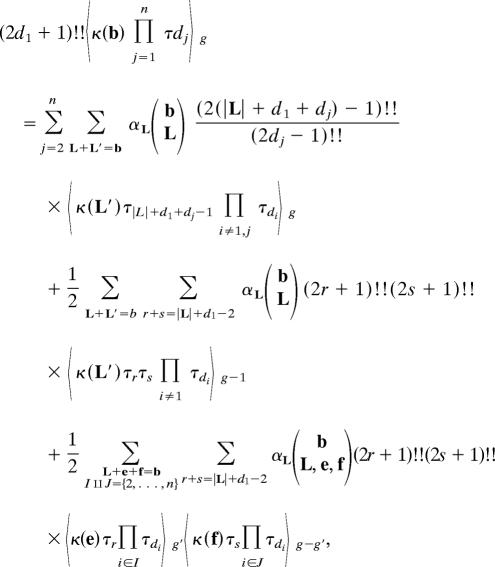where the tautological constants α_L can be determined recursively from the following formula

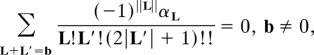namely

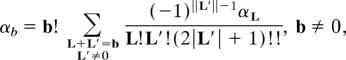with the initial value α₀ = 1.

The proof of the above theorem is to use Witten–Kontsevich theorem, a combinatorial formula in ref. 5 expressing κ classes by ψ classes and the following elementary but crucial lemma (11).

Lemma 1.

Let F (L, n) and G (L, n) be two functions defined on N^∞ × ℕ, where ℕ = {0, 1, 2,…} is the set of nonnegative integers. Let α_L and β_L be real numbers depending only on L ∈ N^∞ that satisfy α₀β₀ = 1 and

Then the following two identities are equivalent.

When b = (l, 0, 0, …), Theorem 3 recovers Mirzakhani's recursion formula of Weil–Petersson volumes for moduli spaces of bordered Riemann surfaces (12–17).

Theorem 3 also provides an effective algorithm to compute higher Weil–Petersson volumes recursively.

In fact, we can use the main formula in ref. 5 to generalize almost all pure ψ intersections to identities of higher Weil–Petersson volumes that share similar structures as Theorem 3. For example, the identities in the following theorem are generalizations of the string and dilation equations.

Theorem 4 (11).

For b ∈ N^∞ and d_j ≥ 0,

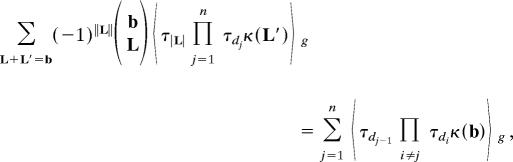and

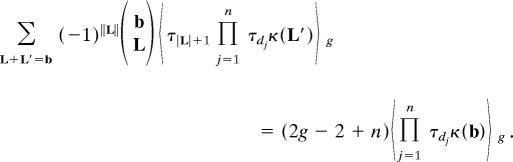Note that Theorem 4 generalizes the results in ref. 18.

New Identities of Intersection Numbers

The next two theorems follow from a detailed study of coefficients of the n-point functions in Theorem 1.

Theorem 5 (8).

We have

1. Let k > 2g, d_j ≥ 0 and Σ_j=1ⁿ d_j = 3g + n − k.

   
2. Let d_j ≥ 1 and Σ_j=1ⁿ d_j = g + n.

   

Theorem 6 (8, 19).

We have

1. Let k > 2g, d_j ≥ 0 and Σ_j=1ⁿ d_j = 3g + n − k − 1.

   
2. Let d_j ≥ 1 and Σ_j=1ⁿ (d_j−1) = g − 1.

   

In fact, it's easy to see that Theorems 5 and 6 imply each other through the following proposition.

Proposition 7 (8).

Let d_j ≥ 0 and Σ_j=1ⁿ d_j = g + n.

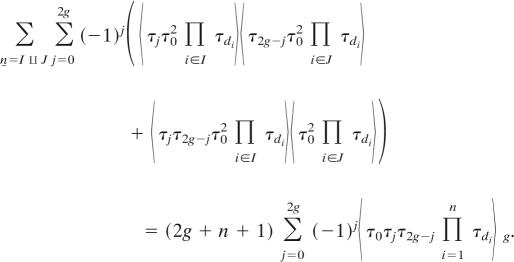Because ch_k (𝔼) = 0 for k > 2g, λ_gλ_g−1 = (−1)^g−1 (2g − 1)!ch_2g−1 (𝔼), by Mumford's formula (1) of the Chern character of Hodge bundles, it's not difficult to see that Theorem 6 implies the following theorem.

Theorem 8 (8, 19).

Let k be an even number and k ≥ 2g, d_j ≥ 0, Σ_j=1ⁿ d_j = 3g + n − k − 2.

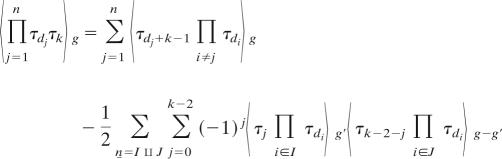Note that, when k = 2g, the above theorem is equivalent to the following Hodge integral identity (20) (also known as Faber's intersection number conjecture; ref. 21)

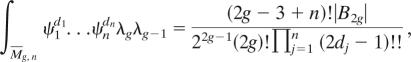where Σ_j=1ⁿ (d_j−1) = g − 2 and d_j ≥ 1.

The above λ_gλ_g−1 integral follows from degree 0 Virasoro constraints for ℙ² announced by Givental (22). However it is very desirable to have a direct proof of Theorem 8 when k = 2g, possibly using our explicit formulae of the n-point functions (see also ref. 23).

As pointed out in the last section, we can generalize all of the above new recursion formulae of ψ classes to identities of higher Weil–Petersson volumes. For example, we may generalize Proposition 7 and Theorem 8 to the following.

Proposition 9 (11).

Let b ∈ N^∞, d_j ≥ 0.

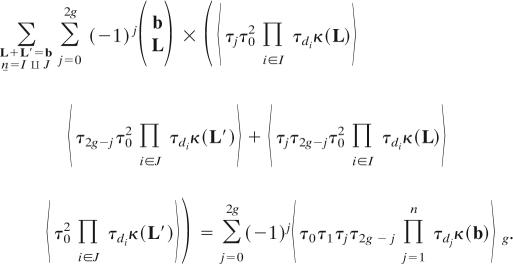Theorem 10 (11).

Let b ∈ N^∞, M ≥ 2g be an even number and d_j ≥ 0.

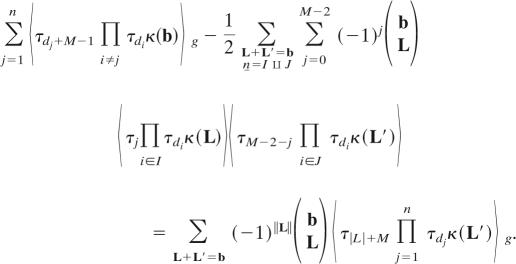We also found the following conjectural identity experimentally, which is amazing if compared with Theorems 6 and 8.

Conjecture 11 (19).

Let g ≥ 2, d_j ≥ 1, Σ_j=1ⁿ (d_j−1) = g.

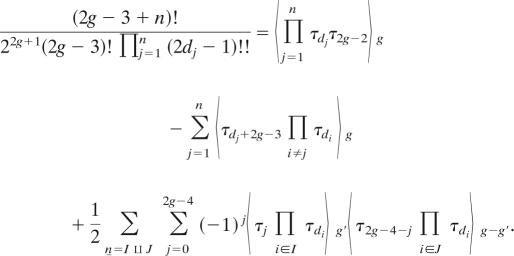Because (2g − 3)!ch_2g−3(𝔼) = (−1)^g−1 (3λ_g−3λ_g − λ_g−1λ_g−2), it's easy to see that the above identity is equivalent to the following identity of Hodge integrals.

Conjecture 12.

Let g ≥ 2, d_j ≥ 1, Σ_j=1ⁿ (d_j − 1) = g.

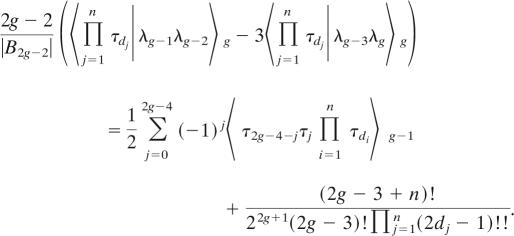Virasoro Constraints and KdV Hierarchy

From Theorem 3, we found new Virasoro constraints and KdV hierarchy for generating functions of higher Weil–Petersson volumes that vastly generalize the Witten conjecture and the results of Mulase and Safnuk (15).

Let s := (s₁, s₂, …) and t := (t₀, t₁, t₂, …), we introduce the following generating function

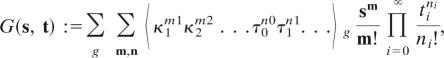where s^m = ∏i≥1 s_i^mi.

We introduce the following family of differential operators for k ≥ −1,

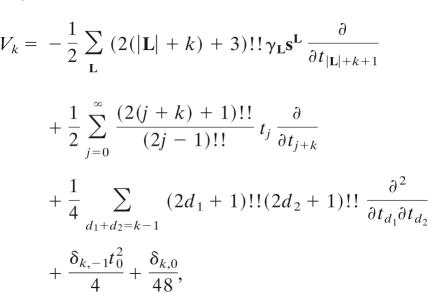where γ_L are defined by

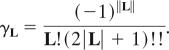Theorem 13 (11, 15).

We have V_k exp(G) = 0 for k ≥ − 1 and the operators V_k satisfy the Virasoro relations

The Witten–Kontsevich theorem states that the generating function for ψ class intersections

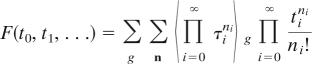is a τ-function for the KdV hierarchy.

Because Virasoro constraints uniquely determine the generating functions G(s, t₀, t₁, …) and F(t₀, t₁, …), we have the following theorem.

Theorem 14 (11, 15).

where p_k are polynomials in s given by

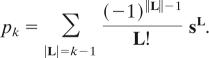In particular, for any fixed values of s, G(s, t) is a τ-function for the KdV hierarchy.

Theorem 14 also generalized results in ref. 24.

Denominators of Intersection Numbers

Let denom(r) denote the denominator of a rational number r in reduced from (coprime numerator and denominator, positive denominator). We define

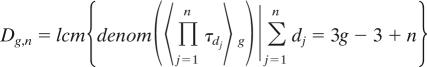and for g ≥ 2,

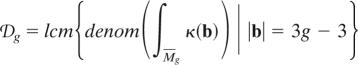where lcm denotes least common multiple.

Because denominators of intersection numbers on M̄_g,n all come from orbifold quotient singularities, the divisibility properties of D_g,n and 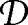_g should reflect overall behavior of singularities.

We have the following properties of D_g,n and 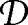_g.

Proposition 15 (25).

We have D_g,n | D_g,n+1, D_g,n | 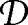_g and 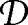_g = D_g,3g−3.

Theorem 16 (25).

For 1 < g′ ≤ g, the order of any automorphism group of a Riemann surface of genus g′ divides D_g,3.

The following corollary of Theorem 16 is a conjecture raised by Itzykson and Zuber (26) in 1992.

Corollary 17.

For 1 < g′ ≤ g, the order of any automorphism group of an algebraic curve of genus g′ divides 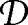_g.

The proof of Theorem 16 needs the following two lemmas (see ref. 25).

Lemma 2.

If p ≤ g + 1 is a prime number, then ord(p, D_g,3) ≥ 2.

Lemma 3 (27).

Let X be a Riemann Surface of genus g ≥ 2, then for any prime number p,

We have also obtained conjectural exact values of 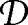_g in ref. 19.