On the relationship between synaptic input and spike output jitter in individual neurons

Abstract

What is the relationship between the temporal jitter in the arrival times of individual synaptic inputs to a neuron and the resultant jitter in its output spike? We report that the rise time of firing rates of cells in striate and extrastriate visual cortex in the macaque monkey remain equally sharp at different stages of processing. Furthermore, as observed by others, multiunit recordings from single units in the primate frontal lobe reveal a strong peak in their cross-correlation in the 10–150 msec range with very small temporal jitter (on the order of 1 msec). We explain these results using numerical models to study the relationship between the temporal jitter in excitatory and inhibitory synaptic input and the variability in the spike output timing in integrate-and-fire units and in a biophysically and anatomically detailed model of a cortical pyramidal cell. We conclude that under physiological circumstances, the standard deviation in the output jitter is linearly related to the standard deviation in the input jitter, with a constant of less than one. Thus, the timing jitter in successive layers of such neurons will converge to a small value dictated by the jitter in axonal propagation times.

When a cortical neuron is presented with the appropriate stimulus it rapidly and reliably increases its probability of firing. Indeed, individual neurons from cortical area MT in the behaving monkey respond to a dynamic random dot motion stimulus with a highly reproducible temporal modulation of their firing rate, precise to a few milliseconds (1). Furthermore, the time that it takes for an MT cell to significantly modulate its firing rate—as determined by averaging over many presentations of an identical stimulus—is almost always less then 10 msec (2). This occurs in neurons that are at least six synapses removed from the periphery. This precision is surprising because the propagation of an input through a multilayer network with continuous mean rates causes rise times to become increasingly shallow (3).

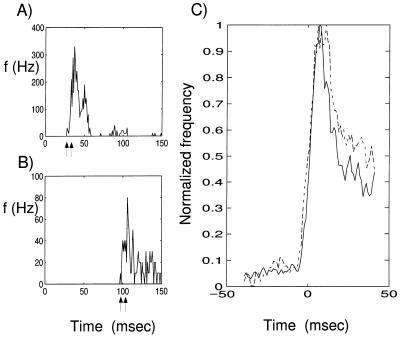
Yet, this does not appear to be the case in cortex. The rise times of signals—as defined via the poststimulus time histogram—in extrastriate areas, such as V4 or MT, can be as rapid as those in primary visual cortex (V1). As the sensory triggered “wave” of activity propagates through many layers of neurons, such a signal does not appear to become appreciably rounded off, but is instead only delayed between consecutive stages. This can be assessed directly by comparing the rise time of neurons in a single cortical area to the same stimulus. The cell in Fig. 1A responded within about 30 msec to the onset of a black and white grating, whereas the neuron in Fig. 1B responded only after 100 msec. Yet the rise time in both neurons is equally fast, even though the signal must have traversed more processing stages in the second case.

Figure 1.

Visual responses from isolated cells in the visual cortex of one behaving monkey. (A and B) Responses from two isolated units that were stimulated with a high contrast, stationary black and white square wave grating that appeared at t = 0 and remained on for the duration of the plot. Each histogram is the average of responses to 100 stimulus presentations. The vertical axis plots responses in units of spikes per second. (A) Responses from a unit in V1 with a very early onset (latency 27 msec, peak 37 msec). Rise time, marked by arrows, is defined as the interval during which response rises from 10% to 90% of the peak, was 6 msec for this neuron. (B) Responses from another V1 unit with much longer latency (99 msec). Although this neuron presumably is situated many synaptic stages later than the neuron in A, its rise time is similar, 7 msec. (C) Comparison of average rise times in cortical visual areas V1 and V4. The solid trace represents the average response profile of 73 units in V1, and the broken trace the average for 183 units in V4. All units were driven with a Gabor stimulus, temporally counter-phased at 4 Hz on an isoluminant gray background. Before averaging, each unit’s response was normalized to the same rate of firing and shifted to bring the time when its response reaches one-half its peak value to t = 0. The average response profiles for V1 and V4 were individually scaled to bring them to the same (arbitrary) peak value. The resulting curves show the average rise times of responses for units in V1 and V4. The rise times are remarkably similar, 8 msec in V1 and 7 msec in V4 (both after smoothing), although the average latency in V1 was 64 msec and that in V4 was 90 msec. The similarity in rise time raises the question of how a volley of synaptic inputs, triggered by a visual stimulus, can propagate through many layers of cortical processing without losing its sharp onset.

Fig. 1C gives further testimony to this. The solid and broken lines show the average rise times for the visual responses of neurons in V1 and a higher order extrastriate cortex area, V4 (see Fig. 1 legend, and ref. 4). The average response latency (measured as the time when the response reaches one-half its peak value) was 64 msec for the V1 neurons and 90 msec for the V4 neurons. This difference in latency presumably corresponds to many synaptic levels of processing interposed between areas V1 and V4. Yet, the average rise time of the firing rate in both sets of neurons is indistinguishable. How can neurons in later stage of processing retain a sharp onset when the signals are processed by neurons with passive membrane time constants of tens of milliseconds?

A similar problem arises in Abeles’s synfire model of cortical processing (5, 6). He proposes that sensory events trigger wave-like patterns that criss-cross cerebral cortex. Underlying this model are small and coupled groups of neurons receiving synchronized input that excite all members of the group. This tightly coupled cell assembly excites a second group of neurons that triggers synchronized spiking activity in a third group of neurons, in a so-called synfire chain. Neurons might belong to more than one group, depending on their connectivity (7). Abeles formulated this model in response to his puzzling finding that the cross-correlation function of firing of cortical cells frequently shows a narrow peak far removed from zero (up to 100 msec), raising the question of how such a wave of synchronized firing activity can propagate through many layers of intervening neurons, where the neurons possess passive time constants on the order of 10–20 msec (8, 9).

We seek to address this issue at the single cell level in the following manner. Suppose an instantaneous sensory event in the world triggers a volley of activity in n synaptic inputs. Let us assume that the arrival time of this input is centered around t = 0 and that its standard deviation in time, henceforth called input jitter, is σ_in. If we further suppose that these n synapses excite a pulse generating neuron, we can compute the standard deviation in time, termed the output jitter σ_out, of the spike triggered in response to this input. If σ_out > σ_in, then it is clear that each consecutive layer of spiking neurons will introduce more and more temporal jitter, compromising the ability of higher level neurons to sharply respond to this sensory input and rendering synfire assemblies difficult. Inversely, if σ_out < σ_in (as we will find) then, depending on other sources of temporal jitter, the temporal variability in spike times response to an abrupt input converges toward a fixed point. In the following, we investigate analytically the case of a perfect integrate-and-fire (I&F) model. Computer simulations using two different single cell models complement our results and confirm that under physiological circumstances, σ_out ≪ σ_in.

The I&F Model

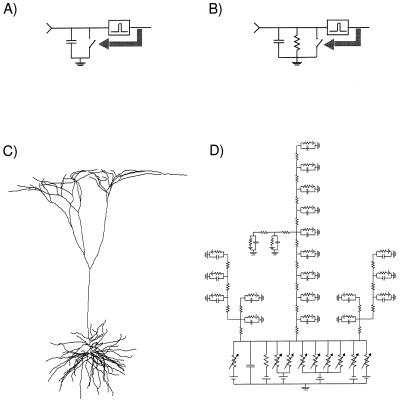
We begin with the simplest model of a spiking cell (10). This I&F model consists of a capacitance, C, and a voltage threshold, V_th (Fig. 2A). Each synaptic input dumps positive or negative charge onto the capacitance, de- or hyperpolarizing the membrane. Once V_th is reached, an output spike is generated and the membrane potential is reset to zero. The I&F unit is assumed to receive input from n excitatory synaptic inputs of equal weight, a_E, each of which can be activated independently of each other.

Figure 2.

Three single neuron models that are investigated for the relationship between temporal jitter in the synaptic input and jitter in the timing of the output spike. (A) I&F unit; each synaptic input charges the capacitance, C. If a voltage threshold, V_th, is reached, an output spike is generated and the voltage is reset (black arrow indicates closing the reset switch). (B) Leaky I&F unit; with the addition of a resistance, the subthreshold regime (i.e., for V_m < V_th) acquires a time constant τ = RC. (C) Morphology of the reconstructed layer 5 pyramidal cell from visual cortex of the anesthetized adult cat (9) that was used. (D) A fraction of the equivalent circuit used in the numerical, compartmental simulations (via the single cell simulator NEURON).

First we assume that n_th = n, where n_th = V_th/a_E is the number of inputs needed to reach threshold. Under these conditions, the time, t_out, for which the I&F unit generates an output pulse is the time that the nth input arrives, given by max(t₁, t₂, … t_n). The probability distribution of spike times for the I&F unit is

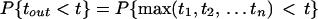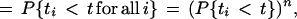1

where P{t₁ < t} is the distribution for all of the synaptic inputs (the last step holds because all synaptic inputs are assumed to be independent of each other). The probability density of spike times, p_out(t), is the derivative of this distribution:

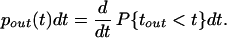2

Using Eq. 1, we can transform this into

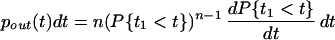3

Here p_input(t) is the probability density of the synaptic input.

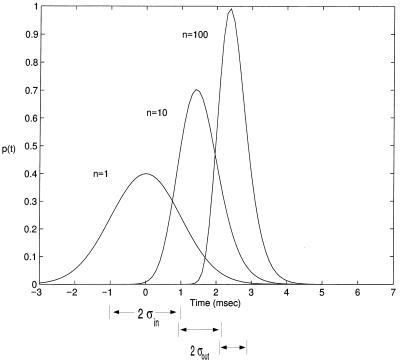
Let us assume that p_input(t) is a normal density with a temporal input jitter σ_in, as in Fig. 3 (for normal density). This allows us to make several observations. For n = 1, it trivially follows that the density of spike times is identical with the synaptic input density. For larger ns, the resulting density becomes narrower. Indeed, it can be shown that the output jitter, i.e., the standard deviation of p_out(t), for n + 1 inputs, is less than the jitter for n inputs. Thus, this rudimentary model achieves the goal of transmitting signals without temporal smear, although activity is significantly delayed. Indeed, jitter would be systematically reduced at each successive level in a multilayer network of such neurons because, as is evident upon inspection of Fig. 3, σ_out < σ_in (in the case of normally distributed synaptic input).

Figure 3.

Probability density of spiking p_out(t) of Eq. 3 associated with the I&F unit of Fig. 2A. Here, n = n_th; that is, the number of excitatory inputs is equal to the number of inputs needed to bring the unit to threshold. n = 1 reproduces the probability density of the synaptic input itself, p_input(t) (assumed to be Gaussian distributed around zero, with σ_in = 1 msec). If n = n_th = 10 inputs are required, the mean of p_out(t) is shifted to 1.6 msec, but becomes narrower, with σ_out = 0.6 msec. This is even more the case if n = n_th = 100 inputs are required to reach threshold: the mean shifts to 2.6 msec with σ_out = 0.4 msec. In other words, as individual synaptic inputs are made smaller and smaller, requiring the summation of more and more inputs, the jitter in the timing of the output pulse becomes less and less. For normally distributed synaptic inputs as used here and for large ns, σ_out ≪ σ_in.

For an arbitrary density, p_input(t), p_out(t) scales with the input jitter. When changing the input jitter from σ_in to 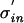one can rescale time replacing t with tσ_in/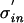. This leads to the same density function times a scaling factor σ_in/ 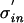(to account for the broader spread of the probability density, which has to sum to one). In other words, increasing the input jitter by α increases the output jitter by α.

Now let us deal with the more general case of n > n_th and where p_input(t) is the uniform density on the interval [0, 1]. (p_input(t) = 1 for t ∈ [0, 1]; p_input(t) = 0 otherwise.) This assures us that at t = 1 the voltage will be exactly na_E (in the absence of a threshold).

The probability that the voltage at time t has attained the value n_tha_E is given by the beta density (11–13):

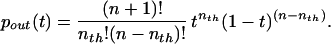4

The standard deviation of this distribution is

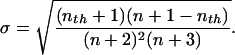5

In the case of the uniform probability density assumed here, σ_in = 1/2 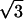. This allows us to rescale Eq. 5, and we can write for the output jitter

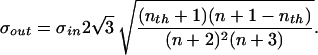6

To arrive at some intuitive feeling for this result, let us assume that the number of inputs n is far above the number needed to reach threshold n_th. Making the approximations that n + 3 ≈ n + 2 ≈ n, that n + 1 − n_th ≈ n, and n_th + 1 ≈ n_th we arrive at (with n_th = V_th/a_E)

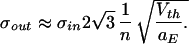7

Or, the output jitter is inversely proportional to the number of excitatory synaptic inputs. This makes sense, since the time it takes to reach threshold will be proportional to the drift that is dictated by n. The jitter in this time is inversely related to the drift. Of course, our derivation only holds under conditions when the membrane leak can be neglected.

The Leaky I&F Model

Although this I&F model has desirable properties, it is not physiologically plausible and leaves many questions open. What happens if p_input(t) is not uniform? Furthermore, neurons are not perfect integrators. Rather, they have a passive membrane time constant that is on the order of 10–20 msec in pyramidal cells in vivo (for review, see ref. 8). If only a small number of synapses are active, the membrane potential can decay significantly between inputs. These concerns are addressed using the leaky or forgetful I&F model. It is obtained from the I&F model by addition of a resistance R, endowing the unit with a passive time constant τ = RC (Fig. 2B). Although quite simple, leaky I&F units have been successfully used to mimic many aspects of the temporal dynamics of cortical pyramidal cells (5, 14–17).

In the subthreshold region, the voltage is governed by

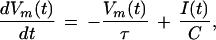8

where the current I(t) is given by the superposition of random excitatory inputs. The input comes in the form of n short, depolarizing current pulses of amplitude a_E, and m hyperpolarizing current pulses of amplitude a_I. Each input has an associated probability density function p_input(t), with a mean of t_mean and input jitter σ_in.

Each excitatory input pulse depolarizes the membrane, pushing V_m closer to the threshold V_th, whereas the inhibitory input displaces V_m away from V_th. Unlike the nonleaky I&F model, V_m decays exponentially to zero in the absence of input. What can we say about the relationship between σ_in and σ_out, that is the standard deviation in time in which V_m reaches threshold? We have not managed to place firm boundaries on the jitter for a leaky I&F unit, forcing us to rely on computer simulations.

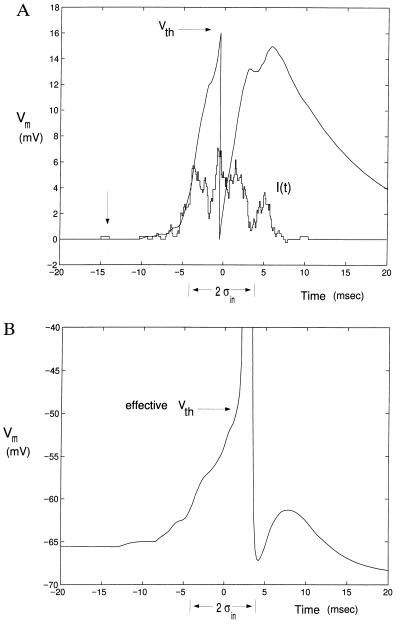
We numerically solve Eq. 8 via Matlab. We assume V_th = 16 mV, τ = 10 msec and a_E = a_I = 0.23 mV, such that n_th = 70 simultaneous excitatory synaptic inputs that are required for the unit to fire. Fig. 4A illustrates one sample path for V_m(t), for excitatory, rectangular current pulses (using α functions did not lead to any significant difference) of 1 msec width, 0.23 nA amplitude, and with a Gaussian input probability density p_input. For n = 250 excitatory inputs in the absence of any inhibition, approximation gives σ_out ≈ 0.116 σ_in (Fig. 5A). The simulated curve is always below the estimate, confirming the intuition that for large number of synaptic inputs the decay can be neglected.

Figure 4.

Sample voltage trace (A) in the leaky I&F unit (Fig. 2B), and the somatic membrane potential (B) in the simulated pyramidal cell (Fig. 2 C and D). p_input(t) is a Gaussian, with a mean at t = 0 and a standard deviation of σ_in = 3.5 msec. The input current for the leaky I&F in A is the staircase-like curve denoted I(t). This is qualitatively similar for the pyramidal cell model (B). All pulses last 1 msec. The membrane time constants are τ = 10 msec (A) and τ = 9 msec (B). One unit of pulse is marked by the arrow on the left. In the pyramidal cell, the input current is delivered by excitatory and inhibitory conductance increasing synapses scattered throughout the dendritic tree (see text for details). Horizontal arrows in A and B indicate V_th. The potential is reset to zero in the leaky I&F unit. Both traces are computed with excitation and inhibition.

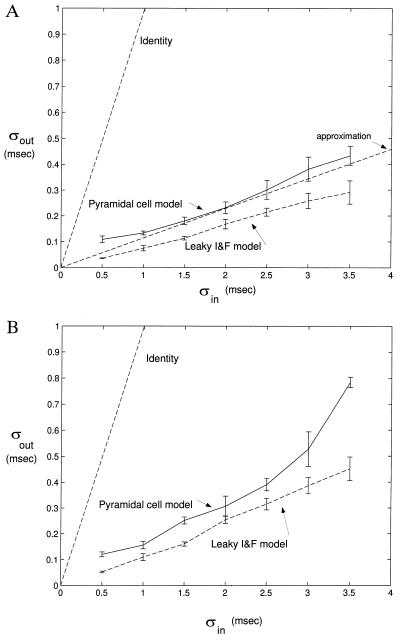
Figure 5.

Relationship between input and output jitter for excitatory input only (A) and with both excitation and inhibition present (B). The approximation we find for the nonleaky I&F (Eq. 7) is indicated in A, with slope of 0.116. We added a line with unity slope for comparison. The numerical simulations always fall below the identity line, as does the output jitter associated with our anatomical and biophysical accurate model of a pyramidal cell with a passive dendritic tree. Error bars correspond to sample standard deviation from 5 runs from 50 threshold passages. These results show that in a cascade of such neurons in a multilayered network and in the absence of large timing uncertainty in synaptic transmission and inhomogeneous spike propagation times (see text), the timing jitter in spiking times will converge to zero.

What happens in the presence of inhibition? On general grounds, one expects the overall jitter to increase, due to the introduction of additional degrees of freedom. Indeed, if 62 inhibitory synapses are added, the output jitter is larger than in the no-inhibition case, yet still substantially below the identity function (Fig. 5B). We conclude that a leaky I&F unit can reduce the jitter in its input in the presence of massive synaptic input.

A Cortical Pyramidal Cell

It could be argued that an I&F unit does not represent a reasonable model of a cortical cell. Although substantial evidence has accumulated in favor of neurons having an abrupt voltage threshold (for a detailed discussion see refs. 17 and 18), voltage-dependent channels inactivate and can change the effective threshold depending on the history of V_m. We address this point by carrying out simulations in a detailed model of a regular-firing, neocortical pyramidal cell. The arcanae of these simulations are described in detail in ref. 18, and we will only summarize the salient points here.

The morphology of this cell (Fig. 2C) was derived from a layer 5 pyramidal cell in primary visual cortex filled with horseradish peroxidase during in vivo experiments in the anesthetized, adult cat (9). Fig. 2D illustrates part of the compartmental model that was simulated using the single cell simulator NEURON (19, 20). In the complete model the cell has 163 branches, consisting from 1 to 10 compartments, with the most distal tip 1387 μm from the soma. The soma comprises only 2% of the total membrane area. The basal dendrites, including the apical obliques that are located in layer 5, account for approximately 60% of the membrane area, with the apical trunk and apical tuft taking the remainder.

We assume here that the dendritic tree is passive, with R_m = 100 kΩcm², R_i = 200 Ωcm, C_m = 1 μF/cm², and E_leak = −66 mV. We mimicked the synaptic background activity by incorporating the steady-state conductance (and driving potential) effect of 4000 excitatory inputs of the voltage-independent AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazoleproprionic acid) type 500 GABA_A and 500 GABA_B inhibitory synapses, all activated independently of each other on the basis of a Poisson process with a rate of 0.5 Hz (21). Synapses are not distributed uniformly along the membrane. Inhibition is more prevalent on and near the soma, whereas excitation is more distal (22, 23). This distribution was modeled by making the surface density of synapses a function of distance from the soma. This lowers the effective R_m to about 11 kΩcm² at the soma (where the density of inhibitory synapses is large) and to 50 kΩcm² for distal locations.

The somatic membrane includes eight voltage-dependent conductances, two sodium conductances (fast and persistent), a delayed rectified potassium conductance, a calcium and a calcium-dependent potassium current, an A and an M type of potassium conductance, and an anomalous or inward rectified conductance (for details, see ref. 18). The final somatic input resistance was 12.5 MΩ, the time constant 9 msec, and the somatic resting potential −65.6 mV. For this cell, the voltage threshold to initiate an action potential V_th ≈ −49 mV.

To mimic the synaptic input, we randomly generated 500 locations for excitatory synapses and 125 locations for inhibitory synapses, taking into account their anatomical distributions (see above). For each block of trials one-half (n = 250 and m = 62, respectively) of these synapses were randomly triggered. Excitation is of the fast, voltage-independent AMPA type and is modeled by an α function with t_peak = 0.5 msec, g_peak=1.5 nS, and E_syn = 0 mV. Inhibitory synaptic input is of the GABA_A type, with t_peak = 10 msec, g_peak = 1 nS, and E_syn = −70 mV. We simulated input jitter times, σ_in of 0.5–3.5 msec. For larger values of σ_in, frequently trials would not lead to the generation of a spike (at our level of excitation). Fig. 4B shows sample traces of V_m at the soma, while Fig. 5 plots the resultant jitter. It is obvious that the variance of the output jitter of this pyramidal cell is approximately linear in the input jitter and always falls below the identity line.

Spiking Jitter Following a Step Increase in Firing Rate

So far we have treated the case of a wave of elevated firing probability arriving at a neuron and triggering a spike. How does this situation relate to a step increase in activity (similar to that generated by an appropriate visual stimuli when recording from a cortical cell)?

Let us assume that the input to a nonleaky I&F unit abruptly switches at t = 0 from a low spontaneous value to a much higher rate. Since the rise time in the average firing rate (Fig. 1C) occurs within a fraction of a time constant, we will neglect the membrane decay during this portion of the input. We will approximate the voltage trace by Wiener process with drift. We will express the new, elevated value for the drift as μ_w = a_Eλ_E − a_Iλ_I and the variance parameter σ_w² =a_E² λ_E + a_I²λ_I, where λ_E and λ_I denote the new excitatory and inhibitory input rate. Assuming that the nonleaky I&F unit had the voltage V₀ at this time, it is straightforward to compute (24–26) that the probability density of the first spike following the input is given by the inverse Gaussian density

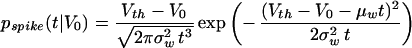9

Assuming that V₀ is uniformly distributed within the interval [0, V_th], we can average over all possible values of V₀:

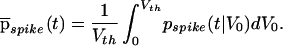10

From this average we can compute the mean and standard deviation of the first spike to occur following the step increase in input. The mean latency is

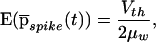11

and the jitter around this latency is

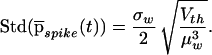12

Assuming that the nonleaky I&F unit discharges at a rate of 50 Hz following the input increase, by back substitution (and assuming, as before, a_E = a_I = 0.23 mV, λ_E = 4λ_I) we have λ_E = 4.63 msec⁻¹ and a latency of first spike of 10 ± 1.55 msec. Thus, we have transformed a problem of jitter following a step increase in the input to the problem treated above, e.g., a probability density of the time of first spike p_spike(t) in output. Instead of a Gaussian density as we have assumed in our simulations, the spikes would be distributed according to Eq. 9. Yet for our parameter values, the difference between these two distributions is negligible. Moreover, the value of standard deviation lies within the range of assumed jitter levels.

Discussion

The aim of this study was to explain some puzzling observations regarding the preservation of highly accurate spike timing in cortical networks. Naive intuition suggests that in a layered network of mean-rate “units” (such as those at the heart of most neural networks), precise temporal information will become smeared out. Experimentally, as we have shown in Fig. 1, this is not true for neurons in different cortical areas in the macaque monkey. We can show analytically that for an uniformly distributed synaptic input to a nonleaky I&F model, a linear relationship exists between σ_out and σ_in, with the constant of proportionality depending inversely on n. Using numerical methods to deal with temporal dispersion and nonlinear processing existing in biophysical realistic models of individual neurons, we can show that under physiological conditions σ_out ≈ α σ_in with α <1. α depends on various parameters, in particular on n_th and n, and is larger if both excitatory as well as inhibitory synaptic input is included. Lastly, we show that the situation of an abrupt increase of the excitatory and inhibitory synaptic input to a nonleaky I&F unit gives rise to a probability distribution of spikes with a certain jitter that now propagates to the following layer of processing.

For a cascade of such neurons the output jitter will converge to zero. However, in real networks this is unlikely to be the case since we have neglected several additional sources of timing variability. The two most dominant sources are likely to be (i) the inhomogeneous spike propagation times between consecutive layers of neurons due to variations in the diameter and length of the associated axons and axonal termination (wiring jitter) and (ii) jitter in the delay between presynaptic spike and the opening of the postsynaptic synaptic channels (synaptic jitter). Thus, even if all neurons in one layer spike at precisely the same time, the synaptic induced conductance change in their postsynaptic target cells will not be perfectly synchronized. Manor and others (27) simulated spike propagation in a highly branched layer 5 pyramidal cell axonal tree from somatosensory cortex and found that the jitter in the arrival times at the different synaptic boutons due to purely geometrical factors was on the order of ±0.5 msec.Thus, the output jitter for many layers of such a network will converge to a fixpoint that is different from zero but bounded by the “jitter” in the anatomical connections and in synaptic jitter, which would presumably be in the order of several milliseconds.

The effect of strong dendritic nonlinearities is unclear. However, if such voltage-dependent membrane components would act to more rapidly depolarize the membrane, such as dendritic spikes, the output jitter should be smaller than estimated here. σ_out can be maximized by combining excitatory inputs with the largest amount of inhibition compatible with the cell still firing (since inhibition increases the variance of the membrane potential). This is precisely the situation we simulated in Fig. 5B: any more inhibition and the cell would have failed to generate spikes in a growing fraction of all trials.

Several groups have previously investigated the preservation of spike timing using the dynamic equations describing network activity (in particular refs. 28 and 29). Not taking into account any processing at the single cell level and assuming a mean-field approach, both studies conclude that the jitter between two consecutive stages decreases as 1/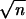; that is, for relatively large number of afferent excitatory synapses, σ_out will remain small. We investigate the specific case of a nonleaky I&F unit, and conclude that the dependency on n could be even stronger (see Eq. 7) and show that this approximation is also valid for a biophysical quite detailed model of a layer 5 pyramidal cell. Thus, our simulations are in qualitative agreement with those of Abeles (29) and Herrmann (28).

We conclude that layers of pulse-generating neurons can preserve the temporal jitter of spike times and that this jitter will converge to a small fixpoint. This property of neurons provides one of the biophysical substrates necessary for exploiting the detailed timing information inherent in spike trains as is frequently asserted (30–32).

Note

. We recently learned that Diesmann et al. (33) have independently studied the relationship between input and output jitter in a different type of neuron model and have arrived at qualitatively similar conclusions.