Structural correlations in protein folding funnels

Abstract

While the overall energy landscape of a foldable protein can be described by means of a few parameters characterizing its statistical topography, specific energetic terms subtly bias the representative structures giving rise to residue pair correlations as in a liquid. We use a free energy functional incorporating an inhomogeneous pair contact energy along with a contact formation entropy and a cooperativity contribution to determine residue-specific contact probabilities in the denatured state and the transition state ensemble. The predicted “hot residues” for the theoretical transition state ensemble reasonably agree with experiment for chymotrypsin inhibitor 2, and generally a strong correlation exists with the measured kinetic effects of mutating residues not involved in highly solvent-exposed regions.

Protein folding is efficient because the energy landscape resembles a funnel (1, 2) dominated by interactions in the native structure that are more favorable than those in alternatives—i.e., there is minimal frustration (3). The multiplicity of folding routes down a funnel implies that discussing folding thermodynamics and kinetics requires the use of ensembles which average over many landscape details. A global statistical characterization of the landscape topography is fundamental, but protein folding funnels are not structurally featureless: At various points along the folding reaction coordinate, the ensembles involve the ordering of different regions of the protein to various extents. Stronger and short-range in-sequence contacts are more likely to form in a partially ordered protein. These structural correlations can be probed by combining protein engineering with measurements sensitive to particular ensembles of structures (4). At the folding midpoint, the rate-limiting step for folding is passage through a transition state ensemble which acts as a largely entropic bottleneck, arising from an imbalance between the rate of entropy loss and free energy decrease as the ensemble descends in the funnel (2, 5). Nonadditivity of forces such as hydrophobicity (6) may also contribute to barriers (7). The location of the thermodynamic bottleneck can be inferred by experiments which modify the funnel topography globally by denaturants or through widespread sequence changes between distantly related proteins (4, 8).

Extrathermodynamic free energy relations (9) between rate and stability then demonstrate that the bottleneck lies midway between folded and denatured states, in accordance with the corresponding states analysis that maps lattice models onto real proteins (10).

The surgical precision of engineered mutations at single sites reveals a wide distribution of residue participation in the ordering at the transition state ensemble both in the laboratory (4) and in lattice models (11). It is tempting to call the most ordered contacts, or “hot spots,” a folding nucleus. The delocalized nature of the nucleus, its relatively large size involving many partially ordered residues throughout the protein (12, 13), requires the term “nucleus” to be used with care. Although the analogy with a first-order transition holds (14), crossing the transition state region for a small protein should be sharply distinguished from classical nucleation in bulk solids (15), where the nucleation event is distinct from later growth. Fersht has used the compound term “nucleation-condensation mechanism” recognizing this (4).

The structural correlations in the transition state ensemble must depend jointly on the native structure, the sequence, the intermolecular forces, and the thermodynamic conditions. These aspects are partially linked through the minimal frustration principle. Using a quantitative form of the minimal frustration principle to design sequences that stably fit given structures and then simulating their folding, Shakhnovich and co-workers (16) have inferred that the most ordered residues in the transition state ensemble, which they call a specific nucleus, are the ones most strongly constrained by the design process for lattice proteins. Extending this idea to real proteins, they argue that the conservation of residues in evolution explains the “hot spots” in the folding kinetics of chymotrypsin inhibitor 2 (CI2). This explanation is incompletely satisfying because it is teleological and appropriate only for evolved proteins that completely satisfy the minimal frustration principle, folding under physiological conditions. It leaves mysterious both mechanistic changes caused by varying thermodynamic conditions and the physical relation of kinetics to underlying forces. While by construction, the constrained residues in designed lattice proteins depend only on the native contact pattern, experiments (8) have shown that the most important residues for folding kinetics vary with sequence and chain connectivity even when the contact pattern is unchanged. A more satisfying approach to structural inhomogeneity in the bottleneck has been explored using fully atomistic molecular dynamics (17). Sampling several unfolding trajectories, snapshots of the protein near its unfolding transition state ensemble are generated. The contact probabilities in this set can be correlated with the protein engineering results. The molecular dynamics technique, applicable to both natural and engineered proteins, is, however, computationally intensive and leaves open the interpretation in terms of the physical forces involved.

We present here an approach to understanding the structural and energetic correlations in the transition state ensemble. Our method generalizes the mean field free energy functions already used to describe the global folding funnel topography (2). The generalized free energy allows for the inhomogeneity of the interactions and is based on functionals introduced earlier by Bohr and Wolynes to discuss the fast events of folding (18) and used, with Wang, to discuss the growth of protein structural domains (19). The free energy functionals resemble ones for random field Ising magnets and inhomogeneous fluids. They treat differentially the tradeoff between the variable energy and entropy loss of contacts. The entropic terms can be approximated with simple polymer theory (20) and specific microscopic interaction forces can be accounted for explicitly. This allows us to dissect the structural correlations in energetic terms both for equilibrium ensembles like the denatured state and for the quasi-equilibrium transition state ensemble.

The free energy function used here is crude, perhaps the simplest to capture the essentials. As we shall see, also, by comparing theory and experiment the details of the sequence-specific forces are incompletely known. Nevertheless, many of the experimentally determined features of the transition state ensemble in the folding funnel are reproduced.

The Funnel Picture and Folding Reaction Coordinates

Even for simple chemical reactions, there is controversy associated with the choice of a reaction coordinate arising from a necessary ambiguity in its definition. Different choices ultimately give the same rate when used in a complete theory. Rate coefficients can be written as the product of an equilibrium factor, giving the probability of achieving a set of “bottleneck” configurations and a transmission coefficient measuring the number of recrossings of the surface defined by the critical value of the reaction coordinate (21). Transition state theory neglects the transmission coefficient giving an upper bound to the rate. Thus when we speak of a reaction coordinate, we may simply choose a progress variable for which the calculation of equilibrium factors is straightforward. Even if the transmission coefficient is nonnegligible but does not vary systematically for thermally occupied transition states, this will be sufficiently good for discussing extrathermodynamic relations. On the other hand, finding a reaction coordinate for which transition state theory without recrossing corrections can be applied exactly is hard. One trades the validity of the nonrecrossing assumption for the complexity of finding the coordinate and evaluating the equilibrium factor. We compromise by using a simple reaction coordinate to determine the ensemble of appropriate structures and then characterize equilibrium structural correlations within that ensemble.

Since tertiary contacts are a dominant source of protein stabilization, a collective coordinate measuring the fraction of such contacts which are correct, Q, has been used in a number of off-lattice and lattice simulations (22–25). The motion of this coordinate for small lattice models is diffusive, and rates are predicted well using a diffusional rate theory (25), since the free energy barrier is broad. It has also been shown that at the folding midpoint of the lattice protein the effects of site mutations faithfully reflect the structural correlations in the ensemble at the top of the barrier (11).

Q also lends itself to treatment in approximate mean field theories of the folding free energy profile (7) which can be written as a sum of two dominant terms: one depending on the energy of native contacts, and the other on their formation entropy cost. There is also a free energy term arising from the interactions’ inhomogeneity. The quantitative treatment reveals that barriers arise subtly, much as in rubber vulcanization. The entropy loss on forming a contact is large when the first few are made but diminishes once many are made, since the structure is already highly specified. The variation of the inhomogeneity energy also contributes to barriers. The overall density of the protein globule couples to the reaction coordinate, requiring the introduction of the so-called “core–halo” model. Residues in their native location are in a high-density core surrounded by a halo of lower-density material, a structure enhanced when nonadditive forces are encountered (7).

Structural correlations in the various funnel ensembles corresponding to values of Q can be computed by using an inhomogeneous free energy functional dependent on the set of pair correlations, {Q_ij}, Q_ij = 〈δ(r_ij − r_ij^T)〉. Q = ∑_ij Q_ij/∑_native Q_ij. {r_ij} is the set of pair distances for the residues, while is that for the native structure (here measured at the β carbons). We suggest in the next section a simple form for the inhomogeneous free energy functional that captures much but not all of the physics of the mean field homogeneous model. It describes an interacting “gas” of contacts. This simplified form might not locate the transition state value Q with great accuracy but should suffice if we are willing to use experimental input about the bottleneck location.

The Free Energy as a Function of the Contact Matrix

A free energy functional for Q_ij can be constructed along the lines already used by Bohr et al. (19). The energy, instead of being linear in the global Q, is represented as a sum reflecting the inhomogeneity of different contact energies: E = +∑_ijɛ_ijQ_ij. The entropy can be represented in a variety of ways: in ref. 19, a complete virial expansion in terms of contacts was used as done earlier by Chan and Dill (26)

1

The lowest-order term is the Jacobson–Stockmayer (27) entropy loss on forming specific contacts: S₀^ij = +k_Blog[ΔV/ |i − j|^3/2]. Assuming the denatured protein can be modeled as a random flight chain, the quantity ΔV=(3/2π)^3/2Δτ/l₀³, where Δτ is the volume corresponding to the interaction range and l₀ is the persistence length of the polymer, can be treated as adjustable within reasonable limits. The virial expansion converges slowly. In the homogeneous mean field theory (20), a separate approximation of the type introduced by Flory for rubber vulcanization is used; namely, contacts nearby in sequence are treated by means of Jacobson–Stockmayer, but for sequentially distant contacts the entropy cost saturates to that of a typical fluctuating segment of the chain, which depends on Q itself. S₀^ij = +k_Blog[ΔV/μ^3/2], where μ is the number of contacts made. For the resulting inhomogeneous functional, the probability of forming a contact depends only on the contact energy, the distance in sequence between the residues (which determines the entropy), and the Q value of the ensemble.

Numerically we use an interpolation for entropy loss:

2

At high Q, the Flory-style resummation breaks down and an entire atom with all of its contacts should be removed from the frozen part of the structure to create entropy—i.e., the major contribution comes from an atomistic gas of contacts clustered together at a site. This suggests a free energy functional of the following form:

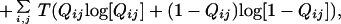3

where 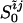is obtained by functionally integrating Eq. 2. The last term is an entropy of mixing arising from the number of ways of making contacts in a partially ordered protein. Nonadditive free energetic effects of contacts can also be described by adding such a term (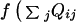) dependent on the local density around a residue. For our purposes here f is quadratic with α_t. Explicit cooperativity for forming α-helices can be introduced:

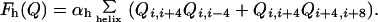4

The residue-specific interaction parameters ɛ_ij are based on statistical potentials obtained by the information theoretic approach (28, 29) or by optimization schemes in the present calculation (30). The cooperativity parameters (α_t, α_h) are chosen to give reasonable thermodynamics and are treated initially as adjustable.

The probability of finding specific residues which are in contact at any particular value of Q*, is obtained by minimizing the inhomogeneous free energy functional subject to the constraint ∑_ij Q_ij/∑_native Q_ij = Q*, giving

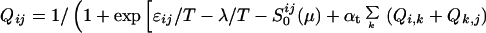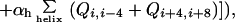5

where λ is a Lagrangian multiplier determined by the equation of constraint.

This equation is explicit when the local cooperativity terms in the functional are absent. When local cooperativity is present, it is solved iteratively.

The contact matrices in the denatured state ensembles can be directly calibrated with NMR structure data. The contact matrices in the transition state ensemble can be averaged in various ways to compare with mutagenesis studies of kinetics. If the ɛ_ij were constant, the φ values representing the change in rate k_f upon mutation (φ= δlog[k_f]/δlog[K] and K is the equilibrium constant) would be the average of the Q_ij involving the site. Generally, φ is given by φ_i = (∑_j Δɛ_ijQ_ij^TST − ∑_j Δɛ_ijQ_ij^UF)/(∑_j Δɛ_ijQ_ij^F − ∑_jΔɛ_ijQ_ij^UF) where Δɛ_ij is the change of the contact energy upon mutation (11). The formation also allows the variation of φ_i with transition state location to be studied by varying Q*.

Calculations and Results

Statistical data base potentials generally have both an arbitrary scale factor and an arbitrary additive term representing the average hydrophobicity undetermined. To specify the thermodynamic conditions we must fix a few parameters governing the temperature scale and overall tendency to collapse. The results presented assume the protein is at a triple point near both the collapse and folding midpoints at folding temperature T_f. The entropic loss for a protein folding from the coil to the folded state is N log(ν), where N is the number of residues and ν is the number of conformations per residue (ν ≈ 9) which must match at T_f the total energetic changes in folding. The entropic loss from coil to folded is N log(ν) = −ɛ_f/T_f, while from the globule it is N log(ν/e) = −(ɛ_f − ɛ_mg^˜)/T_f. Here ɛ_f is the energy of the folded structure and (ɛ̃_mg − ɛ_f) is the difference between the molten globule and folded energies. ɛ̃_mg is computed by averaging the results of threading the sequence through alternate protein structures. The results reported are for optimized contact interactions whose range is 6.5 Å. Within this range, once a contact forms, contacts nearby in sequence form too. We therefore coarse-grain the sequence and ascribe to an ij pair the energy of a renormalized block containing three neighboring residues. When one native contact of the renormalized block forms, the rest of the native contacts in that block also form. With this choice the entropy loss on making all the native contacts properly scales to N log(ν).

The degree of cooperativity in the free energy functional is hard to determine a priori. Direct structural experiments can be used for calibration. We use the NMR experiments of Wüthrich (31, 32) on the phage 434 repressor to determine the relative magnitude of α_h and α_t. Wüthrich finds in the denatured state a conserved region of native structure in the α-helix at the C terminus of the protein. There is no clear indication of tertiary conserved structure in this study. We applied the free energy functional to the denatured state of phage 434 repressor and varied the magnitude of cooperativity to match the conserved structure found. We found that at Q̄ = 0.2, which fits the experimental map well, the theoretical contact map with α_h ≈ 0.45 has a high overlap of contacts in the region of conserved structure as determined by nuclear Overhauser enhancements. Good agreement can also be reached using α_t ≈ 0.05. We note similar data on barnase have become available recently (33).

The 64-residue protein CI2 has been thoroughly studied through kinetics (4) and by means of atomistic molecular dynamics (MD) simulations (17). In our calculations we set the value of Q at the transition state, Q*, equal to 0.2 and take the denatured state as having Q = 0. We choose Q* to match the average φ value of Fersht and co-workers (4), which is an approximately equivalent quantity. Interestingly, chemical denaturants suggest a larger Q* = 0.6.

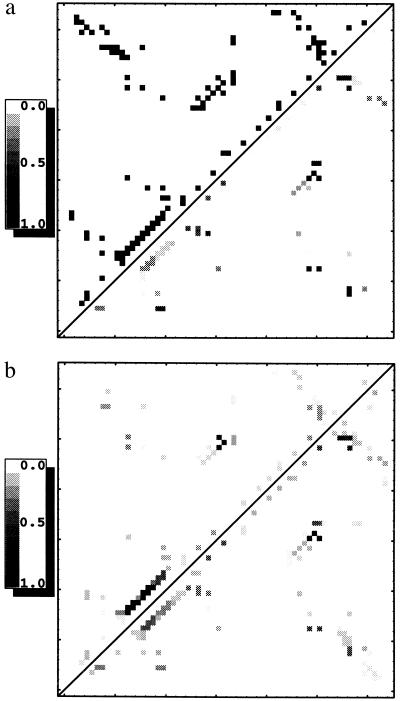
The contact map for the transition state ensemble shows the theoretical contact probabilities, Q_ij. As a point of reference, the upper left of Fig. 1a shows the full native contact map at Q = 1.0. The lower right of Fig. 1a shows the contact map for the transition state ensemble at Q* = 0.2 without either tertiary or secondary cooperativity. Contact probabilities are evenly distributed, with the highest values in the core. Without any cooperativity the α-helix is poorly formed.

Figure 1.

(a) Native contact map (at Q = 1.0) for CI2 shown in the upper left and contact map of calculated contact probabilities (at Q* = 0.2) for the CI2 transition state ensemble without any tertiary or secondary cooperativity in the lower right. (b) Contact map of calculated contact probabilities (at Q* = 0.2) with α_h = 0.45 and α_t = 0.0 shown in the upper left and α_h = 0 and α_t = 0.05 shown in the lower right.

As seen in the upper left of Fig. 1b, adding helical cooperativity (α_h = 0.45 and α_t = 0), helical i, i+4 contact probabilities become well defined hot spots having high average local densities at the expense of nonhelical contacts, maintaining the constraint of a constant sum of all Q_ij values. There is also appreciable contact probability between β-strands three and four, which includes core residues. At very large values of α_h only helical contacts are formed.

Fig. 1b (lower right) shows the Q_ij using tertiary cooperativity alone (α_h = 0.0 and α_t = 0.05). With tertiary cooperativity three localized spots on the map achieve a high average local density. These spots include contacts in the core between β-strands three and four and between β-strands four and five. They also include local interactions in the helix, especially its N terminus.

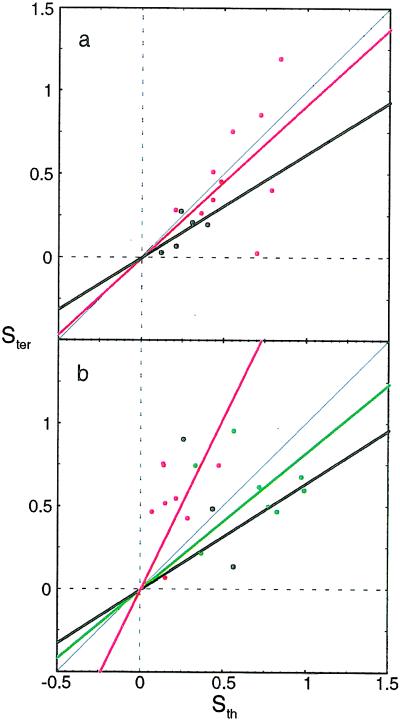
Averaging Q_ij about a given residue, i, gives S_tertiary, a quantity estimated by means of molecular dynamics (17). Fig. 2 shows the correlation between the theoretical S_tertiary (for α_h = 0.45 and α_t = 0) and simulated S_tertiary for each mutated residue. The residues are distinguished by colors according to their environment—i.e., core, α-helix, β-sheet, minicore, and turns and coils, as classified by Fersht and co-workers (4). These values are computed at Q* = 0.45 matching simulations to which we compare.

Figure 2.

Correlation of the energy-unweighted contact density (S_th) to the molecular dynamics S_tertiary (S_ter). Q* = 0.45 is used to match the simulation’s average value of S_tertiary. There is good agreement for core residues and reasonable agreement for helical and sheet residues. The diagonal line S_ter = S_th is indicated in black along with the separate correlation lines for core (red) and sheet (black) in a and α-helical (green), minicore (black), and turn and coil (red) residues in b.

The good comparison for core and sheet suggests that the purely structural predictions from the functional are fine. The energies for turns and helices clearly need improvement. The energy-weighted quantity, φ, is on a better theoretical footing than S_tertiary for comparison with kinetics but depends upon the accuracy with which the pair potential models the real protein.

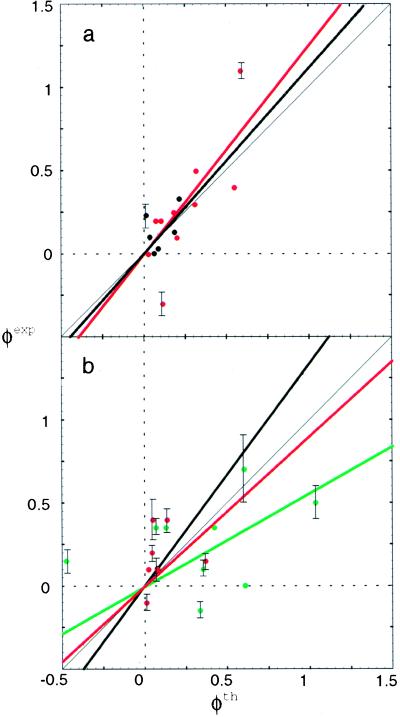
Fig. 3a shows the correlation of our theoretical φ_th computed by the energy-weighted formula to the experimental φ_exp of CI2 by Fersht and co-workers (4) for core and β-sheet mutations. Fig. 3b shows the comparison for helical, minicore, and turn and coil residues that are largely surface-exposed. In all cases the theory and experiment have been averaged over the measured mutants on that site. We see good correlation between the present theoretical φ values and experiment for core and sheet residues, with parameters α_h = 0.45 (an appreciable amount of helical cooperativity comparable to the other free energy terms, but no tertiary cooperativity) and ΔV = 0.1. We see much weaker correlation between φ_th and φ_exp for the mutations in the helix, minicore, and turns and coils than in their structural aspect, as seen in Fig. 3b. The slope of the experimental φ versus theoretical φ is 1.2, with a correlation coefficient of 0.8 for core residues and a slope of 1.1 and a correlation coefficient of 0.4 for β-sheet residues. We have seen that the addition of either helical or tertiary cooperativity improves the agreement for α-helical and β-sheet residues outside the core, but clearly our energy function still must be improved to handle solvent-accessible mutations. This parallels the earlier finding (34) that pair potentials successfully calculate stability changes for core mutations but not for solvent-accessible mutations.

Figure 3.

Correlation of the energy-weighted φ_th to the measured φ_exp for the core and β-sheet residues (a) and the helical, minicore, and turn and coil residues (b), using the same color scheme as Fig. 2. Error bars for a few representative (larger or smaller) experimental values are indicated from data of Fersht and co-workers (4).

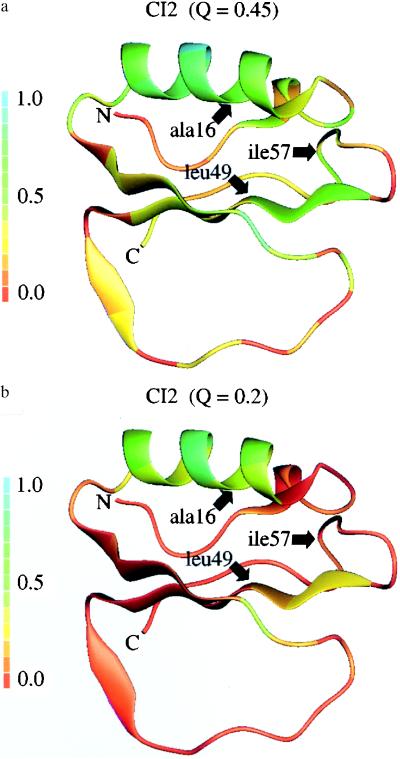
Clearly the quasiequilibrium analysis here yields a rather delocalized entity, but we can certainly examine which residues have the most completed contact set. Fersht and co-workers (4) call residues 16, 49, and 57 the folding nucleus because residue 16 has a large φ value and it interacts with residues 49 and 57. We find φ values to be similar to experimental values for these residues, but we also find residue 20 to have a large φ value. As in experiment, the hot residues are found in the core between the helix and the β-sheet. Still, our calculation, as well as experiment, indicates a significant involvement of a cloud of residues about this group, encompassing a large part of the small protein CI2. Fig. 4 shows the complete folded molecules with residues color coded to represent their involvement in the transition state ensemble as measured by S_tertiary.

Figure 4.

The folded structure of CI2 is shown for ensembles at Q* = 0.45 (a) and Q* = 0.2 (b) with residues colored according to the theoretically predicted energy-unweighted S_tertiary in those ensembles. The specific hot sites identified by experiment are indicated by arrows. The experimental and theoretical energy-weighted φ values are as follows: Ala-16 φ_exp = 1.1, φ_th = 0.6; Leu-49 φ_exp = 0.5, φ_th = 0.3; and Ile-57 φ_exp = 0.1, φ_th = 0.2.

Conclusions

While protein folding dynamically occurs through an ensemble of partially disordered structures, pair correlations exist just as they do in a liquid. Experiment and the present quasiequilibrium theory based on landscape ideas suggest that in small fast-folding proteins these correlations involve a delocalized set of contacts in the protein core. The current calculations describe these pair correlations through the interplay between the entropy of forming contacts and their heterogeneous energies. Cooperativity, which may be largely entropic or perhaps energetic, involving the many-body hydrophobic forces, appears to be a modest perturbation on the simple pair-interaction picture. The theory describes well the buried residues. Clearly a major deficit of the current work is the energy function for surface-exposed residues. Further work refining these terms should help.

At the statistical mechanical level, treating the protein as an interacting gas of contacts is a severe simplification. Explicit effects of random nonnative contacts have been neglected and different degrees of collapse have also not been taken into account. Both effects play a role in determining the actual height and location of the thermodynamic bottleneck. Just as in liquid state theory, higher-order functionals can be developed (35). We believe the present picture is a good step, however, in quantifying the structural energy relations once the bottleneck location is known empirically.

The larger proteins have modular structures, or foldons (36), each being described by a single transition state ensemble. This modular structure would be detected by a perfect free energy functional, but it might be missed by the present one. A more basic difficulty is that the quasiequilibrium assumption of diffusive Q motion may have to be modified for very large proteins. Topological constraints may become important for real proteins, as some recent lattice simulations indicate (37).

A useful avenue for future investigation will be the comparison of the present coarse-grained statistical mechanical theory with detailed atomistic calculations using importance sampling, which are appropriate for kinetic prediction when the quasiequilibrium protein folding funnel picture is adopted (38).