Anomalous compression behavior in lanthanum/cerium-based metallic glass under high pressure

Abstract

In situ high-pressure x-ray diffraction, low-temperature resistivity, and magnetization experiments were performed on a La₃₂Ce₃₂Al₁₆Ni₅Cu₁₅ bulk metallic glass (BMG). A sudden change in compressibility at ≈14 GPa and a rapid increase of resistivity at ≈12 K were detected, whereas magnetic phase transformation and magnetic field dependence of the low-temperature resistivity do not occur at temperatures down to 4.2 K. An interaction between conduction electrons and the two-level systems is suggested to explain the temperature and field dependences of resistivity of the BMG alloy. Although the cause of the unusual change in compressibility at ≈14 GPa is not clear, we believe that it could be linked with the unique electron structure of cerium in the amorphous matrix. An electronic phase transition in BMG alloys, most likely a second-order amorphous-to-amorphous phase transition, is suggested.

Recent studies of amorphous materials have revealed that more than one distinct amorphous phase can be formed from the same substance, a phenomenon that is called amorphous polymorphism (1–4). The nature of amorphous-to-amorphous transition induced by pressure has been a topic of considerable research activity in several substances, e.g., ice, silicon, silica, and carbon (5–13). All these reports have encouraged the search for polymorphic phase transitions in liquids and glasses (14–19). Bulk metallic glasses (BMGs) as a new kind of amorphous material with a maximum size up to ≈70 mm in diameter and wide supercooled liquid regions have been fabricated in the last decade (20, 21). To the best of our knowledge, evidence for an amorphous-to-amorphous phase transition has rarely been reported in metallic glasses. Very recently, parallel to our work, Sheng et al. (22) reported similar amorphous-to-amorphous phase transition in a binary CeAl metallic glass ribbon sample.

For decades, both structural and electronic transitions in pure elemental cerium and its crystalline alloys have been intensively investigated. Cerium, which is the first element in the lanthanide series with one 4f electron, has a complex phase diagram. Depending on pressure and temperature, it can be either a paramagnet, an antiferromagnet, or a superconductor. Cerium is also the only pure element to exhibit a solid–solid critical point in the well known γ ⇔ α isostructural phase transition (23, 24). Many cerium-bearing alloys are heavy-fermion compounds and have anomalous low-temperature resistivity and magnetization behaviors that are relevant to Kondo coupling (25, 26) and also have first-order phase transitions resembling the γ ⇔ α phase transition for pure cerium or second-order phase transitions above a critical point (27). Recently, a LaCe-based BMG with a maximum size up to 10 mm (28) and a La-based BMG with a maximum size up to 20 mm were developed (29). An interesting question has been raised: Do LaCe-based BMGs have electronic phase transitions similar to pure cerium and its crystalline alloys? In this work, we report in situ room-temperature high-pressure x-ray diffraction up to 40 GPa, low-temperature resistivity, and magnetization measurements of a LaCe-based BMG. At high pressures, we found an unusual change in compressibility at 14 GPa for a [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG. At low temperatures, the resistivity rapidly increases and there is a logarithmic temperature dependence below ≈12 K, which resembles a Kondo-like magnetic origin scatting problem in Ce-bearing alloys, but no magnetic dependence was observed. It is proposed to be a characteristic of two-level systems that are the typical excitations of a glassy system and extensively exist in metallic glasses (30–37).

Results and Discussion

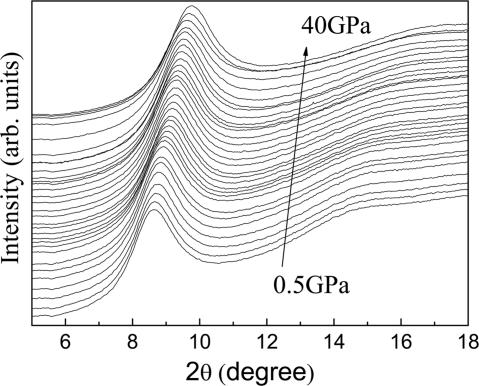
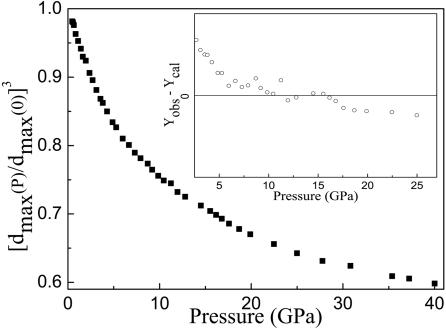
Fig. 1 shows high pressure x-ray diffraction patterns during compression for the [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy. The diffraction data recorded are high quality with high signal-to-noise ratio, which allows us to accurately determine the peak position on the 2θ scale, where the Bragg angle is. The peak positions were estimated from the fit by using a Voigt line profile after subtracting baseline, and they were used to calculate d_max = λ/2 sin θ_max). It is clear that the position of the broad amorphous peak shifts to higher angle with increasing pressure. For metallic glasses, most likely having a dense random packed structure, the parameter of [d_max(P)/d_max(0)]³ in an x-ray diffraction pattern is proportional to the reduced volume of the sample V(P)/V(0), where P and 0 denote the high-pressure and ambient-pressure conditions, respectively (38). In Fig. 2, [d_max(P)/d_max(0)]³ data as a function of P are first fitted by using the third-order Birch–Murnaghan equation of state (39, 40). It was found that the parameter [d_max(P)/d_max(0)]³ decreases with pressure, and no obvious discontinuous change of the parameter was detected within the pressure range used. However, the experimental data cannot be fitted well with the third-order Birch–Murnaghan equation. Many experimental data deviate above the fitted curve at pressures below 14 GPa and below the fitted curve at above 14 GPa, as shown in Fig. 2 Inset. The pressure of 14 GPa appears to be a critical point for the [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy.

Fig. 1.

In situ x-ray diffraction patterns of [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG under pressures at room temperature. The position of the broad amorphous peak shifts to higher angles with increasing pressure.

Fig. 2.

The parameter [d_max(P)/d_max(0)]³, which is proportional to the reduced volume of the sample, V(P)/V(0), as a function of pressure. (Inset) Plot of (Y_obs − Y_cal) vs. P, where Y = [d_max(P)/d_max(0)]³. Open circles stand for the difference between experimental data and the fitting curve (Y_obs − Y_cal), and the solid line is the zero. The (Y_obs − Y_cal) values almost all deviate above zero at pressures below 14 GPa and below zero above 14 GPa. Error bars for experimental data are smaller than the symbol size.

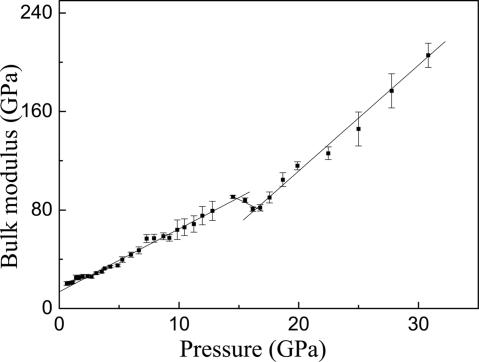
To illustrate this point, we plot local bulk modulus, K = −V(dP/dV), as a function of pressure in Fig. 3, in which linear fitting of every five adjacent data was used to get the slope, dP/dV, of the center point. It is clear that a break of bulk modulus at ≈14 GPa was detected within the experimental uncertainty. The slopes below and above 14 GPa are different. This observation suggests that the BMG alloy exhibits a sudden change in compressibility, which might originate from the Kondo coupling between 4f spin and conductive electrons due to the addition of cerium because an electronic second-order transition was reported in pure cerium and cerium-based compounds (41–46), although it has not been reported previously in any bulk metallic glasses.

Fig. 3.

Bulk modulus K vs. pressure. A distinct break of bulk modulus occurs at 14 GPa, and the slopes below and above 14 GPa are different within the experimental uncertainty.

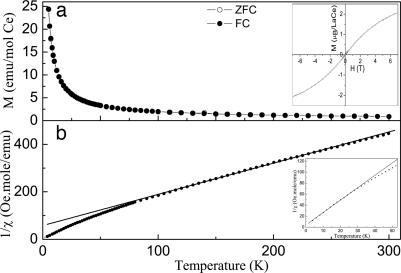
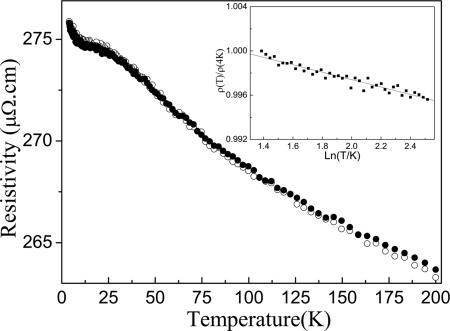
To confirm this hypothesis in [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy, magnetization and low-temperature resistivity measurements were performed on it. Zero-field-cooled (ZFC) and field-cooled (FC) curves at a field of 0.1 T for the [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy are shown in Fig. 4a. The temperature dependences of ZFC and FC magnetization curves for the sample completely coincide from 5 to 300 K, indicating neither spin-glass nor ferromagnetic behavior for the alloy within the temperature range. Magnetization increases monotonically with decreasing temperature. The M–H hysteresis loop of the alloy at 5 K is inserted in Fig. 4a. It reveals that the BMG alloy exhibits no magnetic hysteresis even at 5 K, which shows a characteristic paramagnetic behavior. The thermal dependence of inverse susceptibility χ⁻¹ is shown in Fig. 4b. The high-temperature data (T > 80 K) were fitted to a linear Curie–Weiss law with an effective moment of (2.47 ± 0.01) μ_B per Ce atom, which is lower than the free Ce³⁺ ion (2.54 μ_B), and a paramagnetic Curie point of −44 K. The low-temperature data (T < 30 K) were also fitted in Fig. 4b Inset, showing a second region of paramagnetic behavior with an effective moment of (2.06 ± 0.01) μ_B per Ce atom and a paramagnetic Curie point of −1.7 K, which indicate the existence of antiferromagnetic interactions. Fig. 5 shows the resistivity as a function of temperature for the [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy with applied magnetic fields H = 0 and 4 T. The two curves almost coincide. The slope of the curves, called the temperature coefficient of resistivity, is negative (47). Below ≈12 K, the resistivity ρ(T) rapidly increases, and it shows a negative logarithmic temperature dependence and can be well described by using the relation ρ(T)/ρ(4 K) = α + β ln T; the coefficient β can be determined to be −3.36 × 10⁻³ by linearly fitting the reduced resistivity ρ(T)/ρ(4 K) as a function of ln T in Fig. 5 Inset.

Fig. 4.

Magnetization measurements for [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy. (a) Zero-field-cooled (ZFC) and field-cooled (FC) magnetization curves at a field of 0.1 T for [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy. The temperature dependences of ZFC and FC magnetization curves for the sample completely coincide from 5 to 300 K, and they increase monotonically with decreasing temperature. The M–H hysteresis loop of the alloy at 5 K in the Inset exhibits no magnetic hysteresis. This is characteristic of a paramagnetic behavior. (b) Inverse susceptibility dependence of temperature. At high temperature (above 80 K) and low temperature (below 30 K in Inset), the susceptibility evidently follows a Curie–Weiss behavior. The solid line represents the fit 1/χ = (T + θ)/C. Above 80 K, the Curie constant C = 0.76 electromagnetic unit (emu) K·(mol of Ce)⁻¹·Oe⁻¹, and a paramagnetic Curie point is −44 K. The magnetic moment is ≈2.46 μ_B (Bohr magnetons), which is lower than the value 2.54 μ_B of free Ce³⁺ ion. Below 30 K, the Curie constant C equals 0.53 emu K·(mol of Ce)⁻¹·Oe⁻¹ and the magnetic moment is ≈2.06 μ_B. The paramagnetic Curie point is −1.7 K, which is shown in Inset.

Fig. 5.

Resistivity as a function of temperature for [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloys with applied magnetic fields H = 0 and 4 T. The two curves almost coincide and show no obvious magnetic dependence. The slope of the curves, called the temperature coefficient of resistivity, is negative. Below 12 K, the reduced resistivity ρ(T)/ρ(4 K) shows a logarithmic temperature dependence, ρ(T)/ρ(4 K) = α + β ln T, with a coefficient β = −3.36 × 10⁻³ in Inset.

For the origin of the increase in ρ(T) of metallic glasses at low temperature it is still debated whether it is due to a Kondo-type effect, structural disorder induced two-level systems, and/or weak localization and a Coulomb electron–electron interaction effect. Some reports indicate that the temperature dependence of resistivity for magnetic and nonmagnetic metallic glasses can be fitted to T^1/2 with a negative slope as predicted by Coulomb electron–electron interaction theories (48). In Ce-bearing crystalline alloys (25, 26, 43) a magnetic Kondo effect is usually suggested to explain the anomalous negative coefficient with a logarithmic temperature dependence at low temperature. Both effects mentioned above predict a magnetic field dependence of resistivity (49–52). However, we found that the resistivity of this BMG alloy does not depend on magnetic field applied in Fig. 5. Thus, we suggest that the anomalous behavior of resistivity at low temperature for the BMG alloy could be ascribed to the interaction between conduction electrons and the tunneling two-level systems. Because of the disorder structure in metallic glasses, many local energy minima, corresponding to similar atomic configurations, exist in metallic glasses. Of these, roughly equivalent states that can make transitions within an experimental time scale will contribute to the thermal and transport properties. These changes in configuration or rearrangement of small groups of atoms at the “equivalent” sites are so-called “tunneling levels.” In its simplest form they are the “two-level systems.” The coupling between conduction electrons with the two-level systems affects electron scattering as temperature is lowered just as in the Kondo effect, i.e., a logarithmic temperature dependence of resistivity (34–37). This model does not involve spin, so that no significant dependence of resistivity on the application of external magnetic fields is expected. The resistivity data obtained here are consistent with data reported in the literature for other metallic glass alloys (34–36, 53, 54). During compression, density of the sample increases and the average interatomic distance should be shortened. Consequently, it is not unreasonable to expect a change of the coupling between conduction electron and the two-level system, which might cause the change in compressibility at 14 GPa. More investigation of the mechanism is still needed.

In conclusion, we report results obtained from in situ high-pressure x-ray diffraction, low-temperature resistivity, and magnetization measurements for [La_0.5Ce_0.5]₆₄Al₁₆Ni₅Cu₁₅ BMG alloy. A sudden change in compressibility at ≈14 GPa and a rapid increase of resistivity at ≈12 K for the La₃₂Ce₃₂Al₁₆Ni₅Cu₁₅ BMG were detected, whereas no magnetic phase transformation and no magnetic field dependence of the low-temperature resistivity were observed at temperatures down to 4.2 K. An interaction between conduction electrons and the two-level system was suggested to explain the temperature and field dependences of resistivity of the BMG alloy. Although the cause of the unusual change in compressibility at ≈14 GPa is not clear, we believe that it could be linked with the unique electron structure of Ce in the amorphous matrix. An electronic phase transition, most likely a second-order amorphous-to-amorphous phase transition, is suggested in BMG alloys.

Materials and Methods

Master ingots were prepared by arc-melting a mixture of pure lanthanum (99.5 atom %), cerium (99.5 atom %), aluminum (99.95 atom %), nickel (99.98 atom %), and copper (99.9 atom %) in a zirconium-gettered argon atmosphere. Each of the master ingots was melted five times, then mechanically polished and sucked into copper molds for forming a rod with a diameter of 5 mm or a sheet with dimensions of 2 mm × 10 mm × 90 mm. Rods were sliced to a thickness of 0.5 mm at the middle position for x-ray diffraction and differential scanning calorimeter measurements, and sheets were sliced to a dimension of 2 mm × 4 mm × 8 mm for resistivity and magnetization measurements. The fully amorphous structure of all samples was confirmed by x-ray diffraction using a Thermo Electron (San Jose, CA) ARL X'TRA diffractometer with Cu K_α radiation. Thermal analyses were performed with a PerkinElmer (Waltham, MA) Pyris Diamond differential scanning calorimeter with a heating rate of 20 K/min under argon flow.

In situ high-pressure x-ray diffraction measurements at ambient temperature using a Mao–Bell-type diamond-anvil cell were performed at the High Pressure Collaborative Access Team, Advanced Photon Source, with a beam size of ≈15 × 15 μm² and a wavelength of λ = 0.4116 Å. A total of 56 diffraction patterns for samples compressed up to 40 GPa and then decompressed to ambient pressure were recorded by using a charge-coupled device (CCD) detector. No obvious evidence of hysteresis and broadening or degradation between compression and decompression was found. The sample and tiny ruby powder suspended in a 16:3:1 (vol/vol) methanol/ethanol/water pressure-transmitting medium were enclosed in a 200-μm-diameter hole in a T301 stainless steel gasket. The pressure was measured by the ruby fluorescence method, using the nonlinear pressure scale of Mao et al. (55). Low-temperature electrical resistivity measurements were carried out with a four-probe method using a current of 10 mA and a frequency of 11 Hz on a Quantum Design (San Diego, CA) PPMS-9. Measurements were performed on 2 mm × 4 mm × 8 mm samples in a temperature range of 4.2–200 K without field and with a field of 4 T; measurements were repeated twice for each one. Magnetization measurements were also performed on the Quantum Design PPMS-9 in the range of 5–300 K under applied fields up to 7 T.

Abbreviation

BMG

bulk metallic glass.