Polaron melting and ordering as key mechanisms for colossal resistance effects in manganites

Abstract

Polarons, the combined motion of electrons in a cloth of their lattice distortions, are a key transport feature in doped manganites. To develop a profound understanding of the colossal resistance effects induced by external fields, the study of polaron correlations and the resulting collective polaron behavior, i.e., polaron ordering and transition from polaronic transport to metallic transport is essential. We show that static long-range ordering of Jahn–Teller polarons forms a polaron solid which represents a new type of charge and orbital ordered state. The related noncentrosymmetric lattice distortions establish a connection between colossal resistance effects and multiferroic properties, i.e., the coexistence of ferroelectric and antiferromagnetic ordering. Colossal resistance effects due to an electrically induced polaron solid–liquid transition are directly observed in a transmission electron microscope with local electric stimulus applied in situ using a piezo-controlled tip. Our results shed light onto the colossal resistance effects in magnetic field and have a strong impact on the development of correlated electron-device applications such as resistive random access memory (RRAM).

Materials with a coexistence of a variety of electronic and lattice interactions of similar strength are able to create fundamentally differing electronic ground states (1). In doped manganites (Re_1−xA_xMnO₃; Re and A are rare- and alkaline-earth cations), this includes ferromagnetic metallic, paramagnetic insulating and antiferromagnetic charge and orbital ordered states, representing different collective behavior of the microscopic lattice, charge, orbital, and spin degrees of freedom (2). External fields influence the subtle balance of the interactions and the induced phase transitions between different ground states are related to colossal resistance effects in magnetic (3, 4), electric (5), photon (6), and strain fields (7). They offer great opportunities for new correlated electron devices (8), e.g., in magnetoelectronics and nonvolatile electronic data storage.

Among various interactions, two different basic types of electron–lattice coupling (9) play a distinct role in manganites: One is the effect of the static crystal structure on electron transport and bonding. Different ion radii of the involved Re and A cations generate different internal stress on the MnOMn bonds. The different resulting types of lattice distortions involve transitions from the ideal cubic to hexagonal, rhombohedral, and orthorhombic structures (10, 11), which may induce polar distortions or even multiferroic ordering, i.e., the presence of electric and magnetic order of electrons in a single phase (12). In doped systems, the decrease of the MnOMn bonding angle below 180° due to rigid rotations of the MnO₆ octahedra (for example, see Fig. 2a) results in a strong reduction of the bandwidth of the e_g conduction electrons, the conductivity, and the related ferromagnetic double exchange (13).

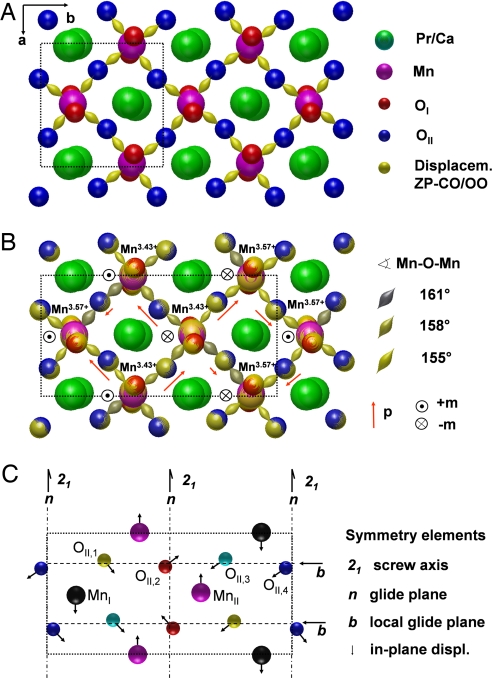
Fig. 2.

Structure projection along the [001] direction. Projected structure of the charge and orbital disordered (A) and the Zener polaron ordered (B) states with a schematic representation of the e_g orbitals for half doping x = 0.5. The displacement of Mn and O sites due to ordering is indicated in yellow. Increasing MnOMn bond angles (color index) result in an enhancement of the ferromagnetic double exchange and orbital occupation by the e_g electrons. The in-plane electric dipole moments p of the MnOMn dimers determined from the noncentrosymmetric atomic displacements are indicated by red arrows. Their canted structure results in a net-polarization P_a along the crystallographic a direction, whereas P_b sums up to zero. The directions of the perpendicular magnetic moments of the Mn atoms m below T_N as expected from CE-type antiferromagnetic ordering are indicated with black arrowheads. (C) Symmetry elements and displacements of the ordered phase. Sites related by the P2₁nm space group are indicated by same colors. Additional pairing in the displacements is due to the local b glide plane of O_II,1 and O_II,2, O_II,3, and O_II,4, respectively. This symmetry element is preserved along the b and c directions.

In addition to this static effect, the electron charge may induce dynamic lattice distortions of the crystal accompanying the moving charge carrier through the crystal lattice. Such a charge carrier can be pictured as being “dressed” by a cloth of lattice vibrations, phonons. It represents a particle-like excitation, a polaron. Depending on the weight of the long- or short-range electron–lattice interactions, simplified models have been developed, including weakly dressed band electrons and heavy Holstein polarons with “cage-like” self-trapping of the electrons as their limits (14). In manganites, there are several important phonon modes, including a volume changing breathing mode for the MnO₆ octahedron, two uniaxial volume preserving modes, and several rotational modes partly accompanied by Mn vibrations (15, 16). Most of these modes are related to energy level shifts of the conduction electrons and thus constitute the Jahn–Teller (JT) effect: A lift of degeneracy of the relevant e_g electrons in the d_3x²−r² and d_3y²−r² Mn orbitals. Strong JT-like electron-phonon coupling results in self-localization of e_g charge carriers in the potential wall of the induced lattice distortion. Thermally activated motion of such JT polarons represents the dominant electronic transport mechanism in the paramagnetic insulating phase (17). The electron–lattice interaction in the ferromagnetic and the charge and orbital ordered ground states is only poorly understood.

Our results on polaron ordering show that the above distinction between static and dynamic electron–lattice interactions is, however, only relative. Similar to the development of static off-center polar distortions in ferroelectric perovskites due to soft phonon modes (18), a softening of JT polaron modes is observed in manganites at the charge and orbital ordering temperature (19). Indeed, the volume density of dynamic JT polarons in doped manganites is high enough to develop strong correlation effects, such as dynamic short-range correlation in a polaron liquid and static long-range ordering of JT distortions, forming a polaron solid. The latter are related to charge and orbital ordering of the involved e_g electrons. Such ordered states are unavoidably related to structural changes. The resulting local order may be much richer than a conventional checkerboard (CB)-type arrangement, comprised of JT-distorted Mn³⁺ and nondistorted Mn⁴⁺ octahedra, as presently discussed for various manganites (20, 21), including off-center ferroelectric distortions.

In general, partially filled d-orbitals in manganites tend to oppose noncentrosymmetric lattice distortions (22) with static displacement of bound cation charges, because the strong Coulomb repulsion favors symmetric ligand arrangements (23). Because magnetic ordering requires partially filled d-orbitals with uncompensated net-spin, there is a general difficulty in uniting long-range electric and magnetic order in single phase multiferroic materials (22). However, complex electron–lattice correlations, influenced by cation radii, additional ligand-type, or magnetic interactions may overcome this Coulomb repulsion and induce noncentrosymmetric second-order JT distortions (24). This effect may give rise to the multiferroic ordering in YMnO₃ (23) and TbMnO₃ (25), but was never considered for static cooperative JT polarons in doped manganites.

An additional challenge is the understanding of the electron lattice interaction in the ferromagnetic metallic state, and its role in the magnetic field assisted phase transition from the insulating to conducting ferromagnetic phases, the colossal magnetoresistance (CMR). The ferromagnetic metallic properties appear to be inconsistent with a pure band picture of a metal. Although the Zener-double exchange is governing the metallic phase, the coupling to the lattice and orbital degrees of freedoms is still evident from optical conductivity (26), resistivity, and specific heat measurements (27). The reorganization of JT polaron modes during the phase transition, leading to band-like behavior, is an essential but unresolved issue. Actual spectroscopic results emphasizes the role of coherent polaron behavior not only for the CMR materials but also as a general phenomena linked to high-T_c superconductivity (28).

For our study of correlated polaron behavior, we selected Pr_1−xCa_xMnO₃ (PCMO) as a representative of hole charge carrier doped perovskite manganites with a strong octahedral tilting (29), a small bandwidth of the 3d e_g electrons and strong JT-type electron-phonon coupling. Charge and orbital ordering is observed below a transition temperature T_c ≈ 250 K over a very broad doping region 0.3 ≤ x ≤ 0.7 (30, 31). Due to the almost equal ion radii of Pr and Ca, it exhibits negligible local lattice strain and no cation ordering.

Zener Polaron Charge and Orbital Ordering

It is often assumed that the ordering in PCMO is of the so-called CB type (32), in which charge ordering is associated with a periodical arrangement of Mn³⁺ and Mn⁴⁺ ions, i.e., a site-centered ordering. This type of ordering is related to even-parity centro-symmetric JT distortions at Mn³⁺ sites with an occupancy difference in the 3d_3x²−r² and 3d_3y²−r² orbitals. From the crystallographic viewpoint, such an arrangement is only compatible with a few space groups (P112₁/m or P11m). However, the detailed structure of the ordered state is controversially discussed in the literature, and an alternative picture of bond-centered charge ordering (21) is developed within the space group P2₁nm. Different structural results are obtained for Pr_0.6Ca_0.4MnO₃ by different authors (33, 34).

An experimental proof of the controversial space groups by macroscopic diffraction measurements is not possible because PCMO is heavily twinned and exhibits six twin domains with twin sizes of <100 nm. This may lead to misinterpretations due to mixing of diffraction spots of Bragg and superlattice reflections from different twin domains. To overcome this problem, we have investigated individual twin domains of various bulk and thin film samples in the doping range 0.32 ≤ x ≤ 0.5 by means of high-resolution transmission electron microscopy (HRTEM).

All samples reveal an electronic and structural phase separation between charge and orbital disordered (Pbnm) and ordered phases with a doubled unit cell along the crystallographic b direction. The supercell lattice parameter b_s is reduced compared with the doubled lattice parameter b of the disordered phase (b_s/2b₀ = 0.983), indicating a change in the specific volume and therefore proofs the phase transition to be of first order. The extinction conditions (see Fig. 1C and D), which are exclusively observed for individual twins, disproves all space groups of the CB-type. They uniquely define the space group P2₁nm for the ordered state. In contrast to the CB-type charge ordering, this type of charge ordering is to a large extend independent of the doping level x consistent to our observation in a doping regime 0.3 ≤ x ≤ 0.5.

Fig. 1.

HRTEM lattice images and diffraction results of the Zener polaron charge and orbital ordered state at room temperature. (A) Lattice fringes of a (b,c) plane. (B) Typical example of structural and electronic phase separation between a Zener polaron type charge and orbital ordered (P2₁nm) and a disordered (Pbnm) structure, as observed in a wide temperature 80 ≤ T ≤ 300 K and doping 0.3 ≤ x ≤ 0.5 regime. The fringes correspond to the superlattice modulation with a doubled lattice parameter in b direction. (C and D) Diffraction patterns of the ordered state along the [010] and [100] zone axis, respectively. C shows extinction of the h0l reflections for h + l = 2n + 1; this confirms the space group P2₁nm for the ordered state with the Zener polaron type of ordering. (D) Nearly extinction of 0kl for k = 4n + 2 confirms the preservation of local b glide planes for subgroups of atoms and therefore gives constraints to the symmetry of the cooperative JT distortions.

This space group together with the preservation of local b glide planes (see Fig. 2) gives insight into the relevant JT modes for the static cooperative JT distortion forming the polaron solid. In contrast to the usually assumed even-parity uniaxial breathing modes, we find a superposition of rotational JT distortions involving odd-parity Mn displacements. The resulting noncentrosymmetric lattice distortion leads to nonequivalent MnOMn bonds (Fig. 2B). Valence sum analysis of the refined structure as well as electron energy loss spectroscopy find negligible charge disproportionation at Mn sites, but confirms the localization of e_g electrons at a preferential MnOMn bond with highest bonding angle [supporting information (SI) Text]. Real space ordering of e_g electrons results in an ordered state of magnetic Zener polarons (ZP) (33): Pairs of JT-distorted ferromagnetically coupled MnO₆ octahedra, linked by MnOMn bonds with a strongly enhanced Zener double exchange interaction. This polaron solid represents bond-centered charge ordering in contrast to site-centered charge ordering of the e_g conduction electrons at Mn³⁺/Mn⁴⁺ sites.

The symmetry elements of the ZP ordered structure indicates that the soft dynamic polaronic JT modes, which are involved in the ordering extend over length scales larger than the unit cell of the disordered paramagnetic insulating Pbnm phase. Fig. 2C shows the Mn and in-plane oxygen sites which are related by the symmetry elements of the P2₁nm space group in the same color settings. One example is the 2₁ screw axis with 1/2,0,0 screw vector. It reflects a strong correlation of the oxygen displacements of MnO₆ octahedra in adjacent Pbnm unit cells. The ordering transition involves symmetry-breaking of the b glide planes at x = 1/4 and x = 3/4: This symmetry element degrades from a global property of the Pbnm unit cell to a local property of the P2₁nm supercell, as revealed by the observed additional extinction condition for 0kl reflections with k = 4n + 2. Therefore, the atoms form pairs, O_II,1 and O_II,2 as well as O_II,3 and O_II,4, keeping the local b glide plane symmetry along the b and c directions, respectively. This pair correlation is an essential ingredient of the ZP feature. Among the various JT modes which coexist in the Pbnm state, the A_g rotational modes with odd-parity Mn displacements seem to play a preferential role for the long range electron–lattice interaction and ordering. This reflects the short range dynamic polaron correlations in the polaron liquid for the disordered Pbnm structure.

Ferroelectric Ordering

An essential property of the Zener polaron ordered structure is the noncentrosymmetric JT distortion of the MnOMn bonds. Their presence depends only on the symmetry but not much on the amplitude of the structure refinement. The related displacements of the bound cation and anion charges of the Mn and oxygen cations create permanent electric dipoles as depicted with red arrows in Fig. 2B. Based on the noncentrosymmetric distortions of the oxygen anions obtained from structure refinement, and a valence state of O²⁻ and Mn^3.5+, a net permanent polarization of P_a ≈ 44 mC/m² parallel to the a axis is calculated, whereas P_b = 0 (see Fig. 2B). We note that the ZP does not contribute to P, because the bonding is more symmetric and screening effects of delocalized e_g electrons in the MnOMn orbitals may be dominant. Because an electrical measurement of a permanent electric polarization interferes with colossal electroresistance effects (see below), we study electric polarization domains with electron microscopy in the Lorenz mode. It follows from the symmetry elements of the ZP ordered phase that ferroelectric domains with a 180° reversal of the net-moment along the a direction represent antiphase domains in the superstructure, where the local b glide plane of the O_II,3 and O_II,4 pair with x = 1/4 ± Δ_x (Δ_x ≈ 0.01 a) is shifted in opposite directions along the a axis.

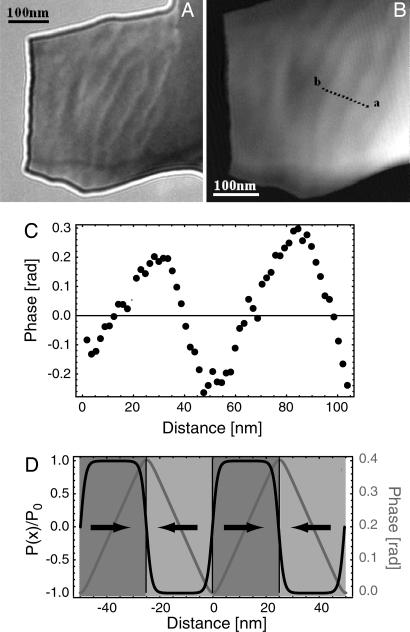
We observe peculiar fringe patterns (Fig. 3A) in some areas at room temperature. The strong increase of the number and size of such areas with fringes with decreasing temperature is correlated with the increase of the volume ratio of the ZP ordered phase. Although similar fringes are rather frequently observed in Lorenz–TEM, and may have different origin (e.g., magnetic domains, thickness modulations, etc.), we ascertain their persistence at room temperature, where magnetic ordering is absent, and their stability in presence of an applied magnetic field, hence ruling out a possible magnetic origin. Furthermore, thickness modulations of such regularity are most unlikely. The observed Fresnel-contrast features are therefore interpreted as an array of head-to-head/tail-to-tail ferroelectric domains. By recording electron diffraction patterns from the same area, we ascertained that domains run parallel to the a axis, with a polarization along the a axis. This observation is in full agreement with our structure refinement.

Fig. 3.

Electron optic evidence for ferroelectric domain structure in PCMO with x = 0.32. (A) Fresnel (out-of-focus) image of a thin area of the sample surrounded by vacuum; the peculiar Fresnel diffraction fringes are clearly visible when the defocus is large enough (we estimate a defocus value of ≈200–300 μm for this picture). (B) Reconstructed phase shift from the electron hologram (not shown) recorded in-focus over the same area as in A. (C) Experimental line scan (dashed line in B) taken across four domains. From the line scan, we can estimate the domain size, o, the order of 25 nm (with relatively large variations), the phase gradient (slope), o, the order of 16 mrad/nm, and the total phase shift associated to each domain, ≈0.4 rad. (D) Simple model describing the ferroelectric polarization P₀ and phase shift across the domains. Full agreement with the profile in C is obtained for a value of 1.2 mC/m² for the quantity P₀/ε_r, where ε_r denotes the static dielectric permittivity.

To further investigate ferroelectric ordering, we recorded electron holograms over one region of the sample showing out-of-focus fringes. After standard reconstruction and unwrapping a phase map is obtained (Fig. 3B) which is related to the projected polarization over the sample thickness. In particular, in the simple scenario sketched in Fig. 3C where the polarization is taken as a smoothed square wave, the phase profile across the array turns out to be a smoothed triangular wave, with a slope proportional to tP₀/ε_r, where t ≈ 20 nm is the determined thickness, P₀ is the electrostatic polarization, and ε_r is the dielectric permittivity. To reproduce P₀ ≈ 40 mC/m² obtained from our structure model, an ε_r of the ordered phase of ≈35 has to be assumed, which is a very reasonable bulk value (35). Indeed, dielectric response shows formation of static electric dipoles at the charge ordering temperature of T_c ≈ 230 K (36), which gives supporting evidence for the domain interpretation.

It is well established that antiferromagnetic ordering sets in the charge and orbital ordered phase at T_N ≈ 140 K (37). Based on the determined Zener polaron type, this order can be pictured as a magnetic ordering of MnOMn dimers, which are coupled antiferromagnetically along the b direction and form ferromagnetic chains along the a direction. Each Zener polaron has a strongly enhanced ferromagnetic double exchange interaction, and, according to a theoretical calculation (38) a magnetic moment of ≈7 μ_B for the Mn pair. Our experiments should be interpreted as strong evidence that the Zener polaron solid exhibits multiferroic order with a high ferromagnetic coupling of the Mn^+3.5±δ pairs and canted permanent electric dipoles with a net moment along the a axis.

Electroresistance as a Polaron Order Disorder Transition

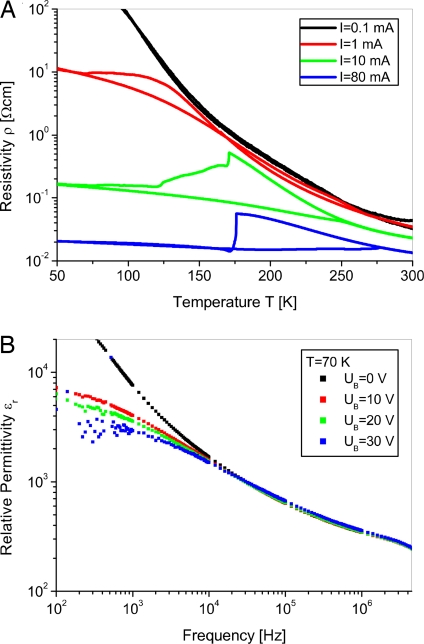
For small currents, the temperature dependence of the PCMO resistivity in Fig. 4A points out the important role of JT polarons in the electronic transport. This temperature dependence is in excellent agreement with the model of thermally activated motion of polarons in the validity range of above one half of the Debye temperature Φ_D: T ≥ $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$Φ_D ≈ 160 K (for the analysis, see SI Text). Alternative models like the variable range hopping or band insulator models do not describe the resistivity, adequately. Our experiments on various bulk and film samples in the doping range 0.3 < x < 0.5 clearly demonstrate, that the electric transport in the phase separated state is dominated by the hopping of small polarons with a hopping length of the Mn–Mn distance and an activation barrier W_h ≈ 110–190 meV. The barrier approximately corresponds to one half of the JT distortion energy (39). However, applying a sufficiently high current, the resistivity is strongly reduced over the whole temperature range and a step-like change (17) occurs at a percolation temperature of about T_p ≈ 170 K (Fig. 4A). Above the threshold, the temperature dependence can be described within the model of thermally activated polaron hopping, where the activation energy decreases with increasing current to 80 meV. This current-dependent activation barrier is a significant fingerprint of the polaron liquid with current dependent dynamic polaron correlations. Below T_p, the strong increase of ρ(T) at low currents reflects the freezing out of the polaron modes. At high currents, the resistivity only marginally depends on temperature (W_H ≈ 25 meV), indicating a transition toward a light polaron and e_g band formation in the current induced polaron disordered state at low temperatures.

Fig. 4.

Colossal electroresistance effect (CER) as a polaron order–disorder transition between the polaron-solid and liquid phases. (A) Temperature dependence of the resistivity ρ(T) for different constant electric currents in a c-axis-oriented epitaxial Pr_0.5Ca_0.5MnO₃ film. At the percolation temperature T_p, a step-like resistivity drop is observed. (B) Frequency dependence of the relative permittivity ε_r(ω) at 70 K as a function of the applied bias. The drop in this excess low-frequency ε_r(ω) is related to a suppression of the static ferroelectric order of the Zener polaron ordered phase.

The frequency-dependent permittivity ε_r(ω) at low temperatures, i.e., in the ordered phase, shows an excess contribution in ε_r(ω) at low frequencies (Fig. 4B). This excess is strongly suppressed by applying moderate bias voltages, i.e., at the onset of the colossal electroresistance effect (CER). In contrast, the dynamic response of mobile (e_g) and bound charge is nearly unaffected at frequencies above 10⁴ Hz (for the frequency dependent resistivity, see SI Text). Therefore, two essential features are associated with the CER, a change in the low-frequency conduction mechanism and a suppression of the low-frequency capacitance, related to disordering of static polarons and disappearance of ferroelectric polarization.

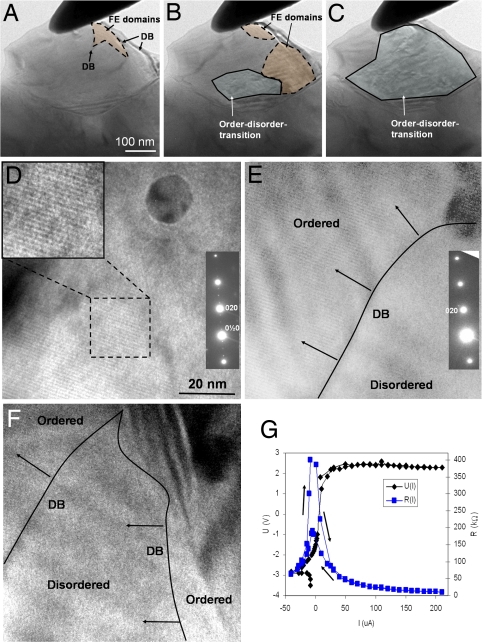
The polaron solid to liquid transition and their cooperative behavior is directly observed in local transport experiment in the TEM (Fig. 5), where we specifically contact grains with a scanning tunnelling tip and observe the structural response of the ordered phase to an electric current or electric field. For point contact configuration, a disordering is observed at currents between 3 and 200 μA and bias between 3 and 10 V (Fig. 5 A–F), depending on the geometrical configuration and the distance of the observed area from the tip. We observe a disordering process that, surprisingly, sets in by current induced motion of 10- to 30-nm large ordered domains. The coherent motion of ordered Zener polarons was observed by selecting a crystal area, where a defect is used as a marker to keep the region of interest in the field of view. Diffraction measurements are performed during all steps of the experiment to rule out movements of lattice fringes due to tilting of the zone axis. We conclude that, at the onset of the disordering process, the superstructure modulation due to ordered JT polarons moves coherently through the crystal lattice (SI Movie 1). Only after a characteristic transient period of some 10 s up to minutes, the moving ordered domains vanish and the areas with sufficiently large current are transform into a polaron-disordered Pbnm state. Simultaneously, or immediately preceding the onset of domain motion, we observed a strong change in a stripe fringe contrast in some areas (Fig. 5 A–C). According to Fig. 3, it is interpreted as a change of the ferroelectric domain pattern at the onset of the disorder transition followed by a complete dissolution of domains in the disordered phase. The direct interplay of the changes in the ferroelectric polarization and the order–disorder transition at electric field values of E_c ≈ 0.5 10⁵ V/m is consistent with the fact that both have the same microscopic origin in the noncentrosymmetric cooperative JT distortion.

Fig. 5.

In situ TEM study of the local colossal resistance (CER) effect at two different PCMO grains induced by a Pt/Ir tip. (A–C) Low-magnification images of the first grain (slightly defocused) visualizing electric domain patterns and the disorder transition at applied current. (A) PCMO grain with a high volume ratio of the ordered phase and some ferroelectric domains at zero current I = 0 μA. (B) Same area with I = 6 μA and bias U = 1 V. The electric domain structure has been strongly modified and the order–disorder transition sets in. (C) I = 10 μA, where the major grain area is involved in the order–disorder transition. (D–F) HRTEM images and SAED patterns (Inset) of a second grain far away from the tip with a defect as a marker. (D) Ordered area with a 2b₀ superlattice immediately before the disorder transition at I = 200 μA. (E) Snapshot of a moving domain boundary (DB) between an ordered and disordered domain 5 s after increase of the current to I = 210 μA (SI Movie 1). (F) Same as E with a second ordered domain moving into the image area, ≈8 s after increasing I to 210 μA. All diffraction patterns are acquired at the [1̄01] zone axis. (G) U–I and R–I curves that are recorded during the experiment at grain 2. Note that a sign reversal of the current is required to obtain a full recovery of the high-resistance ordered state in most of the grain area.

Before approaching the tip into point contact to grains with ordered domains, we perform control experiments, where a vacuum barrier with distances of 10–200 nm between the tip and grain is maintained. In such a zero-current experiment with electric fields of up to 10¹⁰ V/m no changes of the ordered state are observed. This finding is confirmed by electron diffraction and HRTEM lattice imaging (SI Text).

At first sight, the observation that the order–disorder transition and the related decrease of the resistivity is induced by an electric current but not by an electric field alone may indicate that Joule heating is the dominant driving force for the phase transition. The change of the specific volume between the ordered and disordered phases and the latent heat in the disordering transition tend to support the idea that thermal effects could be involved. However, a pure thermal mechanism can be easily ruled out by the observation that after switching off the current to zero, the ordered state does not recover spontaneously at most areas within a time window of several minutes. For the reordering, a sign reversal of the current is required as is also visible in the R(I) hysteresis at low current values in Fig. 5G. Because latent heat is released in the ordering transition, a pure thermal mechanism would require undercooling in contrast to the observed ordering in reversed currents. This argument is even more strengthened by the observation that the ordered phase can be induced by currents in areas, where the ordered phase is absent before applying electric currents.

Summary and Further Impact

In summary, our electron optic and transport study shows that ordering in the charge, orbital and polaron degrees of freedom is directly linked to changes in the crystal structure and breaking of one or more of the symmetries that generate the Pnma space group. Phase separation between ordered and disordered states is thus an intrinsically structural and electronic phenomenon. Due to the first-order type of the phase transition, different crystal lattices coexist. However, the temperature and doping windows 80 K ≤ T ≤ 300 K and 0.3 ≤ x ≤ 0.5 are surprisingly large, respectively. The higher complexity of structural and electronic order can be most clearly established in PCMO due to the small bandwidth, strong electron–lattice coupling, and small local strain. This observation may support evidence that other rich structure of local order than the CB-type, involving localization of holes at distinct oxygen sites, is present in other doped manganites (20, 21, 38).

Our observation of current-induced polaron solid–liquid transition relates the CER to the polaronic degrees of freedom. However, the CER cannot be simply reduced to an electric destruction of the long-range order, because significant current induced resistance change is also observed at room temperature, where polaron liquid is the dominant phase. At room temperature, where the disordered Pbnm phase is dominating, the electroresistance thus may be governed by cooperative effects in the polaron liquid; this is reflected by a moderate reduction of the activation barrier W_h with increasing current density of up to 35%. The strong electrically induced W_h reduction of 80% and more in the low temperature regime of the CER may indicate that the disordering of the Zener polaron solid is related to a drastic reorganisation of the electron–lattice interaction toward large, light polarons and polaron band formation. Therefore, we conclude that the visualization of the electrically induced coherent polaron motion and the solid–liquid transition are only first steps in understanding a much richer cooperative polaron phase diagram. This may include transitions from small polarons with charge self-trapping to current driven dynamic polaron ordering process with long range electron–lattice interactions. It could represent a clue for understanding the magnetic field induced ferromagnetic metallic state, where the double exchange may further enhance long-range electron lattice interaction, thus increase the e_g bandwidth and the MnOMn bond angles.

The Zener polaron-type of charge and orbital ordering represents an illuminating example for complex ordering which is driven by a combination of the electron–lattice and double exchange interactions. Their cooperative action, therefore, does not only represent a key microscopic mechanism for the CMR and CER, but also lay at the core of the formation of a ferroelectric state which is characterized by polar displacements of cations and anions. Due to its origin from static polaron ordering, the ferroelectric properties are hidden by e_g band and polaron conduction and related screening effects. Based on the well established antiferromagnetic order below T_N and our experimental evidence for low-frequency electric ordering, we thus conclude that PCMO represents a multiferroic material, where a connection between magnetic/dielectric ordering and charge/orbital ordering has been established.

The results on current-induced polaron disorder and ordering contribute significantly to the understanding of the recently observed remanent resistance switching effect (40), where charge density as well as electronic interactions could be modified at the vicinity of interfaces to the electrodes. It immediately impacts applications of this type of manganites for resistive random access memory (RRAM) devices, which open up routes for the fabrication of nonvolatile memories with increased data density and reduced power requirements.

Materials and Methods

PCMO material in the doping range 0.32 ≤ x ≤0.5 is prepared by two different methods: Bulk polycrystalline material is obtained from the metal oxides by a solid-state reaction, and epitaxial c-axis-oriented thin films are grown by pulsed-laser deposition on SrTiO₃ and MgO (001) substrates. Bulk and thin film materials show the same type of phase separation and ordering. For the space resolved structural analysis HRTEM is used for real space imaging, electron diffraction and scanning TEM for sample temperatures between 300 and 80 K. Electric domain analysis is performed by Lorentz microscopy and electron holography. The DC and AC transport measurements are performed in a cryogenic system at temperatures between 300 and 10 K using two and four terminal geometries. The local correlation of transport and structural measurements are performed by a TEM setup with a piezo-controlled Pt/Ir Nanotip. See SI Text for details.

Abbreviations

JT

Jahn–Teller

CB

checkerboard

CMR

colossal magnetoresistance

PCMO

Pr_1−xCa_xMnO₃

TEM

transmission electron spectroscopy

HRTEM

high-resolution TEM

CER

colossal electroresistance effect.