On the importance of a funneled energy landscape for the assembly and regulation of multidomain Src tyrosine kinases

Abstract

Regulation of signaling pathways in the cell often involves multidomain allosteric enzymes that are able to adopt alternate active or inactive conformations in response to specific stimuli. It is therefore of great interest to elucidate the energetic and structural determinants that govern the conformational plasticity of these proteins. In this study, free-energy computations have been used to address this fundamental question, focusing on one important family of signaling enzymes, the Src tyrosine kinases. Inactivation of these enzymes depends on the formation of an assembly comprising a tandem of SH3 and SH2 modules alongside a catalytic domain. Activation results from the release of the SH3 and SH2 domains, which are then believed to be structurally uncoupled by virtue of a flexible peptide link. In contrast to this view, this analysis shows that inactivation depends critically on the intrinsic propensity of the SH3–SH2 tandem to adopt conformations that are conducive to the assembled inactive state, even when no interactions with the rest of the kinase are possible. This funneling of the available conformational space is encoded within the SH3–SH2 connector, which appears to have evolved to modulate the flexibility of the tandem in solution. To further substantiate this notion, we show how constitutively activating mutations in the SH3–SH2 connector shift the assembly equilibrium toward the disassembled, active state. Based on a similar analysis of several constructs of the kinase complex, we propose that assembly is characterized by the progressive optimization of the protein's conformational energy, with little or no energetic frustration.

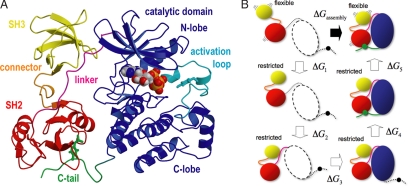
Modular binding domains within large allosteric enzymes play a key role in the regulation of signal transduction pathways in the cell. By virtue of their ability to engage a diverse range of interaction partners, they act as molecular switches turning different pathways on or off. This versatility arises, in part, from the integration of these small modules into multidomain assemblies that are able to adopt different spatial arrangements in response to specific stimuli (1). The functional importance of conformational plasticity in modular-protein assemblies is perhaps best exemplified by the Src tyrosine kinases, a family of enzymes involved in fundamental processes such as cell growth and adaptive immunity; dysfunctional Src kinase activity has also been associated with breast and colon cancers (2). Src-type kinases are membrane-anchored and comprise a tandem of binding modules, one SH3 and one SH2 alongside a catalytic domain. The activity of the kinase is inhibited after the assembly of the SH3 and SH2 modules with the catalytic domain (Fig. 1A), whereas disassembly of the SH3–SH2 tandem leads to activation (3). Regulation of Src depends on the reversible formation of this assembly and is thus a dynamic equilibrium process that is modulated by, among other factors, the interaction with other tyrosine kinases and phosphatases that target a tyrosine side chain at the C terminus of the catalytic domain (Tyr-527 in c-Src). Because this tyrosine side chain can bind to the SH2 domain, the inactive assembled state is favored by phosphorylation of the C-terminal tail, whereas dephosphorylation promotes the activation of the enzyme.

Fig. 1.

Modular assembly of Src tyrosine kinases. (A) Crystal structure of the Src-type tyrosine kinase Hck in the inactive, assembled state (7); the PP1 inhibitor has been replaced by an ATP molecule, as in entry 1AD5 (8). Molecular graphics throughout this work were rendered with Pymol. (B) Virtual thermodynamic cycle used for estimating the shift in the assembly equilibrium induced by mutations in the SH3–SH2 connector (see Results for description).

An intriguing aspect of the modular organization of allosteric enzymes involved in regulatory processes pertains to the functional importance of the interdomain linkers. It is commonly assumed that these short peptide regions merely serve to link the various modules along the polypeptide chain (4). However, there has been increasing evidence indicating that interdomain linkers can play a relatively complex functional role. In Src, for example, a cell growth assay illustrated how a triple glycine substitution in the SH3–SH2 connector rendered the enzyme constitutively active (5). Computer simulations of the molecular dynamics of the kinase complex in the inactive assembled state, in both the wild-type (crystallographic) and mutated (modeled) forms, revealed no significant structural differences upon mutation, but indicated that the dynamic coupling between the SH3 and SH2 domains was markedly reduced (5). Based on this result, it was proposed that the functional role of the connector is to confer rigidity to the regulatory tandem in the assembled state and that this rigidity is required to ensure the inhibition of the catalytic domain (the so-called “snap-lock” mechanism). Upon mutation of the connector, the inhibitory action of the tandem in the assembled state would be compromised by its increased dynamics, and the kinase would no longer be effectively down-regulated. Although such a kinetic view of allosteric regulation of Src is consistent with the experimental observations, seeking to explain the effect of the glycine substitutions solely on the basis of the assembled state assumes implicitly that the SH3 and SH2 domains are completely uncoupled in the disassembled (active) state of the enzyme. In other words, the conformational flexibility of the disassembled state is assumed to be already “maxed-out” in the wild-type protein, and, thus, the mutations in the SH3–SH2 connector would be expected to affect the assembled state only.

In this study, we aim to explore an alternative, and possibly complementary mechanism, based on thermodynamic and energetic considerations rather than kinetic. Specifically, we ask whether the mutations in the SH3–SH2 connector could enhance the activity of the enzyme also by affecting the assembly/disassembly equilibrium and, thus, the formation of the down-regulated complex. This leads to an important question, namely, whether the chemical detail in the linkers between modular domains may be tuned to modulate the energetics of the assembly process and thus enable appropriate regulation.

To assess this idea, we use free-energy calculations to characterize the conformational freedom and preferred organization of the SH3–SH2 tandem in several constructs of the Hck kinase where interactions with the catalytic domain are varied and where glycine substitutions are introduced in the SH3–SH2 connector. Based on these calculations, we quantify the shift in the assembly/disassembly process and point out possible experiments that could be carried out to validate or refute our proposal. This analysis also provides qualitative insights into the nature of the assembly process itself from a mechanistic and energetic perspective.

In summary, the present study provides a perspective not only into the specifics of tyrosine-kinase regulation, but also into the energetics governing the organization and assembly of multidomain proteins.

Results and Discussion

The Importance of the SH3–SH2 Connector for Regulation.

A possible approach to quantify the influence that mutations in the SH3–SH2 connector may have on the assembly/disassembly equilibrium and the activation of the enzyme is to directly simulate this reversible reaction, and evaluate how the populations of each state are affected upon mutation. Such simulation is, however, computationally prohibitive at the present time, as long as atomic-detailed models and explicit solvation are used. Alternatively, it is possible to formulate this problem differently and estimate the assembly free-energy shift upon mutation, ΔΔG_assembly = ΔG_{mut assembly} − ΔG_{WT assmebly}. This formulation, depicted in Fig. 1B, is based on the development of Wang et al. (6) for the computation of absolute binding free energies. The assembly process is separated into a series of virtual steps, each contributing a given free-energy change that can be computed from a simulation. These steps are: (1) the flexible, disassembled SH3–SH2 tandem is restricted to adopt a conformation like that in the assembled state but still disengaged from the kinase domain; (2–4) the restricted tandem binds to the SH2-kinase linker, the C-lobe of the kinase and the C-terminal tail, respectively; (5) the tandem is released from the conformational restriction to recover its full intrinsic flexibility while in the assembled state. The free energy of assembly, ΔG_assembly, is thus

This virtual thermodynamic cycle is advantageous because steps 2–4 are expected to be insensitive by the mutations in the SH3–SH2 connector. This is so because in steps 2–4, the tandem is structurally constrained (which rules out a dynamical effect) and also because the connector itself is distant from the interfaces being formed (which rules out an energetic effect). Thus, we can write ΔΔG_assembly as:

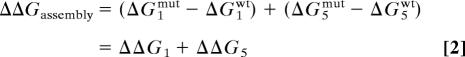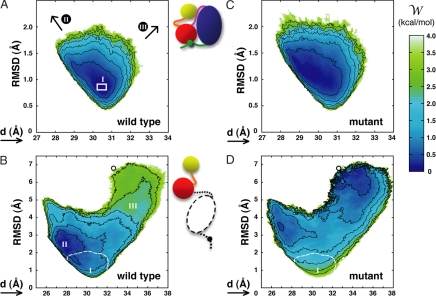
To estimate ΔG₁ and ΔG₅ for either the wild type or the mutant forms, it is necessary to characterize the conformational free-energy landscape of the SH3–SH2 tandem in isolation from the rest of the kinase as well as in the assembled state. To do so, we selected two conformational order parameters that monitor the arrangement of the tandem and calculated a two-dimensional potential-of-mean-force (PMF) surface using umbrella-sampling molecular dynamics simulations (see Methods). Specifically, these conformational coordinates are the distance d between the core region of each domain and their RMS deviation relative to the arrangement in Fig. 1A.

The resulting free-energy surfaces are shown in Fig. 2. We first examine the PMF surface of the wild-type SH3–SH2 tandem in the assembled form (Fig. 2A), because this serves as a control system. This is the down-regulated, inactive state of the kinase, where the arrangement of the SH3 and SH2 domains appears to be tightly configured by their interaction with the catalytic domain, the C-terminal tail, and the SH2-kinase linker (Fig. 1A). It is expected that the conformational freedom of the tandem will be restricted as a result of these interactions. More importantly, the minimum in the computed free-energy surface ought to correspond to the crystal structure, after taking into consideration thermal fluctuations. As shown in Fig. 2A, both expectations are fulfilled. The free-energy surface shows a narrow basin with a minimum around RMSD = 0.86 Å and d = 30.5 Å. As the arrangement of the domains is disturbed away from the minimum, the free energy increases steeply.

Fig. 2.

Potential-of-mean-force surfaces for the SH3–SH2 tandem, in the following constructs: wild-type, assembled state (A); wild-type, disassembled state (B); mutant, assembled state (C); and mutant, disassembled state (D). The mutant constructs include glycine substitutions of residues S138, E140, T141, and E142, in the SH3–SH2 connector. See Methods for definition of the reaction coordinates and further details. Contours (black lines) are plotted for 0.5-kcal/mol increments. The white box in A indicates the location of the four crystal structures in entries 2HCK and 1AD5 of the PDB (8). In B and D, the small circle locates the structure of the SH3–SH2 tandem from the Lck kinase in entry 1LCK (16). Note the change in the scale between graphs; to aid the comparison, the location of regions I, II, and III on the free-energy surfaces is indicated, and, for B and D, the 3.5-kcal/mol isocontour from the surfaces in A and C, respectively, is also shown (dashed white lines). These free-energy surfaces correspond to averages over 10 independent calculations. Standard deviations about these averages (<1 kcal/mol) are given in supporting information (SI) Fig. 4.

For the sake of clarity, two issues are worth noting in regard to the particular projection of the free energy along (RMSD, d). First, it is clear that as the distance between domains increases or decreases, the RMSD of the tandem must change concurrently. Hence, all PMF surfaces in this study display a V-shaped forbidden region that is delineated by the minimum possible RMSD value for a given value of d. This free-energy boundary arises as a result of the choice of projection and has no special mechanistic relevance. Second, it should be noted that the most probable RMSD value with respect to a three-dimensional reference conformation (here an x-ray structure) cannot be zero at T > 0, irrespective of the accuracy of the model. This is simply a consequence of nonlinearly growing density of states along the RMSD reaction coordinate.

The minimum in the free-energy surface shown in Fig. 2A is consistent with the available crystal structures of the Hck kinase. Among these, entry 1QCF (7) was chosen as our reference for the RMSD coordinate, because of its better resolution (2.0 Å). Comparison between this and the other four structures [Protein Data Bank (PDB) entries 2HCK and 1AD5, two molecules per unit cell (8)] yields RMSD values between 0.79 and 0.85 Å, in excellent agreement with the minimum in the PMF calculation for this state. We thus conclude that the current computational framework appears to be capable of providing an accurate description of the free-energy surface underlying the conformational flexibility of the SH3–SH2 tandem.

The assembly/disassembly equilibrium depends on the conformational freedom of the two end states. Thus, in Fig. 2B, we examine the free-energy surface of the wild-type SH3–SH2 tandem in solution. This construct is meant to represent the fully disassembled state, where, by definition, the regulatory tandem has no interactions with the rest of the kinase complex. Two striking observations can be made based on this result; first, it is clear that the intrinsic structural flexibility of the tandem is vastly greater than what can be inferred by inspection of the assembled-state crystal structure. Upon disengagement of the catalytic domain and the SH2-kinase linker, the tandem can adopt a wide range of conformations, which either bring the SH2 and SH3 domains closer together (left branch of the PMF) or further apart (right branch). However, despite the absence of any interactions with the rest of the kinase complex, the free-energy surface of the tandem is funneled toward conformations conducive to the association of the tandem with the kinase. That is to say, the amino acid sequence of the tandem, presumably within the SH3–SH2 connector, appears to be fine-tuned to funnel the search in conformational space toward the assembled, down-regulated state of the enzyme. Interestingly, the global free-energy minimum is shifted from the assembled-like arrangement toward more compact structures (RMSD ≈ 2.5 Å), yielding a “loaded-spring” character to the tandem in the assembled state. Nonetheless, the corresponding free-energy difference is less than ≈2 k_BT, according to our calculations, and thus the strain on the tandem upon assembly appears to be small.

To be able to estimate the assembly free-energy shift that may be induced by the mutations the SH3–SH2 connector, we now proceed to analyze the conformational freedom of the tandem carrying a quadruple glycine substitution similar to that probed by Young et al. (5) in Src. As shown in Fig. 2C, these mutations have a small effect on the conformational preference of the assembled tandem. Although the arrangement of the domains appears to be more dynamical (e.g., note the change in shape of the 0.5-kcal/mol contour), the conformational free-energy minimum remains essentially unchanged (shifting <0.1 Å). In fact, computation of -ΔΔG₅ through integration of the PMF surfaces in Fig. 2 A and C (see SI Text) results in a value of 0.4 kcal/mol. It is in view of this modest effect that we propose that consideration of the assembly equilibrium as a whole, rather than the assembled state alone, is also required to arrive at a compelling rationale that takes into consideration both thermodynamic and kinetic factors.

In contrast to its limited influence on the structural stability of the assembled state, the glycine substitutions in the SH3–SH2 connector have a dramatic effect on the conformational equilibrium of the disassembled tandem. As revealed by Fig. 2D, the free-energy surface is no longer funneled toward the assembled state but is, instead, a rather flat landscape. Thus, upon mutation in the SH3–SH2 connector, the tandem becomes much more flexible than in the wild-type form. Because of this greater flexibility, the probability of reaching conformations conducive to inactivation of the enzyme is much smaller than for the wild-type sequence. Specifically, integration of the PMF surfaces in Fig. 2 B and D yields a value for ΔΔG₁ of 2.7 kcal/mol. From this and the value of ΔΔG₅ derived previously, our estimate of the change in the free energy of assembly upon mutation is then ΔΔG_assembly ≈ 4 k_BT. This value corresponds to a shift in the assembled/disassembled population ratio of ≈98%. For the wild-type protein and a phosphorylated C-tail, it is estimated that the assembled/disassembled ratio is 98:2 (9, 10). According to our calculations, upon mutation of the SH3–SH2 connector, the assembly equilibrium in the mutant protein would approximately shift to a 1:1 ratio. Thus, it seems plausible that the constitutive activation of the catalytic domain reported by Young et al. (5) for Src mutants is to a significant degree because of this marked shift in the assembly/disassembly equilibrium. This effect would add to the loss of dynamic coupling within the regulatory tandem proposed in that same study and its potential impact on the flexibility of the catalytic domain and, thus, on the kinetics of the activation process. Lastly, it is worth noting that the free-energy surfaces in Fig. 2 B and D are also informative (in particular their right-hand branch) of the conformational freedom of the tandem in state where the SH2 domain is bound to the C-terminal tail, whereas the SH3 domain is disengaged from the SH2-kinase linker. This partially disassembled state would also be stabilized by the mutations in the SH3–SH2 connector.

Fine-Tuning of the SH3–SH2 Free-Energy Funnel.

As described above, the free-energy funnel encoded within the sequence and structure of the regulatory SH3–SH2 tandem, and, in particular, in the short connector, appears to be a practical solution to the problem of conformational search faced by the kinase complex during down-regulation. This suggests that multidomain complexes could have evolved a similar strategy for their self-assembly as that evolved by each individual domain for their own folding (11). The notion that isolated SH3–SH2 tandems are flexible and yet retain a propensity to adopt conformations comparable to that characteristic of the assembled state is consistent with NMR and crystallographic analyses. For example, based on NMR studies of the SH3–SH2 tandem of the Fyn tyrosine kinase (12), Ulmer et al. concluded that in solution the tandem is flexible, and that its arrangement appears to be modulated by the SH3–SH2 interface. In their model, derived from residual dipolar couplings, this arrangement not dramatically different from that in the crystal structure of assembled Src (13). Considering the flexibility of the tandem and the fact that the NMR data corresponds to an ensemble average, we interpret these findings to mean that the tandem encodes the aforementioned propensity to adopt conformations conducive to the assembled form. Consistently, the crystal structure of the Fyn SH3–SH2 tandem (14) was found to be also very similar to that of the Src tandem in the full-length assembled state (see SI Fig. 6).

From a fundamental standpoint, it would be of great interest to understand how the primary sequence influences the conformational free-energy landscape of Src-family SH3–SH2 tandems, as a means to rationalize slight but important regulatory differences (14). Src and Fyn are identical in sequence around the SH3–SH2 connector (see SI Fig. 5), which helps explain the similarities observed between the solution and crystal structures of the Fyn tandem and that of the assembled Src complex. Similar analyses of the Lck tandem by NMR (15) and crystallography (16), which is unique in the Src family because it includes two proline side chains in the SH3–SH2 connector, yield noticeably different arrangements from those of the Fyn tandem, especially in the crystal environment. To our knowledge, no analogous structural data are as yet available for Hck and Lyn, which also comprise a family subgroup sequence-wise. Thus, although a direct comparison across sequences may not be meaningful, we propose that the funneling of the free-energy landscape hypothesized here for Hck may be a common feature of the Src family, albeit the details and fine-tuning of this conformational bias may differ among members.

In the case of Hck, it is possible to rationalize the free-energy funnel at the level of the primary sequence. Inspection of the configurations sampled during the simulations indicates that the clustering hydrophobic groups in the SH3–SH2 interface make an important contribution (SI Fig. 7A). These clusters involve Val-84, Leu-86, and Ala-134 in the SH3 domain, Val-136, Glu-140, and Thr-141 in the SH3–SH2 connector, and finally Phe-145 and Lys-147 in the SH2 domain (numbering as in P08631 Swiss-Prot annotation). The significance of these hydrophobic clusters is confirmed upon analysis of the corresponding van der Waals interaction energies along the reaction coordinates used for the PMF surfaces reported above (SI Fig. 7B). It is clear from this calculation that the free-energy funnel of the tandem is well correlated energetically and structurally with the formation of these clusters. A similar analysis reveals that electrostatic interactions mediated by the side chain of Ser-138 also appear to be key (SI Fig. 7 C and D). This side chain is located at the junction between the SH3 and the SH3–SH2 connector and may form hydrogen bonds primarily with the backbone of Arg-135 and the side chain of Glu-140, which may also salt-bridge with Lys-147. These clear correlations help rationalize the impact of the glycine substitutions described in the previous section, in that they remove the hydrophobic or H-bonding potential of several of these seemingly important side chains in both Src and Hck, namely Ser-138, Thr-141, and Glu-140 [Glu-142 was also mutated in our study following Young et al. (5)].

Possible Experimental Validation.

Further experimental work is now required to validate or refute our proposal with regard to the role of the SH3–SH2 connector in the regulation of the kinase. Biophysical and biochemical experiments aimed at characterizing the assembly equilibrium as well as the catalytic activity of the kinase would be particularly informative. For example, structural models of the regulatory tandem derived from NMR have been shown to be sensitive to the sequence in the connector (14, 15); low-resolution structural data for the complex may also be obtained through small- or wide-angle x-ray scattering experiments (17). Our expectation is that the SH3–SH2 connector mutations would enhance the population of the more disordered or extended conformations of the tandem and the complex, with a concomitant impact on the kinase activity.

Whether restoring the assembly/disassembly equilibrium in the mutant protein is sufficient to recover regulation of the enzyme is a key question. Thus, it would be of interest to modulate the intramolecular interactions between the SH3 and SH2 domains and their counterparts while simultaneously introducing the Gly substitutions in the SH3–SH2 connector. If the perspective suggested by the computations is correct, the introduction of a high-affinity substitution in the SH2-kinase linker should recover the wild-type assembly equilibrium partially or fully. SPR experiments indicate that the EWPPQPPS sequence developed by Lerner et al. (18) may be a suitable candidate. Substitution of the high-affinity sequence pYEEI in the C-terminal tail (19) may also have a modulatory effect, but it is less likely to restore the regulation of the kinase by itself. As mentioned above, we anticipate that the SH3–SH2 connector mutations stabilize not only the fully disassembled state but also a partially disassembled state where the SH3 domain is disengaged from the SH2-kinase linker but the SH2 domain remains bound to the C-terminal tail. Because such a state is most likely also up-regulated (20), strengthening of the interaction between the SH2 domain and the C-terminal tail may not be sufficient to counter the effect of the SH3–SH2 connector mutations on the regulation of the kinase.

Step-Wise Assembly of the Complex.

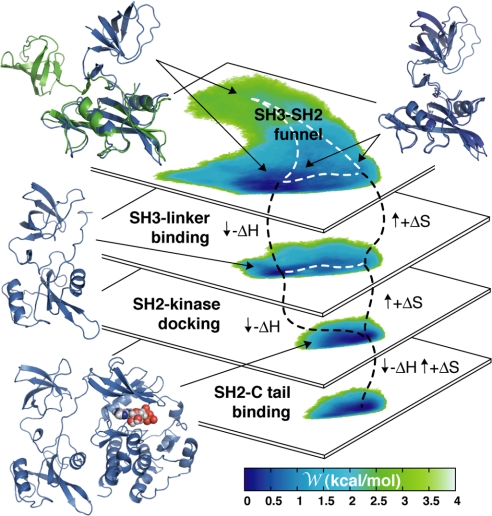
In this last section, we try to exploit the information provided by the different free-energy landscapes to gain further insights into the energetics and mechanism of the assembly process. In particular, we address two open questions with regard to the interactions of the tandem with the rest of the kinase complex. The first issue pertains to the observation that the binding affinity of the wild-type phosphorylated C-tail is per se insufficient to rationalize the degree to which the activity of the enzyme is suppressed by phosphorylation (10, 21). Rather, the assembly of the complex appears to rely largely on conformational preferences elsewhere in the protein, which ensure that the SH2 domain and the C-terminal tail become proximal, thus increasing the effective local concentrations of both binding partners. Prompted by this notion, it is reasonable to ask whether the assembled form depicted in Fig. 1A is a metastable state even in the absence of the interaction between the SH2 domain and the C-terminal tail. The second question pertains to the role of the polyproline SH2-kinase linker during assembly/regulation. As for the C-terminal tail, this is a relatively weak interaction (18, 22) but may serve to mediate the formation of a metastable state during assembly. Therefore, we explore the extent to which binding to the SH2-kinase linker restricts the conformational freedom of the SH3–SH2 tandem.

To address these questions, we carried out a conformational free-energy calculation, analogous to those reported above, for two additional constructs, namely one of the assembled form of the complex lacking the C-terminal tail, and one of the isolated tandem with the SH2-kinase bound to the SH3 domain. The interactions of the tandem with the rest of the complex were not enforced in either of these calculations, despite which no spontaneous disassociation was observed (see SI Fig. 8). Thus, these PMF surfaces inform us as to whether or not these constructs correspond to local free-energy minima and, if so, of their characteristics. The resulting data are shown in the diagram in Fig. 3, alongside the wild-type PMF surfaces from Fig. 2. As far as the assembled state lacking the C terminus is concerned (second from bottom), three observations are noteworthy: first, it is clear that the interactions between the SH2 and the C-lobe of the catalytic domain, and between the SH3 and the SH2-kinase linker, are sufficient to define a local minimum in the conformational free-energy surface of the tandem; second, that this minimum is structurally indistinguishable from that observed for the full kinase (i.e., Fig. 2A); and third, that release of the C-terminal tail while in the assembled state of the kinase increases the conformational freedom of the SH3–SH2 tandem only very slightly. In summary, this calculation suggests that, during assembly/disassembly, the kinase transiently resides in the state represented by this construct. This result is in agreement with the notion that the association of the phosphorylated C-terminal tail and the SH2 domain is promoted by conformational preferences arising from other interactions within the protein and not solely by their binding affinity.

Fig. 3.

Diagrammatic representation of a putative assembly pathway. The conformational free-energy surface of the SH3–SH2 tandem is shown for each step, alongside representative snapshots of the molecular structure (constructs I through IV from bottom to top; see Table 1). The methodological details for the computation of the PMF surfaces of constructs II and III (in the middle) are analogous to those of constructs I and IV, shown in Fig. 2.

With regard to the linker-bound SH3–SH2 construct (second from top in Fig. 3), it is worth noting how the PMF surface of the tandem is unchanged relative to the linker-unbound form, except for the fact that the right-hand branch of the PMF (which corresponds to extended conformations of the tandem) is now forbidden. Therefore, it appears that the role of the SH2-kinase linker may be, as for the funnel itself, to guide the tandem along the assembly reaction by reducing its conformational freedom. Because of the weakness of the interaction between the SH3 domains and the native polyproline linker (22), this is probably a short-lived state. However, the fact that the activity of the kinase is increased upon perturbation of this interaction (23), and, more recently, the crystal structure of a partially disassembled state of Src (24), illustrate that this is an intermediate state of importance for the appropriate down-regulation of the enzyme.

In summary, our analysis indicates that the sequence of the short SH2–SH3 connector in Src can affect the equilibrium of the assembly/disassembly process and the formation of the down-regulated state in a nontrivial way. The assembly of the SH3–SH2-kinase complex is, as far as the conformational free energy of the protein is concerned, mostly a downhill process, where interactions at the interfaces between the SH3, SH2, and kinase domains are progressively configured in a step-wise manner. By contrast, the disassembly of the complex seems to be mostly driven by an increase in conformational entropy. In the language of protein folding, the assembly process appears to not be energetically frustrated (25), i.e., it does not encounter dead-end low-energy states that preclude further progress as the complex assembles. From a methodological standpoint, this finding may provide a justification for the study of the assembly process by using topological models that encode only the native contacts, such as in Go-like representations (26); such simulations are expected to provide further insights into the mechanism of assembly and disassembly of the kinase complex.

Methods

Calculations of the PMF were made. For all systems the free-energy surface was determined along two conformational order parameters. These are the distance between the two domains d, and the RMSD of the tandem, with respect to the assembled-state arrangement, specifically that in PDB entry 1QCF (7). Whereas the RMSD coordinate monitors the deformation of the structure of the tandem, the distance coordinate describes whether this deformation results in its elongation or contraction. The definition of these conformational coordinates involves only the backbone atoms of a subset of ≈20 core residues in each domain. The free-energy surface along these two coordinates, or PMF, was determined through umbrella-sampling molecular dynamics simulations (27), using CHARMM (28). To remove the bias in the sampling, we used the WHAM method (29, 30). Further details are given in Table 1 and in SI Text and SI Figs. 9–12.

Table 1.

Summary of simulation systems and PMF calculations

System name*	Approx no. of atoms	No. of PMF	No. of windows	kRMSD†	kd†	Sampling per window, ns	Sampling total, ns	Approx CPU hours‡
I	47,500	10	17	4.2	4.2	1	170	136,000
II	47,500	10	28	4.2	4.2	1	280	224,000
III	39,000	10	26	4.2	4.2	1	260	190,000
IV	55,000	10	85	4.2	4.2	1	850	1,150,000
I-4G	47,500	10	17	4.2	4.2	1	170	136,000
IV-4G	55,000	10	85	4.2	4.2	1.5	1,275	1,725,000
Total								3,500,000

The total of all sampling totals was 3 μs.

*The constructs are as follows: I, wild type, full-length assembled state; II, wild type, assembled state with truncated C-tail; III, SH3–SH2 tandem with SH2-kinase bound to SH3 domain; IV, SH3–SH2 tandem only; I-4G and IV-4G are the same as I and IV, except that they include a quadruple glycine substitution in the SH3–SH2 connector. Ten independent PMF calculations were carried out in each case. All simulations used the CHARMM27/CMAP force field (31), PME electrostatics, periodic boundary conditions, NPT ensemble at 300 K and 1 atm with a 150 mM NaCl solution.

^†Force constants for umbrella bias potentials in kcal mol⁻¹Å⁻².

^‡The actual wall-time was 15–20% greater than the CPU time. These simulations were performed by using Linux clusters at the National Center for Supercomputing Applications, the Weill Medical College of Cornell University (New York, NY) and the University of Chicago/Argonne National Laboratory (Argonne, IL).

Abbreviation

PMF

potential-of-mean-force.