Abstract
Chromatin function in vivo is intimately connected with changes in its structure: a prime example is occlusion or exposure of regulatory sequences via repositioning of nucleosomes. Cell extracts used in concert with single-DNA micromanipulation can control and monitor these dynamics under in vivo-like conditions. We analyze a theory of the assembly–disassembly dynamics of chromatin fiber in such experiments, including effects of lateral nucleosome diffusion (“sliding”) and sequence positioning. Experimental data determine the force-dependent on- and off-rates as well as the nucleosome sliding diffusion rate. The resulting theory simply explains the very different nucleosome displacement kinetics observed in constant-force and constant-pulling velocity experiments. We also show that few-piconewton tensions comparable to those generated by polymerases and helicases drastically affect nucleosome positions in a sequence-dependent manner and that there is a long-lived structural “memory” of force-driven nucleosome rearrangement events.
Keywords: chromatin assembly, chromatin disassembly
In the nucleus, chromatin undergoes continual structural rearrangement. Chromatin fibers have been observed to undergo large-scale diffusion-like motions (1, 2) and rapid local motions (3), possibly caused by the action of processive enzymes such as nucleic acid polymerases and helicases. At smaller scales, fluorescence recovery after photobleaching studies in vivo have shown histones to be mobile to some degree (4). Both large-scale conformational and nucleosomal rearrangements are biologically important, e.g., through their influence on gene regulation (5, 6).
These in vivo results are complemented by biochemical experiments indicating that DNA can be transiently released from nucleosomes (7, 8) and recent DNA-pulling experiments that show nucleosome disruption by forces ranging from a few to tens of piconewtons (9–12). Single-nucleosome or single-chromatin-fiber experiments carried out in protein-free buffers provide useful quantifications of histone–DNA interaction strengths and force-driven opening rates. However, affinities and rates obtained from studies of isolated fibers may be very different relative from those occurring in vivo because of the very high levels of chromatin-acting enzymes found in the cell. This issue can be addressed by combining cell extracts with single-molecule methods for reading out folding and unfolding of protein–DNA complexes in real time, which permits observation of single-chromatin fiber dynamics under conditions close to those found in vivo (10, 13–16).
Here, we present a theory of chromatin fiber dynamics in Xenopus egg extracts, based on assembly, displacement, and lateral diffusion (“sliding”) of nucleosome units. Recent experimental data for sequence dependence of nucleosome affinities (17), combined with measurements of single-chromatin fiber assembly and disassembly in Xenopus egg extracts, constrain the theory sufficiently to determine force-dependent nucleosome on- and off-rates, the sequence-dependent free energy associated with nucleosome placement, and the nucleosome sliding diffusion constant. Without further input the theory simply explains why constant-force experiments require only ≈4 pN to displace nucleosomes (16), whereas rapid-pull experiments observe a wide range of forces up to 40 pN during nucleosome disruption (10). We also show that moderate (2–5 pN) forces perturb nucleosome distribution in a sequence-dependent manner and that a fiber possesses a “memory” of disturbance of its nucleosomes.
Nucleosome Dynamics in Xenopus Egg Extracts
We consider assembly and disassembly of chromatin fibers by using Xenopus egg extracts (18, 19) onto multikilobase DNAs, where end-to-end extension of the DNA is measured as a function of time, with known forces applied to the fiber (10, 13, 14, 16, 20). Here, we focus on ATP-independent processes that dominate early stages of chromatin assembly and can be studied in extracts depleted of ATP (16, 21). At low force, reduction of extension in time occurs as nucleosomes are formed, because the ≈150 bp wrapped around each nucleosome reduces the overall fiber extension by a length l ≈50 nm per nucleosome (10, 14, 16). After assembly, high forces cause nucleosomes to unravel, leading to observations of quantized increases in end-to-end distance.
A basic feature of any model of such experiments is addition and removal of nucleosomes, leading to appearance and disappearance of length ≈ l. We will begin by determining force-dependent nucleosome on- and off-rates from constant-force experiments in Xenopus egg extracts, where reversible assembly–disassembly occurs (14, 16). These on and off events can be broken into two-step association and dissociation cascades, corresponding to sequenced placement or removal of 2× (H3 + H4) and 2× (H2A + H2B) onto DNA by nucleoplasmin and NAP-1 (13); we note that experiments in egg extracts are dominated by 50-nm events (10, 16, 22), indicating that it is reasonable to treat these cascades as single events.
Placement of nucleosomes during the early phase of an assembly reaction will quickly eliminate the ≈l-sized regions of naked DNA necessary for further assembly. However, if nucleosomes are able to diffuse laterally, a slow reorganization and further assembly can be expected to occur. Despite experiments suggesting that nucleosome sliding occurs (23) and extensive theoretical modeling (24, 25), quantitative measures of nucleosome sliding diffusion rates have not been forthcoming. Intriguingly, a recent study indicates that the ATP-independent histone chaperone NAP-1, which is present in Xenopus extracts, stimulates nucleosome sliding (26). We thus consider nucleosome sliding diffusion with an objective of determining its rate.
Nucleosome positions along DNA are known to be sequence-biased. A recent study has established a quantitative model for nucleosome positioning by sequence (17). We incorporate this model into our theory, with the objectives of first determining the role of sequence in chromatin assembly and disassembly, and second, to permit models of sequence-driven nucleosome positioning to be tested with single-DNA studies with varying-sequence molecules. Our model therefore depends on nucleosome on, off, and sliding rates with sequence and force dependence. We show how existing experimental data and thermodynamic considerations constrain these rates.
Theory
We consider DNA as a 1D lattice of N0 base pairs (molecule length L0 = N0 × 0.34 nm) along which nucleosomes can adsorb, desorb, and diffuse. Sequence effects are modeled by using a nucleosome positioning potential energy Vi as described by Segal et al. (17) [the exponential of this potential, exp(−Vi/kBT) is proportional to the probability of finding a nucleosome starting at base pair i in the limit of low nucleosomal coverage of DNA]. The result is a type of “random sequential adsorption” (27) of particles along the line, subject to a heterogeneous sequence potential, with particle dissociation and sliding diffusion.
Nucleosome Addition and Removal.
Nucleosomes can adsorb at any sterically permitted location on the DNA at rate ron. Adsorption is presumed to result in formation of a chromatosome covering 168 bp of DNA (histone octamer + linker histone) (21). We consider this, less a small correction for thermal fluctuations, to be the experimentally measurable change in end-to-end distance. Depending on the way nucleosomes are packed in 3D space there is a certain length per nucleosome that is not accessible by the other nucleosomes because of steric hindrance; We estimate this amount of additional “blocked” DNA to be ≈7 bp per nucleosome. Thus, when n nucleosomes are present we suppose experiments will observe “loss” of the equivalent of n × 168 bp of DNA length, with 175n bp of DNA inaccessible for other nucleosomes. On an N0-bp DNA, the maximum number of nucleosomes that can be assembled is thus N0/175 (18).
The overall average value of the potential Vi was not determined by ref. 17, because only relative probabilities for nucleosome occupation at different DNA sites were measured. This average value can be obtained from single-DNA experiments in Xenopus extracts, using the observed reversibility of fiber assembly for forces f >3.5 pN (16). At the 3.5-pN “stall force,” the mechanical work done (f × l) equals the average value of −Vi. For l = 49 nm [a small reduction of the length loss l relative to the lost sequence length caused by thermal fluctuations is present at 3.5 pN (28)], the average value of Vi in Xenopus extracts is 〈Vi〉 ≡ V0 = −42 kBT.
More generally, the effect of force can be included in the free energy per nucleosome as a shift from Vi to Vi + fl (29). Given the experimentally observed reversibility and this free-energy difference, the adsorption and desorption rates must satisfy the Boltzmann equilibrium condition
This one constraint does not fully determine the individual on- and off-rates. We use the simplest model consistent with the energy difference between on- and off-states:
Only the two constants r0 and α remain to be specified: the rate r0 is the on-rate at zero force, while the length α describes the position of the transition state between nucleosome assembly and disassembly as a fraction of the total extension change l (30). In Results, we discuss how r0 and α are constrained by experiment.
Nucleosome Sliding.
The ratio of rates for sliding of a nucleosome from DNA site i to site j (di→j), and that of the reverse event from j to i, must satisfy the Boltzmann relation:
Because this sliding transition involves many microscopic intermediate steps, it will likely depend primarily on the potential difference between the initial and final state, i.e., as
Because Vi − Vj has an average value of zero, the quantity D(f) can be taken as a global estimate of the force-dependent nucleosome diffusion constant.
Schiessel et al. (24) have proposed a mechanism and have made quantitative predictions for thermally activated nucleosome sliding diffusion at zero force [D(0); see supporting information (SI) Appendix]. Thermally excited unwrapping and readsorption events known to occur in nucleosomes (7, 8) can cause small intranucleosomal DNA loop-bulges of length ΔL ≈ 10 bp, which can transfer DNA length through a nucleosome (24, 25). In Xenopus extracts the presence of histone chaperones likely assists in this or other pathways for sliding diffusion of nucleosomes (26, 31).
We have generalized the Schiessel model to the case where the nucleosomal DNA is under tension f, causing thermally activated loop-bulge events to require additional mechanical energy f × ΔL. This additional energy cost suppresses the diffusion rate below its zero-force value to:
We require the free energy per length for displacement of DNA from the octamer surface. We use the value appropriate to Xenopus egg extracts of 42 kBT per 147 bp of DNA contact; for tensions of 1 pN (a force value to be considered in detail in Results) this gives D(f = 1 pN) = 3 bp2/s. This result implies a time for a nucleosome to move an appreciable fraction of a nucleosome length over ≈1-h time scale; we note that the zero-force value is approximately a factor of two larger. In experiments where histone chaperones are absent, the DNA–histone interaction free energy may be appreciably larger, which will greatly reduce D(f) (see SI Appendix).
Calculation Method.
We have studied this model by using the Gillespie method (32), where at each step of the computation we stochastically compute the time interval until the next on, off, or slide event. The calculations begin, like experiments, with naked DNA: at time t = 0, there are no nucleosomes on the DNA. Experimentally the overall extension L(t) is measured, which evolves in time dependent on force applied to the DNA, as nucleosomes adsorb, desorb, and diffuse. At time t there are n(t) nucleosomes bound on to the DNA, wrapping 168n bp of DNA. Experiments essentially measure the naked DNA length, N0 − 168 × n(t) but converted from base pairs to extension, as
where x(f) is the known force-dependent extension per base pair for dsDNA (see SI Appendix). We have supposed that the DNA elasticity has no dependence on the distribution of internucleosomal gaps, justified by the near-complete DNA extensions driven by pN forces of interest here.
Constant Force Versus Constant Pulling Rate Experiments.
DNA stretching experiments fall into two broad classes, depending on whether constant forces are applied or end-to-end extension is increased uniformly with time (“constant velocity”). In constant-force experiments, end-to-end extension is measured as a function of time; our theory naturally describes chromatin assembly and disassembly for constant forces, which include experiments with magnetic tweezers (16). Such experiments are characterized by “plateaus” of extension separated by sharp transitions. In constant-velocity experiments, the end-to-end extension is increased at a constant rate, and force is measured as a function of time. Our model can be used to describe constant-velocity experiments [e.g., many optical tweezer experiments (10)] by iteratively recomputing force as extension increases. Constant-velocity experiments typically produce large force “spikes” of magnitudes that increase with pulling velocity.
Results
Assembly Dynamics Determine On-Rates and Sliding Rates.
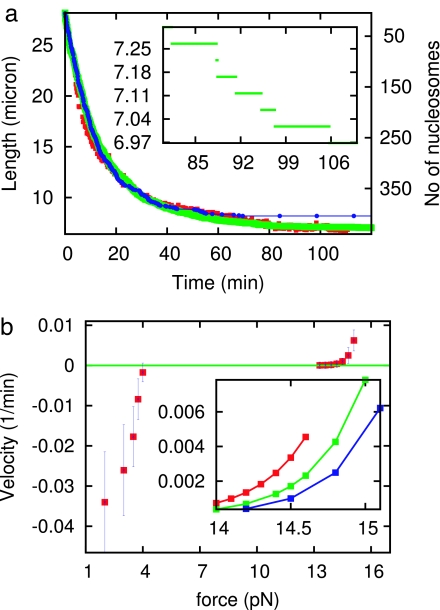
We first show how experimental data for assembly of chromatin against a 1-pN force can be used to determine the on-rates and sliding rates. We consider an initially naked dimer of λ-phage DNA (N0 = 2 × 48,502 = 97,004 bp, ≈33 μm length), under f = 1 pN, as studied experimentally (16). As time progresses, nucleosomes assemble, and the end-to-end extension decreases. Fig. 1a compares experimental data (red) (16) with our theory without sliding (blue) and with sliding (green).
Fig. 1.
Constant-force nucleosome dynamics. (a) Nucleosome assembly onto a 97-kb DNA: end-to-end length (left axis labels) and nucleosome number (right axis labels) of DNA obtained from our theory including sliding (green), compared with experimental data reported in ref. 16 (red). With no sliding (blue), the initial and final dynamics cannot simultaneously follow the experimental result. (Inset) Higher-resolution result for theory showing individual nucleosome assembly steps. (b) Force velocity of assembly and disassembly reactions: rate of end motion at the point where the fiber reaches extension of 2/3 of the DNA contour length L0, normalized by DNA contour length, is plotted. Velocity reaches zero at a stall force ≈3.5 pN. The prominent plateau in velocity between ≈4 and 13 pN is a result of the energy barrier separating assembled and disassembled nucleosome states. (Inset) Detail of force-velocity curves during disassembly following assembly reactions run to end-to-end extensions of L = 0.35 L0 (red), L = 0.3 L0 (green), and L = 0.24 L0 (blue); the disassembly dynamics display a memory of the initial assembly reaction.
Given the 3.5-pN stall force of the assembly reaction (16), and the Boltzmann relation between on- and off-rates (Eq. 1), it follows that the ratio of off- to on-rates at 1 pN is of ≈exp(−2.5 pN·50 nm/4.1 pN·nm) ≈10−14, i.e., at 1 pN nucleosomes are never removed after being assembled. The initial decay (t < 20 min) is thus caused by assembly of isolated nucleosomes and determines the on-rate as ron (1 pN) = 1.0 × 10−3 s−1. Sliding plays little role at early times; our theory with and without sliding produces the same, first-order (single exponential) decay for t < 40 min.
For later times (t > 40 min) experiment shows a new, slow terminal decay regime. Our theory without sliding cannot produce this behavior: without sliding the assembly reaction follows a very nearly first-order time course, governed by “jamming” that occurs during deposition of particles on the line for ≈75% coverage (27). However, inclusion of sliding at the rate D = 5 bp2/s, close to that predicted from the Schiessel model (24) including the effect of the 1-pN force, produces the terminal slow decay observed experimentally.
Fig. 1a Inset shows higher detail for the calculated time course, showing sharp nucleosome addition “steps” that correspond to average extensions after ≈200-nm amplitude thermal fluctuations are averaged out. These steps would be difficult to observe during assembly reactions onto long 97-kb molecules, but could be observed for shorter, few-kilobase DNAs.
Alternatively, it has been suggested that nucleosomes may slide via 1-bp steps by using a twist-defect mechanism (33, 34). However, we find that sequence-dependent potential highly suppresses the 1-bp sliding as discussed in ref. 34. We conclude that the 1-bp twist-defect diffusion (34) cannot explain the late-time dynamics seen experimentally (see SI Appendix).
Determination of Off-Rates.
After determination of the on-rates and sliding rates at 1 pN, our theory needs only one additional on- or off-rate at some other force for both r0 and α of Eq. 2 and therefore all of the dynamics of our theory at all forces to be determined. Experimental data for assembly as a function of force (16) overdetermine the theory; however, choosing r0 = 12 s−1 and α = 0.75 leads to assembly and disassembly dynamics in accord with experiment for all forces, summarized in the “force-velocity” relation shown in Fig. 1b. For forces <3.5 pN this graph shows the rate of contraction of extension with time (velocity), at the point where the end-to-end extension reaches 2/3 of L0 (this quantity is normalized by molecule length L0 to provide a result that is independent of L0). The assembly rate drastically increases in magnitude as force is reduced.
For forces >3.5 pN, positive velocities represent disassembly; these are measured after assembly under a 1-pN force to an extension of 1/3 of L0, by increase of force, and then measurement of rate of disassembly at the point where extension reaches 2/3 L0 (16). The experimental result of a very slow disassembly over the force range 4 to 10 pN is produced by the theory by the force dependence of the on-rates (Eq. 2), and the Boltzmann constraint (Eq. 1). Above 10 pN experiment and theory report a rapid increase in disassembly, indicating that the force level corresponds to the point at which the energy barrier to disassembly is being overcome by mechanical force; the parameter α generates this kinetic behavior. From the relation roff = ra exp((-εb + V0 + f(1 − α)l)/kBT), we compute the energy barrier (11), εb = 24 kBT, which is in addition to the binding energy V0. Here, we have used the attempt rate ra = 107 s−1 (11, 20); roff is obtained from the force-velocity curve. We have also computed the zero force on rate as ron(0) = 12 s−1.
Disassembly Dynamics Display Memory of Nucleosome Configuration.
The assembly (negative) rates shown in Fig. 1 are unique, given the naked-DNA initial condition. However, the disassembly rates display more complex behavior, because the initial condition for disassembly is a partially or completely assembled fiber; the slow internal reorganization dynamics of the fiber gives rise to a long memory of the initial condition, unexpected given the purely first-order nature of the basic kinetic events. To illustrate this, Fig. 1 shows disassembly rates measured at L = 2/3L0 given different initial densities of nucleosomes [L = 0.35L0 (red); L = 0.3L0 (green); L = 0.24L0 (blue)]. When the initial fiber nucleosome assembly is run longer to achieve a higher density and compaction, the subsequent disassembly is slower. This effect is caused by a combination of sliding and sequence, which permit more compact fibers to have significantly more stable nucleosomes, which are more resistant to subsequent disassembly.
Although sequence-dependent nucleosome positioning generates slower disassembly of more compact fibers, one might ask whether nucleosome–nucleosome interaction could contribute to this effect. We found that adding nucleosome–nucleosome interactions of the expected ≈2–3 kBT energy (9) do not change the dynamics; the sequence-dependent binding potential is so large (≈42 kBT) that addition of a few kBT has little effect.
Prediction of Sequence Effects for Constant-Force Experiments.
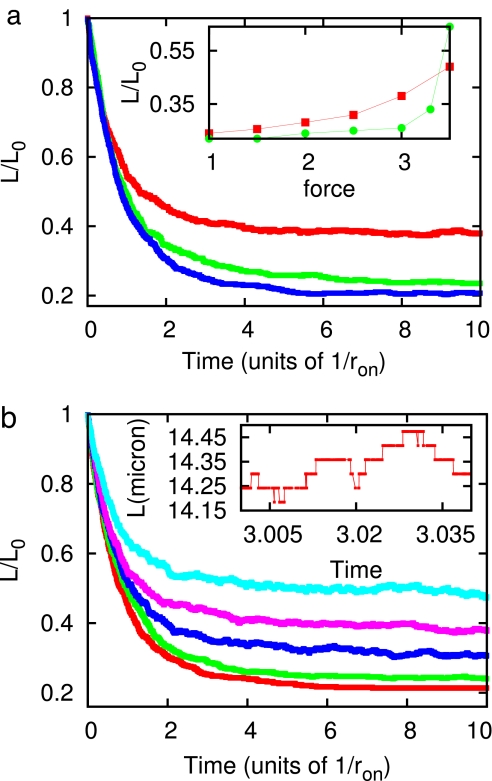
A number of experimentally verifiable effects appear as a result of the sequence dependence of the nucleosome binding potential Vi. The sequence inhomogeneity leads to inhomogeneity in nucleosome assembly onto naked DNA; the effect of this can be readily observed during chromatin assembly against tensions near to ≈3.5 pN. Fig. 2a illustrates this effect for three theoretical assembly reactions run against 3-pN forces, with equal average binding free energy V0 = −42 kBT and therefore equal sequence-averaged stall forces, but with different sequence properties. For λ-DNA sequence (Fig. 2a, red curve) the reaction reaches a final nucleosome density that is much below (a final extension much above) that achieved for a homogeneous potential (i.e., Vi = V0) of the same average binding free energy (Fig. 2a, blue curve). This effect arises from the strong sequence contrast between the left and right portions of λ-DNA; nucleosomes on the left GC-rich half are significantly less well bound, to the degree that at 3.0 pN, nucleosomes are not stable over much of the left half of the molecule. By contrast, in the homogeneous-sequence calculation at 3.0 pN, nearly the whole molecule becomes filled by nucleosomes. Fig. 2a (green curve) shows the prediction for a piece of yeast chromosome (chromosome II of Saccharomyces cerevisiae; constructed by a repeat of two 20-kb pieces, from nucleotides 265000 to 285000, GenBank accession no. NC001134). According to this prediction, the yeast DNA assembles to a more compact form at 3 pN, compared with λ.
Fig. 2.
Predictions of our model. (a) Sequence dependence of nucleosome assembly, for λ-DNA sequence (red curve), a piece of S. cerevisiea chromosome II (green curve), and homogeneous sequence (blue curve) at f = 3 pN. (Inset) Final measured length (normalized to the t = 0 naked DNA length) as a function of force with heterogeneous sequence (red squares) and homogeneous sequence (green circles). (b) Dynamics of assembly of nucleosomes onto λ-DNA for different values of external force. The curves represent 1 pN (red), 2 pN (green), 2.5 pN (blue), 3 pN (pink), and 3.5 pN (light blue). (Inset) Higher-resolution plot for f = 3 pN. Note the discrete steps corresponding to the addition and removal of nucleosomes.
Fig. 2b illustrates the strong force dependence of assembly onto λ-DNA. As force varies from 1 to 3.5 pN (red, 1 pN; green, 2 pN; blue, 2.5 pN; pink, 3 pN; light blue 3.5 pN), the reaction reaches a well defined final length varying from 0.2 to 0.5 of the naked DNA extension at that force. Fig. 2a Inset compares those final lengths for λ-DNA (red) and homogeneous case (green); for λ-DNA the final length varies slowly with force, as a result of different forces destabilizing different groups of nucleosomes. By contrast, the homogeneous case shows a force-width of the filling of only about kBT/l ≈0.1 pN as expected from thermodynamic considerations (29).
Another feature of the assembly reaction for a highly inhomogeneous sequence potential is shown in Fig. 2b Inset. During assembly of nucleosomes onto λ-DNA, large fluctuations of extension can be observed for tensions of 3 pN. For forces from 2 to 3 pN there are many marginally stable nucleosomes that dynamically assemble and disassemble. This effect is absent in the homogeneous potential case when one is >0.2 pN away from the mean stall force.
Kinetic Explanation of Large Nucleosome Displacement Forces Observed During Constant Pulling Rate Experiments.
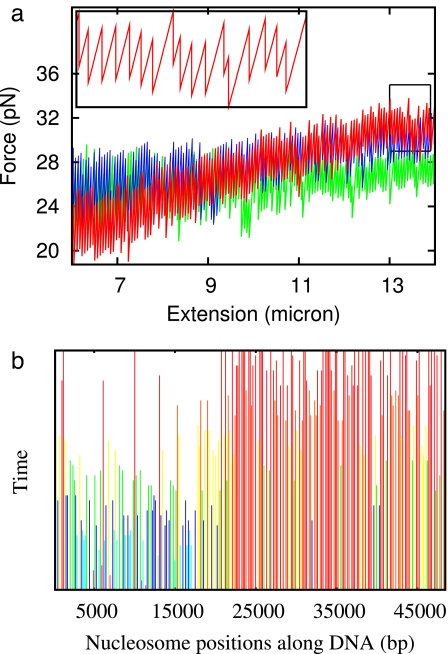
Experiments where the extension of a piece of chromatin is increased with time at a constant rate (constant velocity) observe nucleosome disassembly forces at forces from 10 to 40 pN (10, 11, 35), much higher than the few pN expected from thermodynamic considerations (29). It has been speculated that this result stems from the rapid pull rates in such experiments that usually force full extension of the DNA over 1 or 2 min (10, 11, 35).
Our theory can describe constant-velocity pulling experiments, by using the known extension per base pair x(f) of naked DNA (SI Appendix) to describe the internucleosomal gaps. As extension is increased, the force and the force-dependent transition rates can be calculated. The result for a 1 μm/s pull of chromatin previously assembled onto λ-DNA at 1 pN is shown in Fig. 3a (red curve). The result is a characteristic stretch-release signal, similar to that observed experimentally for λ-DNA (10). The large pull-rate combined with force- and sequence-dependent on/off rates obtained with our model reproduce the kinetics, explaining the large forces seen in such experiments. To closely match with the force ranges (20 to 35 pN) in the disassembly experiment performed after removing the egg extract, one has to increase α to 0.86. This finding suggests that in the absence of chaperones the transition state is slightly closer to fully assembled nucleosomes. Note that α = 0.75 does produce qualitatively the same force-extension behavior but over a narrower force range of 10 to 20 pN.
Fig. 3.
Constant-velocity nucleosome dynamics. (a) Disassembly dynamics during pulling at constant velocity for chromatin assembled onto DNAs of various sequences. The red curve shows the result for λ-DNA, including sequence dependence included by using Vi. The blue curve shows the result of a calculation performed on a 16-μm piece of S. cerevisiae chromosome II. The green curve shows the result for constant Vi = −42 kBT. (b) World lines for nucleosomes on λ-DNA disassembled by using the constant strain rate. Each line indicates the position of one nucleosome with time, terminating when that nucleosome disassociates. Color code runs from blue for unstable nucleosomes to red for more stable (longer-lived) nucleosomes. A 15-s time interval is shown.
Our model predicts how nucleosomes along λ-DNA dissociate. The distribution of nucleosome positions along the molecule during constant-velocity pulling is shown in Fig. 3b: the ending of a line indicates dissociation. The less stable nucleosomes on the left side of the DNA dissociate well before those on the right side. This strong sequence-controlled disassembly is characteristic of λ-DNA. Pulling results for two other ≈48,500-bp sequences are also shown in Fig. 3a: constant Vi = −42 kBT (green) and a 48-kb piece of chromosome II of S. cerevisiae (blue, constructed by a repeat of 20-kb pieces; see previous section) each show a much narrower range of nucleosome disassembly forces.
Discussion
We have presented a theory for assembly and disassembly of nucleosomes, calibrated to describe these processes in Xenopus egg extract solutions without added ATP. Our theory includes force-dependent on- and off-kinetics for nucleosomes and diffusion of nucleosomes along DNA. Our focus on the ATP-independent part of the reaction allows us to analyze thermodynamics and force dependence of nucleosome dynamics and corresponds to analysis of nucleosomes onto DNA that occurs at the beginning of extract-based chromatin assembly reactions, mediated by ATP-independent histone chaperones. This theory addresses many-nucleosome dynamics including effects of DNA tension and sequence and describes the milieu in which ATP-dependent nucleosome assembling and positioning factors work.
Nucleosome Assembly and Disassembly.
Data for fiber assembly using Xenopus extracts allow us to extract rates for nucleosome assembly and disassembly. These are characterized by a critical force ≈3.5 pN, corresponding to a free energy per nucleosome assembled of 42 kBT [27 kcal/(mol·nucleosome)]. Using experimental data, we use our theory to extract the force-dependent rates; the on-rate has a strong force dependence for forces <3.5 pN, whereas the off-rate has a rather weak force dependence >3.5 pN. Considered as a single event, nucleosome assembly/disassembly displays a transition state rather close (in terms of DNA length wrapped, ≈75%) to the assembled state.
Nucleosome Sliding Diffusion.
The on-off dynamics by themselves, which generate essentially a first-order line-filling reaction that “jams” after covering ≈75% of the DNA, cannot describe experiment, where a slow final filling occurs. By adding sliding of nucleosomes along DNA (24, 25) to our theory, we obtain exactly the slow final relaxation observed experimentally, while maintaining the initial first-order-like reaction. Data for the extract-based reactions indicate that nucleosome sliding occurs at a rate 5 bp2/s (≈5 × 10−15 cm2/s).
Although it may appear surprising that the Schiessel et al. (24, 25) model can describe the chaperone-rich extract medium, we note that we use as input the nucleosomal free energy in the presence of chaperones, i.e., including their effect in a self-consistent way (Schiessel et al. considered sliding dynamics in buffer with ≈50% higher nucleosome free energy, leading to much slower rates of DNA dissociation and thus of sliding). It should be noted that recent work (26) has found nucleosome sliding to be facilitated by ATP-independent histone chaperones.
The rates of nucleosome dynamics in extract solutions are known to have a strong concentration dependence (13). Given the higher enzyme concentrations and possibly lower forces in vivo relative to the experiments used to calibrate our theory (16), it is possible that nucleosome sliding diffusion may occur in vivo at rates of up to 100 bp2/s. It would be useful to carry out single-chromatin fiber assembly–disassembly experiments by using a variety of types and dilutions of cell extracts. Yeast nuclear extracts in particular (36) could allow detailed studies of roles of specific factors through use of extracts prepared with knockout mutants.
Predictions for DNA-Sequence Dependence of Chromatin Dynamics.
Our theory makes a number of interesting predictions connected with its sequence dependence. The broadest results follow from the generally lower stability of nucleosomes assembled onto GC-rich DNA. This effect leads to a higher level of stability of nucleosomes on the right end of λ-DNA: for example, we find that during pulling-dissociation experiments nucleosomes release earlier from the left end of λ-DNA than from the right end. This effect is responsible for the broad range of nucleosome release forces seen in rapid λ-chromatin-pulling experiments; our model suggests that the high-force dynamics corresponds essentially to chaperone-independent tearing of DNA off histones. Our detailed predictions for the sequence of nucleosome disruption could be tested by using a fluorescence-based experiment to monitor the spatial distribution of opening events along λ-DNA or study other defined-sequence DNAs with less strong sequence contrast between their ends.
Our theory could be used with experiments to permit precise testing of the sequence dependence of nucleosome stabilities in the model of Segal et al. (17). If one could dynamically monitor nucleosome positions (possibly using fluorescence) for a series of varying sequence-content DNAs in experiments in egg extracts, one might be able to further refine our knowledge of how DNA sequence controls nucleosome and chromatin structure.
Further Development of the Theory.
A number of questions arise from this work, which like the sequence dependence of nucleosome stability, require coordinated experimental and theoretical work. First, the role and effects of noncore-histone proteins, and especially linker histones, could be determined with experiments with extracts depleted of those factors. Understanding the role of linker histones may be of great importance to a second question, which is whether the multiple states observed in single-nucleosome experiments are of importance to nucleosome dynamics in vivo. Pulling experiments on synthetic, isolated nucleosomes assembled with no linker histones show an initial, smooth and reversible “unpeeling” of ≈75 bp of DNA, followed by an abrupt and irreversible ≈25-nm jump thought to correspond to release of the remaining ≈75 bp (11, 12).
Whether or not this two-step disassembly process is relevant in vivo where core histone, linker histone, and histone chaperones are all present at high concentrations is an interesting and open question. Our model, which treats nucleosome assembly and disassembly as single dynamical events, provides a “coarse-grained” description that can be generalized to include multiple-state assembly and disassembly pathways. We have carried out calculations for a generalization of our model that treats nucleosome assembly and disassembly via two steps, each involving ≈30 nm of DNA length: the basic result of a requirement of sliding to produce dynamics matching experiment was maintained. Use of further experiments to more precisely define subnucleosomal transitions involved in assembly and disassembly of nucleosomes would be of great interest. More pressing is the question of how the ATP-free dynamics that we have analyzed here are modified in the presence of ATP-dependent chromatin-assembling and chromatin-remodeling enzymes.
Supplementary Material
Acknowledgments
We thank Prof. J. Widom for helpful advice and Prof. R. Heald and Dr. T. Maresca for advice, comments, and help with the experiments of ref. 16. This work was supported by National Science Foundation Grants MCB-0240998, PHY-0445565, and DMR-0715099.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0701459104/DC1.
References
- 1.Bystricky K, Heun P, Gehlen L, Langowski L, Gasser S. Proc Natl Acad Sci USA. 2004;101:16495–16500. doi: 10.1073/pnas.0402766101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Marshall WF, Straight A, Marko JF, Swedlow J, Dernburg A, Belmont A, Murray AW, Agard DA, Sedat JW. Curr Biol. 1997;7:930–939. doi: 10.1016/s0960-9822(06)00412-x. [DOI] [PubMed] [Google Scholar]
- 3.Levi V, Ruan Q, Plutz M, Belmont AS, Gratton E. Biophys J. 2005;89:4275–4285. doi: 10.1529/biophysj.105.066670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kimura H, Cook PR. J Cell Biol. 2001;153:1341–1354. doi: 10.1083/jcb.153.7.1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Studitsky VM, Kassavetis GA, Geiduschek EP, Felsenfeld G. Science. 1997;278:1960–1963. doi: 10.1126/science.278.5345.1960. [DOI] [PubMed] [Google Scholar]
- 6.Widom J. Science. 1997;278:1899–1901. doi: 10.1126/science.278.5345.1899. [DOI] [PubMed] [Google Scholar]
- 7.Polach KJ, Widom J. J Mol Biol. 1995;254:130–149. doi: 10.1006/jmbi.1995.0606. [DOI] [PubMed] [Google Scholar]
- 8.Polach KJ, Widom J. J Mol Biol. 1996;258:800–812. doi: 10.1006/jmbi.1996.0288. [DOI] [PubMed] [Google Scholar]
- 9.Cui Y, Bustamante C. Proc Natl Acad Sci USA. 2000;79:127–132. doi: 10.1073/pnas.97.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bennink ML, Leuba SH, Leno GH, Zlatanova J, de Grooth BG, Greve J. Nat Struct Biol. 2001;8:606–661. doi: 10.1038/89646. [DOI] [PubMed] [Google Scholar]
- 11.Brower-Toland BD, Smith CL, Yeh RC, Lis JT, Peterson CL, Wang MD. Proc Natl Acad Sci USA. 2002;99:1960–1965. doi: 10.1073/pnas.022638399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mihardja S, Spakowitz AJ, Zhang Y, Bustamante C. Proc Natl Acad Sci USA. 2006;103:15871–15876. doi: 10.1073/pnas.0607526103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ladoux B, Quivy J-P, Doyle P, du Roure O, Almouzni G, Viovy J-L. Proc Natl Acad Sci USA. 2000;97:14251–14256. doi: 10.1073/pnas.250471597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bennink ML, Pope LH, Leuba SH, de Grooth BG, Greve J. Single Mol. 2001;2:91–97. [Google Scholar]
- 15.Wagner G, Bancaud A, Quivy JP, Clapier C, Almouzni G, Viovy J-L. Biophys J. 2005;89:3647–3659. doi: 10.1529/biophysj.105.062786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yan J, Maresca TJ, Skoko D, Adams CD, Xiao B, Christensen MO, Heald R, Marko JF. Mol Biol Cell. 2007;18:464–474. doi: 10.1091/mbc.E06-09-0800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Segal E, Fondufe-Mittendorf Y, Chen L, Thastrom A, Field Y, Moore IK, Wang JP, Widom J. Nature. 2006;442:772–778. doi: 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shimamura A, Tremethick D, Worcel A. Mol Cell Biol. 1988;8:4257–4269. doi: 10.1128/mcb.8.10.4257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Smythe C, Newport JW. Methods Cell Biol. 1991;35:448–468. doi: 10.1016/s0091-679x(08)60583-x. [DOI] [PubMed] [Google Scholar]
- 20.Pope LH, Bennink ML, van Leijenhorst-Groener KA, Nikova D, Greve J, Marko JF. Biophys J. 2005;88:3572–3583. doi: 10.1529/biophysj.104.053074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Almouzni G, Mechali M. EMBO J. 1988;7:4355–4365. doi: 10.1002/j.1460-2075.1988.tb03334.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Claudet C, Angelov D, Bouvet P, Dimitrov S, Bednar J. J Biol Chem. 2005;280:19958–19965. doi: 10.1074/jbc.M500121200. [DOI] [PubMed] [Google Scholar]
- 23.Meersseman G, Pennings S, Bradbury EM. EMBO J. 1992;11:2951–2959. doi: 10.1002/j.1460-2075.1992.tb05365.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schiessel H, Widom J, Bruinsma RF, Gelbart WM. Phys Rev Lett. 2001;86:4414–4417. doi: 10.1103/PhysRevLett.86.4414. [DOI] [PubMed] [Google Scholar]
- 25.Schiessel H, Widom J, Bruinsma RF, Gelbart WM. Phys Rev Lett. 2002;88:129902. doi: 10.1103/PhysRevLett.86.4414. [DOI] [PubMed] [Google Scholar]
- 26.Park Y-J, Chodaparambil J-V, Bao Y, McBryant SJ, Luger K. J Biol Chem. 2005;280:1817–1825. doi: 10.1074/jbc.M411347200. [DOI] [PubMed] [Google Scholar]
- 27.Evans JW. Rev Mod Phys. 1993;65:1281–1330. [Google Scholar]
- 28.Marko JF, Siggia ED. Macromolecules. 1995;28:8759–8770. [Google Scholar]
- 29.Marko JF, Siggia ED. Biophys J. 1997;73:2173–2178. doi: 10.1016/S0006-3495(97)78248-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Evans E, Ritchie K. Biophys J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Luger K. Chrom Res. 2006;14:5–16. doi: 10.1007/s10577-005-1026-1. [DOI] [PubMed] [Google Scholar]
- 32.Gillespie DT. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 33.van Holde KE, Yager TD. In: Structure and Function of the Genetic Apparatus. Nicolini C, Ts'o POP, editors. New York: Plenum; 1985. pp. 35–53. [Google Scholar]
- 34.Kulic IM, Schiessel H. Phys Rev Lett. 2003;91:148103. doi: 10.1103/PhysRevLett.91.148103. [DOI] [PubMed] [Google Scholar]
- 35.Gemmen GJ, Sim R, Haushalter KA, Ke PC, Kadonaga JT, Smith DE. J Mol Biol. 2005;351:89–99. doi: 10.1016/j.jmb.2005.05.058. [DOI] [PubMed] [Google Scholar]
- 36.Robinson KM, Schultz MC. Methods Mol Biol. 2006;313:209–223. doi: 10.1385/1-59259-958-3:209. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.