Quartz Crystal Microbalance Studies of Multilayer Glucagon Fibrillation at the Solid-Liquid Interface

Abstract

We have used a quartz crystal microbalance with dissipation (QCM-D) to monitor the changes in layer thickness and viscoelastic properties accompanying multilayer amyloid deposition in situ for the first time. By means of atomic force microscope imaging, an unequivocal correlation is established between the interfacial nucleation and growth of glucagon fibrils and the QCM-D response. The combination of the two techniques allows us to study the temporal evolution of the interfacial fibrillation process. We have modeled the QCM-D data using an extension to the Kelvin-Voigt viscoelastic model. Three phases were observed in the fibrillation process: 1), a rigid multilayer of glucagon monomers forms and slowly rearranges; 2), this multilayer subsequently evolves into a dramatically more viscoelastic layer, containing a polymorphic network of micrometer-long fibrils growing from multiple nucleation sites; and 3), the fibrillar formation effectively stops as a result of the depletion of bulk-phase monomers, although the process can be continued without a lag phase by subsequent addition of fresh monomers. The robustness of the QCM-D technique, consolidated by complementary atomic force microscope studies, should make it possible to combine different components thought to be involved in the plaque formation process and thus build up realistic models of amyloid plaque formation in vitro.

INTRODUCTION

The ability of certain polypeptides to aggregate into long, thin needle-shaped amyloid structures and their subsequent deposition at plaque sites in different parts of the body is associated with multiple protein-folding disorders (1,2). For instance, a stretch of polyglutamine that repeats in a particular protein has been proposed as the cause of many neurological disorders, including Huntington's disease and spinal bulbar muscular atrophy, and aggregation of other unrelated proteins is correlated with prion disease (PrP aggregation), Alzheimer's disease (Aβ-peptide), Parkinson's disease and amyotrophic lateral sclerosis (ALS) (a-synuclein aggregation), dialysis-related amyloidosis (β-2 microglobulin aggregation), corneal dystrophy (keratoepithelial deposits), and aggregation of islet amyloid polypeptide in >95% of type II diabetes (3). Although the cytotoxic species in the aggregation process has been proposed to be an early prefibrillar oligomer with enhanced cell membrane-permeabilizing properties (4), a detailed understanding of the temporal sequence of events leading up to the nucleation and growth of these fibrillar deposits is important for the development of therapeutic strategies. Fibrillar deposits also serve a useful purpose in their own right for the formation of bacterial biofilm (5), fungal spore production (6), and melansome production in the skin (7), making those interesting biotechnological role models.

Here we investigate the dynamic fibrillation of glucagon, a 29-amino acid peptide amphiphatic hormone connected to the regulation of blood glucose levels and used therapeutically in the treatment of severe hypoglycemia (8). Glucagon has a strong propensity to aggregate under a variety of buffer conditions (pH, temperature, agitation, and salts) (9–11), which limits the stability of the hormone. The ensuing fibrils differ significantly in secondary structure, suggesting an inherent structural plasticity of the hormone, which may also be reflected at the level of the actual fibrils (9–11).

The multifaceted hierarchy of glucagon fibrillogenesis was recently mapped using atomic force microscopy (AFM) by ex situ observing the products of the fibrillation process formed freely in the bulk under acidic conditions and subsequently immobilized on surfaces (12,13). Because in vivo conditions associated with amyloid fibrillation, however, are often dictated by surface and lipid membrane phenomena (1,3), the in situ temporal study of amyloid fibrillation at the solid-liquid interface represents an important and physiologically relevant approach to the study of amyloid fibrillogenesis. This relevance is emphasized by the differences found in fibril morphology in various polypeptide systems depending both on bulk or surface assembly and on the physiochemical properties of the confining interface (14–17).

In situ AFM imaging has revealed unique insight into the initial monomer adsorption and organization of the amyloid-peptide Aβ, depending on a hydrophilic versus hydrophobic surface assembly (14), and in the study of insulin fibrillation on model lipid-water interfaces, the fibril morphology was reported to depend on bulk or surface assembly but also on the electrostatic nature of the lipids (15). Assembly of amylin on mica was likewise found to differ significantly from that grown in the bulk (16), and in one case, by studying the fibrillation of the light chain domain SMA on different functionalized surfaces (negative charged, positive charged, or hydrophobic) (17), it was shown that the surface chemistry and buffer conditions had a strong influence on the fibril formation on negatively charged mica. Furthermore, it was suggested that a secondary surface-induced assembly pathway existed with elongation and accelerated growth from multiple nucleation points (17).

Despite the wealth of structural detail provided at the level of individual filaments by these pioneering AFM studies, it is important to elucidate at a more general level how the surface is colonized by the growing mass of amyloid. The ultimate goal is to allow us to model amyloid plaque formation in vitro. Structural and mechanistic details of its undoubtedly complex formation in vivo remain elusive, but we hope that a realistic reconstruction of the plaque's characteristic mechanical and viscoelastic properties will provide a better understanding of the processes controlling its biological genesis, particularly the contributions made by components such as heparin and apolipoprotein E4 to the buildup and consolidation of the protein deposit. In the long term, this may inspire future therapeutic strategies.

Here we report on the use of a quartz crystal microbalance with dissipation (QCM-D) to follow the dynamic process of glucagon fibrillation at the solid-liquid interface in situ. QCM-D allows us to follow the coupling between initial deposition and structural rearrangements leading to growth in layer thickness and accompanying changes in the deposited layer's viscoelastic properties. We reveal that a clear correlation can be established between the QCM-D response and the dynamic fibrillation process by comparing the temporal QCM-D response to time-lapsed AFM images of the fibrillation. Further, we modeled the experimental results using an extended viscoelastic model, which allowed us to obtain detailed time-resolved insight into the dynamic interfacial response during the fibrillogenesis process.

MATERIALS AND METHODS

Glucagon and film preparation

Pharmaceutical grade glucagon protein powder (Novo Nordisk A/S, Bagsværd, Denmark, purity >98.9%) was dissolved to a concentration of 2.5 mg/ml at pH 2.0 (10 mM HCl and 1 mM Na₂SO₄) and initially incubated at 23°C for 5 min, with great care taken to ensure reproducible mixing conditions during the procedure. This procedure involved using a micropipette to gently aspirate the samples at 23°C a fixed number of times during mixing and making sure not to introduce air bubbles in the procedure.

Standard 5-MHz AT-cut gold-coated quartz crystals (QSense AB, Gothenberg, Sweden) were coated with 500 Å of tantalum (Ta) by e-gun evaporation. From x-ray photoelectron spectroscopy (XPS) results, we can conclude that the exposure of the Ta films to ambient conditions led to the formation of a 20–50 Å thick top layer of native tantalum oxide (Ta₂O₅). All films were UV/ozone (UVO) pretreated for 40 min to ensure a clean, hydrophilic surface.

Quartz crystal microbalance with dissipation

QCM-D experiments were performed in parallel duplicates using two axial flow chambers, QAFC 301 and QAFC 302, from Q-Sense AB. The QCM-D technique (18) has proven to be well suited for in situ dynamic monitoring of both mass and mechanical properties, such as viscoelasticity of absorbed biomolecules (19,20). The AT-cut quartz crystal is piezoelectric and deforms mechanically when exposed to an electrical field. By applying a radio frequency (RF) ac voltage across the crystal, a shear oscillation is induced at the resonance frequency or at overtones 3, 5, and 7; for the crystals used here, the ground resonance frequency is 4.95 MHz. Information about the adsorption process is obtained by the simultaneous measurement of changes in the resonance frequency (ΔF_N) and the dissipation factor (ΔD_N) at each Nth overtone. The shift in dissipation on ΔD_N provides information about the viscoelastic properties of the adsorbed layer. For rigid films displaying little shift in dissipation (ΔD_N < ∼8–10 × 10⁻⁶), the change in the Nth overtone resonance frequency, ΔF_N, is proportional to the change in the total adsorbed surface mass density (Γ) via the Sauerbrey equation (21,22):

(1)

The quantities of ρ₀ and μ₀ are the density and shear modulus of quartz, respectively, whereas F₁ is the baseline fundamental resonance frequency. For increasing viscoelastic layers, the more advanced Kelvin-Voigt formalism is often employed (23–25). This model relates the observed shift in frequency (ΔF) and dissipation (ΔD) to the thickness and viscoelastic properties (shear modulus and shear viscosity) of the forming layer. All experiments were performed at a controlled temperature of 22.9 ± 0.1°C. Samples were injected into the two chambers after a stable baseline buffer signal (drift <0.1 Hz/min on the third overtone) and an initial thermal equilibration of the sample. At least five experiments were performed for each condition, i.e., each result reported (mean ± SD).

Atomic force microscopy

AFM is particularly useful for studying fibrillar ultrastructure, as it permits visualization of individual biological macromolecules at the nanometer scale (26–28). To conduct parallel AFM and QCM-D studies, several Ta-coated quartz crystals were incubated in individual small tubes simultaneously with the injection of freshly prepared glucagon solution into the QCM-D chamber. At each point of interest, a sample was removed from the incubation tubes and imaged using a commercial Nanoscope IIIa MultiMode AFM (Veeco Instruments, Santa Barbara, CA) under ambient conditions at 23°C. To quantitatively check for any influence originating from the differences in experimental conditions between the QCM-D experiments and the incubated samples, all AFM results were additionally repeated by interrupting the QCM-D experiment at certain time sequences and imaging these QCM surfaces directly by AFM. Overall, very good agreement was obtained, implying that the AFM images presented are representative for the temporal evolution corresponding to the QCM-D results. AFM imaging was performed in the tapping mode at scan frequencies of 1–2 Hz with minimal loading forces applied and by optimized feedback parameters. These conditions ensured that any sample distortion by tip compression is reduced to an absolute minimum. Silicon nitride cantilevers (NSG01, NT-MDT, Russia) were used with a typical resonance frequency of 150 kHz, a spring constant of 5.5 N/m, and a typical tip radius of 10 nm. The AFM images were obtained by recording 512 × 512 pixels, and several images were always obtained from separate locations across the Ta-coated crystals at each time point of interest to ensure that data presented are representative of actual surface morphology. All AFM images were globally flattened and visualized using the commercial Scanning Probe Image Processor software (SPIP™, Image Metrology ApS, Version 4.2, Lyngby, Denmark).

RESULTS AND DISCUSSION

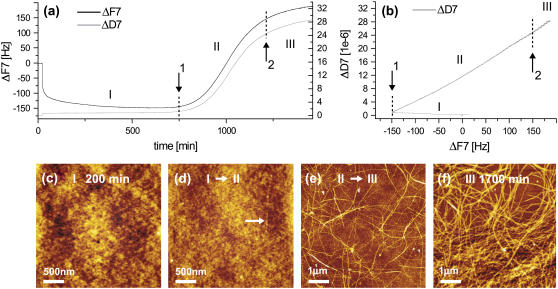
Time-resolved QCM-D data are depicted in Fig. 1 a, where the QCM-D frequency shift ΔF and the dissipation response, ΔD of overtone 7 are displayed as a function of glucagon exposure time. Because of the extended period of observation, additional control experiments on a similar timescale were performed with buffer only injected, in which case no dynamic ΔF or ΔD signals were observed (data not shown). The QCM-D glucagon response can be tentatively divided into three characteristic regions referred to as I, II, and III, respectively, in Fig. 1 a. First, after the injection of glucagon, a ΔF decrease is observed as the adsorption of monomers forms an initially rigid layer as concluded from the small increase in ΔD (<5 × 10⁻⁶) (Fig. 1 a, section I). Both the frequency shift ΔF and dissipation shift ΔD display a behavior corresponding to typical adsorption phenomena (21,23). This observation is further confirmed by the corresponding AFM images (see Fig. 1 c) of the adsorbed layer of biomolecules after the initial fast adsorption (∼200 min). A significant aggregation of particle-like structures is observed, forming a complete homogeneous layer of globular structures across the Ta surface. Similar rigid layer formation has been observed using QCM-D in case of Aβ(1–40) monomer adsorption on various substrates (29) but without monitoring the subsequent fibrillation.

FIGURE 1.

Representative QCM-D and AFM data from a typical experiment, displaying the observed frequency (ΔF7) and dissipation (ΔD7) shifts for overtone 7 (a) along with the combined time-independent ΔD7 versus ΔF7 graphs (b). At important time points, marking transitions of the observed QCM-D signal (arrows 1 and 2 in a and b), corresponding AFM images are displayed (c–e) along with an end-of-experiment image from 1700 min when no further dynamics is observable (QCM-D data displayed only until 1500 min).

After a characteristic lag time of 430 ± 97 min, the adsorbed layer is observed to transform dramatically, becoming notably more viscoelastic as reflected by the significant increase in the dissipation ΔD and frequency ΔF (see Fig. 1, section II). This behavior is ascribed to a result of glucagon fibrillation at the Ta surface, as fibrils start to appear in the AFM images (see Fig. 1 d, indicated by the arrow) as opposed to the previous nonstructured aggregates in the AFM images (Fig. 1 c). A similar fibrillation lag period is also observed in other studies using spectroscopic techniques, such as binding of the fluorescent probe thioflavin T, tryptophan fluorescence, or changes in the far-UV CD signal (9,10).

The dynamic process of fibrillation continuously transforms the interfacial glucagon layer throughout this phase, as depicted from subsequent time points in Fig. 1, e and f. Distinct micrometer-long fibrils are clearly visible, forming locally an increasingly dense and viscoelastic network of fibrils. This observation is in good agreement with earlier AFM studies (12,13) where glucagon fibrillation takes place after a characteristic lag period, resulting in an increasingly elaborate network of fibril species.

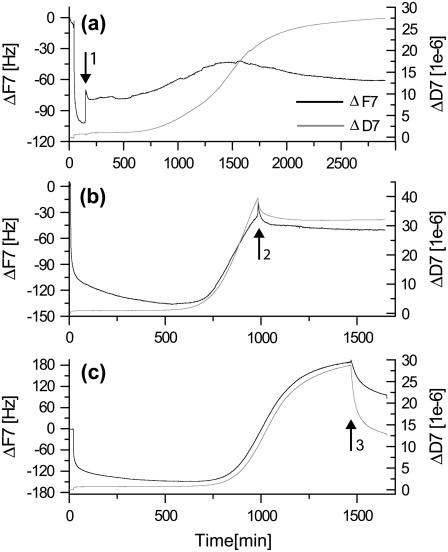
At this stage it was not clear whether the observed increases in ΔF and ΔD were caused by a rapid adsorption or formation of various mature and viscoelastic fibrillar species in the bulk solution or if they were truly a surface phenomenon. To test this, a flushing procedure was performed at different time points. If the observed increases in frequency and dissipation were effects of the change in bulk solution properties only (viscosity and density), the process should be completely reversible by flushing with buffer solution. This, however, is not the case. When the chamber is flushed with buffer midway in the experimental time cycle (Fig. 2 b) or at the end of an experiment (Fig. 2 c), there is a slow desorption curve with a plateau value higher than that seen at the start of the experiment. In addition, if flushing is performed directly after the formation of the initial rigid layer (Fig. 2 a), we still observe the characteristic dynamics of the fibrillation and, in particular, a similar lag time. In all three flushing experiments, the presence of fibrils was confirmed by direct imaging by AFM. On the basis of these observations, we thus conclude that the observed onset of fibrillation is caused by a slow dynamic reconfiguration within the already formed interfacial glucagon layer.

FIGURE 2.

Observed QCM-D response to buffer flushing (arrows 1–3) after the initial rigid layer formation (a), midway during the dynamic fibrillation (b), and at the end of an experiment (c). Notice the similar timescales of b and c in contrast to the approximately twice as long scale in a.

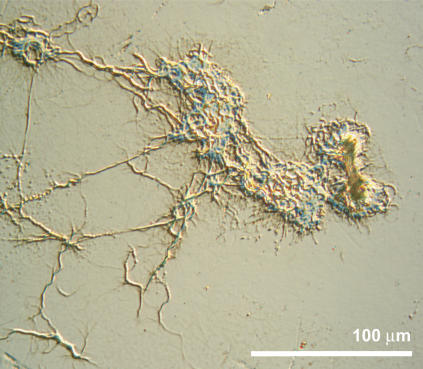
However, during the process, the fibrillation process is not independent of mass transfer from the bulk glucagon solution. Exchange with buffer solution shortly after the initial deposition extends the process time by a factor of ∼2 once the fibrillation has been initiated (Fig. 2 a; notice the longer timescale). Furthermore, the fibrillation process on the crystal can be stopped at a given time point, as seen from Fig. 2, b and c. The final QCM-D response to the fibrillation (Fig. 1 a, section III) shows that the limited availability of monomers in the bulk solution ultimately terminates the growth of fibrils and slowly guides the process into a stable regime with no further dynamic rearrangement of the glucagon observable. This depletion behavior is also evident from the time-independent dissipation ΔD versus frequency ΔF plots (Fig. 1 b), where the final transition between sections II and III (indicated by arrow 2 in Fig. 1 b) does not alter the slope of the ΔD-ΔF curve, which confirms that the process results from depletion rather than a configuration change. Interestingly, the ΔD-ΔF plot provides an unambiguous identification of the transition from phase I to phase II (indicated by arrow 1 in Fig. 1 b), giving a unique fingerprint of the onset of fibrillation and the subsequent growth process. Furthermore, although multiple fibrils are found across the entire crystal interface at this final phase III of the experiment, a large number of dense macroscopic (>100 μm) fibril islands coexist, as displayed in Fig. 3. This coexistence strongly suggests that the fibrillation process is governed by interfacial nucleation sites, as also seen for Aβ(1–40) amyloids (29).

FIGURE 3.

Optical image of a locally dense fibril island present on the tantalum surface in the final phase III of the dynamic process. The presence of multiple islands suggests a fibrillation potentially governed by interfacial nucleation sites.

To obtain further microscopic insight into the dynamic interfacial fibrillation process, we have applied a simple model of the QCM-D frequency and dissipation response. In the initial phase (Fig. 1, section I), a linear scaling of overtones 3, 5, and 7 of ΔF is always observed along with a low dissipation ΔD value (<5 × 10⁻⁶). This observation implies that the change in resonance frequency, ΔF_N of the Nth overtone, can be related to the change in the adsorbed surface mass density Γ via the Sauerbrey equation (Eq. 1).

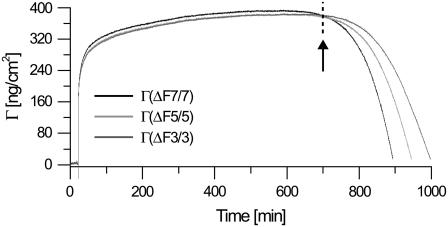
A representative curve of the modeled surface mass density is displayed in Fig. 4. On average, Γ saturates at 420 ± 42 ng/cm². In the approximation of a closely packed side-by-side orientation of extended glucagon monomers in a β-sheet configuration of dimensions 101.5 Å × 10 Å (corresponding to a monomer area of 1.01 × 10⁻¹³ cm², i.e., ∼55 ng/cm²), this is equal to a lower limit of ∼7 adsorbed monolayers.

FIGURE 4.

Representative modeling results for the surface mass density (Γ) according to the Sauerbrey model, for overtones 3, 5, and 7 simultaneously. The model successfully applies for the initial, rigid multilayer formation, showing little overtone dependence. At ∼750 min, however, the system displays a increasing viscoelastic behavior, making the interpretation within the Sauerbrey model invalid (after arrow).

However, because the QCM-D technique measures the complete hydrated mass of the adsorbed biomolecules, the actual number of glucagon molecules on the surface will be significantly smaller (21). Because glucagon monomers are expected to adsorb randomly and not in a well-ordered β-packing across the entire interface, the observed surface mass density still suggests multilayer formation. This suggestion is in correspondence with the AFM data displayed in Fig. 1 a, which reveals a strong aggregation of particle-like structures.

To further describe the continued fibrillation process through phases II and III, we went beyond the simple Sauerbrey model and instead used the more advanced Kelvin-Voigt model (23–25) for the QCM-D data analysis. This application was motivated by the extreme viscoelastic behavior monitored by QCM-D of the rather complex network of fibrils, causing the Sauerbrey model to fail from the onset of fibrillation. As displayed in Fig. 4, the surface mass density shows an inconsistent overtone dependence (cf. Eq. 1) and a marked reduction of the surface mass density, reflecting the increase in frequency in phases II and III. This apparent reduction in density is clearly at odds with the fibril growth observed by AFM, where there is an accumulation of material on the surface. To clarify this paradox, we introduced an expansion of the original Kelvin-Voigt model and include a linear frequency dependence of the shear viscosity (η) and shear modulus (μ) for the multilayers formed, as described by Eqs. 2 and 3. This introduction turned out to be a necessary and sufficient step to obtain a satisfactory correspondence with measured data. In the model, positive coupling constants (α, β) imply that the shear viscosity and shear modulus increase with frequency. Simultaneous fitting of frequency overtones 5 and 7 along with dissipation are done pointwise using a least-squares algorithm, varying the thickness (h₁), shear viscosity, and the shear modulus of the adsorbed layer. These parameters are subsequently recombined to yield the surface mass density Γ (h₁·ρ₁) along with the fitted viscoelastic parameters.

(2)

(3)

This extended three-layer viscoelastic model displays the relationship between the observed Nth overtone frequency (ΔF_N) and dissipation shift (ΔD_N) and the viscoelastic parameters of the forming layer (annotated 1), the extending bulk (annotated 2), and the oscillating crystal (annotated 0). The free model parameters are the shear viscosity (η_1,N), the thickness (h₁), and the shear modulus (μ_1,N) of the adsorbed overlayer for the Nth overtone. The linear dependence of the shear modulus (μ_1,N) and the shear viscosity (η_1,N) are expressed via the coupling constants α,β. For further details concerning Eq. 2, see Voinova et al. (24).

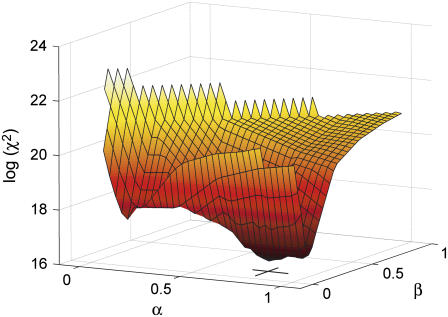
To determine the optimal linear coupling constants (α,β) of the overtone dependence of μ and η (Eq. 3), a grid search χ² analysis was performed, fitting data according to Eq. 2 while at each fit keeping the couplings (α,β) at fixed grid values for the entire data set. Note that the optimized coupling constants often have a large variance depending on the actual data, with large constants (∼0.5) usually corresponding to smaller values of the final surface density and weak couplings (∼0.01) conversely to large values. In all cases, the couplings corresponding to the minimal χ² values were used as final model parameters, as illustrated in Fig. 5. The residuals, between the modeled values and the measured frequency and dissipation response, were always <0.9 Hz and 0.1 × 10⁻⁶ for ΔF and ΔD, respectively.

FIGURE 5.

Three-dimensional plot of χ² grid analysis for a representative experiment in the vicinity of minimum. In this particular case, as indicated by the cross, the optimized couplings α and β were 0.8010 and 0.1501, respectively.

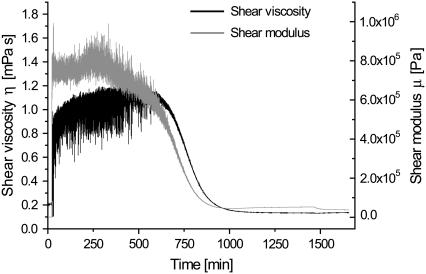
Representative curves for the temporal development of the viscoelastic parameters η and μ are displayed for the fundamental frequency (N = 1) in Fig. 6. Both the shear viscosity and the shear modulus decrease as the fibrils evolve, reaching values of 3.5 ± 0.85 × 10⁻⁴ Pa·s and 7 ± 1.3 × 10⁵ Pa, respectively. The noise present in the early stages of the process is caused by the initially low dissipation values, which make modeling according to Eqs. 2 and 3 and a determination of the viscoelastic properties difficult. From the modeled curves of surface mass density (Fig. 7), one should notice the initial positive correspondence in phase I between the simple Sauerbrey equation and the extended model. It is evident that the continued fibrillation beyond the characteristic lag time gives rise to a significant increase in surface mass densities Γ. This increase marks the onset of growth in the vertical (stacking) or horizontal (more dense surface packing) direction, possibly combined with a change in layer hydration.

FIGURE 6.

Temporal development of the parameterized viscoelastic properties of the fibrillating layer. Both the shear viscosity and shear modulus decrease as the fibrillation evolves.

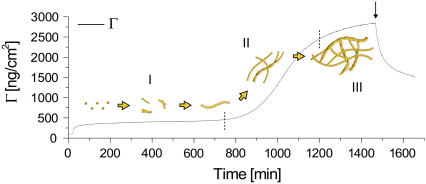
FIGURE 7.

Modeled surface mass density (Γ) according to the extended viscoelastic Kelvin-Voigt model, throughout the three characteristic regimes observed (I, II, and III) for a representative experiment, along with an illustration of dynamic interfacial fibrillation. Note the intuitively correct behavior modeled at the end-of-experiment flushing (arrow), showing a characteristic desorption behavior.

Because of the nature of the Kelvin-Voigt model employed, these modeled parameters can only be interpreted as mean values across the crystal surface. Quantitatively, however, they are in excellent agreement with the observed scenario (Fig. 1, c and d) of monomers or oligomers slowly being excluded from the layer as the fibrils mature. This process gradually forms a dense network with micrometer-long fibrils, continuously growing from multiple nucleation sites. In turn, the layer becomes notably more viscoelastic, with both the density and the height increasing locally as well as globally. In the final phase III of the process, the viscoelastic parameters and the modeled surface mass density level off (Figs. 6 and 7), as the fibrillation process halts because of the depletion of nonfibrillated glucagon material. In regard to the surface mass density, notice the intuitively correct modeled behavior after flushing with buffer, with a subsequent slow decrease in Γ (Fig. 7). This behavior is in contrast to the ΔF data (Fig. 2 c), showing a decrease in frequency, which usually signifies a mass increase within the simple Sauerbrey model. This correspondence clearly demonstrates the applicability of the extended viscoelastic model introduced here.

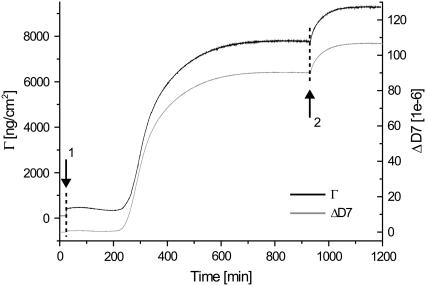
Having successfully identified and modeled the viscoelastic development of a single glucagon injection, we additionally investigated whether this process of interfacial fibrillation could be continued by a secondary injection. As presented in Fig. 8, the introduction of a freshly prepared glucagon monomer solution led to a large, but slow increase in dissipation. On the basis of the slow kinetics displayed and the magnitude of the dissipation shift, we interpret this as a direct continuation of the fibrillation process, but interestingly with no secondary lag period needed. This finding is additionally supported by the modeled surface mass density, showing a significant increase resembling the onset of the initial fibrillation.

FIGURE 8.

Reinjection of glucagon monomers (arrow 2) leads to a dramatic but slow incense in ΔD and Γ. Because of the amplitude and kinetics of the response, as compared with the initial injection of monomers (arrow 1), this indicates a direct continuation of the interfacial fibrillation.

CONCLUSION

In this study, we have successfully applied the QCM-D in combination with parallel AFM imaging to study glucagon fibrillation at the solid-liquid interface. A clear correspondence between the process of interfacial fibrillation and the QCM-D response has been established. From the experimentally observed changes in frequency ΔF and dissipation ΔD, three phases in the dynamic fibrillation were identified, which were additionally evident in the corresponding characteristic ΔD-ΔF curves. Furthermore, we successfully modeled the dynamic QCM-D response using the simple Sauerbrey equation in the initial phase and an extended Kelvin-Voigt model, including frequency-dependent terms, in the late, more viscoelastic regimes. This modeling enabled us to obtain a detailed quantitative description of the fibrillogenesis process, with correlated changes in the surface mass density and viscoelastic properties of the forming layer. In phase I, we observe an initially rigid multilayer formation of glucagon monomers with a subsequent slow rearrangement, when possibly initial oligomers and other early species within the fibrillogenic hierarchy begin to form within the interfacial layer. After a characteristic lag time, the onset of fibrillation and maturing of fibrils passes a transition point, when the layer becomes dramatically more viscoelastic, and the fibrillogenesis process enters phase II. This phase is characterized by a decrease in shear modulus and shear viscosity and a large increase in surface mass density. As illustrated in Fig. 7, we attribute this to the process of monomers or oligomers being excluded from the layer as the fibrils mature, gradually forming a dense polymorphic network of micrometer-long fibrils growing from multiple nucleation sites. In their continuous growth, these fibrils form a still more viscoelastic and elaborate network with increases in both height and density of the layer. Finally, the process progresses into a stable phase III as a result of the finite amount of monomers available, effectively terminating the interfacial fibrillar formation. The process could be continued with a secondary injection of fresh monomers but, interestingly, without a secondary lag time needed.

This work successfully demonstrates for the first time the ability to monitor in detail the temporal development and viscoelastic changes accompanying multilayer amyloid deposition at the solid-liquid interface in situ using QCM-D. The robustness of the technique, consolidated by complementary AFM studies, should make it possible to combine a large number of different components thought to be involved in the plaque formation process and thus build up realistic models of amyloid plaque formation in vitro as well as allow further insight into biological interfacial deposition processes in general.