Computational Prediction of Atomic Structures of Helical Membrane Proteins Aided by EM Maps

Abstract

Integral membrane proteins pose a major challenge for protein-structure prediction because only ≈100 high-resolution structures are available currently, thereby impeding the development of rules or empirical potentials to predict the packing of transmembrane α-helices. However, when an intermediate-resolution electron microscopy (EM) map is available, it can be used to provide restraints which, in combination with a suitable computational protocol, make structure prediction feasible. In this work we present such a protocol, which proceeds in three stages: 1), generation of an ensemble of α-helices by flexible fitting into each of the density rods in the low-resolution EM map, spanning a range of rotational angles around the main helical axes and translational shifts along the density rods; 2), fast optimization of side chains and scoring of the resulting conformations; and 3), refinement of the lowest-scoring conformations with internal coordinate mechanics, by optimizing the van der Waals, electrostatics, hydrogen bonding, torsional, and solvation energy contributions. In addition, our method implements a penalty term through a so-called tethering map, derived from the EM map, which restrains the positions of the α-helices. The protocol was validated on three test cases: GpA, KcsA, and MscL.

INTRODUCTION

Ab initio prediction of membrane protein structure, in the absence of additional experimental data, remains a difficult problem, in part due to the small number (≈100) of high-resolution structures that are known, compared to the >30,000 protein structures that have been solved by x-ray crystallography. Nevertheless, membrane protein structural biology is important because it is estimated that approximately one-third of genes code for membrane proteins (1) and because >50% of the pharmaceuticals in use are targeted to membrane proteins (2). This is so mainly because of technical problems in the expression and crystallization of this class of proteins (3–5). (See Michel's membrane protein website: http://www.mpibp-frankfurt.mpg.de/michel/public/memprotstruct.html and White's membrane protein website: http://blanco.biomol.uci.edu/Membrane_Proteins_xtal.html.)

Advances in electron microscopy (EM) have produced an increasing number of intermediate-resolution (9–6 Å) structures of membrane proteins, which can be utilized as restraints to make the prediction calculations more tractable. In this work we restrict ourselves to the major class of membrane proteins formed by bundles of transmembrane (TM) α-helices and describe a protocol for predicting their structure that uses a given EM map as an aid to restrain the position of the helices.

A number of approaches have been developed in the last several years regarding the structure prediction of membrane proteins. (Extensive lists of references are given in other reviews (6,7).) One of the most widespread approaches is homology modeling, which constructs models that are homologous to other protein(s) (templates) whose three-dimensional structure is known. An important example of the application of this approach is the modeling of ion channels (8) based on the structure of KcsA (9).

In general, methods differ in the kind of energy function they use and/or their sampling strategy to search for low-energy conformations. The core of all of these procedures is the docking of flexible helices. Abagyan et al. (10) first demonstrated that the correct association of two α-helices could be predicted from scratch by global energy optimization. The sampling protocol was capable of identifying the correct arrangement of the two helices, and the energy function, which included van der Waals, torsional, hydrogen bonding, electrostatic and solvation terms, distinguished parallel, antiparallel, and crossed helical conformations. Kim et al. (11) used only the van der Waals energy term, and, starting from a set of random orientations of a pair of helices, optimized the parameters by a Monte Carlo search. In this way, they were able to model simple homo-oligomers (a straight helix repeated two, four, or five times). Gottschalk (12) used only four degrees of freedom for each helix to generate a sparse set of conformations, which were then evaluated using van der Waals and electrostatic energy terms. Park et al. (13) described a scoring function, which they used to perform an exhaustive search of the six degrees of freedom between two helices. A similar approach was used by Fleishman and Ben-Tal (14), while Dobbs et al. (15) used an empirical energy function derived from statistical analyses of known membrane protein structures (16). The replica-exchange Monte Carlo method has been used successfully (17) to reproduce the NMR structure of Glycophorin A (GpA). For this, the authors performed a long replica-exchange Monte Carlo simulation starting from a single conformation of the pair of helices. Molecular dynamics (MD) simulations have also been used in the modeling of transmembrane helices (18). Goddard and co-workers (19) have specifically tailored a method called MembStruk to predict the structures of G-protein coupled receptors. Physicochemical data are used to build an initial coarse-grained model, which is subsequently refined by stochastic sampling and MD simulations. The TASSER method has also been adapted to membrane proteins (20). This approach threads the given sequence on parts of solved protein structures, and then refines the resulting template. Lastly, the Rosetta algorithm for structure prediction has been implemented for TM proteins (21). However, only backbone coordinates are derived due to the computational intractability of a full-atom prediction for membrane proteins, which are usually larger than the small soluble proteins amenable to Rosetta.

Despite the promising progress exemplified by the success of the above methods, they are in general very time-consuming, which makes them applicable only to simple or small cases, such as the fitting of rigid α-helices, or they can only be performed by a sparse search, which degrades their reliability. This is alleviated when some additional constraints are imposed (22). For instance, Sale et al. (23) combined measures derived from statistical analyses with experimental distance constraints to refine an ensemble of initial conformations that matched a set of distance constraints. Beuming and Weinstein (24) proposed a related approach, using distance restraints obtained from EM maps to assemble bundles of ideal α-helices, each of which was individually oriented according to a measure that combined evolutionary residue conservation with their propensities to be exposed to the lipid. A similar methodology was independently suggested by Fleishman et al. (25), which, unlike Beuming and Weinstein (24), provides only C^α coordinates but does not involve any manual adjustments.

The present work also belongs to this category. However, unlike those approaches, we allowed the α-helices to be flexible and performed a fast exhaustive search (made possible by the use of a novel tree-decomposition algorithm) combined with energy minimization. In this way, we were able to obtain predictions that were close to the experimental structures—between 0.9 and 1.9 Å root mean-square deviation (RMSD) for the backbone atoms, depending on the size of the complex.

In our approach we assume that an intermediate-resolution EM map of the transmembrane helical bundle is available and that the helical segments of the sequence have been determined beforehand. We use these input data to construct another map, called a tethering map, which has low values around the helices' backbone atoms, and grows quickly away from them. This map is used as a penalty term (acting on the backbone atoms only) during the energy minimization stage to keep the helices close to their experimental positions as given by the density map. The energy function includes van der Waals, electrostatic, hydrogen bonding, and torsional terms. The effect of desolvation is included by correcting the energies through a solvent-accessibility map, which provides an efficient way to consider this contribution.

METHODS

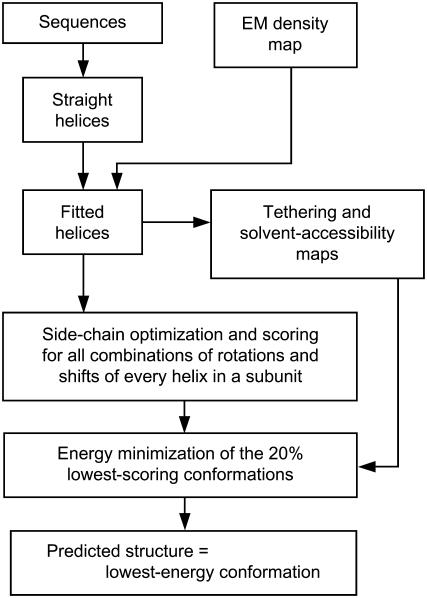
A schematic flow chart of our method is presented in Fig. 1. Details of the various steps are described below. They were performed within the internal coordinate mechanics (ICM) software environment (10); the ICM scripts used in this work are available upon request.

FIGURE 1.

Schematic flow chart of our prediction methodology.

Three-dimensional map and TM α-helix sequences

The input data consisted of an intermediate-resolution density map and the sequences of the α-helical TM segments. For real prediction cases, these segments are assumed to have been identified beforehand by standard hydropathy analysis (26,27) as well as experimental methods such as antibody labeling (28–30). For our simulated test cases, the sequences of the TM segments were based on the experimental structures. We also used the identities of the three amino acids before and the three amino acids after each TM segment, to build initial straight helices as described in the next step.

Modeling the TM α-helices

Using the given sequences, a family of ideal, straight α-helices was constructed by assigning the values −62° and −41° to the φ- and ψ-backbone torsion angles, respectively. As mentioned above, this family of α-helices included shifts along the sequence of up to three amino acids in each direction (keeping the length of each helix fixed, so when a residue was added at one end, another was deleted from the other end).

Fitting the modeled α-helices into the density rods of the EM map

Each of the helices built in the previous step (i.e., for each helical segment of the subunit and for each shift) was rotated around its main axis in steps of 10° and then flexibly fitted (keeping that rotational degree of freedom fixed) into the corresponding density rod of the (simulated) map, by minimizing an energy function that included van der Waals interactions, electrostatic, hydrogen bonding, torsional, and density correlation terms. By means of this procedure (built into ICM (10)) the backbone torsions were optimized to adjust the shape of each shifted and rotated helix to the particular density rod. Two of these fitted helices (for a particular rotation and shift), corresponding to one of the subunits in each of our test cases, are displayed in panels a–c of Figs. 3–5.

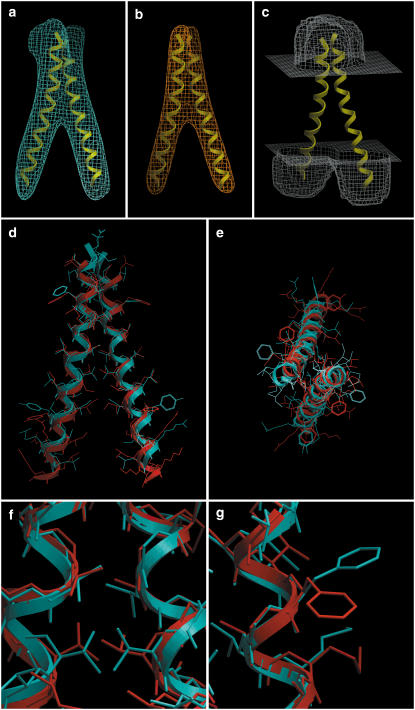
FIGURE 3.

GpA. (a) Isocontour surface of the simulated density map obtained from the NMR structure. (b) Tethering map, used as a restraint during the minimization stage. (c) Solvent-accessibility map, contoured at level 0.8. Displayed for reference are the two TM helices. (d) Side view and (e) top view of the dimer. The NMR structure is in blue, and our prediction (lowest-energy conformation) is in red. The backbone RMSD of this prediction is 0.89 Å with respect to the NMR structure. (f) Closeup of a helix-packing region near the center, where the fit of side chains is close to the NMR structure. (g) Closeup of a region facing the lipid, where, due to lack of packing constraints, the predicted side chains deviated from the NMR structure. Panel heights are: first row, 56 Å; second row, 50 Å; and third row, 12 Å.

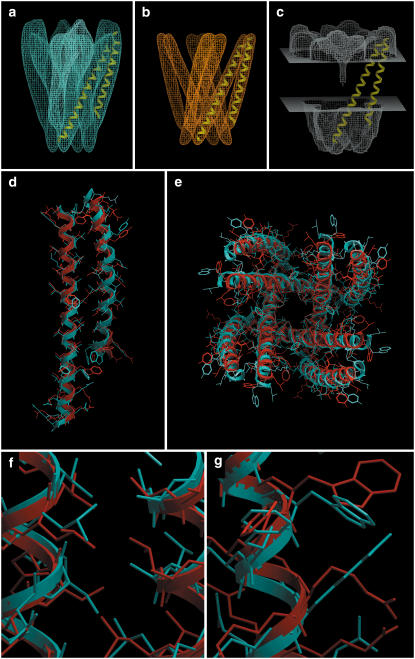
FIGURE 4.

KcsA. (a) Isocontour surface of the simulated density map obtained from the x-ray structure, including the loops and pore helices. (b) Tethering map, used as a restraint during the minimization stage. (c) Solvent-accessibility map, contoured at level 0.8. Displayed for reference are two TM helices of a subunit. (d) Side view of a subunit and (e) top view of the tetramer. The crystal structure is in blue, and our prediction (lowest-energy conformation) is in red. The backbone RMSD of this prediction is 1.59 Å with respect to the crystal structure. (f) Closeup of a helix-helix interface where the predicted side-chain packing is close to the crystal structure. (g) Closeup of a region facing the lipid, where, due to lack of packing constraints, the predicted side chains deviated from the crystal structure. Note that the fourfold symmetry of the side chains is almost perfect, even though it was not imposed. Panel heights are: first row, 80 Å; second row, 70 Å; and third row, 12 Å.

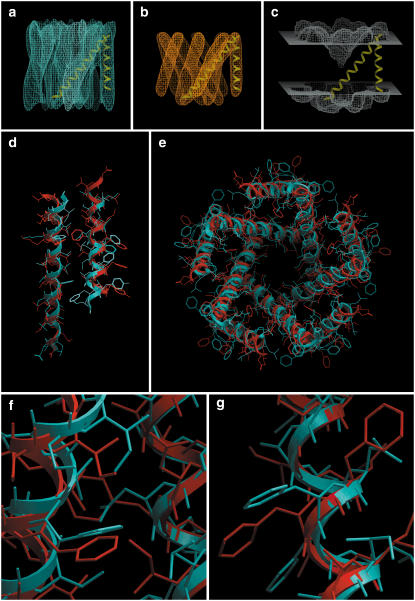
FIGURE 5.

MscL. (a) Isocontour surface of the simulated density map obtained from the x-ray structure. (b) Tethering map, used as a restraint during the minimization stage. (c) Solvent-accessibility map, contoured at level 0.8. Displayed for reference are two TM helices of a subunit. (d) Side view of a subunit and (e) top view of the pentamer. The crystal structure is in blue, and our prediction (lowest-energy conformation) is in red. The backbone RMSD of this prediction is 1.88 Å with respect to the crystal structure. (f) Closeup of a helix-helix interface where the predicted side-chain packing is close to the crystal structure. (g) Closeup of a portion of the shorter helix, for which the prediction exhibits a screw motion along the backbone relative to the crystal structure, but in such a way that there is an approximate substitution of side chains. The fivefold symmetry of the side chains is nearly perfect. Panel heights are: first row, 60 Å; second row, 60 Å; and third row, 12 Å.

Optimizing the amino-acid side chains for each backbone conformation

For each combination of rotations and shifts of the α-helices that made up a subunit, an oligomer was built by repeating the subunit according to the assumed symmetry. (This was the only step in the procedure where symmetry was imposed.) Then, a global side-chain prediction was performed by means of the SCATD algorithm (side-chain assignment via tree decomposition (31)). This algorithm generates the best packing of the side chains based on a simplified van der Waals potential and gives a score for that packing. SCATD takes ≈3 s to predict the side chains for each backbone arrangement of KcsA (264 residues) and large-conductance mechanosensitive ion channel (MscL) (220 residues) (substantially less for GpA). The output of the protocol was a table of scores for all the combinations of rotations and shifts of the independent helices. Parallel processing made this step quite efficient. For example, the score table could be generated in, at most, 15–20 min using 200 processors of the Scripps Linux cluster (64-bit, 3.4 GHz Intel XEON-EMT). (For our cases of two independent helices, there are (36 × 7)² = 63,504 backbone conformations.)

Minimizing the energy of the best conformations obtained in the previous step

This step required two maps. The first one was the so-called tethering map, which was used as a restraint to keep the helices from deviating too much from the experimental map. It was constructed as follows. First a helical bundle was built by taking one of the fitted helices for each density rod, modifying all residues to Gly, and extending each helix by the addition of two glycines at each end. (The latter prevented the final tethering map from being too short due to the lower density values near the ends of the helices.) Then, a new map was obtained by convolving this helical bundle with a Gaussian kernel with σ = 4 Å (emulating 8 Å resolution). This value of σ was not critical. Finally, we transformed this new map by applying the function

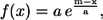where a = 0.25 σ_map, and m is a density value such that the isocontour surface of the new map at level m enclosed the backbones of the fitted helices with a reasonable leeway for their adjustment during the minimization process. The value of m should be independent of the particular structure, and indeed we found an optimal value of m = 11 for the three cases that we tested. The particular functional form has the property that its derivative at x = m is, in absolute value, 1, so it can be considered the point at which the function starts growing quickly. The particular factor 0.25 in the expression for a was chosen empirically to get a sufficiently high rate of increase of the function. The transformed map obtained in this way was our tethering map, which has low values at the helices' positions and grows quickly away from them. Isocontour surfaces of this map at level a for each of our test cases are shown in the b-panels of Figs. 3–5, with two of the previously fitted helices.

The second map needed for the minimization was the solvent-accessibility grid map. This map gave at each position in space a value between 0 and 1, indicating how much a particular atom would be exposed to water. Thus, electrostatic interactions of atoms with water were computed according to the surface-accessibility approximation of the electrostatic solvation energy (see Discussion). The experimental values of the solvation-energy surface densities reflect the electrostatic energy differences between the dielectric constant of 80 for water and the dielectric constant of ≈10 for octanol. In the construction of this map, the hydrophilic headgroups of the membrane were considered as water. The c-panels in Figs. 3–5 show isocontour surfaces of the accessibility maps for our three test cases at level 0.8. The blank region in the middle corresponded to the hydrophobic core of the membrane, for which we tested thicknesses of 22, 26, and 30 Å. The regions above and below were the phospholipid headgroups (7 Å each) and the water itself (cytoplasm and extracellular regions). This map was built by taking, as for the tethering map, one of the fitted helices for each density rod and modifying all residues to Gly. (No extensions were made here. In the KcsA case, we also added the pore helix, modified to all-Gly.) This helical bundle was then used to calculate the accessibility map, which ICM performed by using a fast modification of the algorithm of Shrake and Rupley (32). Finally, the slab corresponding to the hydrophobic core of the membrane was set to 0 (except the central part that included the cavity and channel).

The energy minimization then proceeded as follows. We considered the lowest-scoring 20% of the side-chain-optimized conformations obtained in the previous step. (This cutoff was used because the minimization was significantly slower than the side-chain assignment.) Each of these conformations was first side-chain minimized (i.e., with no backbone motions) to eliminate possible severe clashes between side chains, which could make the structure fail to converge during the minimization process. Next, the structures thus obtained were subjected to a restrained relaxation, by using a sequence of decreasing harmonic restraints. After this, the final energy minimization was performed. The energy function consisted of van der Waals, electrostatic, hydrogen bonding, and torsional energy terms, plus a term that penalized large deviations of the structure from the given EM density map. This penalty term was calculated by evaluating the tethering map, described above, at the positions of the backbone atoms of the structure; that is, by computing the sum of the map values at the positions of the backbone atoms. The positions of the side-chain atoms were not included, so their locations would not be perturbed. The minimized energy was then corrected by adding the desolvation energy, which was calculated by applying the solvent-accessibility map to the minimized conformation (in the same way as just described for the tethering map, except that in this case all atoms were used).

We have experimented with two options for the minimization: free or fixed backbone torsion angles. The former was much more computationally demanding as there were many more variables to optimize. We used this option for the GpA case. But for larger systems (including KcsA and MscL) the flexible-backbone minimization is not feasible, due, in some instances, to an overly slow convergence of the Newton method, or, in other cases, to oscillations. Hence, for the larger systems we used rigid-backbone minimization. We were strict about convergence, demanding that the norm of the energy gradient be <1—a stringent criterion given the large number of variables—and that the energy change between consecutive steps be <4 × 10⁻⁶ × N_res kcal/mol, where N_res is the total number of residues in the structure.

The energy minimization of each conformation took, for the cases presented here, between 30 and 45 s on a single processor of the type described above. Again, this step of our protocol was run in parallel to achieve efficient timings.

The output atomic model

The minimization step produced a table of energies for all the combinations of rotations and shifts of the independent helices. The conformation having the lowest minimized energy was taken as the output of our prediction protocol and was visualized using the ICM software package.

RESULTS

We have validated our methodology, outlined in Fig. 1, on three test cases: GpA, KcsA, and MscL, obtaining very good agreement between the predicted atomic models and the experimental structures (Table 1). For each of the test cases, we generated a simulated intermediate-resolution map having 6 Å in-plane and 20 Å vertical resolution, by convolving (i.e., blurring) the backbone atoms of the experimental structure with an anisotropic Gaussian kernel (Figs. 3–5 a). This emulates the typical resolution of three-dimensional cryo-EM maps derived by merging image data from tilted two-dimensional crystals (33–35). Resolution is significantly degraded due to imaging factors such as specimen drift and charging, crystal imperfections, and the missing-cone artifact due to the limited tilt angle.

TABLE 1.

Summary of RMSD values for our test cases

Molecule	Backbone atoms	All buried heavy atoms	All heavy atoms
GpA	0.89	1.30	2.26
KcsA	1.59	1.96	2.42
MscL	1.88	2.57	3.36
(TM1 / TM2)	(1.17 / 2.21)	(1.37 / 3.38)	(1.78 / 4.34)

The second row of MscL gives values for each of the two subsets of helices independently. The higher values for TM2 reflect its screw motion relative to the x-ray structure.

GpA

Glycophorin A is a sialoglycoprotein of human erythrocyte membranes, and forms dimers by noncovalent association of its membrane-spanning domain. NMR analysis of GpA dimers in dodecylphosphocholine micelles showed that the TM domains associate as a right-handed, parallel, α-helical structure (36). We used this NMR structure (PDB code 1AFO, model 1) for our first test case. However, we should emphasize that we did not impose any symmetry on the dimer, not even when constructing each backbone arrangement. In particular, we considered both vertical shifts and both rotations as independent of one another. In fact, the NMR structure itself is not symmetric, the deviation from symmetricity being 1.7 Å all-atom RMSD (0.9 Å backbone-atom RMSD).

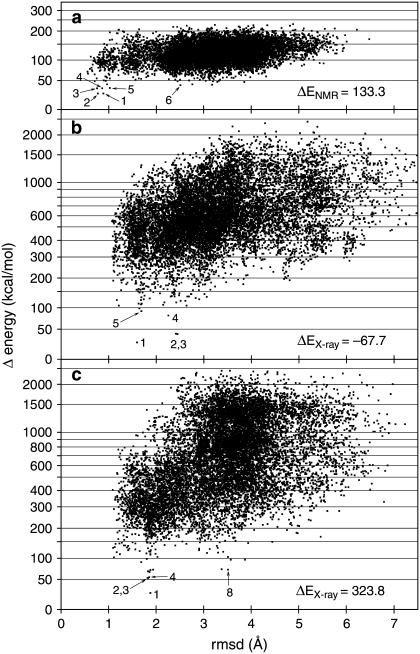
As described in Materials and Methods, the 20% lowest scoring conformations were energy-minimized, and these 12,700 points are shown in Fig. 2 a. The minimization was done, for this particular test case, with free backbone torsion angles, since the small size of this structure allowed full convergence over the whole set of variables. There was excellent agreement between the NMR structure and the best-energy prediction, with a backbone RMSD of 0.89 Å (Fig. 3, d and e). The second-best prediction (0.77 Å RMSD) differed in only 0.01 kcal/mol from the first one. Then there was a jump to the third best solution (0.76 Å RMSD) of almost 10 kcal/mol. Also, the first five solutions belonged to the first energy basin (meaning, the region around a local minimum) shown in Fig. 2 a, with RMSDs ≲1 Å. The bottom of the secondary energy basin (solution number 6) is located at ≈2.5 Å RMSD, with an energy 16 kcal/mol higher than that of the near-native solution.

FIGURE 2.

Plots displaying the 20% (12,700) lowest-scoring conformations that were energy-minimized during the predictions of (a) GpA, (b) KcsA, and (c) MscL. RMSD values, in Å, refer to the backbone atoms. Energy values are in kcal/mol. A logarithmic scale was used on the energy axis to see more detail of the low-energy conformations. In each case, the origin of the energy scale has been set at 25 kcal/mol lower than the minimum energy. The numbers indicate the rankings of the indicated solutions (see text). On the lower right of each plot, the (minimized) energy of each experimental structure is shown. Due to unresolvable clashes, there are many low-RMSD conformations that span a wide range of energy values, especially in cases b and c.

KcsA

The KcsA channel is a bacterial homolog of eukaryotic potassium channels, which regulates, with high selectivity, the transmembrane flux of K⁺ ions. KcsA is a homotetramer, and an x-ray structure at 1.9 Å resolution (9) (PDB code 1R3J) showed that each subunit contains two integral TM α-helices and the so-called P-loop, responsible for the channel's ionic selectivity. In our predictions, we have not considered the P-loop, except for the construction of the solvent-accessibility map (see Materials and Methods).

The x-ray structure and our best-energy prediction were in close agreement, with a backbone RMSD of 1.59 Å (Figs. 2 b and 4, d and e). Note that on the outside of the complex (facing the lipid) the predicted side chains differed more from the experimental coordinates due to lack of constraints (Fig. 4 g), but the interhelical packing was well reproduced (Fig. 4 f). There were three solutions belonging to the secondary energy basin, with RMSDs of between 2.2 and 2.4 Å (Fig. 2 b). In this test case the secondary energy basin (false positives) was 15 kcal/mol higher than the first. We note that the energy span is much larger than for GpA (Fig. 2 a), presumably due to the greater complexity of the structure and because the minimization procedure was done with fixed backbone torsion angles (see Materials and Methods). This resulted in stronger interactions with the tethering map for incorrect backbone geometries. Also, in Fig. 4, d and e, we can see that the shorter helix did not bend enough to fit completely into the corresponding density rod (i.e., to match the experimental helix). This happened, in this particular case, because of the presence of density corresponding to the pore helix, which moved the top part of the helix toward it during the flexible fitting step. No attempt was made to correct this at this time, but its correction would certainly decrease the RMSD values.

MscL

MscL is a specialized class of membrane proteins that mediate the sensing of physical forces and stresses on the membrane by transducing them into electrochemical responses. An x-ray crystal structure at 3.5 Å resolution from Mycobacterium tuberculosis showed that the channel is a homopentamer with two TM helices per subunit (37) (PDB code 1MSL). This third test case represented a higher order oligomeric structure (pentamer versus tetramer for KcsA).

The crystal structure and our best-energy prediction had a backbone RMSD of 1.88 Å (Figs. 2 c and 5, d and e), which is slightly higher than for KcsA and approximately twice the RMSD for GpA. We note that the second-best solution (with 1.83 Å RMSD) was more then 28 kcal/mol higher than the first, and then there were several solutions that proceeded upward in energy while staying at ∼1.85 Å RMSD. The first point of the secondary energy basin was solution number 8, 46 kcal/mol higher than the best solution, with an RMSD of 3.5 Å (Fig. 2 c). An interesting phenomenon occurred in this test case: the shorter helix was rotated and translated (screw motion) relative to the x-ray crystal structure (thus giving an average of 1.88 Å RMSD), in such a way that many of the positions occupied by the experimental side chains were nearly occupied by side chains of different amino acids.

DISCUSSION AND CONCLUSIONS

We developed an efficient method for structure prediction of α-helical membrane proteins when an intermediate-resolution EM density map is available. We make use of a novel and efficient method, SCATD (31), to predict side-chain conformations for a given backbone geometry. The SCWRL method (38), which is commonly used for this purpose, failed in our cases because the annular structure of the channels produces biconnected components that are too large, and therefore intractable by SCWRL. However, SCATD uses an entirely different approach called tree decomposition, which can solve large structures quickly (<3 s). After side-chain optimization and scoring, the best-scoring conformations are minimized using an energy function that includes van der Waals, electrostatic, hydrogen bonding, torsional and desolvation components. It has been postulated that van der Waals interactions are a predominant factor in TM helix packing (39) and in soluble proteins (38,31), but we also observed that other energy terms had a substantial contribution to the total energy and, in many cases, were comparable to the van der Waals energy. For instance, a considerable fraction of the stabilization energy was due to hydrophobic and hydrogen-bonding interactions.

Our method also incorporates a penalty term, through a so-called tethering map, which aids in guiding the minimization process so that the helices remain close to their experimentally determined positions, and avoids searching conformations that would place one or more helices outside of the corresponding density. This restraining map acts only on the backbone atoms of the structure, thus avoiding perturbations of the side chains. Tests that allowed the tethering map to restrain side-chain atoms led to wrong results.

Electrostatic interactions are divided into intramolecular and molecule-solvent interactions. The intramolecular energy was calculated using a distance-dependent dielectric constant ɛ_int = 4R (where R is the distance), whereas protein-solvent interaction was based on solvent accessibilities of the surface atoms: 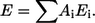The energy densities E_i were derived from water-octanol transfer energies (using a dielectric constant for water (40) ɛ_water = 80). The solvent-accessible areas A_i of each atom were calculated by taking into account both the surrounding atoms and a special grid map describing the membrane and channel geometry. This solvent-accessibility map indicates how accessible to water an atom at a particular point in space would be. In generating the solvent-accessibility map, we initially assumed that the hydrophobic barrier is 22 Å thick, and that the polar lipid headgroups are in the aqueous phase. Since the membrane thickness varies for different kinds of cells, we also carried out the calculations using thicknesses of 26 and 30 Å for the hydrocarbon core of the lipid bilayer. While these model predictions were the same as for a thickness of 22 Å for KcsA and for MscL, the results (not shown) were different for GpA. We surmise that this dependence in the GpA case was due to the very small contact area between both TM helices, resulting in a relatively large influence of the solvation energy.

The use of the tethering map and our approach for computing the solvation energy yielded a significant increase in the overall efficiency of our protocol. This represents an intermediate approach between, on the one hand, considering explicit water molecules or accurate continuous solvent models (Poisson-Boltzmann equation)—both of which are computationally too expensive—and, on the other hand, treating the molecule as if in vacuo, which ignores the solvation contribution altogether. Besides being computationally efficient, our approach allows easy modeling of arbitrary solvent geometries, especially exemplified by the pore regions in the c-panels of Figs. 4 and 5.

We validated our protocol using three test cases: GpA, KcsA, and MscL. These three examples have two independent helices (i.e., helices not related by symmetry). For each case, we computed three RMSDs (Table 1): for backbone atoms only, for all buried heavy atoms, and for all heavy atoms. In addition, for MscL we give separate values for the subsets of helices TM1 and TM2. This shows excellent agreement for TM1 with the crystal structure, but TM2 is off due to the screw motion mentioned in Results. Although the stereochemistry of this structure was quite reasonable, we do not know whether this conformation exists in nature or whether it may even have functional significance. Note that in all cases the buried-heavy-atom RMSDs are substantially lower than the all-heavy-atom RMSDs, confirming that the largest deviations from the experimental structures occur away from interhelical interfaces, due to lack of constraints. We believe that these energetically favorable conformations for the side chains apposed with the lipids could in fact exist.

Notably, our test calculations did not impose any symmetry (other than in building the backbone arrangements for KcsA and MscL), and yet the side-chain conformations of the TM residues in these two cases were virtually symmetric. The RMSDs with respect to perfectly symmetric structures were 0.48 Å for KcsA and 0.57 Å for MscL. These are all-heavy-atom static RMSDs; hence, they include backbone asymmetricity as well. The fact that these deviations are so small is a very positive indication that the procedure attains full convergence.

The predicted conformations for GpA, KcsA, and MscL were close to the experimental structures, with RMSDs between 0.9 and 1.9 Å for the backbone atoms, depending on the size of the complex. At the bottom right of each panel in Fig. 2 are shown the energy values corresponding to the experimental structures. We note that for GpA (Fig. 2 a) and for MscL (Fig. 2 c) these energy values were higher than the respective best solutions obtained by us. This could presumably be due either to imperfections in the parameters or to the functional form of the energy function utilized in the calculations. Another possibility, as suggested by Fleishman and Ben-Tal (7), is that the conformations that we used as templates do not represent the actual native-state structures, but were distorted by crystal packing, detergent interactions, the nonphysiological conditions used for crystallization, or some other reason. Another likely factor that may assign higher-than-minimum energy to the experimental conformation is the presence of extra elements such as the extracellular and intracellular loops, whereas our calculations took into consideration only the TM domains.

A strength of our approach is that it allows for backbone and side-chain flexibility, thereby yielding more realistic results than methods that treat the helices as rigid bodies. Backbone flexibility is incorporated by performing a fine sampling of backbone geometries (every 10°/1.5 Å), flexibly fitting each of these into the EM map, and then using these rigid backbone geometries during the final energy minimizations. This approach is fast and fully convergent, unlike earlier attempts that performed the minimizations over all variables (including backbone torsions), which were slow and, in many cases, failed to converge. An exception was GpA, whose all-variable minimizations fully converged, due to the reduced size of the structure. We expect that all-variable minimizations would be applicable to other membrane proteins with two dissimilar TM helices such as heterodimeric integrins (41).

With current computing power, our protocol can be applied to the prediction of structures containing up to four independent helices. We can expect that further optimization of the protocol and use of more powerful computers will expand the complexity of membrane proteins amenable to our procedure, including systems with more than four independent helices.

Given the lability of many membrane proteins in detergents, we can expect that EM analysis of two-dimensional crystals in lipid bilayers will continue to be a valuable strategy for membrane protein structural biology. Due to crystal imperfections and the difficulty in recording images at high tilt angles, structures determined by two-dimensional electron crystallography are often at an intermediate resolution (9–6 Å). Consequently, the computational methods that we have developed will be particularly useful for fitting atomic-resolution structures that can be validated using other methods such as distance constraints provided by, for example, fluorescence resonance energy transfer (42,43) and electron paramagnetic resonance spectroscopy (44,45). Given that the majority of drug targets are membrane proteins, a robust and reliable structure-prediction protocol would be quite valuable in combination with virtual ligand screening (46).