The Thermodynamic Meaning of Metabolic Exchange Fluxes

Abstract

Metabolic flux analysis (MFA) deals with the experimental determination of steady-state fluxes in metabolic networks. An important feature of the ¹³C MFA method is its capability to generate information on both directions of bidirectional reaction steps given by exchange fluxes. The biological interpretation of these exchange fluxes and their relation to thermodynamic properties of the respective reaction steps has never been systematically investigated. As a central result, it is shown here that for a general class of enzyme reaction mechanisms the quotients of net and exchange fluxes measured by ¹³C MFA are coupled to Gibbs energies of the reaction steps. To establish this relation the concept of apparent flux ratios of enzymatic isotope-labeling networks is introduced and some computing rules for these flux ratios are given. Application of these rules reveals a conceptional pitfall of ¹³C MFA, which is the inherent dependency of measured exchange fluxes on the chosen tracer atom. However, it is shown that this effect can be neglected for typical biochemical reaction steps under physiological conditions. In this situation, the central result can be formulated as a two-sided inequality relating fluxes, pool sizes, and standard Gibbs energies. This relation has far-reaching consequences for metabolic flux analysis, quantitative metabolomics, and network thermodynamics.

INTRODUCTION

¹³C Metabolic flux analysis

¹³C metabolic flux analysis (MFA) has become a widely used tool in Systems Biology and, especially, in Metabolic Engineering (1). The aim of a MFA is the quantitative determination of steady-state fluxes in metabolic pathways of a given organism. The method is based on carbon-labeling experiments in which cells are fed with a ¹³C-labeled substrate. Due to metabolic activity, the labeled material is then distributed throughout the metabolic pathways until, eventually, the labeling state in the system equilibrates and can be measured in cellular compounds. The resulting labeling data is evaluated on the basis of a mathematical model of the carbon flow to estimate the intracellular fluxes. To establish the model, carbon atoms have to be traced through the network. The available methods together with a variety of applications have been reviewed in several recent articles (1–5).

The conceptual and mathematical platform for the evaluation of carbon-labeling experiments is well established (6–9). One basic requirement for all ¹³C MFA procedures is the stationarity of the metabolic network during the time taken by the labeling experiment. Consequently, the stoichiometric equations relating the intracellular fluxes under steady-state conditions are one cornerstone of any flux analysis model. The other building block for MFA is the balance equation system for the transport of labeled carbon atoms through the network. Combining both sets of equations with measurable fluxes (e.g., substrate uptake and product formation) and the labeling data, the intracellular fluxes can be estimated with a parameter fitting procedure. This formalism is described in detail in the literature (10,11). Several computational tools are available for ¹³C MFA (12,13).

In contrast to MFA, different methods for metabolic network analysis (MNA) explore the possible solution space of the stoichiometric equations (14) or optimal flux distributions with respect to certain criteria (15). Only recently, MNA has been combined with thermodynamic constraints derived from metabolite concentrations and standard Gibbs energies (16–18). It is shown in the following that ¹³C MFA yields additional relations between Gibbs energies and fluxes that can be used in the context of flux and network analysis.

Bidirectional reaction steps

Thermodynamic reversibility (in the context of chemical reactions) usually means that the net flux of the reaction can take both directions under different physiological conditions. But even in the case where one direction is strongly preferred, there may still be a simultaneous forward and backward flux present. In fact, any chemical reaction step proceeds in both directions at the same time, i.e., there is a permanent bidirectional exchange of metabolites between the substrate and product pools (19). However, in many cases, one flux direction can be neglected and the reaction is then considered as unidirectional. Otherwise, both forward and backward fluxes must be taken into account in ¹³C MFA.

One remarkable feature of ¹³C MFA is that not only the net fluxes of reaction steps can be determined but also the individual forward and backward fluxes of bidirectional reaction steps (19). This distinguishes ¹³C MFA from methods that are solely based on stoichiometry and/or thermodynamics and, consequently, are restricted to net fluxes. The flux in bidirectional reaction steps has already been quantified in some pioneering ¹⁴C studies (20,21). A prominent example of bidirectionality was given in Marx et al. (22) where large amounts of ¹³C-labeled material arrived at the pentose-5-phosphate pools via the bidirectionally operating transaldolase and transketolase steps of the pentose phosphate pathway, although the net flux was in the opposite direction.

The necessary inclusion of forward and backward fluxes in ¹³C MFA models introduces more degrees of freedom in addition to the unknown net fluxes. For this reason, on the one hand, exchange fluxes are often considered as an unwanted computational and statistical burden for the evaluation of ¹³C-labeling data (23). On the other hand, the resolution of both flux directions can, in some cases, give invaluable information on metabolic cycles suggesting gene knockouts for improving product formation (24,25). Generally, it has never been discussed in the context of MFA how exchange fluxes can be interpreted and what their biological meaning is. This is the purpose of the present article.

Exchange fluxes of elementary reaction steps

Consider an elementary bidirectional reaction S + T … ↔ P + Q + … with a specified nominal flux direction (meaning: left to right side). Elementary here means that the reaction proceeds in one single step governed by a mass action law. Particularly, the products are immediately formed from the substrates without any intermediate states. Clearly, this is an idealization of real reaction mechanisms. In the following, it is strictly distinguished between elementary reaction steps and reaction mechanisms proceeding in several elementary steps as, for example, any enzyme-catalyzed reaction (Fig. 1).

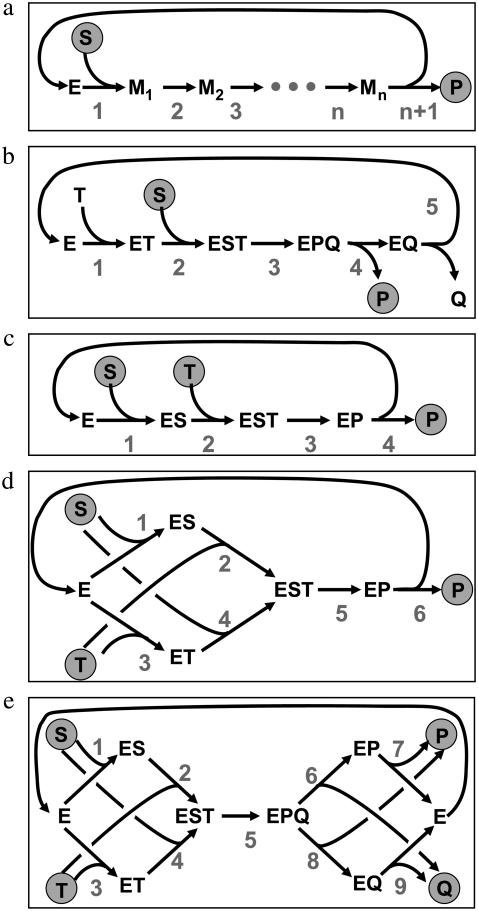
FIGURE 1.

Reaction mechanism examples of increasing complexity used to demonstrate the application of the three computational rules for apparent forward/backward flux quotients: (a) General bidirectional multistep Michaelis-Menten mechanism for a unimolecular reaction S → P. (b) Sequential mechanism for a unimolecular reaction S → P with two cofactors T, Q not taken into account for isotopic labeling. (c) Sequential binding mechanism for a bimolecular reaction S + T → P. (d) Random binding mechanism for a bimolecular reaction S + T → P. (e) Random bi-bi reaction mechanism with multiple substrates and products S + T → P + Q. S, T are substrates, P, Q are products, E is free enzyme, and M_i, ES, ET, EST, and ESPQ are enzyme complexes. Shaded circles indicate the potentially labeled substrates and products.

The forward and backward fluxes of an elementary reaction step under steady-state conditions are denoted by v^→ ≥ 0 and v^← ≥ 0. These two fluxes are unambiguously defined by the amount of molecules per time converted from substrates to products and vice versa. Here, it plays no role which substrate or product is taken to determine the fluxes, because all consumption and production rates are directly coupled by stoichiometry.

Although the two fluxes v^→, v^← are essential to formulate the carbon-labeling balances constituting the backbone of any ¹³C MFA model, they are hard to interpret when the results of a MFA have to be presented. For this reason, the flux pair (v^→, v^←) is equivalently described by the pair of net and exchange flux (v^net,v^xch). The net flux is given by v^net = v^→ − v^←, which has a clear physical meaning and is also the quantity used in classical stoichiometric MFA or in thermodynamic network formalisms (16,26,27). It can be positive or negative with the sign defined relative to the specified nominal direction of the reaction.

In contrast to the net flux, the exchange flux v^xch characterizes the reaction bidirectionality and has no direct counterpart in classical network theories. This led to different definitions in the literature (19,28,29). Since, essentially, all these definitions can be transformed into each other, the most widely used definition is taken here. Precisely, v^xch quantifies the amount of material flowing simultaneously in both directions of a reaction step:

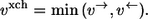Clearly, the nominal direction of a reaction step can be freely chosen. Thus, it is no restriction to assume positive net fluxes in all following investigations. In this case, it simply holds that

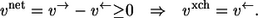(1)

In the following thermodynamic analysis of exchange fluxes, it will turn out that it is more convenient to use the forward/backward flux quotient v^→/v^← to characterize bidirectionality. In the case v^net ≥ 0 this quotient is related to the net/exchange flux quotient by

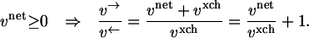(2)

This equation can be used to translate all following results to expressions using exchange fluxes familiar in ¹³C MFA.

Thermodynamic nonequilibrium coefficients

The major aim of this contribution is to relate exchange fluxes to thermodynamic properties of reaction steps under physiological conditions. The thermodynamics of a (not necessarily elementary) reaction step 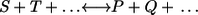is characterized by its equilibrium constant 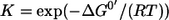where ΔG^0′ denotes the Gibbs energy of the reaction under standard conditions. Assuming standard mass action theory, it holds for the Gibbs energy ΔG′ under physiological conditions (for abuse of notation the same symbols are used both for the names of substance and their concentrations):

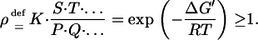(3)

The quantity ρ will be henceforth called the thermodynamic nonequilibrium coefficient (30). It provides for the most compact representation of the following results. Using Eq. 3 all obtained relations can be easily translated to a Gibbs energy formulation. The coefficient is 1 if the reaction is operating in thermodynamic equilibrium. Clearly, because the Gibbs energies of a reaction sequence behave additively, the corresponding nonequilibrium coefficients behave multiplicatively, which will be frequently used in the following.

Related work

During the reviewing process, a second article was published which is concerned with the same topic from another viewpoint (31). Whereas the present article develops all results within the classical framework of mass action kinetics, similar relations between thermodynamic driving forces, and forward/backward fluxes could be proven there for general chemical processes not necessarily governed by mass action laws.

In contrast, the present contribution has a strong focus on the consequences of the exchange flux relations to the practice of MFA. Particularly, the relation between the forward/backward fluxes of multistep reaction mechanisms obtained from classical reaction kinetic formalisms, on the one hand, and from ¹³C-labeling experiments, on the other hand, is investigated. The conceptual difference between reverse fluxes in classical reaction kinetic theory and measured exchange fluxes in ¹³C MFA is elucidated.

Nevertheless, some of the results on Michaelis-Menten-like mechanisms and flux quotients near/far from equilibrium, can be found in both articles. Combining, the present contribution with the results from Beard and Qian (31) significantly extends the generality of most statements. Some of these generalizations are already given in Beard and Qian (31).

MEASURED EXCHANGE FLUXES ARE NOT WELL DEFINED

In this section a pitfall of ¹³C MFA is discussed that has not yet been recognized in the flux analysis community. It is shown that exchange fluxes can only be unambiguously defined for elementary reaction steps. In contrast, metabolic reactions are never elementary but catalyzed by an enzyme operating in several reaction steps. For this reason the practical concept of apparent fluxes will be introduced that characterizes the whole enzymatic reaction mechanism. Unfortunately, it will then turn out that the apparent exchange flux of a reaction mechanism is not a well-defined quantity.

Apparent fluxes

Any enzyme reaction mechanism constitutes a small subnetwork within a metabolic network. As an example, an extended Michaelis-Menten mechanism as shown in Fig. 1 a is taken (S, substrate; P, product; E, free enzyme; and M₁,…,M_n are intermediate enzyme substrate/product complexes). All elementary reaction steps numbered 1,…,n+1 are considered to be reversible. The respective forward and backward fluxes 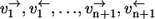are henceforth called the individual forward and backward fluxes of the reaction steps. These fluxes are well defined by mass action laws.

Generally, in ¹³C MFA, it is not possible to resolve the individual steps of an enzyme mechanism because no measurement information on the intermediate complexes can be gathered. Consequently, a complete reaction mechanism is replaced by one single (apparent) step:

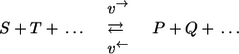(4)

with overall substrates S,T,… and products P,Q,….

By performing an MFA based on the one-step model in Eq. 4, only one single pair (v^→, v^←) of forward and backward flux is measured. These fluxes are henceforth called the apparent fluxes. Apparent fluxes are the central concept of this article. They are of high practical relevance because they constitute the actually measured quantities in ¹³C MFA. Consequently, in the following, all relations between fluxes and thermodynamic quantities have to be formulated in terms of apparent fluxes.

Path dependency of apparent fluxes

Consider now a simple reaction mechanism involving two substrates S,T, which bind to the enzyme in this order and are converted to one product P (Fig. 1 c). Four elementary reaction steps are involved in this mechanism with the individual forward and backward fluxes 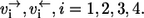Clearly, if a labeled carbon atom is traced through the reaction sequence, its origin can be both in S or T. If an atom of S is chosen to determine the apparent fluxes, it will be involved in all four elementary reactions. In contrast, an atom of P will see only the steps 2–4.

This difference has dramatic consequences as can be shown with an extreme case: Assume that the first step is unidirectional (i.e., 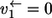) while the others are strongly exchanging. Consequently, there is a high exchange of atoms between P and T whereas it is impossible for any carbon atom to proceed backward from P to S. ¹³C MFA based on S or T labeling then yields inconsistent results because the same reaction seems to be both unidirectional and bidirectional depending on the chosen carbon atom.

In other words, the apparent exchange flux depends on the path an isotope takes when it travels through the network. This property will henceforth be denoted as path dependency of apparent fluxes. Interestingly, this phenomenon is well known from tracer studies in enzyme kinetics (32,33). However, its consequences have never been discussed in the context of ¹³C MFA, although other possible pitfalls of MFA have been recognized (34).

If path dependency has a strong relevance in practice, then the currently used network models for MFA must be changed. Precisely, each enzymatic reaction with multiple substrates must be resolved into its elementary steps. This would introduce so many additional exchange flux parameters that MFA runs into strong identifiability problems. Consequently, a major goal of the following analysis is to quantitate the path-dependency effect to judge its practical relevance.

SOME COMPUTATIONAL RULES

A set of rules is now established that allows us to systematically derive a relation between apparent exchange fluxes and nonequilibrium coefficients for a broad class of enzymatic or transport reaction mechanisms. The basic procedure is outlined as follows:

• Step 1. Fix a substrate molecule for tracing an isotope label through the reaction network. The label will then arrive at exactly one product.

• Step 2. Break down the reaction network into its elementary steps and establish a relation between the apparent fluxes and the individual fluxes.

• Step 3. Relate the individual fluxes to the respective individual nonequilibrium coefficients.

• Step 4. Compare the result with the overall thermodynamics of the reaction mechanism given by Eq. 3.

After introducing the three required computational rules, this procedure will be demonstrated with several examples.

Reaction networks and isotope-labeling networks

The term reaction-network is used here with its common biochemical meaning. It consists of elementary reaction steps with their respective reactands. Reactions with many substrates and products are possible. This is quite different with an isotope-labeling network. Choosing a single substrate for isotope labeling, the corresponding labeling network is obtained by tracing this isotope through the reaction network. By doing this only one substrate and one product is involved in each reaction step, whereas other cosubstrates or coproducts are not recognized by the labeling. Moreover, some reactions may completely vanish because no label is involved. Omitting these reaction steps and all unlabeled cosubstrates and coproducts from the original reaction network, the labeling network emerges. It contains no bimolecular steps and, thus, can be described by a simple directed graph.

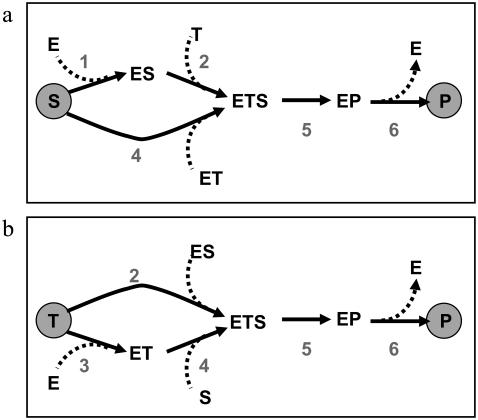
As an example, the bimolecular reaction mechanism from Fig. 1 d is discussed. Depending on the isotope chosen to be traced through the network, two different labeling networks arise (Fig. 2). In each case, one of the reaction steps of the original reaction network (Fig. 1 d) is not recognized by the label flow. Moreover, all unlabeled cosubstrates and coproducts (dashed lines in Fig. 2) are not a part of the labeling network. The resulting network is an ordinary graph with one-to-one edges.

FIGURE 2.

Isotope-labeling networks for the reaction mechanism from Fig. 1 d. (a) Tracing an S atom to P. (b) Tracing a T atom to P. Dashed arrows indicate substances which enter or leave the network but are not considered for isotope tracing.

Clearly, if the reaction network describes a proper enzyme or transport mechanisms, any labeling network derived from the original network has only one single input (the labeled substrate) and one single output (the product receiving the label). Apparent fluxes are always measured relative to this input-output pair. Finally, for any labeling network (being a simple graph) the notion of sequential and parallel reaction steps has a well-defined meaning. For example, in Fig. 2 a, the reaction sequence 1, 2 runs in parallel to reaction 4.

Exchange fluxes and thermodynamics

Based on this preliminary understanding the rules for network analysis can now be given. The rather technical proofs can be found in Appendix A in the Supplementary Material.

Sequential composition rule

Consider two sequential reaction steps 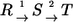in an isotope-labeling network with individual forward and backward fluxes 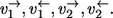Assume that a carbon atom is traced through both reactions. Then it holds for the apparent and individual fluxes of the sequence:

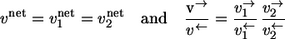It should be noticed that this rule can only be applied if there is no other reaction step involved in the intermediate pool T.

Parallel composition rule

Consider two parallel reaction steps 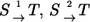in an isotope-labeling network with individual forward and backward fluxes 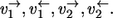Assume that the same isotope is traced through both reactions, arriving at the same position in T. Then it holds for the apparent and individual fluxes of the parallel composition:

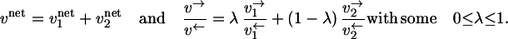Here, the mixing coefficient λ is determined by kinetic properties of the reactions and, thus, cannot be explained within thermodynamic categories.

Elementary exchange flux rule

For any elementary reaction step obeying the mass action law the following relation between forward/backward flux quotient and nonequilibrium coefficient holds:

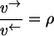SOME EXAMPLES

As proven in the Supplementary Material (Appendix A), the sequential and parallel composition rules can be applied iteratively, i.e., a sequential or parallel composition of two steps can be substituted by one single apparent step with the appropriate flux quotient. Doing this, the network can be reduced step by step until, finally, it collapses to one single apparent reaction step. This is now demonstrated for some illustrative example mechanisms.

General Michaelis-Menten mechanism

For the general reversible Michaelis-Menten mechanism shown in Fig. 1 a, the analysis proceeds as follows:

• Step 1. Since the Michaelis-Menten mechanism has only one substrate and product, there is only one single molecule S that can be labeled. The label finally arrives in P. The corresponding isotope-labeling network is the simple sequence

  
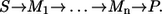
• Step 2. Applying the sequential composition rule iteratively, it turns out

  
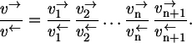
• Step 3. Application of the elementary exchange flux rule now yields

  
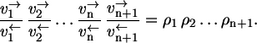
• Step 4. Since nonequilibrium coefficients of individual reaction steps behave multiplicatively, it finally follows that

  

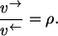
This proves that the elementary exchange flux rule also holds for Michaelis-Menten mechanisms, as already shown for n = 1 in Rolleston (35).

An example with a strict inequality

It is tempting to claim that the exchange flux rule holds for any unimolecular enzymatic reaction sequence with net reaction S → P. However, the example from Fig. 1 b shows that this is not the case. Here, the substrate binding reaction is preceded by the binding of a metabolic cofactor T that might, for example, be ATP. Likewise, the unbinding of the product is succeeded by the unbinding of a cofactor Q (e.g., ADP). Since cofactor carbon atoms are never traced in MFA, application of the rules with S and P now yields the result

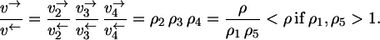However, there is still no path-dependency problem for such mechanisms because there is only one labeling path possible.

An example with path dependency

The bimolecular example from Fig. 1 c used above for demonstrating path dependency of exchange fluxes is now discussed. The two substrates S,T bind sequentially until they are fused to the product P. Two different labeling paths S → P and T → P are possible:

• Case 1. If S is chosen as the label source, the label participates in all steps of the reaction mechanism and it holds that

  

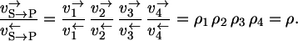
• Here, the subscript S → P indicates the path relative to which the apparent fluxes are calculated.

• Case 2. If T is chosen as the label source reaction step 1 is not recognized. Consequently,

  

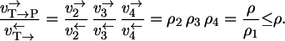
The factor 1/ρ₁ makes the difference and, thus, it precisely quantitates the path-dependency effect. Depending on this factor, the exchange fluxes measured through the two different paths will be more or less different. Path dependency completely vanishes if the first reaction step is in equilibrium.

An example with parallel reaction steps

Consider now the six-step bimolecular reaction mechanism shown in Fig. 1 d, where two substrates S, T can bind in random order until they are fused to the product P. This scheme contains two parallel reaction sequences 1, 2 and 3, 4.

• Case 1. Starting with an S atom for isotope-tracing reaction, Step 3 is not recognized (Fig. 2 a). Reassembling the labeling network from its elementary steps, an iterative combination of parallel and sequential composition rules can be applied. Then, using the energetic relation 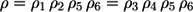(here all reaction steps must be taken into account) and Eq. 3, the exchange flux result is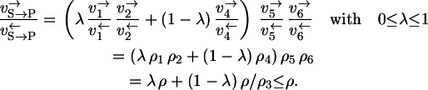

  

• Here, 0 ≤ λ ≤ 1 is the mixing coefficient between the upper 1,2 branch and the lower 4 branch of the carbon flow.

• Case 2. Similarly, if a carbon atom of the other substrate T is traced (Fig. 2 b), a similar result turns out (with another mixing coefficient τ):

  

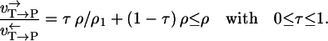
The difference is now given by the terms 1/ρ₃ and 1/ρ₁. They stem from the unrecognized reaction steps in the two labeling paths. A lower bound for the path-dependency effect can be calculated from

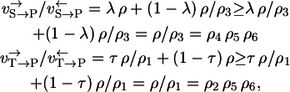from which it follows that

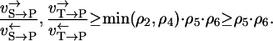Steps 5 and 6 are exactly those steps shared by both labeling networks (Fig. 2, a and b). The worst case happens when one flux quotient is at the upper bound and the other is at the lower bound. This can only happen in the extreme case where one of the reaction branches 1,2 or 3,4 is completely switched off. Thus, the lower estimate is rather pessimistic.

A more realistic lower bound might be obtained by assuming λ = 1/2, τ = 1/2, which should approximately hold in typical enzyme mechanisms. It then holds that

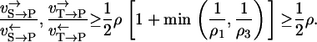A multisubstrate multiproduct example

As a more complex example, consider the mechanism shown in Fig. 1 e with two substrates and two products each binding and unbinding in random order. Four different labeling networks are now possible depending on the substrate that is labeled and the product where the label arrives. However, due to the symmetrical nature of the system it is sufficient to analyze just one combination. If an S atom is traced through the network and arrives at P, the result is

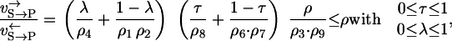where the two mixing coefficients are related to the left and right part of the network. The structure of this expression precisely reflects which reaction steps are not recognized by the label. Comparing all four labeling networks, it can also be shown that a (again rather pessimistic) lower bound for all four apparent flux ratios is

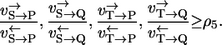Mechanisms with inhibition steps

Enzymes with inhibition are discussed as a last example. Inhibition poses no problem when the binding of an inhibitor (EX → EXI) reversibly inactivates an enzyme or an enzyme substrate complex (which is the usual assumption). Such a reaction constitutes a dead end in the reaction network. Consequently, the net flux of the reaction is zero and it holds v^→/v^← = 1. On the other hand, the enzyme complex and its inhibited state are in equilibrium, i.e., ρ = 1. It follows that inhibition steps leading to dead ends need not be considered when reaction mechanisms are analyzed.

A GENERAL THEOREM

Proper and reducible reaction mechanisms

All examples given in the last section have several things in common:

1. The reaction mechanism starts and ends with the free enzyme.

2. The free enzyme is loaded with the substrates in some random or nonrandom order.

3. The loading is followed by exactly one chemical reaction step. Any path of traced isotopes passes this reaction step exactly once.

4. The reaction step is succeeded by the unbinding of all products in some random or nonrandom order.

5. Additional enzyme state changes without binding or unbinding of a substance are possible.

6. Any enzyme state can have a reversible inhibition. The inhibited state is inactive (i.e., a dead end).

An enzyme reaction mechanism obeying these rules will henceforth be called a proper mechanism. If an isotope-labeling network can be reduced to one single apparent reaction step by applying the composition rules, they will henceforth be called reducible. In fact, most enzyme reaction mechanisms discussed in standard text books (32,33) are proper, and all their labeling networks are reducible. Some few transport mechanisms can also be described in this way (36).

Exchange fluxes of proper enzyme mechanisms

Generalizing the concepts introduced with the examples from the last section, a general theorem can now be stated:

Exchange flux theorem

Consider any proper reaction mechanism. Then it holds for any reducible labeling network derived from this mechanism that

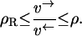Here, ρ is the nonequilibrium coefficient of the overall mechanism and ρ_R is the coefficient of the (elementary) reaction step of the mechanism.

The rather technical proof of this theorem is given in Appendix B in the Supplementary Material. Generally, the lower bound is only reached in special, rather unrealistic situations. On the other hand, if all binding and unbinding steps as well as enzyme state changes are in a rapid equilibrium, the upper bound is reached. In this case, the path-dependency effect vanishes completely.

Exchange fluxes of proper enzyme mechanisms

It should be pointed out that the theorem does not apply to any possible reaction mechanism, i.e., only a subset of all enzyme and transport mechanisms can be analyzed in this way. Exceptions essentially occur if the mechanism is not reducible by applying the parallel and sequential composition rules, or if the mechanism is not proper. This occurs, for example, if a labeling path contains more than one reaction or transport step. In this case, it can even hold v^→/v^← > ρ.Some examples are given in Appendix B in the Supplementary Material.

PRACTICAL RELEVANCE OF THE THEOREM

Due to the definition of the apparent fluxes as those fluxes measured in ¹³C MFA, the proven theorem is not just a theoretical result but also of significant practical relevance. It provides a link between MFA, quantitative metabolomics, and network thermodynamics. Note that with modern MS instruments, metabolome quantitation and labeling data generation can be combined in one single run (37–39).

Relevance of the path-dependency effect

Typically, binding steps operate closer to the equilibrium than reaction steps. Since, for proper mechanisms, ρ is always a product of individual nonequilibrium coefficients including the reaction step (i.e., 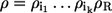), it can be concluded that the flux ratio v^→/v^← is at least in the order of magnitude of ρ. If, moreover, all binding steps and state transformations are close to equilibrium, it will hold v^→/v^← ≈ ρ. On the other hand, if there are unrecognized nonequilibrium state transformations present in the mechanisms (Fig. 1 b), it is impossible to reach the upper bound ρ.

In the practice of MFA, it is well known that the sensitivity of the measured labeling state, with respect to exchange fluxes, is very low. This means that the precise exchange values need not be known to obtain a consistent result. Fortunately, this strongly relaxes the precision requirements for apparent flux quotients. As long as the quotients of different paths are in the same order of magnitude, the path-dependency effect will have little practical relevance. This, finally, provides a rescue for the common procedure in ¹³C MFA, because one (approximate) exchange flux parameter is sufficient to describe the flow of labeled material through all possible paths.

Potential applications

The theorem can be applied in four different ways:

1. To check the consistency of estimated fluxes, measured concentrations, and thermodynamic data (16). To this end, all these data must be available and a rough estimate of ρ/ρ_R must be available.

2. To estimate standard Gibbs energies ΔG^0′ of the reactions in vivo from estimated net and exchange fluxes and measured concentrations in the case ρ_r ≈ ρ. In contrast, the current estimates of in vivo Gibbs energies rely on empirical corrections for intracellular conditions (40).

3. To eliminate exchange fluxes from metabolic flux models by using measured metabolite concentrations and reliable ΔG^0′ data. In contrast to the net fluxes which are strongly constrained by stoichiometry, every exchange flux in the model per se is unknown. Application of the theorem will greatly reduce the computational complexity of MFA methods.

4. To reconstruct hardly measurable in vivo metabolite concentrations (as, for example, oxalo acetate) when all other concentrations in one reaction step are available together with flux data and (reliable) thermodynamic data (16).

Statistical considerations

The statistical quality of the results obtained by one of these applications should be briefly addressed. Clearly, it will depend on the quality of the flux, metabolite concentration, and thermodynamic data:

1. In ¹³C MFA, net fluxes are usually well defined because they are constrained by stoichiometry. In contrast, it is hard to quantify exchange fluxes with a reasonable precision (41). However, it is possible to design special carbon-labeling experiments that produce useful confidence intervals for some chosen exchange fluxes in the focus of interest (25).

2. Likewise, the quantitative measurement of metabolite concentrations is a rapidly developing field (37,42). One of the major problems here is a proper calibration and the potential loss of metabolites in the sample preparation process. Since concentrations appear as quotients on the right side of the theorem, this error is tendentially reduced.

3. Several authors are currently dealing with the precise determination and collection of Gibbs energies under physiological conditions (40,43,44).

Reactions far from or close to equilibrium

There is a long-lasting discussion on the biological meaning of metabolic reaction steps close to and far from equilibrium. Generally, reaction steps with a large Gibbs energy are supposed to have a regulatory function (16,31,35). Using Eqs. 2 and 3, the exchange flux theorem can be reformulated as

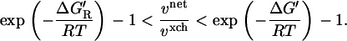This has the following consequences:

1. If the thermodynamic driving force of the reaction step is high (i.e., 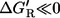), then it must hold v^net ≫ v^xch. This justifies the common assumption that reactions operating far from equilibrium can be assumed unidirectional in MFA.

2. A frequently occurring case in metabolic networks are near equilibrium reaction steps with a significant net flux (i.e., ΔG′ ≈ 0, v^net > 0). In this case, it will hold v^net ≪ v^xch, and high exchange fluxes (relative to the net flux) must be expected.

3. For a vanishing driving force of a reaction (i.e., ΔG′ → 0), it follows v^net → 0. In this situation the relation between net and exchange flux becomes singular and v^xch is no more determined by v^net and ΔG′. In this near equilibrium operation regime the exchange flux is dominated by the enzyme kinetic parameters. A kinetic analysis reveals that an exchange flux is still present when the net flux is zero (see Appendix C in the Supplementary Material).

Exchange fluxes in central metabolism

For several sets of biological reactions in the central metabolism the question of uni- or bidirectionality played an important role in the development of MFA. It is still under discussion which reaction steps can be assumed unidirectional and when both reaction directions have to be considered. The exchange flux theorem now supplies an instrument to decide which decision in appropriate under physiological conditions. A detailed analysis of the thermodynamic driving forces in vivo of all reactions for an Escherichia coli network has recently been undertaken in Kümmel et al. (16). Based on these results recommendations for the choice of the network model used in ¹³C MFA are derived in Appendix D in the Supplementary Material.

CONCLUSION

The analysis of exchanges fluxes from different viewpoints (¹³C MFA, thermodynamics, reaction kinetics) shows that this quantity carries an important information that has long been overlooked. The exchange flux theorem gives a new relation between standard Gibbs energies, metabolite concentrations and fluxes. Because most of these quantities are measurable, the theorem allows us to check the consistency of data and to reconstruct missing information from given measurements. Thus, it has far-reaching consequences for the practice of MFA.

A common assumption in early enzyme kinetic theories was a rapid equilibrium of binding steps, whereas modern formalisms just need a steady-state assumption for the reaction network. In the case of rapid binding equilibria, the exchange flux theorem reduces to an equality. Fortunately, exchange fluxes are, in practice, only determined up to an order of magnitude. This allows us to release the rapid equilibrium condition to the requirement that the reaction step should share a significant part of the overall reaction energy. Some few examples of known reaction velocity constants from literature (32,33) support that this will be the case for the majority of enzymes.

At the same time, the analysis revealed a conceptual problem of ¹³C MFA, which is the path dependency of measured exchange fluxes. Looking closer, it turned out that path dependency is the deeper reason why the exchange flux theorem for enzymes does not yield an exact equality. On the one hand, this effect is a fundamental limitation for the precision of ¹³C MFA. On the other hand, it could be shown that the quantity of this effect is not significant in most practical applications. However, being rigorous, the precise conditions for path independency must still be checked for every individual enzyme.

The theorem is proven for the class of proper reducible enzyme or transport mechanisms. This covers many mechanisms commonly published in text books. However, there are still mechanisms which do not belong to this category. It has to be investigated in the future how far the theorem can be generalized. One important step has already been taken in Beard and Qian (31) by generalizing the elementary exchange flux rule to arbitrary mechanisms not necessarily governed by mass action laws.

Although some basic results were already available in the 1970s it took until now that its value for MFA has been recognized. These developments are obviously driven by the recent experimental progress in ¹³C MFA, quantitative metabolomics, and network thermodynamics that make the theorem practical. Clearly, the practical application in various situations will be the next step in research.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.