Chlorophyll Ring Deformation Modulates Q_y Electronic Energy in Chlorophyll-Protein Complexes and Generates Spectral Forms

Abstract

The possibility that the chlorophyll (chl) ring distortions observed in the crystal structures of chl-protein complexes are involved in the transition energy modulation, giving rise to the spectral forms, is investigated. The out-of-plane chl-macrocycle distortions are described using an orthonormal set of deformations, defined by the displacements along the six lowest-frequency, out-of-plane normal coordinates. The total chl-ring deformation is the linear combination of these six deformations. The two higher occupied and the two lower unoccupied chl molecular orbitals, which define the Q_y electronic transition, have the same symmetry as four of the six out-of-plane lowest frequency modes. We assume that a deformation along the normal-coordinate having the same symmetry as a given molecular orbital will perturb that orbital and modify its energy. The changes in the chl Q_y transition energies are evaluated in the Peridinin-Chl-Protein complex and in light harvesting complex II (LHCII), using crystallographic data. The macrocycle deformations induce a distribution of the chl Q_y electronic energy transitions which, for LHCII, is broader for chla than for chlb. This provides the physical mechanism to explain the long-held view that the chla spectral forms in LHCII are both more numerous and cover a wider energy range than those of chlb.

INTRODUCTION

The chlorophyll (chl) molecule, in its different chemical forms, is involved in the photosynthetic process of plants and bacteria, where it plays essential roles in light gathering and charge separation processes. In the photosynthetic membrane, chl is bound to a number of proteins in the so-called chl-protein complexes.

The chl molecule, in a dry diethyl ether solution at room temperature (RT), has its central Mg atom in a pentacoordinated configuration with the four nitrogens and an external ligand (1–5). This is considered to be the usual configuration in nonpolar solvents (2). However, a coordination change to the hexacoordinated state has been proposed on lowering the temperature (5). High-resolution crystal structure analyses of both ethyl chlorophyllide a and b (6,7) show a pentacoordinated Mg displaced by 0.39 Å from the nitrogen N1-N2-N3 plane (NB-NC-ND, according to Protein DataBank (PDB) nomenclature). Moreover, all the nonhydrogen atoms of the chlorin ring are displaced out of the nitrogen plane (6,7), indicating that the chl molecule has skeletal flexibility.

The fundamental question of whether deformations observed in crystals are due to the crystal packing and whether the deviations from planarity observed in crystals are also maintained in solution was clearly formulated by Fajer (8). A comparison between crystal structure and extended x-ray absorption fine-structure analysis of differently distorted Ni-porphyrin samples and using the sensitivity of the Ni-N distance to distortion indicates that distorted conformations observed in solution are maintained in crystal hosts (9,10).

The conformational variations affect the porphyrin molecular orbitals (10,11) and can modulate the redox and light absorption properties of chromophores (8), with a marked red-shift of the lowest energy optical transition of distorted porphyrins with respect to the planar conformation (9). A relationship between the red shift of the porphyrin absorption transition and the conformational changes from planar to nonplanar structure has been proposed and thoroughly analyzed for both synthetic and natural porphyrins (10–14). The distortion-induced porphyrin absorption red shift was theoretically described as being due to changes of the highest occupied molecular orbitals (HOMOs), with little effect on the lowest unoccupied molecular orbitals (LUMOs), leading to a smaller energy gap between HOMOs and LUMOs (10).

The lowest energy Q_y absorption bands of (Bacterio)chl-protein ((B)chl) complexes from photosynthetic organisms, where only (B)chls contribute, are red-shifted with respect to (B)chl absorption in solvents (15–20) and are spectrally congested due to the presence of a number of (B)chl forms that absorb at different energies (18,21,22). Analyses of in vitro reconstituted chl-protein complexes, after mutation that selectively eliminated a protein Mg ligand, show that these point mutations have a selective impact on the absorption spectrum (23,24). Besides, in PSI antenna complexes, chla molecules have been identified (25,26) which have huge red shifts that set their absorption at lower energies than the PSI reaction center (red spectral forms). The spectral forms are generally loosely ascribed to interactions with the host protein and/or to the presence of excitonic interaction between the chls that split the unperturbed electronic energy transitions leading to lower energy contributions.

Among the chl-protein complexes, the Bchla protein of Prosthecochloris aestuarii, known as FMO protein, was the first isolated and crystallized (27,28) and its structure determined at a relatively high crystallographic resolution. Seven Bchl molecules were resolved and analyzed. They displayed a systematic departure from the best least-squares plane of the atoms of the conjugated part of the macrocycle (28) and, on this basis, were divided into two different distortion classes. Moreover, a deviation of the pentacoordinated Mg atom from the least-squares plane and toward the side of the ring plane facing the protein ligand was described for each Bchl. These out-of-plane displacements are in the range 0.43–0.54 Å. The presence of distorted Bchla was confirmed, some years later, by crystal analysis of the Bchla protein from Chlorobium tepidum (29), but with lower Mg out-of-plane distances (in a range 0–0.22 Å) than previously observed. The comparison between the two structures show differences also in the planarity of tetrapyrroles (29). The occurrence of distortions of the tetrapyrrole ring away from planarity was associated with interactions with the protein backbone and their involvement in generating the different spectroscopic properties of the two complexes was hypothesized (29). Room temperature FT-Raman spectroscopy of light-harvesting complexes from different bacteria show that bound Bchla molecules have significant and conserved distortions (30), an indication that chl distortions also exist in a noncrystallized protein host. On the basis of Bchl crystal coordinates of the FMO complex, Gudowska-Nowak et al. (21) theoretically predicted that different molecular conformers and different residues in the cromophore neighboring region gave rise to the different spectral properties of the seven Bchls.

In recent years, a number of photosynthetic complex crystal structures containing chla and chlb have been analyzed, revealing the architecture of the photosynthetic systems and identifying the spatial position of the different chl molecules (31–37). The crystal analyses span a wide interval of resolutions and different chl molecule models have been used to elucidate the structures. As a result, not all the chl-protein complexes analyzed contain reliable information about possible chl ring deformations. This information is, however, present in the crystal analysis of the Peridinin-chlorophyll-a-protein (PCP) complex (32) from a dinoflagellate and of the LHCII complex (35) from spinach. The recent crystal structure of LHCII by Liu et al. (35), while substantially confirming the findings of the first published structure (31), yields, at relatively high resolution (2.72 Å, R = 0.128), information about 10 monomeric LHCII chl-protein complexes, nine of which are organized in three different antenna trimers, with the direct identification of 80 chla and 60 chlb molecules with their different ligands. The possibility of having the atomic coordinates of all the atoms comprising the chl molecules, present in the Liu et al. (35) structure, allows analysis of chl ring distortions for LHCII, as already done for Bchl. In this latter case, the root mean-square deviation of the conjugated atoms with respect to a least-squares molecular plane was taken as a measure of the Bchl molecule distortion (21,28). More recently, Shelnutt and co-workers proposed a different method to quantify and classify the structural deformations of the porphyrin macrocycle (12,13,38). They analyzed the structure of porphyrins in terms of equivalent displacements along the out-of-plane and in-plane normal coordinates, developing a theoretical framework and a computational procedure to decompose the total distortion in terms of normal deformations. Shelnutt's laboratory has made their normal-coordinate structural decomposition (NSD) procedure available for use (http://jasheln.unm.edu).

In the present study, the following points are addressed:

1. The unperturbed energy gaps between HOMOs and LUMOs, characteristic of the chlorin planar macrocycle conformation, are evaluated on the basis of the results obtained by NSD analysis of the crystal data for isolated chls.

2. The chl out-of-plane deformation modes and deformation energies of two different chl-protein complexes, namely PCP from Amphidinium carterae and LHCII, are determined using NSD analysis.

3. The energy changes due to deformation, obtained by NSD analysis, are used with the unperturbed energy terms to estimate the chl site intrinsic structural energies, i.e., the Q_y transition energies in the absence of other sources of energy modulation than the deformations.

4. The impact of nonspecific solvatochromic effect on the Q_y transition energies is considered as a function of the refractive index.

It is shown that macrocycle deformation plays an important role in chla and b Q_y electronic energy modulation in chl-protein complexes.

MATERIALS AND METHODS

To obtain a method to classify and quantify the displacement from planarity of porphyrin structures, Shelnutt and co-workers developed a computational procedure for determining both out-of-plane and in-plane displacements along the normal mode coordinates of a porphyrin macrocycle (NSD). Their approach is thoroughly discussed in a series of articles (12,13,38) where the normal modes of a porphyrin structure, given in terms of (x,y,z) coordinates of its atoms, are described in terms of normal deformations. Each of these normal deformations is defined as having the square root of the sum of the squares of the displacements of the N atoms of the macrocycle from a reference position equal to 1 Å. This set of normal deformations represents the basis vectors set used to decompose the spatial conformation of a porphyrin molecule macrocycle.

Shelnutt and co-workers (12,13,38) have also shown that metalloporphyrin out-of-plane deformations, evaluated with respect to the mean plane defined by the atomic coordinates of the observed macrocycle structure (39), can be described using a reduced set of the total (N-3) out-of-plane normal modes. This reduced set contains only six modes that are the lowest-frequency normal modes of the different symmetry types having the smallest restoring forces. These six modes correspond to the so-called minimal basis for the deformation representation and are named saddling (B_2u), ruffling (B_1u), doming (A_2u), waving(x) (E_g(x)), waving(y) (E_g(y)), and propellering (A_1u). The symmetries are indicated in parentheses, according to the D_4h point group nomenclature usually used to classify porphyrins or chlorin modes although, in this case, the presence of an additional ring lowers the symmetry. The total macrocycle out-of-plane deformation is then described as a linear combination of the six deformations comprising the minimal basis, weighted by the proper displacement d_n. The displacement d_n along each of the low frequency out-of-plane symmetry types is the square-root of the sum of the squares of the vertical (z) displacements of each atom of the macrocycle from the mean plane. With the NSD computational procedure, the observed porphyrin nonplanar distortion is then represented in terms of the six lowest frequency out-of-plane normal modes allowing determination of the contribution of each normal mode to the analyzed structure. The calculated nonplanar porphyrin macrocycle distortion is then an approximate description of the observed distortion due to the use of a reduced set of deformations. To evaluate the goodness of the calculated structure of the macrocycle to describe the crystallographic observed conformation, the mean deviation between the calculated and observed out-of-plane displacements and the mean positional error in the x-ray crystallographic data (40,41) are compared (42). When the mean deviation is lower or of the order of the mean positional error, the description in terms of the minimal basis is considered a good representation of the observed distortion (42). It is evident that structures having low mean positional errors must be considered to obtain reliable information. This is the case for the structures analyzed here. An upper limit of the mean positional error for an atom in a three-dimensional structure can be set in the range 0.05–0.1 of the given crystallographic resolution (40,41). It should be noted that only out-of-plane displacements are considered in the following and the errors in the vertical (z) displacements are lowered further by a factor of ∼0.5, due to the reduced dimensionality (38). As a rough indication, when the simulated macrocycle conformation fulfill the above requirements, the ratio between the total out-of-plane distortion of the macrocycle obtained by the simulated structure and by the observed structure is ≥0.85–0.9. The total out-of-plane distortion is defined as the square root of the sum of the squares of the out-of-plane displacements of the atoms comprising the chl macrocycle.

To obtain the exact description of an out-of-plane macrocycle deformation, besides the six lowest frequency deformation of each symmetry, the contributions due to deformations along higher frequency modes are required (38). The six lowest frequency out-of-plane deformation modes represent the softest deformation modes, i.e., those modes that require the least deformation energy to induce a distortion giving rise to a specified displacement with respect to the reference plane and, thus, have the highest probability of occurring (38). On the other hand, the high frequency normal deformations require higher energy to cause the same displacement and then, usually, small displacements from the in-plane reference are involved. In the limit of small total macrocycle deformation, the displacements connected with high frequency modes are usually smaller than those connected with the low frequency modes and smaller than the statistical positional uncertainties in the x-ray coordinates of protein crystal structures at the presently available resolutions. Then, while the displacements connected to the lowest frequency deformations can be, at least in principle, reliably obtained this is precluded for the displacements connected with the high frequency out-of-plane normal modes. Moreover, as the strain energy involved in the deformation modes is, in the harmonic approximation, proportional to the squared frequency of the mode, it is clear that the contributions due to high frequency modes to the macrocycle out-of-plane deformation energy turn out to be strongly emphasized. While taking into account the high-frequency contributions give only a small contribution to the total macrocycle out-of-plane deformation description, this adds a dominant noise contribution to the estimated total deformation energy, ruling out a reliable analysis and preventing an assessment of the real physical effect of interest. It is also interesting to note that the use of x-ray coordinates, at the actual resolution obtained with chl-protein complexes, as input data for calculation of electronic structure or full spectroscopic properties of cofactors has serious drawbacks as an incorrect representation of one bond length is sufficient to dramatically change the results (43).

On the basis of the structural decomposition of the porphyrin crystal structure coordinates in terms of the lowest out-of-plane deformation modes, it is possible to estimate the deformation energy (E_D) related to the softest deformation modes, using the deformation energy δE_n of each of the six deformation modes (38) comprising the minimal basis,

(1)

where k_n is the force constant [kJ mol⁻¹ Å⁻² or cm⁻¹ Å⁻²] and d_n is the displacement related to the n^th normal mode obtained by NSD analysis. The k_n values for the different normal modes were calculated by Jentzen et al. (38) for a macrocycle model and are shown in Table 1, with the characteristic frequency of each deformation mode defined according to Jentzen et al. (38).

TABLE 1.

The force constant k and the frequency ν related to the six low frequency normal modes comprising the minimal basis for NSD analysis

Mode	k [cm−1 Å−2]	ν [cm−1]
B2u	761	65
B1u	1379	88
A2u	3461	135
Eg(x,y)	5626	176
A1u	19,929	335

The k- and ν-values for the different normal modes were calculated by Jentzen et al. (38) for a macrocycle model. The values of k represent the energy related to a 1 Å distortion.

The different electronic transitions of a porphyrin (chlorin) molecule have been represented, in the context of the Gouterman model (44,45), as involving a combination of one electron promotion between the two highest occupied (HOMO) and the two lowest unoccupied (LUMO) molecular orbitals. The role of conformational variations in modifying these HOMOs and LUMOs levels has been suggested and analyzed for Bchls (21). Moreover, as already mentioned in the Introduction, a correlation exists between bathochromic (red) optical shift and a reduced HOMO-LUMO energy gap, due to modifications of the energy levels of these frontier orbital induced by macrocycle distortion ((10,14) and references therein). In addition, a correlation also exists between changes in porphyrin redox potentials and energy levels of the HOMOs and LUMOs (9) for structurally distorted synthesized porphyrins, which tends to suggest that macrocycle distortion mainly acts by modifying the frontier orbital properties.

It has been shown (46) that for chla and Bchla, and using the D_4h symmetry nomenclature also for these molecules, the HOMO correspond to the a_1u symmetry, the HOMO-1 to the a_2u, the LUMO to e_g(x), and LUMO+1 to e_g(y). These symmetries are also that of four of the six normal modes comprising the minimal basis used to describe the total deformation of the porphyrin macrocycle in the NSD framework. We considered that, for small deformations, the energy level of the orbital with the n^th symmetry is perturbed by the deformation along the normal mode with the same symmetry. The energy E_n of the molecular orbital with n^th symmetry is represented as the sum of a zero-order energy term, and a first-order energy change, (Eq. 1), due to deformation

(2)

where n numbers the four different symmetries a_1u, a_2u, e_g(x), and e_g(y). The parameter k_n then describes how a change in deformation affects the energy level. is the energy in the absence of deformation and is termed unperturbed energy for the n^th symmetry, a characteristic of the porphyrin planar form. The δE_n values for the lowest frequency normal mode are evaluated using the displacements d_n obtained by NSD analysis. The energy transitions involved in the and ) electronic promotions can then be written as

(3)

in terms of the energy gaps of the unperturbed molecule, ΔE⁰, plus the changes of the energy gaps, ΔδE, due to ring deformation.

The Q_y transition is described, in the four-orbital Gouterman's model (44,45), as a subtractive combination of the two electron promotions HOMO → LUMO and HOMO-1 → LUMO+1, due to a mixing by configurational interaction. Despite the approximation, this approach gives a good estimate of the Q_y electronic transitions due to the marked separation of the highest HOMOs and lowest LUMOs from the other chl levels (47,48).

The dominant contribution to the chls and Bchls Q_y excited-state transition is the HOMO → LUMO, which is the shortest energy gap, with minor contribution from the HOMO-1 → LUMO+1. There is a general consensus (21) that the HOMO → LUMO contribution is >90% for Bchla and the energy gap ΔE_H→L then coincides with the Q_y transition energy. A clearcut indication for chla is lacking. However, a number of theoretical studies suggest a contribution of between 74% and 82% for the HOMO → LUMO (46,48,49), indicating a divergence between the Q_y energy transition and the HOMO → LUMO gap. The estimation of the chl Q_y energy transition then requires further considerations.

The Q_y transition energy ( ) for the chl molecule is evaluated, following Gouterman and Wagniere (45), in terms of one of the eigenvalues of the matrix

(4)

in the form

(5)

where C is the term that mixes the two pure states; it is considered as a characteristic of the molecule. ΔE_H→L and ΔE_H−1→L+1 are the energy gaps between HOMOs and LUMOs. The two energy gaps can be written in terms of the unperturbed contribution plus a perturbation term (Eq. 3) and Eq. 5 can be simply rewritten as

(6)

where the contribution due to the perturbation of the planar macrocycle conformation, δΔE, are pointed out. To evaluate the modulation of the transition energy in the presence of chl macrocycle deformation, knowledge of the reference set including the energy gaps of the unperturbed conformation, is necessary. The values of the two unperturbed energy gaps and characteristic of the planar conformation, are obtained using the crystallographic data for isolated chla and chlb (6,7). This is done in the first part of Results and Discussion, where the crystal data are analyzed by NSD and the energy changes evaluated.

The value of C is obtained by simple inversion of Eq. 5,

(7)

when the two energy gaps ΔE and the corresponding transition energy, of a chl reference structure are known. The numerical evaluation of C is in the first part of Results and Discussion, using chl in solution as the reference structure.

Of course, the wavelength maximum of the chl absorption spectrum is also influenced by a number of interactions between chls and their microenvironment (50) and, then, other sources of energy modulation than just ring deformation must be considered. The solvent effect is certainly involved in modulating the transition energy as well as the excitonic interaction, when present. Of these two main sources of energy modulation, only the solvent effect will be considered in the following.

The chl Q_y energy transition in the presence of an host medium is influenced by the nonspecific solvatochromic effect that plays a major role in solution (5,15), but, presumably, also in the presence of a protein host, modifying the chl intrinsic absorption maximum. This effect was analyzed for chla (5,15) using its wavelength absorption maximum, λ, measured in a number of different solvents. A parameterized linear equation (51) that contains the refractive index, n, and the dielectric constant, D, of the solvents was obtained (5). The result, written in terms of the fit parameters, has the form

(8)

where λ₀ = 645.8 nm (15,485 cm⁻¹) is inferred as the chla Q_y wavelength transition independent of nonspecific solvent effects (vacuum transition). It is not clear which values of the parameters n and D are the most appropriate for chl in a protein environment.

The choice of the refractive index is particularly important in the description of the excitation energy transfer in chl-protein complexes and two opposite views are usually considered (52). In the first, the refractive index is a property of the medium separating the interacting molecules (local picture); in the second, it is characteristic of the solvent (solvent picture). The wide usage of the bulk solution refractive index as the appropriate index of refraction in the Förster energy transfer process between chromophores in protein, as suggested by Moog et al. (53), was criticized by Knox and van Amerongen (52). Kleima et al. (54), using a PCP-complex, estimated n = 1.6, and adopted a local description. A value of n = 1.54 for the refractive index of photosynthetic protein complexes has been estimated (55) on the basis of the carotenoids energy shift and n = 1.51 was estimated for CP47 (56). The value n = 1.54 is used in a recent analysis of LHCII (57) although, in a previous study, arguments are expressed in favor of the use of the solvent refractive index (58). It is interesting to note that the refractive index of adsorbed protein layers in the range 1.36–1.55 was proposed as a function of the size of the protein (59). In our analysis, we considered an interval of refractive indices between 1.3 and 1.7.

The other parameter that plays a role in the solvatochromic effect is the dielectric constant D (Eq. 8). A value in the range 4.6–6.8 (60,61) was estimated for protein although dielectric constants up to 20 are often utilized. This parameter has, however, only a small effect on the red shift of the electronic transition (not shown), as described by Eq. 8. To give an idea of the impact of nonspecific solvent effect on the wavelength transition, it can be seen (Eq. 8) that this effect, per se, determines, for n = 1.54, a red shift >21 nm.

RESULTS AND DISCUSSION

Chlorophyll a and b

In two companion articles, Strouse and co-workers (6,7) published the crystal analyses of ethyl chlorophyllide a and b for crystals grown from an acetone-water mixture. They gave the fractional coordinates for the atoms of both molecules that, after suitable conversion into orthogonal coordinates (not shown), can be used for the NSD analysis. In the same year, Kratky and Dunitz (62) published an independent structural analysis of chla. The observed agreement between the two sets of positional parameters lends value to the chl crystallographic model obtained. The crystal analyses of both chla and chlb gives molecular structures that are puckered with respect to the nitrogen NB-NC-ND plane (according to PDB nomenclature) with the fivefold coordinated Mg atoms being displaced by 0.39 Å as a mean (6,7). A water molecule occupies the fifth coordination site. The out-of-plane displacements of the chla macrocycle atoms are shown in Fig. 1, using their crystal coordinates (6,7).

FIGURE 1.

The observed chla atoms out-of-plane displacements. The distances of all the atoms comprising the chl macrocycle with respect to the nitrogen plane NA-NB-NC are shown in an (x,z) projection. For clarity, the mirror image with respect to the CHC atom of the II, III, and V rings is shown. The Mg atom is also displayed (pentagon). The coordinates of the chl atoms are those given by Chow et al. (7). The nomenclature is according to PDB.

The chl macrocycle conformation is described in terms of the normal-coordinate structural decomposition (NSD) using the minimum set of out-of-plane deformations. The results for both chla and b molecules (Fig. 2) show that all the low frequency modes comprising the minimal basis contribute to the macrocycle deformation. The B_2u and E_g(x) modes have a relatively greater displacement (contribution). This set of low modes can, in principle, contribute to the vibronic spectrum of chl, indicating the possible presence of low frequency modes (≥65 cm⁻¹) also in the absence of protein interactions.

FIGURE 2.

Out-of-plane displacements for isolated chla and chlb. The values are obtained by NSD analysis of the crystallographic data (7) using the minimal set of normal modes ((38), Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature).

The deformation energy associated with each mode can be estimated using Eq. 1 with the deformation parameters (displacement) d_n obtained by NSD analysis (Fig. 2). Values of the total deformation energies are E_D = 436 cm⁻¹ for chla and E_D = 358 cm⁻¹ for chlb. In Fig. 3 A, the deformation energies and associated with the A_1u, A_2u and the two E_g(x,y) modes are shown. These modes are those with the same symmetries of the four molecular orbitals involved in determining the Q_y energy transition (46) on the basis of the Gouterman model. The values of the deformation energies of the different modes are used to obtain the two energy perturbation terms ΔδE_H→L and ΔδE_H−1→L+1 (Eq. 3). Their values, shown in Fig. 3 B, are positive for both chla and chlb and are almost equal for chlb. The positive perturbation of the two HOMO-LUMO energy gaps (Fig. 3 B) means that a blue shift of the Q_y transition is expected for the distorted molecule.

FIGURE 3.

Energy contributions due to chl macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation-induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for isolated chla and chlb obtained using the deformation energies of panel A.

To evaluate the perturbation induced by macrocycle deformation on the chla transition energy (Eq. 6), a choice of the set to be used as a reference, is necessary. This set contains the two HOMO-LUMO gaps characteristic of the planar chl macrocycle conformation (unperturbed gaps). A reference value of and the related two HOMO-LUMO gaps are required to estimate the value of C (Eq. 7) to be used as a characteristic of the chl molecule. In addition, the value of must be independent of solvent effects (λ₀, vacuum transition). Krawczyk (5), fitting the absorption maxima of chla in solution in a number of different solvents, determined a value of λ₀ = 645.8 nm ) (see Eq. 8), which is used as the transition energy reference value in Eq. 7. To define the two HOMO-LUMO gaps related to this energy transition, the two following possibilities are contemplated:

The isolated chl crystallographic model, with its distortions, is considered a representation of the chl conformation in solution

Hanson (46), using the isolated chla crystal coordinates (7), gave an estimation of the two energy gaps ΔE_H→L = 18,800 cm⁻¹ and ΔδE_H−1→L+1 = 29,500 cm⁻¹. These values, regarded as representative of chla in solution, are then used in Eq. 7 and the value C_a = 6816 cm⁻¹ is obtained. To extend the analysis also to chlb, and in the absence of other information, we assume that the two energy gaps are the same as those of chla. Using Eq. 8, with the chlb absorption maxima measured in Acetone and Diethylether (17) and the values of the respective refractive indexes n and dielectric constants D, the vacuum value λ₀ = 629.3 nm () is obtained. From Eq. 7, the value C_b = 6292 cm⁻¹ is then calculated. To obtain the two unperturbed energy gaps, the values of ΔδE_H→L and ΔδE_H−1→L+1 (Fig. 3 B) for both chla and b are used in Eq. 3, with ΔE_H→L = 18,800 cm⁻¹ and ΔδE_H−1→L+1 = 29,500 cm⁻¹ calculated by Hanson (46) using the crystal data. Values of and ΔδE_H−1→L+1 = 29,472 cm⁻¹, for chla, and and for chlb, are obtained. When the crystal structure is taken as representative of chl in solution, the reference sets for both chla and chlb are then {18,735; 29,472; 6816}_chla and {18,723; 29,416; 6292}_chlb.

However, the origin of the distorted chl conformation (Fig. 1), as due to the crystal packing, cannot be ruled out. The chl molecules in the crystal appear as aggregated in a one-dimensional polymer connected to form a two-dimensional aggregate due to a network of hydrogen bonds. This is, presumably, not the case in solution. Hemes are expected to be nearly planar in the absence of external perturbations (63) although an influence of the metal size on the conformation is recognized (63). Moreover, the conclusion that, in solution and in the absence of other interactions, the planar conformation is the stable conformation for chromophores containing large metals, as for chlorophyll, was reached (63). If this is the case, then:

The macrocycle planar conformation is considered as the representation of chl conformation in solution

In this case, the two unperturbed energy gaps, and characteristic of the planar conformation, are considered as a characteristic of the chl in solution and then used to evaluate C. With this choice, and using the values of the unperturbed energy gaps, obtained above for chla, in Eq. 7, the value of C_a = 6742 cm⁻¹ is obtained for chla. Assuming, also in this case, that the two unperturbed chla energy gaps are representative of the chlb molecule in solution, the value C_b = 6215 cm⁻¹ is obtained (Eq. 7). When the planar macrocycle conformation and the unperturbed energy gaps are considered as representative of chl in solution, the two reference sets {18,735; 29,472; 6742}_chla and {18,735; 29,472; 6215}_chlb are obtained for chla and chlb, respectively.

The reference set is now completely defined for both chla and chlb and as a function of the previously discussed choice of the reference structure. These sets are used in the following to evaluate the perturbation induced by the chlorophyll macrocycle deformation on the energy transition in the chl-protein complexes.

It is interesting to note that the calculated eigenvectors of the Gouterman matrix (Eq. 4), using the values ΔE_H→L, ΔE_H−1→L+1 defined by Hanson (46) and the values of C obtained previously, give a contribution of the H→L transition to the lowest energy state Q_y of ∼81% (with the condition that the sum of the squares of the eigenvectors is 1). This contribution is of the order of those published for chla ((46,48,49); and see above).

Peridinin-chlorophyll-a-protein

Peridinin-chlorophyll-protein (PCP) is a water-soluble light-harvesting complex that is present in most photosynthetic dinoflagellates. This complex transfers energy to PSII and contains peridinin, as the main light-absorbing pigment, as well as chla. The pigments are organized in two clusters of four peridinin and one chla each (64). The relative simplicity of this complex renders it an ideal system to study chl-protein interaction (65–69). Its high-resolution (2.0 Å, R-value = 0.179) x-ray structure ((32), PDB ID 1PPR) reveals a trimeric organization with each polypeptide that binds eight peridinin and two chla molecules (CLA1 and CLA2, PDB nomenclature). The peridinin pigment does not contribute to the chla absorption at 670 nm (54,65). The two chla molecules are ∼17 Å apart and interact weakly (32,66). There is a general consensus about a spectral heterogeneity between chl pigments (66–68), although the exact energy of the two chl contribution is still under debate (69).

In the following, the structural data of the three chl couples bounded to the PCP trimer (32) are all used for the NSD analysis in terms of the minimal set of out-of-plane deformations. The obtained NSD decompositions are good representations of the total observed macrocycles out-of-plane deformations when judged in terms of the crystal resolution, as discussed in Materials and Methods. The resulting mean deformations are shown in Fig. 4, with the evaluated errors. Both molecules have a complex distortion pattern with three major deformations onto the three lowest frequency modes. The greatest contribution is the B_2u mode. This last mode has an estimated characteristic frequency, for the porphyrin model, of 65 cm⁻¹ (38). It is interesting to note that PCP fluorescence line-narrowing spectrum (66), measured at 4 K, shows a broad phonon wing with a clear shoulder, suggested to lie at ∼65 cm⁻¹.

FIGURE 4.

Out-of-plane displacements for PCP chlorophylls. The values are obtained by NSD analysis of the crystallographic data (32) using the minimal set of normal modes ((38), Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature). For each chl molecule, the values are the mean of the results obtained analyzing the chl crystal coordinates of three different PCP monomers. The error bars are also shown.

The deformation parameters obtained by NSD analysis (Fig. 4) are used (Eq. 1) to obtain the deformation energy associated with each mode. The values of the total deformation energies are E_D = 290 cm⁻¹ for CLA1 and E_D = 305 cm⁻¹ for CLA2. The deformation energies for the four modes having the same symmetries as the orbitals involved in the Q_y transition are shown in Fig. 5 A. It can be seen that while the HOMOs are clearly perturbed, the LUMOs are substantially unperturbed. The deformation energies have values in the same range obtained for the chla crystal (Fig. 3), but in this latter case the LUMO levels are clearly perturbed (Fig. 3 A).

FIGURE 5.

Energy contributions due to PCP chla macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for PCP chla obtained using the deformation energies. All the values are obtained using the mean values of Fig. 4.

To estimate how the energies associated with the HOMO and LUMO levels are modified by the macrocycle deformation, the contributions ΔδE_H→L and ΔδE_H−1→L+1 (Eqs. 3 and 6) have been calculated for the two chla (Fig. 5 B). It can be seen that both contributions are negative, a result opposite to that obtained for isolated chla and b (Fig. 3 B). Thus, for PCP chls, the two perturbed energy gaps are reduced, with respect to the unperturbed gaps, by molecule distortion, leading to a red shift of the Q_y transition.

The values of ΔδE_H→L and ΔδE_H−1→L+1, with the unperturbed energy gaps and obtained previously for chla, gives the ΔE_H−L and ΔE_H−1→L+1 (Eq. 3) values used to calculate the Q_y intrinsic-structural energy transitions of both PCP chls as eigenvalues of the Gouterman matrix (Eq. 5). When the value of C_a = 6742 cm⁻¹, obtained using the unperturbed energy gaps, characteristic of the planar conformation, as representatives of chla in solution, is used, (15,417 cm⁻¹) for CLA1 and 649.0 nm (15,409 cm⁻¹) for CLA2. The two transitions are red-shifted by ∼3 nm with respect to the vacuum chla transition (645.8 nm) and are practically isoenergetic. Two isoenergetic chls were suggested by spectroscopic analysis (66). The excitonic coupling between the two chls in a monomer of the PCP-complex was estimated to be ∼10 cm⁻¹ (54,66). This would slightly shift the two intrinsic-structural transitions to (15,424 cm⁻¹) for CLA1 and 649.3 nm (15,402 cm⁻¹) for CLA2, increasing the difference between the two to ∼1 nm.

Instead, when the value of C_a = 6816 cm⁻¹, obtained using the crystal structure as representatives of the chl in solution, is considered, (15,359 cm⁻¹) for CLA1 and (15,349 cm⁻¹) for CLA2. Also in this case the two transition are nearly isoenergetic and are red-shifted up to 2.5 nm with respect to the previous estimation.

To compare the chla transition energy with measured absorption spectra, the nonspecific solvatochromic contribution must be considered. The solvatochromic effect is independent of the wavelength but depends on the refractive index and, less strongly, on the dielectric constant of the surrounding (Eq. 8). This contribution then determines the same displacement toward longer wavelengths (5) of the transition energy of the two chls that remain substantially isoenergetic. The Q_y wavelength transition for both PCP chla as a function of refractive index and dielectric constant D = 5 is shown in Fig. 6, when data obtained using the unperturbed energy gaps as representatives of chla in solution are considered. Using D = 20, the changes are negligible (not shown). The RT PCP chl absorption maximum was reported at 667.5 nm (66). From Fig. 6 it can be seen that a reasonable value for the PCP chla site energy, that include the nonspecific solvatochromic effect, is obtained for refractive index values n ≤ 1.46. For n = 1.6, the proposed value for PCP (54), the absorption maxima of the two chls are well on the red side of the experimental RT PCP absorption maximum. If the small excitonic interaction is also considered, a refractive index n ≈ 1.45 is estimated as the effective protein refractive index of this chl-protein complex. This value decreases to n = 1.36–1.37 when the value of C_a = 6816 cm⁻¹, obtained using the chla crystal conformation as representatives of the chla in solution, is considered.

FIGURE 6.

The PCP chla Q_y transitions in the presence of nonspecific solvatochromic effect. The wavelength red shift due to solvatochromic effect is calculated using Eq. 8 (5), with the dielectric constant D = 5, as a function of the refractive index n. The horizontal line is the wavelength of the RT absorption maximum of the chla in PCP complex (667.5 nm, (54)). The two PCP chla without excitonic contribution, ——; the two PCP chla with the excitonic contribution, ⋯⋯⋯. Using D = 20, very small changes are observed (not shown).

Light harvesting complex II

LHCII, the external antenna of PSII, is the most abundant chl-protein complex in thylakoid membrane. It is organized as a trimer with up to 15 chla and chlb molecules plus 3–4 carotenoids (35) per monomer. It has complex spectroscopic characteristics with a congested Q_y absorption band due to the presence of a number of chl spectroscopic forms (70–72). The origin of these chl forms has been substantially ascribed to chl-protein interaction as well as to the presence of excitonic interaction between the densely packed pigments (72). The chl forms, when compared to chl in solvents (15), have absorption spectra with narrower bandwidth (71) and some of them have a red-shifted absorption maximum. The LHCII complex, extracted from pea, was crystallized in 1994 (31) and 12 tetrapyrroles were modeled. No identity distinction (chla and b) and orientation axes were obtained at that time. Biochemical studies, in particular using point mutations in reconstituted chl-protein complexes, provided information on the ligand-binding sites (24,73), with the proposal of mixed chla, chlb binding sites (24). Attempts to assign the directions of transition dipoles analyzing the optical spectra have also been performed (74).

Recently, a much more detailed structure of LHCII, at 2.72 Å resolution (R-value = 0.128), was published (35). In the derived model of the x-ray structure, the identities of the chls have been obtained with an accurate location and orientation of 14 chls and four carotenoids within each monomer. Eight chls a and six chls b per monomer, for a total of 10 monomers, with the complete sets of spatial coordinates, were described, which allows determination of the out-of-plane deformations. The individual chl binding sites are occupied by only one type of chl and no mixed binding sites were found, as was initially suggested by biochemical analyses (24). A number of chla and chlb are packed to a minimal distance of ∼9 Å, and interacting nearest neighbor couples with estimated interaction energies in the range between 54 and 145 cm⁻¹ (35) were proposed. The given estimation of the transition dipole moment orientations permits calculation of the transition energy splitting and oscillator strength redistribution between interacting chls when the site energies of the chls are known.

In the following, the NSD analysis is applied to all the LHCII chls described by Liu et al. (35) to determine the deformation energies and their impact to the Q_y absorption spread associated with the chl spectral forms. Analysis of the atomic coordinate of the chl macrocycle atoms (PDB ID 1RWT (75)) indicate that

1. The Mg atoms are displaced outside the nitrogen plane thorough NA-NB-NC (according to PDB nomenclature) (x,y plane) by a distance in the range of 0.07–0.18 Å for chlb and 0.11–0.25 Å for chla, less than the distance in isolated chla crystal (0.39 Å (7)).

2. All the other atoms are displaced with respect to the nitrogen plane indicating, also for LHCII, a puckered conformation of the chl ring.

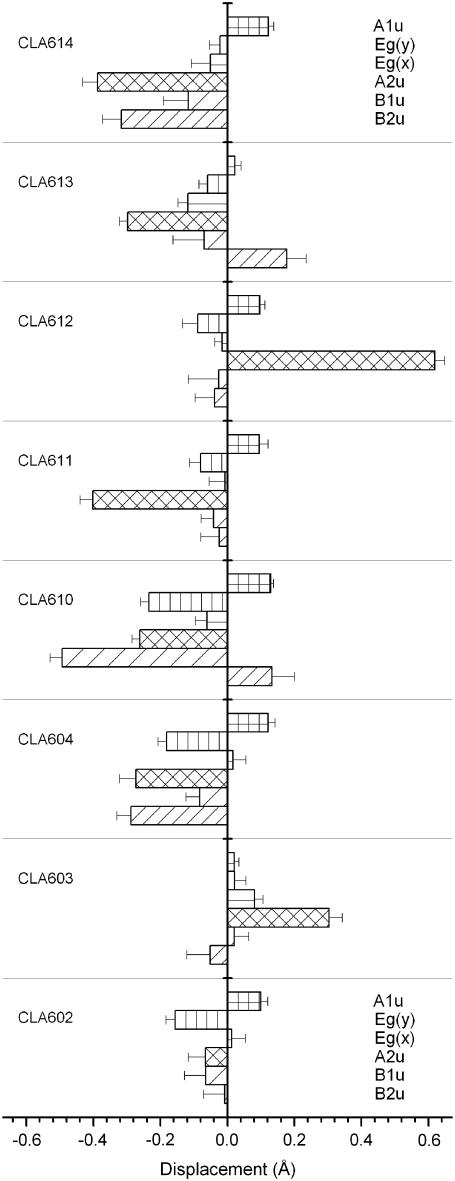
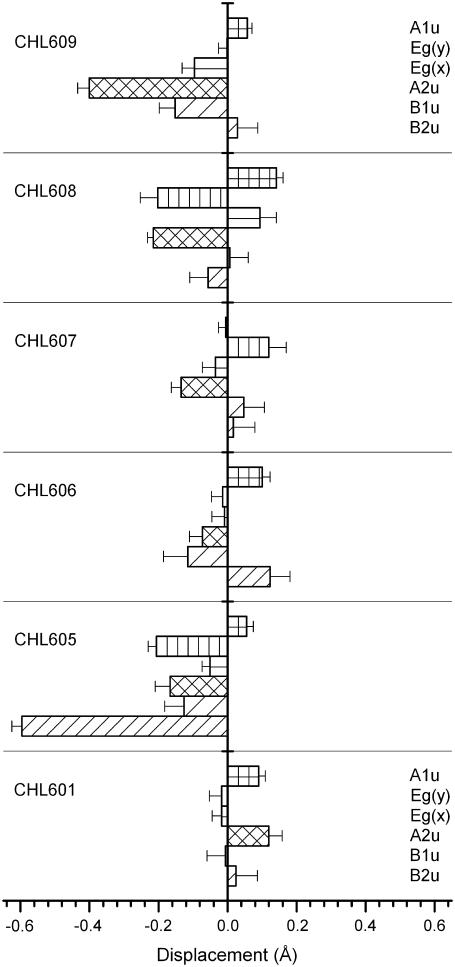
To visualize the different chl conformations, the out-of-plane spatial distribution of the atoms comprising the tetrapyrrole ring of all the chla and chlb molecules are shown in Figs. 7 and 8. To describe and quantify the deformation of the porphyrin macrocycle, the NSD analysis in terms of the six low frequency modes of deformation (38) has been applied to the 126 chls of the three trimers described in the LHCII crystal model. In all these cases, a good description of the total observed chl macrocycle deformations is obtained (not shown), judged by the comparison between the simulated and observed out-of-plane displacements with the crystallographic errors (see Materials and Methods). The results for the six low frequency modes comprising the NSD minimal basis of the out-of-plane deformations, in terms of the displacement d_n defining the contribution of the n^th deformation mode to the total deformation, are shown in Fig. 9, for the eight chla, and in Fig. 10 for the six chlb. The availability of atomic coordinate for fourteen sets of nine equivalent chls permits an estimation of the deformation variability defined as the standard deviation of the displacements d_n for the chls in each set. These standard deviations are shown in Figs. 9 and 10 as the error bars. Both chla and chlb show complex patterns of deformation with contributions of all the out-of-plane modes comprising the minimal NSD basis. For LHCII, the displacements reach values higher than those obtained for crystallized chla and b and for PCP-protein (see Figs. 2 and 4).

FIGURE 7.

Linear plot of the LHCII chla macrocycle. The atoms comprising the chla macrocycle are shown in an (x,z) projection with nitrogen NA, NB, and NC (PDB nomenclature) that lie on the (x,y) plane. The Mg atom is also displayed (pentagon). The chl molecules are shown in a linearized mode, after taking the mirror image of the II, III, and V rings with respect to the CHC atom (PDB nomenclature).

FIGURE 8.

Linear plot of the LHCII chlb macrocycle. The atoms comprising the chlb macrocycle are shown in an (x,z) projection with nitrogen NA, NB, and NC (PDB nomenclature) that lie on the (x,y) plane. The Mg atom is also displayed (pentagon). The chl molecules are shown in a linearized mode, after taking the mirror image of the II, III, and V rings with respect to the CHC atom (PDB nomenclature).

FIGURE 9.

Out-of-plane displacements for the LHCII chlorophylls a. The values are obtained by NSD analysis of the crystallographic data (35) using the minimal set of normal modes ((38), Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature). For each chl molecule, the values are the mean of the results obtained analyzing the chla crystal coordinates of three different LHCII trimers. The evaluated errors are also shown. On the basis of the displacements and using Eq. 1, the total deformation energy E_D (cm⁻¹) for each chl can be evaluated: and

FIGURE 10.

Out-of-plane displacements for the LHCII chlorophylls b. The values are obtained by NSD analysis of the crystallographic data (35) using the minimal set of normal modes ((38) Materials and Methods). These modes have the symmetry types shown in figure (D_4h group nomenclature). For each chl molecule, the values are the mean of the results obtained analyzing the chlb crystal coordinates of three different LHCII trimers. The evaluated errors are also shown. On the basis of the displacements and using Eq. 1, the total deformation energy E_D (cm⁻¹) for each chl can be evaluated: and

The A_2u mode represents the major contribution to deformation modes for five of the eight chla (Fig. 9). In one case (CLA604, PDB nomenclature), the B_2u and A_2u modes have equal contribution. Moreover, B_1u and B_2u modes are often involved with intense contribution, as is the case of CLA610 where the B_1u mode is the major contribution. These two modes have different symmetries with respect to the orbitals mainly involved in the Q_y transition. The A_2u mode has, according to Jentzen et al. (38), a characteristic frequency of ∼135 cm⁻¹ (whereas the other two have characteristic frequencies of 65 and 88 cm⁻¹, respectively; see Table 1). The presence of a low frequency vibronic mode (ν ≈ 120 cm⁻¹), giving rise to a vibronic band in the red tail of the absorption spectrum, has been proposed to explain the thermal behavior of the LHCII absorption spectrum (71) as well as to explain the nonlinear polarization spectroscopy in the frequency domain RT spectrum of LHCII (76). A contribution due to a low frequency vibrational mode at 135–138 cm⁻¹, plus a broad contribution at ∼97 cm⁻¹, was also proposed by fluorescence line-narrowing analysis, at 4 K, of LHCII (72,77) albeit with a very weak apparent coupling. It is interesting to note that the presence of clear shoulders at wavenumbers at ∼52, 86, and 175 cm⁻¹ in the broad phonon wing of chla were observed by fluorescence line narrowing of isolated CP43 complex (78).

In the case of chlb (Fig. 10), three molecules have a deformation distribution comparable with chla, while the other three show a less distorted pattern. The most intense contribution is due to the B_2u mode on CHL605 (PDB nomenclature).

The deformation parameters d_n obtained by NSD analysis (Figs. 9 and 10) are used to calculate the deformation energies (Eq. 1). The total deformation energy is in the range 355–1563 cm⁻¹ for chla and 154–843 cm⁻¹ for chlb. The values of the deformation energies are, on average, much higher that those obtained in the PCP complex, indicating a stronger impact of the chla deformation in LHCII. The deformation energies associated with the four modes A_1u, A_2u, and E_g(x,y), having the same symmetries as the orbitals mainly involved in the Q_y transition, are shown in Fig. 11 A for chla and 12A for chlb. The greatest contributions are, in general, due to the A_1u and A_2u modes, having both the same symmetry of the HOMO molecular orbitals. Instead, the E_g modes, associated with the LUMOs, are substantially unperturbed or slightly perturbed (CLA602, 604, and 610).

FIGURE 11.

Energy contributions due to LHCII chla macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation-induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for LHCII chla obtained using the deformation energies. All the values are obtained using the mean values of the out-of-plane displacements of Fig. 9. The displacement errors are used to determine the uncertainties on deformation energies (A) as well as energy gaps perturbation (B). These uncertainties are shown as error bars.

To estimate how the energies associated with the HOMO and LUMO levels are modified by the macrocycle deformation, the contributions ΔδE_H→L and ΔδE_H−1→L+1 (Eqs. 3 and 6) have been calculated for chla (Fig. 11 B) and chlb (Fig. 12 B). The majority of energy changes are negative, indicating that HOMO-LUMO gaps are decreased by molecular distortion. This source of energy modulation defines the site energies of the chl molecules in chl-protein complexes in the absence of other sources of energy modulation (intrinsic-structural energy).

FIGURE 12.

Energy contributions due to LHCII chlb macrocycle deformations. (A) Deformation energies for the normal modes of the minimal set used to decompose the macrocycle deformation and having the same symmetry of the HOMO (a_1u), HOMO-1 (a_2u), LUMO (e_g(x)), and LUMO+1 (e_g(y)). (B) Deformation induced perturbation of the HOMO → LUMO and HOMO-1 → LUMO+1 energy gaps for LHCII chlb obtained using the deformation energies. All the values are obtained using the mean values of the out-of-plane displacements of Fig. 10. The displacement errors are used to determine the uncertainties on deformation energies (A) as well as energy-gap perturbation (B). These uncertainties are shown as error bars.

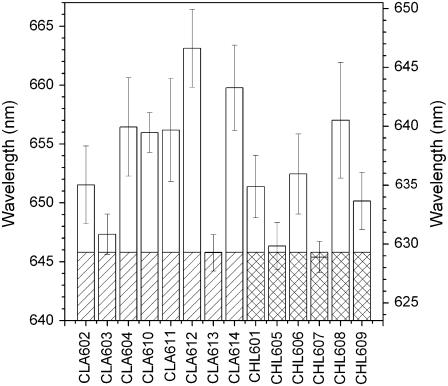
The two perturbed energy gaps ΔE_H→L and ΔE_H−1→L+1 (Eq. 3) are estimated by the unperturbed energy gaps = 18,735 cm⁻¹ and obtained previously, and the values of ΔδE_H→L and ΔδE_H−1→L+1 (Figs. 11 B and 12 B) obtained using NSD analysis, as already done for the PCP complex. These values, with the parameters C_a = 6742 cm⁻¹ and C_b = 6215 cm⁻¹ obtained using the unperturbed energy gaps as representative of the chl molecule in solution (see Chlorophyll a and b, above), are used in the Gouterman matrix (Eq. 4) to calculate the energy transitions for chla and chlb (Eq. 6). The results are shown in Fig. 13, where it can be seen that a Q_y transition energy distribution for both chla and b come about as a result of chl macrocycle deformation. The ring deformations induce a shift of the wavelength transitions toward long wavelengths by up to ∼17 nm for chla and 11 nm for chlb. The CLA612 has the greatest red shift, and is at 663.1 nm (Δλ = 17 nm), whereas CLA613 is at 645.8 nm, the vacuum transition energy. Among chlb, CHL608 has the greatest red shift (640.5 nm), whereas CHL605 and CHL607 are nearly at the same wavelength (629.8 and 628.9 nm, respectively) as the vacuum chlb transition (629.3 nm). This provides the first clear physical mechanism to explain the long-held view that the chla spectral-forms in LHCII are both more numerous and cover a wider energy range than those of chlb.

FIGURE 13.

The intrinsic-structural Q_y transitions of the LHCII chls. The wavelengths are obtained as eigenvalues of the Gouterman matrix (Eq. 5) as outlined in Materials and Methods, using the data of Fig. 11 B and Fig. 12 B and the two reference sets for both chla and chlb obtained when the unperturbed energy gaps are considered as representatives of chl in solution ({18,735; 29,472; 6742} for chla and {18,735; 29,472; 6215} for chlb). The shaded areas represent the unperturbed wavelengths of chla and b whereas the open areas are the changes related to macrocycle deformation. The uncertainties are obtained propagating the uncertainties of the energy gap perturbations induced by the macrocycle deformations.

When the reference sets {18,735; 29,472; 6816}_chla and {18,723; 29,416; 6292}_chlb, defined using the crystal structure as representatives of the chl in solution (see Chlorophyll a and b, above) are considered, the Q_y transition distribution obtained for both chla and chlb are red-shifted with respect to the previously calculated distribution (not shown). In this case, the major red shifted chla and chlb are at wavelengths of 665.8 nm (CLA612) and 643.7 nm (CHLB608), respectively.

As already discussed for PCP, other contributions to transition energy modulation must also be considered; among them the solvent effect and the excitonic contribution, when interaction among chls take place, as is the case for LHCII (35,57,74). These other sources of modulation are hypothesized to act independently and to change the intrinsic-structural energy levels imposing either a constant wavelength red-shift contribution (nonspecific solvatochromic effect) or inducing an energy splitting that further broadens the intrinsic-structural energy distribution (exciton effect).

The solvatochromic contribution adds a constant wavelength red-shift contribution to the chls intrinsic-structural energies evaluated above and determines the chl intrinsic energy levels. This contribution is evaluated as outlined in Materials and Methods, for refractive indices between 1.3 and 1.7. The results are shown in Fig. 14. For n ≈ 1.54, the index of refraction used for the LHCII complex (57), the CLA612 wavelength Q_y transition is shifted to 684 nm. This chl (a₂ in (31)) has been identified, by mutant analysis, as the chromophore with the redmost Q_y transition in LHCII (24,73). The red shift of CLA612 is usually explained as the results of excitonic interactions. We show here that this chl is characterized by the lowest energy transition already at the level of its intrinsic-structural energy.

FIGURE 14.

The LHCII chla Q_y transitions in the presence of nonspecific solvatochromic effect. The wavelength red shift due to solvatochromic effect is calculated using Eq. 8 (5), with the dielectric constant D = 5, as a function of the refractive index n. Using D = 20, very small changes are observed (not shown).

In LHCII a complex relationship of interactions between chromophores is present, with suggested interaction energies of up to 150 cm⁻¹ (35,57). Excitonic interactions then act as a further source of modulation of the intrinsic energy transition distribution. For example, CLA612 interacts with CLA611 (E_int = 145 cm⁻¹, (35)) and, although the two molecules are nonresonant (see Fig. 13), this excitonic interaction will act to red shift the CLA612 intrinsic energy transitions further on. The effect of excitonic contribution on the energy transition distribution has not been analyzed in the present work. The analysis of the excitonic contribution on the transition distribution is in progress.

CONCLUSIONS

The crystal analysis of isolated chl (6,7), PCP complex (32), and LHCII (35) show a complex pattern of distortion of the chl molecules macrocycles with respect to the reference plane. The total chl macrocycle deformations have been decomposed in terms of a set of the six lowest frequency out-of-plane normal mode deformations using the normal-coordinate structural decomposition (NSD) method (38). In this set of lowest frequency deformations, four have the same symmetry of the HOMOs and LUMOs molecular orbitals mainly involved in determining the Q_y electronic transition. It must be considered that, due to the approximations used in the analysis and the intrinsic errors of the input data, the numerical results must be taken with caution. However, it is certainly possible to conclude that the energy involved in each out-of-plane deformation mode determines a structural induced perturbation of the HOMOs and LUMOs energy levels. Then, the deformation-induced energy acts to modulate the HOMO-LUMO energy gaps and, as a consequence, to modulate the Q_y transition energy of chl. A number of conclusions of the present analysis can be summarized:

1. In PCP complex, the main contributions to the total deformation are due to the lowest frequency out-of-plane normal modes. These frequencies are observed in the hole-burning measurements of this complex. The total deformation energies for the two chls in the complex are 290 and 305 cm⁻¹, respectively.

2. The two chla in the PCP complex come out as being substantially isoenergetic. This property remains when the nonspecific solvatochromic effect, that determines a red shift, is considered. A value of the refractive index n ≤ 1.45 is consistent with Q_y transitions in the range of the observed RT absorption maximum (667.5 nm (66)).

3. In LHCII, all the chla and chlb molecules have a complex deformation pattern and the total deformation energy is estimated in the range 355–1563 cm⁻¹ for chla and 154–843 cm⁻¹ for chlb.

4. The A_2u mode, with a characteristic frequency at ∼135 cm⁻¹, is the major contribution to macrocycle deformation for five of the eight LHCII chla.

5. The LHCII chl macrocycle deformations shorten the HOMO-LUMO energy gaps, inducing an estimated red shift of up to 17 nm, for chla, and 11 nm, for chlb, with respect to the unperturbed reference transition energies. The CLA612 has the major intrinsic-structural red shift (17 nm).

6. The deformation-induced distribution of the chlorophyll Q_y electronic energy transition is broader for chla than for chlb.

7. The nonspecific solvatochromic effect adds a nearly constant red shift, as a function of the refractive index, to the intrinsic-structural energy distribution. This contribution, added to the intrinsic-structural energy, determines the chl site energy. When a refractive index n = 1.54 is considered, the lowest energy transition obtained (CLA612) shifts to 684 nm.