Temperature-Dependent Folding Pathways of Pin1 WW Domain: An All-Atom Molecular Dynamics Simulation of a Gō Model

Abstract

We study the folding thermodynamics and kinetics of the Pin1 WW domain, a three-stranded β-sheet protein, by using all-atom (except nonpolar hydrogens) discontinuous molecular dynamics simulations at various temperatures with a Gō model. The protein exhibits a two-state folding kinetics near the folding transition temperature. A good agreement between our simulations and the experimental measurements by the Gruebele group has been found, and the simulation sheds new insights into the structure of transition state, which is hard to be straightforwardly captured in experiments. The simulation also reveals that the folding pathways at approximately the transition temperature and at low temperatures are much different, and an intermediate state at a low temperature is predicted. The transition state of this small β-protein at its folding transition temperature has a well-established hairpin 1 made of β1 and β2 strands while its low-temperature kinetic intermediate has a formed hairpin 2 composed of β2 and β3 strands. Theoretical results are compared with other simulation results as well as available experimental data. This study confirms that specific side-chain packing in an all-atom Gō model can yield a reasonable prediction of specific folding kinetics for a given protein. Different folding behaviors at different temperatures are interpreted in terms of the interplay of entropy and enthalpy in folding process.

INTRODUCTION

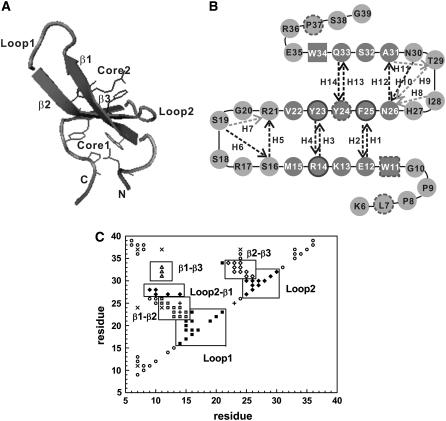
Slow folding rates of β-proteins make it computationally challenging to study their folding kinetics. As a result, most simulation studies on folding of β-proteins are limited to small β-sheet domains (1–6) with a few exceptions (7–10). WW domains constitute a family of three-stranded antiparallel β-sheet proteins comprised of ∼34–44 amino acids (11–14). They are named after two highly conserved tryptophans in the strands. Some WW domains are suitable for theoretical folding studies (15–22) because they unfold and refold reversibly and cooperatively (two-state kinetics) (23,24). Moreover, they are amenable to well-defined mutagenesis without significant changes in their structures (16,25–27). Protein Pin1 is a two-domain protein that regulates early mitotic events. Its WW domain binds proline-rich peptides, and another domain of Pin1 catalyzes the proline cis/trans-isomerization. The high-resolution x-ray structure of the Pin1 WW domain has been determined (1.35 Å) and only residues 6–39 are visible (28). The domain contains two hydrophobic clusters at the opposite side of strands. Core 1 contains Leu⁷, Trp¹¹, Tyr²⁴, and Pro³⁷; Core 2 has Tyr²³, Phe²⁵, and the n-propyl portion of Arg¹⁴, as shown in Fig. 1 A. The NMR structure of this domain adopts a more flexible loop 1 (residues Ser¹⁶ to Arg²¹) in solution compared to the x-ray structure (29).

FIGURE 1.

(A) A cartoon display of the global-minimum-energy structure of an all-atom off-lattice model of Pin1 WW domain (Lys⁶ to Gly³⁹). Three β-strands, two loop regions and coil regions, the hydrophobic Core 1 (Leu⁷, Trp¹¹, Tyr²⁴, Pro³⁷), and Core 2 (Arg¹⁴, Tyr²³, Phe²⁵) are specifically indicated. Drawn with VMD (65). (B) Two-dimensional presentation of the Pin1 WW domain. In addition to the secondary-structure elements, the two conserved Trp residues are highlighted by squares. Ten main-chain H-bonds and four side-chain H-bonds are also shown by the dark dashed lines and the light dashed lines, respectively, and each H-bond is indicated by an arrow from a hydrogen donor to the associated hydrogen accepter. Core 1 is highlighted with a dashed-line border, while Core 2, with a solid-line border. (C) The contact map of the native structure. A residue is in contact with another residue if there is at least one square-well atomic contact between them. Square symbols denote β1-β2 contacts; diamonds, β2-β3 contacts; triangles, β1-β3 contacts; crosses, contacts among Core 1 residues; pluses, contacts among Core 2 residues; the solid squares indicate contacts between loop 1 residues and other residues; the solid diamonds refer to contacts between loop 2 residues and other ones; and other contacts are labeled with circles. The total number of native residue-residue contacts (|i−j| ≥ 2) is 91. The number of nonlocal native contacts (|i−j| > 2) is 65.

The folding transition of Pin1 WW domain has been studied intensively by experimental techniques. A series of well-designed side-chain mutagenesis by Gruebele group (26) suggested that the locally interacting loop 1 controls the folding rate of the Pin1 WW domain with nonclassical φ-values >1 at the physiological temperature, while the formation of the hydrophobic Core 1 contributes significantly to thermal stability. The main-chain amide-to-ester (A-to-E) mutation studies of the Pin1 WW domain also demonstrated that its folding transition state (TS) has nativelike main-chain hydrogen bonds (H-bonds) in loop 1, less developed H-bonds in loop 2 and other regions at 50°C, which is close to the midpoint temperature of thermal denaturation (T_m = 59°C) (27).

Pin1 WW domain has also been studied theoretically. Karanicolas et al. compared the folding kinetics and thermodynamics of three WW domains and found that the difference in hydrophobic packing leads to different folding behaviors (biphasic kinetics of FBP WW domain versus two-state kinetics of Pin1 WW domain and hYAP WW domain) (17,18). Brown et al. (30) refolded proteins L and G with a three-letter code sequence (the hydrophobic, hydrophilic, and neutral) and found that this model could also lead to a correct folding of the Pin1 WW domain. Different folding pathways, however, have been suggested by different theoretical studies. Karanicolas et al. proposed that the hairpin β2-β3 (hairpin 2) of the Pin1 WW domain folds before hairpin β1-β2 (hairpin 1) and the hydrophobic Core 1 forms at last (19) by an improved C_α model including nonnative interactions. More recently, Cecconi et al. studied the transition state ensemble (TSE) of the Pin1 WW domain by a C_α-based model with three-letter codes and found that the folding of the Pin1 WW domain was initiated from the hydrophobic contacts in β1-β2 and β2-β3 and completed by zipping the hairpin β1-β2 and hairpin β2-β3 toward loop 1 and loop 2, respectively (20).

In this article, we make an in-depth study of the folding pathway of the Pin1 WW domain based on an all-atom Gō model (31). The constant-temperature discontinuous molecular dynamics (MD) simulation was employed to examine the thermodynamic and kinetic behaviors of the Pin1 WW domain. The simulation technique and the associated Gō model have been used successfully to simulate folding thermodynamics and kinetics of a three-helix bundle and a β-hairpin (32–35). Here, we use the discontinuous MD technique because a discontinuous MD simulation with a square-well potential is computationally more efficient than a normal MD simulation for the following reasons. First, only short-range interactions are involved; second, force calculations are not required in the discontinuous MD simulations; and third, particles move at constant velocities between collisions and there is an efficient search algorithm for the collision time.

Here, we found that there are two distinct folding kinetic pathways at different temperatures for the Pin1 WW domain. At the transition temperature, Pin1 WW domain folds without any intermediates, and its transition state is characterized by a mostly formed hairpin 1. At a lower temperature, however, Pin1 WW domain folds via a kinetic intermediate with a mostly established hairpin 2. Theoretical results are compared with available experimental data.

METHODS AND SIMULATIONS

Model

The detail description of the discontinuous MD method could be found elsewhere (32–35). Here, we give a brief summary of the model in simulation. First, all the heavy-atom positions of the WW domain were acquired from the x-ray structure (residues 6–39 of Protein DataBank 1pin) (28). The N-terminus and n-methyl C-terminus of the polypeptide were capped with acetyl and amine groups, respectively. The CHARMM program (36) was used to create the initial positions of polar hydrogen atoms. Steric clashes were removed by 100 minimization steps with the CHARMM polar hydrogen parameter set 19 and distance-dependent dielectric constants (37). Thus, all heavy atoms and polar hydrogens are included in the model and the total number of atoms is 361.

We constrain two bonded atoms, as well as any 1,3 angle-constrained atomic pair and 1,4 aromatic carbon pair, i and j, to a center-to-center distance between 0.9σ_ij and 1.1σ_ij, where σ_ij is the atomic distance obtained by the CHARMM energy minimization as mentioned above. This constraint is denoted by an infinitely deep square-well potential

(1)

We apply a bondlike potential for improper dihedral angels to maintain the L-form chirality about a tetrahedral extended heavy atom (ω₀ = 35.26439°) and to keep certain planar atoms (ω₀ = 0°). A 20° fluctuation is used to increase the flexibility and folding rate. That is,

(2)

The nonbonded i, j pair interactions are represented by a hard-core and square-well potential

(3)

where 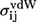are the van der Waals parameters from the CHARMM polar hydrogen parameter set 19 (37) and B_ij are the nonbonded bead interaction strengths. The factor of 0.8 is the typical ratio between the hard-core diameters and the van der Waals parameters in the Weeks-Chandler-Andersen perturbation theory (38), while a ratio of 1.5 (= 1.2:0.8) between the square-well and hard-core diameters is typical for small molecular systems (39).

We remove all initial hard-core overlaps in the CHARMM minimized structure by a short discontinuous MD simulation. To ensure that the original native contacts found in the x-ray structure are maintained during the process, the square-well interactions for these native contacts are set to be a large negative energy (−100). The initial hard-core diameter between any two overlapped atoms is regarded as the distance found in the energy-minimized structure. We modify the hard-core diameters at each time step until the true hard-core diameters are reached and the simulation continues until all initial overlaps are removed. The resulting structure has a main-chain root-mean-squared deviation (RMSD) from the x-ray structure of only 0.69 Å and is regarded as the global minimum structure for the protein (Fig. 1 A). In all, there are 2398 square-well atom-atom overlaps (including both backbone and side-chain contacts) in the global minimum structure. Henceforth, these shall be regarded as native atomic contacts.

To make sure that the energy of the native structure (shown in Fig. 1 A) is at the global minimum, a Gō interaction (31) is adopted. In a Gō model, a square-well interaction energy between two atoms is –ɛ (B_ij = −1) for a native contact, and 0 (B_ij = 0), otherwise. Henceforth, the internal energy, E* (= E/ɛ), and the reduced temperature, T* (= k_BT/ɛ, in which k_B is Boltzmann constant), are scaled in units of ɛ. A reduced time unit t* is also used [t* = t 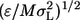where M is the average mass of the atoms and σ_L is 1 Å]. The total number of native residue-residue contacts is 91 (the neighbor contacts between i and i ± 1 are omitted, shown in Fig. 1 C), and the number of nonlocal native contacts (|i−j| > 2) is 65.

The formation of an H-bond is defined by a cutoff distance of 2.88 Å between a donor H atom and an accepter O atom. Ten backbone H-bonds of the native structure are labeled in Fig. 1 B, which are the same as those shown in Fig. 1 of Jäger et al. (26) and in Fig. 1 of Deechongkit et al. (27); other native side-chain H-bonds are mainly located in two loop regions (26).

Simulations

The discontinuous MD simulations of a single Pin1 WW domain were carried out in the canonical ensemble. Ghost-solvent particles were employed to maintain a constant temperature by their collisions with protein atoms (40–42). Simulations were conducted at 18 temperatures from T* = 2.5 to T* = 4.8 for the thermodynamic analysis. The thermodynamic properties at the temperatures that are not simulated can be obtained through the weighted histogram method (43), which is a least-square optimization method for extracting the degeneracy factors of the energy levels and the partition function Z from multiple simulations at different temperatures. The energy and the heat capacity can be calculated from the partition function Z as

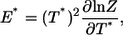(4)

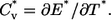(5)

We investigated the folding kinetics at T* = 2.7, 3.0, and 3.6. For folding kinetics at T* = 2.7 and 3.0, the initial coil-like configurations and velocities were obtained from equilibrium simulations at T* = 4.0. Seventy-seven and 135 kinetic simulations were performed for t* = 200,000 at T* = 2.7 and 3.0, respectively. The coordinates were recorded every 100 reduced time units for later analysis. For folding kinetics at T* = 3.6, both folding and unfolding behaviors were observed at equilibrium simulation. The coordinates were recorded every 50 reduced time units. A progress variable Q, the fraction of nonlocal native contacts (|i – j| > 2) between residues (total number is 65, shown in Fig. 1 C), is used to monitor the folding process. Two residues are regarded as in contact if there are any square-well atomic overlaps between them.

φ-value

The experimental data for analyzing the folding transition state are φ-values obtained from protein engineering experiments (44). These experiments measured the change in the active energy of the transition state relative to the change in the free energy of the native state upon a perturbative mutation (substitution). The φ-values are often interpreted as the fraction of native structure or the so-called nativeness of each residue in the folding transition state. Thus, one way to predict φ-values is to calculate the fraction of native contacts in the TSE (45–47). That is,

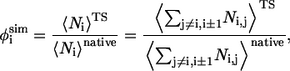(6)

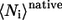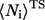where and are the average of native heavy atomic contacts between residue i and other residues in the native condition and that at the transition state, respectively. A contact is considered to exist when the distance of any heavy atoms of the two nonadjacent residues is less than the square-well width (pairs i, i ± 1 are excluded). Our Gō model does not have attractive interactions for nonnative interactions; however, it does have atomic packing interactions from nonnative contacts. Considering the possibility that the nonnative packing might also contribute to φ-values, we also calculate

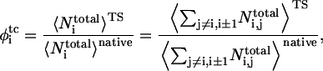(7)

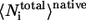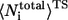where and are the average of all heavy atomic contacts between residue i and other residues in the native condition and that at the transition state, respectively. In this article, 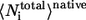and 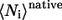were calculated from the configurations of equilibrium simulations at T* = 2.7.

RESULTS

Thermodynamics

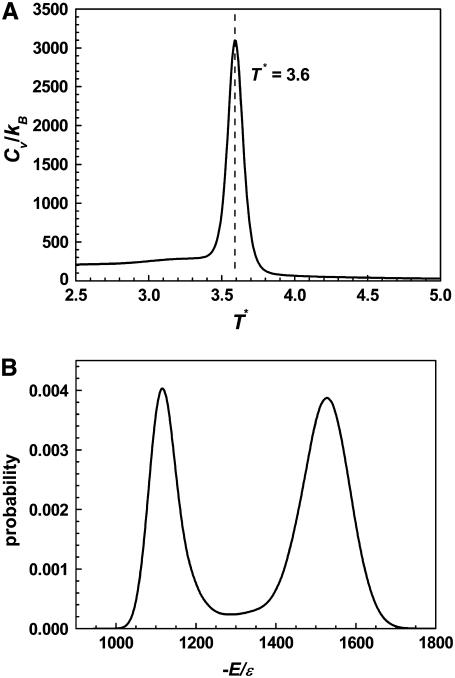
The heat capacity as a function of temperature for Pin1 WW domain is shown in Fig. 2 A. A sharp peak is observed at T* = 3.60, which indicates a thermodynamic transition. This transition is, according to the weighted histogram analysis, accompanied with a bimodal distribution of energies (Fig. 2 B). Thus, the observed transition is a first-order-like two-state transition. Analysis of the structures further demonstrates that the underlying transition is a folding transition between coil-like structures (the average RMSD of main-chain atoms at T* ≥ 4.0 is >14 Å) and folded structures (the average RMSD of main-chain atoms at T* ≤ 3.4 is <3.0 Å).

FIGURE 2.

(A) Reduced heat capacity (C_v* = C_v/k_B) as a function of reduced temperature (T* = k_BT/ɛ). The folding transition temperature is near T* = 3.60. (B) Probability distribution of energy at the transition temperature T* = 3.59. The results were obtained from the weighted histogram method.

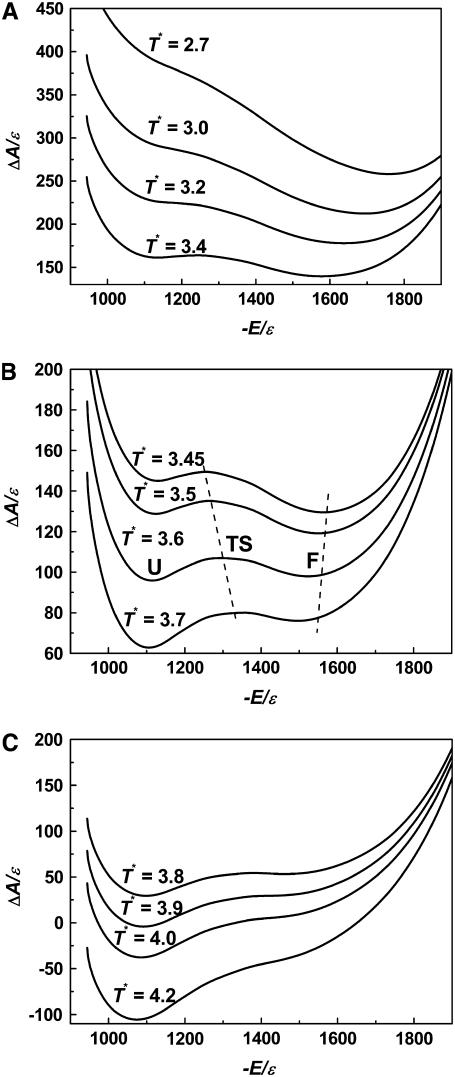
The two-state behavior observed above is also reflected from the free energy profiles as a function of reduced energy at different temperatures (Fig. 3). At the transition temperature (T* = 3.6), there are two stable states corresponding to an unfolded state (with a reduced energy E* ∼ −1110) and a folded state (E* ∼ −1530), respectively. The transition state has an energy E* at ∼−1290 ± 30. When temperature increases, the unfolded state becomes more stable than the native state as expected. Fig. 3, A and C, also illustrate that only one thermodynamically stable state is observed at a very high temperature or a very low temperature.

FIGURE 3.

Free energy profiles as a function of reduced energy (A) at low temperatures; (B) at approximately the folding transition temperature; (C) at high temperatures. The positions of the transition states and native states change with temperature, as indicated by the dashed lines. U, unfolded state; TS, transition state; F, folded state.

If the reduced energy is a correct order parameter, a transition state can be defined based on the peak between the coil and folded states. Fig. 3 further indicates that the transition state becomes more nativelike as temperature increases (see, for instance, from E* ∼ −1250 at T* = 3.45 to E* ∼ −1350 at T* = 3.7), exhibiting the Hammond behavior (48), while the folded state becomes less stable (E* from −1570 at T* = 3.45 to −1500 at T* = 3.7), which is consistent with the ground state effects for proteins (49). (Energy can be used very well to determine the location of transition states at the transition temperature. However, it cannot be used for determining transition states at low temperatures because a kinetic intermediate exists; see below.)

Folding kinetics at the transition temperature

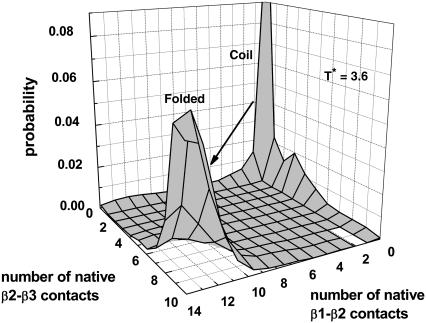
Fig. 4 plots the probability distribution of the number of native contacts between β1 and β2 residues and that between β2 and β3 residues at the transition temperature T* = 3.6. At this temperature, no detectable kinetic intermediate is observed (Fig. 4). This is true when the distribution is plotted against some other progress variables.

FIGURE 4.

Probability distribution of the number of native contacts between β1 and β2 residues and that between β2 and β3 residues. A total of 5,130,000 configurations of eight trajectories at T* = 3.6 were collected for statistics.

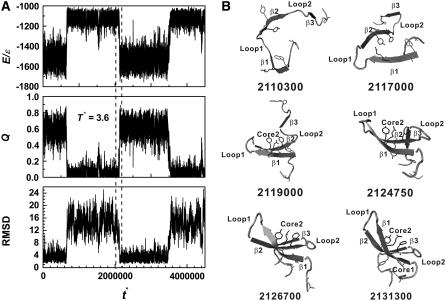
A typical folding and unfolding trajectory is shown in Fig. 5 A, where reduced energy E*, the fraction of nonlocal native contacts Q, and RMSD in various regions are plotted as a function of time. A series of snapshots in the folding process are shown in Fig. 5 B. The folding process starts from the local contacts of loop 1 that initiates the formation of β1 and β2 hairpin. This is followed by three native hydrophobic contacts of Core 2 and the stable hairpin β1-β2. Then, local contacts of loop 2 bring β2-β3 together, to yield the final folded state.

FIGURE 5.

A folding trajectory at T* = 3.6. (A) The reduced energy (E/ɛ), the fraction of native contacts between residues (Q), and the RMSD of Pin1 WW domain are plotted as a function of reduced time (t*). (B) A series of snapshots at the marked reduced times which are in a folding regime indicated by the dashed lines in panel A. The snapshots are displayed with the same symbols as those in Fig. 1 A.

Transition state at the transition temperature

In this article, a snapshot or a conformation is defined as a transition state if its reduced energy is within −1290 ± 30 (Figs. 2 B and 3) and it also belongs to the region of an abrupt structural change in a folding or unfolding event in Fig. 5 A (50). This method of determining TSE is equivalent to the criterion of Q (51–53). We have also tried several other methods including the use of multiple progress variables and the folding probability along a trajectory (P_fold) (54). The resulting ensembles are essentially the same. Details will be discussed in a separate article. Here, we present transition state structures generated by the energy criterion only.

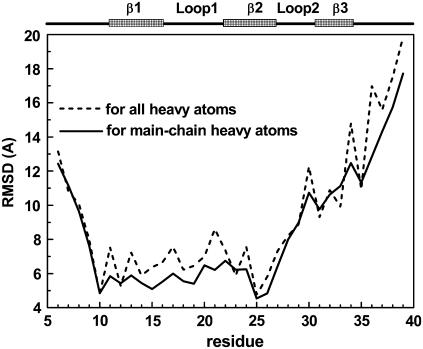
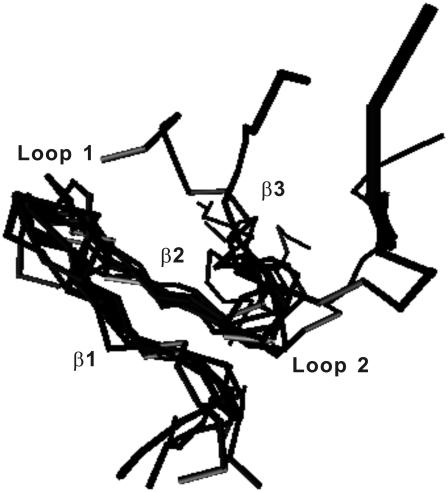
The samples in the TSE are made of 883 configurations collected from the folding/unfolding transitions. (We use the structures in both folding/unfolding transitions because a careful analysis indicates that the structures are the same regardless of folding or unfolding events.) The 883 configurations have an average fraction of nonlocal native contacts Q = 0.27 ± 0.05 and an average radius of gyration R_g = 13.7 ± 1.4 Å. The average main-chain-heavy-atom RMSD and all-heavy-atom RMSD values are 9.33 ± 1.65 Å and 10.24 ± 1.62 Å, respectively. The RMSDs of main-chain heavy atoms and all heavy atoms from the global minimal structure as a function of residue index number are shown in Fig. 6. Hairpin 1 and loop 1 have much smaller deviations from the global minimum structure than loop 2 and β3. Both N- and C-terminus are considerably flexible. Some typical snapshots of TSE are shown in Fig. 7. All of them have a well-established hairpin 1 but a yet flexible loop 1, loop 2 and β3.

FIGURE 6.

Average main-chain-heavy-atom RMSD (solid line) and all-heavy-atom RMSD (dashed line) of the transition-state structures from the native structure for each residue.

FIGURE 7.

Ten snapshots in the transition-state ensemble at T* = 3.6.

Table 1 shows the probabilities of the native H-bonds that are formed in TSE. The probabilities of the four backbone H-bonds between β1 and β2 strands (H1 to H4) are much higher than those of the two backbone H-bonds between β2 and β3 strands (H13 and H14). This confirms that hairpin 2 is not formed in TSE whereas hairpin 1 is well established. The H-bonds in the loop 1 region have higher values: 0.25 for H6 (H-bond between the N-H of Ser¹⁹ and the C=O of Ser¹⁶), 0.06 for H7 (H-bond between the O-H of the Ser¹⁹ side chain and the N-H of the Arg²¹ main chain); and the probability of H5 between the N-H of Ser¹⁶ and the C=O of Ser²¹, the two residues that define the loop 1, is 0.27. In contrast, the probability in loop 2 is only 0.02 for H10 (H-bond between the N-H of Asn³⁰ and the C=O of Asn²⁶); and 0.05 for H12 (H-bond between the N-H of Asn²⁶ and the C=O of Ala³¹). The probabilities of the three local side-chain H-bonds H8, H9, H11 in the loop 2 region are 0.41, 0.25, and 0.05, respectively. Thus, loop 2 has only local native contacts. The probabilities of the four backbone H-bonds between β1 and β2 strands are higher than the probabilities of H-bonds in loop 1 region, which means the H-bonds of the loop 1 are moderately stable compared to H-bonds in hairpin 1.

TABLE 1.

Probability of H-bond formation in TSE at T^* = 3.60 (near transition temperature)

Serial*	Donor†	Acceptor†	Probability	Location
H1	Glu12	Phe25	0.69	β1-β2
H2	Phe25	Glu12	0.51
H3	Arg14	Tyr23	0.37
H4	Tyr23	Arg14	0.46
H5	Ser16	Arg21	0.27	Loop 1
H6	Ser19	Ser16	0.25
H7	Ser19 (O-H)	Arg21 (N-H)‡	0.06
H8	Ile28	Asn26 (O=CNH2)	0.41	Loop 2
H9	Thr29	Asn26 (O=CNH2)	0.25
H10	Asn30	Asn26	0.02
H11	Ala31	Thr29 (O-H)	0.05
H12	Asn26	Asn31	0.05
H13	Tyr24	Gln33	0.00	β2-β3
H14	Gln33	Tyr24	0.00

^*Indicated in Fig. 1 B.

^†The side-chain groups are shown in brackets.

^‡Backbone N-H.

φ-value analysis

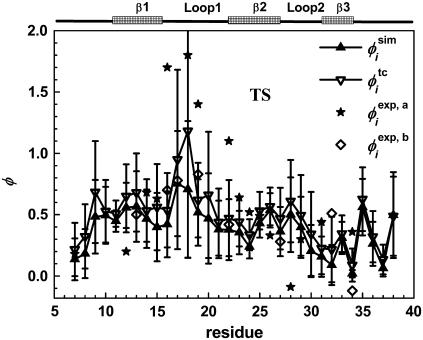
The φ-values obtained from our simulations are shown in both Fig. 8 and Table 2. The data were calculated according to the fraction of the number of native heavy atomic contacts (Eq. 6). The correlation coefficient between φ^sim and φ^exp (side-chain mutation) is 0.39. There is one outlier caused by the negative experimental φ-value for Ile²⁸. Removing this residue improves the correlation coefficient between φ^sim and φ^exp from 0.39 to 0.50. It is of interest to note that the theoretical φ-values have a better agreement with experimental φ-values based on main-chain A-to-E mutation. The correlation coefficient between φ^sim and φ^exp of A-to-E results is 0.74 for eight experimental points.

FIGURE 8.

The simulated φ-values 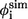(just native contacts involved) and 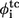(containing total contacts) of each residue. The experimental 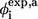from side-chain mutation and 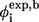from main-chain mutation (A-to-E mutation) both measured by Gruebele group (26,27) are also shown. The secondary-structure elements are indicated above the diagram.

TABLE 2.

Contact residues in TSE and φ-values from simulations (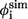) and experiments ()

Residue*	Contact residues†		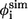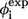‡	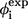§	Location
L7	P9, W11	0.14	0.18		Nonsheet
P8	G10, W11	0.18
P9	L7, W11, N26, I28	0.48
G10	P8, E12, F25, N26, H27, I28	0.49
W11	L7, P8, P9, Y24, F25, N26	0.45			β1
E12	G10, R14, Y24, F25, H27	0.56	0.2
K13	M15, V22, Y23, Y24	0.57		0.50
R14	E12, S16, V22, Y23, Y24, F25	0.47	0.68
M15	K13, R17, S19, G20, R21, V22, Y23	0.40	0.63
S16	R14, S18, S19, R21, Y23	0.42	1.7	0.70	Loop 1
R17	M15, S19	0.75		0.78
S18	S16	0.71	1.8
S19	M15, S16, R17, R21	0.52	1.4	0.83
G20	M15, V22	0.47
R21	M15, S16, S19, Y23	0.38
V22	K13, R14, M15, G20	0.38	1.1	0.42	β2
Y23	K13, R14, M15, S16, R21, F25	0.35	0.64
Y24	W11, E12, K13, R14, N26	0.24	0.52
F25	G10, W11, E12, R14, Y23, H27, N30, A31, S32	0.43	0.49
N26	P9, G10, W11, Y24, I28, T29, N30, A31	0.54	0.33
H27	G10, E12, F25, T29, N30	0.36		0.28	Loop 2
I28	P9, G10, N26, N30	0.50	−0.09
T29	N26, H27, A31	0.40	0.3
N30	F25, N26, H27, I28, S32	0.20
A31	F25, N26, T29, Q33	0.16	0.44		β3
S32	F25, N30	0.09		0.51
Q33	A31, E35, R36, P37	0.31
W34	R36	0.02	0.36	−0.12
E35	Q33, P37	0.56			Nonsheet
R36	Q33, W34, S38, G39	0.26
P37	Q33, E35	0.06
S38	R36	0.50

The boldface type indicates that the associated φ-value(s) is (are) experimentally available.

^*Name of a residue is abbreviated with a single-letter and a serial number.

^†Native contacts in TSE with probabilities >0.1. A residue is in contact with another one if there is at least one square-well heavy atomic contact between them.

^‡Results from side-chain mutation (26).

^§Results from A-to-E mutation (27).

It is of interest to note that some nonnative contacts (due to nonnative side-chain packing in this article) are found in TSE. The φ^tc values based on total contacts (including both native and nonnative contacts) have a somewhat better agreement with φ^exp values. The correlation coefficient between φ^tc and φ^exp is improved to 0.53 (for experimental side-chain mutation) and 0.75 (for experimental A-to-E mutation), compared to 0.39 and 0.74 between φ^sim and φ^exp, respectively. The main difference between φ^sim and φ^tc comes from two residues (Arg¹⁷ and Ser¹⁸). It is interesting that both φ^tc and φ^exp of side-chain mutation have nonclassical φ-values (φ > 1) at loop 1. Although our study implies that nonnative contacts in the transition states might play a role in folding, the relation between nonclassical φ-values and nonnative attractive interactions is still an open question, because in a Gō model, only native contacts are attractive. Further studies are needed for the effect of nonnative attractive interactions.

Folding kinetics at T* = 2.7

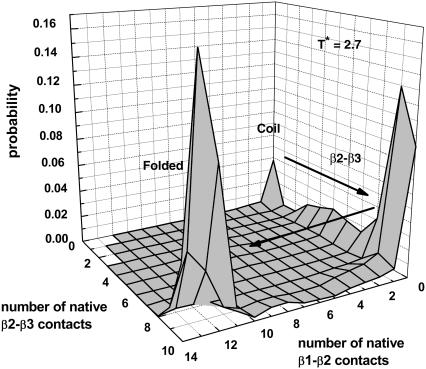
Fig. 9 plots the probability distribution of the number of native β1-β2 residue contacts and the number of native β2-β3 residue contacts at a low temperature T* = 2.7. At this temperature, we found a kinetic intermediate with a mostly formed hairpin β2-β3 (with 9∼10 nonlocal native β2-β3 contacts). At a slightly higher temperature T* = 3.0, a hairpin β1-β2 intermediate was observed in addition to the hairpin β2-β3 intermediate. Twenty-two out of 102 folded trajectories folded via the formation of hairpin β1-β2. Thus, the folding pathway of the Pin1 WW domain is altered as temperature changes.

FIGURE 9.

Probability distribution of the numbers of native β1-β2 and β2-β3 contacts at T* = 2.7. Seventy-seven trajectories were run, and 2000 configurations for each trajectory were collected for statistics.

DISCUSSION

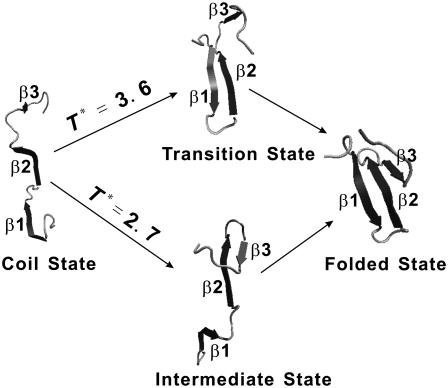
In this article, an all-atom Gō model of Pin1 WW domain was simulated with the discontinuous MD technique. The model exhibited a two-state folding thermodynamics. The folding also exhibited a two-state folding kinetics at the transition temperature with a transition state of a mostly formed hairpin β1-β2. At a low temperature, a drastically different folding behavior was, however, observed. There was a kinetic intermediate with a mostly formed hairpin 2 made of β2 and β3 strands. In between, two kinetic intermediates with either hairpin 1 or hairpin 2 were observed.

The drastically different folding kinetics and pathways (Fig. 10) can be understood as follows. The most entropically favorable way for forming the hairpin 1 (or the hairpin 2) is the formation of loop 1 (or loop 2) that brings β1 and β2 (or β2 and β3) together. Local contacts of loop 2 are more likely to form than those of loop 1 because loop 2 is shorter (32). However, the formation of the hairpin 2 is unlikely to complete folding by recruiting β1, because at high temperature, their intradomain interactions are not strong enough to survive for a relative long time needed for the formation of the long loop 1. Moreover, loop 2 requires long-range interactions to be stable (Fig. 1 C). Thus, the transition state is made of more stable hairpin β1-β2 instead of hairpin β2-β3, although longer time is required for the formation of local contacts in loop 1. Once the hairpin 1 forms, it is stabilized by the hydrophobic contacts and H-bonds between strands β1 and β2, and it is relatively easy to bring β3 to fold because of a short loop 2. Situation is, however, different at low temperatures. The hairpin β2-β3 is, once formed, stable against thermal fluctuation. It becomes a kinetic intermediate while waiting for the formation of the long loop 1 to bring β1 to fold (Figs. 9 and 10), although thermodynamically, this protein is a two-state protein (Figs. 2 and 3). Above explanation reflects that folding results from an interplay between entropy (local contacts form first) and enthalpy (interaction). At approximately that transition temperature, interaction energy guides the folding because only the most stable region can survive thermal fluctuation to yield a productive folding event. At a low temperature, some early local contacts produce a kinetic trap.

FIGURE 10.

A schematic presentation of the two folding pathways at approximately the transition temperature and at a low temperature.

Recent studies devote significant efforts to find the relationship between the folding rates and various physical parameters of the structures of native proteins (55–59). These studies suggest that topology and the number of folded residues rather than detailed energetic interactions play dominant roles in determining the folding rates of small proteins (60–63). Bai et al. have found that the folding rate is correlated to the critical nucleation size of the transition state more than that of the native structure (64). Here, we find that the TSE of the Pin1 WW domain has a critical nucleation size of 18 if the criterion of 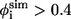is used to define the critical nucleation residues. This size from our simulation is in a reasonable agreement with that from the previous studies, i.e., 16, based on a simple analytical model (64). Our simulations reveal that the nuclear residues include residues 9–20 and residues 25–29. These residues are mainly located at loop 1, β1 and β2.

The above described simulation results are consistent with several experimental observations. It is known that the Pin1 WW domain folds in a two-state behavior thermodynamically and kinetically (26). At approximately temperature 45°C, which is slightly lower than the transition temperature (59°C), the φ^exp values in strands β1 and β2 are higher than φ^exp in β3 strand. This suggests that the hairpin 1 is more nativelike than the hairpin 2 in the TSE (26). The A-to-E mutation also shows that the transition state has a mostly formed backbone structure for hairpin 1 but a yet flexible β3 strand (27). Our simulation also predicted the different pathways of the Pin1 WW domain. The temperature dependence, however, is yet to be tested experimentally. Experimental temperature dependence so far was conducted at temperature near or higher than transition temperature (26,27). This region, however, is very difficult to perform simulations in, because folding rarely occurs at temperatures higher than transition temperatures.

To the best of our knowledge, this work is the first detailed folding kinetic study of Pin1 WW domain on the all-atom level. Using C_α models, Karanicolas et al. (19) predicted that the hairpin 2 of Pin1 WW domain folds before hairpin 1 while Cecconi et al. (20) suggested a zipping mechanism after the formation of a collapsed hydrophobic core. However, our study shows that the hairpin 1 is formed before the hairpin 2 near the transition temperature. Our result is consistent with experimental observations by Gruebele et al. (26,27). Previously, we have argued that it is difficult to reproduce the specific folding behavior of a β-hairpin by a C_α model, while it is relatively easy by using an all-atom model (34). This study confirms the above finding, that is, packing and native atomic contact interactions play an important role in the folding mechanism of proteins. (Certainly, it is possible that a sophisticated C_α-based model may be parameterized to reproduce the behavior of an all-atom model.) A similar conclusion was obtained in a separate folding kinetic study of a three-helix bundle fragment B of Staphylococcal protein A (33).

Interestingly, some theoretical studies of other WW domains agree with our findings on Pin1 WW domain. For example, the simulations of YAP 65 (15,16) and FBP 28 (22) indicate that the β2 and β3 strands of hairpin 2 are dissociated first in unfolding. This can be considered as the reverse of the folding process of Pin1 WW domain observed here. The transition state of FBP 28 also has a well-established hairpin 1 and flexible strand 3 (21,22). Moreover, loop 1 is more flexible compared to the contacts between β1 and β2 strands (21). Some misfolded intermediate states exist at low temperatures (22). These results are consistent with our results on Pin1 WW domain.