Steric Selectivity in Na Channels Arising from Protein Polarization and Mobile Side Chains

Abstract

Monte Carlo simulations of equilibrium selectivity of Na channels with a DEKA locus are performed over a range of radius R and protein dielectric coefficient ɛ_p. Selectivity arises from the balance of electrostatic forces and steric repulsion by excluded volume of ions and side chains of the channel protein in the highly concentrated and charged (∼30 M) selectivity filter resembling an ionic liquid. Ions and structural side chains are described as mobile charged hard spheres that assume positions of minimal free energy. Water is a dielectric continuum. Size selectivity (ratio of Na⁺ occupancy to K⁺ occupancy) and charge selectivity (Na⁺ to Ca²⁺) are computed in concentrations as low as 10⁻⁵ M Ca²⁺. In general, small R reduces ion occupancy and favors Na⁺ over K⁺ because of steric repulsion. Small ɛ_p increases occupancy and favors Na⁺ over Ca²⁺ because protein polarization amplifies the pore's net charge. Size selectivity depends on R and is independent of ɛ_p; charge selectivity depends on both R and ɛ_p. Thus, small R and ɛ_p make an efficient Na channel that excludes K⁺ and Ca²⁺ while maximizing Na⁺ occupancy. Selectivity properties depend on interactions that cannot be described by qualitative or verbal models or by quantitative models with a fixed free energy landscape.

INTRODUCTION

The selectivity of nerve membranes for Na⁺ allows nerve cells to conduct action potentials and has been recognized as a crucial property of membranes since the ionic hypothesis was formulated by Hodgkin et al. in 1949 (1,2). The binding of substrates like Na⁺ plays a crucial role in selectivity (in enzymes (3,4) and channels (5)) and thus the molecular and atomic basis of Na⁺ selective binding (6,7) is a biological problem of great importance. Indeed, in a functional and historical sense, channels (then called conductances) were defined by their selectivity, transport, and binding properties before Mullins suggested that channels were pores in membranes (8,9), and Narahashi (10,11) suggested that pores were in channel proteins at different locations in the membrane (10–12). The atomic (tertiary) structure of the channel protein is of great importance because it helps determine the function of the channel, along with the thermodynamic properties of surrounding solutions and the forces arising from the structure of the protein itself. Unfortunately, the structures of Na and Ca channels are not known.

It is natural (5) to imagine that selective binding arises from chemical effects involving some type of specific localized chemical bond between an Na⁺ ion and binding site of the channel protein but it is difficult to convert this natural idea into a physical model that reproduces the binding of a channel as measured over a range of concentrations of many ions. Computations of properties over a range of conditions are needed to compare models of selectivity with experimental measurements of selectivity. If models of selectivity do not predict experimental measurements, it is difficult to see how one model can be distinguished from another.

Predicting macroscopic channel function from properties of a chemical bond is difficult because the prediction involves quantum mechanics of a solvated ion in an inhomogeneous system that couples atomic scales of the chemical bond to macroscopic scales of the electrochemical potential. The macroscopic scale is unavoidable because the natural function of the Na channel is to change the transmembrane potential, a macroscopic quantity. The natural function of Ca channels and many other channels is to change the concentration of ions, another macroscopic quantity. Discussions and models of biological channels need to compute selectivity as it is actually used by biological systems. They must compute macroscopic quantities. Constructing a model that reaches from atomic scales of femtoseconds and Ångstroms to macroscopic scales of milliseconds and micrometers while simulating chemical bonds and number densities (concentrations) of micromolar is a challenge that cannot be met with present technology, in our view. Nor is it clear how a model with so much detail would yield insight. We choose to consider a simpler model. When simpler reduced models using only physical variables explain biological data and function with a few adjustable parameters, they are of considerable help in understanding the system well enough, for example, to build an abiotic equivalent. When physical models explain a biological function, one might propose the working hypothesis that other, more chemical effects were not selected by evolution to perform that function.

We choose to compute physical effects first because we think we (more or less) know how to do this, building on the large literature describing ionic solutions in general (13–22). In our reduced model, selective properties are outputs of the model that arise from the balance between electrostatic and steric forces in the confined space of a channel. Our model includes the same electrostatic and steric specific (i.e., selective) properties that characterize the free energy of concentrated salt solutions found in experiments (16,23). To these forces we add the dielectric forces and steric confinement produced by the channel protein to make a reduced description of the structure of the channel.

We show here how Na⁺ selectivity can arise (at equilibrium) using a reduced model in a pore that only detects the radius and charge of ions (24,25). This pore balances steric effects of ionic excluded volume against electrostatic effects of ionic charge and uses polarization charges at the dielectric boundary (between protein and pore) to amplify the electrostatic effects. Selectivity arises from the steric competition for space (26,27) between mobile ions like Na⁺ and structural ions, amino-acid side chains tethered to the channel protein in the highly concentrated and charged environment of the selectivity filter that resembles an ionic liquid (28,29) more than an electrolyte solution. The competition between space and charge gives the charge/space competition (CSC) (24–27,30–48). CSC is closely related to models used to compute the free energy of binding of K⁺ in the K channel (49–51).

Reduced models of this type have dealt quantitatively with many properties of several types of channels including the ryanodine receptor (RyR) and OmpF porin (24–27,30–50). In RyR, such models successfully predicted an anomalous mole fraction effect before it was measured (30,52,53). These models also explain RyR mutations that reduce the structural charge density (of side chains with permanent charge) from 13 M to zero (46,54). Models of this type account for the selectivity of K channels (49–51). Similar models produced a successful plan for the conversion of a nonselective bacterial channel OmpF porin into a decent Ca channel (43,55–57). In particular, Vrouneraets et al. (57) verified one of the important features of the CSC mechanism by showing that decreasing pore volume increases selectivity.

Our approach is quantitative in that it reproduces the actual binding curves reported in physiological experiments over a range of concentrations and in mixtures of ions (6,54,58–62); it is distinct from verbal models popular in structural biology (5,63–66) or simulations with large extrapolations (see Discussion) that discuss selectivity but do not reproduce binding curves actually measured in experiments. Models that discuss selectivity without presenting binding curves are hard to deal with. It is difficult to distinguish one model from another if they do not reproduce binding curves measured in experiments.

We use Monte Carlo (MC) simulations developed originally for bulk fluids (67,68) and then extended to include some of the inhomogeneities introduced by the channel protein. The simulations include 1), the energies of the electric field produced by the very large density of side chains (i.e., structural charges) of the channel protein, some 30 M in these proteins (see Methods, Channel Model); 2), the energies that polarize dielectric boundaries between the channel protein and its pore; and 3), the very large steric repulsive energies (produced by excluded volume of ions, side chains, and the rest of the channel protein) that balance the electrostatic forces that crowd spherical ions to these densities. We invoke only the forces and energies present in macroscopic electrolyte solutions and likely to be present in channels (24,25,36,37,40,48,69–82). These forces and energies are used to describe the distinctive properties of the channel environment. The narrow space of the channel is produced by the excluded volume of the protein and its side chains. The dielectric environment of the protein is included in the model. The electrostatic field is computed from the charges of the ions and protein, including polarization charges at the dielectric boundary between channel protein and the pore of the channel. The number of sampled configurations was between 5 × 10⁸ and 2.5 × 10⁹, depending on the parameters. More configurations were used to smooth density profiles and/or for smaller values of the pore radius R.

The energies associated with structural charge, dielectric charge, and steric repulsion produced by excluded volume are all needed to explain the biologically important selectivity of Na channels for both Na⁺ versus Ca²⁺ and Na⁺ versus K⁺ and how it varies under a range of conditions. Our model contains no special processes, forces, or energies particular to proteins (83,84). No special effects like cation-π interactions are needed to reproduce selectivity data from the DEKA Na channel or DEEA Ca channel in a wide range of solutions (see Results), just as they are not used in some successful computations of K channel selectivity (49–51). Traditional electrostatic models (64) and simulations (85–89) do not describe a range of conditions including physiological Ca²⁺ concentrations and/or do not deal with Na⁺ versus Ca²⁺ and Na⁺ versus K⁺ selectivity (87). Traditional kinetic models (5,66) are not relevant because they use an inappropriate prefactor, independent of friction, taken from the theory of gases (90,91) instead of the appropriate prefactor for condensed phases (92,93). The prefactor for condensed phases includes friction and so produces ∼20,000 times less flux than the friction free prefactor of the gas phase, other things being equal (69,94).

In our model, Na channels exclude K⁺ by steric repulsion because the selectivity filter is very small and densely packed with mobile and structural ions. Indeed, the selectivity filter resembles an ionic liquid (28,29) more than an ideal ionic solution. Because of the crowded space, densely packed filters of this sort contain reduced amounts of Na⁺, and thus are likely to carry less current. However, a low dielectric protein around the filter increases the Na⁺ content of the filter while still excluding K⁺. The polarization charge induced at dielectric discontinuities amplifies the net charge and thus electrostatic energies of the selectivity filter, increasing charge selectivity between Na⁺ and Ca²⁺ while maintaining size selectivity between Na⁺ and K⁺.

The balance of steric repulsion (from the excluded volume of mobile ions and protein side chains) and electrostatic attraction (between mobile ions and protein side chains)—amplified by the surrounding dielectric protein—can account for the main properties of the Na channel in this model. In our model, any small pore with a −1 permanent charge and side chains that occupy a significant volume is an Na-selective channel. In our results, the balance between steric repulsion and electrostatic attraction forms a design principle for selectivity likely to be used in many channels (95–98), transporters (99–101), proteins (102–106), and enzymes (107). The lysine K does not play a special role in this balance in our model beyond its volume and charge. Thus, our vision of the design principle needs to be refined to understand the particular role of lysine in the DEKA Na channel as well as other atomic detail when that detail is determined from structures of these channels.

METHODS

Channel model

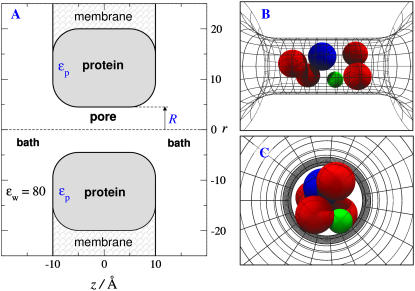
The channel protein is represented as a dielectric continuum that surrounds the selectivity filter with a hard wall. Similar dielectric descriptions of solvation are widely used in physical chemistry. Tomasi (108) reviews this enormous literature and describes the strengths and weaknesses of such descriptions. The selectivity filter contains mobile ions Na⁺, K⁺, Ca²⁺, and Cl⁻ and structural ions representing charged side chains of some of the amino acids of the protein (Fig. 1). The structural ions of the selectivity filter mix with the mobile ions and the dielectric that represents water implicitly (109). Mobile ions are charged hard spheres with radii Na⁺ = 1, K⁺ = 1.33, Ca²⁺ = 0.99, and Cl⁻ = 1.81 Å. The structural ions are charged hard spheres used to (crudely) represent side chains of the protein with permanent negative (acidic) charge or permanent (basic) positive charge. The permanent charge of the carboxyl COO⁻ groups of the acidic aspartate D and glutamate E side chains are assumed to be spread uniformly on the two oxygens of the carboxyl group because the oxygens are indistinguishable and an ordinary single bond joins the carbon of the carboxyl to the rest of the amino acid. These structural ions are represented as two independent negative half-charged structural ions, each an oxygen ion O^½− of radius 1.4 Å, confined within the pore. The amino group of the basic lysine K side chain is a positively charged structural ion, represented here as an 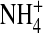ion with radius 1.5 Å. Alanine A is not represented because it is small. A selectivity filter of radius 3 Å and length 10 Å has a volume of 283 ų. A DEKA Na channel will have four oxygen ions O^½− and one 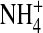giving an average concentration of structural ions of 30 M. This article deals mostly with the natural Na⁺ selective channel wild-type DEKA (Asp-Glu-Lys-Ala, permanent charge −1e), and the Ca²⁺ selective DEEA mutant (Asp-Glu-Glu-Ala, permanent charge −3e). A neighboring EEDD locus is known to influence permeation in Na channels but has not been included because it modifies conductance, not selectivity (110).

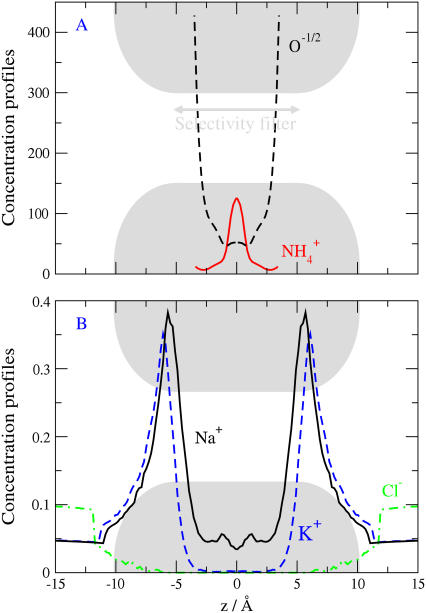
FIGURE 1.

The channel model. Computations are done in a much larger region than shown (see text). (A) Baths containing bulk solution on either side of a membrane containing a channel protein. (B,C) Snapshots of ions in the pore (−10 Å < z < 10 Å). The cross-sectional view Fig. 1 C vividly shows the crowding of ions and the competition for space in the narrow pore. The dielectric coefficient of the bulk solution is ɛ_w = 80. The dielectric coefficient of the protein is ɛ_p, ranging from 2 to 80. Side chains are restricted to the central region of the channel (−5 Å < z < 5 Å) which is called the selectivity filter for that reason. The selectivity filter has spatially nonuniform selectivity (see Fig. 7) and so later figures plot occupancy in the central most selective region of the filter ±2.5 Å from the center of the pore.

The dielectric coefficient ɛ_w of all solutions containing mobile ions is ɛ_w = 80, while the dielectric coefficient ɛ_p of the protein has various values between ɛ_p = 2 and 80. Bulk solutions are thus represented as a primitive model electrolyte, namely as spherical ions in a dielectric continuum (16,22,111). The qualitative effect of dielectric discontinuities depends on the sign of ɛ_w − ɛ_p (in this article, ɛ_w − ɛ_p ≥ 0). Polarization charge induced at dielectric boundaries (see Eq. 20 of Nadler et al. (79)) varies as (ɛ_w − ɛ_p)/(ɛ_w + ɛ_p), and thus one ion induces a charge of the same sign as the ion itself in our simulations. The ion is repelled by the polarization charge the ion itself induces at the dielectric boundary (although the net charge at the dielectric boundary, produced by all ions, might be of either sign so the net dielectric boundary force might be of either sign). Computation time is reduced by assigning a dielectric coefficient of 80 to the membrane, but this value does not change our results (47).

In our model, the structural ions of the selectivity filter of the protein mix with the mobile ions in a dielectric continuum that represents water implicitly. The mixture of water, mobile ions (here Na⁺, Ca²⁺, K⁺, and Cl⁻), and structural ions (here D, E, and K) form a liquid self-adjusting environment resembling an ionic liquid (28,29), which allows the mobile ions (from the surrounding bulk solutions) to enter the selectivity filter. All ions, both mobile and structural, are represented as charged hard spheres and cannot overlap with the walls of the channel pore or the membrane; these are hard walls the ions cannot cross. The spherical structural ions are also entirely confined longitudinally to the selectivity filter (±5 Å from the center of the pore, Fig. 1 A). The selectivity filter has spatially nonuniform selectivity (see Fig. 7) and so we chose to plot occupancy in the central, most-selective region of the filter ±2.5 Å from the center of the pore after considering several possible choices, and many conditions, beyond those illustrated in this article. Confinement is with a hard-wall potential and enforced by rejecting MC moves; springlike restraining forces are not used. Future computations should compare different types of restraining forces.

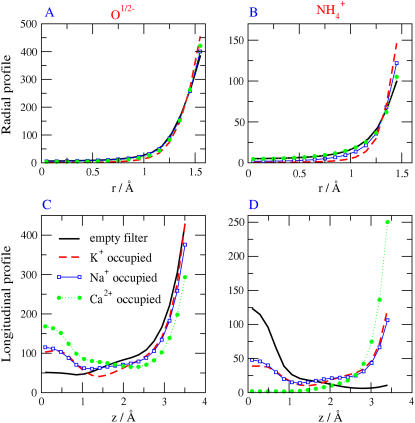
FIGURE 7.

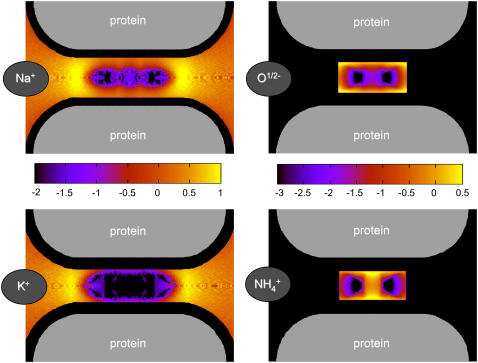
Contour plots in and around for various ions in the DEKA locus (R = 3Å, ɛ_p = 10, and [NaCl] = [KCl] = 0.05 M). Black represents negligible concentration. Plots show log₁₀(c/c_ref) where c_ref is a reference concentration. The value c_ref is the bulk concentration for the K⁺ and Na⁺ ions (0.05 M), while it is the average concentration in the filter for the structural ions (66.6 M) for O^1/2− and 18.9 M for 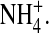These average concentrations are determined using the volume accessible to the centers of each type of ions.

It is important to remember that the effective radius of the pore is reduced dramatically by the side chains of the channel protein, the structural ions. The side chains exclude volume that would otherwise be available to the mobile ions. The channel protein provides a pore with an effective diameter smaller than the distance between the walls of the pore because the side chains extend into the pore from the walls. So little space is available in the pore that ions pile up outside the pore proper, as we shall soon see. When side chains pile up at the ends of the region in which they are constrained, ±5 Å from the center of the pore, the effective length available to ions is reduced as well.

All ions, including structural ions, assume configurations of minimal free energy, which vary depending on experimental boundary conditions imposed on the bulk solution (bulk electrolyte composition, temperature, pressure). Configurations depend also on the charge, composition, and assumed structure of the channel protein itself (e.g., DEKA versus DEEA). Different configurations of structural (and mobile) ions produce different electric fields, and different steric interactions (produced by excluded volume) between mobile and structural ions. Thus, the spatial distribution (i.e., profile) of both electrical and chemical free energy in the selectivity filter varies with experimental conditions imposed on the bulk solution and also with the composition of the channel protein itself. In this way, the mixture of water, mobile ions (here Na⁺, Ca²⁺, K⁺, and Cl⁻) and structural ions (here D, E, and K) form a liquid self-adjusting environment that allows the mobile ions (from surrounding bulk solutions) to enter the selectivity filter and carry electric current.

Simulations

Calculations are performed in a cylindrical compartment forming a simulation box much larger than shown in Fig. 1. The simulation box and procedure has been shown (see Supplementary Material of Boda et al. (47)) to allow the formation of bulklike solutions in both baths. The compartment has a 75 Å radius representing two baths (each 170 Å long) separated by a membrane 20 Å thick containing a protein with a pore (radius R) through it. MC moves that put an ion outside the simulation box are rejected. Electrostatic boundary conditions are not imposed on the simulation box. Rather the dielectric material ɛ_w extends to infinity. Electric potentials are found at the edge of the simulation box, if, for example, ions are of different diameter, as arise in any double-layer calculation (112,113). Care is taken to be sure these potentials do not reach the channel. (See Supplementary Material of Boda et al. (47) for computation and discussion of these effects.)

Occupancy of species i is defined as the number of (centers of) ions of that species in the central region, namely the 5 Å of the selectivity filter −2.5 Å < z < 2.5 Å. The occupancy determined in MC simulations is an average. If a channel were occupied half of the time by one ion, and the other half of the time by zero ions, the occupancy we determine would be 0.5.

Snapshots from an MC simulation illustrate our reduced model of the selectivity region (Fig. 1, B and C). Fig. 1 C particularly shows the crowding of ions and the competition for space. The central, cylindrical part of the pore contains charged side chains extending from polypeptide backbone of the channel protein into the pathway for ionic movement: the side chains are free to move inside the selectivity filter of the channel, and in this sense are dissolved, but they cannot leave the selectivity filter; they are kept within it.

We perform calculations for cylindrical selectivity filters of fixed length 10 Å with hard walls at radii between R = 3 Å and R = 5 Å. Roth and Gillespie (114) have shown that a cylinder of protein surrounding a pore of radius ρ (representing the wall of a channel) has properties similar to those of a cylinder with hard, smooth walls surrounding a pore of slightly larger radius ρ + Δρ when the cylinder of protein is represented as a fluid of wall particles.

We simulate an equilibrium system in the canonical ensemble with temperature T = 298 K. The volume of the computational compartment and the number of atoms of the various ionic species are fixed. The length and radius of the simulation box are chosen so that the number of Na⁺ determines a previously chosen bath concentration. In a few cases, where small bath Ca²⁺ concentrations were computed, we simulated the grand canonical ensemble. We simultaneously inserted (or deleted) one Ca²⁺ and two Cl⁻ ions while maintaining a fixed chemical potential for CaCl₂ (47). All bath concentrations, including Ca²⁺ concentrations in the bath, are outputs of the calculations in every simulation of this article.

An essential part of our MC procedure is a biased particle exchange between the channel and the bath to accelerate the convergence of the average number of various ions in the channel (27,39), but the acceleration of convergence does not change our results. The electrostatic energy of the system is determined using the induced-charge computation method (45), which numerically solves an integral equation for the surface charge induced on dielectric boundaries. Previous work (see Supplementary Material of Boda et al. (47)) has shown the accuracy of the method and the need to check that accuracy when boundaries are curved (44,45).

RESULTS

We simulate selectivity in a reduced model of a channel protein over a wide range of conditions and show that a treatment involving only a few forces can do quite well. The protein in our model is represented by a dielectric boundary surrounding structural ions described in Methods and Fig. 1. The highly concentrated and charged selectivity filter resembles an ionic liquid (28,29) more than an ideal dilute electrolyte solution.

Charge selectivity Ca²⁺ versus Na⁺

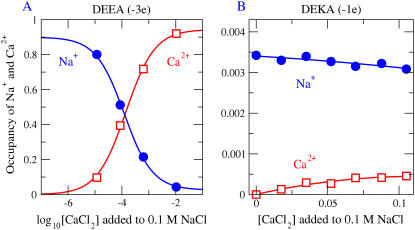
Fig. 2 shows the dramatic effect of the side chains of the channel protein on the contents (occupancy) of the selectivity filter. Simulations were done in which a variable amount of Ca²⁺ was added to a constant, approximately physiological, concentration of Na⁺ (100 mM). Simulations compare a Ca²⁺-selective DEEA mutant (Asp-Glu-Glu-Ala, permanent charge −3e, Fig. 2 A with logarithmic abscissa) with the natural Na⁺ selective channel wild-type DEKA (Asp-Glu-Lys-Ala, permanent charge −1e, Fig. 2 B with linear abscissa). DEEA has been shown to conduct substantial Ca²⁺ currents: Ca²⁺ can easily enter this channel (54,115,116). In our simulations of DEEA, Ca²⁺ easily enters the channel to give the titration curve (Fig. 2 A, logarithmic abscissa) typical of a Ca channel (58–60,117–133).

FIGURE 2.

Simulations give titration curves typical of a Ca²⁺ or Na⁺ channel. Titration curves show Na⁺ versus Ca²⁺ selectivity for a DEEA Ca²⁺ channel (charge −3e) and a DEKA Na channel (charge = −1e) for R = 3 and ɛ_p = 10. The concentration of NaCl is kept fixed at 0.1 M while CaCl₂ is gradually added. We measure the number (occupancy) of the various cations (Na⁺ and Ca²⁺) as a function of [CaCl₂] in the 5 Å long central portion of the 10 Å filter, the most selective region of the pore (see Fig. 7). The mutation of the DEKA locus into DEEA changes a lysine K (+1 charge) into a glutamate E (−1 charge). In our model, the side chains of DEEA are represented as six half-charged oxygen ions (O^½−); the side chains of DEKA are represented as four oxygen ions and one 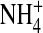ion. The effect of charge and excluded volume is clearly seen in the plot: DEEA is highly Ca²⁺ selective in our model, while the DEKA is highly Na⁺ selective in these solutions. Genetic drift and stochastic mutation could frequently convert K ↔ E and vice versa, giving evolution repeated chances to select the side chain best for each cellular function.

As Ca²⁺ is added to the bulk solutions, more and more Ca²⁺ enters the channel, displacing Na⁺ from the selectivity filter. In the case shown, half of the Na⁺ in the selectivity filter is replaced with Ca²⁺ when [Ca²⁺ ]_bulk is just 10⁻⁴ M, compared to [Na⁺]_bulk = 10⁻¹ M. This DEEA Ca channel has an apparent binding constant of 10⁻⁴ M under these conditions. In calcium channels, Ca²⁺ at just 10⁻⁴ M successfully competes for space with the Na⁺ counterions at 10⁻¹ M and displaces them from the crowded selectivity filter, as we have described previously (47). The filter of the DEEA Ca channel is crowded because structural ions are at high concentration ([O^½−]_{selectivity filter} ≃ 35 M) comparable to the concentration of oxygens in a bulk water solution. Six oxygen ions O^½− are in a cylinder of radius 3 Å and length 10 Å, containing cylindrical volume 283 ų. The volume accessible to any one oxygen ion is substantially less than the cylindrical volume because of the other ions in the channel.

Mutating one negative (acidic) side chain to a positive (basic) side chain changes selectivity dramatically (Fig. 2 B, note the linear abscissa). DEKA (−1e protein permanent charge) is selective for Na⁺; DEEA (−3e) is selective for Ca²⁺. In the DEKA Na channel (−1e), Na⁺ is found at the same small occupancy in the selectivity filter, whether Ca²⁺ is absent (left-hand side of Fig. 2 B) or present (compare Fig. 2 B with Fig. 2 A, the DEEA calcium channel).

Blockade of Na⁺ current by physiological or smaller concentrations of Ca²⁺ is a characteristic property of natural Ca channels but not Na channels. Small concentrations of Ca²⁺ in bulk solutions dramatically reduce the Na⁺ conductance of natural Ca channels as if they reduce the amount of Na⁺ in the selectivity filter. We expect that Na⁺ current in the DEKA Na channel (−1e) will not be reduced (blocked) very much by physiological Ca²⁺ because its small structural negative charge is not enough to attract much Ca²⁺ (see experimental work (115) supplemented and reviewed in Favre et al. (7) and Ch. 14 of Hille (5)). Our results (Fig. 3 C) show that the Ca²⁺ occupancy of the DEKA channel is in fact small. Mutating the negative glutamate E to the positive lysine K should remove the blockade, because the DEEA channel rich in glutamates is so much more crowded with Ca²⁺ counterions than the Na channel (compare the scale of the ordinate in Fig. 3, B and C).

FIGURE 3.

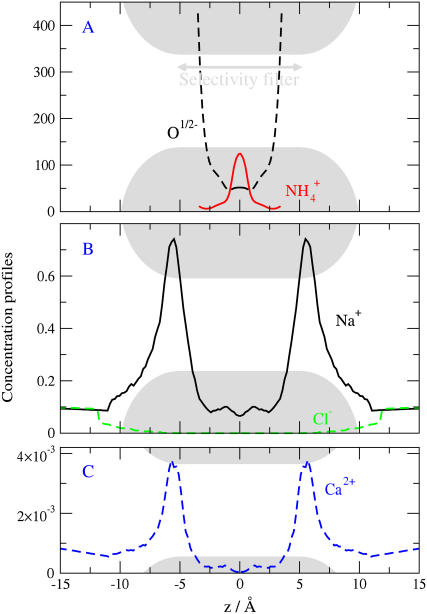
The distribution along the central axis of the channel of structural ions (upper panel A) and mobile ions (lower panels) in a DEKA Na⁺ channel of radius 3 Å; with protein dielectric coefficient 10; in bathing solutions [CaCl₂] = 1 mM and [NaCl] = 100 mM. The channel boundaries are represented by shaded ∪ and ∩ lines touching the horizontal lines that define the figure. The location of the peaks of concentration depends on conditions. A binding site at a fixed location does not describe the peaks of concentration. Ion-specific effects (selectivity) are more apparent in the central part of the channel z = 0, where the concentration of Ca²⁺ is nearly zero, than at the peaks of concentration. The concentrations in this and other figures are determined using the volume accessible to the center of each type of ion. The spatial localization of binding is discussed in Results and in the caption to Fig. 6.

Spontaneous structure of side chains

Our model allows side chains and ions to move—it imposes only minimal structural constraints—so it is interesting to see what self-organized structures arise spontaneously in the filter. The electrostatic interactions of mobile and structural ions balance the steric repulsion and dielectric boundary forces in different ways under different conditions leading to different distributions of matter, charge, and potential. In particular, one must expect the distribution of structural ions to change with experimental conditions imposed on the bulk solution (bulk electrolyte composition, temperature, pressure) and with the charge, composition, and assumed structure of the channel protein itself (e.g., DEKA versus DEEA).

Fig. 3 shows the distribution of side chains (upper panel), i.e., structural ions, and mobile ions (lower panels) in a DEKA Na channel of radius 3 Å; with protein dielectric coefficient 10; in bathing solutions [CaCl₂] = 1 mM and [NaCl] = 100 mM. The channel boundaries are shown by shaded ∪ and ∩ regions touching the horizontal lines that outline the box of the figure. The concentrations shown in this and other figures are averaged 1), over the cross section of the pore accessible to the center of each type of ion; and 2), over the course of the simulations.

Both structural and mobile ions distribute in distinct patterns. The structural oxygen ions (of D and E) sandwich the ammonium ion (of K), and the mobile ions respond to the high density and net charge of structural ions in the selectivity filter: the concentration of coion Cl⁻ is very small throughout the pore, and the concentrations of counterions Na⁺ and Ca²⁺ are equal or smaller in the filter region than in the baths. The maximal value of the concentrations of Na⁺ and Ca²⁺ are just outside the selectivity filter for reasons described later in Results and in the caption to Fig. 6.

FIGURE 6.

Longitudinal concentration profiles for various ions in the DEKA Na channel (charge = −1e). R = 3Å, ɛ_p = 10, and [NaCl] = [KCl] = 0.05 M. This figure shows selectivity by depletion within the filter and binding outside the filter. The binding is not selective and occurs because the pressure arising from the excluded volume of ions and side chains forces the counterions to dwell near rather than in the filter region. Counterions accumulate at the filter entrances to the filter because they are electrostatically attracted to it but they cannot fit within the filter. This is an essential feature of the charge-space competition mechanism of selectivity.

The distribution of ions shown produces the minimal free energy in a system with the imposed bath concentrations. The distribution (and free energy) in the real channel is determined by the sum of all forces not just by nearby chemical bonds, just as the sum of all forces—not just nearby chemical bonds—determines the secondary and tertiary structure of proteins in general. In our model, localized chemical bonds (134) play no role. Chemically specific effects arise only from the diameter and charge of ions, and the structure of the protein dielectric, in our model, just as chemically specific effects (23) arise in bulk solution from the diameter and charge of ions, and the dielectric properties of water (16,21,22,111,135).

Note that the Ca²⁺ concentration is less in the filter region than in the bulk solutions: Ca²⁺ is excluded from the DEKA Na channel. Na⁺ concentrations are similar in the filter and baths. Na⁺ ions are not concentrated in the selectivity filter, but they are not diluted either. The rather small cation concentrations of the filter region indicate that the steric (excluded volume) repulsive forces exerted by the structural ions (and the rest of the channel protein) actually exceed the attractive electrostatic forces arising from the net charge of the structural ions (in this region). The depression of the Ca²⁺ concentration in the central region (Fig. 3 C) is correlated with the peak of the 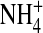distribution there (Fig. 3 A), which makes the net structural charge positive in this vicinity. The low occupancy of the DEKA Na channel suggests that it operates in a different regime than the DEEA Ca²⁺ channel. The electrostatic field outside the selectivity filter of the DEKA Na channel is far more important than the electrostatic field outside the filter of the DEEA Ca channel.

Fig. 4 shows thought experiments designed to study the effect of ion contents on profiles in a DEKA Na channel. The left-hand column (Fig. 4, A and C) shows the distribution of O^½−; the right-hand column (Fig. 4, B and D) shows the distribution of 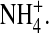In these simulations, the central 5 Å of the channel (i.e., the central part, −2.5 Å < z < 2.5 Å of the selectivity filter) either is empty or contains a single ion constrained to the filter, either one Na⁺ ion, one K⁺ ion, or one Ca²⁺ ion. In this calculation, the constrained ion was treated as if it were a structural ion. MC moves outside the filter were not allowed for the constrained ion. We used different bath solutions depending on the ion. When the filter was forced to hold a single Na⁺ ion, we used 0.1 M NaCl as the external bath solution. When the filter was forced to hold a single K⁺ ion, we used 0.1 M KCl as the external bath solution. When the filter was forced to hold a single Ca²⁺ ion, we used 0.05 M CaCl₂ as the external bath solution. The curve labeled “empty filter” is actually three superimposed curves separately computed for the three external solutions 0.1 M NaCl, 0.1 M KCl, and 0.05 M CaCl₂. The empty filter contained only side chains—namely the structural ions O^½− and 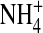—but no Na⁺, K⁺, Ca²⁺, or Cl⁻.

FIGURE 4.

The effect of ion contents in profiles in a DEKA Na channel. (A,C) Distribution of O^½−; (B,D) Distribution of 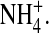The selectivity filter has spatially nonuniform selectivity (see Fig. 7) and so we define and plot occupancy in the central most selective region of the filter ±2.5 Å from the center of the pore. This region is either occupied by one Na⁺ ion; or one K⁺ ion; or one Ca²⁺ ion; or the filter is empty. The longitudinal distribution of side chain structural ions (O^½− and 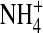) is shown in the lower two panels of C and D. The radial distribution of side chains is shown in the upper two panels of A and B. Filters labeled empty contained side-chain structural ions but no Na⁺, K⁺, or Ca²⁺ ion.

The longitudinal distribution of side-chain structural ions (O^½− and 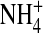) is shown in the lower two panels of Fig. 4, C and D, and is very different in filled and empty channels. When the monovalent Na⁺ or K⁺ occupy the channel, both types of side chains are longitudinally displaced. The divalent Ca²⁺ has an even larger effect. The radial distribution of side chains is shown in the upper two panels of Fig. 4, A and B. The side chains are displaced radially toward the walls of the pore (r ≅ 1.5 Å in Fig. 4, A and B), when the channel is occupied by Na⁺, K⁺, or Ca²⁺.

Monovalent ion selectivity: Na⁺ versus K⁺

Biological Na channels prefer Na⁺ to K⁺ and this size selectivity is crucial to the role of Na channels as generators of the inward current that produces the action potential of nerve and muscle. Our simulations demonstrate that selectivity between ions of the same charge—but different size—cannot be understood as a purely electrostatic phenomenon, in contrast to the conclusions of the literature (85–89).

We simulate K⁺ and Na⁺ in a DEKA selectivity filter with radius R = 3 Å, with bulk solutions containing 0.1 M NaCl and different added concentrations of KCl (Figs. 5 and 6). The original experimental work (115) is supplemented and reviewed in Favre et al. (7) and Ch. 14 of Hille (5). Results are shown for mutant channels DEEA and DEAA as well. The model filter contains Na⁺ in large excess over K⁺. (Note that the K⁺ concentrations shown in Fig. 5 have been multiplied by 10.) This binding ratio for DEKA reaches >35 for a pore of radius 3.0 Å (Fig. 8 A) and is within the range of Na⁺ versus K⁺ selectivities reported in the experimental literature for Na channels (5). Fig. 6 shows how the structural and mobile ions distribute in a simulation when the bulk contains 0.05 M NaCl and 0.05 M KCl. The structural ions arrange themselves much as they did in Fig. 3 (which was computed with different ions in the bulk). The mobile ions, again, are somewhat concentrated outside the mouths of the selectivity filter, but have lower concentrations in the filter itself as discussed previously.

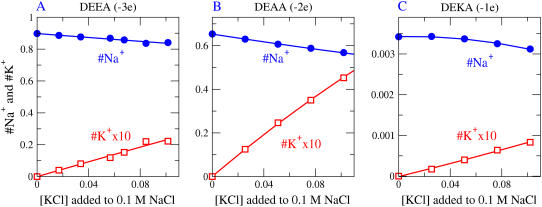
FIGURE 5.

The occupancy of the central selectivity filter ±2.5 Å from the center of the pore as a function of [KCl] for the DEEA Ca channel (charge = −3e), the DEAA mutant channel (charge = −2e), and the DEKA Na channel (charge = −1e).

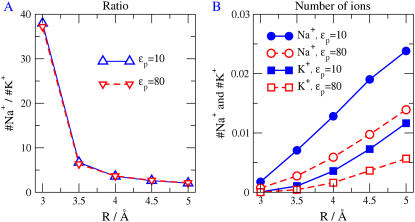
FIGURE 8.

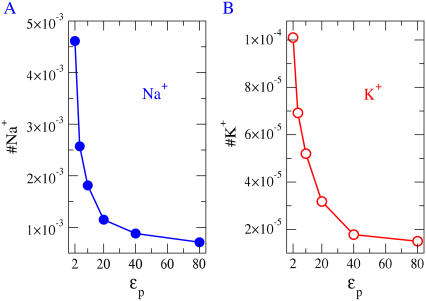
The occupancies of Na⁺ and K⁺ ions as a function of R for two different protein dielectric coefficients of the protein (ɛ_p = 10 and 80). (A) The ratio of the occupancies of Na⁺ and K⁺ as a function of R. The electrolyte is equimolar: [NaCl] = [KCl] = 0.05 M. The protein dielectric coefficient has no effect on the ratio and thus on this measure of size selectivity. (B) The protein dielectric coefficient has a large effect on occupancy and thus we suspect on the conductance of the channel. The selectivity filter has spatially nonuniform selectivity (see Fig. 7) and so we define and plot occupancy in the central most selective region of the filter ±2.5 Å from the center of the pore.

Fig. 6 shows selectivity by depletion within the filter and binding outside the filter. The binding is not selective and occurs because the pressure arising from the excluded volume of ions and side chains forces the counterions to dwell near rather than in the filter region. Counterions accumulate at entrances to the filter because they cannot fit within the filter: the side chains of the filter occupy much of the small volume of the pore. This is an essential part of the charge-space competition mechanism of selectivity, competition between mobile ions, and side chains for space within the filter, with competition enforced by steric constraints imposed by the protein and the electric field generated by deviation from electroneutrality.

The crucial factor here is that there is essentially no K⁺ in the center of the selectivity filter (z = 0) while the Na⁺ concentration there is more or less at its bulk value. The Na⁺ in the selectivity filter is almost 40× the concentration of K⁺ (compare K⁺ and Na⁺ curves at z = 0 in Fig. 6), when the bulk solution contains equal concentrations of Na⁺ and K⁺, although the peak concentrations of Na⁺ and K⁺ are more or less equal (compare K⁺ and Na⁺ curves at z = ±6 Å in Fig. 6). Selectivity here works by K⁺ exclusion, not Na⁺ enrichment. No selectivity is seen where K⁺ and Na⁺ are most concentrated.

Fig. 7 shows contour plots of concentrations in both the radial and axial dimensions of the filter. The structural and mobile ions distribute in intricate patterns in which regions of low concentrations stand out as the most distinct features of the fluid in the pore. The structural ions O^½− and 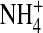representing side chains are found at the pore walls, for the most part. The monovalent mobile ions Na⁺ and K⁺ are excluded from the centerline of the pore, particularly the larger K⁺ ion, which is excluded more than Na⁺. The regions accessible to Na⁺ and K⁺ differ and this difference contributes importantly to the selectivity of the channel, again illustrating the competition between charge and space.

Fig. 7 shows that chemical specificity can be produced from complex interactions of simple physical forces in an oversimplified structural representation of a channel. The interactions are difficult to summarize in the simple language of traditional models. Complex effects are produced by the simple forces and simple structures of our model, essentially the electrostatic attraction between counter and structural ions and steric repulsion between the excluded volume of all ions in a narrow pore between dielectric boundaries. Even the oversimplified structures (Fig. 1) of our reduced model of channels produce intricate patterns that vary dramatically as bath composition is changed.

Effects of radius R and protein dielectric coefficient ɛ_p

It is interesting to investigate variables that the protein (and evolution) might use to control selectivity: the pore radius R of the selectivity filter and the dielectric coefficient ɛ_p of the surrounding protein. Fig. 8 A shows the effect of R on the ratio of Na⁺ occupancy to K⁺ occupancy for two values of protein dielectric coefficient. The ordinate gives the number ratio of Na⁺ versus K⁺ in the central 5 Å of the selectivity filter −2.5 Å < z < 2.5 Å. Changing the protein dielectric coefficient between 10 and 80 has no effect on the number ratio. Polarization charge has no significant effect on selectivity under these conditions, in contrast to the conclusions of the literature (85–89).

The filter radius is the crucial determinant of selectivity under these conditions: a slight widening of the pore drastically reduces selectivity. As the pore is made more narrow, the structural ions extending into the pore become packed more densely. Large mobile ions have more difficulty finding a niche of sufficient size in this crowded space. Such excluded volume effects are known to increase in a strongly nonlinear way in crowded solutions (16,22). Indeed, reducing the pore radius from 3.5 to 3 Å increases the observed size selectivity by almost an order of magnitude. The strong dependence on the pore radius indicates that excluded volume determines this selectivity (136,137), not the strength of the electric field produced by the charges in the pore (64,85–89).

Na⁺ versus K⁺ selectivity of Na channels has received much attention in the classical literature (e.g., (5,64,136–138)) where analysis was qualitative. Our work uses a quantitative analysis explicitly computing both steric repulsion (137) and electrostatic interaction (64). Specifically, Na⁺ versus K⁺ selectivity has classically been suggested to arise from electrostatic interaction of the mobile ion with oxygen atoms in a rather wide selectivity filter (5). One expects classically (Hille/Eisenman) that electrostatic effects of ion diameter contribute to selectivity, independent of the diameter of the channel itself; but our results show that substantial selectivity requires a stronger effect, namely the competition between the charge, the excluded volume of the ions, and the space available within the channel itself, i.e., the CSC mechanism.

The competition effect is shown clearly by the effects of filter radius R. As R is reduced, the fixed charge of protein side chains becomes more concentrated. Nonetheless, fewer ions are attracted into the filter (Fig. 8 B) because there is no room for them in the small space between the walls of the selectivity filter. Our work shows that the electrostatics are less important than the steric repulsion produced by volume exclusion under these conditions. We see that the high selectivity of model pores of small radii (Fig. 8 A) is dominated by steric effects; the center of the channel is almost empty with an average occupancy <0.035 Na⁺ (Figs. 8 B, 5 C, and 2 B). Steric forces arising from excluded volume vary so steeply with radius (as does the Lennard-Jones potential (139)) that they allow the channel to select effectively between Na⁺ and K⁺ . It would be harder for Coulombic forces themselves, which vary much less steeply, to produce such selectivity.

Electrostatics itself is a complex phenomenon in this channel because it involves terms of opposite signs and several kinds of charge: dielectric polarization charge, mobile ion charge, and structural side-chain charge. We have already seen that different loci with different side chains and structural charge (e.g., DEEA, DEAA, and DEKA) produce very different selectivities (Figs. 2 and 5). But, the dielectric properties of the protein also play a crucial and multifaceted role in selectivity. For example, the dielectric boundary force in narrow model pores is important in determining the occupancy of the channel (Fig. 8 B), and thus its conductance—but it is not essential for size (Na⁺ versus K⁺) selectivity (Fig. 8 A).

Fig. 9 illustrates the role of the protein polarization. It shows the numbers of Na⁺ (and K⁺) ions in the central region of the filter, computed for bulk concentrations of 50 mM NaCl and 50 mM KCl, as a function of the dielectric coefficient of the pore wall. The similar shape of the curves shows that the Na⁺ versus K⁺ ratio does not depend on the protein dielectric coefficient ɛ_p (compare with Fig. 8 A). Reducing the dielectric coefficient of the protein from 80 to 2 substantially increases the average number of ions in the pore. The conductance of a channel is likely to increase as the number of mobile ions in its pore increases.

FIGURE 9.

The occupancies of Na⁺ and K⁺ ions as a function of ɛ_p for R = 3 Å. The electrolyte is equimolar: [NaCl] = [KCl] = 0.05 M. The protein dielectric coefficient has a large effect on occupancy and thus (most likely) on the conductance of the channel even though it has little effect on the selectivity, i.e., the ratios of occupancies seen in Fig. 7 A, left-hand panel. The selectivity filter has spatially nonuniform selectivity (see Fig. 7) and so we define and plot occupancy in the central most selective region of the filter ±2.5 Å from the center of the pore.

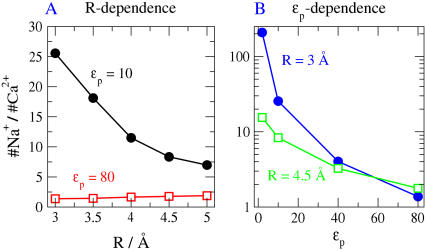
The effects of protein dielectric coefficient ɛ_p on occupancy are even more complex when considering charge selectivity between Na⁺ and Ca²⁺. When ɛ_p = 80 and the pore radius is changed, the ratio of Ca²⁺ to Na⁺ is remarkably unchanged (Fig. 10 A). However, when ɛ_p = 10, the DEKA locus becomes highly Na⁺-selective as the pore radius is decreased (Fig. 10 A). For a given pore radius, this Na⁺ selectivity is a highly nonlinear function of protein dielectric coefficient (Fig. 10 B: note the logarithmic ordinate).

FIGURE 10.

The ratio of the occupancies of Na⁺ and Ca²⁺ ions (A) as a function of pore radius R for two different protein dielectric coefficients of the protein (ɛ_p = 10 and 80) and (B) as a function of ɛ_p for two different radii of the pore (R = 3 and 4.5 Å). The bath Ca²⁺ concentration is 17.5 mM. Protein dielectric coefficient has little effect on Na⁺ versus Ca²⁺ selectivity when the protein dielectric coefficient is large, but it has a substantial effect when the protein dielectric coefficient is small. The radius of Na⁺ and Ca²⁺ are nearly the same (Na⁺ = 1, Ca²⁺ = 0.99 Å) so this graph shows charge selectivity. The selectivity filter has spatially nonuniform selectivity (see Fig. 7) and so we define and plot occupancy in the central most-selective region of the filter ±2.5 Å from the center of the pore.

The structural net charge of the DEKA selectivity filter of our model is −1e. This charge can be locally balanced by one Na⁺, with no net charge remaining to be balanced outside the selectivity filter. One Ca²⁺ in the filter, on the other hand, would not locally balance the fixed charge of the DEKA locus. One Ca²⁺ would change the net charge of the filter region from −1e to +1e and that net charge would be balanced elsewhere, outside the filter. The filter also has net charge if it is empty, namely −1e. Both the empty case and the Ca²⁺-filled case are expected to be electrostatically unfavorable. Reducing the protein dielectric constant ɛ_p around the DEKA locus is expected to further increase the electrostatic energy of these unbalanced configurations. Hence, a reduction of ɛ_p is expected to reduce the probability of unbalanced configurations. A reduction of ɛ_p reduces the Ca²⁺ content of the filter while it increases the Na⁺ content of the filter, as expected. The ratio of Na⁺ to Ca²⁺ then increase substantially (see Fig. 10 B).

It is interesting that a reduction of pore radius increases Na⁺ versus Ca²⁺ selectivity when the dielectric coefficient is small (Fig. 10 A). Reducing the radius increases the repulsion produced by excluded volume. Nonetheless, the ion that packs the smaller charge in the same particle volume (i.e., Na⁺ compared to Ca²⁺) becomes the favored counterion in the DEKA locus because the need for local charge neutrality in the filter overwhelms the steric constraints arising from excluded volume (when both radii and dielectric coefficients are small; see Fig. 10 A). Both steric repulsion and electrostatic attraction are important, but the relative importance must be calculated and cannot be determined by qualitative discussion. The relative importance depends on the quantitative size of interacting terms.

The selectivity (occupancy ratio) for ions of different charge like Ca²⁺ and Na⁺ depends much more on pore radius, than for ions of the same charge, as would be expected from the dielectric boundary force for these ions (see Eq. 20 of Nadler et al. (79)). The dielectric boundary force is much stronger in small than large channels (44,47,48,79,140,141) and contributes to selectivity only when it is strong compared to the forces arising from the structural charge of side chains. Structural charge produces a monopole field, to use the classical language of electrostatics that expands Coulomb's law into a series of multipoles. Monopoles like the structural charge on carboxyl oxygens of D and E and amino nitrogens on K produce strong forces in both wide and narrow channels because monopole fields are long-range; dielectric charge at the edge of the channel creates a dipole field that has much shorter range and so is more important in narrow channels. The crowding of hard spheres into the narrow volume of a selectivity filter produces even shorter-range forces and so crowded charge effects depend even more on the diameter of the selectivity filter. The interplay of diameter, protein dielectric coefficient, and structural charge on an ion must be actually computed to be understood (Figs. 8–10).

Simulations were also done to assess Na⁺ versus K⁺ selectivity in model pores representing mutants in which the lysine residue of the DEKA locus is replaced by other residues. We tested DEEA and DEAA (Fig. 5). With the pore radius fixed at 3 Å, these mutant models yield Na⁺ versus K⁺ selectivities comparable to those of the DEKA model, which is different from experimental observations (115,116). The fraction of pore volume occupied by structural ions is substantial, ∼20%, 0.244 in DEEA, 0.163 in DEAA, and 0.213 in DEKA. Size selectivities should be similar if they depend mostly on excluded volume. However, small changes in pore radius would drastically change size selectivity (see Fig. 8), and perhaps mobility, and so are a plausible explanation of the difference between our simulations and experiments. In our view, reduced models of the type considered here have limited ability to resolve this sort of issue. Direct measurements of structure or mobility do much better.

DISCUSSION

Selectivity in our model

We show here how (equilibrium) Na⁺ selectivity can arise in a pore that only detects the radius and charge of ions (24,25). We consider a model that does not include local chemical bonds between a specific permeating ion and a binding site. (Chemical bonding here means the change in the shape of electron orbitals that characterizes a chemical bond (134).) We find that many of the experimentally measured selectivity properties of Na⁺ channels can be understood by a model that does not involve localized chemical bonding of this type. Selectivity in other systems is likely to depend on both chemical bonding and the more physical effects computed in our model.

We have deliberately chosen an overly-reduced model of the Na channel and the surrounding baths with the idea that if this simple system produces much of the complex behavior of the Na channel, then the origin of these properties is clear. All-atom simulations will add more important details, but it will also add other details not so relevant to selectivity. The underlying principles of selectivity may well be easier to find if they have been previously identified in a reduced model. (Or to put the same thing another way: a higher resolution model can be used to test the working hypothesis that selectivity can arise in a pore that only detects the radius and charge of ions.) By stripping away a myriad of atomic interactions, leaving only the steric and electrostatic interactions, we have shown that many—but certainly not all—properties of Na channel selectivity can be produced by these two fundamental interactions.

In our reduced model, the protein that makes the pore provides the strong structure that allows balance between steric effects of ionic excluded volume and electrostatic effects of ionic charge. The protein provides polarization charges at dielectric boundaries to amplify the electrostatic effects. Selectivity arises from the balance of electrostatic attraction and steric repulsion: attraction occurs between counterions and structural charge of protein side chains; repulsion arises from steric competition for space (26,27) between mobile ions like Na⁺ and structural ions (amino-acid side chains tethered to the channel protein). Either attraction or repulsion occurs at dielectric boundaries depending on the sign of the jump in dielectric coefficient across the boundary. In this article, ɛ_p ≤ ɛ_w = 80, so that all ions induce a charge of the same sign as the ion itself (see Methods and Eq. 20 of Nadler et al. (79)). In this article, the dielectric boundary force between the ion and the charge it induces in the wall of the channel are repulsive.

Physiologically, Na channels like DEKA need to conduct Na⁺ while excluding K⁺ and Ca²⁺. At the same time, Na⁺ current needs to be as large (and quickly turned on) as possible so the action potential can propagate as rapidly as possible. In our model of a small, dense selectivity filter (Fig. 1), the DEKA Na channel excludes K⁺ by steric repulsion arising from excluded volume. This kind of selectivity filter, however, reduces Na⁺ occupancy as well as K⁺ occupancy (Fig. 8 B). To maximize the Na⁺ current, Na⁺ occupancy can be increased (while still excluding K⁺) by surrounding the selectivity filter with a low-dielectric coefficient protein (Fig. 9). The dielectric sheath always increases occupancy in these highly-charged channels because it amplifies the electrostatics of the unoccupied filter, but this does not affect Na/K ratio at all (Fig. 8 A). The low-dielectric sheath has the added benefit of excluding Ca²⁺ (Fig. 10 B) because, again, the electrostatics of the filter is amplified by the low-dielectric protein. The role of the dielectric (and electrostatics) in our results is different from that proposed by Corry and Chung (87), who do not consider the size selectivity between Na⁺ and K⁺.

In comparing our results on Ca²⁺ channels in this and other articles (24–27,30–48,142,143) it is important to note the different range of Ca²⁺ concentrations: we simulate physiological Ca²⁺ concentrations down to 10⁻⁵ M using the grand canonical ensemble (see Methods). Corry and Chung use Ca²⁺ concentrations of 1.8 × 10⁻² M, some 10⁴× larger than those inside cells. Extrapolation of properties over a range of 3–4 orders of magnitude is always problematic, particularly when properties are known experimentally to change dramatically over that range.

Our model accounts for several classical experiments. For example, Na channels are known not to show single file behavior (7,54,144) in contrast to K channels (145) and this result is hard to explain in classical models of Na channels as long narrow pores. In our model, the lack of single filing is a natural consequence of the low occupancy of the channel. Ions do not encounter each other often enough to force single-file behavior. Long narrow channels need not have single-file behavior if their occupancy is low. Single-file behavior can arise in many ways (30,46)

Our simulations also explain how mutations control selectivity (54,115,116). The mutation K → E converts a Na channel into a Ca channel (115) because the mutants have different charges, and different sizes, changing both the electric field (and thus free energy landscape) and the excluded volume (and thus the steric competition for space). Genetic drift and mutation could frequently convert K ↔ E and vice versa, stochastically, giving evolution repeated chances to select the side chain best for each cellular function.

Our simulations show binding sites outside the channel. Similar sites have been seen directly in structures of the K channel (146,147), but there is no direct evidence they exist in Na or Ca channels because their structures are unknown. Indirect evidence known since the work of Frankenhaeuser and Hodgkin (148), investigated much more thoroughly in other laboratories (149–152), suggests that Na⁺ concentrations are elevated immediately outside channels so the extracellular region does not become rapidly depleted of Na⁺ during prolonged activity or depolarization. Depletion of this sort would severely limit the physiological function of nerve fibers to carry repeated trains of action potentials so binding sites just outside a channel have an important functional role.

Role of structure

The structure of our model is not determined by the amino-acid sequence of the channel protein alone. The structure depends on the ionic concentrations in the bath as well and varies as they vary. The side chains of the channel protein assume positions that minimize the energy of the system as they would in almost any model or simulation of a channel protein with secondary and tertiary structure. Our simulation allows polar or charged side chains to comingle with mobile ions. The locations of protein side chains are an output of our simulations. No special ion binding forces particular to proteins are used in our simulations. Our model includes only properties of electrolyte solutions although other special forces may well be needed to explain more specialized functions of particular channels (84) and enzymes (83,107).

Selectivity even in our reduced model depends on many different effects, including changes in peak concentrations (binding), changes in minimum concentrations (depletion), and changes in the location of peaks and valleys of concentrations, all of which vary with ionic concentration, with ionic charge, and with protein dielectric coefficient and diameter. More realistic models than ours (that include kinetic effects of ion mobility, for example) are unlikely to have simpler behavior. The rich behavior of selectivity and binding (seen in Figs. 2 and 8–10) is beyond what can be captured by scaling models (64), kinetic models (5,66), electrostatic models (85–89), let alone structural discussions of selectivity (63,136,137,146,147,153–160). Those approaches to selectivity do not produce curves like those shown in Figs. 2–11 and some approaches do not produce curves at all. Depletion is likely to be particularly effective in controlling ion movement (30) because small changes in concentration in a depletion zone have large effects, particularly when the depletion zone is in series with the channel. Depletion zones control much of the behavior of transistors for this reason (73,161).

FIGURE 11.

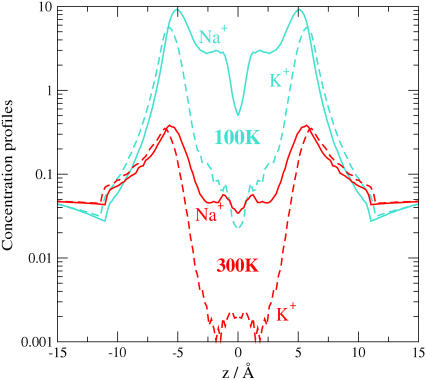
Longitudinal concentration profiles for Na⁺ and K⁺ ions in the DEKA locus for crystallographic temperature 100 K (blue lines) and biological temperature 300 K (red lines). Pore radius is R = 3 Å, protein dielectric coefficient is ɛ_p = 10, and [NaCl] = [KCl] = 0.05 M, the same situation as in Fig. 5. Note the profound effect of temperature. Barriers and wells are frozen into the structure at crystallographic temperatures because entropy is low. The profile shows little such structure at biological temperature where entropic disorder is much larger. Measurements made at one temperature give qualitatively different results from those at another.

Binding sites found in crystal structures are extraordinarily important constraints to theoretical models. Models must agree with the measured crystal structures when the models are computed under the conditions of crystallization. But the structures and binding should not be assumed to have the same location under other conditions (162) as is shown by simulations in the Appendix of this article and is obvious from the most simple-minded comparison of TS at the temperature T at which the channel functions and at which its diffraction pattern is measured (25). ΔT is typically 200 K. Diffraction patterns are measured in the cold in part because patterns are significantly better defined in the cold. Diffraction patterns are better ordered in the cold because structures have less entropy S and less disorder.

Binding sites

Mobile ions distribute in distinctive patterns in our model and in that sense are bound to particular locations. For us, a binding site is the location of a (significant) maximum in the spatial distribution of concentration of ions like Na⁺, K⁺, Ca²⁺, or Cl⁻. These binding sites are consequences of the summation of all forces in the model.

Binding sites are not consequences of just local covalent interactions and thus cannot be represented by fixed structures at definite locations independent of experimental conditions imposed on the bulk solution. Binding sites seen in crystals of proteins are the locations of excess concentration of bound ions under the conditions of crystallization and observation. Those locations are expected to vary with conditions (e.g., composition and concentration of the bulk solution) and with temperature (see Appendix) just as the driving force for ion movement and other thermodynamic quantities involved with binding vary with conditions and temperature.

The free energy landscape of the channel is thus different when different experimental (i.e., boundary) conditions are imposed on the protein (by nature or by the experiment) and in that sense the conformation of the channel is different as well (73,161). The free energy landscape and thus the effective conformation depends on boundary conditions as much as on the channel protein itself. The flexible free energy landscape of our model reflects a general property of energy landscapes of proteins. Landscapes will be flexible whenever the forces between mobile ions and protein are comparable to the forces that hold the side chains and/or protein in their conformation, which means almost always (163).

Note that the free energy that enforces the localization of mobile and structural ions in our model is a free energy of binding that comes entirely from the electrostatic (including dielectric) and excluded volume interactions of mobile ions, side chains, and the rest of the channel protein. No chemical binding is present in our model because no covalent bond formation or partial delocalization of electron orbitals is allowed in our model. For example, our model has no cation-π interactions (84). Our model only includes the electrostatic and van der Waals forces (of steric repulsion) involved in the secondary and tertiary structure of proteins. The specific binding of our model comes from the physical properties of charged hard spheres, dielectric boundaries, and their interactions with each other.

It is interesting to compare the selectivity seen in our model to the classical view of selectivity by ion binding to a specific site determined only by the protein structure. In classical models, ions of different types or concentrations are usually assumed to bind at the same location. But Figs. 3 and 5–7 show that selectivity of our Na⁺ channel is not determined by a region with a large ion concentration like that of a classical binding site. The selectivity arises from the exclusion of K⁺ from the central region of the selectivity filter. Fig. 6 shows no selectivity in the regions where Na⁺ and K⁺ are most concentrated. The Na⁺ concentration in the most selective region is approximately equal to that in the bath.

Problems in our model

A problem with our model is its oversimplified treatment of hydration in the bulk and solvation in the pore of the protein (compare with (108,164)). Our model includes significant energies of hydration, dehydration, and resolvation as it compares ions in the bulk and the selectivity filter, but it computes these energies from an implicit solvent model (109), with water and protein solvation represented only as dielectric interactions, in the traditions of many treatments of solvation in the chemical literature, reviewed in Tomasi et al. (108). Our model assigns the same dielectric coefficient to the selectivity filter and the bath, when a more realistic treatment would use different dielectric coefficients. We are working on this problem now.

More generally, it is not clear why such a low resolution description of solvation is able to account well for such a wide range of phenomena as we show here. The same is true, we point out, for implicit solvent (primitive) models of concentrated bulk solutions. They do surprisingly well in reproducing thermodynamic properties of solutions over a large range of concentrations while describing the solvent only as a dielectric (16,21,22,108,109,111,135), but concentrations in our selectivity filter far exceed bulk solubilities. Perhaps ideas of solvation nurtured by the study of dilute electrolyte solutions may not be well suited to concentrated highly charged ionic liquids (28,29) like the selectivity filter of our model or concentrated salt solutions, for that matter.

Implicit models of solvent are likely to remain important, in our view, until models of water approximately reproduce polarization effects over the entire range of times (femtoseconds to seconds) involved in hydration and solvation. A huge experimental literature on the dielectric properties of simple ionic solutions (23) shows that polarization varies by at least a factor of 40 in that time domain and depends dramatically on the type and concentration of ions. Polarization is not likely to have simpler properties in complex mixtures of several ions (like extracellular or intracellular solutions in biological systems) or in spatially inhomogeneous systems like the interface between an ionic solution and a metal or colloid (112,113), or the active site or selectivity filter of a protein or channel, where ions can interact sterically or electrostatically with nearby charges in the protein, producing dielectric friction, resonance, stochastic resonance, or other complex phenomena in nearly any frequency range.

Another problem with our model is that it does not have a specific role for the lysine K in the DEKA Na channel; in principle, all that is needed to make a Na channel is a crowded selectivity filter (to exclude K⁺) and a −1 net charge in the filter (to exclude Ca²⁺). In the context of our analysis, we must wonder why the DEKA Na channel contains lysine. One possibility is that lysine contributes to an asymmetrical property of the channel which is not seen in our equilibrium MC simulations using the same solutions inside and outside the channel. Perhaps the lysine is located so its positive charge helps repel K⁺ coming from the intracellular space (in the biological situation) without repelling the Na⁺ coming from the extracellular space. Another possibility is that the lysine is needed to make a channel of just the right size. Tiny changes in size can make large differences in selectivity when competition for space is severe as in the selectivity filter. Of course, channels are not just selectivity filters. The lysine may have an important role in a different channel function altogether, or the channel polypeptide might require the positive charge of the lysine to be able to fold into a channel protein with a narrow selectivity filter. Our model suggests that the side chains of the mutant Asp-Gln-Gln-Ala (DQQA, charge −1e) should be bulky. The DQQA channel should be as selective as DEKA for both Na⁺ versus K⁺ and Na⁺ versus Ca²⁺ if the selectivity filter of DQQA has the same size and mechanical properties as DEKA. If the experiment can be done and we are wrong, it will be interesting to see why.

Experimental predictions

Experimental predictions and checks of reduced models are of great importance. Reduced models of the ryanodine receptor (46)—similar to those considered here in their treatment of charge-space competition—have predicted anomalous mole fraction effects before they were measured; indeed they predict the dependence of the anomalous mole fraction effect on ionic concentration. Models of the L-type Ca²⁺ channel (24–26,34,35,44,47,48) have been used to design and build synthetic channels starting with bacterial OmpF porin that has no structural homology or similarity to the eukaryotic Ca²⁺ channels (43,55–57,165). These synthetic channels become more and more like the L-type Ca²⁺ channel as crowding is increased (55,57).

Further experimental checks of this sort should be possible. Miedema's OmpF mutants can be modified to see if they become Na⁺ selective as our model predicts. Specifically, the DEKA, DEEA, and DQQA loci can be placed in the constriction zone of OmpF porin and selectivity measured under a variety of conditions. The α-hemolysin system of Braha and Bayley (166–173) provides powerful control albeit of a very large diameter channel and so probably would provide the most stringent test of our reduced models, if the nanopore volume of the nonselective α-hemolysin channel can be reduced to the nearly picopore volumes of highly selective Na, Ca, or K channels, whether natural (174) or synthetic (43,55,57,165). Specifically, chemical adapters (167,168,175–177) might be used to study the properties of DEKA, DEEA, DEAA, and DQQA in α-hemolysin pores of different size and chemical composition using the mathematical theory of inverse problems (reverse engineering) to design suitable and efficient experiments (178). Abiotic nanopores (179–182) can be modified to see if they acquire Ca²⁺ and Na⁺ selectivity when they are built with suitable shape, size, charge, and chemical composition, as suggested by mathematical analysis (183), when they are studied in ionic environments (e.g., ionic strength) appropriate to the nanometer diameter of the nanopore.

Further experimentation is clearly needed on the original preparations of Ca²⁺ channels: effects of ionic strength in suitable conditions may reveal subtleties in selectivity not properly captured in our simple reduced model. Indeed, more quantitative experimentation under a variety of conditions with a range of mutants is likely to stretch our model beyond its limited range of validity.

Selectivity in general

It is easier to discuss selectivity than to compute binding curves like Fig. 2, curves 8–10. Selectivity between ions of widely different concentrations is a striking feature of nearly all protein function: nearly all proteins function in a physiological salt environment of some 200 mM K⁺, 20 mM Na⁺, 20 mM Cl⁻, 10⁻⁶ M Ca²⁺, and various organic anions (if the proteins are intracellular) or some 200 mM NaCl, 5 mM KCl, 2 mM CaCl₂ (if the proteins are extracellular). Most proteins are controlled by trace concentrations (<10⁻⁶ M) of ions, called vitamins, cofactors, coenzymes, first or second messengers, allosteric effectors, cytokines, etc., in various disciplines at various times (3,107). Calculation of selectivity in binding must then span at least six orders of magnitude of concentration. Indeed, given the large concentrations of mobile and structural ions found at active sites of proteins, calculations must reach to ∼70 M concentrations, i.e., from ∼10⁻⁷ to 70 M, approximately nine orders of magnitude. Treatments of selectivity that do not yield binding curves obviously cannot be said to reproduce physiological selectivity phenomena that are measured over a wide range of concentrations.

Selectivity involves energies much less than those of covalent bonds; selectivity involves energies comparable to the energies of secondary and tertiary structural interactions that hold proteins in a particular conformation (4,163). These energies are similar to the energies of interaction of dissolved organic molecules, usually ions. Understanding selectivity starts with understanding solvation (49,50,108,164,184,185). Selectivity involves solvation by the channel protein as well as solvation by the bulk solution. Solvation of ions in the active site or selectivity filter of proteins resembles interactions in ionic liquids (93,94).

Any of the intermolecular interactions of organic molecules and their solvents (186–189) might be exploited by evolution to create selectivity. These include (134):

1. Electrostatic forces produced by the net permanent charge of the molecules independent of the spatial distribution of that charge;

2. Electrostatic interactions dependent on the spatial distribution of permanent charge on the molecule (which is often striking asymmetrical);

3. Electrostatic interactions of induced (i.e., polarization) charge that occurs at boundaries that separate weakly charged molecules or environments (in which charge moves only a little in an applied electric field) from charged (i.e., polar) molecules or environments (in which charge moves substantially in an applied electric field);

4. Weak hydrogen bonds, chiefly electrostatic in nature (190);

5. Strong hydrogen bonds involving electron delocalization and redistribution into the region between individual water molecules;

6. Entropic effects produced by the finite volume of the molecules;

7. Entropic effects produced by tumbling;

8. Special effects like cation-π interactions (84).

And this list is no doubt incomplete. Calculation of these energies may well be possible without quantum mechanics (except for the strong hydrogen bonds (190) and cation-π interactions (84)), but such calculations are difficult to calibrate in bulk solution (164,185), let alone in the inhomogeneous concentrated environment of the selectivity filter (49–51), and few attempts have been made to do such calculations over a range of ionic conditions including physiological concentrations of Ca²⁺. Calculations have not yet been shown to reproduce experimental data like density versus temperature and pressure, polarization (i.e., protein dielectric coefficient) versus frequency (necessarily from the timescale of atomic motions, 0.1 fs to the biological timescale of milliseconds), and so on. Indeed, it is not clear that the purely electrostatic interactions of rigid macroscopic models of complex molecules have been calculated in a calibrated way.

Reduced models

Physicists use reduced models and avoid vague verbal discussions of one ionic trajectory or concentration subjectively chosen to represent the staggering number of trajectories of ions moving in channels. Physicists developed statistical mechanics (191–193) because it is needed to objectively (139,189,194–196) compute energies and entropies—even concentrations—from sets of states (in equilibrium systems) or trajectories (in nonequilibrium systems) and to objectively determine average paths of atomic motion. Discussions of selectivity (popular in structural biology) that use subjectively selected trajectories (5,63,65,154,158,160,197–201) or concentrations at fixed subjectively chosen locations (3–5,65,197) ignore the statistical realities of the structure of matter on the atomic scale.

We do not believe that simulations (85–89) based on extrapolations of the main phenomena of interest over many orders of magnitude of concentration are much better than subjective structural discussion because

1. Proteins behave differently as concentrations are changed drastically. Many intracellular and channel proteins change properties, lose function, or denature (i.e., lose function irreversibly) when exposed to the nonphysiological Ca²⁺ concentrations actually used in the simulations (2,85–89); and

2. Conclusions of the simulations depend on the details of extrapolation. Those details can only be determined (we suspect) by a simulation or theory that itself does not involve extrapolation and thus could be used to directly reproduce experimental results.

The pessimists among the authors originally felt that reduced models involving accurate calculation of only a few energies were unlikely to be helpful, although reduced models are very widely used in the chemical treatment of solvation (108). What about the other energies, those left out of the reduced models? Counterexamples were too easy to imagine. One could easily imagine systems in which selectivity depends on the energies not included in a particular reduced model. It seemed that reduced models could work, and successfully reproduce a range of experimental data, only if evolution used the same energies included in the model.

Despite these worries, reduced models had some appeal. At least one knew which energies to include when dealing with simple ions. One should include energies known to determine the chemical potential (free energy per mole) of homogeneous densely packed solutions of ions. At least one could tell if reduced models worked by checking whether they could reproduce binding curves for several types of ions, over a wide range of concentrations in natural and mutated proteins.

It seems clear now that the pessimists were too pessimistic: binding of at least some simple molecules—nonpolarizable spherical atomic ions like Na⁺, Ca²⁺, and K⁺—to some channel proteins can be well described by reduced models (24–27,30–50). One concludes that in those cases the forces in the model are more or less the forces evolution uses to produce this kind of selectivity.

The size and charge selectivity that we model here for the DEKA Na channel has also arisen in proteins that do not include a DEKA motif. Some of those proteins are channels (95–98), others are transporters (99–101), enzymes (107), or binding proteins (102–106). Although such proteins use different atomic structures, they could use the same principles of selectivity that our simulations have revealed. Indeed, the energies we consider here must arise in those systems, although of course other types of energy may be involved in selectivity in these and other proteins and active sites.

We deal here, however, with ancient proteins that may work in particularly simple ways when confronting their ancient companions, the hard spherical substrates Ca²⁺, K⁺, and Na⁺. Simple models involving only a few kinds of energy seem to be enough to deal with a significant range of complex properties of these ancient systems, properties of considerable biological and medical importance.

APPENDIX: TEMPERATURE EFFECTS

The Monte Carlo simulations presented in the body of this article have shown how the essential physiological selectivities of a Na channel can arise in a system without the fixed energy barriers and wells of a definite free energy landscape, the standard elements used by protein biochemists and channologists in models of protein function (83) and permeation (5).

The output of our simulations are the average ion distribution profiles in the pore. Such profiles, which could previously be only inferred by modeling, have now become more directly accessible to observation by crystallography (63). Crystals of K channels have been formed and diffraction patterns are measured ex situ from crystals in a vacuum at temperatures of ∼100 K. The composition and state of the solution surrounding the protein is not well known and the protein may not be at equilibrium with that solution. Analysis of these crystals reveals a nonuniform distribution of ions along the pore, as if ion binding sites were interspersed with energy barriers, much like the chemical kinetic descriptions of K⁺ permeation. Crystallographic results are from proteins in an unknown, perhaps nonequilibrium state some 200 K different in temperature from that of biological interest and so temperature artifacts are not unlikely. The significance and reality of such artifacts in the crystallographic descriptions of proteins has recently been addressed (162).

Using the opportunity provided by our simulations of the Na channel, we were interested to learn how the distribution of Na⁺ in our physically well-defined model system might be changed when we simulate the system at 100 K rather than at 300 K. Such a simulation must not be regarded as a simulation of a physical system. Clearly, water is not a fluid at 100 K. In addition, the experimental situation is unlikely to be at equilibrium whereas our simulations are at equilibrium. Nonetheless, such an idealized thought (gedanken) experiment provides useful insight into the effect of temperature on channel energetics.

Fig. 11 shows profiles of Na⁺ and K⁺ concentrations from simulations at these two different temperatures. The effect of temperature is dramatic. Generally, the concentrations of ions in and near the selectivity filter are greatly increased at lower temperatures (note the logarithmic scale of the ordinate). Entropy is less, disorder is less, so ions are less dispersed and more concentrated at crystallographic temperatures. Ions can be frozen in place by cold enough water. After all, the improvement in diffraction patterns produced by the increase in order in the protein is one motivation for using these temperatures.

In particular, at crystallographic temperatures much of the pore attracts a large concentration of Na⁺, thus forming a wide binding site. The total amount of mobile ions present in the filter is some 10× larger at 100 K than at 300 K, so that the ion occupancy observed at 100 K is a very poor estimator of the occupancy at 300 K.

Temperature T also produces qualitative changes in the system. K⁺ is mostly attracted at 100 K but repelled at 300 K. Small, apparently insignificant local variations of ion concentration seen at 300 K near the center (z = 0) are much increased at 100 K. Distinct barriers and wells only appear at crystallographic temperatures where they are frozen in, reducing ionic dispersion and thus producing crystallographic order not present when the channel is functioning at biological temperatures.

Temperature change has large effects on both the distribution of ions (i.e., structure) and the driving forces involved in ion permeation and selectivity because TS is so different at crystallographic and biological temperatures. The driving forces of thermodynamics include entropy S, and entropy is very different at 100 K and 200 K.

Temperature effects on ion distribution (i.e., structure) arise in our model because the ion distribution is governed by two opposing forces. Cations are attracted electrostatically into the pore by the net negative charge of the structural ions of the DEKA locus. Particles tend to be excluded from the pore because the side chains of the DEKA locus fill much of the space available in the pore. This exclusion is due to geometry, and hence is independent of temperature (the ions in our model are incompressible and we assume unrealistically that the diameter of the channel/filter does not change with temperature). The extent to which the electrostatics can accumulate ions in the pore depends on the amount of thermal agitation of the particles and ion accumulation becomes greater at low temperature. The two opposing effects that control ion distribution scale differently with temperature. Hence, temperature has strong effects on ion distribution as it is likely to have in any model. The two forces included in our model are necessarily present in any system of charged particles that have finite dimensions. They are the dominant forces in ionic liquids.

These simulation results demonstrate that simulation and theory are needed to extend crystallographic observations at 100 K to biological temperatures. Driving forces of electrodiffusion depend on entropy and thus most likely on temperature. The structure of the system is likely to depend on temperature as well. The simulation and theory must start with the observed structures. But the structure must not be assumed to be independent of temperature, or—in our view—of type of ion, concentration of ion, etc. Conclusions about binding sites based only on low temperature ex situ experiments are unlikely to be valid in channels operating under physiological conditions. Extrapolation to biological temperatures requires an explicit model and calculation, because models that seem the same at one temperature can involve different amounts of entropy and thus give different results.