Solvation Effect of Bacteriochlorophyll Excitons in Light-Harvesting Complex LH2

Abstract

We have characterized the influence of the protein environment on the spectral properties of the bacteriochlorophyll (Bchl) molecules of the peripheral light-harvesting (or LH2) complex from Rhodobacter sphaeroides. The spectral density functions of the pigments responsible for the 800 and 850 nm electronic transitions were determined from the temperature dependence of the Bchl absorption spectra in different environments (detergent micelles and native membranes). The spectral density function is virtually independent of the hydrophobic support that the protein experiences. The reorganization energy for the B850 Bchls is 220 cm⁻¹, which is almost twice that of the B800 Bchls, and its Huang-Rhys factor reaches 8.4. Around the transition point temperature, and at higher temperatures, both the static spectral inhomogeneity and the resonance interactions become temperature-dependent. The inhomogeneous distribution function of the transitions exhibits less temperature dependence when LH2 is embedded in membranes, suggesting that the lipid phase protects the protein. However, the temperature dependence of the fluorescence spectra of LH2 cannot be fitted using the same parameters determined from the analysis of the absorption spectra. Correct fitting requires the lowest exciton states to be additionally shifted to the red, suggesting the reorganization of the exciton spectrum.

INTRODUCTION

In photosynthesis, light-harvesting proteins efficiently capture incoming solar photons, and transfer the resulting excitation energy to reaction centers, where it is transduced into chemical potential energy (1). Compared to plants, the light harvesting system of photosynthetic purple bacteria is relatively simple, thus, it has been extensively used for over two decades as a model system to investigate the very early steps of excitation evolution during the photosynthetic process. As a result, the light-harvesting proteins from these organisms, namely light-harvesting complexes 1 and 2 (LH1 and LH2), are among the best-characterized membrane proteins from a structural and functional point of view. However, defining the precise relationship between the structural, spectroscopic, and functional properties of these proteins still represents a major challenge.

The structure of the LH2 (or peripheral light-harvesting) complex of Rhodopseudomonas (Rps.) acidophila (now Rhodobastus (Rbl.) acidophilus) (2) was elucidated over a decade ago (3). This complex is arranged as a highly symmetric ring of nine protein-pigment subunits, each containing two helical trans-membrane polypeptides, the α-polypeptide on the inner side and the β-polypeptide on the outer side of the ring. The carboxy-terminal domain of this protein binds, in the hydrophobic membrane phase, a ring of 18 tightly coupled bacteriochlorophyll (Bchl) molecules with a center-to-center distance of <1 nm between neighboring pigments. This ring is responsible for the intense absorption of LH2 at 850 nm (B850 ring). Due to the relatively small distances between the pigments in the B850 rings, the interaction between the pigments will play an important role in determining their spectroscopic and functional properties. Indeed, the magnitude of the nearest neighbor dipole-dipole coupling matrix elements were estimated to be ∼300 cm⁻¹ (e.g., see (3–9)). A second ring of nine weakly interacting Bchls is bound by the amino-terminal domain of LH2 (pigment-pigment distance of ∼2.1 nm) and is largely responsible for the absorption at 800 nm (B800 ring). The availability of detailed structural information for LH2 has stimulated efforts to model the observed electronic properties of the Bchl molecules using exciton theory (9,10).

The spectroscopic properties of the Bchl molecules are also influenced by interactions with their surrounding environment. Proteins provide to their bound cofactors a complex, anisotropic, and flexible environment, the dynamics of which proceeds on timescales ranging from femtoseconds to hundreds of nanoseconds (11). Pigment-protein interactions should thus be time-dependent. Fluctuations that occur on timescales longer than the excited state lifetime of the pigment do not directly manifest themselves in the optical experiment; therefore, over an ensemble of a large number of molecules the electronic transition frequencies of the individual pigments will just be randomly distributed around a mean value. This results in an inhomogeneous broadening of the observed electronic transitions and the corresponding distribution is commonly referred to as an inhomogeneous distribution function (IDF). Since the IDF is related to the slow dynamic components of the surrounding protein, it is referred to as static disorder. Rapid fluctuations, related to vibrations of the pigments and the surrounding protein, will define the homogeneous line shape and can be characterized by the spectral density function (SDF). All basic spectroscopic features can thus be described and understood on the basis of a model that includes SDF along with the intrinsic pigment site energy disorder and the excitonic coupling between the pigments (9,12,13).

An obvious way of discriminating homogeneous from inhomogeneous broadening is their different behaviors according to temperature. Evidently, the homogeneous broadening should be temperature-dependent, as is the population of the vibrational states, while the inhomogeneous broadening, accounting for the static distribution of the system in the ensemble, is not, at least in a particular temperature range where no phase transitions are observed. The temperature dependence of the absorption spectra can thus be used for monitoring both IDF and SDF values. In particular, the temperature dependence of the absorption spectra of J-aggregates (14), and of LH2 complexes (4,15) has been characterized. These systems are somewhat similar, J-aggregates being linear molecular structures, while the pigments in LH2 are organized as cyclic aggregates. However, differences in the molecular surroundings of the pigments in these two systems result in differences of temperature dependences of their absorption spectra.

In a previous study we analyzed the temperature dependence of the absorption spectra of detergent-purified LH2 complexes from Rhodobacter (Rba.) sphaeroides in a glycerol-water mixture (this complex exhibits the same basic architecture as the LH2 from Rps. acidophila (16,17)) using the exciton model based on the known structure (18). According to this analysis the experimentally observed temperature dependence of the spectral parameters deviate from the theoretical calculations. This deviation was qualitatively attributed to the temperature dependence of the static dielectric constant of the glycerol-water solution. To confirm this statement and to better understand and further characterize the mechanisms underlying the solvent effect on the transitions, more thorough studies were needed, requiring in particular studies on complexes in different solvent environments. In this present work, we have performed further studies on the same pigment-protein complex from Rba. sphaeroides under different solvent conditions: 1), detergent-purified LH2 in the absence of glycerol; 2), detergent-purified LH2 in the presence of extraneous glycerol; and 3), native membranes containing LH2 in the presence of extraneous glycerol. The semiempirical method described above was used for the analysis and permitted us to ascribe values for the IDF and SDF to the Bchl molecules in the B800 and B850 rings as a function of solvent environment. The IDF and SDF values are compared to previous experimental measurements, in particular fluorescence spectroscopy and fluorescence line-narrowing (FLN) spectroscopy (19).

A somewhat similar approach was also applied recently by analyzing the absorption spectrum of LH2 from Rhodospirillum molischianum by using ab initio calculations on the basis of combined molecular dynamics and quantum chemistry methods at fixed temperature (12,13) and the temperature dependence of the absorption spectrum of J-aggregates attributing it to the exciton interaction with acoustic phonons (20,21). The possible effects of acoustic phonons on the exciton absorption spectrum in LH2 will be also discussed.

MATERIALS AND METHODS

Rhodobacter sphaeroides 2.4.1 was grown anaerobically at 30°C in liquid Böse medium (22). Strict anaerobic conditions ensure that the carotenoid present in LH2 is predominately spheroidene (97% spheroidene, 3% spheroidenone). Isolation of LH2 complexes was based on Gall and Robert (23). Cells were harvested by centrifugation. Rupturing the whole cells in a French press allowed the isolation of the photosynthetic membranes after centrifugation. The membranes were solubilized using n,n-dimethyldodecylamine-n-oxide (Fluka, Buchs, Switzerland), and the LH2 pigment-protein complexes were purified as previously described (23). To simplify the main body of the text, the detergent-buffer mixture, which is a microemulsion, is referred to as the buffer solution. For the membrane-glycerol measurements, a RC⁻LH1⁻ strain was used. In this strain, which was a kind gift from P. Braun (Department I der Universität München), the predominant carotenoid in the LH2 complex is spheroidenone.

For electronic absorption experiments, the LH2 samples with glycerol were prepared in 0.1% (w/v) n,n-dimethyldodecylamine-n-oxide (Fluka, Buchs, Switzerland), 20 mM Tris. Cl., pH 8.5. Since glycerol-water solutions exhibit a phase transition at ∼200 K, the complete temperature cycle could be only measured by progressively decreasing the temperature. Absorption measurements in the 4–200 K range were also achieved by slowly raising temperature. To ensure the equilibrium between the sample and the helium bath, the sample was stabilized at each measured temperature for at least 15 min. The low temperature absorption spectra of detergent-purified LH2 complexes in the absence of glycerol and native membranes in the presence of glycerol were obtained using a thin pathlength cuvette to minimize light scattering in the frozen sample. The cuvette consisted of a sandwich of two glass microscope coverslips and a spacer such that the optical path-length was 80 μm. Electronic absorption spectra were collected using a Cary E5 spectrophotometer (Varian, Les Ulis, France). The temperature of the samples was maintained by a Helium bath cryostat (Maico Metriks, Tartu, Estonia).

The electronic fluorescence measurements were obtained with a 488 nm excitation provided by an Argon laser (Innova 100, Coherent, Palo Alto, CA). Detection was ensured using a Jobin Yvon U1000 spectrometer, equipped with a N₂-cooled CCD detector (Spectrum 1, Jobin Yvon, Longjumeau, France). The temperature of the samples of fluorescence measurements was maintained using a Helium flow cryostat (Air Liquide, Sassenage, France).

ABSORPTION MEASUREMENTS

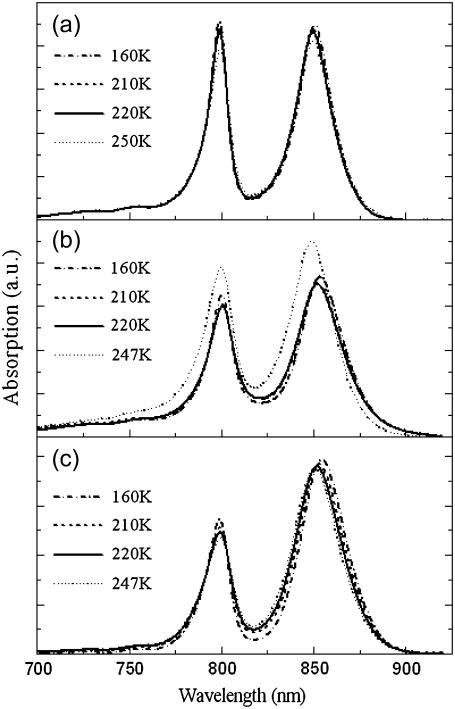
Shown in Fig. 1 is the temperature dependence of the near-infrared (740–900 nm) electronic absorption spectra of LH2 complexes in the presence, or absence of glycerol, as well as that of native membranes in the presence of extraneous glycerol. As discussed above, the two major electronic transitions located at 800 nm and 850 nm, which contribute to these spectra, arise from the rings of weakly and strongly interacting Bchl molecules, respectively. Increasing the temperature induces small shifts in the position of both these transitions, as well as changes in their broadening.

FIGURE 1.

Evolution of the absorption spectra of LH2 from Rba. sphaeroides as a function of temperature (150–250 K) and environment. (a) Detergent-purified LH2 in 60% (v/v) glycerol/detergent/water, (b) detergent-purified LH2 in detergent/water, and (c) native membranes in 60% (v/v) glycerol/water.

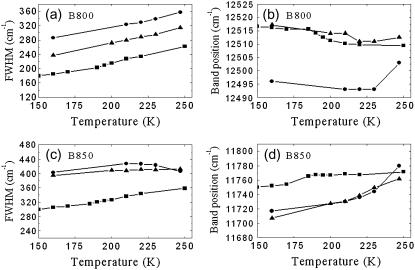
In the presence of 60% (v/v) glycerol (similar trends were observed at higher glycerol concentrations, data not shown) both the B800 and B850 absorption bands broaden when the temperature increases (Fig. 2, a and c) and their position shifts slightly, toward longer wavelengths for the B800 band (see Fig. 2 b) and toward the shorter wavelengths for the B850 band (Fig. 2 d).

FIGURE 2.

Temperature dependences of (a,c) the bandwidth and (b,d) peak positions of the absorption spectra of detergent-purified LH2 in 60% (v/v) glycerol/detergent/water (solid squares), detergent-purified LH2 in detergent/water (solid circles), native membranes in 60% (v/v) glycerol/water (solid triangles). These data correspond to the absorption spectra shown in Fig. 1.

In the absence of glycerol the absorption transitions of B800 and B850 exhibit different temperature dependences. The temperature dependence of the B850 bandwidth is weaker than that of B800 (Fig. 2, a and c). Above 250 K (data is not shown, see (18)), the bandwidth of B800 does not change with temperature, while that of B850 reduces somewhat. The peak positions of B800 and B850 shift to the red and blue, respectively, when temperature increases up to 230 K (Fig. 2, b and d). Furthermore, the B850 position is clearly more sensitive to temperature changes under these conditions (Fig. 2 d). Additionally, there is a clear change in the behavior of the bands at higher temperatures and may indeed be crudely considered as an inflection point.

The peak positions and bandwidths of B800 and B850 at 160 K as a function of glycerol content are summarized in Table 1. When the LH2 complexes are embedded in the native membrane and in the buffer containing 60% (v/v) glycerol the B800 and B850 electronic transitions exhibit mixed properties, sometimes similar to those they show when they have been measured in buffer lacking glycerol (the bandwidth and the peak position of the B850, between 130 and 230 K), sometimes similar to those obtained when isolated in the water/glycerol mixture (compare to peak position of the B800).

TABLE 1.

The experimental full widths at half-maximum (FWHM) and band-maximum positions for the B800 and B850 Bchl molecules at 160 K as a function of LH2 environment

	FWHM (cm−1)		νmax (cm−1)
LH2 environments	B800	B850	B800	B850
60% (v/v) Glycerol	185	320	12,516	11,752
70% (v/v) Glycerol	215	311	12,516	11,736
80% (v/v) Glycerol	204	306	12,517	11,746
Buffer/water	286	413	12,506	11,722
Membranes in 60% glycerol	237	395	12,517	11,707

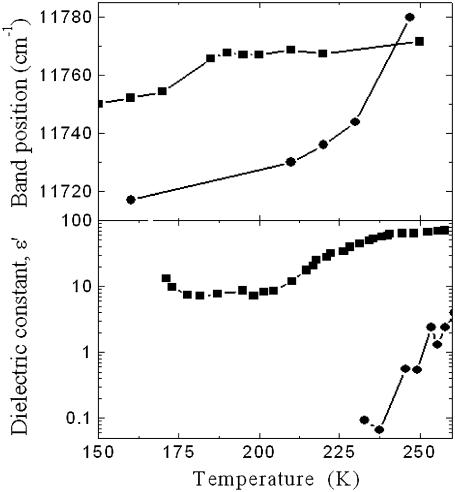
The temperature dependence of the B850 peak shift can be better understood by comparing it to the temperature dependencies of the dielectric constants of different water-glycerol solvents (24) (see Fig. 3). The dielectric constant of water exhibits a strong increase with temperature between 250 and 280 K, with an abrupt change at ∼275 K. In the case of the 60% (v/v) glycerol-water mixture, the variation of the dielectric constant between 200 K and 250 K is less steep with the ascent midpoint at ∼225 K. The correlation between the observed variations of the B850 band position with the change of the dielectric constant of the solvent is remarkable despite the fact that the ascent midpoint for the B850 position is shifted to 237 K for the pure buffer, and to 180 K in glycerol.

FIGURE 3.

Temperature dependences of the peak positions of the B850 absorption band in 60% (v/v) glycerol/detergent/water (solid squares), detergent-purified LH2 in detergent/water (solid circles) solutions (upper plot), and of the dielectric constant of 50% glycerol/water (solid squares), water (solid circles), and solvents (bottom plot), redrawn with permission from Yu (24).

The specific behavior of solvent molecules in the immediate neighborhood of proteins and membranes has been observed by neutron scattering studies (25). It must also be noted that changes of the dielectric constant with temperature of these solvents relates to their general properties in the vicinity of the phase transition. However, it is unclear at this stage whether the dynamic properties of the solvents, or their dielectric constants itself, influence directly the Bchl dipole transitions of B800 and B850 rings.

EXCITON MODEL

To explain the temperature broadening and shift of the absorption spectra we can make use of the exciton model (18). According to structural and spectroscopic data (3,7) the excitons in the B850 and B800 rings can be considered as additive units since their mutual influence is negligible. Therefore, the B850 and B800 spectra can be calculated independently, although the coupling between both exciton subsystems may be important to the excitation transfer (9,10,26).

The absorption spectrum of the ringlike molecular aggregate can be defined in terms of the Frenkel exciton (9,27). The line-shape function of the exciton spectrum is determined by the exciton interaction with the bath, the latter being well characterized by a set of harmonic oscillators (vibrations/phonons). Dynamic theory of the absorption line shape was formulated by Lax in 1952 (28), and developed by others (9,29–31) as well as in a number of articles devoted to linear and nonlinear spectroscopic applications (32–34). Since we will use the parametric form of the SDF, we apply the simplest version of this theory taking into account the diagonal part of the excitation coupling with phonons/vibrations only, and explicitly discriminating against static diagonal disorder (32)

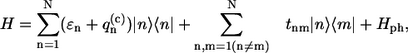(1)

where |n〉 and 〈n| represent ket and bra vectors, respectively, of the molecular excitation localized on the n^th molecule in the aggregate. Due to the ensemble of the LH2 complexes considered, the excitation energy ɛ_n is assumed to be the Gaussian random variable with mean ɛ₀ and the full width at half-maximum (FWHM) Γ^inh of the IDF:

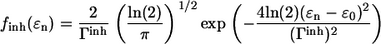(2)

Matrix elements t_nm denote the interpigment resonance interaction (V ≡ max(t_nm)) between the pigments on the sites n and m. These matrix elements are calculated according to the LH2 structural data of Rps. acidophila (see (35) for the details). The 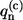value represents the bath energy fluctuation upon the excitation of n^th molecule. All relevant information about the dynamic exciton interaction with the bath is contained in the correlation function of this energy fluctuation, the Fourier transform of which is related to the SDF of the separate Bchl molecule (29). Assuming that the baths acting on different molecules are uncorrelated, the latter is defined as

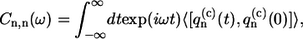(3)

where the bath average and time evolution are taken in respect of the free phonon Hamiltonian H_ph. Additionally assuming also that baths for all molecules are equivalent, the following simplification can be used:

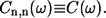(4)

Introducing exciton states,

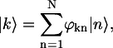(5)

where ϕ_kn is the coefficient describing the participation value of the n^th excited molecule in the k^th exciton state, the Hamiltonian given by Eq. 1 is obtained in its diagonal form,

(6)

where the exciton energy E_k, the exciton energy fluctuation 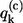as well as the correlation function C_k,k(ω) relate to the site characteristics as follows (9,31)

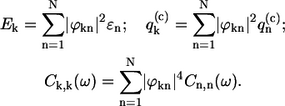(7)

The polarization operator representing linear coupling of the aggregate with the optical field can be given by

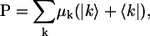(8)

where 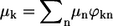and μ_n are transition dipole moments related to the exciton state k and to the n^th molecule, respectively.

With these data at hand, the cumulant expansion technique provides the expression for the aggregate absorption spectrum (29,33)

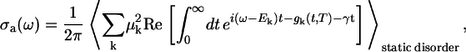(9)

where γ is the mean intraband exciton relaxation time, and the spectral broadening function g_k(t) is derived as

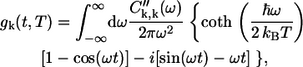(10)

where C″_k,k(ω) is the imaginary part of the Fourier transform of the correlation function C_k,k(ω). The exciton relaxation/dephasing time within the B850 band deduced from ultrafast spectroscopies is of the order of 50 fs (10,36), which corresponds to the phenomenological homogeneous broadening constant γ ≈ 100 cm⁻¹. When applied to the absorption spectra simulations at various temperatures, this strong broadening requires the assumption of an unrealistic small static disorder. It is well established that Γ^inh ≥ V for LH2 complexes (9). Therefore, γ = 50 cm⁻¹ has been introduced to take into account the exciton intraband relaxation. This value is also applicable for the B800 band (10).

It should be noted that, when dropping the sum over excitonic states k, Eq. 9 takes the form of the absorption spectrum of a single molecule embedded into the phonon bath characterized by C_k,k(ω) ≡ C(ω). During the numerical calculations, the imaginary part of the correlation function C″(ω) can be approximated and expressed in a more convenient parametric form (34),

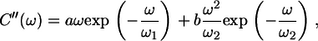(11)

where the four variable parameters a, b, ω₁, and ω₂ are directly related to the reorganization energy λ as (see (29) for its definition)

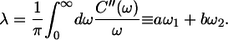(12)

The two-exponent terms in Eq. 11 can be also interpreted thus as contributing from two distinct spectral distribution modes.

The imaginary part of the correlation function C″(ω) is related to the SDF. Indeed, by introducing the following relationship between the excitation energy fluctuations 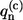and phonon/vibration modes,

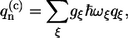(13)

where g_ξ is the strength of the excitation energy coupling with the particular vibrational mode ξ of frequency ω_ξ, the SDF describing the distribution of oscillations can be determined as follows:

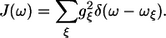(14)

According to this definition the C″(ω) function is related to the SDF function accordingly:

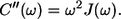(15)

Recently, using FLN the SDF was determined in a parametric form for the B777 subunit (37,38). This subunit, containing a single Bchl molecule bound to an α-helix (either the α- or the β-polypeptide) is obtained by dissociating the core light-harvesting complex, LH1, using high concentrations of detergent (39). Therefore, it is characterized solely by the pigment-bath interaction. The obtained SDF can be also approximated in an elementary function form (38)

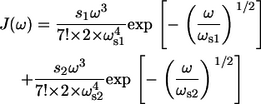(16)

The normalization factor introduced in Eq. 16 is chosen to fulfill the definition of the Huang-Rhys factor S as a sum of the corresponding factors of two distinct spectral distribution modes, s₁ and s₂:

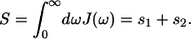(17)

It is noteworthy that the Huang-Rhys factor determines the strength of the exciton interaction with the vibrational/phonon modes, i.e.,

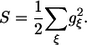(18)

Thus, the SDF can be defined unambiguously by using the approximation for C″(ω) (Eq. 11) from the relationship given by Eq. 15, or by using its direct approximation (Eq. 16). By also applying the approximate series expansion for 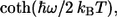analytical integration for the spectral broadening function g_k(t), Eq. 10, can be then easily performed giving algebraic expressions with the help of the approximation of C″(ω) (40). Therefore, the form of Eq. 11 has been used for further simulations.

ANALYSIS OF THE EXPERIMENTAL DATA

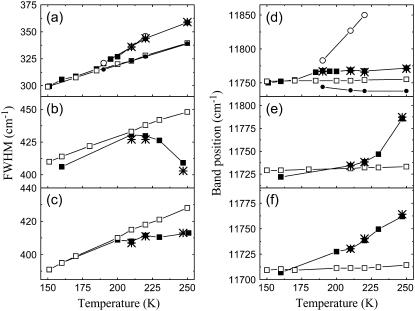
Modeling of the B800 and B850 absorption bands versus temperature was performed using the parametric form of C″(ω) (Eq. 11) with four adjustable parameters, namely, a, b, ω₁, and ω₂, and also alternating the value of inhomogeneous broadening, Γ^inh (see (18) for the details). The below-presented simulation data have been obtained by averaging over ensemble of 100,000 realizations of the disorder in the LH2 for a particular temperature. By using the relationship given by Eq. 15 the corresponding parameters of the SDF, as defined by Eq. 16, were also determined. During the fitting of the B800 band the weak interactions between the Bchl molecules in the ring are not taken into account, i.e., we assume that these molecules are not interacting. For the B850 band, which arises from closely packed Bchl molecules, the excitonic coupling has been taken into account as described in the previous section. The least-deviation between the measured and simulated FWHM of the absorption spectra of the LH2 complexes at different temperatures was used as the criterion of goodness of the SDF as performed previously (18). The results of simulations of the FWHM and the correspondingly calculated band peak positions together with the experimental data are presented in Fig. 4. The best fitting parameters for the IDF and SDF for the B800 and B850 bands, as well as the resonance interaction used for fitting the B850 band, are given in Tables 2 and 3. It is evident that calculated results with fixed resonance interactions and the IDF at all temperatures deviate from the experimental at higher temperatures for the glycerol-water solution as previously demonstrated (18). Furthermore, this deviation is most sensitive when the solvent system lacks glycerol.

FIGURE 4.

Measured (solid squares) and simulated (with the best fit at low temperatures; open squares) temperature dependences of the FWHM and peak positions of the B850 band of the LH2 complexes in 60% buffer-glycerol solution (a,d), in buffer with water (b,e), and in membranes with 60% buffer-glycerol solution (c, f). Fitting parameters of the B850 band at high temperature takes into account the observed shift of the B800 band position due to the dispersive interaction (see Fig. 2 for the experimental data). Taking into account this shift only, results in a fairly large red shift (solid circles, d). After additional change of the resonance interaction V while keeping the same inhomogeneous broadening Γ^inh = 362 cm⁻¹, it gives the band shift to the blue side (open circles). Here is the best fit (stars) obtained when taking into account all three factors with dominant contribution from the inhomogeneous broadening (see Table 3 for the obtained fitting parameters).

TABLE 2.

Calculated parameters of SDF at the low temperature range (4–160 K)

		C″(ω) function parameters				J(ω) function parameters
Band	λ(cm−1)	a	b	ω1 (cm−1)	ω2 (cm−1)	s1	s2	ωS1 (cm−1)	ωS2 (cm−1)
B777	108	0.5	0.58	100	100	0.8	0.5	0.556	1.936
B800	112	0.130	0.583	10	190	0.183	0.34	1.149	3.891
B850	220	4.911	5.696	10	30	4.9	3.4	0.15	0.605

Note that a and b are linear parameters of the C″(ω) function; ω₁ and ω₂ are characteristic frequencies of the first and second exponent of the C″(ω) function (see Eq. 11); s₁ and s₂ are linear parameters of the J(ω) function; ω_S1 and ω_S2 are characteristic frequencies of the first and second exponent of the J(ω) function (see Eq. 16); and λ, defined according to Eq. 12, is the reorganization energy (half of the Stokes shift) of the Bchl molecule. The parameters presented for B777 are taken from Renger and Marcus (38). Note that these parameters have been determined for the 60% glycerol solution and are kept the same for other solvents.

TABLE 3.

B850 exciton band parameters at different high temperatures obtained by changing the resonance interaction, V, inhomogeneous broadening, Γ^inh, and taking into account the shift of the Bchl excitation energy in accordance with the experimental B800 band shift due to dispersive interaction (see Table 4 below)

	V (cm−1)					Γinh (cm−1)
LH2 B850	160 K	210 K	220 K	250 K	300 K	160 K	210 K	220 K	250 K	300 K
60% Glycerol	342	325	325	322	—	362	377	386	390	—
Buffer-water	342	332	331	309	307	564	547	538	466	416
Membranes	342	328	321	310	301	532	510	506	482	475

As stated above, there is a clear correlation between the B800 and B850 peak shifts and the dielectric constants of the solvent (Fig. 3). This corresponds to the temperature range where the deviation is observed between the calculated and experimentally measured data. It is thus a likely hypothesis that this deviation arises from the changes of the properties of solvent phase with temperature. The Bchls of both B800 and B850 ring aggregates can be considered to be in a similar environment when LH2 complex being immersed into glycerol of water solvent indeed. In the absence of intermolecular resonance interactions, the variations of the B800 peak position induced by the changes of the solvent dielectric properties can be only related to the changes in the dispersive interaction of the pigment with its surrounding environment. If we use this response of the dispersive interaction to predict the behavior of the Bchl transition energy in the B850 ring with temperature (ɛ_n in Eq. 1), we are not able to improve the calculated temperature dependence of the bandwidth and the peak position (see solid circles in Fig. 4 d). The response of the latter to changes of the solvent properties must thus depend on an additional phenomenon.

Changes in the dielectric constant with temperature can modulate the intermolecular resonance interaction (9). We may introduce the intermolecular interaction as a free fitting parameter for the B850 absorption bandwidth in the region of strong temperature dependence, and use the deduced changes in the intermolecular resonance interaction to calculate the temperature dependence of the peak position. The result of this calculation is shown in Fig. 4 d (open circles). It is clear that the peak position deviates even more from the experimental data than the previous model. It is thus impossible to account for the correct behavior of both bandwidth and peak position of the B850 transition by just assuming that they depend 1), on the influence of the dielectric constant; 2), on the dispersive interactions; and 3), on the intermolecular resonance interactions.

Fitting both temperature dependence of the bandwidth and peak position thus requires the assumption that the width of the IDF varies with temperature as a result of the structural reorganization of the solvent around its phase transition point. When the width of the IDF is assumed to be a free variable parameter in the fitting procedure, fitting both temperature dependences of the bandwidth and of the peak positions is easily attained (see stars in Fig. 4). It is noteworthy that the resonance interaction, which was also chosen as a free fitting parameter, experiences an abrupt change near to the phase transition point as well, being 342 cm⁻¹ at low temperatures (below 160 K), and 322 cm⁻¹ and 310 cm⁻¹ above the point of the phase transition for the glycerol solvent (180 K) and for the buffer solution (237 K), respectively. In the simulations where the width of the IDF is assumed to be variable, the resonance interaction remains almost unaltered, only slightly increasing for the glycerol solutions and decreasing for the buffer without glycerol (see Table 4).

TABLE 4.

Inhomogeneous broadening (Γ^inh) and dispersive bandshifts of the B800 excitation energies in the high temperature range

	Γinh (cm−1)	Shift of the band position, (cm−1)
LH2 B800	160K	160 K	210 K	220 K	250 K	300 K
60% Glycerol	120	−5	−13	−14	−15	—
Buffer-water	208	−16	−17	−17	−17	−16
Membranes	165	−4	−8.5	−13	−12	−13

It is important to note that the parameters of the SDF remain the same for all temperatures under consideration.

DISCUSSION

To describe the temperature dependence of the absorption spectra of LH2 complexes in various environments we have used a semiempirical approach based on the exciton model. According to this approach, the spectra are characterized by free fitting parameters, and in this aspect are different from ab initio calculations (12,13). This semiempirical approach provides the possibility to address the origin of the observed temperature dependence. Initially, the two parameters that describe the exciton model, namely the interpigment resonance interaction and the IDF of the molecular transition energies were considered as free temperature-independent fitting parameters. The temperature dependence of the shape of the absorption spectra was simulated using a parametrically defined SDF function, including four fitting parameters varied to fit the low temperature experimental data (18) (Table 2). It is noteworthy that the values of parameters vary slightly with sample preparation. The spectral bandwidths and peak positions for different glycerol concentrations are presented in Table 1. As main fitting criteria, we used the temperature dependence of the peak positions and of the widths of both absorption bands at 800 and 850 nm, since the first two momenta of the bandshapes are dominating for a particular transition band according to the linear line shape theory (28). When such a calculation is performed, systematic deviations are observed between the simulated and experimental bandwidths and peak positions at higher temperatures (160–250 K).

These deviations correspond to events occurring during the phase transitions of the solvents. They appear in the temperature range where dielectric constants of the different solvents become temperature-dependent (see Fig. 3). As the actual deviations take place at the temperatures slightly lower than the solvent phase transition, they are likely to be due to the fact that solvent molecules, in close proximity with the protein, do not display exactly the properties of the free solution (25). This correlation between the observed deviations and the phase transition temperature of the solvents can be used to explain the deviation of the calculated bandwidths and peak positions of the absorption bands from the experimental data at high temperature (18). In a second step, we tried to explain these deviations by taking into account the temperature dependence of the dielectric constant. The latter may have two major effects, either influencing the dispersive forces, or modulating the dipole strength of the molecular electronic transition.

As the interpigment resonance interaction in the B800 band is weak, we can consider this band as a benchmark of the exciton spectrum calculation for fitting the B850 band. Upon neglecting the intermolecular interactions in this band, the changes of the peak position with temperature can be solely attributed to changes in the dispersive interaction of the isolated Bchl molecules with their surrounding, which occur when the protein environment is affected by the solvent changes. Using this value, we calculated what should be the temperature dependence of the peak position of the B850 band. However, this did not result in spectacular improvements during the fitting of the absorption band parameters (see Fig. 4). The temperature dependence of the dielectric constant can modulate the dipole strengths of the molecular transitions and, in turn, influence the intermolecular resonance interaction. However, we were unable to fit simultaneously both the bandwidth and the peak position when using the intermolecular interaction as a free parameter.

As a result of the changes in the solvent properties the IDF can also become temperature-dependent around the phase transition point. To span the deviation of the initial results at higher temperatures, we had to assume that this was the case, and that both the IDF and the resonance interaction (because of the temperature dependence of the dielectric constant) change with temperature (see Fig. 4). We conclude that the value of the resonance interaction changes from 342 cm⁻¹ at low temperatures to 325 cm⁻¹ at the solvent phase transition point when the protein is in glycerol solvent mixtures, dropping to 310 cm⁻¹ when it is in a buffer without glycerol (see Table 3). The slight difference of the values at the critical points correlates well with the peak values of the dielectric constants behind the phase transition points of the solvents (see Fig. 3).

Above the phase transition point, the resonance interaction becomes nearly constant while the width of the IDF, Γ^inh, has to be assumed to be variable. It slightly increases for glycerol solutions and drops for the buffer-water mixture. This opposite variation of the IDF for glycerol and water can be related to the different nature of these solvents. Glycerol converts from glass to liquid at the phase transition point, releasing more degrees of freedom for the LH2 complexes. Water or buffer without glycerol converts from a complex microcrystalline state to complex liquid (25). It is likely that, in the microcrystalline state, the inhomogeneity increases with temperature due to the reorganization of the water and its complex H-bond network around the proteins. In this case, the transition toward liquid results in a decrease of the inhomogeneity of the sample. It should be noted that, for water at temperatures higher than the phase transition point, the parameter Γ^inh is larger than the one obtained for glycerol below the phase transition point. Therefore, even minimal static disorder for water is larger than the maximal one obtained for the water-glycerol environment. As Γ^inh relates to the excitation energies of the Bchl molecules to the slow conformation motions of the protein, the variation of this parameter as a function of solvent indicates a strong solvent influence on the flexibility of LH2. However, as the phase transition of the two solvents used (water and water-glycerol solution) occur at very different temperatures, we cannot exclude that, in the case of glycerol (the phase transition temperature is lower), the slow conformational motions with large amplitudes are progressively frozen when decreasing the temperature. This results in an apparently restricted conformational space of LH2. In contrast, the absence of glycerol the phase transition temperature is much higher and the sudden freezing of the large amplitude motions may result in a higher static disorder for the LH2.

The IDF of both the B800 and B850 bands clearly differ depending on solution used to surround the detergent-isolated LH2 complexes or if they are embedded in native membranes. The Γ^inh value obtained for the B850 band is largest for the buffer-water solution (see Table 3) demonstrating some reduction of this value (up to 26%, as compared to the low temperature value) when approaching room temperature. For membrane-embedded LH2, the width of the IDF of the B850 band is close to the Γ^inh values obtained in buffer-water, but with a slightly smaller value (10%) at room temperature. The weaker temperature dependence of the IDF in the membrane samples suggests that the membrane phase protects the LH2 from the microenvironments created during the solvent phase transition, which results in a jump of this parameter. This is consistent with the notion that the detergent sheath surrounding purified photosynthetic complexes only protects the most hydrophobic region of the trans-membrane domain and does not thus fully emulate the native membrane (41–43). Qualitatively, the same solvent effect on the Γ^inh value is observed for the B800 band (see Table 4). These findings indicate the crucial role of water in the solvation of the LH2 pigment-protein complex since the water molecules might cause constraints in the proteins resulting in slightly different environments for each individual LH2 complex in a bulk sample.

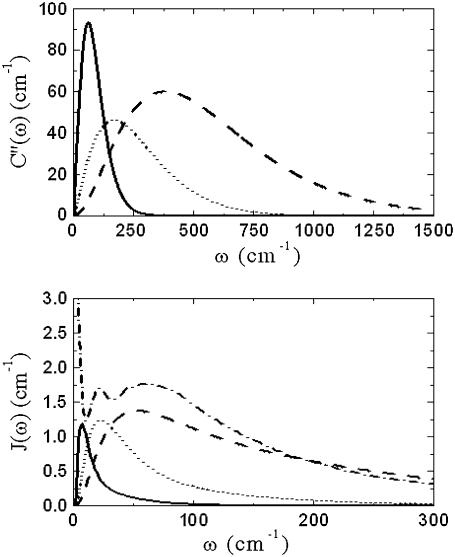
It is worth noting at this stage that, as Γ^inh is virtually the only parameter showing response of the B850 and B800 bands, broadening depending on the LH2 solvent. The shapes of the SDF determined from the fitting of the B800 and B850 absorption bands are presented in Fig. 5. They demonstrate striking differences from each other and that from the SDF determined for the B777 complex (38). The SDF obtained by fitting the B800 band is a broad function with a maximum at 50 cm⁻¹, while the SDF corresponding to the B850 band is much narrower with the maximum at 8 cm⁻¹. This shift could be caused by the appearance of a new low-frequency vibrational mode strongly coupled with the electronic excitation of the pigments in the B850 ring. Such type of vibrations might be attributed to the interpigment interaction between the α- and β-Bchls. However, an increase of the damping parameter in the Brownian oscillator model is another reason of shifting the maximum of the SDF toward the lower frequencies (29). Such an increase of the damping parameter might also be a plausible assumption for the results obtained for the B850 ring. The value of the SDF obtained by fitting the absorption band of the B777 complex (see Table 2) should be attributed to the very different environment surrounding the Bchl molecules and/or to the difference in the experimental conditions: FLN experiments were used to determine the SDF (38). A different FLN approach was also used recently to determine the SDF for the B850 (19), which was shown to be more complex in that it contains two peaks at 20 cm⁻¹ and 60 cm⁻¹ (see Fig. 5). However, the latter method cannot be used to detect reliable signals at frequencies as low as 8 cm⁻¹. In that case, the observed differences in the SDF values might be caused simply by the different methods used to collect experimental data.

FIGURE 5.

C″(ω) and J(ω) functions for the B850 band (solid line) and for the B800 band (dashed line) as calculated J(ω) for B777 (dotted line); adapted with permission from Renger and Marcus (38), copyright 2002 American Chemical Society. According to parameters presented in Table 2, C″(ω) for B777 (dotted line) and J(ω) for LH2 Rba. sphaeroides in 66% buffer-glycerol solution (dashed-dotted line); adapted with permission from Timpmann et al. (19), copyright 2004 American Chemical Society, is also presented for reference.

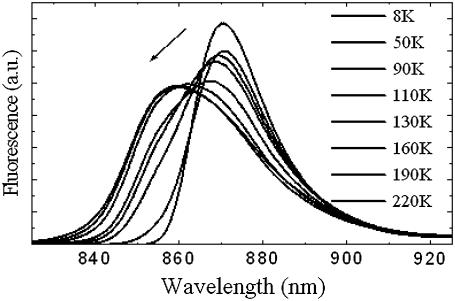
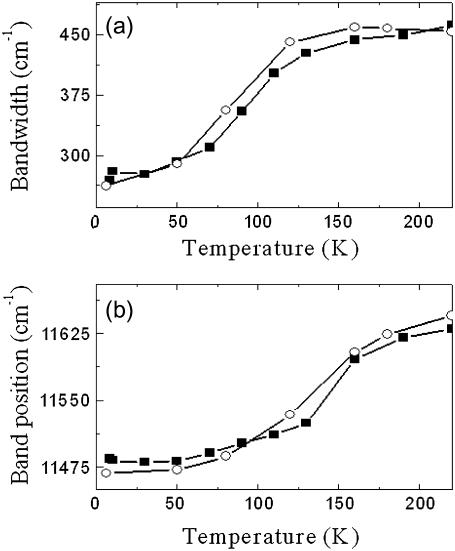
We applied our model to analyze the temperature dependence of the LH2 fluorescence spectra described above. The reorganization energy determined by Eq. 12 for the B850 band is approximately twice as large as that for the B800 band and is similar to the value found when simulating the fluorescence from a single LH2 complex (44) and by describing the fluorescence of the LH2 ensemble spectra (45). It indicates that the exciton-phonon coupling for the Bchl molecules in B850 is much stronger than in B800. Indeed, the Huang-Rhys factor determined according to Eq. 17 equals to 8.3 for the B850 band and to 0.523 for the B800 band. To verify this possibility we also fitted the fluorescence spectra obtained at different temperatures (see Fig. 6). The temperature dependence of the bandwidth and of the maximum of the fluorescence spectrum can be fitted with the same parameters determined above from absorption spectroscopy, only assuming an additional red shift of the lowest exciton state by 90 cm⁻¹ and of the next exciton state by 30 cm⁻¹. The results of this fit are presented in Fig. 7. These shifts of the exciton states are necessary for fitting these spectra. They can be attributed to the reorganization of the exciton states caused by the exciton-phonon coupling resulting in the exciton self-trapping (45).

FIGURE 6.

Fluorescence spectra of purified LH2 from Rba. sphaeroides in 60% buffer-glycerol solution in the 8–220 K temperature range. The arrow indicates the spectral changes with increasing temperature.

FIGURE 7.

Measured (solid squares) and calculated (open circles) of the temperature dependences for the FWHM (a) and peak position (b) of the fluorescence spectra in 60% Tris. Cl.-glycerol solution. The shift and broadening of the fluorescence band have been properly reproduced with the low temperature SDF and IDF just after additional shifting-down of the two lowest excitonic levels (k = 0 and k = 1) by 90 cm⁻¹ and 30 cm⁻¹, respectively, and with Γ^inh = 419 cm⁻¹.

It is worth noting that the difference in the SDF determined by using the absorption and fluorescence spectra could arise from the fact that, as suggested by our modeling, different states are responsible for absorption and fluorescence. It is well established that the B800 and B850 bands under applied high pressure also experience the shift and broadening (46,47). Evidently, the pressure broadening of the absorption bands in LH2 is akin to the effect of the increasing the temperature. In this respect, the inability to properly simulate the temperature shift and broadening of the steady-state fluorescence with the SDF and IDF parameters obtained from the absorption data is better understandable because the pressure broadening of the fluorescence spectra is much stronger than the absorption spectra (48). This provides further support for the conclusion that the fluorescent states of the B850 band differ from the absorbing ones.

As a final point, we wish to underline that the temperature dependences of the bandwidths of the B800 and B850 bands follow the power laws:

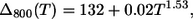(19)

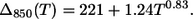(20)

In J-aggregates a much larger power exponent, 3.4, is observed (14), and such strong dependence was attributed to the exciton interaction with acoustic phonons (20,21). LH2 exhibits much weaker temperature dependence as follows from Eqs. 19 and 20, thus the dominant phonon modes responsible for the SDF maxima as determined from B850 cannot be attributed to the acoustic phonons of the Bchl ring. Most probably, this type of vibration is damped by the protein scaffold surrounding the Bchl molecules.

In conclusion, we demonstrated that the IDF is sensitive to the external conditions of the LH2 complexes in the temperature ranges close to the phase transitions of the solvents used in this study. Taking into account this sensitivity, we are able to determine the SDF of the Bchl molecule in both ring arrangements (B800 and B850) of LH2 for the of 4–300 K temperature range. However, the SDF determined for the B850 band is different from that of the B800 band, demonstrating the presence of different vibrational/phonon modes predetermining its shape. It is also noteworthy that the SDF determined from the absorption spectra and fluorescence measurements differ. Since the temperature dependence of the fluorescence spectra does not correspond to the exciton states as determined from the B850 absorption spectrum, this could indicate the possible formation of the different fluorescing states in the LH2. This suggestion could be also used to explain the difference on the SDF determined by the absorption and fluorescence measurements.