A Mechanical Explanation for Cytoskeletal Rings and Helices in Bacteria

Abstract

Several bacterial proteins have been shown to polymerize into coils or rings on cell membranes. These include the cytoskeletal proteins MreB, FtsZ, and MinD, which together with other cell components make up what is being called the bacterial cytoskeleton. We believe that these shapes arise, at least in part, from the interaction of the inherent mechanical properties of the protein polymers and the constraints imposed by the curved cell membrane. This hypothesis, presented as a simple mechanical model, was tested with numerical energy-minimization methods from which we found that there are five low-energy polymer morphologies on a rod-shaped membrane: rings, lines, helices, loops, and polar-targeted circles. Analytic theory was used to understand the possible structures and to create phase diagrams that show which parameter combinations lead to which structures. Inverting the results, it is possible to infer the effective mechanical bending parameters of protein polymers from fluorescence images of their shapes. This theory also provides a plausible explanation for the morphological changes exhibited by the Z ring in a sporulating Bacillus subtilis; is used to calculate the mechanical force exerted on a cell membrane by a polymer; and allows predictions of polymer shapes in mutant cells.

INTRODUCTION

Despite their simplicity when compared to eukaryotes, bacteria display a remarkable degree of internal structure. This is particularly apparent during cell division, which involves carefully choreographed chromosome and plasmid segregation, division septum assembly, and cell membrane rearrangements (1–3). Some species, such as Escherichia coli, divide to form essentially identical daughter cells, whereas others, including Caulobacter crescentus, form morphologically different daughter cells. Largely driven by new experimental techniques, intracellular bacterial structure is the focus of much current research. As well as being intrinsically interesting, results are also helping to explain eukaryotic cell structure and are showing the ways in which living systems are assembled from otherwise inanimate molecules.

Several recently discovered bacterial structures are multiprotein polymers that are bound to the inside of the cell membrane, which often take the forms of rings or helices (Fig. 1). These polymers serve various functions: some help define the cell morphology (4–6), others form a septum that contracts upon cell division (7,8), and yet others are involved in locating the cell division site (9,10). Presumably, the shapes and locations of the polymers are essential to their functions; but what gives them their shape, and what positions them in the cell?

FIGURE 1.

Examples of coiled protein polymers in bacteria, which are bound to the inside of the cell membrane. (A) MreB in E. coli (15), (B) FtsZ in B. subtilis (both the central ring and the helix) (13), and (C) MinD in E. coli (15). In all images, the polymerizing proteins were fused to, and imaged with, fluorescent protein markers. The membrane is made visible in panel B with an orange membrane stain, and the cell cytoplasm is shown in panel C with red fluorescent protein. In this article, a mechanical explanation for these polymer structures is shown to be consistent with the experimental images. (Figures are reprinted with permission from the referenced articles: panels A and C are copyright 2003 National Academy of Sciences USA, and panel B is copyright 2002 Elsevier.)

We focus on the membrane-bound protein polymers that are shown in Fig. 1: MreB, FtsZ, and MinD. MreB is a cytoskeletal protein that is found in E. coli and other bacteria which forms helices that extend the entire length of the cell and back, apparently forming closed loops (11). It helps determine the shape of a cell, probably by directing cell-wall synthesis during growth and division (4,12). FtsZ, which is widespread among prokaryotes, copolymerizes with several other proteins in a so-called Z ring (7,8). Typically, the Z ring forms at the cell center to form the cell division septum and then contracts to divide the mother cell into two daughter cells. It also exhibits remarkable dynamics during Bacillus subtilis sporulation (13): the centrally located Z ring converts into a helix, expands to span the length of the cell, separates and transforms into separate rings around each pole, and then one ring contracts to separate the spore from the mother cell. The final protein, MinD, forms a polymer in E. coli that primarily spirals about one cell pole, but also extends toward the other pole (14–16). It helps position the E. coli Z ring at midcell through an oscillatory mechanism in which MinD alternately polymerizes and depolymerizes at opposite ends of the cell (9).

In this article, we show that mechanical interactions between membrane-bound polymers and cell membranes are sufficient to explain the rings, helices, and polar-targeted structures that are observed for MreB, FtsZ, and MinD. It also provides a plausible explanation for the dynamics of the Z ring during B. subtilis sporulation. To explore these ideas, we used a combination of numerical and analytical techniques to investigate the low-energy structures of stiff unbranched polymers that are bound to rigid spherical, cylindrical, or rod-shaped membranes.

Description of the model

In our model (Fig. 2), a polymer is a sequence of identical monomers, where each of these monomers may represent several individual proteins, proteins in neighboring filaments of a polymer bundle, and possibly even several kinds of protein. The polymer shape is characterized as a sequence of turning angles as one progresses from the back of the polymer toward the front (much like actin which has pointed and barbed ends, the structures considered here are likely to be directionally asymmetric as well (5,17,18)). This polymer model was used with straight monomers and finite bends for simulations, and in an analogous continuous form for analytical work. It is a variant of the classic wormlike chain of Kratky and Porod (19) and of several models that were used more recently to investigate the mechanics of DNA (20–22).

FIGURE 2.

Polymer models used for simulations and analytical theory. (Top) Discrete model with finite length monomers in which the j^th bend has yaw, pitch, and roll angles a_φ,j, a_θ,j, and a_ψ,j, respectively. (Bottom) Continuous model in which the yaw, pitch, and roll curvatures at pathlength position s are α_φ(s), α_θ(s), and α_ψ(s), respectively.

We follow the Tait-Bryan convention (23) for rotational angles, commonly used for ships and airplanes, because it leads to more intuitive results for small bending angles than do the conventions that are more common in the polymer physics literature such as the Euler (23) or Flory conventions (24). In our model, the membrane-binding side of each monomer is called its bottom, so that rotation tangent to the membrane surface is rotation toward the monomer's left or right. This is called yaw. Rotation out of the tangent plane is up or down in the monomer's frame of reference and is called pitch. Rotation around the polymer axis is called roll. Because the word pitch can also be used to describe the spatial period of a helix, we reduce confusion by only using the word pitch for the pitch-rotation, and using helix-period for the alternate definition. Following the convention (23), yaw, pitch, and roll rotations are indicated with φ, θ, and ψ subscripts, respectively.

A bending energy is defined to make modeled polymers stiff, with an intrinsic shape. For the discrete case, the energy for the j^th bend is defined as

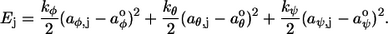(1)

The variables a_φ,j, a_θ,j, and a_ψ,j are the yaw, pitch, and roll angles for the j^th bend; a_φ°, a_θ°, and a_ψ° are called the preferred bending angles, which describe the intrinsic polymer curvature; and k_φ, k_θ, and k_ψ are the bending force constants, which produce polymer stiffness. Only these low order terms of an implicit Taylor expansion of a more complicated energy function are included because the angles are typically small and because our focus is on low energy conformations. For the continuous model, the bending energy density is defined as

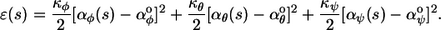(2)

Here, s is the pathlength along the polymer from the back to the front, κ_φ and κ_θ are flexural rigidities (25), κ_ψ is the torsional rigidity, and the α-values are the actual or preferred curvatures. Using χ to represent any of φ, θ, or ψ, the correspondence between the discrete and continuous parameters, in the limit of short monomer length, l, is α_χ = a_χ/l, α_χ° = a_χ°/l, κ_χ = k_χl, and ɛ = E/l. For both models, we ignore interactions between non-neighbor monomers such as excluded-volume effects.

For all of the figures and some of the equations presented in this work, the three bending rigidities are set equal to each other. This is equivalent to treating the polymers as though they are solid cylindrical rods in which the compositions are isotropic and have a Poisson ratio of 0 (significantly more compressible than typical solids). We do this to simplify the analysis and so that fewer parameter effects need to be explored. More importantly, moderate inequalities in the bending rigidities do not affect most results that are presented below; they are discussed where they do. There is very little experimental evidence on which to evaluate this assumption of equal rigidities. The best is that MreB is a structural homolog of actin for which the three rigidities have in fact been found to be very similar to each other, using experimental mechanical measurements (26–29). On the other hand, microscopy experiments indicate that the torsional rigidity of actin may be much smaller than the flexural rigidity (30,31). Furthermore, rheological properties of MreB gels have been shown to differ some from those of actin gels (32), implying that there may be mechanical differences between MreB and actin filaments.

It is even harder to estimate the preferred curvatures in the model. In principle, they could be derived from protein crystal structures and models of molecular interaction potentials. In practice, this is impossible because the arrangement of individual proteins in these filaments is largely unknown; there are many contact points between neighboring proteins in filaments, and the bending angles that are involved are very small. Because of this lack of information, we explore our model over wide ranges of preferred curvature values. In Discussion, our results are used to estimate the preferred curvatures for MreB, MinD, and FtsZ.

Simulation methods

Statistical mechanics simulations were performed using a program based on the Metropolis algorithm (33) (the source code can be downloaded from: genomics.lbl.gov/∼sandrews/software.html). Briefly, a simulation starts with an initial polymer structure, computes its bending energy using Eq. 1, makes a random change to create a trial structure, computes the new bending energy, and replaces the initial structure with the trial structure if 1), the trial energy is less than the initial energy; or 2), a uniformly chosen random number between 0 and 1 is less than exp(−ΔE/k_BT), where ΔE is the difference between the bending energies and k_BT is the thermal energy. This cycle repeats until a total of 20,000 trial moves are accepted, after which point essentially no substantial changes are made. Each trial structure is created with either of two equally likely changes: a random internal angle is changed a small amount, which pivots the entire polymer from that point to a randomly chosen end; or the polymer is treadmilled one step by adding a monomer to a random end of the polymer, with a small random angle, and a monomer is removed from the other end. Both possibilities are used because preliminary work showed that either one alone led to the simulation getting stuck in local energy minima early in the optimization process. Trial moves are reversible, ergodic, and unordered, which are essential for achieving accurate statistics with the Metropolis algorithm (33). In a method called simulated annealing, the thermal energy is started with a high value to rapidly explore the space of possible polymer structures and is gradually decreased to isolate a low-energy structure. Final structure morphologies and bending energies were quite consistent over different runs, were independent of the starting polymer structure, and did not change with more conservative parameter choices (more iterations, slower annealing rate, fewer monomers, etc.). These indicate that the simulation results accurately represent the desired minimum energy structures.

In the simulation program, polymers are mapped from a flat plane to the surface of a sphere, cylinder, or rod. It is impossible to map points from a plane to these curved surfaces while preserving local distances, so the program instead maps angles: a turn to the left or right on a plane is mapped to the corresponding three-dimensional bend (yaw, pitch, and roll) for the appropriate surface. Constraints are that monomer ends are in contact with the curved surface and the bottom faces of monomers are plane-parallel to the surface beneath the center of the monomer. These mathematics are described in the Appendix.

RESULTS

Entropy contributions

In preliminary studies, we investigated the shapes of polymer structures over a range of simulated thermal energies to investigate the role of entropy. Results are what one would intuitively expect: as the effective temperature increases, the polymer shapes become less ordered. At high effective temperatures, the polymers are completely unordered random walks on the membrane surface. No phase transitions or other interesting behaviors were observed.

Because MinD, MreB, and FtsZ all appear to polymerize with multifilament bundles (17,34–37), their rigidities are probably comparable to or larger than those of actin, which is a two-filament bundle (38). Actin has a bending persistence length of ∼16 μm (26,28), which is several times the width of rod-shaped bacterial cells. Thus, for all of the polymers that we focus on, mechanical factors are expected to be more important in determining polymer shapes than entropic ones.

Because entropy contributions are likely to be minor for these systems, we focus the rest of our discussion on the low-energy results.

Spherical membrane

On a spherical surface, low-energy polymer structures are invariably circular (Fig. 3 A). A preferred yaw curvature of zero leads to a great circle around the sphere and larger absolute values of α_φ° yield progressively smaller circles. Seen from the outside, with the circle on the close side of the sphere, the polymer turns clockwise or counterclockwise for positive and negative α_φ° values, respectively. The preferred roll and pitch curvatures were found to have no effect.

FIGURE 3.

A polymer on a sphere. (A) Examples of low-energy structures with α_φ° = 0 and α_φ° = 1.5/R. (B) Example of a potential energy surface for polymer curvature, illustrated for parameter values α_θ° = −0.7/R and α_ψ° = 0.3/R. Here, and in other figures, blue is low energy and red is high energy. Quantitative color scales are not shown because flexural rigidities are unknown for the polymers that we focus on. However, color scales are consistent between comparable figure panels, which in this case are panels B and C. On a sphere, the actual α_θ and α_ψ values are constrained to the pink dot marked sphere constraint. (C) Minimum attainable energy density as a function of the parameter values. (D) Radial force on the spherical membrane by the polymer, as a function of the parameters; α_φ° has no effect on the force.

These simulation results can be understood analytically. For a continuous polymer that is constrained to the inside of a sphere of radius R, it is shown in the Appendix that the pitch-and-roll curvatures are constrained to −R⁻¹ and 0, respectively. Because these are fixed, variation of the corresponding preferred values cannot change the actual pitch or roll curvatures, and thus cannot select specific low-energy structures; but this variation does affect the polymer-bending energy density, shown in Fig. 3 B. In contrast, the yaw curvature is unconstrained, so the lowest energy structure is attained when the actual yaw curvature equals the preferred value. Quite generally, a constant transverse curvature, with no rolling curvature, yields a circular shape. This is the situation here, which is in agreement with the simulations.

Several properties of the polymer circle can be calculated. Firstly, the circle radius is the inverse of the total curvature, [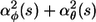]^1/2, so the circle radius is

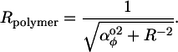(3)

The polymer-bending energy density is found from Eq. 2 and the constraints to be

(4)

shown in Fig. 3 C. Finally, the polymer exerts a force on the spherical membrane. The overall outward force that is exerted by the polymer is the derivative of the energy density with respect to the sphere radius, which is

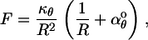(5)

shown in Fig. 3 D. It is noteworthy that the total inward or outward force that the polymer applies to the membrane is independent of α_φ°, and thus of the polymer shape. There are no forces parallel to the membrane because our modeled membrane does not restrict motion in the membrane plane; in this way, it conforms to the commonly accepted fluid-mosaic model of biological membranes. Naturally, if the membrane were sufficiently flexible to respond to the force given above, the polymer would not simply change the sphere radius but would distort it. Membrane and cell wall deformation is sufficiently complex (25,39), and distinct from the focus of this work, that we do not consider it further.

As an interesting aside, Spakowitz and Wang showed that if one removes our constraint that the bottom face of the polymer must be plane-parallel to the surface, then quite different structures result (40). In this case, the polymer forms a complex pattern of overlapping cycles.

Cylindrical membrane

A greater diversity of structures is found on cylindrical surfaces, shown in Fig. 4 A. These are right- and left-handed helices of various pitches, rings around the cylinder, straight polymers that parallel the cylinder axis that we call a line-morphology, and loops that form circles on a side of the cylinder.

FIGURE 4.

A polymer on a cylinder. (A) Examples of low-energy structures, which we call a right-handed helix, a ring, a line, and a loop, respectively. (B) Example of a potential energy surface for polymer curvature, illustrated for parameter values α_θ° = −0.7/R and α_ψ° = 0.3/R. On a cylinder, the actual α_θ and α_ψ values are constrained to the circle shown with a pink dashed line. The inset shows the height of the energy surface as a function of the position around the constraint circle, for which one full turn is an increase of b from 0 to π. Asterisks show the lowest energy value that obeys the constraints. (C,D) Phase diagrams for α_φ° = 0 and α_φ° = 0.5/R, respectively. (Green, right-hand helix; pink, left-hand helix; blue, loops; black line, ring; and dashed line, line. Gray lines connect parameter values that yield helices with the same helix-pitch.) (E,F) Minimum attainable energy densities for α_φ° = 0 and α_φ° = 0.5/R, respectively, using the same color scale. In both cases, the energy is minimum at the constraint circle. In panel F, the dashed line indicates the boundary of the loops region, which is also a local energy maximum. (G,H) Radial force on the cylindrical membrane for α_φ° = 0 and α_φ° = 0.5/R, respectively. In both cases, the radial force is zero at the constraint circle.

As on a sphere, the pitch-and-roll curvatures are also constrained on a cylinder. It is shown in the Appendix that, at any point along the polymer, these curvatures are constrained according to the equations

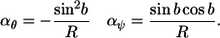(6)

The variable b is the absolute direction of the polymer on the cylinder surface, relative to the cylinder axis. In other words, if the cylinder were unrolled into a plane with the x axis of the plane defined to be parallel to the cylinder axis, then b is the angle of the polymer, relative to the x axis. If b is constant over the length of the polymer and equals 0, or another integer multiple of π, then the polymer is parallel to the cylinder, resulting in a line morphology. Values of ±π/2 imply that the polymer direction is perpendicular to the cylinder axis, yielding rings around the cylinder. Other constant values of b produce helices with different spatial periods.

In Fig. 4 B, the pitch-and-roll components of the curvature energy are shown as functions of the actual pitch-and-roll values. The curvature constraints appear in this figure as the circle that is described by the equation (derived from Eq. 6)

(7)

The value of b increases linearly as one moves counterclockwise around the constraint circle, going from 0 to π in one full rotation. We define U(b) to be the pitch-and-roll curvature energy as a function of the position on the constraint circle. It is the height of the energy graphed in Fig. 4 B over the constraint circle and it is also the last two terms of Eq. 2; U(b) is graphed in the inset of Fig. 4 B.

Assume for now that α_φ°, the preferred yaw curvature, equals zero. We show below that this implies that the actual yaw curvature, α_φ, also equals zero over the length of the minimum-energy structure. Because there is no left-right curvature, b is constant over the length of the polymer and the morphology is a ring, line, or helix. What is the value of b? In both portions of Fig. 4 B, the coordinate with the lowest attainable energy is shown with an asterisk. It corresponds to a certain b value, and thus a certain helix period. More generally, whenever κ_θ = κ_ψ, the lowest attainable energy point will be at the intersection of the constraint circle and the line from the circle center to (α_θ°, α_ψ°), which can be inferred from Fig. 4 B. This yields the absolute polymer angle:

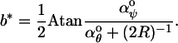(8)

This result, interpreted as a polymer morphology, is shown in Fig. 4 C as a phase diagram.

If κ_θ ≠ κ_ψ, the parabolic energy basin shown with colors in Fig. 4 B becomes distorted so that the sides are steeper on one axis than the other, thus changing its shape from that of a bowl to that of a trough. This also changes the shape of U(b), possibly causing it to have not one but two minima. Two minima would create bistability, meaning that either of two polymer conformations would be stable to perturbations. For example, it was mentioned above that actin may have a much lower torsional rigidity than flexural rigidity (30,31). Supposing that this inequality is the case for, say MreB, then the U(b) function for MreB would have two minima at equal α_θ values, with nearly the same energies. These would lead to an equal prevalence of right- and left-handed helical MreB polymers, both with the same helical period. Quite generally, bistability can also lead to switching behaviors. Here, small changes in the preferred curvatures, or in the rigidities, would change the relative energies of the two minima and could thus abruptly switch the morphology from one shape to another.

Equation 2 only includes three terms of the nine that might reasonably be included. Omitted are cross-terms, such as κ_φθ[α_φ(s)−α_φ°][α_θ(s)−α_θ°]/2. Inclusion of these terms again distorts the parabolic energy basin that is shown in Fig. 4 B, but now so that the trough orientation is not necessarily parallel to the α_θ or α_ψ axes (these are just the off-diagonal terms of a three-variable Taylor expansion (41)). Again, this changes the precise shape of U(b) and changes the position of the energy minimum (or minima). It is impossible to analytically solve for energy minima when κ_θ ≠ κ_ψ or when these cross-terms are included, but they are easily found with numerical minimization algorithms (42). (C-language code for this is available in the Supplementary Material.)

Now consider a non-zero α_φ°; this makes the polymer “want” to curve either left or right in the plane of the surface. Considering a very long polymer so that end effects are unimportant, this was shown by simulation to have either of two effects: either the polymer curves continually, or it does not curve at all. In the former case, the polymer adopts a looping morphology on the side of the cylinder, while the latter case leads to rings, lines, or helices, exactly as before. Considering the loops, a non-zero α_φ(s) causes the absolute angle of the polymer on the cylinder, b(s), to increase or decrease as one progresses from the back to the front of the polymer. This curvature is represented in Fig. 4 B by motion around the constraint circle, and around the periodic function U(b). Continuous curving can reduce the energy in the yaw term of Eq. 2, but, because it makes b(s) usually unequal to b*, the pitch-and-roll terms of the equation are nearly always greater than their minimum values. In contrast, a noncurving polymer can minimize the energies for pitch and roll, but not for yaw; in this case b(s) is constant and equals b*. Thus, there is an energy tradeoff. Large absolute values of α_φ° lead to loop shapes, while small absolute values lead to the noncurving rings, lines, and helices. Also, looping is favored when U(b) is relatively flat, which occurs when α_θ° and α_ψ° are near the center of the constraint circle.

Fig. 4 D shows a phase diagram for polymer shapes on a cylindrical surface in which α_φ° is non-zero. The looping region that is shown in blue was identified from simulations and the logic presented above, but its exact radius can only be found by calculating the minimum energy densities for the nonlooping and looping structures, described next.

The curvature energy density for a ring, line, or helix is simply Eq. 2, but with substitutions for the minimum energy curvature angles:

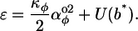(9)

This energy density is graphed in Fig. 4 E and in the outer (nonlooping) portion of Fig. 4 F. It is seen that the energy density is lowest when the preferred curvatures are on the constraint circle because this allows the actual curvatures to equal the preferred ones.

For the looping situation, the energy density varies over the polymer pathlength because the curvatures vary. Thus, the energy density average needs to be calculated. Rather than finding it by integrating over the pathlength s, it turns out to be easier to integrate over the absolute angle b. Following is the average energy density for half of a polymer loop, for which b is taken from 0 to π:

(10)

The term in brackets inside the second integral is the energy density as a function of angle b, mostly from Eq. 2 and the definition of U(b). The function α′_φ(b) gives the yaw curvature for absolute angle b, exactly as α_φ(s) represents the yaw curvature at pathlength s. The other term in the second integral weights the energy density by the pathlength that the polymer spends at each absolute angle to address the fact that the integral is over b rather than s. Because α′_φ(b) is the bending angle per unit of pathlength, 1/α′_φ(b) is the amount of pathlength per unit amount of bending angle, which is the desired weighting factor. Finally, the first term in the equation corrects for the effect of the weighting factor within the second integral. By symmetry, the energy density of one half of a polymer loop is identical to that for the other half, so Eq. 10 also represents the average energy density for a whole loop. Also, the average energy density of a sufficiently long polymer approaches that for each loop.

To solve Eq. 10 for the average energy density of a minimum-energy loop, one needs to optimize it not for single value (comparable to b* in Eq. 9), but for the optimal function α′_φ(b). This type of problem is called the calculus of variations (41). This particular optimization cannot be solved analytically so we use a numerical variational treatment: α′_φ(b) is expanded with a 24-term Fourier series because it is a periodic function; then, a greedy algorithm that employs a random walk in Fourier parameter space optimizes the coefficients to achieve the minimum average energy density (the C-language code is available in the Supplementary Material). The resulting average energy density is compared to that from Eq. 9 to determine if the lowest energy structure is a looping or nonlooping structure. In the former case, the appropriate portion of the phase diagram is colored blue in Fig. 4 D and the average energy density is graphed in the inner portion of Fig. 4 F. Results from this calculation agree well with both the qualitative discussion presented above and those from simulations.

As was done for the spherical surface, the radial force exerted by a polymer on a cylindrical surface is found by differentiating the curvature energy density by the radius, which is now the cylinder radius. This force is shown in Fig. 4, G and H, for zero and non-zero α_φ° values, respectively. There is no force when the preferred curvatures lie along the constraint circle. There is a net inward force on the membrane when these parameters lie outside the circle, and vice versa. This radial force, whether inward or outward, is strongest for ring shapes, decreases with longer-period helices, and becomes zero for lines.

Thus far, the energy densities that have been minimized are averages over the entire polymer. However, if a polymer grows rapidly and cannot rearrange once it is formed, then the relevant energy density is only that at the growing end. This does not affect the discussions presented above for a polymer on a sphere, or on a cylinder where α_φ° was considered to equal zero. However, a different conceptual picture is required for a polymer on a cylinder with non-zero α_φ°. Now, it is best to think of the preferred yaw value as applying a curvature force at the polymer terminus (this can be seen by analogy between Eq. 2 and Hooke's law). The polymer responds by curving, as it grows, until an equal opposing curvature force is applied by the pitch-and-roll constraints. This latter force is proportional to the slope of U(b) (Fig. 4 B). Once equality is reached, if it can be achieved, the polymer grows thereafter as a ring, line, or helix. On the other hand, the yaw force may exceed the maximum opposing pitch/roll force, in which case the polymer continues to turn indefinitely to form a loop morphology. Returning to the former case, the absolute angle of the ring, line, or helix is found by setting the net curvature force to zero,

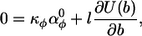(11)

and solving for b. A complication seen here is that the relative importance of the yaw and pitch/roll forces depend on the monomer length, l. The reason is that for extremely short monomers, the local cylinder surface is effectively flat so the yaw force dominates; the opposite is true for long monomers. Biologically, the effective monomer length is the amount of the polymer terminus that is relatively free to move on the membrane surface.

Rod-shaped membrane

For the most part, structures on a rod-shaped membrane combine the results for the spherical and cylindrical membranes. If the polymer energy density can be lower on the cylinder portion of the rod than on one of the hemispherical endcaps, it targets the cylinder portion and adopts a ring, line, helix, or loop morphology, depending on the preferred curvatures. On the other hand, if the energy density is lower on a sphere, the polymer becomes polar-targeted, meaning that it forms a circle about one of the hemispherical endcaps. As shown in Fig. 5, A and B, polar-targeting is possible when there is a non-zero preferred yaw angle.

FIGURE 5.

Phase diagrams for polymer morphologies on a rod-shaped membrane. Colors and symbols are the same as for Fig. 4, but now with orange to indicate polar-targeting. RH, right-handed helix; LH, left-handed helix; Rn, ring; Ln, line; Lp, loops; and PT, polar-target. (A,B) Phase diagrams for α_φ° = 0 and α_φ° = 0.5/R, respectively. Selected simulated low-energy structures are shown for the indicated parameter choices. (C) The pitch-yaw plane of the three-dimensional phase diagram at α_θ° = 0. The dotted region indicates line morphologies. (D) Phase diagram in which the abscissa is the position around the cylinder constraint circle, measured with the angle b, and the ordinate is the preferred yaw curvature. The black dot represents a ring morphology. In panels C and D, numbered black diamonds indicate the parameters of the respective simulated structures that are shown on panels A and B.

The phase diagram for the morphology as a function of the preferred yaw, pitch, and roll angles is fundamentally a three-dimensional concept. Four slices of this volume are shown: the pitch-roll plane at α_φ° = 0 (Fig. 5 A), the pitch-roll plane at α_φ° = 0.5/R (Fig. 5 B), the pitch-yaw plane at α_ψ° = 0 (Fig. 5 C), and a slice that is taken about the cylinder constraint circle (Fig. 5 D). The first two are analogous to ones shown earlier for cylindrical membranes. The others show that polar-targeting and loops become increasingly dominant structures as preferred yaw angles get farther from zero. In contrast, rings are low-energy structures in only the special case that both α_φ° and α_ψ° equal zero and α_θ° < −0.5/R. As discussed below, many protein polymers probably do not exert strong forces on the membranes, which allows the relevant portion of the three-dimensional phase diagram to be reduced to only that shown in Fig. 5 D. Here, the parameter possibilities that give rise to rings reduce to a single point, while those for left- or right-handed helices become finite areas.

Long polymers that are targeted to the cylindrical portion of the cell do not necessarily fit there. In these cases, the polymer simply wraps around the endcaps as few times as possible, with radii of curvature that are dictated by the preferred yaw angle (Eq. 3). Near the boundary of the polar-targeted and either the helix or loop regions of the phase diagram, there is minimal energy difference between the two possibilities. Simulated polymers with parameters near these boundaries frequently adopted hybrid shapes in which different parts of the polymer took on different morphologies.

Most of the polymer structures that are possible on rod-shaped membranes have been observed in live cells. FtsZ forms a ring (8), MreB forms helices (11), and MinD is a hybrid of polar-targeted and helical (15). TubZ is a recently discovered member of the FtsZ/tubulin superfamily that exhibits line-shaped structures (43). The sole morphology that has not been observed yet in bacteria is the loops structure.

DISCUSSION

Dynamics and mobility

Our model is defined for a polymer that is static in composition and that can move freely within the plane of a membrane. This is in marked contrast to the biological situation. All three protein polymers that we focus on are highly dynamic: MinD polymers form and disassemble approximately every 20 s in an oscillation from one cell pole to the other (44), Mbl (a protein that is similar to MreB) proteins turn over with a half-time of ∼8 min (45), and FtsZ proteins turn over with a time-constant of ∼30 s (46). Mobility of these polymers on the cytoplasmic membrane varies. MinD binds the membrane directly with an amphipathic helix (47) and does not appear to associate with other membrane proteins (16), so is probably relatively free to rearrange. FtsZ appears to initially bind the cytoplasmic membrane through its own interactions and through associations with the membrane-binding proteins ZipA and ZapA, which FtsZ recruits to the Z ring (48–51). In this case, there does not appear to be any prior structure that directs FtsZ to a ring (although see (52), where it is shown that successive division planes alternate orientations in spherical cells), but the structure may be anchored to the membrane once it is formed. Finally, MreB may bind to the transmembrane proteins MreC and MreD, of which MreC binds to the cell wall (53,54). In apparent contrast, it was also shown that MreC helices in C. crescentus occur even in the absence of MreB, and, when MreB is present, the two helices do not overlap but are instead out of phase (55). In any case, it is likely that MreB binds to proteins that are largely immobilized.

Our model can be applied to these situations by considering the likely effects of dynamics. When a polymer grows at a terminus, each monomer will, most likely, preferentially adopt a configuration that is close to the lowest energy one that is available. This could happen because reaction rates into low-energy states are faster than those into high-energy states; because monomers with high-energy configurations would tend to dissociate rapidly; or through small rearrangements on the membrane occurring after a monomer binds. Whatever the mechanism, if the net growth of the polymer is slow compared to the rates of reactions and rearrangements at its terminus, equilibrium statistical mechanics assures us that low-energy conformations will dominate the result (entropic contributions are minor here because the only degree of freedom is the bending angle of the terminal monomer). Depending on the mechanical parameters, it was shown above that minimum-energy growth structures are, or are close to, the morphologies that minimize the curvature energy of the entire polymer. Thus, polymers are expected to naturally grow into reasonably low-energy shapes. These initial structures should relax into even more mechanically favorable conformations if the polymer is at least somewhat mobile within the membrane, or through a turnover of internal monomers. The latter case is an example of a dynamic equilibrium so any small rearrangements that are made in monomer positions will necessarily, on average, reduce the local free energy of the polymer. Thus, our model was not defined with compositionally dynamic polymers, but such dynamics are a mechanism by which polymers would be expected to adopt mechanically favorable shapes. The rapid dynamics of the MreB, MinD, and FtsZ polymers do not invalidate our model, but actually allow it to be applicable despite their lack of free movement within the plane of the cytoplasmic membrane.

MreB

It is relatively easy to find curvature values from fluorescence images. From the MreB image in Fig. 1 A, the ratio of the spatial helix period to the helix diameter is ∼3.0. Assuming a typical E. coli cell diameter of 0.8 μm, this corresponds to a helical density, ρ, of ∼0.4 turns per micron. Simple geometry converts this to the absolute angle of the polymer on the cylinder surface,

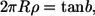(12)

yielding b ≈ ±46°. Fig. 1 A is of a MreB-YFP construct (15), which was shown to produce more extended MreB helices than those from the wild-type protein. A statistical survey of random images of wild-type MreB found an average helical density of 1.6 ± 0.3 turns per μm (16), corresponding to an absolute angle of ± (76 ± 3°). The absolute angle is converted to the actual curvatures, which are then used to infer the preferred curvatures. Because a helix is observed on the cylindrical portion of the cell, Eq. 6 is used to find α_θ ≈ −0.94/R and |α_ψ| ≈ 0.23/R. Current models of MreB suggest that the polymer does not apply strong inward or outward forces to the membrane, but instead acts more like a scaffold for membrane and cytoskeletal construction (4,56). If this is the case, then our results on polymer forces imply that the preferred curvatures are likely to lie near the cylinder constraint circle, meaning that they are close to the actual curvatures. Two pieces of evidence suggest that the preferred yaw angle is small. Firstly, Fig. 5 D shows that a polymer with a b angle of 76° (∼0.42π radians) would not form a helix, but would target the poles, if |α_φ°| were >∼0.24/R. Also, the few published MreB images that reveal the polymer shape on the cell poles (15,57) seem to show that the polymer adopts great-circle shapes. Thus, we find that the intrinsic curvature values for an MreB protein are |α_φ°| < 0.24/R, α_θ° ≈ −0.94/R, and |α_ψ°| ≈ 0.23/R. Substituting in our assumed radius of 0.4 μm and converting from radians to degrees yields intrinsic curvatures of |α_φ°| < 34°/μm, α_θ° ≈ −135°/μm, and |α_ψ°| ≈ 34°/μm. These results are listed in Table 1 along with analogous results for other protein polymers. Also shown are simulation results, using the inferred parameters, which can be seen to compare favorably with experimental images.

TABLE 1.

Curvature parameters of polymers

	ρ	|b|	|αφ°|	αθ°	|αψ°|	Diagram
Yfp-MreB*	0.4	46°	< 0.64/R ∼ 92°/μm	−0.52/R ∼ −74°/μm	0.50/R ∼ 72°/μ
MreB†	1.6	76°	< 0.24/R ∼ 34°/μm	−0.94/R ∼ −135°/μm	0.23/R ∼ 34°/μm
MinD†	2.2	80°	0.19/R ∼ 27°/μm	−0.96/R ∼ −139°/μm	0.18/R ∼ 25°/μm
FtsZ rings	∞	90°	0	−1/R ∼ −143°/μm	0
FtsZ helices‡	2.5	81°	< 0.15/R ∼ 21°/μm	−0.98/R ∼ −140°/μm	0.15/R ∼ 22°/μm
FtsZ contracting	∞	90°	0	< −1/R ∼ −143°/μm	0

Curvature parameters of protein polymers, inferred from fluorescence images. The value ρ is the helical density, b is the absolute angle of the polymer on the cylinder surface, and α_φ°, α_θ°, and α_ψ° are the preferred yaw, pitch, and roll curvatures, respectively. In all cases, the cell radius is assumed to be 0.4 μm. With the exception of the FtsZ contracting line, it is assumed that the polymer exerts minimal inward or outward force on the cell membrane.

^*Extended form, measured from Fig. 4 of Shih et al. (15).

^†Value is from Shih et al. (16).

^‡Measured from Fig. 1 of Ben-Yehuda and Losick (13).

The preferred curvature values allow predictions to be made about MreB structures on different shape membranes. On spherical cells, including minicells, the small α_φ° value implies that great-circle structures are expected. For the same reason, MreB would be expected to form straight filaments on a planar membrane, as one might create in vitro. In this case, the polymer would apply a force to the membrane in the direction that would cause it to curl toward the protein. On mutant cells with diameters that are larger than normal, MreB would be expected to exhibit a helix with a larger absolute angle than usual and produce an inward force on the membrane. Unusually small diameter cells would produce the opposite effects.

MinD

Analysis of the MinD helices, using an average helix density of 2.2 turns per μm (16), implies that the pitch-and-roll curvatures for MinD are −0.96/R and 0.18/R, respectively. As with MreB, it is expected that MinD does not exert a significant force on the cell membrane, so these are also the preferred curvatures. MinD is observed to both target cell poles and form coils the length of the cell, suggesting that α_φ° is such that the MinD polymer parameters are close to both the polar-targeting and helix phases of parameter space, which is achieved when α_φ° is 0.19/R. Our simulations showed that this boundary of phase space is quite sharp since slight differences in α_φ° drove simulated polymers completely to either the polar or cylindrical portions of the cell. Thus, either evolution has led MinD proteins to have precisely the correct shape so that they will polymerize onto both the cell poles and the cell center or, more likely, additional mechanisms are involved in targeting one end of the MinD polymers to the cell poles (a factor that is also required for dynamic models that have been described by Drew and Cytrynbaum (58,59)).

Many studies have investigated MinD polymerization in wild-type cells and in alternate systems, although it is hard to reconcile the results with each other or with the theory presented here. On round E. coli cells, MinD is seen covering entire membrane regions, in filamentous structures, and in very small circles (16). The circle diameters suggest that α_φ° is ∼700°/μm, which is 26 times the value estimated above. In vitro, MinD polymerizes to form short straight filaments in the absence of lipids (17); in the presence of lipid vesicles, MinD tubularizes them, with MinD tightly wrapped around their outsides (60). Neither in vitro result is consistent with any of the others. Thus, there is clearly much more to learn about MinD polymers.

FtsZ

As described in the Introduction, the FtsZ-dominated Z ring exhibits remarkable dynamics during B. subtilis sporulation in which it transitions from a ring to a helix, to a ring near a pole, and then finally constricts. Our mechanical model provides a plausible explanation for these changes.

Bacterial Z rings are not merely comprised of FtsZ, but also FtsA, ZipA, ZapA, and many other proteins (8). Because these proteins bind to FtsZ, they may affect its mechanical properties. They might change the mechanics directly through their incorporation into the Z ring or by causing the dominant FtsZ proteins to switch between native structures (61). Similarly, it has been proposed that phosphate release from GTP hydrolysis by FtsZ could trigger deformation of FtsZ filaments, which would cause Z-ring contraction (3,37). These provide mechanisms for the cell-cycle regulatory network to control the intrinsic curvature parameters of the Z ring: it could vary expression levels of specific Z-ring proteins, or control the FtsZ-GTP abundance through various reactions. Perhaps SpoIIE or FtsA convert the Z ring from a ring to a helix (13), other proteins from a helix to polar-targeted rings, and phosphate release from GTP hydrolysis would create a constrictive force that would invaginate the septum (62). This hypothetical trajectory is illustrated in Fig. 6.

FIGURE 6.

A proposed model for the dynamics of the Z ring during B. subtilis sporulation, shown as a trajectory in the three-dimensional parameter space. Structures are: (a) ring, (b) helix, (c) polar-targeted rings, and (d) constricting ring.

This mechanism relies on the observed rapid reassembly of the Z ring (46) both for the shape transitions to occur, and so that the cell cycle regulatory network could exert a tight control over the Z-ring shape. It is also consistent with experiments that showed that Z-ring depolymerization is not required for ring constriction (63), in contrast to some other models (64). Finally, it agrees as well with observations that the Z ring can constrict and deform the cell wall even if the ring is incomplete or is a spiral (62).

CONCLUSIONS

We propose a simple mechanical model for membrane-bound protein polymers. In it, polymers are characterized by their flexural and torsional rigidities and by their intrinsic three-dimensional curvature on the yaw, pitch, and roll axes. Minimization of the bending energy of the polymers, while constraining them to surfaces that have the same shape as rod-shaped bacteria, produce five distinct classes of morphologies: rings, lines, helices, loops, and polar-targeted circles. The specific low-energy shape that is achieved depends on the values of the parameters, of which the preferred curvatures are the most important. Many of these morphologies agree well with structures that have been observed for membrane-bound protein polymers including FtsZ, MreB, and MinD. While not investigated here, the shapes of Mbl, MreC, ParA, LamB, TubZ, and many other membrane-bound protein polymers are sufficiently similar that the same model may apply to them as well.

Although the model definition does not specifically address hindered movement of polymers on the cytoplasmic membrane, or dynamic compositions of polymers, it is nevertheless consistent with these aspects of bacterial polymers. In fact, it was shown that monomer (or protofilament) turnover can promote the relaxation of polymers to low-energy structures despite hindered movement within the membrane. Moreover, a changing polymer composition could provide a mechanism for the bacterial cell-cycle regulatory network to direct the structures of specific polymers. This was proposed as a mechanism for several Z-ring transformations that occur during B. subtilis sporulation, as well as for normal Z-ring constriction.

It is unlikely that this simple mechanical model is the only determinant of membrane-bound polymer shape. However, the likely stiffness of cytoskeletal polymers make these mechanics almost certain to contribute significantly. From images of fluorophore-tagged protein polymers, it is straightforward to estimate the primary model parameters, which are the intrinsic curvatures on each bending axis. These parameters can be used to predict polymer structures in new shapes, including in elongated or round mutant cells, in vesicles, or on a planar-supported bilayer.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX

In this section, we present the mathematics for constraining polymers to cylindrical or spherical curved surfaces, for both finite and infinitesimal length monomers. It also applies to rod-shaped bacteria because they have nearly cylindrical center sections and hemispherical ends.

We start by mapping a sequential pair of monomers from a plane to a cylinder, shown in the left column of Fig. 7. These monomers each have length l. Their directions, meaning the directions of the vectors that go from the backs of the monomers to the fronts, relative to the x axis of the plane, are b₁ and b₂. The angle between these directions is a. To map this bend from a plane to a cylindrical surface, the “paper” on which the monomers are drawn is creased so that the crease intersects the bend and is parallel to the cylinder axis, which is taken to be the x axis. The paper is folded until the monomer ends are at the cylinder surface, as shown at the bottom of Fig. 7; the folding angle is denoted χ. Note that the monomers are plane-parallel to the portion of the cylinder surface that is directly below their centers.

FIGURE 7.

Methods for mapping a polymer to a curved membrane. (Left column) Mapping to a cylindrical surface. The polymer is defined on a flat plane which is then folded, parallel to the cylinder axis, so that each monomer endpoint touches the cylinder surface. The middle panel is viewed from the right side to yield the bottom panel. (Right column) Mapping to a spherical surface. The polymer is defined on a flat disk which is then cut and shaped into a cone, so that each monomer endpoint touches the sphere surface. The middle panel is viewed from below to yield the bottom panel.

Before the paper was folded, the relative direction of the second monomer was a = b₂−b₁, which can be thought of as the following process: start with the monomers parallel, rotate the second monomer backwards by b₁ to the x axis, and then rotate forwards by b₂. This process can also be expressed with direction cosine matrices, A_plane = R_z(b₂)R_z(−b₁), where R_z(φ) is the rotation matrix for rotation about the z axis by angle φ,

(13)

7For brevity, c is used for cosine and s for sine. An analogous process finds the relative direction between the monomers after folding: start with the monomers parallel, rotate the second monomer backwards by b₁ to the x axis, fold along the x axis by χ, and then rotate the monomer around the new z axis by b₂. This is A_cyl = R_z(b₂)R_x(χ)R_z(−b₁), which expands to

(14)

The yaw, pitch, and roll angles are found from this direction cosine matrix to be

(15)

For the continuous model, these are taken in the limit of short monomers that have small bends between them. Using α as the polymer curvature on the flat plane and b as the absolute direction on the plane (b₁ and b₂ become identical in this limit), the yaw, pitch, and roll curvatures are found to be

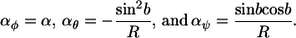(16)

The latter two equations represent the constraints that are imposed by the cylindrical surface.

A similar procedure constrains a polymer to a spherical surface, shown in the right column of Fig. 7. Monomers are drawn on a flat circle of paper and the paper is made into a cone by removing a wedge that surrounds the first monomer, and bringing the new edges together. The resultant cone bends the monomers up from the x,y plane by angle χ, which puts the monomer ends at the surface of a sphere and leaves the monomers plane-parallel to the portion of the sphere that is directly beneath their centers. Mathematically: start with the first monomer correctly positioned in the sphere and the second monomer parallel to it, rotate the second monomer about the y axis by –χ to bring it up into the x,y plane, rotate about the z axis (the axis of the cone) by a′ = a/cosχ to achieve the proper left-right bend, and finally rotate it again on the y axis by –χ to bring it up to the cone. This is A_sph = R_y(−χ)R_z(a′)R_y(−χ), which is

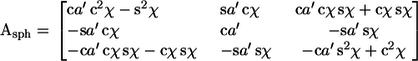(17)

The yaw, pitch, and roll angles are

(18)

The short-monomer limit yields the polymer curvatures,

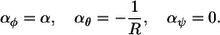(19)

Again, the latter two equations represent the constraints that are imposed on a polymer, this time by a spherical surface.