Tectorial Membrane Stiffness Gradients

Abstract

The mammalian inner ear processes sound with high sensitivity and fine resolution over a wide frequency range. The underlying mechanism for this remarkable ability is the “cochlear amplifier”, which operates by modifying cochlear micromechanics. However, it is largely unknown how the cochlea implements this modification. Although gradual improvements in experimental techniques have yielded ever-better descriptions of gross basilar membrane vibration, the internal workings of the organ of Corti and of the tectorial membrane have resisted exploration. Although measurements of cochlear function in mice with a gene mutation for α-tectorin indicate the tectorial membrane's key role in the mechanoelectrical transformation by the inner ear, direct experimental data on the tectorial membrane's physical properties are limited, and only a few direct measurements on tectorial micromechanics are available. Using the hemicochlea, we are able to show that a tectorial membrane stiffness gradient exists along the cochlea, similar to that of the basilar membrane. In artificial perilymph (but with low calcium), the transversal and radial driving point stiffnesses change at a rate of –4.0 dB/mm and −4.9 dB/mm, respectively, along the length of the cochlear spiral. In artificial endolymph, the stiffness gradient for the transversal component was –3.4 dB/mm. Combined with the changes in tectorial membrane dimensions from base to apex, the radial stiffness changes would be able to provide a second frequency-place map in the cochlea. Young's modulus, which was obtained from measurements performed in the transversal direction, decreased by −2.6 dB/mm from base to apex.

INTRODUCTION

It has been shown that the tectorial membrane is extremely important for the sensitivity and frequency selectivity of the mammalian inner ear. Mutation of the gene that encodes α-tectorin resulted in tectorial membrane detachment from stereocilia and disruption of its noncollagenous matrix (1). The structural changes caused by this mutation were limited to the tectorial membrane, but hearing function was severely compromised. Although it has been shown that the tectorial membrane plays an important role in cochlear micromechanics, the mechanisms by which the tectorial membrane contributes to the ear's frequency selectivity and sensitivity remain equivocal. More than a century ago, ter Kuile (2) proposed a cochlear model, in which the tectorial membrane acts as a stiff beam. The physical separation between the pivot point of the basilar membrane and that of the tectorial membrane produces a shearing motion between the two structures and results in bending of the stereocilia bundles. ter Kuile's view remained unchallenged until, almost 80 years later, the ideas of basilar membrane segmental vibration (3) and of a resonant tectorial membrane (4–6) were proposed. It took another 16 years before the first set of experimental data on tectorial membrane dynamics was published (7–10). Measurements made by Ulfendahl and colleagues (7) in the guinea pig temporal bone apex seemed to confirm ter Kuile's assumption that the tectorial membrane moves as a rigid beam at all frequencies, with a pivot point at the spiral limbus. In contrast to Ulfendahl's findings, Gummer and co-workers found a resonance in the tectorial membrane's motion in a similar temporal bone preparation (8,11). They reported that the tectorial membrane motion is resonant at a frequency that is ∼0.5 octaves below the basilar membrane resonant frequency at the same longitudinal location. Moreover, they stated that the radial component of the tectorial membrane vibration was 30 dB larger in amplitude than that of its transversal component. More recent in vivo experiments, performed in the apex of the guinea pig cochlea, differ from the results of the Gummer group (10). Dong and Cooper state that the tectorial membrane follows the vibration of the organ of Corti and basilar membrane below the basilar membrane's best frequency and exhibits complex but small vibrations above the basilar membrane's best frequency. Measurements in the hemicochlea at very low frequencies (12) and at audio frequencies (13) show similar behavior.

To shed new light on this controversial subject, our set of experiments tested whether the tectorial membrane's physical properties would support a second resonant system in the cochlea and whether this resonant system had a gradation of best frequencies along the length of the cochlea. In particular, we examined whether the driving point stiffness of the tectorial membrane changes from base to apex.

METHODS

The hemicochlea

The method to prepare a hemicochlea has been described elsewhere in detail (12,14–18). After a lethal sodium pentobarbital injection (180 mg/kg bodyweight), gerbils (Meriones unguiculatus) were decapitated, and the bullae were removed. One of the bullae was opened, and the cochlea was exposed in an oxygenated artificial perilymph solution: 5 mM KCl, 10 mM HEPES, 45 mM NaCl, 105 mM NaOH, 100 mM lactobionic acid (18,19), 310–317 mOsm, and pH 7.3. Replacement of most of the external chloride ions by lactobionic acid in the bath solution can prevent the cells from visible deterioration for time periods up to and beyond 3 h (19). Experiments were also performed in endolymph-like medium: 1.3 mM NaCl, 126 mM KCl, 31 mM KHO₃, and 0.023 mM CaCl₂. The osmolarity was 304 mOsm, and pH was adjusted to 7.4 after at least 30 minutes of bubbling the solution with carbogen (95% O₂ and 5% CO₂). Next, the cochlea was cut into two parts along a plane containing its modiolus. One of the resulting hemicochleae was positioned in a petri dish and immersed in the bathing medium. To avoid edge-effects related to the cut through the tissue, all measurements were made at least 100 μm from the cut edge.

Stiffness measurements with a piezoelectric probe

Use and calibration of the stiffness measurement system have been described in detail (18). In short, the stiffness sensor consisted of a needle tip (diameter, 25 μm) attached to a piezoelectric “sensor” bimorph, which was attached in turn to a piezoelectric “driver” bimorph; the needle had no opening at its tip (Fig. 1 B). The driver bimorph was cemented to a static actuator system consisting of a rigid glass rod, a piezo-pusher (PZL-007, Burleigh, Fishers, NY), and a stage-mounted 3-axis manual micromanipulator (MMW-203, Narishige, Tokyo, Japan). The static actuator system allowed for positioning of the entire sensor system to a precision of 1 μm, and the driver bimorph was used to deliver 10 Hz sinusoidal motion to the sensor bimorph and needle. For a given tissue location, the actual stiffness measurements were based on a series of interleaved static and dynamic displacements. The static displacements were used to move the sensor tip in 1-μm steps toward and onto the tissue; to be more specific, the sensor base (i.e., the proximal end of the driver bimorph) was moved in 1-μm steps. Any DC response generated by static flexion of the sensor was filtered out by AC-coupling of the voltage signal from the sensor bimorph. After each of these static steps, a 10-Hz dynamic measurement (100 ms) was taken to determine the tissue stiffness (which could change as a function of tissue compression). This latter measurement was effectively a “chord” measurement, where the incremental force in response to an incremental displacement was measured using a low-frequency sinusoid; the exact magnitude of the displacement did not need to be known but was instead accounted for in the sensor calibration. The frequency of 10 Hz was chosen to enable filtering out of any DC response from the sensor while at the same time minimizing inertial responses from the tissue. In practice, the inertia of the sensor itself resulted in a measurable voltage on the sensor bimorph and had to be corrected for in the data analysis (see below). Because the sensor system itself was statically compressed and the tissue was statically indented over the course of a measurement series, the exact position of the sensor tip had to be approximated using an iterative algorithm that incorporated the known position of the sensor base, the known input stiffness of the sensor system (determined during sensor calibration), and the incremental external load on the sensor (derived from the dynamic measurements).

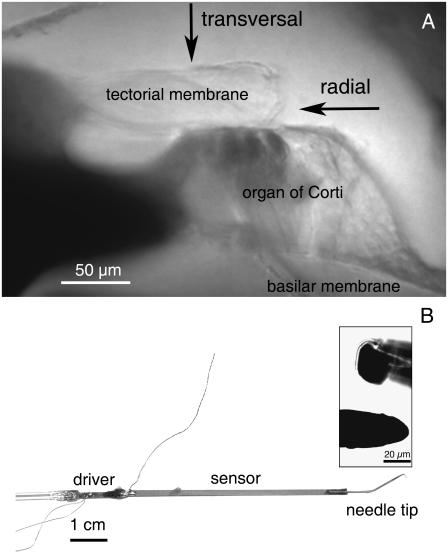
FIGURE 1.

(A) Image of a radial cross section of a gerbil cochlea at a middle-turn location. Shown are the basilar membrane, the organ of Corti, and the tectorial membrane. The osseous spiral lamina can be seen in the lower left side of the image. The arrows indicate the points on the tectorial membrane selected for stiffness measurements and the directions in which the measuring probe was advanced. (B) Image of the sensor system used to measure stiffness. It consists of a solid needle tip (diameter, 25 μm) attached to a piezoelectric “sensor” bimorph, attached in turn to a piezoelectric “driver” bimorph. The insert shows magnified views of the probe tip from the side (inset, lower) and head-on (inset, upper).

Before the experiments, the sensor was calibrated by measuring the 10-Hz sensor response against a range of known stiffness loads (calibrated glass fibers). The measurement series was similar to that used for the actual tissue measurements. The glass fibers had been calibrated previously for their absolute stiffnesses on a “string instrument” (18,20). The sensor calibration data confirmed that the 10-Hz dynamic voltage response from the sensor bimorph was independent of the magnitude of static compression of the sensor itself, up to several hundred microns.

For the measurements on the tissue, hemicochleae were mounted on the stage of an upright microscope (Ergolux AMC, Leitz, Wetzlar, Germany) sitting on a vibration isolation table (RS4000, Newport, Foster City, CA). Tectorial membrane stiffness was measured as a function of static tissue deflection at five different sites along the length of the cochlea and for different sensor orientations, as shown in Fig. 1. Measurements were made by initially positioning the sensor tip in scala media at least 100 μm away from the cut edge of the hemicochlea. For each measurement site, a curve of stiffness versus static tissue deflection was constructed. These curves were fit with a quadratic function (Fig. 2), based on a parallel beam model, originally formulated for the basilar membrane (21,22). The constant term from this fit was taken as the value for the “plateau” stiffness, which has been argued to represent the physiologically relevant stiffness of the basilar membrane (23,24). Because of the relatively short duration of these experiments (<2 h), the material properties and structural relationships of the cellular and noncellular components of the hemicochlea are expected to remain constant. We have validated this assertion in a previous report (18), based not only on the constancy of repeated stiffness measurements obtained in a hemicochlea over an extended time period but also on the equivalence of hemicochlea stiffness data and in vivo stiffness data.

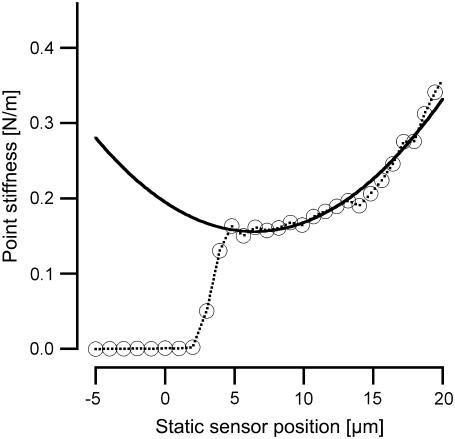
FIGURE 2.

Example of stiffness of tectorial membrane as a function of static sensor tip position. Point stiffness (in N/m) is shown on the ordinate. The abscissa represents the position of the sensor tip (in μm) as it is moved toward and onto the tissue: initial contact with the basilar membrane occurs at 0 μm. The measurement shown was obtained at the basal-turn location. The curve has been fitted with the following quadratic function to obtain a plateau stiffness value of 0.16 N/m: k = 0.16 + 0.0095 (x − 6.4)².

Data analysis

Stiffness values as a function of static tissue deflection were derived from the sensor signal after processing the acquired waveforms off-line using Igor Pro (Wavemetrics, Lake Oswego, OR). Response magnitudes and phases were determined for the 10-Hz voltage response measured at each static displacement step. For the purpose of our discussion here, a “measurement waveform” is defined as any one of these 10-Hz response waveforms. To correct for intrinsic inertial forces due to the combined mass of the needle and the sensor bimorph, a set of 10 measurement waveforms with the sensor in “free field” (i.e., in the fluid before contacting the tissue) was selected from the initial steps of the sensor advancement, and these 10 measurement waveforms were averaged and subtracted from all measurement waveforms measured in the series. By averaging and subtracting the entire waveforms, both magnitude and phase information were included in the inertia correction. After this correction, the magnitude of each measurement waveform was computed and converted to a stiffness value based on the sensor calibration data. Note that although there was a need to correct for inertial forces, viscous forces were assumed to be negligible based on the observation that the response from the sensor did not change before and after immersing the sensor tip into the bathing fluid.

After the analysis described above, a curve of stiffness (based on the 10-Hz dynamic measurements) versus static tissue deflection could be constructed for each measurement site. During the experiments, only the exact static position of the sensor base, x_base (proximal end of the driver bimorph), was known. However, for analyzing and plotting the data, the static position of the sensor tip, x_tip, was required. Therefore, it was necessary to take into account the static compression of the sensor system itself. The static sensor tip positions were estimated from the known sensor base positions using a sequential algorithm (18) that took into account the relative values of the sensor's input stiffness and the measured sequence of tissue stiffness (derived from the 10 Hz dynamic measurements). In effect, for each 1 μm advancement of the sensor base, the incremental static compression of the sensor was a function of the sensor's internal stiffness and the incremental static load presented by the tissue. Figs. 3 A and 4 A show the voltage measurements obtained from the sensor. The voltage reading could be converted into stiffness values. The sensor used in these experiments had an input stiffness of 2.04 N/m.

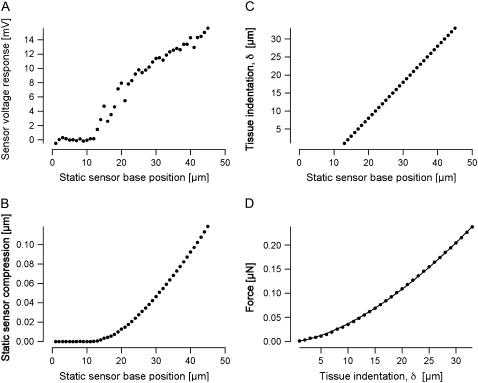
FIGURE 3.

Measurement series obtained from a middle-turn location. (A) Responses at 10 Hz voltage recorded from the sensor as it was dynamically driven at static advancements onto the tissue. (B) Static compression of the sensor as it was advanced onto the tissue. The compression was calculated by an iterative method, as described in the text. Note that the abscissa is referenced to the starting position of the measurement series, when the sensor tip was in the fluid away from the tissue. For this particular measurement series, the sensor tip first contacted the tissue when the sensor base reached a position near 14 μm. (C) Tissue indentation δ as a function of position of the sensor base. Indentation is equivalent to the position of the sensor tip (relative to initial contact with the tissue) and is computed simply as the difference between the sensor base position (relative to initial contact) and the sensor compression. Note that, because of the relatively small internal compression of the sensor itself, the tissue indentation is almost equal to the displacement of the sensor base. (D) Applied force as a function of tissue indentation. The force was calculated from the static compression of the sensor in conjunction with the known input stiffness of the sensor. The solid circles show the values derived from the measurements, and the solid line is the result of fitting the modified Hertz model, as described in Methods.

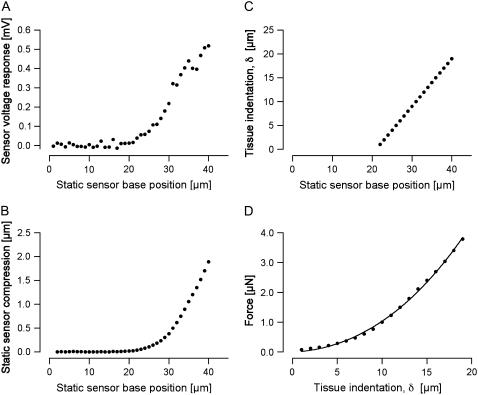
FIGURE 4.

Measurement series obtained from a basal-turn location. The layout of this figure is the same as that of Fig. 3.

Young's modulus E

To compare our data with those in the literature, Young's modulus was extracted from the measurements using a model describing a sphere indenting an elastic material (25,26). A detailed derivation of the model, originally described by Hertz, is given in Dimitriadis et al. (26). In this study, it is assumed that the sample (i.e., the tectorial membrane) is not bonded to the supporting substrate (i.e., the reticular lamina). The applied force F as a function of indentation is given by

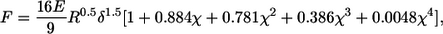where δ denotes the tissue indentation, E the Young's modulus, R the radius of the indentor, and h the thickness of the specimen; χ is derived from the other parameters and is equal to 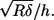The indentation δ is known from the sensor's tip position after touching the tissue (Figs. 3 C and 4 C) and is calculated simply as the advancement of the sensor base minus the internal compression of the sensor (Figs. 3 B and 4 B). The applied force F can be calculated independently (Figs. 3 D and 4 D) from the static sensor compression and the sensor's input stiffness, which was determined experimentally as described in the previous section. The tectorial membrane height h and probe radius R are constant and known for each experiment. The only unknown is Young's modulus, which can be derived from fitting the model and the data.

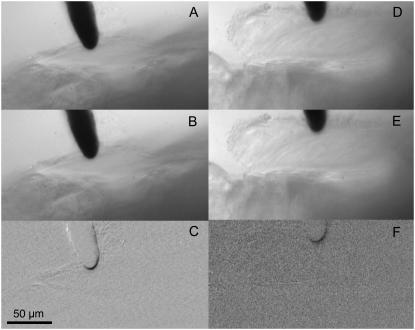
Since there are multiple models that can be used to estimate Young's modulus, one has to be aware of some limitations of our particular approach. We selected a modified Hertz model because the tectorial membrane is assumed to be an elastic layer (of known thickness) resting on the reticular lamina (with a contribution from the pillar heads). From previous measurements (27,28) we know that the reticular lamina has some elasticity, and so it is possible that the lower surface of the tectorial membrane is not “rigid” and that the entire tectorial membrane bends or is displaced during the measurements. Such a displacement would result in an underestimation of Young's modulus. Three methods were applied to confirm that the bending or displacement of the tectorial membrane is negligible: 1), visual observation, 2), basic image subtraction, and 3), optical flow analysis. During visual observation of the displacement of the sensor and the tectorial membrane, even for tectorial membrane indentations of 20 μm with the sensor approaching from the scala media side, no significant displacements of the tectorial membrane could be detected on the reticular lamina side. The raw visual observations were supplemented using image subtraction in NIH image (Fig. 5). Two examples, one in each column, represent the maximum excursions (∼1 μm peak) during an individual stiffness measurement Fig. 5, A, B, D, and E), made after each incremental static advancement of the sensor base. The images at the extrema of the measurement were subtracted from each other, and the subtracted images are shown in the bottom row of Fig. 5, C and F. If no movement occurs in a particular region, the corresponding region in the difference image should be gray. However, if a structure is displaced, it shows up as a darkened region on the difference image. The bottom panels in Fig. 5 show that the region near the sensor tip is clearly displaced but no movement is seen on the reticular lamina side of the tectorial membrane. To further quantify the motion of the sensor tip and the tectorial membrane at its reticular lamina surface, we measured displacements using a video flow technique, which has been described previously (12,13,29). The results of this latter analysis show that the displacement of the tectorial membrane at the sensor tip during an individual measurement is about an order of magnitude larger than the displacement of the surface of the tectorial membrane facing the reticular lamina. The relative difference in displacement magnitude at the two surfaces of the tectorial membrane was similar for measurements in the base and in the apex of the cochlea. Any bulk displacement of the tectorial membrane would result in an overestimation of the indentation and a subsequent underestimation of Young's modulus. On the assumption that the relative displacements quantified in Fig. 5 are representative of those across an entire measurement series for each of our experiments, it is possible to quantify the extent to which our Young's modulus value might be underestimated. From Fig. 5, we can approximate that the indentations are actually 10% smaller than the values we have used. Using the smaller indentation values in the calculations for the example from Fig. 3, we find that our reported Young's modulus value would be an underestimate by ∼6%. In a worse case, assuming that the indentations are actually 20% smaller than the values we have used, Young's modulus will be underestimated by ∼13%.

FIGURE 5.

Sensor indentation shown for a basal- and a middle-turn location. (A–C) Images for a basal-turn location. (D–F) Images for a middle-turn location. (Upper and middle) Different sensor indentations. (Lower) Subtracted images of the indentations shown in A and B (C) and D and E (F). Regions that exhibit displacement show up as darkened areas in C and F.

For the Young's modulus calculations, it is also crucial to determine the point at which the sensor first touches the tectorial membrane. Initially, this zero point was guessed by visual inspection of the plot of static sensor base position versus static sensor compression (see, e.g., Figs. 3 A and 4 A). After the first estimate of Young's modulus, the χ-square value of the goodness of fit between the model and data was calculated. The zero point was then changed by increments of 1 μ in the positive and negative directions. The reported value for Young's modulus was obtained from the fit with the lowest χ-square value. In general, the initial guess for the zero point yielded the lowest χ-square value.

Detachment of the tectorial membrane

The driving point stiffness of the tectorial membrane may be influenced by the stiffness of the stereocilia bundles of the outer hair cells. To determine whether and how much these stereocilia contribute to the tectorial membrane stiffness in situ, measurements were made for two different conditions: 1), the hemicochlea was not altered, so that the outer hair cell stereocilia bundles were presumably not detached from the tectorial membrane (but see below); and 2), using a small hook, the organ of Corti was removed from below the tectorial membrane before the measurements, to detach the stereocilia from the tectorial membrane.

Statistics

Mean, standard deviation, and standard error were calculated for the stiffness data obtained at each of the five sites along the length of the hemicochlea. An analysis of variance was performed, followed by the Tukey HSD test (Igor, Wavemetrics).

Experimental procedures followed the National Science Foundation guidelines and have been approved by the Northwestern University Animal Care and Use Committee.

RESULTS

Tectorial membrane stiffness was measured in the radial and transversal directions at five locations along the gerbil cochlea: basal, upper basal, middle, upper middle, and apical locations. The corresponding distances from the basilar membrane basal end were 2.9 ± 0.55, 5.5 ± 0.53, 7.3 ± 0.44, 8.5 ± 0.46, and 9.8 ± 0.5 mm. The results are summarized in Table 1.

TABLE 1.

Stiffness summary

		Plateau stiffness (transversal) (N/m)		Plateau stiffness (radial) (N/m)
Cut edge	Distance from base (mm)	Artificial perilymph	Artificial endolymph	Pristine hemicochlea	Stereocilia detached	Young's modulus(kPa)	Basilar membrane stiffness (N/m)*
Base	2.9 ± .055	0.166 ± 0.05 (N = 13)	0.131 ± 0.06 (N = 7)	0.288 ± 0.124 (N = 7)	0.255 ± 0.151 (N = 3)	3.0 ± 0.36 (N = 13)	3.2 ± 0.11
Upper base	5.5 ± 0.53	0.061 ± 0.03 (N = 13)	0.048 ± 0.01 (N = 6)	0.121 ± 0.050 (N = 6)	0.111 ± 0.055 (N = 3)	1.9 ± 0.26 (N = 9)	0.12 ± 0.07
Middle	7.3 ± 0.44	0.029 ± 0.01 (N = 13)	0.0253 ± 0.006 (N = 6)	0.033 ± 0.011 (N = 5)	0.041 ± 0.018 (N = 2)	0.86 ± 0.08 (N = 11)	0.09 ± 0.03
Upper middle	8.5 ± 0.46	0.021 ± 0.01 (N = 9)	0.0156 ± 0.005 (N = 5)	0.013 ± 0.007 (N = 3)	0.020 ± 0.014 (N = 3)	0.53 ± 0.14 (N = 7)
Apex	9.8 ± 0.50	0.005 ± 0.006 (N = 3)	0.009 ± 0.003 (N = 4)	0.007 ± 0.005 (N = 5)	0.009 ± 0.010 (N = 4)	0.32±0.07 (N = 5)
Slope		−4 dB/mm	−3.4 dB/mm	−4.9 dB/mm	−4.3 dB/mm	−2.6 dB/mm	−4.4 dB/mm

^*For comparison, our basilar membrane data are shown, which were measured between the midpectinate zone and the outer pillar foot (18).

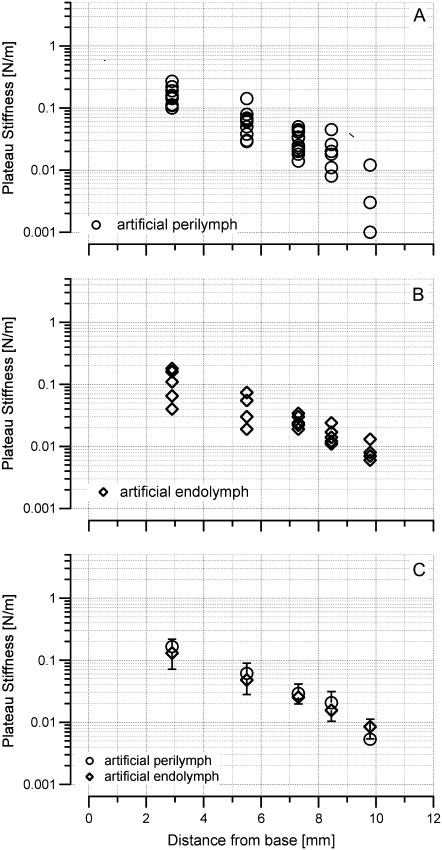
Transversal point stiffness measurements

Measurements were taken at the surface of the tectorial membrane above Hensen's stripe. Fig. 6 and Table 1 show the stiffness values obtained at different locations along the length of the cochlea. For the basal-turn location, the mean stiffness was 0.166 ± 0.05 N/m (N = 13), for the upper basal turn 0.061 ± 0.03 N/m (N = 13), for the middle turn 0.029 ± 0.01 N/m (N = 13), for the upper middle turn 0.021 ± 0.01 N/m (N = 9), and for the apical turn 0.005 ± 0.006 N/m (N = 3) in artificial perilymph. In artificial endolymph, these values were 0.131 ± 0.06 N/m (N = 7) for the basal turn, 0.048 ± 0.01 N/m (N = 6) for the upper basal turn, 0.0253 ± 0.006 N/m (N = 6) for the middle turn, 0.0156 ± 0.005 N/m (N = 5) for the upper middle turn, and 0.0085 ± 0.003 N/m (N = 4) for the apical turn (Fig. 6, Table 1). Although there was no significant difference between stiffness measured in endolymph versus stiffness measured in perilymph at a given location, stiffness did change significantly along the length of the cochlea: −4 dB/mm in artificial perilymph and –3.4 dB/mm in artificial endolymph.

FIGURE 6.

Driving point stiffness obtained in the transversal direction above Hensen's stripe. Stiffness values are plateau stiffnesses. Transversal stiffness decreases from base to apex. (A) Measurements performed while the hemicochlea was immersed in artificial perilymph. (B) Measurements obtained while the hemicochlea was bathed in artificial endolymph. The two sets of data are not significantly different (C).

Radial point stiffness measurements

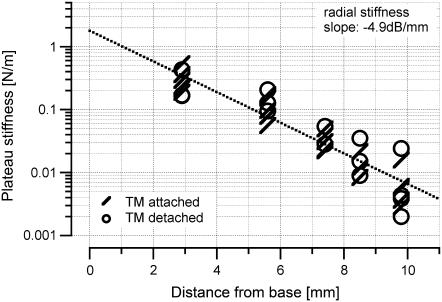
Radial tectorial membrane stiffness was determined in artificial perilymph for two hemicochlear conditions: 1), when the preparation was unaltered; and 2), when the organ of Corti was removed with a small hook before the measurements. The second set of experiments was performed to determine whether or not the stiffness of the stereocilia bundles of the outer hair cells contributes to the radial stiffness measurements taken at the tectorial membrane.

When the preparation was unaltered, stiffness values for individual locations were 0.288 ± 0.124 N/m (N = 7) for the basal turn, 0.121 ± 0.050 N/m (N = 6) for the upper basal turn, 0.033 ± 0.011 N/m for the middle turn (N = 5), 0.013 ± 0.007 N/m (N = 3) for the upper middle turn, and 0.007 ± 0.005 N/m (N = 5) for the apical turn. After detaching the stereocilia bundles before the measurements, these values were 0.255 ± 0.151 N/m (N = 3) for the basal turn, 0.111 ± 0.055 N/m (N = 3) for the upper basal turn, 0.041 ± 0.018 N/m (N = 2) for the middle turn, 0.020 ± 0.014 N/m (N = 3) for the upper middle turn, and 0.009 ± 0.010 N/m (N = 4) for the apical turn (Fig. 7). Stiffness values were not significantly different for the two conditions. In both conditions, there was a significant longitudinal gradient of the radial stiffness: −4.9 dB/mm with the tectorial membrane attached to the outer hair cell stereocilia bundles and −4.3 dB/mm with the tectorial membrane detached.

FIGURE 7.

Plot shows plateau stiffness values in the radial direction determined at different locations along the cochlea. Measurements were done in artificial perilymph. One set of data (slashes) was acquired from unaltered preparations, whereas the second set of data (circles) was acquired from preparations in which the organ of Corti was removed before the measurements. This manipulation was performed to determine whether or not the stiffness of the stereocilia bundles affected the results of the radial stiffness measurements. Stiffness values were not significantly different for the two conditions.

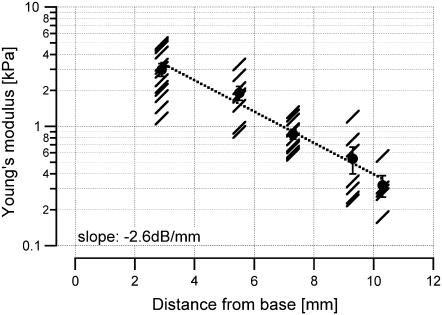
Young's modulus

The data used to determine the driving point stiffness were also used to extract Young's modulus. For the different locations along the cochlea, the Young's modulus was 3.0 ± 0.36 kPa (N = 13) for the basal turn, 1.9 ± 0.26 kPa (N = 9) for the upper basal turn, 0.86 ± 0.08 kPa (N = 11) for the middle turn, 0.53 ± 0.14 kPa (N = 7) for the upper middle turn, and 0.32 ± 0.07 kPa (N = 5) for the apical turn. The longitudinal gradient of Young's modulus was –2.6 dB/mm (Fig. 8).

FIGURE 8.

Mean values and standard errors are shown for the Young's modulus, which was determined for the transversal direction. Slashes are individual measurements. A gradient in Young's modulus is present along the length of the cochlea.

DISCUSSION

Tectorial membrane stiffness has been measured by several groups. Measurements were made on isolated tectorial membranes (25,30,31), in vitro (32) and in vivo (20,33). Except for the measurements by von Békésy, longitudinal gradients were not examined systematically. Available data are summarized in Table 2. In contrast to previous experiments, the measurements in this study were made in the gerbil hemicochlea, which allowed us to determine the radial and transversal stiffness of the tectorial membrane in situ at multiple locations along the cochlea. Simultaneous access to all of these locations provides an ideal tool to study cochlear stiff ness gradients. Here, we were able to answer the question of whether or not the tectorial membrane itself may constitute a graded second resonant system, similar to that provided by the basilar membrane.

TABLE 2.

Reference	Range of point stiffness (N/m)	Probe type	Stiffness per unit length (103 N/m2)	Stiffness per unit area (106 N/m3)	Shear modulus (kPa)	Location along the cochlea	Animal
This work	0.008–0.3	Metal probe; diameter, 25 μm	0.32–12	16.3–61	0.1–1.2	Base to apex	Gerbil
von Békésy (32)	0.1–10	hair				Base to apex	Human
Zwislocki and Cefaratti (20)	0.116–0.125	Glass fiber, 1 μm	0.625			Midcochlea	Gerbil
Abnet and Freeman (35)	0.18	Magnetic bead, radius ∼10 μm					Mouse
Hemmert et al. (9,11)	0.1∼0.6	AFM cantilever <1 μm	∼10–60	∼320–1900		Apex	Mouse
Freeman et al. (30,31)	0.06–0.34	AFM cantilever <1 μm/magnetic bead				Apex	Mouse
Shoelson et al. (25)		AFM cantilever <1 μm			1.2–8.6	Three segments along the cochlea	Guinea pig
Gueta et al. (38)	0.019–0.014	AFM cantilever (tip radius, 20 nm)				Base to apex	Mouse
Masaki et al. (37)	0.0009					Base to apex	Mouse

Previous measurements

Von Békésy was the first to measure the stiffness of the tectorial membrane along the cochlea (32). He used a hair of known stiffness and pushed on the tectorial membrane from above (34). By measuring the bending of the hair, he determined the stiffness of the tectorial membrane of the human cadaver to be 0.1 N/m, with little change along the cochlea. In other words, von Békésy could not find gradients in transversal stiffness of the tectorial membrane along the cochlea. Moreover, by the oval shape of the indentation caused by the stiffness probe, von Békésy suggested a greater stiffness in the radial direction compared to the longitudinal direction (32,34).

Results of a second series of stiffness measurements obtained from the gerbil tectorial membrane have been published by Zwislocki and Cefaratti (20,33). Using a calibrated glass fiber, they determined the tectorial membrane stiffness in the transversal and radial directions. Measurements were only taken at one location in the cochlea, ∼5–6 mm from the basal end of the tectorial membrane. Their values for the transversal and radial stiffnesses were 0.125 N/m and 0.116 N/m, respectively. Thus, radial and transversal stiffness were similar to each other. At an equivalent location along the cochlea, we measured 0.03 N/m for both the transversal and radial components of the tectorial membrane point stiffness. Again, transversal and radial stiffnesses were similar, but the values of the measurements presented here were ∼4 times smaller than those of Zwislocki and Cefaratti. When the size of the probe is taken into account and the stiffness per unit length is calculated, Zwislocki and Cefaratti measured stiffness at 625 N/m², whereas our value is ∼1200 N/m².

Abnet and Freeman (35) harvested mouse tectorial membranes and placed them on a coverslip. Deformation was achieved via magnetic beads placed on the surface of the tectorial membrane, to which a force was applied via an electromagnetic field. Stiffness values in the radial and longitudinal directions were ∼0.25 N/m and 0.15 N/m, respectively. Measurements were taken at different stimulus frequencies. Magnitude and phase plots suggested that the isolated tectorial membrane behaves like a viscoelastic solid. In another set of experiments, Freeman et al. (30,31) placed a section of an isolated tectorial membrane in a cell-tack coated chamber and vibrated this chamber with a piezo actuator at frequencies between 10 Hz and 14 kHz. At the same time, they recorded the mechanically induced vibrations of the tectorial membrane with an atomic-force cantilever with known mechanical impedance. The vibration magnitude of the tectorial membrane decreased with a rate between 0 and −20 dB/decade of frequency, and the phase angle was between 0 and −90°. The conclusion drawn from these latter experiments supported their previous demonstration that the impedance spectrum of the tectorial membrane is that of a viscoelastic element.

In a more recent article by Shoelson et al. (25), sections of isolated guinea pig tectorial membranes from the base, middle, and apex of the cochlea were used to measure Young's modulus. Measurements were made with an atomic force cantilever. Stiffness values between 1.3 and 9.8 kPa were reported. Although tectorial membrane stiffness values varied with radial location, the authors could not detect any systematic changes along the length of the cochlea. When tectorial membrane stiffness was compared with stereocilia stiffness (36), comparable values were found: 4.36 kPa (tectorial membrane) and 1.62 kPa (stereocilia bundle). The authors did not comment on their observation that although the stiffness of the stereocilia bundles changes along the cochlea, the stiffness of the tectorial membrane does not change.

Masaki and co-workers (37) used osmotic stress to determine the poroelastic bulk properties of the mouse tectorial membrane. The equilibrium stress-strain relation of the tectorial membrane was determined by adding polyethylene glycol (molecular mass of 511 kDa) to the bathing solution. The experiments showed a gradient in the transversal stiffness along the radial axis of the tectorial membrane and along the longitudinal axis of the cochlea: the transversal stiffness was ∼20% greater in the modiolar region than in the lateral wall region, and samples from the base of the cochlea were stiffer than samples from the apical half of the cochlea. The authors have compared the strains in the different directions and have argued that their method provides them with the longitudinal modulus, for which they measured an average value of 0.45 kPa. To compare their data with values previously reported in the literature, Masaki et al. used their longitudinal modulus data to estimate transversal stiffness. The transversal stiffness estimate was 0.009 N/m, which is close to the lower end of the previously published data (37).

Recently, Gueta et al. have published a set of tectorial membrane stiffness measurements that are very different from previously reported values (38). They measured the tectorial membrane stiffness using an atomic force microscope probe and in agreement with previous reports (37,39) demonstrated that the tectorial membrane stiffness decreases from base to apex and varies along the radial axis. With regard to actual magnitudes, however, their stiffness values at equivalent radial and longitudinal positions on the isolated mouse tectorial membrane were at least an order of magnitude stiffer than data published previously. The source of the differences is not clear. Gueta et al. suggest that the differences in stiffness value are due to differences in the indenter size. They used a 2-μm probe, which is smaller than the 10-μm probe used by Shoelsen et al. (25), or the 25-μm probe, which was used in our study. Gueta et al. state that their finite element modeling shows that for an approximate 350-nm indentation the 2-μm probe will deform an area of 6 μm in diameter and a 10-μm probe will deform an area of 20 μm in diameter. They argue that measurements carried out with 10-μm probes may include contributions from other radial zones, and thus represent an average stiffness value. This explanation does not address the fact that their overall values for stiffness are one order of magnitude larger than those reported by others. The issues related to differences in probe size have also been addressed by Dimitriadis et al. (26), who showed that the use of sharp tips tends to overestimate Young's modulus.

Tectorial membrane stiffness gradient

In contrast to previously published results, the set of data presented here systematically examines the tectorial membrane point stiffness in situ at several locations along the length of the cochlea. We found that the transversal component of the tectorial membrane stiffness has a longitudinal gradient of –4.0 dB/mm in artificial perilymph and –3.4 dB/mm in artificial endolymph. The radial component of the tectorial membrane stiffness has a longitudinal gradient of −4.9 dB/mm, which is similar to a previous estimate of −4.4 dB/mm for the gradient of the transverse stiffness of the basilar membrane (18,39–41). The data here are the first to show a longitudinal stiffness gradient for the tectorial membrane. Such a gradient could provide the substrate for a second frequency-place map, associated with the tectorial-membrane-stereocilia complex (4–6).

Tectorial membrane versus stereocilia stiffness

A rationale for measuring tectorial membrane stiffness is to quantify the interaction of the tectorial membrane with other cochlear structures, in particular the outer-hair-cell stereocilia bundles. Tips of outer-hair-cell stereocilia are embedded in the tectorial membrane, which has often been represented as a rigid beam (e.g., (2)). It is assumed that the relative movements between the reticular lamina and the tectorial membrane deflect the stereocilia bundles and stimulate the hair cells. For this traditional model, it is also assumed that the tectorial membrane is stiffer than the stereocilia bundles. There is sufficient information available to assess the validity of this hypothesis for the mode of ciliary displacement. The mechanical coupling within the tectorial membrane has been approximated by space constants that quantify the extent of deformation produced by a driven magnetic bead (35). In their study, Abnet and Freeman found that tissue displacement decreased exponentially with increasing distance from the bead, with space constants of 27.1 μm in the longitudinal direction and 20.7 μm in the radial direction. Note, the measurements were made on tectorial membranes from apical cochlear locations. For the calculations, we assume that the spatial constants are similar along the cochlea. The spatial extent covers a distance spanning ∼3 hair cells along the longitudinal axis and two hair cells along the radial axis, for a total of ∼6 hair cells. In these experiments, the tectorial membrane radial stiffness measured with a 25-μm probe at the middle turn (∼6 mm from the basal cochlear end) was ∼0.03 N/m. Normalizing this measurement to the area coupled to a single point on the tectorial membrane (∼27.1 μm × 20.7 μm), we obtain an effective stiffness of 0.033 N/m. The translational stiffness of an average single stereocilia bundle in the middle cochlear turn is ∼2 × 10⁻³ N/m (36). If six hair cells are covered, the combined stiffness is 0.012 N/m. The measured tectorial membrane stiffness is ∼3 times greater than the reported ciliary stiffness. A similar calculation can be made for basal and apical locations in the cochlea. In the apex, the applicable tectorial membrane stiffness is 0.008 N/m. The combined translational stereocilia stiffness for six apical-hair-cell stereocilia bundles is ∼0.005 N/m (6 × 0.8 × 10⁻³ N/m (36)). In the base, the applicable tectorial membrane stiffness is 0.34 N/m. The combined translational stereocilia stiffness for six hair-cell stereocilia bundles is 0.033 N/m (6 × 5.5 × 10⁻³ N/m (36)). Apart from the base, our data show that the difference in effective stiffness between the tectorial membrane and the stereocilia bundles is less than an order of magnitude: 0.008 N/m vs. 0.005 N/m in the apex and 0.033 N/m versus 0.012 N/m in the middle. In other words, the tectorial membrane and stereocilia bundles appear well matched in stiffness at these cochlear locations. Previous studies have addressed this same question. Freeman et al. (31) concluded that the tectorial membrane is stiffer than the stereocilia bundles. Zwislocki and Cefaratti (20) found that the tectorial membrane is seven times more compliant than the stereocilia bundles. Schoelson et al. (25) estimated that stereocilia bundles are stiffness matched with the tectorial membrane.

If the stereocilia are normally physically coupled to the tectorial membrane, we would expect our measurements to show differences in the driving point stiffness of the tectorial membrane before and after detaching the organ of Corti. In this analysis, we assume that, if coupled, the translational stiffness of the hair bundles is acting in parallel (i.e., summing) with the radial component of the tectorial membrane stiffness. For example, for the middle-turn location, where we estimated that the tectorial membrane stiffness in the intact preparation is ∼3 times greater than the stereocilia stiffnesses, we would expect a detachment of the organ of Corti to manifest itself as a decrease in the radial component of the driving point stiffness measured at the tectorial membrane by a factor of (0.03 + 0.012)/0.03 = 1.4. In the apical location, we would expect a decrease by a factor of (0.008 + 0.005)/0.008 = 1.63. In the basal location, we would expect a decrease by a factor of only (0.34 + 0.033)/0.34 = 1.097, which may be too small to be detectable with our instrumentation. Our data indicate that, in fact, there is no significant difference of driving point stiffness of the tectorial membrane with and without the organ of Corti attached. At face value, these results suggest that the stereocilia are not coupled to the tectorial membrane; consequently, we need to address a potential pitfall in our experimental technique.

Namely, for our measurements on “unaltered” preparations, the stereocilia may already have been abnormally detached from the tectorial membrane. In a recent article, Dallos (42) calculated for the gerbil cochlea the stereocilia deflection for given low-frequency basilar membrane displacements. His kinematic model suggested that the range of basilar membrane deflections is limited to <1 μm to yield physiological magnitudes of cilia rotation. In the cochlear base, the ratio between ciliary rotation and basilar membrane displacement was ∼40 deg/μm. Clearly, a basilar membrane deflection >2 μm would flatten the bundle. Taking into account that the tectorial membrane is deflected several micrometers for our stiffness measurements, the angle of deflection can be estimated by the arctg of the stereocilia displacement divided by the stereocilia height. The angle for a 5-μm displacement is ∼45°. The cilia are most likely pulled out of the tectorial membrane. In other words, the large displacements themselves detach the cilia, regardless of whether the organ of Corti has been removed. Consequently, we assert that all of our stiffness data presented here are, in fact, from the tectorial membrane alone, without any contribution by the stereocilia. This latter assertion helps to reconcile our tectorial membrane data with the stereocilia data from Strelioff and Flock.

Young's modulus

Young's modulus E was also computed from our data. The results provide estimates for E between 0.3 and 3.6 kPa. Considering that the tectorial membrane is composed primarily of incompressible fluid, the shear modulus G can be calculated as 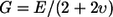(43). The Poisson ratio υ is 0.5 (43). For our experiments on the gerbil tectorial membrane, the shear modulus would be between 0.1 and 1.2 kPa, which is ∼5-fold smaller than the values reported by Shoelson et al. (25) for the guinea pig tectorial membrane. Several parameters may contribute to the differences, including the difference in species, the probes' size, and the indentation depth. The tectorial membrane of the gerbil appears drastically different from the tectorial membrane of the guinea pig. Although the radial cross section of the gerbil tectorial membrane looks like a thick plate, the cross section of the guinea pig tectorial membrane looks like a cone that is particularly thin over the outer hair cells (44). Based on the geometry alone, we might expect the Young's modulus of the guinea pig tectorial membrane to be smaller in the region over the outer hair cells than that of the gerbil tectorial membrane, but it is possible that the stiffness shown by Shoelsen et al. (25) includes a contribution from the stiffness of Hardesty's membrane. Furthermore, in the experiments presented here, the probe had a relatively large tip with a diameter of 25 μm, whereas Shoelsen et al. (25) used the tip of atomic force cantilever. Finally, it must be noted that our measurements were made on the scala media surface of the tectorial membrane, whereas Shoelsen et al. measured the reticular lamina side of the tectorial membrane.

Further considerations

In a previous report (18), we discussed some cautionary points with regard to driving point stiffness measurements made on the basilar membrane. Here, we reiterate those points in the context of our tectorial membrane study. Under physiological conditions, the stimulus driving the cochlear tissues is a distributed fluid pressure. In contrast, for each stiffness measurement described in this and previous studies, the stimulus is a focal point-force applied by a probe at a single position on the tissue. Associated with this difference in stimulation mode is a difference in the magnitude of the tissue deflection. Normal physiological tectorial membrane motion is assumed not to be larger than the basilar membrane motion, which itself is in the submicron range, even for high-level sound stimulation (e.g., (45)). The stiffness measurements presented here were based on tissue deflections on the order of tens of microns. These deflections are significantly larger than sound-induced motion in vivo, and it is important to consider some potential pitfalls with these measurement methods. Previous investigators (22,23,46,47) have argued that the physiologically relevant return force from the basilar membrane is attributed to the embedded radial fibers and that the measured plateau stiffness represents the stiffness of these fibers. Here, we extend this same interpretation to the tectorial membrane. In all cases, there is the possibility that the relevant stiffness occurs at much smaller tissue deflections and may be buried in the noise. Moreover, the large deflections during stiffness measurements (on either the basilar membrane or the tectorial membrane) are likely to produce immediate damage to the stereociliary complex. If this complex normally contributes to the stiffness at the tectorial membrane, its contribution will not easily be observed with any point stiffness measurement technique. Acknowledging that some caution is necessary, we maintain for our discussion here that point force measurements can provide a useful indication at least of spatial gradients of mechanical properties within the cochlea. Further caution is likely necessary when comparing these measurements directly to values of in vivo response properties.

Our use of a quadratic fit for the stiffness-deflection curves for the tectorial membrane follows previous work in which the basilar membrane is approximated by parallel beams sustaining transverse deflections (21,22). Studies of the tectorial membrane using immunocytochemistry have demonstrated that Type II collagen is an important constituent of its fibrous components (25,48,49). Although the biomechanical properties will, of course, depend on the exact configuration of the collagen fibrils and on the nature of other proteins in the tissue, to a first approximation we expect general response characteristics of the tectorial membrane to be similar to those seen in other types of tissue with this collagen content. One example of this tissue type is cartilage, for which the stress-strain relation at small deformations has been modeled using a power law function (e.g., (50)). For our purposes, however, we maintain use of the quadratic fitting function, rather than a higher-order power law function, because the primary purpose of our fit is to obtain values for the plateau stiffness (i.e., the constant term). The plateau has been observed consistently in our data and in previous work. Although ultimately it may be more appropriate to fit the rising portion of the stiffness-deflection curves with a nonquadratic function, we believe that for the purpose of obtaining plateau values, the quadratic fit is accurate and sufficient.

Stiffness gradients and frequency-place mapping

Using our estimate for the gradient of tectorial membrane stiffness along the length of the cochlea, we examine whether the tectorial membrane could constitute the substrate for a second frequency place map along the cochlea. Similar to our previous analysis for the basilar membrane (18), a relatively simple lumped-parameter model incorporating a one-dimensional spring-mass resonance was used. In this analysis, some gross simplifications of the cochlea's mechanical behavior are applied. First, the tectorial membrane is conceptually divided along its longitudinal dimension into many short segments, with each segment modeled as a friction-free lumped-parameter system having a single mass suspended by a single spring, attached to a rigid support. Such a system exhibits a resonance at a radian frequency equal to (k/m)^0.5, where k is the stiffness and m is the mass (51). Second, the stiffness of the entire tectorial membrane cross section at a given longitudinal location is approximated with its plateau stiffness, and the mass is assumed to be proportional to the local cross-sectional area of the tectorial membrane. Best frequencies have already been measured directly in the hemicochlea (29), yielding values at the basal- and middle-turn locations of 9.4 and 2.0 kHz, respectively, corresponding to a decrease by a factor of 4.7 (2.2 octaves) between these two locations. Note, the best frequency determined for different structures at a given measuring site was the same (29). If the spring-mass resonance model applies, then (k/m)^0.5 also should change by a factor of 4.7. Data from the study presented here indicate that the average tectorial membrane stiffness decreases from 0.34 N/m at the basal-turn location to 0.034 N/m at the middle-turn location, equivalent to a decrease in k by a factor of 10. The tectorial membrane cross-sectional area is 3500 and 8500 μm² for the basal and middle locations, respectively (17), corresponding to an increase of mass m by a factor of 2.4. Note that we avoid the issue of directly computing the mass at each location by instead computing an estimate of the mass ratio between the two locations. Combining the measured stiffness change with the estimated mass change yields an expected decrease of resonance frequency from the basal location to the middle location by a factor of 4.9. This predicted decrease is similar to the measured change of best frequency, which decreases by a factor of 4.7 (2.2 octaves).

The analysis from the model suggests that the combined stiffness and mass gradients of the tectorial membrane do yield the known change of best frequency along the length of the gerbil cochlea. It should be clear that, although it is informative and intuitive, the spring-mass model used here is a greatly simplified interpretation and is insufficient to represent the details of either the active response of the cochlea (i.e., action by the outer hair cells) or the stimulation of the hair bundles of the hair cells. Nevertheless, inasmuch as the stiffness and mass gradients of the basilar membrane are presumed to be the primary bases of cochlear spectrum analysis, our demonstration of a second structure with a graded stiffness and an appropriately-matched stiffness range is of potential significance. In this vein, we recall the suggestions (5,6,8,52) that a second system providing frequency analysis is required for proper cochlear function. It is also worth noting that graded tectorial membrane stiffness could interact with the inherently oscillatory nature of stereocilia (53) to yield locally tuned mechanical input to outer hair cells.