Maximum penalized likelihood estimation in a gamma-frailty model

Abstract

The shared frailty models allow for unobserved heterogeneity or for statistical dependence between observed survival data. The most commonly used estimation procedure in frailty models is the EM algorithm, but this approach yields a discrete estimator of the distribution and consequently does not allow direct estimation of the hazard function. We show how maximum penalized likelihood estimation can be applied to nonparametric estimation of a continuous hazard function in a shared gamma-frailty model with right-censored and left-truncated data. We examine the problem of obtaining variance estimators for regression coefficients, the frailty parameter and baseline hazard functions. Some simulations for the proposed estimation procedure are presented. A prospective cohort (Paquid) with grouped survival data serves to illustrate the method which was used to analyze the relationship between environmental factors and the risk of dementia.

1 Introduction

Inference for Cox proportional hazards model (Cox, 1972) was developed under the assumption that the observations are statistically independent, at least conditionally upon covariates. However, this assumption may be violated. Thus in many epidemiological studies, failure times are clustered into groups such as families or geographical units: some unmeasured characteristics shared by the members of that cluster, such as genetic information or common environmental exposures could influence time to the studied event. In a different context, correlated data may come from recurrent events, i.e. events which occur several times within the same subject during the period of observation. In frailty models, dependence is produced by sharing an unobserved variable which is treated as a random effect, or frailty (Clayton, 1978; Hougaard, 1995; Petersen, Andersen and Gill, 1996).

Semi-parametric inference for frailty models was introduced by Klein et al. 1992 and Nielsen et al. 1992, and as suggested by Gill (1985), they used an EM algorithm applied to the Cox partial likelihood. Hastie and Tibshirani (1993) proposed a general model with time varying coefficients and suggested estimation through penalized partial likelihood. Therneau and Grambsch (2000) noted a link between the gamma frailty model and a penalized partial likelihood. In the approach of the present paper, we penalize the hazard function(s) while Therneau and Grambsch (2000) penalize the frailties.

The aim of the present paper is to propose a method for semi-parametric inference in a stratified gamma frailty model: our focus is on the nonparametric estimation of the hazard function, and the approach is based on the penalized full likelihood (as opposed to the penalized partial likelihood). Parner (1998) proved the consistency of the nonparametric maximum likelihood estimator in the shared gamma-frailty model (and for the more general correlated gamma-frailty model). However, the usual nonparametric maximum likelihood estimation method leads to a discrete distribution and the hazard function cannot be derived from the estimated cumulative hazard. The article is structured as follows. In section 2, the shared frailty model is presented, and inference with Maximum Penalized Likelihood Estimation (MPnLE) is developed in section 3. In section 4 we describe simulation studies conducted to ascertain the properties of the proposed method and to compare it to a semi-parametric EM algorithm. We have also performed simulations to illustrate the estimation of the hazard function. In section 5 the method is applied to a study of the effect of aluminum on the risk of dementia in a large cohort (see Letenneur et al., 1994) possibly presenting intra-group correlations.

2 The shared gamma-frailty model

2.1 The model

We consider models in which the hazard function partly depends on an unobservable random variable thought to act multiplicatively on the hazard, so that a large value of the variable increases the hazard. We treat the case of right-censored and left-truncated data, and allow for stratum-specific baseline hazards. For the j^th (j = 1, …, n_ih) individual of the h^th stratum (h = 1, …, K) and the i^th group (i = 1, …, G), let T_ihj denote the survival times under study and let C_ihj be the corresponding right-censoring times. The observations are Y_ihj = min (T_ihj, C_ihj) and the censoring indicators δ_ihj = I_{{Tihj≤Cihj}}. The survival times may be left-truncated: only subjects with $T_{\mathit{ihj}}>{\mathcal{L}}_{\mathit{ihj}}$ are observed; we assume that the left-truncation times ${\mathcal{L}}_{\mathit{ihj}}$ are independent of the survival times T_ihj.

Our frailty model specifies that the hazard function conditional on the frailty is:

$${\lambda }_{\mathit{ihj}}(t\mid Z_i)=Z_i{\lambda }_{0h}(t)exp({\beta }^{\prime }{X}_{\mathit{ihj}})$$ (1)

where λ_0h(t) is the baseline hazard function for stratum h; X_ihj = (X_1ihj, …,X_pihj)′ denotes the covariate vector for the j^th individual of stratum h and group i, and β is the corresponding vector of regression parameters.

Conditionally on the frailty Z_i, the failure times T_ih1, T_ih2, …, T_ihnih are assumed to be independent. It is assumed that the Z_i’s are independently and identically distributed from a gamma distribution with mean 1 and unknown variance θ; the probability density function is thus:

$$g(z)=\frac{z^{(1/\theta -1)}exp\left\{-z/\theta \right\}}{\mathrm{\Gamma }(1/\theta ){\theta }^{1/\theta }}$$

Large values of θ signify a closer positive relationship between the subjects of the same group and greater heterogeneity among the groups. As discussed by Nielsen et al. 1992, we assume the censoring times C_ihj to be independent of the failure times and of the frailties Z_i.

2.2 Inference in the shared gamma-frailty model

The idea of the Cox partial likelihood does not carry over in a simple manner, since the integration over frailties induces a complicated form for this likelihood. Instead, we use the full likelihood. In the gamma-frailty model, a compact formula for the full likelihood can be obtained by integrating out the frailty Z_i from the joint likelihood (Klein et al., 1992; Nielsen et al., 1992). For treating left-truncation we must write a likelihood conditional on $T_{\mathit{ihj}}>{\mathcal{L}}_{\mathit{ihj}}$. This is obtained by dividing by the likelihood of $T_{\mathit{ihj}}>{\mathcal{L}}_{\mathit{ihj}}$ (for i = 1, …, G; h = 1, …, K; j = 1, …, n_ih). Moreover, we can avoid using gamma functions in the expression of the log-likelihood, thus making it easier to compute. The full log-likelihood for left-truncated data can then be written:

$$\begin{array}{ll}l({\lambda }_0(.),\beta ,\theta )=& \underset{i=1}{\overset{G}{\Sigma }}\{\underset{h=1}{\overset{K}{\Sigma }}\underset{j=1}{\overset{n_{ih}}{\Sigma }}{\delta }_{\mathit{ihj}}\left\{{\beta }^{\prime }{X}_{\mathit{ihj}}+ln({\lambda }_{0h}(Y_{\mathit{ihj}}))\right\}\\ & -(1/\theta +m_i)ln\left[1+\theta \underset{h=1}{\overset{K}{\Sigma }}\underset{j=1}{\overset{n_{ih}}{\Sigma }}{\mathrm{\Lambda }}_{0h}(Y_{\mathit{ihj}})exp({\beta }^{\prime }{X}_{\mathit{ihj}})\right]\\ & +1/\theta ln\left(1+\theta \underset{h=1}{\overset{K}{\Sigma }}\underset{j=1}{\overset{n_{ih}}{\Sigma }}{\mathrm{\Lambda }}_{0h}({\mathcal{L}}_{\mathit{ihj}})exp({\beta }^{\prime }{X}_{\mathit{ihj}})\right)\\ & +I_{\{m_i\ne 0\}}\underset{k=1}{\overset{m_i}{\Sigma }}[ln(1+\theta (m_i-k))]\}\end{array}$$ (2)

with λ₀(.) = (λ₀₁(.), …, λ_0K(.)′; ∧_0h(.) are the cumulative baseline hazard functions and $m_i={\Sigma }_{h=1}^K{\Sigma }_{j=1}^{n_{ih}}{I}_{\{{\delta }_{\mathit{ihj}}=1\}}$ is the number of observed events in the i^th group. If a parametric baseline hazard function is specified, then maximum likelihood estimates are available by directly maximizing (2) (see Costigan and Klein, 1993).

3 The penalized likelihood approach

We introduce a semi-parametric approach to jointly estimate the parameters β, θ and the baseline hazard function λ₀(t), which is assumed to be smooth. A possible means for introducing such an a priori knowledge is to penalize the likelihood by a term which has large values for rough functions (O’Sullivan, 1988; Joly, Commenges and Letenneur, 1998). Thus for the vector of baseline hazard functions, λ₀(.) = (λ₀₁(.), …, λ_0K(.))′, we define the maximum penalized likelihood estimators (MPnLE) of λ₀(t), β and θ as maximizing:

$$pl({\lambda }_0(.),\beta ,\theta )=l({\lambda }_0(.),\beta ,\theta )-\underset{h=1}{\overset{K}{\Sigma }}{k}_h{\int }_0^{\infty }{\lambda }_{0h}^{″2}(t)dt$$ (3)

where l(λ₀(.), β, θ) is the full log-likelihood defined in (2), and k_h ≥ 0, (h = 1, …, K) are positive smoothing parameters for each stratum. In practice, the range of the integral is restricted to the period when at least one subject is still at risk. This expression represents a trade-off between faithfulness to the data, as represented by l(.), and “smoothness” of the solution, as represented by the squared norm of the second derivative. For large k_h;, the term $\int {\lambda }_{0h}^{″2}(t)dt$ will be forced toward zero and the curves λ̂_oh (.) will approach linear functions of time. If k_h is small, then the main contribution to pl (.) will be the log-likelihood l(λ₀ (.), β, θ) and the curve estimate λ_0h will track the data closely, but will be more irregular.

3.1 Spline-based approximations

When the penalized likelihood is used to estimate nonparametric regression functions, it can be shown that the estimators are cubic splines with knots at every observed data point (see Silverman (1985)). In the present context of hazard function estimation, there is no such simplification. Exact computation of these estimators is not possible and the MPnLE of λ₀(t) must be approximated using splines. Splines are polynomial functions which are combined linearly to give ${\stackrel{\sim }{\lambda }}_{0h}(.)={\Sigma }_{i=1}^m{\stackrel{\sim }{\eta }}_{hi}{M}_i(.)$, where the M_i (.) are cubic M-splines, i.e. splines of order 4 (Ramsay, 1988). By direct integration and with the same vector of coefficients η_h = (η_h1, …, η_hm)′, it is also possible to obtain the cumulative intensity function: ${\stackrel{\sim }{\mathrm{\Lambda }}}_{0h}(.)={\Sigma }_{i=1}^m{\stackrel{\sim }{\eta }}_{hi}{I}_i(.)$ where I_i(.) are I-splines defined as $I_i(x)={\int }_0^x{M}_i(u)du$. In our approach, although there are different strata, we use the same basis of splines for each stratum, so only the coefficients η_hi are different for the distinct strata.

Note that the estimator is the MPnLE λ̂(.), while λ̃(.) is an approximation to the estimator λ̂(.). The approximation error can be made as small as desired by increasing the number of knots.

3.2 Variance of the estimates

We drew our inspiration from Gray’s work (Gray, 1992; Gray, 1994). To simplify notations we will consider only the unstratified case. We make the assumption that λ₀(.) belongs to the space generated by m splines, so the model is specified by a parameter vector ${\zeta }^{\prime }=({\eta }_1^{\prime },\dots ,{\eta }_{\mathbf{K}}^{\prime };{\beta }_1,\dots ,{\beta }_p;\theta )$ where ζ belongs to a subspace χ⊂IR^K+p+1. In the general case this is only an approximation. The penalized log-likelihood can then be written as:

$$pl({\lambda }_0(.),\beta )=l(\zeta )-P_G(\zeta )$$

where P_G(ζ)) the penalization term, depends on the number of groups G and on ζ but not on the data. P_G(ζ) may be a weighted sum of squared norms of second derivatives of the λ₀(.) as in (3), but the theory applies to other choices of penalization.

We can show that the MPnLE ζ̂ asymptotically follows a multivariate normal distribution with mean

$$E(\widehat{\zeta })={\zeta }_0-\underset{G\to \infty }{lim}{H}_G^{-1}({\zeta }_0)\left(\frac{\partial P_G}{\partial \zeta }({\zeta }_0)\right)$$ (4)

and variance-covariance matrix

$$var(\widehat{\zeta })=H_G^{-1}({\zeta }_0)var\left(\frac{\partial l}{\partial \zeta }({\zeta }_0)\right)H_G^{-1}({\zeta }_0)$$ (5)

where $H_G({\zeta }_0)=I_G({\zeta }_0)+\frac{{\partial }^2{P}_G}{\partial {\zeta }^2}({\zeta }_0)$ and $I_G({\zeta }_0)=-\frac{{\partial }^{2}l}{\partial {\zeta }^2}({\zeta }_0)$, and ζ₀ is the true value of ζ.

It follows from (4) that a necessary condition for consistency is

$$\underset{G\to \infty }{lim}{H}_G^{-1}({\zeta }_0)\left(\frac{\partial P_G}{\partial \zeta }({\zeta }_0)\right)=0$$

or, under a condition of steady increase of information with G $(H_G({\zeta }_0)=O_p(G)):\frac{\partial P_G}{\partial \zeta }({\zeta }_0)=o_p(G)$. If $P_G=k_G{\int }_0^{\infty }{\lambda }_0^{″2}(t)dt$, this condition is equivalent to k_G = o_p(G). We conjecture that this is also a sufficient condition.

Two estimators may be proposed for var(ζ̂).

• If the distribution of the observations belongs to the class of models considered, we have $var\frac{\partial l}{\partial \zeta }(\zeta )=I_G(\zeta )$ and by substituting ζ̂ in (5) we obtain:

  $$\widehat{va{r}_1}(\widehat{\zeta })={\widehat{H}}_G^{-1}(\widehat{\zeta }){\widehat{I}}_G(\widehat{\zeta }){\widehat{H}}_G^{-1}(\widehat{\zeta })$$ (6)

  with ${\widehat{I}}_G(\widehat{\zeta })=\left[-\frac{{\partial }^{2}l}{\partial {\zeta }^2}(\widehat{\zeta })\right]$ and ${\widehat{H}}_G(\widehat{\zeta })=\left[-\frac{{\partial }^{2}pl}{\partial {\zeta }^2}(\widehat{\zeta })\right]$.

• A variance estimator deduced from a bayesian approach was proposed by O’ Sullivan (1988) for a similar problem. In this approach ζ is considered as a random variable. Up to a constant, the penalty term is regarded as the prior log-likelihood for ζ and the penalized log-likelihood as the posterior log-likelihood. After some manipulation we obtain a multivariate gaussian approximation distribution for ζ and this makes it possible to use ${\widehat{H}}_G^{-1}(\widehat{\zeta })$ simply as a variance estimator.

These estimators for var(ζ̂) do not take into account the variability due to the choice of the smoothing parameters.

3.3 Confidence bands

From ${\stackrel{\sim }{\lambda }}_{0h}(.)={\Sigma }_{i=1}^m{\stackrel{\sim }{\eta }}_{hi}{M}_i(.)$ we deduce that var(λ̃_0h(t)) = M′(t)[var(η̂_h)]M(t), so point-wise 95% confidence bands are of the form

$${\stackrel{\sim }{\lambda }}_{0h}(t)\pm 1.96\sqrt{{\mathbf{M}}^{\prime }(\mathbf{t})\left[\widehat{var}({\widehat{\eta }}_h)\right]\mathbf{M}(\mathbf{t})}$$

where M′(t) = (M₁(t), …, M_m(t)) is the spline vector in t, and estimators $\widehat{var}({\widehat{\eta }}_h)$ can be taken from one of the estimators of var(ζ̂). Wahba (1983), Silverman (1985), and O’Sullivan (1988) proposed such confidence bands based on Ĥ⁻¹(η̂_h) for conventional problems.

3.4 Choice of smoothing parameter

To be practical, it is sometimes sufficient to choose the smoothing parameter heuristically, by plotting several curves and by choosing that which seems most realistic. We briefly present two other approaches to determine the smoothing parameters.

In each stratum the smoothing parameters could be chosen by maximizing an approximate cross-validation score which was detailed by O’Sullivan (1988) for a Cox model:

$$\overline{CV(k)}=\frac{1}{n}{l}_j(\widehat{\eta }(k))-\frac{1}{n}\text{trace}\left({\left[\widehat{\text{I}}(\widehat{\eta })+2k\mathrm{\Omega }\right]}^{-1}\widehat{\text{I}}(\widehat{\eta })\right)$$ (7)

where l_i is the log-likelihood contribution of individual j, $I(\eta )=E\left(-\frac{{\partial }^{2}l}{\partial {\eta }^2}(\eta )\right)$ is the information matrix $\left(\widehat{I}(\widehat{\eta })=-\frac{{\partial }^{2}l}{\partial {\eta }^2}(\widehat{\eta })\right)$, and H(η) = I(η) + 2kΩ is minus the converged hessian of the penalized log-likelihood (Ĥ(η̂) = Î(η̂) + 2kΩ) and $\mathrm{\Omega }=\int {\left(\frac{{\partial }^{2}M}{\partial u^2}\left(u\right)\right)}^{\prime }\frac{{\partial }^{2}M}{\partial u^2}\left(u\right)du$. As in Gray (1992), if we interpret trace ([Î(η̂) + 2kΩ]⁻¹ Î(η̂)) as an effective number of parameters or as the model degrees of freedom, $\overline{CV(k)}$ is equivalent to an AIC criterion (Akaike, 1974).

Another approach introduces a priori knowledge, by fixing the number of degrees of freedom to estimate the hazard function (e.g., Buja et al., 1989; Hastie and Tibshirani, 1989; Gray, 1992). We thus use the relation linking the model degrees of freedom and the smoothing parameter k to evaluate the smoothing parameter. Indeed, it is easier to specify a number of degrees of freedom to estimate a given curve, rather than specify a smoothing parameter. For example, if we want to estimate a straight line, we choose a number of degrees of freedom equal to 2, while a quadratic curve has 3 degrees of freedom.

4 Simulations

We first present the computing algorithm, then two simulation studies: one to compare our results to those of Nielsen et al. 1992, and the other to illustrate a more realistic situation.

4.1 The algorithm

The estimated parameter ζ̂ was obtained by the robust Marquardt algorithm (Marquardt, 1963) which is a combination between a Newton-Raphson algorithm and a steepest descent algorithm. This algorithm is more stable than the Newton-Raphson algorithm but preserves its fast convergence property near the maximum. To be sure of having a positive function at all stages of the algorithm, we restricted all the spline coefficients η_hi to be positive for all i. This restriction does not have a major adverse effect on the approximation, while being very convenient numerically. We also imposed a positivity constraint for the variance parameter. When θ is very small, numerical problems may arise. When θ̂ ≤ 10⁻⁶, we used an alternative formula of the log-likelihood (2) based on a third-order expansion in the expression of the log-likelihood. Thus, we replaced the two terms of the form 1/θ log(1 + θΔ) by Δ − θΔ²/2 + θ²Δ³ with Δ stands for ${\mathrm{\Delta }}_{1,\mathit{ihj}}={\Sigma }_{h=1}^K{\Sigma }_{j=1}^{n_{ih}}({\mathrm{\Lambda }}_{0h}(Y_{\mathit{ihj}}))exp({\beta }^{\prime }{X}_{\mathit{ihj}})$ or ${\mathrm{\Delta }}_{2,\mathit{ihj}}={\Sigma }_{h=1}^K{\Sigma }_{j=1}^{n_{ih}}({\mathrm{\Lambda }}_{0h}({\mathcal{L}}_{\mathit{ihj}}))exp({\beta }^{\prime }{X}_{\mathit{ihj}})$.

4.2 First simulation study

We conducted a simulation study to investigate the sampling properties of the MPnLE for θ. Our aim was to compare the statistical properties of the proposed method with the EM algorithm used by Nielsen et al. 1992. For the selected value of the variance parameter θ, we generated G independent pairs (t_i1, t_i2) of survival times with two strata of equal sample size and with only one subject (n_ih = 1) in each stratum of each cluster. An example of this two-sample model with dependence between some of the individuals would be a study of a disease in a number (G) of families with K = 2 corresponding to husbands (h = 1, n_i1= 1) and wives (h = 2, n_i2 = 1). For each simulation run of M replicates (500 under H₀ and 200 under H₁), the random variates were generated by the frailty model as follows:

$$\begin{array}{l}{v}_{ih},i=1,\dots ,G,h=1,2\hspace{0.17em}\text{i}.\text{i}.\text{d}.\hspace{0.17em}exp(1)\hspace{0.17em}\text{random}\hspace{0.17em}\text{variates}\\ z_i,i=1,\dots ,G,\hspace{0.17em}\text{i}.\text{i}.\text{d}.\hspace{0.17em}\text{gamma\hspace{0.17em}}(1/\theta ,1/\theta )\\ t_{ih}=v_{ih}/z_i.\end{array}$$

The survival times were not left-truncated (entry times equal to zero). All failure times were censored at fixed times (t = 2) determined as the value that would censor 10% (in expectation) of the entire sample.

We used cubic splines to approximate each hazard function. The number of knots was 8 for all simulations. For the first replicate of each simulation (i.e., for a given θ and number of groups G) we evaluated in each stratum a value of k_(θ,G) using the fixed degrees of freedom method. Since the hazard function is a constant function equal to 1, we had to specify a reasonable value for the smoothing parameter in order to obtain a linear hazard function close to a linear function of time. The numerical evaluations allowed us to find a smoothing parameter corresponding to a model degrees of freedom close to 2 (between 2.0 and 2.1). Thereafter k_(θ,G) was the same for the M replicates of the simulation. The empirical standard deviation S.D.(θ̂) was estimated, and two estimators of standard error were computed; $\widehat{SE}(\widehat{\theta })=\sqrt{{\widehat{H}}_{\theta \theta }^{-1}}$ and the sandwich estimator $\widehat{SE}(\widehat{\theta })=\sqrt{{\widehat{H^{-1}I{H}^{-1}}}_{\theta \theta }}$. The hypothesis “θ = θ” can be tested using a score test (Commenges and Andersen, 1995) but we do not present results using this test here.

For the analyses of the uncensored life times, the results are summarized in Table 1. We observed a negative bias for θ̂ for small number of groups. Conversely, we obtained an over-estimation of θ̂ when the number of groups increased. Nevertheless, this bias decreased with increasing G for a given value of θ. As expected, the sandwich standard error estimator of $\widehat{\theta }\left(\sqrt{{\widehat{H^{-1}I{H}^{-1}}}_{\theta \theta }}\right)$ was smaller than the bayesian standard error estimator $\left(\sqrt{{\widehat{H}}_{\theta \theta }^{-1}}\right)$. Both estimators under-estimate the empirical standard error (S.E.(θ̂)).

Table 1.

Estimations of mean(θ̂) and standard errors of θ̂ for G pairs of uncensored life-times and M simulated samples (M=500 under H₀ and M=200 under H₁); θ is the true value of the variance of the frailty variables.

Uncensored life-times
G	θ	Mean (θ̂)	empirical S.E.(θ̂)	Mean S.E.(θ̂) ( $\sqrt{{\widehat{H^{-1}}}_{\theta \theta }}$)	Mean S.E.(θ̂) ( $\sqrt{{\widehat{H^{-1}I{H}^{-1}}}_{\theta \theta }}$)
1000	0.0	0.013	0.019	0.015	0.014
	0.1	0.104	0.034	0.035	0.033
	0.2	0.202	0.036	0.041	0.039
500	0.0	0.019	0.028	0.021	0.019
	0.2	0.205	0.056	0.057	0.057
	0.4	0.398	0.066	0.066	0.064
200	0.0	0.028	0.045	0.031	0.028
	0.2	0.206	0.087	0.077	0.070
	0.4	0.406	0.109	0.106	0.132
100	0.0	0.038	0.064	0.041	0.035
	0.2	0.194	0.127	0.110	0.102
	0.4	0.390	0.163	0.187	0.224
	0.6	0.561	0.187	0.161	0.174
	0.8	0.752	0.201	0.165	0.161
	1.0	0.918	0.191	0.182	0.181

The same general tendencies were observed when times were censored at t = 2 (Table 2 vs Table 1). Nevertheless, the mean value of θ̂ was greater than θ in the censored case, whatever the sample size. As expected, the standard deviation of θ̂ was larger in the censored than in the uncensored case.

Table 2.

Estimations of mean(θ̂) and standard errors of θ̂ for G pairs of censored life-times and M simulated samples (M=500 under H₀ and M=200 under H₁); θ is the true value of the variance of the frailty variables.

Censored life-times
						Nominal coverage of the 95% CI
G	θ	Mean (θ̂)	empirical S.E.(θ̂)	Mean S.E.(θ̂) ( $\sqrt{{\widehat{H^{-1}}}_{\theta \theta }}$)	Mean S.E.(θ̂) ( $\sqrt{{\widehat{H^{-1}I{H}^{-1}}}_{\theta \theta }}$)	*	**
1000	0.0	0.021	0.029	0.023	0.022	93.0	93.0
	0.1	0.104	0.041	0.031	0.029	88.0	86.0
	0.2	0.208	0.048	0.047	0.044	93.0	92.0
500	0.0	0.025	0.036	0.026	0.025	97.0	95.0
	0.2	0.204	0.071	0.065	0.062	94.0	92.0
	0.4	0.409	0.096	0.080	0.075	90.0	87.0
200	0.0	0.037	0.056	0.043	0.041	96.8	94.6
	0.2	0.210	0.115	0.099	0.092	91.5	91.0
	0.4	0.415	0.148	0.122	0.112	92.5	91.0
100	0.0	0.053	0.078	0.061	0.056	97.2	93.0
	0.2	0.218	0.158	0.133	0.123	87.0	86.0
	0.4	0.428	0.202	0.177	0.164	92.5	87.5
	0.6	0.625	0.244	0.212	0.197	92.0	89.0
	0.8	0.839	0.260	0.249	0.232	93.5	89.5
	1.0	1.013	0.303	0.281	0.263	91.0	90.0

^*using the estimator ${\widehat{H^{-1}}}_{\theta \theta }$ of the variance estimator θ̂,

^**using the estimator ${\widehat{H^{-1}I{H}^{-1}}}_{\theta \theta }$ of the variance estimator θ̂.

The estimator $\stackrel{\vee }{\theta }=\widehat{\theta }+{\left[{\widehat{H}}_G^{-1}(\widehat{\zeta })\left(\frac{\partial P_G}{\partial \zeta }(\widehat{\zeta })\right)\right]}_{\theta }$, which is theoretically less biased, was almost identical to θ̂.

Figure 1 illustrates the theoretical and estimated baseline hazard functions for a single simulation of 400 subjects and a variance parameter θ = 0.4. We also represented the estimated marginal hazard function which was estimated using a proportional hazard model without frailty variables. The marginal hazard function is connected with the average hazard in the population, and corresponds to the hazard for an average value of the frailty variable among the surviving individuals. Thus in this example, the population hazard function and the individual hazard function (using the frailty model) deviate more and more as time passes, because the most frail subjects have already died. The confidence bands for the estimated baseline hazard function were obtained using the standard error estimator of the spline parameters $\sqrt{{\widehat{H^{-1}I{H}^{-1}}}_{\theta \theta }}$ (using $\sqrt{{\widehat{H^{-1}}}_{\theta \theta }}$yielded nearly the same result).

Figure 1.

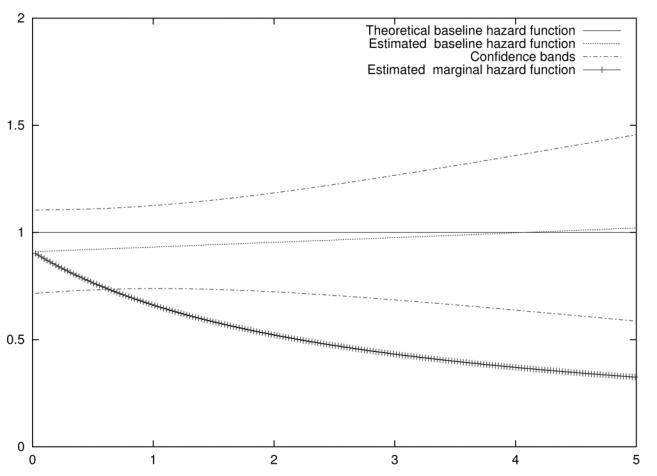
Theoretical and estimated baseline hazard functions and estimated marginal hazard function for a frailty variance θ = 0.4 for a simulated dataset.

4.3 Numerical illustration

We also carried out a different simulation study to illustrate the quality of the estimation for a non-linear hazard function. A sample with similar features as the Paquid cohort (see section 5) was generated: there was 2,698 subjects and varying group sizes, between 13 and 232 subjects by group, (but without explanatory variables). The failure times were generated using a mixture of Weibull distributions (for stratum 1 : 0.35W(t; 20, 0.013) + 0.65W(t; 20, 0.0102); for stratum 2 : 0.35W(t; 15, 0.0107) + 0.65W(t; 15, 0.0107)). A shared frailty variable for each group of subjects was generated using a gamma distribution (with θ = 0.2). The data were left-truncated and right-censored at a fixed value, and the percentage of censoring was around 10%. The estimation of the hazard function for stratum 1 with three different numbers of knots (therefore, three different smoothing parameters) is illustrated by Figure 2. In each stratum we estimated a value for k using the automatic cross-validation method. Many authors have pointed out that the automatic cross validation method for estimating k often leads to an undersmoothed hazard function. In fact, we observed a slight oversmoothing. Figure (2) also shows that we obtained a good estimate of the theoretical hazard function. The more knots we used, the closer the approximation of MPnLE was to the true hazard function. Nevertheless, the benefit of using 15 knots compared with 8 knots was small. We also conducted a simulation run (for θ = 0.2) with this irregularly-shaped function to assess the inference for θ̂. The results obtained for 200 replicates were: mean(θ̂) = 0.232, empirical SE(θ̂) = 0.143, mean SE(θ̂) = 0.123. We again observed that the standard error estimators slightly under-estimated the empirical standard errors and θ̂ had a slight upward bias.

Figure 2.

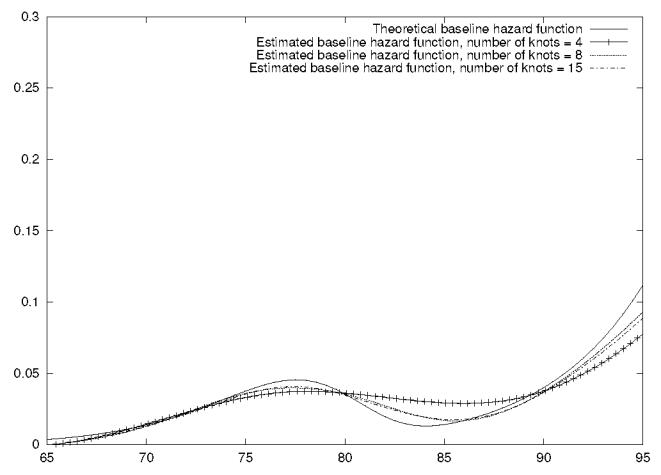
Theoretical and estimated baseline hazard functions for survival times generated from a mixture of Weibull.

5 Application to dementia in geographical areas

Although the hypothesis of a link between aluminum and Alzheimer’s disease has been supported by several epidemiological studies (Martyn et al., 1989; Rondeau et al., 2000), there is much controversy regarding these findings and their interpretation. We analysed data from the Paquid cohort, a large cohort randomly selected from a population of subjects, aged 65 years or more, living at home in two administrative areas of southwest France (Gironde and Dordogne). The present study is based on 70 areas for which measures were available. For each drinking water area, we computed a weighted mean of all the available measures of each drinking water component of interest. An active search for demented cases was undertaken. Details can be found in Jacqmin et al. 1994 and Rondeau et al. 2000.

One of the characteristics of the Paquid cohort is the grouping of the individuals in geographical areas. Thus, subjects from the same group who may share the same environmental exposure are likely to be more similar than subjects from different groups. Our objective was to establish whether there was heterogeneity of the incidence rates of dementia between areas. If this were the case, our aim was to explain it by individual-specific or group-specific variables. We also wanted to correct the variance of the regression coefficients, especially for group-specific variables. For this analysis we used data on 2,698 subjects regularly followed-up for 8 years (1, 3, 5 and 8 years after the initial visit). Among these, 253 subjects were diagnosed with dementia during the 8-year follow-up.

We chose to carry out a stratified analysis on gender and estimated a value for k in each stratum using the automatic cross-validation method described in Section 3.4. We used 8 knots and cubic M-splines to approximate each hazard function. Age, an important risk factor in dementia, was taken as the basic time-scale. We considered only subjects free of dementia at entry into the cohort. Subjects still unaffected at the last visit were right-censored at that time. Deceased subjects who were unaffected at the last visit were right-censored at that date. For a demented subject, we considered half of the time between the last visit at which they were nondemented and the first visit at which dementia was diagnosed.

In a first analysis using a gamma-frailty model, we did not adjust for explanatory variables but age was chosen as the basic time scale and the model was stratified on gender. The variance of the random effects was estimated by θ̂ = 0.018 with P=0.045 for testing θ = 0 with the Wald test. This significant variance indicates an heterogeneity of the incident cases of dementia between the different areas. The heterogeneity of the risk of dementia may be explained by subject-specific factors other than age and sex, such as educational level, or group-specific factors such as the exposure to aluminum and silica in tap water. We first adjusted for educational level in two classes (did not graduate from primary school vs graduated from primary school). The estimated variance of the frailty decreased to θ̂ = 0.001 (P=0.35). Then, we added exposure to aluminum (as a binary variable with the threshold of 0.1 mg/liter) and to silica (coded as a binary variable with 11.25 mg/1, the median in our sample, as the cut-off); the variance of the frailty decreased to θ̂ = 0.00036 (P=0.45).

We compared three approaches: a classical proportional hazards model using a Cox partial likelihood, a proportional hazard model with a penalized likelihood estimation for the hazard function (Joly, Commenges and Letenneur, 1998), and a shared gamma-frailty model using a penalized likelihood estimation. Table 3 shows the estimated regression coefficients and the standard errors. The different models and estimation methods led to very close estimates, which is not surprising in view of the low intra-group correlation. Although we did not find any intra-area dependency, we had to validate our previous results by using a model taking into account the potential correlation of the data. Furthermore, the advantage of the frailty model was to show that since the area variation (θ) was so small, we were unlikely to find other area-specific factors strongly correlated with the hazard of dementia.

Table 3.

Estimates and standard errors of the regression coefficients for dementia in the Paquid Cohort after 8 years of follow-up, using a shared gamma-frailty model or a model for independent data (with partial or penalized likelihood).

	Model for independent data		Shared gamma-frailty model
Variables	(partial Likelihood) β̂(S.E.*)	(penalized Likelihood) β̂ (S.E.*)	(penalized Likelihood) β̂ (S.E.*)
educ. †	0.589(0.127)	0.617(0.116)	0.607(0.116)
Aluminum‡	0.751(0.254)	0.774(0.249)	0.765(0.249)
silica⋄	−0.293(0.127)	−0.270(0.109)	−0.270(0.109)
			θ̂(S.E.) = 0.00036(0.0029)

^*standard errors estimated with $\sqrt{{\widehat{H^{-1}}}_{\theta \theta }}$

^†educational level: without versus with primary school diploma

^ೠ0.1 vs <0.1 mg/liter of aluminum

^⋄≥ 11.25 vs <11.25 mg/liter of silica

The results confirmed a higher risk of dementia for subjects exposed to high concentrations of aluminum (≥ 0.1mg/l) and low levels of silica (< 11.25mg/l).

Figure 3 shows the estimated hazard functions of dementia obtained with a shared frailty model. We distinguished women from men and subjects exposed to high levels of aluminum from those exposed to low levels. Since the basic time-scale is age, the hazard function is the age-specific incidence of dementia. It steadily increased with age, and again an increased risk of dementia for subjects exposed to high levels of aluminum was observed. Of course, we cannot exclude the possibilities that these results were obtained either by chance, or because of misspecification of the model. Furthermore we did not completely deal with the interval-censoring problem, which requires the evaluation of an integral in the estimation of the likelihood. There is probably little difference in considering interval-censoring or the middle of the interval (see Commenges et al. 1998) as long as we stay in the framework of survival models. A better approach would be an illness death model as in Joly et al. 2002; however extending frailty to multistate models requires further work.

Figure 3.

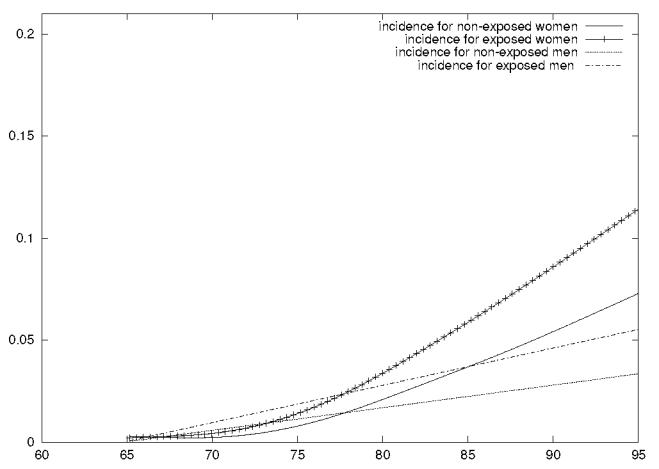
Age-specific risk of dementia estimated with a shared gamma-frailty model for women and men exposed to high levels of aluminum (≥ 0.1 mg/l) or low levels of aluminum (< 0.1 mg/l).