Modelling the influence of MDR1 polymorphism on digoxin pharmacokinetic parameters

Abstract

Objectives

Digoxin is a well-known probe for the activity of P-glycoprotein. The objective of this work was to apply different methods for covariate selection in non-linear mixed effect models to study the relationship between the pharmacokinetic parameters of digoxin and the genotype for two major exons located on the MDR-1 gene coding for P-glycoprotein.

Methods

Thirty-two healthy volunteers were recruited in three pharmacokinetic drug interaction studies. The data after a single oral administration of digoxin alone were pooled. All subjects were genotyped for the MDR1 C3435T and G2677T/A genotypes. The concentration-time profile of digoxin was established using 12 to 16 blood samples taken 15 minutes to 72 hours after administration.

We modelled the pharmacokinetics of digoxin using non-linear mixed effect models. Parameter estimation was performed using the stochastic approximation EM method (SAEM). We used three methods to select the covariate model: selection from a full model using Wald tests, forward inclusion using the log-likelihood ratio test and model selection using the Bayesian Information Criteria.

Results

The three covariate inclusion methods led to the same final model. Carriers of two T alleles for the C3435T polymorphism in exon 26 of MDR1 had a lower apparent volume of distribution than carriers of a C allele. The only other covariate effect was a shorter absorption time-lag in women.

Conclusion

The apparent volume of distribution of digoxin is lower in TT subjects, probably reflecting differences in bioavailability. Non-linear mixed effect models can be useful to detect the influence of covariates on pharmacokinetic parameters.

Introduction

Pharmacogenetics is a recent field of research investigating the variability in drug effect due to genetic factors. Genetic variation occurs at many levels: drug absorption, distribution and metabolism, receptors for drug action, and drug elimination. Single-Nucleotide Polymorphisms (SNPs) have been identified which induce modifications of the pharmacokinetics (drug course through the body) or pharmacodynamics (drug efficacy and safety). SNPs have namely been shown to modify bioavailability [1, 4], decrease excretion [25] sometimes inducing severe toxicity [10] and have been linked to drug efficacy [6, 13]. Thus, pharmacogenetics are the next step to provide individualised treatments.

The studies including pharmacogenetic data have become more numerous over the last few years. In an overwhelming majority of these studies, non-compartmental analysis (NCA) is used to compare pharmacokinetic measurements such as AUC or maximum concentration between groups. This technique requires a large number of sampling points for every subject. On the other hand, modelling approaches can take advantage of sparse individual designs and can be used in patients with routine clinical data [26], but these more sophisticated approaches are seldom used. One issue with these approaches is the method used for covariate selection and hypothesis testing, since detecting a gene effect can be thought of as a model selection problem. A wide variety of approaches have been proposed. The mainstream method consists in stepwise selection [23, 17], possibly following prior screening of relevant candidate covariates. The criterion for model selection is usually the likelihood ratio test, which is widely used to compare nested mixed effect models. Tests assessing the statistical significance of the final parameters in the final model, such as the Wald test, can also be used as a selection criterion [26]. Other criteria can be used in model selection, such as the Akaike (AIC) or the Bayesian Information Criterion (BIC) [22]. Regardless of the method used, the clinical relevance is sometimes also assessed by examining the magnitude of the effects found.

In a previous paper, Verstuyft et al. estimated the AUC of digoxin, a probe for the activity of P-glycoprotein, in healthy volunteers using non-compartmental analysis and showed an increase in subjects carrying the TT genotype for the C3435T polymorphism of MDR-1 [38]. The objective of the present paper was to reanalyse the data in [38] by a modelling approach, using three covariate model selection methods: likelihood ratio tests, backwards selection from a full model using Wald tests, which take into account potential correlations between covariates, and model selection using the BIC, which considers all the potential models. A related problem in covariate selection is that the false positive rate (type I error) of the tests has been shown to increase when the estimation methods rely on linear approximations to the likelihood [7, 40]. In this work, we therefore use a recent estimation method, the stochastic EM algorithm SAEM [20]. Although the three methods can be applied with other estimation algorithms, SAEM allows estimation of the likelihood without approximation, via stochastic simulation, and has been shown to have better statistical properties than linearised methods [33].

Materials and methods

Data

Pharmacokinetic data was collected from 32 healthy volunteers included in three pharmacokinetic interaction studies dealing with oral digoxin [38]. Seven subjects participated in a macrogol-digoxin interaction study [30], 12 in a grapefruit juice-digoxin interaction study [2], and 13 in a dipyridamole-digoxin interaction study [39]. The three studies were performed in accordance with the Declaration of Helsinki and its amendments. Protocols were approved by the Ethics Committee of the Pitié-Salpêtrière Hospital (CCPPRB), Paris, France, and written informed consent was obtained from all subjects. The 3 studies took place in the same clinical unit under the supervision of the same research team.

All subjects received a 0.5 mg oral dose of digoxin with a glass of water after an overnight fast. Pharmacokinetic samples were obtained at times 15, 30, 45 minutes, 1, 1.5, 2, 4, 6, 8, 12, 24 and 48 hours after the dose for two of the studies [2, 39]. For the last study [30], samples were taken at 15, 30, 45 minutes, 1, 1.5, 2, 2.5, 3, 4, 6, 9, 12, 16, 24, 48 and 72 hours.

The three studies included 23 men and 9 women, with a mean age of 25.8±5.2 years (range 19–35). Patients were genotyped for two MDR1 polymorphisms, C3435T polymorphism in exon 26 and G2677T/A polymorphism in exon 21. In study [39], patients were genotyped prior to inclusion to balance the genotypes for the C3435T polymorphism while in the 2 other studies, genotyping was performed after inclusion. As a result, the genotypes of the 32 patients for this polymorphism included 10 TT (mutant homozygotes, 31%), 8 CT (heterozygotes, 25%) and 14 CC (wild-type homozygotes, 44%). G2677T/A genotyping revealed 12 GG (38%), 11 GT (34%), 7 TT (22%), 1 GA (3%) and 1 AA (3%) subjects, with a linkage disequilibrium between the two polymorphisms (Somer’s D’=0.72).

Digoxin was measured using a modified enzyme multiplied digoxin immunoassay (EMIT 2000, Dade Behring, Calif., USA), with a quantification limit of 0.1 ng/ml. MDR1 C3435T and G2677T/A genotypes were determined by TaqMan allelic discrimination. More details concerning the analytical methods can be found in [38, 37].

Statistical methods

Pharmacokinetic model

The pharmacokinetics of digoxin were described using a two-compartment model [15] with first-order absorption and elimination, and an absorption time-lag, using the analytical form of the model. We assumed a proportional variance model for the residual error. This model included six parameters: k_a, k_el, V_c/F, T_lag and the two transfer rate constants k_1,2 and k_2,1. Interindividual variability was estimated for the first four parameters, with no covariance between them (diagonal variance matrix Ω).

Denoting f the function describing this model, the statistical model for concentration y_{i j} in individual i at time t_{i j} is:

$$y_{i\hspace{0.17em}j}=f({\theta }_i,t_{i\hspace{0.17em}j})+{\epsilon }_{i\hspace{0.17em}j}$$ (1)

θ_i denotes the vector of parameters for individual i and its components are assumed to follow a log-normal distribution:

$${\theta }_i={\theta }_0{e}^{{\eta }_i}$$ (2)

where ${\eta }_i\sim \mathcal{N}(0,\mathrm{\Omega })$ is the vector of individual random effects.

The residual errors ε_{i j} are assumed to be independent, with distribution $\mathcal{N}(0,{\sigma }_{i\hspace{0.17em}j}^2)$, where the variance of the error is modelled using a proportional error model: ${\sigma }_{i\hspace{0.17em}j}^2={\sigma }^{2}f{({\theta }_i,t_{i\hspace{0.17em}j})}^2$.

The model for covariate effect describes the relationship between the individual pharmacokinetic parameters and a given covariate. The effect of polymorphism in exon 26 on a component θ^(k) of the vector of parameters θ was modelled as:

$${\theta }_i^{(k)}={\theta }_0^{(k)}{(1+{\beta }_{\text{CT}}^{(k)})}^{CT}{(1+{\beta }_{\text{TT}}^{(k)})}^{TT}{e}^{{\eta }_i}$$ (3)

Thus, the expected value of ${\theta }_i^{(k)}$ is ${\theta }_0^{(k)}$ for subjects with genotype CC, ${\theta }_0^{(k)}(1+{\beta }_{\text{CT}}^{(k)})$ for subjects with genotype CT and ${\theta }_0^{(k)}(1+{\beta }_{\text{TT}}^{(k)})$ for subjects with genotype TT. This model was used for the 4 parameters with variability (k_a, k_el, V_c/F, T_lag). In the following, we will drop the superscript ^(k) for simplicity. For each parameter in the model, there are 5 possible models for the gene-parameter relationship: the full model with three classes as in equation 3 (denoted H₁ in the following), three intermediate models with two classes that we denote H_0a: {β_CT = 0}, H_0b: {β_TT = 0} and H_0c:{β_CT − β_TT = 0} and the model with no gene effect H₀: {β_CT = β_TT = 0}. In the following, we first illustrate the three covariate selection approaches using the polymorphism in exon 26, then we apply these methods considering all the available covariates.

Backward covariate selection using the Wald test

One approach to select the covariate model is to estimate the parameters of a full model and perform a significance test using the Wald statistics to select which parameters should be kept in the model [26]. The advantage of this method is that model selection is performed in one step, and that interactions between covariates are taken into account in the estimation of the parameters. Given the model described in equation 3, we test if the three parameters β_CT, β_TT and (β_CT − β_TT) are significantly different from zero by comparing the corresponding Wald statistics to the critical value of a χ² with one degree of freedom.

A screening step is often performed to eliminate candidate covariates which have a very small probability of influencing the parameters, to improve the estimation of the remaining parameters in the model. We choose an arbitrary value of 0.25 as the significance threshold, and we eliminate the covariates for which the p-values of the 3 tests corresponding to the 3 null hypotheses H_0a, H_0b and H_0c are higher than 0.25. This yields a simplified model where some parameters are modelled according to model H₁ and some parameters are the same regardless of the genotype. This step eliminates relationships that are totally irrelevant from the model and increases the precision of estimation of the other, possibly meaningful, parameters.

In the next stage, we estimate again the parameters and their standard errors using the simplified model. For each parameter modelled using H₁, the p-values of the three Wald tests are used to select the appropriate relationship, after correction for multiple tests by applying the Simes procedure [35, 3]. This method allows to control the family-wise error rate for the three simultaneous tests performed. For a given parameter, the final model for the gene-parameter relationship depends on which hypotheses are rejected. For example, if H_0a and H_0c are simultaneously rejected for a parameter, equation 3 simplifies to:

$${\theta }_i={\theta }_0{(1+{\beta }_{\text{CT}})}^{CT}{e}^{{\eta }_i}$$ (4)

This procedure leads to the final model.

Forward covariate selection using the log-likelihood ratio test

Convergence problems and non-identifiability may occurr when trying to estimate the parameters of a full model with many covariates. The alternative is to build the model using forward selection. Different forms of this approach are used in most studies using nonlinear mixed effect models [23, 17].

For forward selection, we start from a model without covariates (basic model) and compute empirical Bayes estimates (EBE) of the individual parameters. One-way analysis of variance (ANOVA) is used to test for a difference between the three genotypes for each parameter [23]. As previously, we begin by a screening step: candidate relationships are selected as those where the p-value of the ANOVA is less than 0.25. We then model the candidate relationships as in equation 3 one at a time, starting with the most significant according to the LRT. We stop when none of the remaining relationships provide a significant improvement in the model according to a LRT. We then test for all parameter-gene relationships the three submodels H_0a, H_0b and H_0c using the LRT again, correcting the p-values using the Simes procedure. The best model for the corresponding relationship is selected as in the previous strategy, based on the p-values for the three corresponding tests.

Covariate selection using the Bayesian Information Criterion

We compared the two previous selection methods with model selection using the Bayes Information criterion (BIC) given by:

$$\mathit{BIC}=-2LL+Plog(n_{\mathit{tot}})$$ (5)

where P is the number of parameters (fixed and variance) in the model and n_tot is the total number of observations.

The best model is defined as the model with the lowest BIC. For model selection using the BIC, we also consider models close to the lowest BIC. From the definition of Bayes factor as a ratio of posterior to prior odds used in Bayesian model selection, Raftery shows that the strength of evidence of one model versus the other is limited when models are within 3 points of BIC while a larger difference provides positive evidence [29, 18].

A practical problem is the number of models to test. For each parameter in the model, there are 5 possible models when considering the genotype for exon 26 alone. To test all possible combinations for the 4 parameters with variability would require generating and fitting 625 models. Although technically feasible here, this would soon become impractical with more covariates or more parameters, therefore we propose a simplified approach. In a first step, for each parameter, we keep the model with the lowest BIC, as well as models within 3 points of BIC to the lowest. The model without covariate (H₀) is also added to this list of possible models. In a second step, we build combined models where the possible models for one parameter are combined with each of the models for the other parameters. We estimate the corresponding BIC, and the best model s selected as the model having the lowest BIC overall. Again, we also examine models with BIC close to the lowest value.

Estimation method

The parameters are estimated using maximum likelihood approaches. Because the regression function is nonlinear with respect to the random effects, the likelihood function has no closed form. The most commonly used estimation methods rely on approximations of the likelihood function through first-order Taylor expansions, and have been implemented for instance in the nlme package in R/Splus [27], and in the NONMEM software [34]. To avoid this approximation, Bayesian approaches have been proposed which integrate the likelihood using Monte-Carlo Markov chains (MCMC) [36]. An alternative approach is to consider random effects as missing data and to use the EM algorithm [9]. An algorithm called SAEM has been recently developed using the EM approach: stochastic approximation combined with MCMC methods to simulate the random effect in the E-step provides a convergent algorithm and consistent estimates of the population parameters [8]. This method has better statistical properties since no linearisation is involved in the computation of the likelihood and hence the statistical tests based on the results have better properties [20]. It has also been recently applied in two applications, the study the pharmacokinetics of saquinavir in HIV patients [21] and the modelling of the viral load decrease to compare two treatments in a clinical trial [32].

The SAEM algorithm is implemented in the MATLAB language in the software MONOLIX, available on the author’s website (http://www.math.u-psud.fr/~lavielle/monolix/logiciels.html). We used version 1.1 of MONOLIX, in a Linux environment (Red Hat 9.0, GNU Fortran compiler), with MATLAB version 7. The analysis of the results was handled using the R statistical and graphical environment [28]. MONOLIX provides an estimate of the parameters (fixed effects and variance of the random effects) as well as an estimate of the estimation error via the Fisher information matrix [20].

The likelihood is computed by an importance sampling procedure [31]. Since a good estimate of the log-likelihood was required to perform likelihood ratio tests, we used the average of five successive estimations of the likelihood to obtain a more stable estimate.

Model building

The three strategies described above were applied to the digoxin data considering the exon 26 polymorphism. We then performed the same analysis for exon 21. For the G2677T/A polymorphism in exon 21, 5 different genotypes were found in the population (GG, GT, GA, TT and TA). We performed first an analysis taking them all into account, and second an analysis where we regrouped the mutant alleles, yielding 3 groups (group 1: GG, group 2: GT or GA, group 3: TT or TA). The influence of the polymorphism in exon 21 was analysed first independently from the results of the analysis including exon 26, then including the model developed for exon 26 alone. We also considered the homozygous wild-type diplotype (combined genotype) CC-GG, combining the GG genotype at position 2677 in exon 21 and the CC genotype at position 3435 in exon 26, versus all other diplotypes. The functional haplotype has previously been shown to influence the AUC of digoxin [16]. Other haplotype analyses were not performed since the number of subjects was too small. Finally, full covariate analysis was performed; the following covariates were available in the study in addition to gene effect: gender, age, weight, body mass index and smoking status. Renal function was not evaluated in these subjects.

We examined the following plots to evaluate the goodness of fit of the final model provided by each approach: scatterplots of predictions (population and individual) versus individual observations; population weighted residuals versus predictions and versus independent variable (time); absolute individual weighted residuals versus individual predictions. In addition, model validation was performed using prediction distribution errors [5], which are computed as the quantiles of the observations in the predicted distribution. The predicted distribution for each observation was obtained through 1000 simulations of the data set given the final model. The prediction distribution errors were decorrelated as proposed in [5] to take into account the correlation induced by the multiple observations within one subject. If the model is adequate, the distribution of the prediction distribution errors is expected to follow a uniform distribution over the interval [0–1], and we used a Kolmogorov-Smirnov test to test this assumption.

Results

Backward covariate selection using the Wald test

A full model including the effect of exon 26 genotype on all parameters was fit. The volume of distribution was the only parameter for which at least one of the p-value of the Wald tests for the gene effect was lower than 0.25. The results are shown in figure 1: for each parameter, we show the estimate of β_CT, β_TT and the difference β_CT − β_TT as well as the corresponding confidence interval. The horizontal line represents the expected value of 0 in the absence of effect. As seen from this figure, only β_TT and β_CT − β_TT for parameter V_c/F were found to be significantly different from zero using Wald tests.

Figure 1.

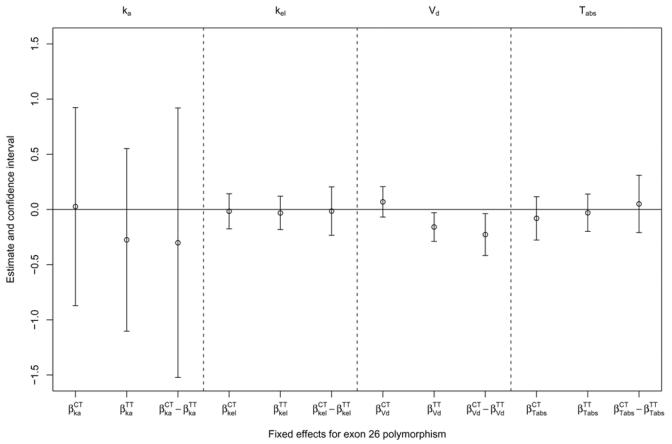
Estimates of the genetic fixed effect for the different parameters in the model.

The model was then re-run with only V_c/F, yielding the following estimates for the gene effects: β_CT = 0.065 (NS), β_TT = −0.164 (p<0.01), β_CT − β_TT = 0.229 (p<0.02). A final model was therefore run, including only a different V_c/F for TT subjects.

Forward covariate selection using the log-likelihood ratio test

Figure 2 displays the empirical Bayes estimates of the four parameters with intraindividual variability (k_a, k_el, V_c/F, and T_lag), separated according to the genotype for exon 26. As with the Wald test, only V_c/F was found to have a significant relationship with the MDR-1 polymorphism on exon 26 (p<0.017 according to the ANOVA), the three other tests yielding p-values larger than 0.4. Including the full gene effect in the model for V_c/F led to an improvement in the model (p=0.007 according to a LRT, df=2).

Figure 2.

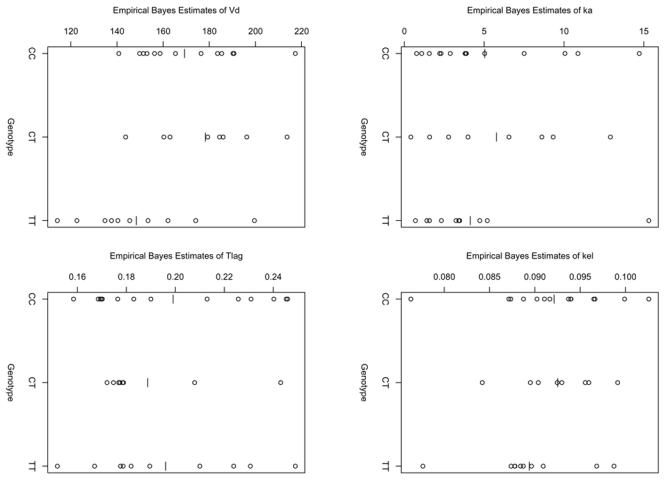
Empirical Bayes estimates of k_a, k_el, V_c/F and T_lag with the model without covariate.

In the next and final stage, we then tested the three submodels versus H₁ using LRT yielding the following p-values: p=0.003 for H_0a ={β_CT = 0}, p=0.29 for H_0b ={β_TT = 0}, and p=0.049 for H_0c =(β_CT − β_TT = 0}. Using the Simes procedure, the final model selected was the model where TT subjects have different V_c/F from the two other groups. For the effect of exon 26 polymorphism, the model selected by this strategy was therefore the same as for the selection based on Wald tests.

Covariate selection using the Bayesian Information Criterion

The selection for each parameter separately yielded the following results: for V_c/F, the best model was a model with different population mean for TT subjects; for the other parameters, the best model was a model without covariates and there was no model within 3 points of BIC of the lowest model. The results are illustrated in figure 3, which shows the BIC of the five models tested for each parameter. For each parameter, the model with the lowest BIC is shown as a full circle.

Figure 3.

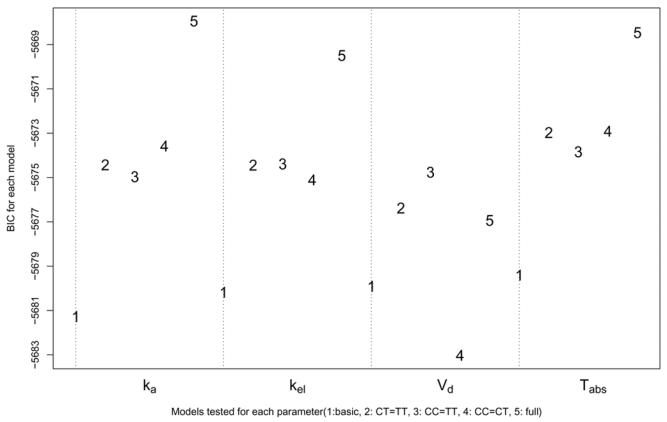
BIC for the five models tested for each parameter: basic model (no gene effect), submodels with β_CT = β_TT, β_CC = β_TT or β_CC = β_CT, full model with β_CC and β_TT

The models were then combined, and again, the best model overall was here the model with different population mean for V_c/F in TT subjects.

Final model

For the analysis of exon 26 alone, the three methods led to the same final model, a model where the carriers of the TT genotype have a different population mean for V_c/F.

The same analyses were done considering the genotype for exon 21. We found no significant parameter-genotype relationship when considering the five genotype group for exon 21 but some genotypes were present in few subjects, suggesting a lack of power. When regrouping the subjects in three groups according to the number of mutant alleles, the estimate of the volume of distribution was slightly lower in group 3 (TT or TA) versus the other groups (p<0.04). However, when the model for exon 26 was taken into account, this relationship disappeared, showing that the difference is accounted for by exon 26 because of the strong linkage between the two exons (Somers D’=0.72). The three approaches presented above therefore gave the same results for the selection of genetic covariates in the model.

In addition, 11 subjects carried the CC-GG diplotype, and a slight difference was found between the estimates of the volume of distribution for these patients when using a Wald test (p=0.045). However, the two other methods (BIC and EBE) did not pick this difference up.

In the final step, we then added the other covariates to the model. Because of the strong linkage disequilibrium between the two exons, the full covariate model included only exon 26. Using the Wald test approach, the final model included different population mean for V_c/F in TT subjects, as previously, as well as smaller absorption time-lag in women. Using the LRT approach, a small increase in T_lag (2.5%) was also found for smoking patients, but the size of the effect was not clinically significant and thus the final model was the same as with the Wald approach. The BIC approach was not implemented for the full covariate selection because of time constraints.

The parameter estimates and estimates of the standard errors are given in table I. The parameters were all well estimated, with standard errors lower than 20% except for the two covariate effects, for which it was less than 40%. The residual (intraindividual) error was also small (17%). In this model, subjects with the TT genotype have a volume of distribution lower by 17% relative to carriers of at least a C allele, and women have a 54% shorter absorption time relative to men. The within-subject variability was largest for the absorption rate constant k_a.

Table I.

Estimates of the population pharmacokinetic parameters for the final model.

Parameter	Population mean (SE as %)	Variability as % (SE on ω2 as %)
ka (hr−1)	3.15 (20)	85 (32)
kel (L.hr−1)	0.09 (6)	17 (63)
Vc/F (L)	172.70 (5)	15 (30)
βV,TT(−)	−0.17 (31)	-
Tlag (hr)	0.21 (8)	28 (42)
βTlag,women (−)	−0.43 (27)	-
k1,2 (hr−1)	0.32 (7)	-
K2,1 (hr−1)	0.10 (7)	-
σ(%)	0.18 (4)	-

^†p=0.001 according to Wald test

^††p=0.0002 according to Wald test

A plot of the concentrations of digoxin as a function of time for the three genotypes for exon 26 is shown in figure 4. Overlayed is the corresponding population predictions for the group. Diagnostic graphs for this model are shown in figure 5. The two upper graphs show respectively the population (left) and individual (right) predictions versus observed concentrations. The two bottom graphs show the individual predictions for the first two subjects in the dataset. The graphs show a satisfactory fit, and the absorption phase is well described. A slight underestimation can be seen around 24 hours, as the model does not capture a small rebound at that time. We tested two alternative models, one with a double absorption phase and one assuming enterohepatic recycling, but both encountered numerical difficulties and unphysiological estimates, and the bias in the model was not improved. Therefore, the two-compartment model was kept. We performed model validation for the final model; using prediction discrepancies, we did not reject the hypothesis that the data observed could have been obtained under the model (NS, p=0.49) and considered the model to be adequately qualified.

Figure 4.

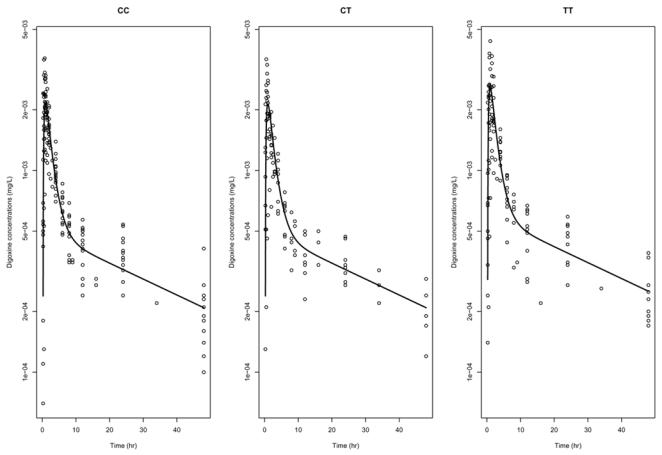
Concentration versus time data for digoxin, for the three genotype classes for exon 26 polymorphism (in log-scale). Overlayed is the line corresponding to the predictions using the population parameters in each group, for men.

Figure 5.

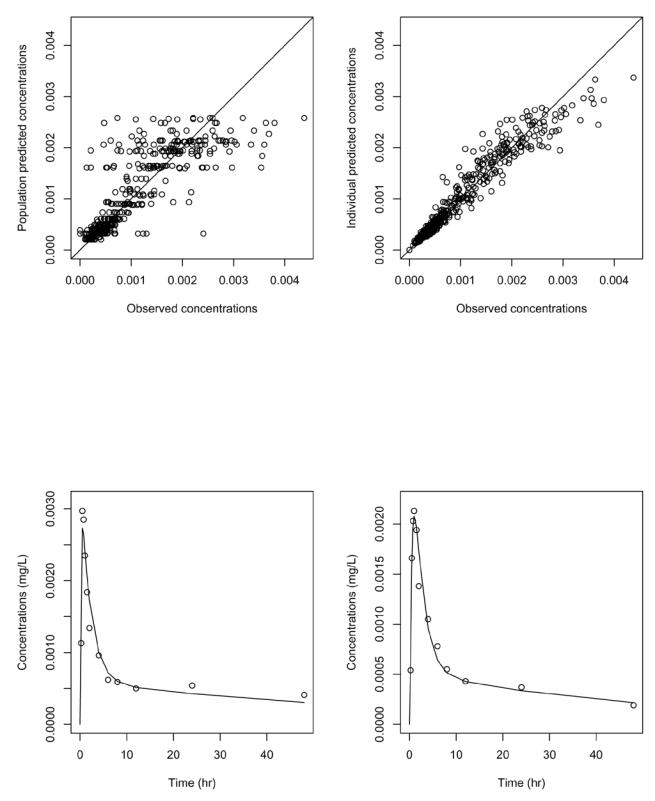
Goodness of fit plots for the final model. Top: population predicted concentrations versus observed concentrations (left); individual predicted concentrations versus observed concentrations (right). Bottom: predicted concentrations (line) overlayed on observed concentrations (dots) for the first man (left) and the first woman (right) in the dataset.

Discussion

With the recent availability of cheaper genotyping methods, it is now possible to collect genetic information related to drug transporters, metabolic complexes or receptor structure on a routine basis in clinical trials or before a patient is given a new treatment. In pharmacokinetics (PK) and pharmacodynamics (PD), the time course of drug concentrations or effects is described using models with a small number of parameters, and pharmacogenetic data is being increasingly used to characterise their variability. There are now reports of pharmacogenetics studies for a large variety of drug classes, confirming the widespread interest and potential applications of pharmacogenetics.

The statistical analysis in these studies however is usually limited to using non-compartmental approaches to study the influence of genotype on AUC, apparent clearance or maximum or trough concentration. Only a few papers report the use of more sophisticated methods such as mixed effect models or Bayesian analysis, despite the fact that these approaches can be more informative. They can take advantage of sparse designs, which could be useful to design studies for screening genetic factors or during therapeutic monitoring. Here we present the first pharmacokinetic population model for digoxin including pharmacogenetics.

In this study, we used three different methods to explore the relationships between the pharmacokinetic parameters and the genetic covariates: forward step wise selection, Wald test-based selection, and criteria-based selection. Although in the present application, they led to the same final model, the three methods all have different characteristics and strengths.

The tests for the three approaches are asymptotic, that is, they assume that the number of subjects as well as the number of points per subject is large enough. All three methods require good estimates of the likelihood, and the Wald test requires in addition good estimates of the standard errors. The only approximation in the computation of the estimated standard errors of estimation involved in SAEM lies in the asymptotic approximation applied to the finite dataset [20], so that we expect better statistical properties of the tests based on estimates obtained by SAEM relative to more traditional methods based on first-order linearisation such as are implemented in NONMEM [34] or in the library nlme for R [28]. Indeed, the standard errors of estimation of the parameters estimated using the SAEM software have been shown to be accurately predicted [33].

Genetic covariates (genotypes or haplotypes) are usually modelled as categorical covariates, except for some genes such as CYP2D6 where a numeric variable representing the number of mutant alleles has been used as the genetic covariate [19]. Categorical covariates bring specific challenges. We need to estimate one parameter for each possible genotype and the number of possible covariate models increases exponentially with the number of genotypes. Also, the dataset is often unbalanced, with sometimes a very small number of patients for the rarer genotypes, which can generate problems for parameter estimation.

Given these specific challenges, being able to select the covariate model in one step with the Wald test is appealing, and has been proposed by Panhard [26]. All the potential relationships are included in the model and a simultaneous estimation of the significance of all the parameters is provided. This approach could be most interesting in sparse data settings where the empirical Bayes estimates (EBE) do not contain as much information as they do in our example where the pharmacokinetic sampling was rich. The three methods described above can be applied regardless of the estimation method, and have been used for instance in NONMEM [17] and nlme [26]. Using the new algorithm SAEM, we can obtain good estimates of the parameters and their estimation error, allowing us to select the covariate model by backwards deletion from a full model. Compared to the two other methods, the Wald test requires an additional assumption, in that the confidence interval for the estimated parameters is assumed to be symmetrical, which makes it less robust than the LRT.

The likelihood ratio test, by contrast, does not require any additional hypothesis beyond that of the asymptotic. Stepwise inclusion is therefore the main method used for covariate model selection in PK/PD models. However, it suffers from a number of known problems: inflation of type I error due to multiple testing during the building process, selection bias, collinear variables and no guarantee that the final model selected using these methods is the correct model [41]. Inflation of the type I error is also inherent to the first-order linearisation of the log-likelihood used by NONMEM [7], while the stochastic approximation of the log-likelihood performed by SAEM retains a type I error closer to the nominal value, as shown in simulation studies [14]. Variants of stepwise methods include building generalised additive models using the empirical Bayes estimates of a model without covariate [24], however they do not address the issues mentionned above. An interesting combination of the LRT approach and the Wald approach could be outlined as follows: first, build a full model with all potential covariates included, and keep as candidate covariates those for which the Wald test is significant; finally, build the covariate model using LRT-based forward or backward selection from these candidate covariates. This would reduce the number of models to test in the selection while allowing for combination of covariates to enter the model.

Finally, the advantage of criterion-based strategies lies in their systematic exploration of all possible models. The use of model selection criteria such as AIC or BIC is more frequent in the Bayesian litterature [29] and has solid theoretical background in information theory. In practice however, AIC often proves anti-conservative and has been shown to be non-consistent [42], and here we use the BIC. Criterion-based strategies have two main drawbacks. The first drawback is that the number of possible models increases exponentially with the number of covariates, although we can simplify the number of possible models by considering prior physiological knowledge to eliminate unlikely parameter-genotype relationships. The second drawback is that there is no formal test of the relative performance of two models. Kass and Raftery propose to use the difference in BIC as a measure of the strength of evidence of one model versus another [18], but one can be left with several competing models of similar strength using that approach.

In summary, despite known problems we recall here, stepwise selection strategies are less computationally cumbersome than criteria-based selection, while more robust to poor estimations of the standard errors than selection based on the Wald test. However, it can be useful to explore candidate relationships using this last method, especially in the presence of a large number of covariates, because as shown here it can provide reliable estimates in one step and because effects due to a combination of several covariates may be missed by stepwise approaches.

The strategies outlined in this work can be used for all types of covariates (demographic data, clinical characteristics, biological measurements…), as well as for building the structural model.

Our main finding, the difference in volume of distribution found for TT subjects, explains the higher AUC observed for these subjects in the previous non-compartmental analysis performed using this data [38]. It can be interpreted as a higher bioavailability in TT subjects relative to CC or CT subjects. This result should be confirmed in patients receiving digoxin, and probably does not warrant dose adjustment for digoxin, especially considering the high variability in absorption. A possible exception would be to adjust dosage in certain populations such as elderly patients or patients receiving other comedications. The proportion of digoxin-treated patients experiencing therapeutic drug monitoring has been shown to increase with the number of PgP inhibitors received [11], which could make it useful to determine the genotype governing PgP activity [12].

In conclusion, we modelled the pharmacokinetics of digoxin including pharmacogenetic data, using nonlinear mixed effect models. Our main finding was that carriers of the TT genotype for the C3435T polymorphism in exon 26 of the MDR-1 gene have lower apparent volume of distribution. Several methods can be used to test for genetic effects. In addition to the usual stepwise selection method, we recommend using the Wald test to screen candidate covariates.

Appendix

The SAEM algorithm is implemented the MATLAB language in the software MONOLIX, available on the author’s website (http://www.math.u-psud.fr/~lavielle/monolix/logiciels.html). We used MONOLIX version 1.1.

The dataset was prepared in R as a two-dimensional array, with columns representing subject ID, time and observed concentrations. A column representing the dose was also added (with the same value at all times and for all subjects). To code for the categorical covariates representing the genotypes of MDR1, we used dummy variables. For example, to code for the exon 26 polymorphism, we defined 3 dummy variables, one with value 1 for the subjects with CC genotype and 0 for the other two genotypes, one with value 1 for the subjects with CT genotype and 0 otherwise, and one with value 1 for the subjects with TT genotype and 0 otherwise. Each dummy variable was entered as an additional column in the dataset. Exemples of datasets used with MONOLIX are included in the Zip file containing the program.

The following code was used to define the pharmacokinetic model (lines beginning with the symbol % are comments), using the explicit analytical equation:

	function [f,g]=dig_funct(phi,x,id);
	%%%%%%%%%%%%%%%%%%%%%%%
	d=x(:,1,:);
	t=x(:,2,:);
	%%%%%%%%%%%%%%%%%%%%%%%
	ka=exp(phi(id,1,:));
	ke=exp(phi(id,2,:));
	V=exp(phi(id,3,:));
	Tlag=exp(phi(id,4,:));
	k12=exp(phi(id,5,:));
	k21=exp(phi(id,6,:));
	%%%%%%%%%%%%%%%%%%%%%%%
	bet=(ke+k12+k21-sqrt((k12+k21+ke).^2-4*k21.*ke))./2;
	alp=(k21.*ke)./bet;
	f=d.*ka./V.*(((k21-ka)./((alp-ka).*(bet-ka))).*exp(-ka.*(t-Tlag))+...
	((k21-alp)./((ka-alp).*(bet-alp))).*exp(-alp.*(t-Tlag))+...
	((k21-bet)./((ka-bet).*(alp-bet))).*exp(-bet.*(t-Tlag)));
	g=f;

The program MONOLIX is run from within MATLAB. A window opens in which the user specifies the dataset, the model function and the number of covariates to include in the analysis. In our analysis, the variance-covariance matrix was set to diagonal and the variance for parameters k_1,2 and k_2,1 was set to 0. The covariate model was also specified via the graphical interface as a linear combination of the dummy covariates defined above.

Version 1.1 of the software requires some tuning of the numerical procedure to ensure convergence of the Markov chain during the stochastic approximation step (see the user manual on the website). We used the following sequence of four stepsizes in the algorithm:

$$\{\begin{array}{ll}{a}_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=0\hfill & \text{during\hspace{0.17em}}{K}_1=500\hspace{0.17em}\text{iterations}\hfill \\ a_2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=0.5\hfill & \text{during\hspace{0.17em}}{K}_2=100\hspace{0.17em}\text{iterations}\hfill \\ a_3\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=0.8\hfill & \text{during\hspace{0.17em}}{K}_3=100\hspace{0.17em}\text{iterations}\hfill \\ a_4\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=1\hfill & \text{during\hspace{0.17em}}{K}_4=2000\hspace{0.17em}\text{iterations}\hfill \end{array}$$ (6)

The output from MONOLIX consists in a series of graphs as well as a table of parameter estimates with their associated standard errors. Hypothesis testing opens a new window in which the two models compared are specified and the corresponding criteria (AIC, BIC, log-likelihood) are shown after the fit of each model is performed. Empirical Bayes Estimates (EBE) of the individual parameters are obtained as the mean of the posterior distribution and the standard errors on these parameters (the standard deviations of the posterior distribution) are also reported.