Abstract
This paper provides transcendental and algebraic framework for the classification of identities expressing π and other logarithms of algebraic numbers as rapidly convergent generalized hypergeometric series in rational parameters. Algebraic and arithmetic relations between values of p+1Fp hypergeometric functions and their values are analyzed. The existing identities are explained, and new exhaustive classes of new ones are presented.
1. Introduction
This paper is devoted to the exposition of the algebraic relations between generalized hypergeometric functions and algebraic functions and their logarithms. We strive to explain some of the newly found identities expressing π (and not 1/π as in ref. 1) as rapidly convergent generalized hypergeometric series in rational parameters, discovered by W. Gosper and others (2). In our explanation, identities expressing logarithms of algebraic numbers (with the most notable examples of π, ln 2, ln 3) in terms of generalized hypergeometric functions can be classified by using transcendental and algebraic means. On a simpler, transcendental level, the classification involves an easy problem of determination of all cases, when solutions of generalized hypergeometric equations are expressible in term of logarithms of algebraic functions only. This immediately leads to a finite set of irreducible cases described by extensions of finite reflection groups, and one to a multiparameter case. On a relatively complicated algebraic level, the classification provides the explicit algebraic equations on algebraic functions, whose logarithms are involved in the identities. Additionally, the algebraic formalism provides with arithmetic conditions that explicitly describe all allowed identities for logarithms of specific numbers. These last arithmetic conditions take the form of multiplicative relations among roots of algebraic equations; in the most interesting multiparameter case these algebraic equations are trinomials of arbitrary degrees.
We describe all of the formalisms above, including explicit algorithms of the classification problem and closed form expressions for low degree cases. We also list some of the most interesting identities for simpler logarithms (π, ln 2, ln 3) in terms of generalized hypergeometric series with coefficients that are ratios of binomial coefficients. Among other things we show that though there is a finite classification of “irreducible” identities, each identity generates an infinite family of “reducible” series identities, whose convergence increases at the expense of the increased order of hypergeometric functions.
This paper deals primarily with extensions of Schwarz’s list for 2F1 series and nFn−1 series that have coefficients as products of simple binomial functions of indices and are defined over integers. We postpone for another paper the explicit description of the remaining 20-plus cases of individual finite reflection groups that describe specific hypergeometric functions and involve algebraic numbers of higher degrees.
There are other classical and Gosper’s identities that involve generalized hypergeometric functions depending on a free parameter expressing ratios of Γ functions of this parameter. Many of these identities also can be covered by formalisms presented in this paper, including the analysis of extensions of reducible generalized hypergeometric equations, and hypergeometric series with coefficients that are products of special Γ functions of indices.
At the end of the paper we list some of the more interesting (series of) identities for lower order hypergeometric functions, and we present an application that provides a measure of irrationality. More diophantine applications can be derived from the “master formula” (Eq. 11).
2. Hypergeometric Equations
We refer to ref. 3 for basic definitions of classical (univariate) generalized hypergeometric functions pFq of parameters ai, bj : i = 1 … p; j = 1 … q and a variable z:
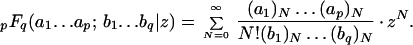 |
Here (a)N is the Pochhammer symbol: (a)0 = 1, (a)N = a ⋯ (a + N − 1). In addition to their importance as special functions, these generalized hypergeometric functions and their immediate multivariate generalizations are suspected to be able to describe all linear differential equations with “arithmetic” properties—having solutions that are G–functions in Siegel’s sense (that is, having series expansions with algebraic coefficients with slowly growing denominators) see ref. 4. Generalized hypergeometric equations are among few classes of linear differential equations that do not depend on accessory parameters, and the monodromy (Galois) group can be determined explicitly in terms of parameters ai, bj.
New identities for values of logarithms of algebraic numbers, including π, in term of generalized hypergeometric functions, can be classified, provided they are imbedded into a one-parameter family of functional identities, involving a logarithm and generalized hypergeometric functions. For such a functional identity to occur, the differential operator, annulling corresponding hypergeometric functions have to be reducible over a ring of differential operators with algebraic function coefficients. This condition of reducibility, expressed through the properties of the monodromy group of the generalized hypergeometric equations, allows one to classify all possible cases of functional identities expressing logarithms of algebraic functions through generalized hypergeometric functions. The most famous class is related to Schwarz’s list of algebraic functions among Gauss’ 2F1 hypergeometric functions.
In this paper we concentrate only on a subclass of hypergeometric identities that can be written by using binomial coefficients (that is, B factors, rather than more general Γ factors). These identities involve only hypergeometric sums of the form
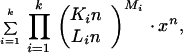 |
where Ki, Li and Mi are integers (and Ki, Li are positive). For generalized hypergeometric functions with parameters ai, bj this means that all ai, bj are rational and if one has ai0 ≡  (mod 1) for (p, q) = 1 then among ai there are all
(mod 1) for (p, q) = 1 then among ai there are all  (mod 1) for all r, (r, q) = 1. These conditions severely restrict algebraic cases under consideration. Two of the most interesting classes of examples in this series correspond to the dihedral Dn and symmetric Sn groups. From the point of view of diophantine approximations one would like to keep the order of the hypergeometric functions low and their rate of convergence high (i.e., Mi should be negative).
(mod 1) for all r, (r, q) = 1. These conditions severely restrict algebraic cases under consideration. Two of the most interesting classes of examples in this series correspond to the dihedral Dn and symmetric Sn groups. From the point of view of diophantine approximations one would like to keep the order of the hypergeometric functions low and their rate of convergence high (i.e., Mi should be negative).
We start with reducible equations arising from 2F1 functions. The first nontrivial case corresponds to a series
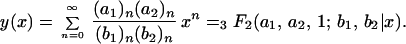 |
1 |
These functions, though 3F2, satisfy inhomogeneous second-order differential equations, and can be integrated in terms of the fundamental solution of the Gauss hypergeometric functions with parameters a = a1 − b2 + 1, b = 1 + a2 − b2, c = 1 + b1 − b2.
For the dihedral group case this means that we are dealing with representations of algebraic functions (1 +  )1/n or (1 +
)1/n or (1 + 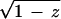 )1/n. Keeping in mind the requirement of binomial coefficient representation, we end up only with three possible cases of functions (Eq. 1):
)1/n. Keeping in mind the requirement of binomial coefficient representation, we end up only with three possible cases of functions (Eq. 1):
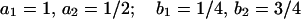 |
2 |
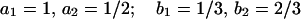 |
3 |
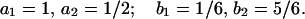 |
4 |
In these cases explicit integration of the corresponding dihedral equations gives a closed form expression between two logarithms of algebraic functions and y(x). Differentiating these expressions one gets a set of two equations for y(x) and y′(x) involving these two logarithms. This allows us to express each logarithm as a linear combination of y(x) and y′(x). This provides two families of identities (typically for logarithms and arctan) as sums of rapidly convergent binomial series. The cases Eqs. 3 and 4 are new. The case Eq. 2 had been originally derived by Gosper (2) in 1990 in a very interesting form. According to our classification below, this is a “reducible” case, and with some tedious algebra one can recover its expression from classically known series for arcsin(x/2), arcsinh(x/2).
Let us start with the case Eq. 3. The relevant parametrization of x in terms of a new variable T is the following: x = (4T3)/(T3 + 1)2. Then y(x) is a linear combination over Q of two functions of T f1(T) = (T ⋅ (T + 1)/(T3 + 1)) ⋅ ln((T2 − T + 1)/(T + 1)2), f2(T) = 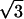 (T ⋅ (T − 1)/(T3 + 1)) ⋅ arctan((2T − 1)/(
(T ⋅ (T − 1)/(T3 + 1)) ⋅ arctan((2T − 1)/(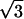 )).
)).
This allows us to represent fi(T) : i = 1, 2 as a linear combination of y(x), y′(x) over Q(x). Choosing rational values of x that correspond to important logarithms like π or ln 2 one gets interesting families of identities (see below). Two identities corresponding to y(x) and y′(x) at x = 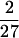 are the most important, because they allow us to prove measures of diophantine approximations to π. The fastest convergent identity we present in this series corresponds to x = −
are the most important, because they allow us to prove measures of diophantine approximations to π. The fastest convergent identity we present in this series corresponds to x = −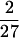 .
.
In the case Eq. 4 we are looking at Schwarz’ list entry (1/2, 1/2, 2/3). The uniformization variable T allows us to express the corresponding y(x) as a linear combination of two logarithmic functions f1(T), f2(T) over Q(x): x = (4 ⋅ T3)/(T3 + 1)2, f1(T) = (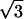 ⋅ (T2 + 1)
⋅ (T2 + 1)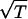 /(T3 + 1)) ln((T −
/(T3 + 1)) ln((T − 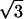
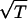 + 1)/(T +
+ 1)/(T + 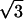
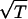 + 1)), f2(T) = ((T2 − 1)
+ 1)), f2(T) = ((T2 − 1)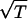 /(T3 + 1)) ⋅ arctan((T2 − 4T + 1)/(3
/(T3 + 1)) ⋅ arctan((T2 − 4T + 1)/(3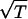 (T − 1)).
(T − 1)).
This allows us to represent fi(T) : i = 1, 2 as a linear combination of y(x), y′(x) over Q(x). Two of the most interesting values are x = 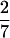 and a very spectacular x =
and a very spectacular x = 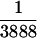 (giving the fastest convergent hypergeometric series for ln 2). These identities are presented at the end of the paper.
(giving the fastest convergent hypergeometric series for ln 2). These identities are presented at the end of the paper.
All other Schwartz cases of the dihedral group give rise to the function y(x) in Eq. 1 whose coefficients cannot be represented as products of binomials.
For generalized hypergeometric equations of an arbitrary order, there is only one infinite sequence of equations having algebraic solutions only (with the monodromy group as a symmetric group Sn). Up to the obvious transformations, this sequence of functions is described completely by algebraic function solutions to trinomial algebraic equations, as covered below in the master formula. In addition there is a finite set of exceptional equations with finite reflection Galois groups, see ref. 5. If, as before, we restrict ourselves only to hypergeometric series whose coefficients are products of factors of binomial coefficients, than, in addition to the cases mentioned above, there are 26 additional nFn−1 hypergeometric functions that have to be considered for n in 4 … 8, requiring cyclotomic extensions of Q. We return to explicit expressions for these exceptional cases in another publication.
Note that in the cases above, as everywhere else in this paper, one can exchange parameters ai and bj (this corresponds to expansion near ∞ rather than near 0). Very often this “exchanged series” is not desirable because the rate of convergence of corresponding “exchanged” series drops dramatically. For example, series corresponding to logarithms of solutions yk of the trinomial equation yn − Tys − 1 = 0 that follow from the master formula are contiguous to the series ΣN=1∞ ((−1)n−sTn)N/(NsNn)—corresponding to (relatively) small T, whereas “exchanged” series relate logarithms of yk in terms of ΣN=1∞ (NsNn)/N ⋅ ((−1)n−sTn)N—corresponding to (relatively) large T (and are known historically, see ref. 6 and below).
3. Lagrange Inversion Formula and Logarithms of General Algebraic Functions
The original and still most efficient method to derive expansions of algebraic functions in terms of coefficients of equations they satisfy is the use of Lagrange’s inversion formula. We use this formula to derive the explicit series representation for sums of logarithms (squares of logarithms) of all branches of an algebraic function defined by a sparse polynomial. In the case of a trinomial equation we get the master formula.
We use Lagrange’s formula in Birkeland representation (7). In the most general case, we are looking at the root y of the equation
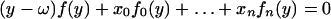 |
5 |
where f(y), f0(y), … , fn(y) are series convergent in the neighborhood of ω, and f(ω) ≠ 0, fi(ω) ≠ 0, i = 0 … n. The expansion of y near xi = 0 : i = 0 … n has the following form
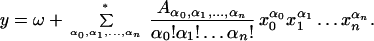 |
6 |
In Eq. 6 the range of summation is over all non-negative αi : i = 0 … n, excluding a point αi = 0 : i = 0 … n. We use below the following abbreviations:
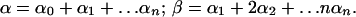 |
Lagrange’s formula give the expression for the coefficients Aα0,α1, … ,αn in either of the following two forms:
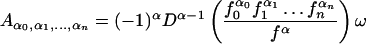 |
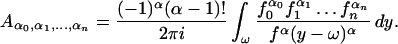 |
In applications that we need, we actually sum over all roots ω of the corresponding initial (unperturbed) algebraic equation.
The most interesting applications arise from considering powers yγ of solutions of the sparse algebraic equation
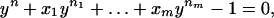 |
7 |
considered as the perturbation of the cyclotomic equation yn − 1 = 0 at xi = 0 : i = 1 … m. Then from the Lagrange’s formula above we get
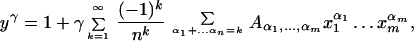 |
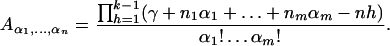 |
Because a general solution of Eq. 7 is given by ɛy(ɛn1x1, … , ɛnmxm) for ɛn = 1, starting from a given solution y(x1, … , xm), we can sum ykγ over all solutions yk : k = 1, … , m of Eq. 7. This expression is a very useful one (see below for the trinomial m = 1 case), but we are interested primarily in its specialization as γ → 0. In this case we get the following multivariant generalization of the master formula:
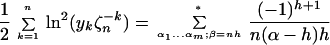 |
8 |
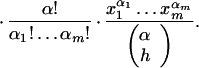 |
Here, as above, the summation excludes αi = 0 : i = 1 … m, and α = α1 + ⋯ + αm, β = n1α1 + ⋯ + nmαm.
In the case of our primary interest, the trinomial equation
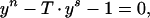 |
9 |
the expression for the sum of yγ specializes to a relatively simple formula. We will assume the “irreducible” case of (n, s) = 1, and denote by yk : k = 1, … , n roots of Eq. 9 ordered in the way that yk → ζnk as T → 0 for ζnk = e2πik/n. Then we have the first simple formula:
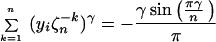 |
10 |
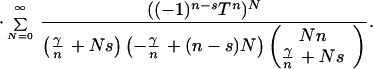 |
Finally, specialization at γ → 0 give the master formula that we use below:
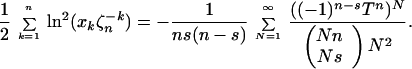 |
11 |
4. Trinomial Equations and Logarithms of Their Roots
The most general case of the Galois group of the generalized hypergeometric equation with algebraic solutions only is that of a symmetric group. We find the explicit realization of the action of this group, and its extension, that provides generalized hypergeometric equation whose solution space is spanned by logarithms of algebraic functions. An explicit realization of these generalized hypergeometric equations is given by Cayley’s or resolvent linear differential equation satisfied by all branches of the solution of the trinomial algebraic equation. We had studied this subject in detail in ref. 8 in connection with analytic and numerical solution of sparse polynomial equations. Historical notes on hypergeometric expansions of solutions of trinomial equations (including the famous Lambert–Lagrange–Ramanujan expansions), together with the remark that the Galois group of the trinomial is symmetric can be found in ref. 8. A detailed derivation of different generalized hypergeometric expansions of solutions of trinomial algebraic equations is best dealt with by Birkeland in his papers (7, 9). In these papers (especially the latter), Birkeland looks also at the expansion of logarithms of solutions of trinomials, but at a rather dull domain T → ∞. By the way, similar expansion of the logarithm can be found in Whittaker–Watson (6) where it is attributed to McClintock. Much more interesting range of expansion is T → 0, that leads to rather surprising identities starting from Eq. 11.
4.1. Consequences of the Master Formula.
From the master formula (Eq. 11), expressing sums of the ln2 of all branches of trinomial algebraic functions, we can derive explicit expressions of individual ln of branches in terms of full system of contiguous generalized hypergeometric functions. This way we explicitly exhibit the reducibility of the corresponding generalized hypergeometric equations. This explicit representation is the key for the most generalized hypergeometric series representations of logarithms of algebraic numbers.
The primary hypergeometric function is
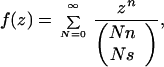 |
and the (example of the) full system of contiguous hypergeometric functions is
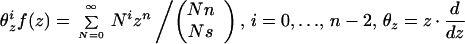 |
Let us denote
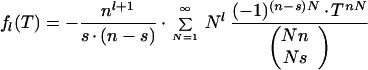 |
12 |
for l = −2, −1, … , . We can rewrite Eq. 11 in these notations
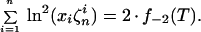 |
13 |
Here, as above, xi are all roots of the trinomial equation
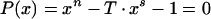 |
14 |
(as functions of T), with the normalization of xi|T=0 = ζn−i = e−2πi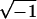 /n, i = 1, … , n.
/n, i = 1, … , n.
We are differentiating the main formula (Eq. 13) using the derivative θT = T ⋅ d/dT. To establish the main rules of the chain differentiation in the algebraic function field K = C(T, xi(T)) (or even Q(T, xi(T))), we notice that for r = r(x, T), we have
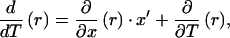 |
15 |
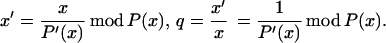 |
16 |
The first application of T ⋅ d/dT to Eq. 13 gives
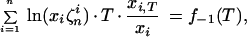 |
17 |
and the second application of T ⋅ d/dT gives
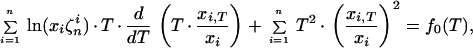 |
18 |
etc. The general form of these equations is the following
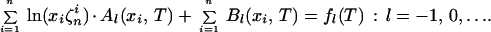 |
19 |
The recursion formulas connecting Al, Bl following from the differentiation rules (Eqs. 15 and 16):
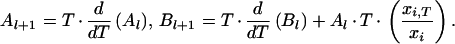 |
20 |
4.2. Explicit Representation of Logarithms.
We can built linear combinations of successive differentiations of the master formula to express ln(xiζni) as linear combinations of n − 1 generalized hypergeometric functions contiguous with the “primary” function F0(z) = ΣN=1∞ zN/(NsNn). See ref. 10 for the proper definition of a full system of contiguous functions—basically a maximal system of functions having the same monodromy group. The canonical family of contiguous functions we consider here is defined simply by Fi(z) = ΣN=1∞ NizN/(NsNn) for i = −1, 0, 1, … . It is easy to see that the functions Fi(z) : i = −1, … , n − 2 are linearly dependent over Q(z), thus to have simpler identities (with a polynomial of N in the numerator at the expense of the increase in the sizes of coefficients), we choose as the canonical complete system of contiguous functions the following one:
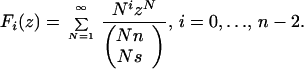 |
As before, we consider an irreducible case of (n, s) = 1. The algebra is made easy by considering the algebraic extension Q(T, x) of Q(T) for the equation P(x) = for P(x) = xn − T ⋅ x − 1. The differentiation rules for elements of this extensions are very simple: first define x′ = dx/dT = x/P′(x) mod P(x), and then apply the chain rule: dr/dT = (∂r/∂x) ⋅ x′ + (∂r/∂T). To solve the system of equations on ln(xiζni), we need a simple symbolic expression for the solution of the system of Vandermonde equations. One obtains it readily with the help of the Lagrange interpolation polynomial L(y, x), defined as
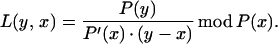 |
Writing L(y, x) as L(y, x) = Σj=1n Lj(x)yj−1, we form matrices from the coefficients of Al(x), Bl(x) and L(y, x) as follows: L = (Ljk)j,k=1n; Ljk = Lj(xk); A = (Ajk) : j = 1 … n, k = 0, 2, … n − 1; for Al(x) = Σj=1n Ajlxj−1, and B = (Bjk) : j = 1 … n, k = 0, 2, … n − 1; for Bl(x) = Σj=1n Bjlxj−1. Because (n, s) = 1, the matrix A from Mn(Q(T)) is nonsingular, and we can define the matrix C as C = A−1 ⋅ L, to obtain the expression
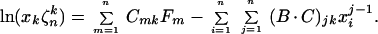 |
Taking into account the properties of the Lagrange interpolation polynomials and the simple formulas for the power-sum symmetric functions of xi, we have the final expressions in the form:
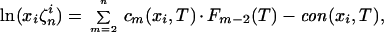 |
with cm(x, T) = Σl=1n (A−1)mlLl(x), and con(x, T) = Σl=1n Ql(T) ⋅ Ll(x), and Ql(T) = (B ⋅ A−1)1ln + (B ⋅ A−1)(n−s+1)l(n − s)T.
It is easy to see that the coefficients cm(x, T) and con(x, T) are rational functions from the algebraic extension Q(x, T)/Q(T) resulting from P(x) = 0 algebraic equations. Simple scaling arguments immediately imply that cm, con depend on T, xi in a simpler fashion. Because n and s are relatively prime (and without the loss of generality, by the symmetry x → 1/x, one can assume that 2s < n), we have two positive integers a, b such that bn − a(n − s) = 1. Then cm(x, T), con(x, T) are actually polynomials in t = x ⋅ Ta of degrees at most n − 1, with coefficients from Q(Tn). This shows that the new identities represent ln (xiζni) as power series in Tn with coefficients depending algebraically on ti = xi ⋅ Ta. The general expression for each individual ln (xiζni) thus has the form:
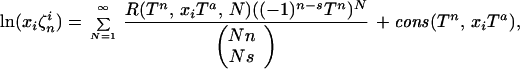 |
for R(Tn, xiTa, N)—polynomial with rational coefficients of degree at most n − 2 in N and at most n − 1 in xiTa, and rational in Tn.
4.3. Multiplicative Relations.
Because all linear relations with algebraic coefficients among logarithms are reducible to linear relations with rational (integer) coefficients, it means that different classes of expressions of logarithms of individual algebraic numbers (such as π or ln 2), based on the master formula, are derived from multiplicative relations between the roots of the trinomial equations. Similarly, expressions of logarithms of roots of arbitrary polynomial equations in terms of multivariable generalized hypergeometric functions, bring the important question of the nontrivial multiplicative relations between the roots of the algebraic equations. Galois group gives a good vehicle to establish (non-)existence of such relations. If, say, we restrict ourselves to the representation of logarithms of numbers from a multiplicative group M(S) of rational numbers, generated by primes from the set S, then we are trying to determine the rank of the Abelian group MR(xi) of all multiplicative relations:
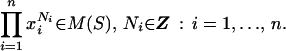 |
[The vectors (Ni) in these relations form a group because a product of two such multiplicative relations is yet another relation.] We leave the subject of explicit determination of the rank of MR(xi) for another publication, and concentrate only on simplest case of S ⊂ {1, 2, 3} corresponding to three logarithms: π, ln 2, ln 3. To make the setting over Z(Q), we have assume that Tn is a rational number, and within the radius of convergence of the hypergeometric function - |Tn| < nn/ss(n − s)n−s. In general, we have to distinguish between the cases S = {1, p} and |S| > 2, because when S contains two primes (>1), there are infinitely many examples of trinomial equations xn − Txs − 1 = 0, giving rise to a positive rank of MR(xi) and a representation of a linear combination of ln p for p ∈ S as a convergent series of the above-mentioned form with a rational number Tn (and rational coefficients of a numerator polynomial R(N)). On the other hand, when |S| = 1 (like formulas involving only π or only ln 2), then for every n there are only finitely many distinct (not reducible to each other) trinomials of degree n, with rational Tn and convergent series, representing ln p for S = p (or representing π for S = {1}). This can be proved by an asymptotic analysis of the resolvents of the Galois groups of the trinomial equations. Thus we can classify all representations of a single logarithm of a rational (algebraic) number (like π) as generalized hypergeometric series with (NsNn) in the denominator and (p/q)N ⋅ R(N) in the numerator for a polynomial R(N). A representative list of such identities is shown below for small values of n.
5. The Hierarchy of Reducible Identities
So far we have covered the “irreducible” hypergeometric series ΣN=1∞ zN/(NsNn), corresponding to the trinomial xn − T ⋅ xs − 1 = 0, when (n, s) = 1. Whenever (n, s) > 1, the root of xn − T ⋅ xs − 1 = 0 are obviously multiplicatively dependent. The corresponding hypergeometric function ΣN=1∞ zN/(NsNn) satisfies the hypergeometric equation that is a lift of an irreducible hypergeometric equation via the Kummer mapping z → zd, d = gcd(n, s). Such equations and their solutions are known as Kummer reducible. We show now how reducible equations are handled in the same framework as irreducible ones. We also show that any identity from the irreducible case can be lifted to the whole family of reducible series arising from this one (though not in an entirely trivial fashion). In this respect (and only in this) there is an infinite series of identities whose rate of convergence increases ad infinum. However, there is a little sense in using these series for rapid computations of π or other constants, because the complexity of computations with these series stay the same.
To deal with a reducible case, we start with an irreducible one, corresponding to integers n and s, n ≥ s ≥ 0 and (n, s) = 1. As before we look at roots xi = xi(T) of xn − Txs − 1 = 0 for T within the area of convergence: |Tn| < nn/(ss ⋅ (n − s)n−s). There are obvious transformation formulas for xi(T) as T → T ⋅ ζni. We can write this formula in the form xi(Tζnj) = xi−j(T) ⋅ ζn−j, where i − j is defined in {1, … , n} mod n.
Let us chose for the degree of reducibility an integer m, m ≥ 2. We rely on our master formula that we apply for m values of T : T ⋅ ζnmj : j = 0, … , m − 1. Choosing as before the order of roots xi(T) such that xi(T) → ζn−j as T → 0, we simply add up m copies of the master formula:
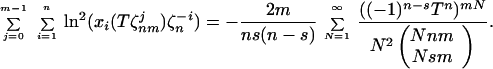 |
21 |
Note that the algebraic equation we are dealing with is not xnm − Tmxsm − 1 = 0, but rather ∏j=1m−1 (xn − Tζnmj ⋅ xs − 1) = 0. As in the calculations above, we differentiate Eq. 21, applying θT = T ⋅ d/dT. The discussion is identically to the one above, if one replaces the set {xi = xi(T), n, s} in the expression above by {xi(Tζnmj), nm, sm}. We get the expression
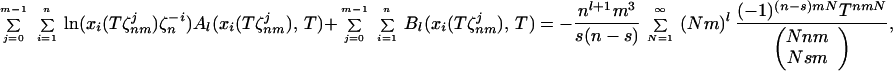 |
22 |
with the same recursion formulas for Al, Bl as above. We supplement these formulas (Eq. 22) for l = −1, 0, … by m obvious identities Σi=1n ln(xi(Tζnmj)ζn−i) = 0 for j = 0, … , m − 1. To express the logarithms in terms of functions
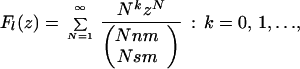 |
we may restrict k to the range 0 ≤ k < m ⋅ (n − 1), and obtain the general expression of the form:
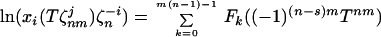 |
23 |
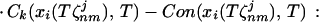 |
i = 1, … , n; j = 0, … , m − 1. Here Ck(xi(Tζnmj), T) and Con(xi(Tζnmj), T) are polynomials in Tnm and in xi(Tζnmj) ⋅ Ta (with bn − a(n − s) = 1).
The existence conditions of the identities for logarithms of rational number (π including) are the same as above—they are the conditions of the existence of the multiplicative relations on roots xα of
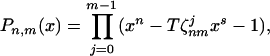 |
in addition to the requirement for Tmn to be rational within the radius of convergence: |Tn| < nn/(ss ⋅ (n − s)n−s).
Consequently, if there is an identity for logarithms of rational numbers in the case of (n, s, T), then the identity continues to exists in all reducible cases (nm, sm, Tm) : m ≥ 2. We give below a rather simple list of such identities arising from a classical expression for π (that one gets from arcsin(x/2) power series expansion).
6. Some Identities
We present here some interesting identities for π, ln 2 (or ln 3) that immediately follow from our explicit expressions and the multiplicative relations between the roots of the corresponding trinomial equations. This is not a complete list, but is rather representative in the “irreducible” case, because most important classes of the multiplicative relations in the case of S = {1, 2, 3} are presented here.
A) Identities:
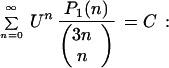 |
1) U = 8/3; P1(n) = 49n + 1; C = 81 + 16π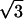 ; 2) U = 8/3; P1(n) = −245n + 338; C = 162 − 6π
; 2) U = 8/3; P1(n) = −245n + 338; C = 162 − 6π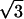 − 18 ln 3; 3) U = −27/16; P1(n) = −90n − 177; C = 64 ln 2 − 120; 4) U = −8/9; P1(n) = 3575n + 1999; C = 1215 − 432 ln 3; 5) U = 1/2; P1(n) = 50n − 6; C = π (Modified Gosper’s identity); 6) U = 1/2; P1(n) = 275n − 158; C = 6 ln 2 − 135; 7) U = −1/4; P1(n) = 17 − 728n; C = 24 ln 2 + 54;
− 18 ln 3; 3) U = −27/16; P1(n) = −90n − 177; C = 64 ln 2 − 120; 4) U = −8/9; P1(n) = 3575n + 1999; C = 1215 − 432 ln 3; 5) U = 1/2; P1(n) = 50n − 6; C = π (Modified Gosper’s identity); 6) U = 1/2; P1(n) = 275n − 158; C = 6 ln 2 − 135; 7) U = −1/4; P1(n) = 17 − 728n; C = 24 ln 2 + 54;
B) Identities:
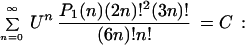 |
1) U = 8; P1(n) = 350n − 17; C = 15π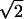 + 27; 2) U = 1/36; P1(n) = 1173874n − 202577; C = 720 ln 2 − 202176;
+ 27; 2) U = 1/36; P1(n) = 1173874n − 202577; C = 720 ln 2 − 202176;
C) Identities:
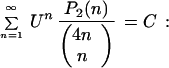 |
1) U = 8; P2(n) = 520 + 6240n − 430n2; C = −45π − 1164; 2) U = −16/3; P2(n) = −710 + 240n − 2150n2; C = 15 ln 3 + 388; 3) U = 3; P2(n) = 480 − 15215n + 7175n2; C = 40π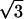 + 1872; 4) U = 9/8; P2(n) = −5692 − 6335n + 5415n2; C = 576 ln 2 − 288π
+ 1872; 4) U = 9/8; P2(n) = −5692 − 6335n + 5415n2; C = 576 ln 2 − 288π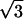 − 324; 5) U = 9/8; P2(n) = −7514 − 1145n − 18050n2; C = 576 ln 2 − 1008π
− 324; 5) U = 9/8; P2(n) = −7514 − 1145n − 18050n2; C = 576 ln 2 − 1008π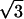 − 7587; 6) U = −1; P2(n) = 51406 − 196341n + 246323n2; C = −720 ln 2 − 7278; 7) U = −1/8; P2(n) = 113930 − 482295n + 769825n2; C = 2880 ln 2 − 9354;
− 7587; 6) U = −1; P2(n) = 51406 − 196341n + 246323n2; C = −720 ln 2 − 7278; 7) U = −1/8; P2(n) = 113930 − 482295n + 769825n2; C = 2880 ln 2 − 9354;
D) Identities:
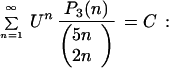 |
1) U = −1/2; P3(n) = 3028 + 482n − 77362n2 + 89012n3; C = 240 ln 2 + 15π − 528; 2) U = −1/2; P3(n) = 32132 − 168944n + 32425n2 + 117623n3; C = 1080 ln 2 + 99π − 882;
E) Identities for Σ xn/(n5n):
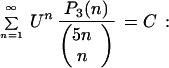 |
1) U = −1; P3(n) = 1556188 − 9734011n + 2663836n2 − 17091891n3; C = −9240 ln 2 − 202436; 2) U = 1/2; P3(n) = 1556188 − 9734011n + 2663836n2 − 17091891n3; C = −9240 ln 2 − 202436; 3) U = −1/16; P3(n) = −3810109 + 48164564n − 132390804n2 + 126626274n3; C = −73920 ln 2 − 382391;
F) Known identity:
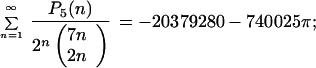 |
P5(n) = −65979888 + 1181293644n − 6191776770n2 + 17657815350n3 − 18752083422n4 + 5314039086n5.
G) New identity:
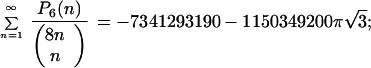 |
P6(n) = 79371060090 + 148314047723n + 1480383303223n2 + 5565398860353n3 − 2545104522979n4 + 17229124728424n5 − 8645263491354n6.
H) Modified Gosper’s identity:
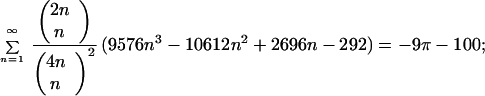 |
The list of progressively faster convergent “trivial = reducible” identities for π and Σ xLn/(Ln2Ln):
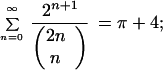 |
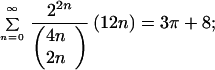 |
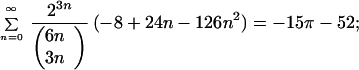 |
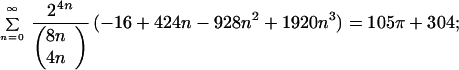 |
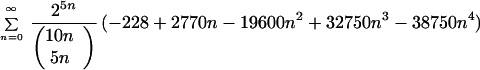 |
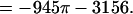 |
7. Some Diophantine Applications
One can convert rapidly convergent series given above into sequences of rational approximations to corresponding logarithms these series represent. For this one should use Padé approximations of the second kind to generalized hypergeometric functions described in detail in ref. 11. As an example we use the case Eq. 3 on the Schwarz list, with contiguous hypergeometric functions representing both π and ln 2.
In this case we take a function
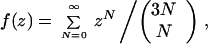 |
satisfying second-order inhomogeneous linear differential equation over Q(z) arising from the trinomial algebraic equation x3 − Tx − 1 = 0 with the identification z = T3, and z = ½. The system of Padé approximations to generalized hypergeometric functions was explicitly constructed in section 5 of ref. 4. This system of dense rational approximations now bounds the measure of linear independence of π, ln 2 (see, e.g. lemma 2.5 in ref. 4):
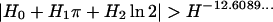 |
for sufficiently large H, H = max{|H0|, |H1|, |H2|}.
This result is based on contiguous identities 5) and 6) from the list A) in section 6:
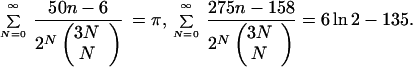 |
There are interesting polylogarithmic extensions of all identities above, derived by integrating the master formula. For example, there is a natural counterpart to pair 5)-6) in A), section 6 of cubic trinomial identities given above, that expresses π and ln 2. This is a tri-logarithm identity involving the Catalan constant G and ζ(3):
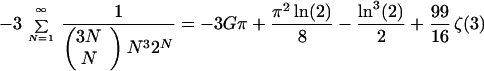 |
Not-trivial multiplicative relations between the roots bring in other interesting diophantine approximations. The simplest pair of formulas for the same rational x, representing π in two different ways—a nontrivial multiplicative relation for S = 1—is the following addition to the list D) of section 6.
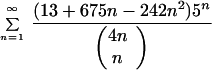 |
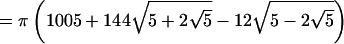 |
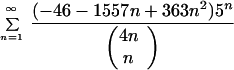 |
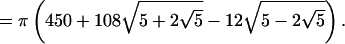 |
Acknowledgments
With great pleasure we acknowledge illuminating inputs from R. Askey and W. Gosper.
References
- 1.Chudnovsky D V, Chudnovsky G V. In: Ramanujan Revisited. Andrews G, et al., editors. New York: Academic; 1988. pp. 375–472. [Google Scholar]
- 2.Gosper W. Hypergeometric Identities. New York: Springer; 1998. , in press. [Google Scholar]
- 3.Bateman H, Erdelyi A. Higher Transcendental Functions. Vol. 1. New York: McGraw-Hill; 1953. [Google Scholar]
- 4.Chudnovsky, D. V. & Chudnovsky, G. V. (1989) Proc. Symp. Pure Math. Am. Math. Soc. 49, Part II, 167–232.
- 5.Beukers F, Heckman G. Invent Math. 1989;95:325–354. [Google Scholar]
- 6.Whittaker E T, Watson G N. A Course of Modern Analysis. Cambridge: Cambridge Univ. Press; 1927. [Google Scholar]
- 7.Birkeland R. Math Zeitschrift. 1927;26:566–578. [Google Scholar]
- 8.Chudnovsky D V, Chudnovsky G V. In: Computers in Mathematics. Chudnovsky D, Jenks R, editors. New York: Dekker; 1990. pp. 109–232. [Google Scholar]
- 9.Birkeland R. Avh Norske Videnskaps Oslo Mat-Naturv Klasse. 1927;8:1–23. [Google Scholar]
- 10.Chudnovsky D V, Chudnovsky G V. Lect Notes Physics. 1980;126:136–169. [Google Scholar]
- 11.Chudnovsky D V, Chudnovsky G V. In: Computer Algebra. Chudnovsky D, Jenks R, editors. New York: Dekker; 1988. pp. 1–82. [Google Scholar]


