Implications of a primordial origin for the dispersion in D/H in quasar absorption systems

Abstract

We explore the difficulties with a primordial origin of variations of D/H in quasar absorption systems. In particular we examine options such as a very large-scale inhomogeneity in the baryon content of the universe. We show that very large-scale (much larger than 1 Mpc) isocurvature perturbations are excluded by current cosmic microwave background observations. Smaller-scale ad hoc perturbations (∼1 Mpc) still may lead to a large dispersion in primordial abundances but are subject to other constraints.

There has been a recent flurry of activity in measurements of potentially primordial D/H in quasar absorption systems. If the measured values of D/H are, in fact, primordial, then they are of paramount importance to Big Bang nucleosynthesis (BBN) because the predicted D/H abundance is a rapidly varying and monotonic function of the single unknown parameter in the standard model, namely the baryon-to-photon ratio, η (see e.g., Walker et al. and references therein, ref. 1). An independent determination of η, in addition to enabling a critical test of BBN based on the other light element isotopes (2), has far-reaching consequences on the nature of dark matter and the composition of galactic halos. A simple interpretation based on the recent D/H measurements, however, is complicated by the fact that they may not be uniform. In fact, published values span an order of magnitude in D/H. Taking the extremities of the range of values leads to very different cosmological interpretations. Nevertheless, all measurements are consistent with the basic BBN prediction that deuterium is primordial and the nucleosynthetic prediction (2, 3) that the primordial D/H ratio is higher than present-day values. However, the different extra-galactic measurements, if proven universal, would imply very different chemical evolution histories with high primordial values indicating large amounts of stellar processing and lower values indicating perhaps that our galaxy presently is receiving primordial infall. Although it is necessary to be highly cautious at this stage (as is the case with any new set of data), and indeed any one (or all) of the reported measurements may not represent the primordial abundance of D/H, here we explore the alternate (and even more exotic as we shall see) possibility that both high and low D/H measurements are accurate and uncontaminated. Indeed, it has been suggested (4–6) that a possible explanation of differing measurements of primordial D/H is the presence of an inhomogeneity in the baryon number on large scales. We will explore the implications of very large-scale inhomogeneities on the cosmic microwave background, where, if allowed, we then would expect a dispersion in the height of the Doppler peak to be observable.

In the past few years there have been several reported values and limits of the primordial D/H abundance in high redshift quasar absorption systems. These values have ranged from ∼2 × 10⁻⁴ (7–9) and a new observation with a similarly high value (10) to ∼ 2.5 × 10⁻⁵ (6, 11). More recent data have suggested that one of the systems with a low reported D/H abundance is more consistent with D/H ≥ 4 × 10⁻⁵ (12). Given the appropriate amount of caution regarding these measurements, we now consider the constraints on any real spread in the primordial D/H over distance scales appropriate to quasar absorption systems. In the remainder of this paper, we would like to detail the consequences of assuming fluctuations in D/H on very large scales.

As we stated earlier, the BBN prediction for primordial D/H is a very rapidly changing monotonic function of the baryon-to-photon ratio, η. As such, any measurement with some degree of confidence of primordial D/H, can in principle very accurately pin down the value of η. If there is a real dispersion in primordial D/H as would be the case if both the highest and lowest D/H measurements were accurate, then we have evidence of a real inhomogeneity in the baryon number on large scales. In addition, the amplitude of the fluctuations producing these inhomogeneities must be large [𝒪 (1)] at the time of BBN as the D/H dispersion corresponds to values of η from ∼1.5 to ∼7.0. The various possibly observed quasi stellar object absorption systems in which the D/H measurements are made are all at large redshift (ranging from z = 2.5–4.7) and thus are separated by cosmological distance scales. We stress that inhomogeneities on scales as large as this are very different from the baryon inhomogeneities inspired from the quantum chromo-dynamics phase transition [see e.g., Malaney and Mathews (13) and Thomas et al. (14)] and from the small-scale baryon isocurvature fluctuations (15) that give rise to inhomogeneous BBN. In these cases the inhomogeneities were produced on small scales (sub-horizon at the time of BBN), whereas the inhomogeneities we are considering must be nearly horizon scale today, meaning that these are inhomogeneities on scales much larger than the horizon at the time of BBN. That is, within a horizon at the time of BBN, we still are dealing with homogeneous BBN. Nucleosynthesis with large-scale inhomogeneities has been considered recently (16, 17). These studies focused on inhomogeneities that have mixed and would not lead to inhomogeneities in the observed abundances without the imposition of an arbitrary cutoff in the power spectrum.

We also would like to emphasize the implications of a large-scale baryon inhomogeneity of the type we have been discussing on standard BBN. The abundance of a single light element isotope that can be associated with its primordial value is enough to constrain BBN and determine a value for η. To test the theory, we need the abundances of two or more light element isotopes. For example, this can be and is achieved by using ⁴He and ⁷Li (18, 19). If the universe was homogeneous in baryon number, then a primordial measurement of D/H in quasar absorption systems would lead to a strong test of the theory. However, if the dispersion in D/H in these systems is real and indicates a real large-scale baryon inhomogeneity, then unless a second isotope (e.g., ⁴He or ⁷Li) can be observed in the same absorption system, the D/H measurements will yield information regarding the baryon-to-photon ratio in those systems, in addition to information on the inhomogeneity. These measurements alone could not be used to test BBN as they could not be directly compared with the predictions based on ⁷Li, which is observed in our own galaxy, or ⁴He, which though is observed in external galaxies, these all are relatively local (i.e., they are all at very low redshift).

One important and viable mechanism for the production of the baryon asymmetry of the universe is realized in supersymmetric extensions of the standard model of electroweak interactions (20–22). The minimal supersymmetric standard model contains many additional particle degrees of freedom over the standard model, corresponding to the supersymmetric partners of ordinary particles. The potential for the scalar fields contains directions for which the potential is perfectly flat, that is, certain combinations of these fields are allowed to take arbitrarily large vacuum expectation values at little (or none, if supersymmetry is unbroken) cost in energy. During inflation, De Sitter fluctuations drive these scalar fields to large expectation values, and the subsequent evolution of these fields (which store baryon and lepton number) produces a baryon asymmetry. The final baryon asymmetry is, in general, quite model-dependent as it depends on quantities such as the expectation value produced by inflation, the inflation mass, the grand unified mass scale, and the supersymmetry breaking mass scale.

In the course of the evolution of the scalar fields, sfermion density fluctuations are produced (22, 23), which lead to isocurvature fluctuations in the baryon density with an amplitude that is given by (24)

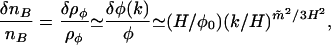1

where H is the Hubble parameter during inflation, m̃ is the sfermion mass, and φ_o is the vacuum expectation value of the sfermion fields, φ, produced during inflation. Thus, isocurvature baryon number fluctuations are produced with an amplitude that depends primarily on the ratio H/φ_o and may take values from ∼10⁻⁸ to ∼1. To have an impact on the D/H abundances, δn_B/n_B must take values of order 1.

The overall baryon to entropy ratio is given by (22)

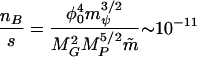2

for φ_o ∼10⁻⁶M_P, an inflation mass, m_ψ∼ φ_o, a grand unified theory mass of order 10⁻³M_P, and a sfermion mass, m̃, of order 100 GeV. First, it is important to stress that in models such as these, the baryon density ρ_B ≪ ρ_total so that even though δρ_B/ρ_B may be of order unity (if H ∼ φ_o), δρ_B/ρtotal ∼ 10⁻⁹ is very small at the time the sfermion oscillations have decayed, and ρ_total is the total energy density that is dominated by the dynamics of inflation. Thus, these baryon perturbations are not responsible for structure formation in the universe. Second, the spectrum of isocurvature perturbations in the baryons is very nearly flat, because m̃/H ≪ 1, is present on exponentially large scales, and is completely independent of the adiabatic fluctuations produced by inflation. Note that adiabatic perturbations do not influence BBN because δη/η= 0. (More accurately, δ(n_B/s) = 0 for adiabatic perturbations.) Thus, the overall large-scale structure believed to have been seeded by inflation remains a flat adiabatic spectrum of density fluctuations. Baryons, however, have in addition an isocurvature component with an amplitude that may be of order unity. Such a model provides a plausible physical origin for baryon inhomogeneities on very large scales without affecting the evolution of large-scale structures.

We note that the perturbation spectrum we have just described is simply one that is plausibly obtained by inflation and that contains power on scales larger than the horizon at the time of BBN as is required. Because of its flatness, the spectrum also possesses power on very large cosmological scales as would any spectrum that is not sharply peaked or cut off. We do not imply that this spectrum is unique; we use it below to obtain constraints because of its simplicity. We will comment on the possibility of other spectra below.

We begin our discussion of the constraints by first considering the presence of very large-scale inhomogeneities on angular scales θ ≥ θ_LS ∼ 2°. Thus the scales we are considering enter the horizon after last scattering, and they will induce fluctuations in the cosmic microwave background (CMB) because of the inhomogeneities in the gravitational potential from the variations in the baryon density, i.e., the Sachs–Wolfe effect, on scales θ ≥ θ_LS ∼ 2°.

The total temperature fluctuations in the CMB for isocurvature perturbations including the intrinsic fluctuations and those induced by the Sachs–Wolfe effect are

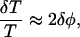3

where δφ is the Newtonian potential (25). This expression is accurate to ∼10%. For isocurvature perturbations the fluctuations in the potential are

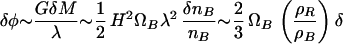4

at the time when a scale λ ∼ H⁻¹ enters the horizon. Here

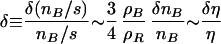5

is the fluctuation in the number of baryons per comoving volume and ρ_R is the energy density in radiation at late times. This expression (Eq. 5) is valid for ρ_B ≫ ρ_R. The temperature fluctuations are suppressed by two effects. First by the density of baryons in the universe, Ω_B, which create the potential well. The second suppression comes from the fact that super-horizon-sized perturbations cannot grow because δρ = 0.

As one can see from Eq. 4, the potential fluctuations δφ are time-independent on a particular scale λ, before horizon crossing as λ²δn_B/n_B ∝ R³ ∝ t², and H² ∝ t⁻². However as can also be seen from Eq. 4, these fluctuations are scale-dependent. Before horizon crossing, the suppression factor (ρ_R/ρ_B) induces a scale dependence, and we can scale δφ to the present by noting that δφ ∝ R⁻¹ and that the scale λ enters the horizon at a time t ∝ λ³. Because R∝t^2/3 in the matter-dominated era

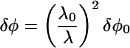6

in terms of the potential fluctuations today, δφ₀. For λ₀ ∼ H₀⁻¹ and δ ∼ 1 the restriction δT/T ≤ 10⁻⁵ leads to λ ≥ λ₀. This is our main result. The large-scale, large-amplitude baryon inhomogeneity needed to explain the apparent dispersion in the D/H abundances measured in quasar absorption systems makes a contribution to the microwave background anisotropy induced by the Sachs–Wolfe effect, which is in excess of the observed anisotropy for all scales λ < λ₀ ∼ H₀⁻¹ that have entered the horizon.

On angular scales somewhat smaller than 2°, the Sachs–Wolfe effect is not operative but a similar constraint may be derived. For scales that enter the horizon between the epochs of matter domination and last scattering, i.e., between ∼20′ h⁻¹ and 2°, corresponding to length scales between ∼35 h⁻² Mpc and 200 h⁻¹ Mpc, there is a contribution to δT/T, which is caused by Doppler shifts across fluctuations at last scattering. This gives (26)

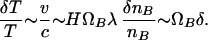7

Thus large fluctuation in n_B/s are excluded at these scales as well.

To avoid these CMB constraints we need to consider smaller scales where the fuzziness of the last scattering surface suppresses temperature fluctuations so that at scales below 30" the fluctuations are acceptably small. Alternatively, we can consider scales that have not yet been probed by the CMB. However, we do not want to consider scales that are so small that many such perturbations would make up one quasar absorption cloud. In this case we would expect the regions to mix. Observations in our galactic neighborhood preclude this mechanism from producing the large fluctuations in the D/H abundance (16, 17). Very large fluctuations mix in regions with high ⁷Li abundances producing a final abundance inconsistent with present observations. Fluctuations with δ ≤ 0.15 can be made consistent with the light element abundances (16) but are not sufficiently large to explain the observed quasi stellar object D/H abundance variations.

Clearly, the type of spectra we have considered (flat spectra produced by inflation) though naturally produced are not capable of explaining the D/H dispersion. Instead, we find that a rather specific baryon perturbation spectrum is required. To circumvent both of these bounds one is forced to consider a scale in the middle, large enough to encompass an entire quasar absorption cloud, but small enough to avoid the CMB bounds. This leaves us only with a scale of ∼1 Mpc that corresponds to θ ∼ 30" at last scattering. Extra-galactic HII regions, the best sites for observing ⁴He have been probed on these scales. Both D and ⁷Li have been probed in our galactic neighborhood on scales smaller than this. Thus, we would not expect to see variations in the observed galactic D and ⁷Li abundances but would expect to see them in the observed ⁴He abundances. Observations from the lowest metallicity extra-galactic HII regions are consistent with a scatter of δY_p ∼ 0.01 (27), which corresponds to δη ∼ 3. However the uncertainties are large and the scatter is consistent with the assigned error bars of individual ⁴He measurements. We note, however, that picking out a single scale for the baryon number fluctuations strays far from our original motivation of flat directions from supersymmetry, which generally lead to a flat spectrum on very large scales. Thus, we cannot motivate the 30" scale from the model described above.

At present the published observations of deuterium in quasar absorption systems roughly fall around two values that differ by an order of magnitude. Though it is probably still premature to identify either (or any) set of observations as primordial, we see from our above discussion that it would be extremely difficult for both of these to represent primordial values. To be primordial we need large-scale, large-amplitude isocurvature perturbations. Standard BBN then would lead to the observed dispersion in D/H. Supersymmetry provides one model where an isocurvature spectrum can be produced.

For scales that enter the horizon after last scattering, θ > θ_LS ∼ 2°, the dominant contribution to the CMB is the Sachs–Wolfe effect. Perturbations on all scales that have entered the horizon after last scattering that could explain the D/H dispersion lead to CMB fluctuations that are larger than observed. For scales smaller than this, 20′h⁻¹ ∼ θ ∼ 2°, Doppler shifts across fluctuations at last scattering also would be too large for these fluctuations. Only on smaller scales can the CMB limits be avoided. However, scales smaller than those of a quasar absorber would be well mixed, thus homogenizing the BBN products. Fluctuations of the amplitude we are considering here are not possible because of light element constraints (16, 17). Only on scales λ ∼ 1 Mpc, θ ∼ 30" can we avoid all constraints. But such a spectrum seems quite ad hoc and unmotivated. Observations of ⁴He in extra-galactic HII regions probe these scales but the data are too uncertain to test for these perturbations. Even so, we do not have a model that will produce large-amplitude perturbations on just these scales.

ABBREVIATIONS

BBN

Big Bang nucleosynthesis

CMB

cosmic microwave background