Abstract
Fluorescence blinking in nanocrystal quantum dots is known to exhibit power-law dynamics, and several different mechanisms have been proposed to explain this behavior. We have extended the measurement of quantum-dot blinking by characterizing fluctuations in the fluorescence of single dots over time scales from microseconds to seconds. The power spectral density of these fluctuations indicates a change in the power-law statistics that occurs at a time scale of several milliseconds, providing an important constraint on possible mechanisms for the blinking. In particular, the observations are consistent with the predictions of models wherein blinking is controlled by diffusion of the energies of electron or hole trap states.
Keywords: fluorescence intermittency, power spectrum, nanocrystals
High-quality, monodisperse semiconductor nanocrystals can be produced in large quantities by colloidal-synthesis techniques (1). These nanocrystals, known as quantum dots (QDs), can exhibit bright luminescence, whose wavelength is controlled by the size of the nanocrystals (2). This property makes colloidal QDs attractive candidates for several applications, including light-emitting diodes (3), solid-state lasers (4), and biological labeling (5, 6). Such applications, however, may be compromised by fluctuations in the QD luminescence. In particular, individual QDs emit light intermittently, switching irregularly between bright (“on”) and dark (“off”) states (7). Widespread interest in this blinking phenomenon was stimulated by the surprising observation that the durations of bright and dark periods follow power-law statistics (8, 9). Specifically, the blinking periods are described by probability densities of the form
with a value of ν between 0.4 and 1.0. The power-law behavior holds regardless of sample temperature (9), QD size or composition (10), nanoparticle shape (11), or excitation intensity (12).
So far, though, experimental studies of QD blinking have been limited in their temporal resolution. A resolution of 200 μs was achieved in one of the earliest measurements (8), and a small number of later experimental studies have included analysis of submicrosecond blinking dynamics (14, 16, 17, 41). The remainder of the quantitative characterizations have been restricted to time scales of several milliseconds or longer. In this paper, we report measurements of fluctuations in QD fluorescence on time scales from microseconds to tens of seconds. We observe a change in the fluctuation dynamics for time scales less than several milliseconds.
This observation is consistent with the predictions of a class of models where blinking is controlled by slow diffusion of the energies of electron or hole trap states. In these models, the fluorescence of a QD is quenched through the trapping of a carrier, which occurs when the energy of the trap state fulfills a resonance condition. The duration of the blinking periods is determined by the diffusion of the energy of the QD-trap system about this resonance condition. This diffusion-controlled mechanism predicts the existence of a critical time below which the power-law blinking statistics change, in agreement with our measurements.
Measurements of Fluorescence Fluctuations
Blinking-Time Probability Densities.
Most previous experimental studies have characterized blinking statistics in terms of the probability densities of bright and dark periods. We begin by calculating these functions for our data, as a clear demonstration of the power-law blinking statistics. Fluorescence measurements are performed on CdSe/ZnS core-shell QDs, synthesized according to established methods (13). The diameters of the QDs were chosen such that the emission wavelength is 615 nm. Photons emitted by single QDs are collected and detected, and the time of each photon detection is recorded, as described in supporting information (SI).
To calculate the blinking-time probability densities, the recorded photon arrival times are converted into a time series by grouping the photon detection events into time bins of fixed width, as illustrated in Fig. 1. The minimum bin size that can be used is dictated by the need to clearly distinguish bright and dark states. More specifically, the average number of detected photons per time bin must be significantly greater than unity, or it will not be possible to differentiate between the detection of photons emitted from the dot and background counts. This minimum usable bin size thus depends on the emission rate from the QD, the photon collection and detection efficiency, and the background photon-count rate; for our experiment, a bin size of at least 5 msec is necessary.
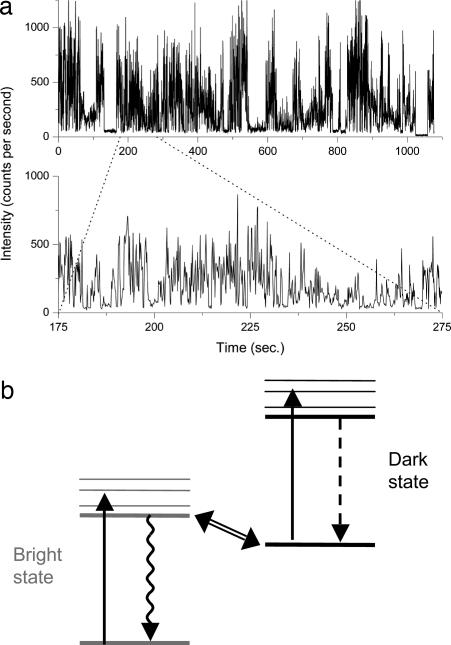
Fig. 1.
Blinking of quantum dots and diffusion-controlled model. (a) Intensity of fluorescence as a function of time measured from a single CdSe/ZnS core–shell nanocrystal QD. The two tracings show the same data on different time scales, grouped into time bins of 100 msec (Upper) and 5 msec (Lower). (b) Schematic of the states involved in QD blinking. The dot is excited from a lower-energy to a higher-energy state by absorption of a photon. If the dot is in a bright state, relaxation occurs by photon emission; if it is in a dark state, relaxation occurs by a nonradiative mechanism. Blinking corresponds to transitions between the bright and dark states.
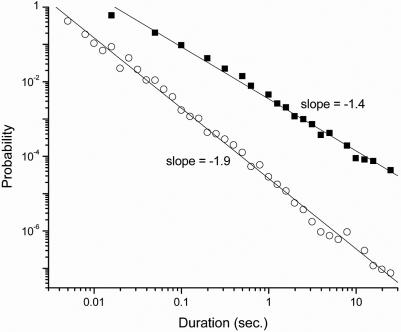
A threshold is applied to the binned data, with all signals above the threshold taken to be on states, and all signals below the threshold taken to be off states. Blinking-time histograms are calculated from the thresholded data, as shown in Fig. 2. The dark and bright periods both show power-law behavior over the measured time scales, with exponents νoff = 0.4 and νon = 0.9, respectively. Similar behavior was seen for several other dots.
Fig. 2.
Probability density of duration of blinking periods for the time trace shown in Fig. 1, using 5-msec time bins. Filled squares indicate dark periods, and open circles indicate bright periods. The absence of points for short bright periods is due to the limited statistics for the finite duration of this data run.
Although some of our experimental probability densities show a hint of a change of slope on millisecond time scales, identification of any change in dynamics requires that the characterization be extended to significantly shorter times. Because of the required time binning, though, we cannot use the probability densities to investigate blinking dynamics on submillisecond time scales.
Autocorrelation Function.
The photon autocorrelation function, defined as G(2)(τ) = 〈i(t)i(t + τ)〉, where i(t) is the rate at which photons are counted experimentally, can be calculated directly from the photon counts without the need for additional binning, as described in the SI. To allow comparison with theory, we calculated the normalized correlation function, g(2)(τ) = G(2)(τ)/(〈i1(t)〉〈i2(t)〉).
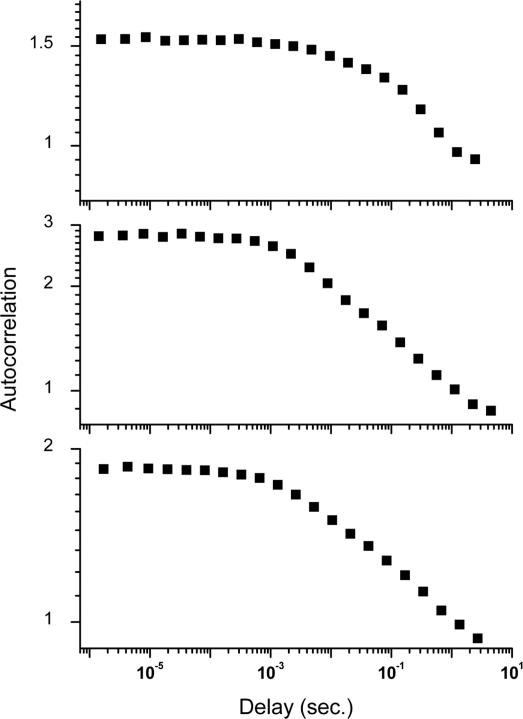
Fig. 3 shows representative experimental correlation functions. By inspection, it is clear that the correlations change slope on the millisecond time scale. Interpretation is complicated, however, by the nearly flat form of g(2)(τ), which changes by only a factor of ≈2 over seven orders of magnitude of time delay. This very gradual change has inhibited prior observation of short-time dynamics, even though submillisecond correlation functions have previously been reported (14).
Fig. 3.
Autocorrelation function of fluctuations in fluorescence measured from three individual QDs. The correlation functions are normalized by the mean intensity; however, due to the power-law probability density of blinking periods, this mean depends on the duration of the experiment, and the short-time values of the functions do not approach unity. Average count rates, from top to bottom, are 5,200, 1,700, and 3,000 counts per sec.
Verberk and Orrit (15) have derived an expression for the autocorrelation function that arises from the blinking-time probability density of Eq. 1. However, the probability density diverges at short times and is not normalizable, which necessitates the imposition of arbitrary lower and upper limits of integration in the derivation. The result is a correlation function of the form g(2)(τ) = 1 − Cτ1−ν, where the constant C depends on both these arbitrary limits. This dependence on arbitrary parameters presents a difficulty in comparing the prediction to experiment, particularly in determining whether there is a minimum time scale below which the blinking-time probability density of Eq. 1 does not hold.
We note that the slowly varying correlation function arises because the probability density functions of bright and dark periods are both power laws. Certain samples of QDs, consisting only of CdSe cores, have been observed to exhibit power-law blinking only for the dark periods, with exponential probability density functions for the bright periods; in this case, the form of the correlation function is expected to be g(2)(τ) ∝ τν−1 (15). For these uncapped QDs, this power-law correlation function has been observed experimentally to persist down to microsecond time scales, with no evidence for a change in dynamics on short time scales (16, 17).
Power Spectral Density.
The difficulties with interpreting the correlation functions of fluorescence fluctuations can be avoided by evaluating instead their power spectral density (18). The power spectrum is defined as P(f) = |I(f)|2, where I(f) is the Fourier transform of the photon count rate, i(t), for frequency f. As for the autocorrelation function, no additional binning of the data is necessary to calculate the power spectrum. The spectrum is formally equivalent to the Fourier transform of the autocorrelation function G(2)(τ), and thus provides, in principle, the same statistical information. However, the expected power spectrum that arises from the blinking-time probability density of Eq. 1 has a particularly convenient form (18–20):
Although derivation of this function requires the imposition of lower and upper time limits, tmin and tmax, the resulting power spectra apply for 1/tmax < f < 1/tmin. Within this frequency range, P(f) depends on the time limits only through an overall arbitrary proportionality constant. Moreover, a log–log plot of the power spectrum should result in a straight line with an easily identifiable slope. For all previous observations of QD blinking, ν is between 0 and 1, and the first form in Eq. 2 is expected to apply. As we show below, however, the diffusion-based theory gives both forms in Eq. 2 in the short- and longer-time limits.
Eq. 2 holds exactly only if the on and off blinking periods are described by the same power-law probability density. In most cases, including the present data, they are described by two separate power laws, with different exponents νon and νoff, as illustrated in Fig. 2. In this case, the power spectrum is dominated by the process that contributes the larger noise. For our data, this is the on-time probability density, and Eq. 2 holds approximately, with ν equal to νon. Evaluating the fluorescence fluctuations in terms of their power spectrum, then, means losing independent information about on and off times, as a tradeoff for the ability to examine significantly shorter time scales.
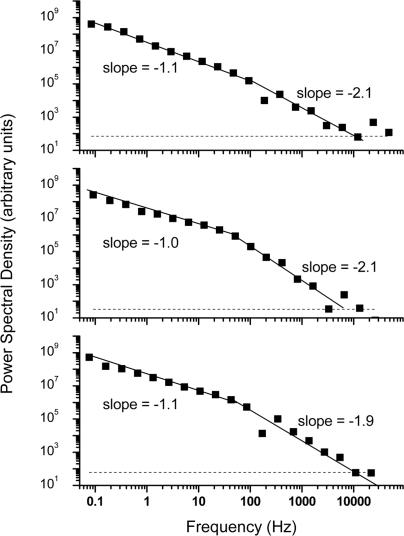
Fig. 4 shows representative power spectra, calculated as described in the SI. At the highest frequencies, the power spectra are dominated by shot noise of photons from the QD and of background counts. This noise limits the maximum frequency that can be examined, a disadvantage compared with the autocorrelation function. Nevertheless, the current data show a clear change in the slope of the power spectra on millisecond time scales.
Fig. 4.
Power spectral density of fluctuations in fluorescence measured from three individual QDs. Results are for the same time series as for Fig. 3. Solid lines are fitted power laws to low-frequency and high-frequency portions of the power spectra, and horizontal dashed lines are expected shot-noise levels. Statistical errors are expected to be less than the size of the plotted points.
This effect is quantified by separately fitting low- and high-frequency parts of the power spectra according to Eq. 2. Nonlinear least-squares fitting of the lower frequencies consistently gives a slope of −1.1 ± 0.1; this corresponds to a value of ν = 0.9, in agreement with the measured probability density of bright periods. The higher-frequency parts of the power spectra, on the other hand, have slopes of −2.1 ± 0.15; according to Eq. 2, this would seem to imply a negative value of ν. The crossover point between the low-frequency and high-frequency regimes can be estimated as the point where the two fitted curves intersect, and it is found to lie in the range of 5–35 msec, with significant variation from QD to QD.
Comparison to Models
Distributed-Trapping Models.
The observed change in the statistics of QD fluorescence fluctuations on time scales below 5–35 msec is an important new piece of information that must be taken into account when considering possible mechanisms for the fluctuations.
A popular model of QD blinking, due to Efros and Rosen (21), proposes that a bright dot blinks off when it loses a charge to a surface-trap state. The extra charge remaining behind in the dot quenches fluorescence through rapid, nonradiative Auger recombination, and the dot blinks back on when the charge returns from the trap and reneutralizes the QD. The key difficulty with this model is that, if blinking could simply be described by electron transfer at fixed rates to and from a single surface trap, then the durations of bright and dark periods would follow exponential probability densities. A static distribution of trap states, with a corresponding distribution of electron-transfer times, could explain the power-law statistics of off times, but would still produce an exponential probability density of on times (22).
It was proposed by Verberk et al. (16) that the extended on times could be produced by trapping of a hole on the QD shell; this trapped hole does not quench luminescence, but prevents further ionization of the QD by Coulomb blockade. An alternative proposal, by Kuno et al. (12, 22), is that the electron-transfer rate could fluctuate rapidly because of environmentally induced fluctuations in tunnel-barrier heights or widths. These two models, however, imply a sensitivity of the blinking statistics to the QD environment, in contradiction to subsequent experimental observations (18). Moreover, these models cannot naturally account for the present observation of modified blinking statistics on submillisecond time scales.
Diffusion-Controlled Models.
Models based on diffusion can account in a straightforward fashion for the change in statistics of photon emission, as well as previous measurements of QD blinking. A diffusion-based model was proposed by Shimizu et al. (9), who suggested that the trap-state energy undergoes a random walk, with charge transferred between the QD states and the trap only when their energy levels align. The duration of a blinking period is thus given by the time that the trap energy takes to diffuse away from and back to this resonance condition. This first-passage time is known to yield a probability density with a universal value of ν = ½.
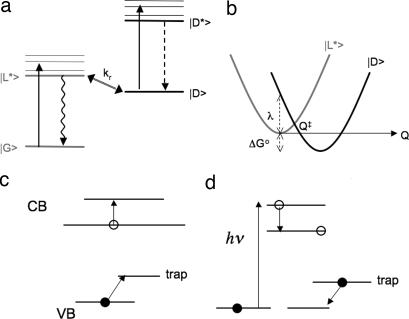
This idea of diffusion-controlled electron transfer (DCET) was developed into a detailed model by Tang and Marcus (23), illustrated schematically in Fig. 5a. It involves four states: the ground and excited states, |G〉 and |L*〉, of a bright dot, and the ground and excited states, |D〉 and |D*〉, of a dark dot, with |D〉 lying slightly lower in energy than |L*〉. In the original DCET model, |D〉 is assumed to correspond to a QD with an electron trapped in a conduction-band-edge surface state, but the same formalism also applies for a different charge-separated state, such as a valence-band (VB)-edge trap. As depicted in Fig. 5b, the transition between |D〉 and |L*〉 is controlled by slow diffusion of the system along an energy-difference reaction coordinate, Q. This coordinate converts the distribution on the many-dimensional coordinate space, by statistical mechanics, into a free-energy profile as a function of Q. The energy of the system with the QD in state |L*〉 is taken to be quadratic in Q: E = κQ2/2, where κ is the curvature of the assumed energy parabola. Likewise, in state |L*〉, E = κ(Q − a)2/2 + ΔG°, where λ = κa2/2 is the reorganization energy and ΔG° is the free-energy gap for electron transfer; for simplicity, the same κ is assumed for the two parabolas. The transition between the two states |D〉 and |L*〉 occurs at the crossing point Q‡ of these two energy curves. Motion on these parabolas and transitions between them provide the classical counterpart of quantum phonon-assisted transitions. A validation of the usefulness of this approach is seen in the fact that spectral diffusion, which is due to the diffusion of the vertical energy difference between the parabolas for the |G〉 and |L*〉 states, exhibits a nearly classical behavior at all but the lowest temperatures (23). The model thus predicts a broadening of single-QD emission lines that is consistent with experimental observations.
Fig. 5.
Schematic of models for QD blinking. (a) Energy levels in the DCET model. Transitions from |G〉 to |L*〉 or from |D〉 to |D*〉 are driven by incident light. Transitions from |L*〉 to |G〉 are primarily radiative, whereas transitions from |D*〉 to |D〉 are primarily nonradiative. (b) Free energies of energy levels in the DCET model, as a function of reaction coordinate Q. Transitions from |L*〉 to |D〉 occur by electron transfer, at rate kr, when the system is at reaction coordinate Q‡. (c) Schematic of trapping mechanism in the Auger-assisted model. Holes are trapped in deep-band states through the promotion of an electron in the conduction band (CB). (d) Schematic of the suggested photo-assisted detrapping mechanism.
In the DCET model, blinking events correspond to phonon-assisted transitions, at the crossing point Q‡, between electronic states of the entire QD. Time intervals between blinking events are determined by diffusion along the reaction coordinate with a sink at Q‡. The probability density for QD bright or dark periods then takes the following limiting forms (23):
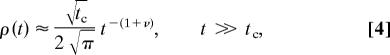 |
where ν = ½. If we approximate the rate constant for electron transfer at the crossing point by kr(Q)δ(Q − Q‡) (24), then the critical time tc is given by
where tdiff is the relaxation time for motion on a parabolic energy surface.†† Values of ν different from 0.5 can be obtained by considering anomalous diffusion in a non-Debye dielectric medium (26). Eq. 4 applies for times long compared with tc but short compared with the “saturation time,” 1/Γ ≈ (8tdiffλkBT)/(λ ± ΔG°)2, where the positive sign is for bright periods and the negative sign is for dark periods (23). For times comparable to this saturation time, the probability density is approximately . This exponential roll-off has been observed in the distribution of bright periods for times on the scale of several seconds to several minutes (9). Here, we focus on short time scales, limiting our observations to time scales shorter than this saturation time.
Certain of the characteristics of the DCET model of Tang and Marcus (23) also apply to an alternative model of QD blinking, developed by Frantsuzov and Marcus (27). In the latter model, illustrated in Fig. 5c, it is assumed that there is a band of trap states, with a sharp edge, deep in the band gap. The electron transition in the conduction band from the lowest-lying state, 1Se, to a higher-lying state, 1Pe, may be in or out of resonance with a transition of a hole from the VB to the band of trap states. When the two transitions are not in resonance, the QD fluoresces upon absorption of a photon. When the two transitions are in resonance, there is a continuous cycling from 1Se to 1Pe and from the VB to the trap, followed by a relaxation from 1Pe to 1Se and a phonon-assisted transition from the trap to the VB. This process is assumed to be much faster than the radiative relaxation, so the QD is dark.
In this model, there is a diffusion of the 1Se to 1Pe energy difference ε into and out of resonance with the transition energy ε* between the VB and the band of trap states. The solution of the standard first-passage-time problem for the diffusion equation, starting with ε = ε* at the initial time and with an absorbing boundary at ε = ε*, gives rise to the t−3/2 probability density of blinking times.
A modification of the Auger-assisted transition between light and dark periods can be combined with the mathematical formalism of the Tang-Marcus DCET model (Z. Zhu and R.A.M., unpublished work). The various transitions can again be described in terms of free-energy curves and their intersections. For example, there is a free-energy parabola for the 1Se plus VB states, one for the 1Pe plus trap states, one for the unexcited system, and so on. Resonance corresponds to the system being near the intersection, or “avoided crossing,” of two curves. Transitions between the parabolas from bright to dark states are assumed to be Auger-assisted, and the boundary condition at the intersection Q‡ is the “radiation boundary condition” used in ref. 27. In the event that the reverse transition also occurs (see below), the resulting equations for the blinking-time probability densities are formally similar to Eqs. 3–5, except that the transition rate, kr, has a different, Auger-assisted, meaning. Indeed, the power-law probability density of the blinking times and the crossover at tc are natural consequences of any model of one-dimensional diffusion with an absorbing sink. Differences between alternative diffusion-based models enter into the meaning of tc and its dependence on physical parameters.
The merits of using an Auger-assisted transition are severalfold. The Auger coupling is relatively weak, so that small values of kr are not unreasonable. The kr value for bright-to-dark transitions can now be different from the kr for the dark-to-bright transitions, because of a different mechanism for the transitions. For example, as illustrated in Fig. 5d, a 1Se state can be produced by the usual optical absorption to higher-energy states and downward relaxation, with a transition en route from 1Pe to 1Se in resonance with a hole transition from trap state to VB state. In this case, the lifetime of the dark state would be prolonged, and the transition would be sensitive to excitation energy. This mechanism might apply only to long-lived traps, in the millisecond rather than the nanosecond regime.
Autocorrelation Functions.
The form of the blinking-time probability density predicted by the diffusion-based models removes the need to apply arbitrary time bounds in the derivation of the autocorrelation function. It is, in fact, possible to derive an explicit expression for the autocorrelation function by using the more general expression for the blinking-time probability density, of which Eqs. 3 and 4 are limiting forms. The Laplace transform of this probability density is given in ref. 26 and can be substituted into the general expression for the Laplace transform, g̃(2)(s), of the autocorrelation function (15, 28). Considering times short compared with the saturation time, 1/Γ, we obtain
where T+ is the mean duration of the bright periods. Limiting forms for the inverse transform can then be determined:
However, a difficulty remains: to compare these predictions to the experimental results, the measured correlation functions must be normalized by the mean photon count rates. If the duration of the experiment is not long compared with the saturation time 1/Γ, this mean is not well defined, but increases with the duration of the experiment (28–30). In other words, the magnitude of g(2)(τ) depends on the total time for which data are collected, if this time is less than 1/Γ (14). Indeed, an accurate quantitative estimate of the correlation function cannot be obtained unless the duration of the experiment exceeds the saturation time by at least two orders of magnitude (31). Saturation times of several seconds to several minutes, depending on temperature and excitation power, have been observed for bright periods (9), and saturation times of more than an hour have been inferred for dark periods from ensemble fluorescence-decay measurements (32). Because our measurement times are on the order of several minutes, we are unable to use g(2)(τ) to make a quantitative comparison to the predictions of the diffusion-based theories.
Power Spectral Density and Critical Time.
The difficulty with normalization is removed if we again turn to the power spectral density. Because the power spectrum is the Fourier transform of the autocorrelation function, it can readily be obtained from the Laplace transform, Eq. 6, by using the fact that g(2)(τ) is real-valued and symmetric about τ = 0. Taking the appropriate limits, we obtain
in agreement with the predictions of Eq. 2, above. As shown above, and as illustrated in Fig. 4, the experimental data are in excellent agreement with these expressions: experimental exponents below and above the critical times, tc, are −1.1 and −2.1, respectively. By fitting Eqs. 9 and 10 to the low- and high-frequency parts of the spectra, as shown in Fig. 4, and by taking the intersection of the two fitted curves, we can obtain an estimate of tc; this value is found to vary from dot to dot, within the range of 5–35 msec. We have not observed any systematic dependence of the results on the intensity of the illuminating laser light, within the range considered (4–12 kW/cm2).
The significance of the critical time can be seen by examining the physical interpretation of Eqs. 3–5. We introduce the fact that the classical amplitude, ΔQ, of vibrational motion on a free-energy parabola at a temperature T satisfies κ(ΔQ)2 = kT, and we note that the diffusion constant, D, for the motion along Q is approximately equal to (ΔQ)2/2tdiff. From Eq. 5, it then follows that
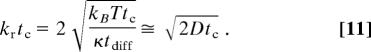 |
We can approximate the delta function δ(Q − Q‡) in the expression for the rate constant at the intersection crossing point at time tc by a Gaussian of width . Eq. 11 then corresponds to a statement that tc is the time for the population, which has expanded in this time to occupy a width , to largely disappear into the “sink” at Q‡, forming in the process a population gradient there, with an effective population at the intersection of approximately zero. The power spectrum for high frequencies, corresponding to times less than tc, thus has the 1/f2 form characteristic of Brownian motion, whereas the power spectrum at low frequencies has a power-law form, reflecting the modified diffusion process after a concentration gradient has developed.
The experimental value of tc could be used to set a value of the rate constant kr, according to Eq. 5, if one knew the relaxation time, tdiff. However, while tdiff is known at time scales of 10–100 sec from spectral diffusion data, many dynamical processes are known to have a distribution of relaxation times, the values at very short times being much smaller than the limiting value at long times. [An example is the case of dielectric relaxation time at high frequencies, as compared with the Debye limit at long times (33).]
We can, however, attribute the significant dot-to-dot variation in tc to variation in the physical parameters of Eq. 5, with the most likely candidate being the transition rate, kr. There is evidence for a wide range of trapping times in QDs, from picoseconds to thousands of seconds (32, 34–36); those on picosecond and nanosecond times will not contribute to the current data, but slower transitions may play a role. The trapping times, and thus tc, may be relatively slow for core–shell QDs, because of the physical separation between the surface states and states confined in the QDs. Furthermore, tc is likely to be sensitive to the QD composition and preparation, and can thus be significantly different for different samples. This sample-specific character explains why previous measurements, both of blinking-time distributions with 200-μs time resolution (8) and of correlation functions with nanosecond time resolution (14), have not revealed the existence of tc. Nonetheless, the observation of tc for our samples supports a diffusion-based process for QD blinking, which may be generally applicable to a range of samples.
Surface Traps.
Although the diffusion-based models invoke particular mechanisms for fluorescence quenching, the same formalism should apply for other, related, mechanisms. Electrochemical experiments have shown that QD fluorescence is quenched by injection of charges into trap states (37), and they have also shown that QDs can fluoresce even if they contain an extra confined charge (38). These results suggest that the quenching of fluorescence may be a direct consequence of the occupation of the surface trap by charges. If this is the case, blinking can still correspond to electron transfer from the QD into and out of those surface states, which is still controlled by diffusion along a reaction coordinate. The direct quenching of QD luminescence by charges in trap states would account for the recently observed collective blinking of several closely packed QDs (39): charging and neutralization of traps would cause the blinking of all nearby dots. Multiple traps are likely to exist on the surface of a QD, each with a different efficiency of quenching QD luminescence. Hopping of carriers into and out of these states will lead to switching between several different levels of luminescence, with different corresponding recombination rates; such a distribution of emissive states has recently been inferred for single-dot luminescence data (40). Incorporating multiple surface traps into the diffusion-based models will require the consideration of additional system states, beyond the bright and dark states currently considered.
Conclusions
We have extended measurements of fluctuations in the fluorescence from individual nanocrystal QDs to time scales shorter than have previously been examined. The power spectral density clearly reveals a change in the fluctuation dynamics below a critical time, tc, of 5–35 msec. These results provide a significant constraint on possible models of QD blinking. In particular, they agree with models in which the blinking is controlled by a diffusion process, because such models predict a corresponding change in blinking statistics at tc.
The existence of tc is largely independent of the microscopic details of the models, although its value depends on the physical parameters that enter the model. Determination of the molecular mechanism responsible for blinking, and further verification of the diffusion-based model, will thus require an investigation of the dependence of the critical time on QD composition, size, and temperature. Investigation of the dependence on laser power will clarify whether the observed behavior contains contributions from photon-induced processes. Improved data-collection techniques should allow the extension of the measurements to even shorter time scales, down to the recombination time of carriers in the QDs. The insight we have gained is thus a key step toward understanding, and eventually controlling, the blinking of QD fluorescence.
Supplementary Material
Acknowledgments
We thank Prof. Philippe Guyot-Sionnest for providing the QD samples and for valuable discussions, and Dr. Pavel Frantsuzov for helpful comments. This work was partially funded by National Science Foundation Grant CHE-0616663 (to N.F.S.), National Institutes of Health Grant R01GM67961 (to N.F.S.). The Center for Nanoscale Materials is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Contract DE-AC02-06CH11357. R.A.M. thanks the Office of Naval Research and the National Science Foundation for support. N.F.S. acknowledges the J. S. Guggenheim Foundation for a fellowship.
Abbreviations
- DCET
diffusion-controlled electron transfer
- QD
quantum dot
- VB
valence band.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0706164104/DC1.
Here, kr corresponds to the value (2πV2/ℏ)(1/(∂U12/∂Q))that appears in the form of a term 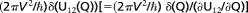 in equation 1c of ref. 25. In this equation, we note that the difference of the slopes of the energy parabolas at their intersection, ∂U12/∂Q, equals κa, and the reorganization term λ equals ½κa2. Using these results, one sees that the present value of tc corresponds to the value given in the line following equation 2b in the same reference.
in equation 1c of ref. 25. In this equation, we note that the difference of the slopes of the energy parabolas at their intersection, ∂U12/∂Q, equals κa, and the reorganization term λ equals ½κa2. Using these results, one sees that the present value of tc corresponds to the value given in the line following equation 2b in the same reference.
References
- 1.Murray CB, Norris DJ, Bawendi MG. J Am Chem Soc. 1993;115:8706–8715. [Google Scholar]
- 2.Hines MA, Guyot-Sionnest P. J Phys Chem. 1996;100:468–471. [Google Scholar]
- 3.Colvin VL, Schlamp MC, Alivisatos AP. Nature. 1994;370:354–357. [Google Scholar]
- 4.Eisler H-G, Sundar VC, Bawendi MG, Walsh M, Smith HI, Klimov V. Appl Phys Lett. 2002;80:4614–4616. [Google Scholar]
- 5.Bruchez M, Moronne M, Gin P, Weiss S, Alivisatos AP. Science. 1998;281:2013–2016. doi: 10.1126/science.281.5385.2013. [DOI] [PubMed] [Google Scholar]
- 6.Chan WCW, Nie S. Science. 1998;281:2016–2018. doi: 10.1126/science.281.5385.2016. [DOI] [PubMed] [Google Scholar]
- 7.Nirmal M, Dabbousi BO, Bawendi MG, Macklin JJ, Trautman JK, Harris TD, Brus LE. Nature. 1996;383:802–804. [Google Scholar]
- 8.Kuno M, Fromm DP, Hamann HF, Gallagher A, Nesbitt DJ. J Chem Phys. 2000;112:3117–3120. [Google Scholar]
- 9.Shimizu KT, Neuhauser RG, Leatherdale CA, Empedocles SA, Woo WK, Bawendi MG. Phys Rev B. 2001;63:205316. [Google Scholar]
- 10.Kuno M, Fromm DP, Gallagher A, Nesbitt DJ, Micic OI, Nozik AJ. Nano Lett. 2001;1:557–564. [Google Scholar]
- 11.Wang S, Querner C, Emmons T, Drndic M, Crouch CH. J Phys Chem B. 2006;110:23221–23227. doi: 10.1021/jp064976v. [DOI] [PubMed] [Google Scholar]
- 12.Kuno M, Fromm DP, Hamann HF, Gallagher A, Nesbitt DJ. J Chem Phys. 2001;115:1028–1040. [Google Scholar]
- 13.Talapin DV, Mekis I, Götzinger S, Kornowski A, Benson O, Weller H. J Phys Chem B. 2004;108:18826–18831. [Google Scholar]
- 14.Messin G, Hermier JP, Giacobino E, Desbiolles P, Dahan M. Opt Lett. 2001;26:1891–1893. doi: 10.1364/ol.26.001891. [DOI] [PubMed] [Google Scholar]
- 15.Verberk R, Orrit M. J Chem Phys. 2003;119:2214–2222. [Google Scholar]
- 16.Verberk R, van Oijen AM, Orrit M. Phys Rev B. 2002;66:233202. [Google Scholar]
- 17.Huff RF, Swift JL, Crumb DT. Phys Chem Chem Phys. 2007;9:1870–1880. doi: 10.1039/b617115j. [DOI] [PubMed] [Google Scholar]
- 18.Pelton M, Grier DG, Guyot-Sionnest P. Appl Phys Lett. 2004;85:819–821. [Google Scholar]
- 19.Jensen HJ, Christensen K, Fogedby HC. Phys Rev B. 1989;40:7425–7427. doi: 10.1103/physrevb.40.7425. [DOI] [PubMed] [Google Scholar]
- 20.Kertész J, Kiss LB. J Phys A: Math Gen. 1990;23:L433–L440. [Google Scholar]
- 21.Efros AL, Rosen M. Phys Rev Lett. 1997;78:1110–1113. [Google Scholar]
- 22.Kuno M, Fromm DP, Johnson ST, Gallagher A, Nesbitt DJ. Phys Rev B. 2003;67:125304. [Google Scholar]
- 23.Tang J, Marcus RA. J Chem Phys. 2005;123 doi: 10.1063/1.2128409. 054704. [DOI] [PubMed] [Google Scholar]
- 24.Sumi H, Marcus RA. J Chem Phys. 1986;84:4894–4914. [Google Scholar]
- 25.Tang J, Marcus RA. J Chem Phys. 2005;123:204511. doi: 10.1063/1.2128409. [DOI] [PubMed] [Google Scholar]
- 26.Tang J, Marcus RA. Phys Rev Lett. 2005;95:107401. doi: 10.1103/PhysRevLett.95.107401. [DOI] [PubMed] [Google Scholar]
- 27.Frantsuzov PA, Marcus RA. Phys Rev B. 2005;72:155321. [Google Scholar]
- 28.Margolin G, Barkai E. J Chem Phys. 2004;121:1566–1577. doi: 10.1063/1.1763136. [DOI] [PubMed] [Google Scholar]
- 29.Brokmann X, Hermier J-P, Messin G, Desbiolles P, Bouchard J-P, Dahan M. Phys Rev Lett. 2003;90:120601. doi: 10.1103/PhysRevLett.90.120601. [DOI] [PubMed] [Google Scholar]
- 30.Margolin G, Protasenko V, Kuno M, Barkai E. J Phys Chem B. 2006;110:19053–19060. doi: 10.1021/jp061487m. [DOI] [PubMed] [Google Scholar]
- 31.Zwanzig R, Ailawadi NK. Phys Rev. 1969;182:280–283. [Google Scholar]
- 32.Chung I, Bawendi MG. Phys Rev B. 2004;70 165304. [Google Scholar]
- 33.Hsu C-P, Song X, Marcus RA. J Phys Chem B. 1997;101:2546–2551. [Google Scholar]
- 34.Fisher BF, Eisler H-J, Stott NE, Bawendi MG. J Phys Chem B. 2006;108:143–148. [Google Scholar]
- 35.Shim M, Shiloy SV, Braiman MS, Guyot-Sionnest P. J Phys Chem B. 2000;104:1494–1496. [Google Scholar]
- 36.Burda C, Link S, Mohammed M, El-Sayed M. J Phys Chem B. 2001;105:12286–12292. [Google Scholar]
- 37.Wang C, Shim M, Guyot-Sionnest P. Science. 2001;291:2390–2392. doi: 10.1126/science.291.5512.2390. [DOI] [PubMed] [Google Scholar]
- 38.Wang C, Wehrenberg BL, Woo CY, Guyot-Sionnest P. J Phys Chem B. 2004;108:9027–9031. [Google Scholar]
- 39.Yu M, van Orden A. Phys Rev Lett. 2006;97 doi: 10.1103/PhysRevLett.97.237402. 327402. [DOI] [PubMed] [Google Scholar]
- 40.Zhang K, Chang H, Fu A, Alivisatos AP, Yang H. Nano Lett. 2006;6:843–847. doi: 10.1021/nl060483q. [DOI] [PubMed] [Google Scholar]
- 41.Biebricher B, Sauer S, Tinnefeld P. J Phys Chem B. 2006;110:5174–5178. doi: 10.1021/jp060660b. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.