Coupling of Fast and Slow Modes in the Reaction Pathway of the Minimal Hammerhead Ribozyme Cleavage

Abstract

By employing classical molecular dynamics, correlation analysis of coupling between slow and fast dynamical modes, and free energy (umbrella) sampling using classical as well as mixed quantum mechanics molecular mechanics force fields, we uncover a possible pathway for phosphoryl transfer in the self-cleaving reaction of the minimal hammerhead ribozyme. The significance of this pathway is that it initiates from the minimal hammerhead crystal structure and describes the reaction landscape as a conformational rearrangement followed by a covalent transformation. The delineated mechanism is catalyzed by two metal (Mg²⁺) ions, proceeds via an in-line-attack by CYT 17 O2′ on the scissile phosphorous (ADE 1.1 P), and is therefore consistent with the experimentally observed inversion configuration. According to the delineated mechanism, the coupling between slow modes involving the hammerhead backbone with fast modes in the cleavage site appears to be crucial for setting up the in-line nucleophilic attack.

INTRODUCTION

The emerging view is that long-range or global and short-range or local motions in biomolecules with a diverse range of timescales tend to couple to bring together the essential elements required for chemical catalysis (1–7). The coupling of fast and slow modes poses limitations on the conformational sampling and plagues the use of computationally demanding quantum mechanics molecular mechanics (QMMM) modeling approaches to characterize complex reaction pathways. In this article, we investigate the effect of coupling between the slow dynamical modes and the fast (reactive) dynamical modes on the phosphoryl transfer pathway of the minimal hammerhead ribozyme.

The discovery that RNA can catalyze certain biochemical reactions has raised the fundamental question of how RNA enzymes work (8–15). Many principles governing the catalytic mechanisms are unique to RNA enzymes (or ribozymes), and many others overlap with protein enzymes (16–26). These features are beginning to be exploited in a variety of biochemical applications (10–12,15), particularly in the design of riboswitches.

Hammerhead RNAs are small self-cleaving RNAs (11,27–30) with a conserved motif consisting of three basepaired stems flanking a central core of 15 conserved nucleotides (27,28). The conserved central bases, with few exceptions, are essential for ribozyme's catalytic activity (28). In terms of the structure (31–36) and in terms of the cleavage chemistry—kinetic studies (37–39), folding studies (29,40–44), effects of ion binding and rescue (45–55), elemental substitution at the cleavage site (49,56), cross-linking (28), effects of protonation and proton transfer (57–60), single molecule studies (42,61–63), phosphoryl transfer mechanism (37,64–70), alternative reaction mechanisms (71,72)—the hammerhead is a widely characterized ribozyme (28,36).

The phosphoryl transfer reaction in the hammerhead RNA results in the self-cleavage of the phosphate backbone. There exists a debate over whether a “two-metal-ion” catalyzed phosphoryl transfer mechanism—believed to be common to phosphoryl transfer reactions across several biomolecules (73)—is operational in hammerhead catalysis (69,70). In the two-metal-ion catalyzed phosphoryl transfer, one divalent metal (Mg²⁺) ion (termed catalytic) sets up the in-line attack of the nucleophilic anion on the phosphorous and possibly even plays a direct role in the deprotonation of the anion before attack, and a second metal (Mg²⁺) ion is believed to facilitate product dissociation. Experimental and theoretical evidence suggests that the resulting nucleophilic attack proceeds via a conformation resembling a trigonal-bipyramidal transition state formed by a pentacovalent phosphorous intermediate (19,74,75). A body of experimental studies involving several enzymes indicate that phosphoryl transfer reactions can proceed either via an associative or a dissociative mechanism (75–77). Recently, direct structural evidence based on x-ray crystallography for a partially-associative transition state in β-phosphoglucomutase was reported, in which the critical distance between nucleophilic oxygen and the target phosphorous was 2.0 Å (75). A similar geometry was also observed in the crystal structure of a group I intron splicing catalytic RNA (19). The most recent structural study involving the full-length hammerhead construct reveals an active site almost poised for an in-line attack, with a nucleophile to phosphorous attack distance of 3.2 Å and an in-line attack angle of 160° in the ground (crystal) state (36).

The native structure of the minimal hammerhead construct (18,30,32–35,78) differs significantly from its full-length counterpart (36). One of the prominent features of the full-length hammerhead ribozyme structure (Protein Data Bank (PDB) code, 2GOZ), which is not present in the minimal hammerhead (PDB code, 379D) is that the tertiary stem II loop/stem I bulge interactions appear to induce structural organization of the catalytic core. This difference translates into a dramatic change in the cleavage (or active) site: in the minimal hammerhead crystal the attacking 2′-oxygen is nearly 90° removed from that required for an in-line attack for S_N2(P) cleavage, whereas in the full-length structure, this angle is within 20° of the ideal transition state value. (That is, the full-length hammerhead ribozyme is almost poised for an in-line attack). Moreover, the average distance between the phosphates of the so-called rescue (A9, G10) and cleavage sites in the minimal construct is ∼20 Å, in stark contrast to a value of 7 Å in the full-length construct. For the full-length hammerhead molecule, this latter aspect was inferred in pioneering earlier biochemical experiments: specifically, metal ion rescue experiments with full-length hammerheads containing two phosphorothioates at A9 and the scissile phosphate suggested that the A9/G10.1 metal site (referred to as the rescue site) and the scissile phosphate (referred to as the cleavage site) coordinate the same Mg²⁺ ion in the transition state (49).

The striking differences in structure between the minimal and full-length hammerhead ribozymes together with a large body of functional (mutation) data suggest that the minimal hammerhead molecule likely undergoes a dramatic conformational isomerization before cleavage to catalyze the self-cleavage (79). The existence of several alternative mechanisms for the hammerhead ribozyme catalysis has been postulated (33,71,72) but not carefully characterized.

Computational annotations of the transphosphorylation reaction in fragment models constructed to mimic the ribozyme catalytic reaction have been reported by Gregerson et al. (80). These authors find that the in-line attack mechanism is associative in character and proceeds via two concerted transition states. The relative heights of the barriers depend on the context, i.e., different for native versus thio substituted fragments. In different studies, the authors have also reported kinetic isotope effects (81) and pesudorotation in oxyphosphoranes (82). These ab initio studies in RNA-like active-site fragments provide detailed insights into the possible contexts of phosphoryl transfer, which makes our extension to the cleavage reaction of a fully solvated ribozyme here possible.

In this article we employ several computational protocols with the objective of gaining insight into the catalytic pathways of the minimal hammerhead ribozyme. In particular, we hope to gain some insight on how a coupling between fast and slow modes (which is inevitable under the requirement of a conformational isomerization) will affect the pathway of phosphoryl transfer. Based on classical molecular dynamics (MD), correlation analysis of coupling between slow and fast dynamical modes, and free-energy (umbrella) sampling using classical as well as mixed QMMM force fields, we uncover a possible pathway for phosphoryl transfer in the self-cleaving reaction of the minimal hammerhead ribozyme. Although, we cannot guarantee its uniqueness, the significance of this pathway is that it initiates from the minimal hammerhead crystal structure and describes the reaction landscape as a conformational rearrangement followed by a covalent transformation. The delineated mechanism is catalyzed by two metal (Mg²⁺) ions, proceeds via an in-line attack by CYT 17 O2′ on the scissile phosphorous (ADE 1.1 P), and is therefore consistent with the experimentally observed inversion configuration. Our computed pathway suggests a strong coupling between the ribozyme backbone motion and the fast motions in the active site, which is crucial to transform the catalytic geometry into one that is poised for direct in-line attack.

METHODS

System preparation

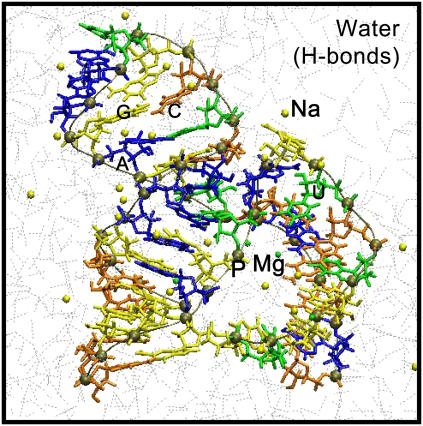
Two models of the minimal hammerhead molecule are constructed from published x-ray crystal structures of Scott et al. (PDB codes, 379D and 301D) (34,35). Missing hydrogen atoms are added and the crystallographic divalent ions are replaced with Mg²⁺ ions. The protonation states of the nucleic acid residues are chosen based on their individual pKa values and assuming an aqueous environment at a pH of 7.0. The models are solvated in a cubic box of water molecules using the software package SOLVATE 1.0 (83), which also neutralizes the system by placing Na⁺ and Cl⁻ ions at an isotonic concentration (0.154 mol/l) and in accordance with a Debye-Huckel potential distribution at a temperature of 300 K. The solvated complex contains 41 ribozyme nucleotide bases consisting of 1321 atoms (see sequence and naming convention in Supplementary Table S1), 5 Mg²⁺ ions, 37 Na⁺ ions, 8 Cl⁻ ions, and 5276 water molecules. (A snapshot of the solvated neutral system with a total of 17,199 atoms is depicted in Fig. 1.) Structures are visualized and snapshots are rendered using the program VMD (84).

FIGURE 1.

Cropped image of the simulation cell depicting the phosphorous backbone (tan) of the minimal hammerhead, explicit water, Mg²⁺ ions (green), Na⁺ ions (yellow), and Cl⁻ ion (cyan).

Molecular dynamics

Several MD simulations of explicitly solvated ribozyme systems with classical force fields yielding stable and reliable results have been reported (see review by Westhof et al. (85)). In general, there are a variety of critical issues in a simulation of nucleic acids that need to be considered. These include properly representing the effects of the environment, in particular, ionic strength and identity effects, overcoming conformational sampling limitations, developing and applying more accurate and representative force fields, and further characterizing known artifacts of the methods. It was concluded that even for extreme polyelectrolyte systems such as nucleic acids, the force fields provided adequate representation in many contexts: the observation of phased A-tract bending and other sequence-dependent DNA fine structures, the precise description of the importance of specific hydration and ion association in nucleic acids, the ability to estimate the conformational free-energy differences of different nucleic acid structures, and the reliable representation of the environmental dependence of nucleic acid structures give great promise for the future predictive studies (86).

Conformational fluctuations of a double-stranded RNA oligonucleotide have been obtained from molecular dynamics including explicit waters and ions and from a harmonic mode analysis. The qualitative pattern of atomic position and helical descriptor fluctuations along the sequence was similar for both approaches (87,88). Specific to the application of the CHARMM force field to RNA systems, MD studies have explored the stabilizing role of loop-closing residues in kissing interactions in trans-acting responsive element and aptamer systems (89). MD simulations and free-energy calculations of base flipping in dsRNA have also been reported using the CHARMM force field (90). The general consensus from these studies is that the force field provides a satisfactory representation of the overall conformational dynamics for explicitly solvated systems.

Recently, the role of cations and hydration in catalytic RNA has been studied by MD simulations of the hepatitis δ-virus ribozyme by Krasovska et al. (91). The simulations find that one Mg²⁺ cation binds stably, by both inner- and outer-sphere contacts, to the electronegative catalytic pocket of the reaction precursor; according to the authors, this position potentially supports the notion of a concerted reaction mechanism in which C75 and hydrated Mg²⁺ act as general base and acid, respectively.

Our (explicitly solvated) structures of the hammerhead ribozyme are subjected to two rounds of energy minimization and constant temperature equilibration runs using the CHARMM27 force field (92) at 300 K, first with ribozyme atoms and Mg²⁺ ions fixed, and subsequently with no constraints. The systems are then subjected to two independent 30-ns constant pressure (1 atm) constant temperature (300 K) MD simulations with periodic boundary conditions enforced and long-range electrostatics treated through the particle mesh Ewald method. These dynamics runs are carried out using the NAMD package (93) and the resulting aggregate 60-ns trajectory is used in further analysis.

Principal component analysis

Principal component analysis (PCA) (94) is performed by constructing a covariance matrix σ (here, the underscore represents a matrix) whose elements are given by: σ_ij = 〈(x_i − 〈x_i〉)(x_j − 〈x_j〉)〉, where i and j run from 1,…,3N, N being the total number of atoms, x represents the position vector in a Cartesian system of coordinates, and the average is calculated over the aggregate 60-ns trajectory. The diagonalization of the covariance matrix produces a set of eigenvectors (principal components (PCs)), which represents the set of independent directions of atomic motions about the average structure. Each calculated eigenvalue (ev) is a measure of the amplitude of motion along the corresponding eigenvector. The first few principal components (in decreasing order of eigenvalues) describe the largest positional fluctuations. Using the CARMA software (95), the top five principal components are visualized.

QMMM simulations

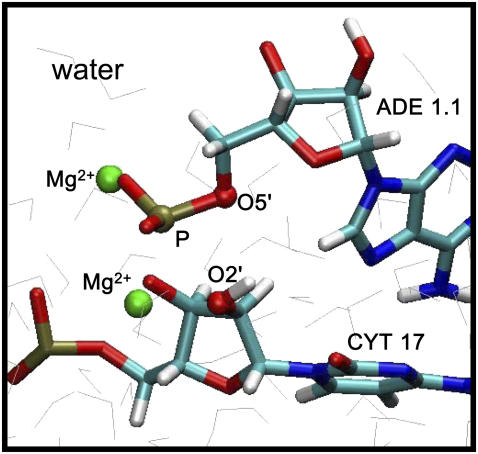
The QMMM approach we adopt is based on an existing interface between GAMESS-UK (96) (an ab initio electronic structure prediction package) and CHARMM (97). The crux of the QMMM approach is to perform wave function optimizations in the QM region according to a density functional theory. That is, the forces in the quantum region are calculated on-the-fly assuming that the system evolves on the Born-Oppenheimer surface. The forces on the classical region are calculated using a classical force field. We choose C17, A1.1, C1.2 (see Fig. 2) of the hammerhead ribozyme, the two Mg²⁺ ions in the vicinity of the cleavage site (ADE 1.1 P), and water molecules within 4.5 Å of the Mg²⁺ ions, amounting to a total of 64 atoms (including three link atoms; see below) as the quantum region and treat them quantum mechanically using density functional theory with a B3LYP exchange correlation functional and a 6-311G** basis set (98). The remaining nucleic acid atoms, ions, and solvent molecules are treated classically using the CHARMM27 force field. Because the QMMM boundary cuts across covalent bonds, we use the single link atom procedure (99) to satisfy the valencies of those atoms in the QM region that host the broken bonds. Three link atoms are placed and constrained to stay on the following bonds between the classical host and the quantum host atoms: CYT 17 C5′ and CYT 17 C4′; CYT 17 N1 and CYT 17 C1′; ADE 1.1 C4′ and ADE 1.1 C5′. In our simulations electrostatic interactions between the quantum atom and the classical atom hosting a link atom between them is discarded; this choice has been shown to provide enhanced accuracy in the resulting energies and geometries (100). These choices are identical to our prior application for pol β and have yielded reliable results (101). Energy minimizations and molecular dynamics simulations are performed in accordance with the QMMM Hamiltonian. The system is minimized using the Steepest Descent method for 100 steps followed by adapted basis Newton-Raphson for 10,000 steps. The system is then equilibrated for 5 ps at 300 K using a Verlet integrator with a 1-fs time step. The electrostatic and van der Waals interactions are smoothed to zero at 12 Å. The accuracy of the force field and the QMMM Hamiltonian at the level of theory employed here is expected to be within 2 kcal/mol, which is sufficient for a quantitative delineation of the energy landscape.

FIGURE 2.

Active (cleavage) site of the hammerhead ribozyme. The scissile phosphorous (tan, ADE 1.1 P), the attacking nucleophile (red, CYT 17 O2′), and the leaving oxygen (red, ADE 1.1 O5′) are in ball notation.

Umbrella sampling

This procedure enables the calculation of the potential of mean force (free-energy density) along an a priori chosen set of reaction coordinates (or order parameters χ_i), from which free-energy changes are calculated by numerical integration; see Chandler (102), for example. For the free-energy calculation, the probability distribution P(χ_1, χ₂) is calculated by dividing the range of order parameter χ_i into several (five to 10) windows. The histograms for each window are collected by harvesting trajectories in that window. To enhance the sampling in each window, two harmonic restraints with force constants of K = 20 kcal/mol/Ų were applied along χ₁ and χ₂. The restraints are set up by adding the harmonic term (1/2) × K × (χ_i − χ_i,0)², χ_i,0 being the target distance along the restrained coordinate for that window. The calculation of the multidimensional potential of mean force (along multiple reaction coordinates) using the weighted histogram analysis method (WHAM) is reviewed by Roux (103). We adopt this recipe for removing the applied bias and combining the results from different windows.

To obtain the free-energy landscape of a conformational change, umbrella sampling is performed with the classical molecular dynamics trajectories to obtain the free-energy landscape along a specified principal component, PC_i. To achieve this task, we generate two coordinate files, the first corresponding to the initial equilibrated state X₀ and the second corresponding to X_f = X₀ + 4 × ev_i × PC_i. This second coordinate corresponds to traveling along the chosen PC_i by a normalized distance (i.e., weighted by the eigenvalue ev_i) which is four times the value captured in the 60-ns MD trajectory. The two order parameters χ₁ and χ₂ are chosen as root mean-square deviation between the conformation X(t) at time t and X₀, and X(t) and X_f, respectively. In total, 25 windows are sampled as a uniform 5 × 5 grid along χ₁ (2.5–4.5 Å) and χ₂ (2.5–5.5 Å), with each window harvesting a classical MD trajectory of 500 ps. The error bars are calculated by repeating one of the 25 windows using a different initial condition and calculating the standard deviation. This is found to be 0.9 k_BT, and is taken to be the same for all the other windows.

To obtain the free-energy landscape associated with the chemical step, umbrella sampling is performed using QMMM MD simulations with χ₁ and χ₂ chosen as CYT 17 O2′- ADE 1.1 P and CYT 17 O2′- Mg²⁺ distances in the cleavage site (see Fig. 2). In total, 25 windows are sampled as a uniform 5 × 5 grid along χ₁ (1.5–3.4 Å) and χ₂ (1.5–2.8 Å), with each window harvesting a QMMM MD trajectory of 2 ps. The calculated error bar (see procedure described above) is found to be 1.5 k_BT.

The total CPU time for umbrella sampling using the classical force fields was 12 h per umbrella window per processor on four processors of a 3.2-GHz Intel Xeon cluster with an aggregate total of 1200 CPU hours for 25 windows. The CPU time for umbrella sampling using the QMMM MD required 24 h per processor per umbrella window on 32 processors yielding an aggregate total of 19,200 CPU hours.

The analysis of correlations through the PCA approach relies on the harmonic approximation in the ground state to be valid until the system reaches the transition state. This approach is expected to be valid if the ground state and transition states are similar in conformational terms but may break down for large conformational differences. Thus, extensions of our approach that do not make this assumption are possible by incorporating a local direction for slow modes in path space by defining isocommittor surfaces (104), to replace the eigenvectors obtained from PCA.

RESULTS

The aggregate 60-ns classical MD trajectory initiated from the crystal structure of the minimal hammerhead ribozyme (34,35) did not reveal any global conformational rearrangements. However, the molecule is observed to be highly dynamic with amplitudes of relative motion between some domains recording 4–7 Å. (see Supplementary Fig. S1, Supplementary Material). A PCA of the MD trajectory allowed us to dissect the motion along specific modes or PCs (Supplementary Fig. S1). The active site constituted by four successive bases U, C17, A1.1, C1.2 (see Fig. 2 and sequence in Supplementary Table S1; the cleavage site is between CYT 17 and ADE 1.1 bases) undergoes a small local conformational rearrangement in one of the two 30-ns trajectories as a result of a sugar-repuckering transition in bases A1.1 and C 1.2 (Supplementary Fig. S2). However, as a result of this change, the geometry of the active site is not perturbed in any significant fashion (key measures are depicted in Supplementary Fig. S3). In particular, the distances and angles associated with the attacking nucleophile (CYT 17 O2′), the scissile phosphorous (ADE 1.1 P), and the leaving oxygen (ADE 1.1 O5′) are relatively stable: O2′-P distance ∼4 Å, O5′-P distance ∼4 Å, and the O2′-P-O5′ angle of 90°, which as such, are far from conforming to an in-line nucleophilic attack.

In contrast to these stable active site distances and geometries, the landscape of Mg²⁺ motion appears to be relatively diffuse (Supplementary Fig. S4): in our trajectories, we observe the bound Mg²⁺ ions at the cleavage site (in the vicinity of ADE 1.1 P) and the rescue site (in the vicinity of GUA 10.1 N7) to be stable in a 10-ns timescale (Supplementary Fig. S4, A and N); their escape is observed over the course of the 30-ns (Supplementary Fig. S4 I). We also observe a different Mg²⁺ or even a surrogate Na⁺ ion replace the original bound ion at the two sites (Supplementary Fig. S4, J and L). Moreover, on several instances, a diffusely bound second Mg²⁺ ion at the cleavage site is observed to be transiently stable with a residence time of 10–100 ps (Supplementary Fig. S4 D). This transient reconstruction of two-metal-ion geometry in the cleavage site occurs several times and appears to be diffusion limited.

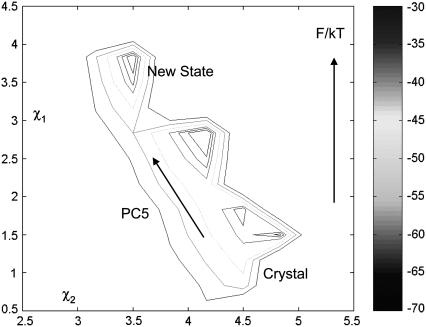
Because the minimal hammerhead ribozyme is a flexible biomolecule, we sought to find a relationship between the conformational flexibility of the phosphate backbone of the ribozyme and the dynamics of the active-site degrees of freedom. To explore this relationship between global (delocalized) and local modes, we perform PCA of the 60-ns MD trajectory (Supplementary Fig. S1) to look for the coupling of principal (slow) modes with key distances in the active site. In particular, we identify a dynamic coupling (strong correlations) between principal component or PC 5 and a fast mode constituting angular fluctuations involving the scissile phosphate, namely, O2′-P-O5′, O5′-P-O1P, and O3′-P-O5′ angles at the cleavage site. (None of the other top 10 modes showed any correlation with the active site motion). To capture the effect of this coupling beyond that captured in the 60-ns trajectory, we perform umbrella sampling along PC 5 (free-energy landscape depicted in Fig. 3; also see Methods) to find that the hammerhead ribozyme molecule assumes two conformationally distinct stable states with reference to the 301D or the 379D crystal structure. The free-energy minimum labeled new state in Fig. 3 is more stable than the crystal state by 3 k_BT. The calculated free-energy barrier for the transition is 35 k_BT (corresponding to a rate of 80 min⁻¹), which is 100-fold greater than the experimentally observed cleavage rate for the minimal hammerhead molecule.

FIGURE 3.

Free-energy landscape based on umbrella sampling along PC 5 (PC5). The emergence of two metastable states conformationally distinct from the state closest to the crystal structure is evident. χ_i-values are in angstroms.

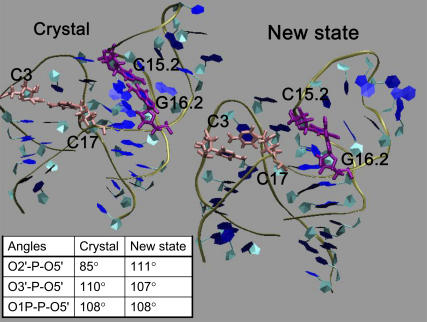
The overall backbone conformation of the new state is not drastically different from the minimal hammerhead crystal structure as depicted in the comparison in Fig. 4. In particular, a majority of the stacking interactions and Watson-Crick basepairs are preserved during this conformational change including: G2.5:C1.5, U2.4:A1.4, G2.3:C1.3, G2.2:C1.2, and U2.1:A1.1. However, the Watson-Crick basepair C15.2:G16.2 gets disrupted and A15.1:U assumes a wobble basepair conformation in the new state. To compensate for this disruption, the interaction between CYT 3 and CYT 17 is stabilized in the new state (hydrogen bond distances between CYT 3 O2 and CYT 17 H42 of 1.8 Å and between CYT 3 N3 CYT 17 H5 of 2.5 Å) in comparison to the crystal state (the respective distances being 2.3 and 5.6 Å); see Fig. 4. The differences in basepair interactions between the two states (labeled crystal and new in Fig. 4) translate into a subtle but crucial difference in the active-site geometry. Namely, the O2′-P-O5′ angle is always less than the O3′-P-O5′ angle in the crystal state, whereas the trend is reversed in the new state; see inset in Fig. 4. This difference sets up the possibility of an in-line attack by the O2′ nucleophile in the new state, whereas the crystal state is far from being poised for an in-line attack.

FIGURE 4.

Depiction of conformations in crystal (379D) and new states. The disruption of the Watson-Crick basepair between C15.2:G16.2 (purple) in the new state is evident. Also apparent is the change in the interaction between C3 and C17. The effect of the conformational change on the active-site geometry is evident from the table (inset).

Next, we explore the effects of the conformational isomerization (between the crystal and the new state) on the self-cleaving reaction landscape of the hammerhead ribozyme. Specifically, we perform umbrella sampling with the QMMM Hamiltonian to map the phosphoryl transfer reaction pathway and the associated energetics from the crystal state as well as from the new state.

Starting from a transiently assembled two-metal-ion conformation observed in the course of our classical MD simulations in the crystal state (see t < 10 ns in Supplementary Fig. S4 and Fig. 2) and by employing molecular dynamics with a QMMM Hamiltonian (density functional theory using a B3LYP functional and a 6-311G** basis set) we perform two-dimensional (WHAM) umbrella sampling (103); we are able to compute the phosphoryl transfer free-energy landscape as a function of key variables: CYT 17 O2′-ADE 1.1 P and CYT 17 O2′-Mg²⁺ distances and observe the self-cleaving reaction (Supplementary Fig. S5). We find that the reaction proceeds via a pentacovalent transition state around the central phosphorous atom, but not through an in-line attack. At the transition state, the CYT 17 O3′-ADE 1.1 P-ADE 1.1 O5′ angle was 180° with the two bond distances assuming 1.86 Å. The CYT 17 O2′ anion, instead, coordinated the ADE 1.1 P at 1.73 Å and made 120° angles of O2′-P-O1P and O2′-P-O1P. There is a concomitant proton (H2′) transfer from O2′ to a neighboring water molecule and subsequently through a Grotthuss hopping mechanism (105) to ADE 1.1 O5′. The phosphoryl transfer occurs in one step and relies on a transiently bound second metal to complete the two-metal-ion geometry; this conformation was spontaneously observed on several occasions in our aggregate 60-ns simulations. The reaction results in a stereoisomer with a retention conformation about the central phosphorous with a calculated free-energy barrier of 40 k_BT, as opposed to the experimentally observed inversion conformation; the free-energy barrier (using transition state theory) translates to a cleavage rate of 1 min⁻¹; even though the experimental cleavage rate for a minimal hammerhead is also ∼1 min⁻¹, we have to conclude that the near-perfect agreement of calculated and experimental rates is rather fortuitous because it is known that the B3LYP functional underestimates free-energy barriers.

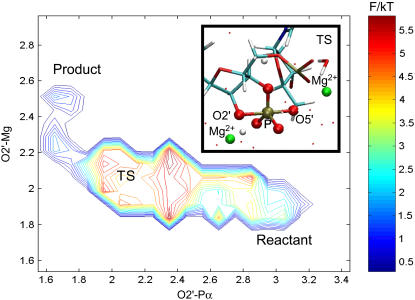
Intriguingly, however, the free-energy landscape obtained through umbrella sampling from the new state using the QMMM Hamiltonian (B3LYP and 6-311G**) along the distances of O2′-P and O2′-Mg yields the correct stereoisomer (inversion about the scissile phosphate) as the product, and the reaction proceeds via an in-line attack (see Fig. 5); the calculated free-energy barrier for the phosphoryl transfer step is 6 k_BT, much lower than that for the conformational change, indicating that the conformational change is rate limiting. The coupling between the slow backbone motion and the dynamic fluctuations in the active site manifests by selecting a phosphoryl transfer reaction pathway leading to an inversion, which in its absence, proceeds via a retention configuration about the scissile phosphorous. Therefore, the coupling between slower modes resulting from the enzyme's backbone motion with the fast modes involved in the reaction, which leads to the conformational isomerization, completely alters the reaction channel for phosphoryl transfer.

FIGURE 5.

Umbrella sampling with QMMM dynamics initiated from the new state leads to the correct (experimentally observed) reaction mechanism. Inset depicts the transition state with a trigonal-bipyramidal geometry around ADE 1.1 P.

DISCUSSION AND CONCLUSION

A common thread that has emerged from experimental as well as theoretical studies on a wide range of enzyme-substrate systems is that the ubiquitous coupling of fast and slow dynamical modes in biomolecular dynamics drives catalytic mechanisms (1–5). Here, we suggest through molecular simulation studies that for the minimal hammerhead ribozyme, the coupling manifests by selecting a reaction pathway leading to a phosphoryl transfer with inversion, which in its absence proceeds via a retention configuration about the scissile phosphorous, and is therefore crucial in capturing the physical pathway.

Our delineation of the overall mechanism for the hammerhead cleavage has revealed a conformational change preceding the phosphoryl transfer. The identity of the conformational change is highlighted by the observation that even though the overall backbone conformation of the new state is not drastically different from the crystal structure, differences do arise in base interactions in the vicinity of the cleavage site, which lead to a reversal of trend in relative values of O2′-P-O5′ and O3′-P-O5′ angles (Fig. 4). The significance of the conformational change is clear: the conformational state resulting from this change is poised for a two-metal-ion catalyzed phosphoryl transfer through an in-line nucleophilic attack. Indeed the phosphoryl transfer from the new state proceeds with a small activation free-energy barrier of 6 k_BT and the reaction proceeds via a trigonal-bipyramidal geometry around the scissile phosphorous and a partially associative mechanism. Concomitant proton transfer from O2′H mediated through two water molecules is crucial in stabilizing this transition state. Relaxation from the transition state to product involves a pseudorotation about the scissile phosphorous. Overall, similar evidence for geometry of the active site for the hairpin ribozyme is also garnered from recent computational studies based on classical simulations (106). In our simulations, the cleaved product is characterized by a stereoisomer with an inversion configuration about the scissile phosphorous and according to our calculations, the dominant barrier along the reaction pathway is that for the conformational change (35 k_BT), making it (as opposed to the covalent transformation) the rate-limiting step.

The physical relevance of the described reactive channel is subject to the usual well-appreciated limitations of our modeling strategy, i.e., the effect of CHARMM27 force field on RNA conformational energetics and our quasiharmonic approximation to the slow modes. However, mechanisms inferred from ab initio calculations on fragment models of the hammerhead ribozyme active site are in qualitative agreement with our suggested pathway. In particular, our umbrella sampling results suggests a barrier associated with pseudorotation about the scissile phosphorous consistent with the report of York et al. (82). Moreover, Murray et al. proposed alternative mechanism involving a conformational rearrangement of the cleavage site nucleotide during minimal hammerhead catalysis, which first involves positioning of the attacking nucleophile in-line with the 5′-oxygen leaving group of the RNA similar to that observed in an crystallized intermediate structure (33,78). This proposed alternative mechanism did not address the question of how the 5′-oxygen leaving group is stabilized (or how a proton is abstracted).

Irrespective, we underscore the importance of the identified dynamic coupling between modes: without the coupling, we get a fundamentally different transition state and product; with the coupling the transition state reflects the in-line attack and the product results in the physically observed stereoisomer. Thus, neglecting this coupling in the delineation of reaction free-energy landscapes in ribozymes and enzymes can have severe consequences. In the future, a simultaneous sampling of the slow and fast modes by combining umbrella sampling with path sampling will be attempted to make this approach more generally applicable.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.