Light-controlled self-assembly of reversible and irreversible nanoparticle suprastructures

Abstract

Nanoparticles (NPs) decorated with ligands combining photoswitchable dipoles and covalent cross-linkers can be assembled by light into organized, three-dimensional suprastructures of various types and sizes. NPs covered with only few photoactive ligands form metastable crystals that can be assembled and disassembled “on demand” by using light of different wavelengths. For higher surface concentrations, self-assembly is irreversible, and the NPs organize into permanently cross-linked structures including robust supracrystals and plastic spherical aggregates.

Self-assembly (1) induced and controlled by light^‡ is of continuing interest as a promising route to new types of structures and materials (2–4) with potential applications in optics (5), sensing (6), and delivery systems (7). Although considerable progress has been achieved in implementing light-induced self-assembly (LISA) at both colloidal (8, 9) and (macro)molecular scales (10, 11), the underlying phenomena and/or experimental methods have not proven effective at the nanoscale. For example, nanoscopic components of dimensions significantly smaller than the wavelength of light cannot be efficiently addressed and assembled by using optical confinement techniques [e.g., laser interference (8) and optical trapping (9)], on which virtually all colloidal LISA systems are based. At the same time, LISA based on light-induced interactions between nanoscale components coated with photoswitchable molecules (12, 13) has invariably led to disordered precipitates rather than crystalline assemblies. Here, we describe a system that circumvents these limitations, and in which photoisomerization of dithiol molecules bound onto the surfaces of metal nanoparticles (NPs) mediates their LISA into ordered, three-dimensional suprastructures: light-reversible or irreversible crystals (Figs. 1A and 2) and supraspheres of various sizes (Figs. 1A and 3). The degree of structural reversibility depends on the strength of light-induced, dipole–dipole interactions between the NPs and on the extent of covalent binding between them. Remarkably, for low surface concentrations of dithiol ligands, the assemblies are fully reversible and can be toggled between crystalline and disordered states multiple times by using light of different wavelengths. For higher concentrations, the ligands can permanently cross-link the assemblies, making them either mechanically/thermally robust (crystals) or flexible (spherical aggregates, “supraspheres”).

Fig. 1.

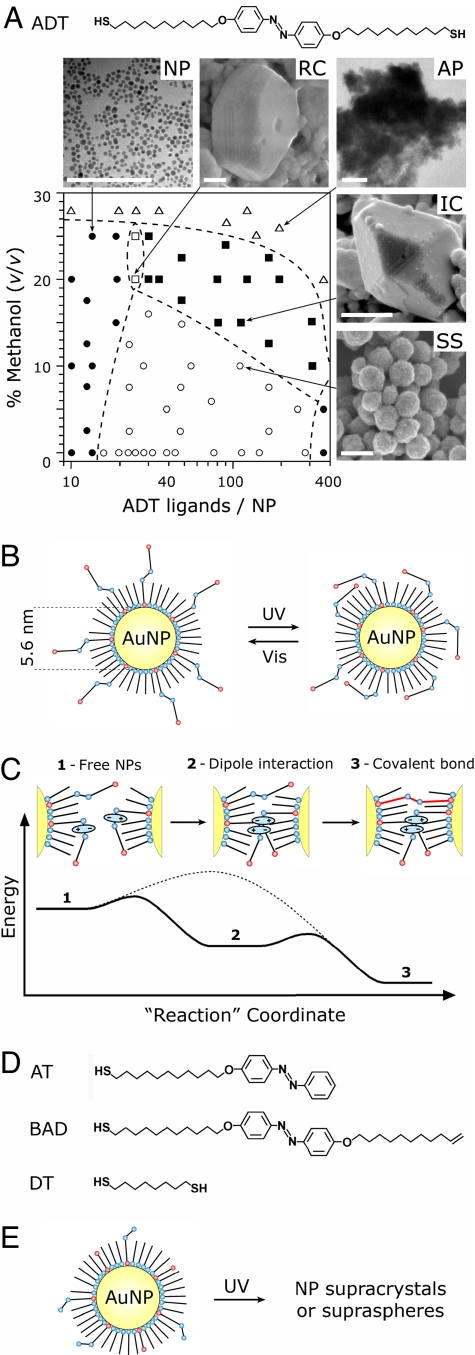
Phase diagram and mechanism of LISA. (A Upper) Structure of the photoswitchable dithiol azobenzene ligand (ADT) mediating LISA of nanoparticles. (Lower) Phase diagram showing various types of suprastructures obtained by LISA for different numbers of ADT ligands adsorbed onto each NP and for different concentrations of methanol in methanol/toluene mixtures. Each point corresponds to a separate experiment. NP, unaggregated NPs; RC, light-reversible crystals; AP, amorphous precipitate; IC, irreversible crystals; SS, supraspheres. (Scale bars: 100 nm.) The numbers of ligands per one NP were determined from solution concentrations according to the method described in detail in SI Appendix, sections 3 and 4. (B) The azobenzene groups of ADT ligands can be toggled between trans and cis conformations by using, respectively, UV and visible light. (C) Light-induced dipoles of cis-ADT ligands mediate NP self-assembly and allow covalent cross-linking of the assembled particles. Dashed line represents qualitatively an energy barrier for cross-linking in the absence of dipole–dipole interactions. After initial aggregation because of dipole–dipole interactions (Center), the NPs can bind covalently via dithiol linkages displacing weakly bound DDA (Right; note that cross-linking via the trans isomer is shown only for clarity; in reality, the alkyl chains of ADT ligands should be long enough to allow cross-linking by the cis-dithiols as well). (D) Model compounds used to investigate the roles of dipole–dipole forces and cross-linking effects in LISA. (E) A scheme of a nanoparticle coated with “decoupled” photoswitchable (AT), cross-linking (DT) molecules, and DDA capping agent. With all these components present on the surface, NPs can self-assemble into ordered phases analogous to those formed by NPs covered with ADT/DDA. This approach, however, is impractical because it requires adjustment and control of the surface concentrations of three species, DDA, AT, and DT.

Fig. 2.

LISA of reversible and irrreversible nanoparticle crystals. (A) (Upper) Reversible nanoparticle crystals form upon UV irradiation of AuNPs having low surface concentration of ADT ligands (thin, red halos). These crystals can be dissolved by exposure to visible light, and the light-induced assembly-disassembly cycle can be repeated multiple times. Pictures on the Left and on the Right show the same vial before (red solution of free AuNPs) and after (clear solution with dispersed black powder of crystals) LISA. (Lower) The SEM image on the Left shows a freshly prepared, faceted, reversible crystal. The TEM image on the Right shows how the crystal exposed to daylight for several seconds starts dissolving by detachment of individual NPs from its walls. (Scale bars: 100 nm in the main images and 50 nm in Inset.) (B) With higher concentration of ADT ligands (thick, red halos), the irradiated particles self-assemble and cross-link into irreversible, permanent crystals. The SEM images show crystals of various morphologies. (Scale bars: 200 nm.) (Lower Right) Magnified image of a hexagonal (100) face characterized by interparticle distance of 7.9 nm. (Scale bar: 50 nm.) (C) Small-angle powder XRD spectrum of the irreversible crystals. Solid line is the fit to experimental data (solid markers); dashed lines have the individual peaks resolved. The identified Bragg reflections on planes specified by Miller indices presented in Inset are characteristic of an hcp structure. Here, broadening of the XRD peaks is due to factors such as the finite size of the crystals, their mechanical deformations, defects, polydispersity of the constituent NPs, and the presence of residual amorphous phase.

Fig. 3.

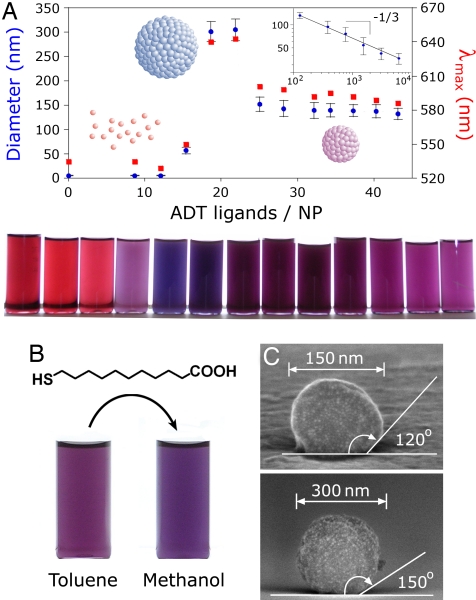
Nanoparticle supraspheres prepared by LISA. (A) Diameters (blue markers) and the wavelengths of maximal absorption (λ_max, red markers) for supraspheres formed by UV irradiation in pure toluene from NPs covered with various numbers of ADT ligands. Below the critical number of surface ligands per NP (here, ≈16), the photoinduced interactions between NPs are too weak to cause their aggregation. Above this limit, nucleation and growth of supraspheres occurs. (Inset) Suprasphere diameter decreases with increasing ADT concentration as D ∼ (C_ADT/C_NP)^−1/3, in agreement with the predictions of the nucleation-and-growth model (black line); here, the x axis refers to the total number (i.e., both surface-bound and free) of ADT ligands per NP. The vials in the bottom row are solutions of supraspheres arranged in the order of increasing ADT/NP ratio and correspond to the points in the plot. (B) Permanently cross-linked supraspheres can have their surfaces further derivatized (here, with 11-mercaptoundecanoic acid) and can be transferred to a more polar medium (here, methanol). (C) SEM images of two supraspheres adhered to and deformed on a silicon surface. Interestingly, the observed increase of the contact angle with increasing SS diameter suggest that these materials have plastic properties.

Results and Discussion

Interparticle Interactions.

Our experiments were based on gold nanoparticles (5.6 nm in diameter) prepared according to a modified literature procedure (14) (also see Materials and Methods). The AuNP solutions in toluene/methanol (0–30% v/v methanol content) were stabilized by dodecylamine (DDA) capping agent and didodecyldimethylammonium bromide (DDAB) surfactant. To such solutions, different amounts of photoactive trans-azobenzene dithiol ligands [4,4′-bis(11-mercaptoundecanoxy)azobenzene (ADT); compare Fig. 1A] were added under vigorous stirring. Low-intensity UV irradiation (365 nm, 0.7 mW/cm²) caused rapid trans-cis isomerization (13) of the ADTs (Fig. 1B Right) and induced molecular dipoles on the azobenzene units [μ = 4.4 debye for the cis (7) form vs. 0 debye for trans]. Importantly, only the isomerization of the ADTs bound to the NPs was significant for self-assembly. This conclusion was supported by two experimental observations: (i) when the surface coverages of ADTs on the NPs were high (>75%), the sterically crowded azobenzene units could not isomerize and the NPs did not aggregate even upon prolonged UV irradiation; (ii) likewise, when NPs were coated with alkane thiols (instead of weakly bound DDA), and the ADTs could not adsorb onto the particles [see supporting information (SI) Appendix for a discussion of competitive adsorption equilibrium], the trans-cis isomerization occurred only in solution. This isomerization, even with high ADT concentrations, had no effect on the stability of free NPs, which remained unaggregated as verified by UV-Vis spectroscopy and TEM.

The fact that the NPs assembled only upon induction of cis-ADT dipoles suggests that LISA is mediated by dipole–dipole interactions and, possibly, by the accompanying solvophobic effects. Based on this premise, the interaction energy between two NPs of radii R and suspended in a toluene/methanol environment can be approximated as the favorable adhesion energy gained by bringing these particles into close contact, E_ad = A_eff(σ₁₁ − 2σ₁₂). In this formula (15), the effective contact area is A_eff ≈ 2πRa, where a is a characteristic molecular scale (here, a ∼ 5 Å is taken as the smallest spacing between two cis-ADT dipoles; see SI Appendix), σ₁₁ is the surface energy of the NP–NP interface (here, due primarily to dipole–dipole interactions), and σ₁₂ is the surface energy of the NP-solvent interface.

If each NP is coated with N_azo randomly distributed cis-ADT ligands, the σ₁₁ term can be expressed as the product of the average number of dipole–dipole pairs per unit area of contact, estimated as ρ_dd = N_azo/4πR², and the energy of one such pair, E_dd, which is ≈0.5 kcal/mol. Here, the dipole–dipole energy is calculated as E_dd(r) = −(μ²/4πε₀εr³)²/3kT for the Boltzmann-averaged interaction between two freely rotating, permanent dipoles, where ε is the dielectric constant of the medium (e.g., ε_toluene = 2.379), μ is the dipole moment, r is the distance between dipole centers, k is Boltzmann's constant, and T is the temperature (compare SI Appendix, section 2). The values of σ₁₂ are estimated from literature data for chemically similar interfaces (n-alkane/toluene and n-alkane/methanol) noting that σ_{alkane/toluene} ≪ σ_alkane/MeOH, σ₁₂ can be approximated as σ_{12 =} xσ_alkane/MeOH, where x is the volume fraction of methanol in solution. Combining expressions for σ₁₁ and σ₁₂ and substituting numerical values, the interaction energy is then written as E_ad = −(0.045 kcal/mol)N_azo − (3.3 kcal/mol)x. This equation indicates that only a small number of dipoles on each NP is necessary to make the magnitudes of interparticle interactions comparable with the thermal energy of AuNPs (3/2 kT ∼ 0.9 kcal/mol) and thus to bring these particles together (e.g., for x = 0, E_ad = 3/2 kT when N_azo ∼ 19). Indeed, we observed that, even with as few as ≈16 ADT ligands per one AuNP, the NPs could aggregate (see Figs. 1A and 3A).

It is important to note, however, that aggregation based solely on the dipole–dipole interactions is not sufficient to self-assemble NPs into ordered structures. When the azobenzene ligands had one of their “tails” lacking (e.g., molecule AT in Fig. 1D) or the end of one tail was blocked for Au binding (BAD in Fig. 1D), the NPs in pure toluene formed only transient, disordered assemblies with AuSPR peak at 590 nm, diameters of ≈200 nm by transmission electron microscopy (TEM), and disintegrating in solution within few minutes after the UV irradiation ceased. In addition, experiments in which the photoisomerization and cross-linking effects were “decoupled” by tethering onto the NPs ligands that could photoisomerize but not cross-link (e.g., AT in Fig. 1D) and/or ligands that could cross-link but not photoisomerize (e.g., 1,8-octanedithiol, DT) demonstrated that LISA of supracrystals occurs only when each NP carries ligands of both types (i.e., AT and DT; Fig. 1E). Overall, these observations indicate that, whereas the dipole–dipole forces and solvophobic effects certainly facilitate self-assembly (Fig. 1C Center), cross-linking of the NPs by the dithiol ligands is necessary to overcome thermal fluctuations and enable LISA of crystalline and/or permanent phases (Fig. 1C Right).

With both of these key elements present in the ADT ligands, the types of structures that formed and the degree of their reversibility depended on, and could be regulated by, the relative magnitudes of the dipole–dipole forces, the extent of covalent NP cross-linking, and on solvent properties. The phases that appear under various conditions are summarized in Fig. 1A and are discussed in detail below.

Reversible Crystals.

When the number of adsorbed azobenzene dithiol ligands per NP was low (≈20) and the content of methanol relatively high (20–25%), the UV-irradiated NPs organized into three-dimensional, reversible crystals (phase RC in Figs. 1A and 2A). These micrometer-sized crystals were stable only under continuous UV-irradiation, and could be reverted to the “free” NP phase either thermally or upon exposure to visible light (UV-Vis spectrum of the redissolved phase was identical to that of the initial “free” NP phase). The full NP–RC–NP cycle took ≈10 min to complete and could be repeated multiple times without noticeable changes in the crystals' quality (we verified up to 15 times).

A plausible explanation for such reversibility is that the interparticle binding energy due to both the light-induced dipoles and sparse ADT cross-links is only slightly greater than the thermal energy disrupting the aggregate. Consequently, the loss of dipole–dipole interactions upon cis-trans reisomerization weakens the NP binding energies sufficiently such that the crystals disintegrate as the result of thermal fluctuations. For example, neglecting the energetic contribution of thiol cross-linkers, which are assumed to be very sparse in the RC phase, the adhesion energy between NPs for N_azo ∼ 20 and methanol fraction, x ∼ 0.2, is estimated at ≈1.6 kcal/mol, that is, greater than the thermal energy, 3/2 kT ∼ 0.9 kcal/mol. In the absence of cis-ADT dipoles, however, this energy is reduced to ≈0.7 kcal/mol, resulting in rapid dissolution of the crystals upon irradiation with visible light.

Permanent Crystals.

With increased number of ADT ligands per NP, the crystals gained permanence. Because of strong cross-linking by ADT ligands, the large (up to 0.8 μm), regularly faceted crystals (phase IC in Figs. 1A and 2B) that formed were irreversible and stable not only to light but also to extensive heating (up to ≈100°C), prolonged sonication, all common solvents [e.g., toluene, methanol, dichloromethane, water, DMSO, and dimethylformamide (DMF)], and exposure to excess of chemicals that could potentially displace the ADT ligands (e.g., various alkyl thiols). Interestingly, this extreme stability is in sharp contrast to other NP supercrystals reported in the literature (14, 16), which disintegrate relatively easily upon environmental changes.

The stability and the high-yield of LISA crystals allowed us to analyze crystal structure by small-angle, powder x-ray diffraction (XRD). The XRD spectrum in Fig. 2C shows four peaks located at 2θ = 1.297°, 1.375°, 1.510°, and 2.492°. This diffraction pattern is characteristic of a hexagonal close-packed structure with the lattice constant, a = 7.86 ± 0.42 nm, the axial ratio c/a = 1.609, and with peak positions corresponding to Bragg reflections on planes specified by Miller indices (100), (002), (101), and (103), respectively. The lattice constant agrees with the value of a = 7.84 ± 0.15 nm obtained from scanning electron microscopy (SEM) measurements (Fig. 2B).

Supraspheres.

Finally, when the strength of interparticle interactions was reduced (either by lowering the methanol content or by decreasing the ADT surface concentration), the NPs formed internally disordered, spherical assemblies (“supraspheres”). The transition between crystals (C phase) and supraspheres (SS phase) can be understood in terms of their free energies accounting for energetic and entropic contributions. Specifically, the energetic difference can be estimated as the sum of bulk and surface energies for each aggregate phase, ΔE = E_C − E_SS ≈ (0.5Δn − 1)E_ad, and accounts for the difference in the number of close NP–NP contacts, Δn, and in the surface areas of the two phases (ΔE > 0 favoring supraspheres; compare SI Appendix, section 6 for details). On the other hand, the per-particle entropy of the supraspheres (17) is higher than that of crystals by approximately S_C − S_SS ≈ −k, and so the Gibbs free energy difference is ΔG = G_C − G_SS ≈ (0.5Δn − 1)E_ad + kT. Overall, when interparticle interactions are weak (i.e., ΔG > 0), the entropic term dominates and supraspheres are favored; when the interactions are strong (i.e., ΔG < 0), the potential energy overcomes the entropic effects and crystals form. Interestingly, this qualitative reasoning suggests that the coexistence curve between the two phases defined by ΔG = 0, should be a decreasing and concave function of N_azo in the (N_azo, x) plane, which agrees with the experimental phase diagram. We note briefly that, although spherical NP aggregates have been observed in other experimental systems (18, 19), our light-induced supraspheres were significantly more stable because of cross-linking by ADTs, even to the extent that their outer surface could be further chemically derivatized, thus allowing their transfer to various other solvents (Fig. 3B). At the same time, the spheres were surprisingly deformable (Fig. 3C) and adhesive with respect to one another, suggesting their possible uses as building blocks for higher-order structures.

Controlling the Sizes of the Suprastructures.

For all phases described above, the sizes of the assemblies could be controlled either by changing the concentration of ADT ligands, C_ADT, or by adjusting the times of UV irradiation, t_UV. In the first case, irrespective of solvent polarity, the dimensions to which both the crystals and supraspheres grew decreased with increasing C_ADT (Fig. 3A). This effect can be explained by a nucleation-and-growth (N&G) mechanism (20), in which the free NPs initially nucleate into small, thermodynamically stable (unless smaller than a critical size) clusters that subsequently grow by the addition of single NPs until all NPs available are used. Briefly, the average number of NPs per aggregate, <N>, can be estimated from the ratio of the initial concentration of NPs in solution, C_NP, and the equilibrium concentration of critical nuclei, C_Nuc, that is, <N> ∼ C_NP/C_Nuc. Because C_Nuc is proportional to the number of nucleation “sites” (21) (here, proportional to the concentration of ADT ligands), it follows that C_Nuc ∼ C_ADT (provided that C_ADT is larger than some critical concentration, C*_ADT, required for aggregation; Fig. 3A and SI Appendix for details). Therefore, <N> should be proportional to the ratio C_NP/C_ADT, and consequently, the average aggregate diameter, D, should scale with this ratio as D ∼ (C_ADT/C_NP)^−1/3, which is in quantitative agreement with the experimental data for supraspheres (Fig. 3A Inset). For crystals, the overall trends are similar with reversible (low C_ADT) crystals up to five times larger than irreversible ones (high C_ADT; Fig. 2A).

The second method based on changes in t_UV allowed for “real-time” control of the aggregates' sizes during their growth. At short times (t_UV ∼ 10 s, Fig. 4A), the NPs began arranging into regularly shaped clusters of only few particles and subsequently (t_UV ∼ 30–60 s; Fig. 4 B and C) grew into aggregates composed of tens to hundreds of NPs. Because these assemblies remained in solution, their growth could be halted and restarted by, respectively, pausing or resuming the irradiation. Such dynamic control was not possible with larger aggregates (≈300 nm, Fig. 4D), which precipitated from solution.

Fig. 4.

Examples of aggregates whose sizes were controlled by the times of UV irradiation. (A) The smallest ordered structures formed at high C_ADT ([ADT] = 0.12 mM; 1:4 v/v methanol/toluene) and were made of only a few cross-linked NPs. Upon further irradiation, more free NPs attached to such growing “nuclei” to give ordered structures composed of hundreds (B and C) to millions (D) of NPs. The assemblies in (A–C) were all soluble; large crystals like the one in D precipitated from solution. (Scale bars: A, 5 nm; B, 20 nm; C, 50 nm; D, 200 nm.)

Conclusions

In summary, we have shown that light can be used to guide and control self-organization of nanoscopic components into larger architectures of various internal orderings and overall dimensions. The use of ligands that simultaneously mediate LISA and endow the assemblies a desired level of permanence offers a new route to nanostructred materials of controllable stability (from metastable to irreversible) and mechanical properties (from flexible to extremely rugged). In the future, LISA could be combined with other types of forces/effects [e.g., electrostatic (14) or entropic (22)] to provide a basis for a “photoregulated” synthesis of more complex and/or adjustable nanostructures and devices.

Materials and Methods

All experiments were based on gold nanoparticles prepared according to a modified literature procedure (14). Briefly, DDAB (925 mg) was dissolved in toluene (20 ml) to make a 100 mM stock solution. Fifty milligrams of tetrachloroauric acid trihydrate (HAuCl₄·3H₂O) and 450 mg of DDA were added to 12.5 ml of the DDAB stock solution and dissolved by sonication. To this mixture, 125 mg of tetrabutylammonium borohydride (TBAB) dissolved in 5 ml of the DDAB stock solution was added dropwise under vigorous stirring. The obtained solution was left to “age” for 24 h. Seven milliliters of the aged solution was then added to 50 ml of toluene containing 200 mg of HAuCl₄·3H₂O, 1.00 g of DDAB, and 1.85 g of DDA. Finally, 131 μl of hydrazine in 20 ml of the stock solution was added dropwise under vigorous stirring. The procedure gave gold nanoparticles of average diameter <d> = 5.6 nm and dispersity σ = 9%.

The AuNP solutions (2.0 mM) in toluene/methanol (0–30% v/v methanol content) were stabilized by DDA (35 mM) capping agent and DDAB (10 mM) surfactant. To such solutions, different amounts (up to 2.4 mM) of photoactive trans-azobenzene dithiol ligands (ADT; compare Fig. 1A and SI Appendix for synthetic details) were added under vigorous stirring. Because excess surfactant and capping agent helped to minimize van der Waals forces between the NPs (by reducing the dielectric contrast, Δε, between the particles and the solvent) and prevented the spontaneous cross-linking of nearby NPs via their divalent ADT ligands, the unirradiated solutions were stable up to methanol content ≈25% for many weeks (Fig. 1B Left). Without this stabilizing effect, the magnitude of vdW interactions was large (e.g., E_vdw ∼ 2kT estimated with a Hamaker constant A = 0.4 × 10⁻²¹ J for interacting alkane-chain molecules in toluene), and the NP solutions precipitated via ADT cross-linking even in the absence of irradiation.

All synthesized assemblies were characterized by SEM (LEO 1525; Carl Zeiss SMT, Cambridge, U.K.; accelerating voltage 3–12 kV) and/or TEM (H-8100; Hitachi, Tokyo, Japan; accelerating voltage 200 kV). Structure of the permanent crystals was solved by small-angle, powder XRD on a Rigaku ATX-G high resolution (Rigaku, Tokyo, Japan), grazing incidence x-ray diffractometer with rotating anode, and with Cu Kα₁ radiation (λ = 1.54056 Å), operated at 50 kV and 240 mA. The sample was prepared by placing acetonitrile suspension of nanocrystals on a polystyrene support (≈1 mm thick) and evaporating acetonitrile. The resulting thickness of the sample was 5–10 μm. Positions of the peaks in XRD spectra were determined by using the MDI Jade 6.5 profile fitting software. Suprasphere sizes were measured by Dynamic Light Scattering (BI-9000; Brookhaven Instruments, Brookhaven, NY; operating wavelength 514 nm; scattering angle 90°) and their UV-Vis spectra were recorded on Cary Model 1 UV-VIS spectrophotometer (Varian, Palo Alto, CA) in the range 300–800 nm in an optical glass cell (1-mm path length).

Abbreviations

NP

nanoparticle

DDA

dodecylamine

DDAB

didodecyldimethylammonium bromide

ADT

4,4′-bis(11-mercaptoundecanoxy)azobenzene

LISA

light-induced self-assembly

XRD

x-ray diffraction.