Electrical Potentials of Plant Cell Walls in Response to the Ionic Environment

Abstract

Electrical potentials in cell walls (ψ_Wall) and at plasma membrane surfaces (ψ_PM) are determinants of ion activities in these phases. The ψ_PM plays a demonstrated role in ion uptake and intoxication, but a comprehensive electrostatic theory of plant-ion interactions will require further understanding of ψ_Wall. ψ_Wall from potato (Solanum tuberosum) tubers and wheat (Triticum aestivum) roots was monitored in response to ionic changes by placing glass microelectrodes against cell surfaces. Cations reduced the negativity of ψ_Wall with effectiveness in the order Al³⁺ > La³⁺ > H⁺ > Cu²⁺ > Ni²⁺ > Ca²⁺ > Co²⁺ > Cd²⁺ > Mg²⁺ > Zn²⁺ > hexamethonium²⁺ > Rb⁺ > K⁺ > Cs⁺ > Na⁺. This order resembles substantially the order of plant-root intoxicating effectiveness and indicates a role for both ion charge and size. Our measurements were combined with the few published measurements of ψ_Wall, and all were considered in terms of a model composed of Donnan theory and ion binding. Measured and model-computed values for ψ_Wall were in close agreement, usually, and we consider ψ_Wall to be at least proportional to the actual Donnan potentials. ψ_Wall and ψ_PM display similar trends in their responses to ionic solutes, but ions appear to bind more strongly to plasma membrane sites than to readily accessible cell wall sites. ψ_Wall is involved in swelling and extension capabilities of the cell wall lattice and thus may play a role in pectin bonding, texture, and intercellular adhesion.

The cell wall (CW) is composed of various cross-linked units (macrofibrils, microfibrils, micelles, cellulose units, and linked agents such as neutral sugars, pectin, proteins, and ions; Cosgrove, 1997; Buchanan et al., 2000). The CW behaves as an ion exchanger where the fixed CW charges interact with exchangeable ions in the surrounding solution (Briggs and Robertson, 1957; Gillet and Lefèbvre, 1981; Sentenac and Grignon, 1981; Irwin et al., 1985; Richter and Dainty, 1989a, 1989b, 1990a, 1990b; Grignon and Sentenac, 1991). The net CW charge is negative and results from weakly dissociating acidic groups having pK_a values similar to those of poly-GalUA, the principal origin of the negative charges (Ritchie and Larkum, 1982; Saftner and Raschke, 1981; Richter and Dainty, 1989a; Buchanan et al., 2000). Some positive charges occur too, mainly associated with CW proteins (Cassab and Varner, 1988; Buchanan et al., 2000).

The CW determines cell dimensions (Taiz, 1984) and intracellular volume. The volume of the CW is a consequence of the dimensions of its internal spaces, i.e. the distances between the intra-CW units (Shomer et al., 1984; Shomer and Levy, 1988), which are determined by the repulsive strengths of diffuse double layers (Shomer et al., 1991). The swelling of parenchyma CW is restrained by the increase of valence and concentration of the exchangeable ions and with the decrease of the dielectric constant of the bulk solution (Shomer et al., 1991; Shomer, 1995). Although cell expansion and CW extension have been studied comprehensively (Cosgrove, 1997), the properties governing the volume of the CW, from the point of view of the dimensions of its internal spaces, deserve further elucidation. In any case, the volume of a CW matrix is affected by its electrical properties.

Several studies have demonstrated the importance of cell-surface electrical properties on plant-ion interactions. These include studies of ion uptake (Zhang et al., 2001; Kinraide, 2001, 2003), intoxication by ions such as Al³⁺, H⁺, and Na⁺ (Wagatsuma and Akiba, 1989; Suhayda et al., 1990; Nir et al., 1994; Yermiyahu et al., 1997; Kinraide, 1999), and alleviation of intoxication by Ca²⁺ and other ions (Kinraide, 1998). When whole cells or tissues, rather than plasma membrane (PM) vesicles, were used in the studies, the site of the electrostatic interactions was ambiguous and may have resided in the PM or CW or both.

The ζ-potentials (the near-surface potentials measured by electrophoresis) of protoplasts or PM vesicles have been measured from diverse sources and allow confirmation of a Gouy-Chapman-Stern model for the calculation of PM surface potentials (ψ_PM) in response to several monovalent, divalent, and trivalent ions (measurements compiled by Kinraide et al. [1998] and Kinraide [2001]). These studies agree remarkably well with studies of ion sorption by PM vesicles (Yermiyahu et al., 1997). ζ-Potentials of CWs have been measured (O'Shea et al., 1990), and CW potentials (ψ_Wall) have been measured with microelectrodes pushed against the surfaces of cells (Nagai and Kishimoto, 1964; Spanswick et al., 1966; Saftner and Raschke, 1981). Nevertheless, studies of ψ_Wall have been few and have included few ions (no highly intoxicating ions, other than H⁺, such as trivalent or heavy metal ions) and few combinations of ions. Indirect studies of CW electrical properties have been more common but have not led to estimations of ψ_Wall. These studies included atomic adsorption analysis and potentiometric titration of exchangeable ions (Bush and McColl, 1987; Allan and Jarrell, 1989; Richter and Dainty, 1989b), charge density measurements (Richter and Dainty, 1990a), electron spin resonance (Irwin et al., 1985), and x-ray microanalysis (Campbell et al., 1981).

Consequently, we are not in a position to predict ψ_Wall with the confidence with which we can predict ψ_PM. Preliminary to an attempted comprehensive treatment of electrostatic effects across the whole cell surface (wall and membrane), we have undertaken this study in which CW electrostatic behavior was monitored directly while changing the ionic conditions and pH of the bathing solution. The study included several novel or unusual features: The results were not influenced by the activity of viable PMs; ψ_Wall was measured at the outer and inner surfaces of the CWs; ψ_Wall was monitored continuously during transitions of ion type and concentration; responses to nearly 20 ions (including trivalent and heavy metal ions) were measured; interactive effects of two or more ions were measured; ψ_Wall was considered in terms of electrostatic (Donnan) theory coupled to ion-binding models; and ψ_Wall and ψ_PM were compared.

THEORY

Electrostatic and Ion-Binding Models

The electrical measurements were considered in terms of Donnan electrostatic theory coupled to ion-binding models. When the Donnan theory is combined with ion binding, we shall refer to it as the Donnan-plus-binding model. In an ideal system, the Donnan theory may be developed from the Nernst equation (Noble, 1991; and see below).

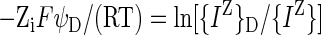1

describes the partition of ion I^Z according to its activity in the Donnan phase ({I^Z}_D), its activity in the bulk phase ({I^Z}), its charge (Z_i), and the electrical potential of the Donnan phase relative to the bulk phase (ψ_D). F/(RT) is the Faraday constant divided by the gas constant and the temperature. Equation 1 may be divided by Z_i, and additional ions (e.g. J^Z) may be added, yielding these equations.

2

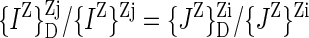3

The balance of charge within the Donnan phase may be written

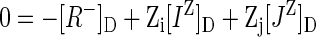4

In this equation, [R^-]_D is the concentration of confined or immobile charges, such as CW charges, and [I^Z]_D and [J^Z]_D are concentrations of ions I^Z and J^Z confined to the Donnan phase. The equation could be extended for any number of ions beyond I^Z and J^Z, but for simplicity, think of I^Z and J^Z being the cation and anion, respectively, in a single-salt solution. Furthermore, Equation 4 assumes no binding of ions to R^-.

Equation 1 may be rewritten

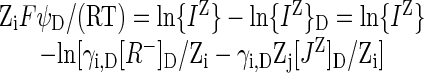5

The expression γ_i,D[R^-]_D/Z_i - γ_i,DZ_j[J^Z]_D/Z_i (= γ_i,D[I^Z]_D = {I^Z}_D) is derived from Equation 4. γ_i,D is the activity coefficient of ion I^Z in the Donnan phase. Often, activity coefficients are omitted from considerations of Donnan equilibria, implicitly setting them all to 1. Equation 5 indicates that ψ_D is a linear function of ln{I^Z} to the extent that ln{I^Z}_D is constant and that {I^Z} dominates the solution. As {I^Z} becomes very small, other ions such as H⁺, OH^-, HCO₃^-, or contaminants will dominate the system, even in supposedly single-salt solutions, and ψ_D will come to a constant value, giving curvature to plots of ψ_D versus ln{I^Z} or log₁₀{I^Z}.

Because [R^-]_D is the origin of the negative charges, a change in [R^-]_D will alter ψ_D, as indicated in Equation 5. [R^-]_D will change as cations bind to R^- in the reaction R^- + I^Z → RI^Zi-1. In those cases, Equation 4 is incomplete because it should contain the species RI^Zi-1. The equations above can be expanded if the binding stoichiometry and an equilibrium constant (K_R,I in units M^-1) for the binding reaction, can be obtained. With that, the concentration of RI^Zi-1 can be computed from

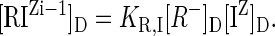6

where [I^Z]_D is the concentration of ion I^Z in the Donnan phase. R^- represents the negative binding sites in the Donnan phase. R^- is a composite because a CW may have several classes of binding sites, and some may be much more accessible than others. Un-charged binding sites may be designated P⁰, and the concentration of PI^Zi can be computed from

7

In addition, binding stoichiometries may differ. For example, 1:1 charge-to-charge binding will produce only neutral R complexes (Z_iR^- + I^Z → R_ZiI⁰).

In an ideal system, a Donnan phase is a homogeneous, macroscopic phase (such as the contents of a dialysis bag) in which all charges, including the confined charges R^-, behave as freely mobile point sources of charge. In such a system, the location of a measuring electrode is not in doubt, and the precise computation of activity coefficients and Donnan-phase volumes is possible. Certainly the CW is not such a simple system. It is a meshwork of unevenly distributed, stationary charges. A microelectrode (large relative to the CW components) may have incomplete access the Donnan phase of the CW as we shall discuss later. Although the CW is not ideally suited to analysis by a simple Donnan-plus-binding model, we nevertheless applied the model to our data. Our approach was to optimize the parameters for the model so as to minimize the sum of squares of the difference between observed and computed ψ_Wall. The parameters for the model included R_Total (the total concentration, in M units, of negative sites assuming no ion binding), a similar parameter for P_Total, K_R,I (a binding constant for each ion I^Z for the R^- binding site), and K_P,I (a binding constant for each ion I^Z for the P⁰ binding site). The method of evaluating parameters is described in “Materials and Methods.”

RESULTS

Some Features of the Potentiometric Measurements

The electrical potentials for microelectrodes (actually glass micropipette salt bridges) in the tissue-bathing solution (the tip potentials) were less negative than -20 mV. Near the CW, the potentials became more negative, depending upon the bathing solution. Upon touching the CW, the ψ_Wall acquired a constant value that did not change even as the electrodes were driven against the CW surfaces with greater force, thereby causing greater deformation. Eventually, the electrodes entered the cell interiors where the potentials jumped to about -120 mV in living cells.

In wheat (Triticum aestivum), values for ψ_Wall were similar for living and heat-killed roots. Moreover, ongoing studies in Shomer's laboratory in Israel show that immunogold labeling of pectin in the CW itself is similar in both boiled potato (Solanum tuberosum) tubers and viable tubers, whereas the middle lamella is removed by boiling. Because ψ_Wall was measured at the outer surface of whole roots (wheat) and at the inner and outer surface of potato cells (Fig. 1), the loss of pectin from the middle lamella would be expected to have little effect.

Figure 1.

Possible locations of the microelectrode tip in ghost cells of potato tuber.

The electrodes appeared to record ψ_Wall very sensitively. Substitution of one bathing medium for another (NaCl for KCl or CaCl₂ for MgCl₂) caused changes in ψ_Wall of a few millivolts, consistently in the same direction. The 2 or 3 m KCl electrode filling solution appeared not to affect the measurements. Addition of 0.1 mm KCl to a perfusion solution of 0.1 mm NaCl caused 20 mV depolarizations, indicating that the CW region under measurement was not swamped with concentrated KCl. Furthermore, micropipette filling solutions of 20 mm KCl produced the same values as 2 m KCl filling solutions.

Unbroken microelectrodes (tips generally taken to be <1 μm in diameter) and deliberately broken microelectrodes (tips >> 1 μm) yielded similar readings for ψ_Wall. Furthermore, repeated measurements were similar. One may again and again withdraw the electrode from the cell surface, move the electrode to a new position, press the electrode onto the surface of the cell gently or firmly and observe similar readings each time.

Potato Cells

ψ_Wall of ghost cells of potato tubers were measured as depicted in Figures 1 and 2 and as described in “Materials and Methods.” ψ_Wall responded sensitively to changes in NaCl concentration in the bathing solution (Fig. 3A) and became less negative with increasing concentration. No hysteresis was apparent in ψ_Wall with increasing or decreasing concentrations. KCl solutions affect ψ_Wall nearly the same as NaCl (Figs. 4A). For both NaCl and KCl, ψ_Wall increased by 30 to 35 mV from about -61 mV over the 100-fold concentration change from 0.1 to 10 mm.

Figure 2.

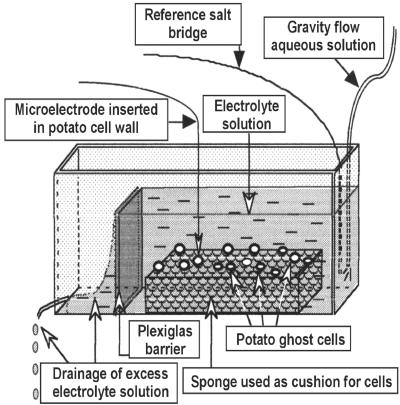
A schematic representation of the experimental setup for measurement in ghost (heat killed) cells of potato tuber.

Figure 3.

CW potentials of potato tuber in changing concentrations of NaCl (A), CaCl₂ (B), and AlCl₃ (C). Arrows and values indicate times of solution changes and the concentrations in millimolar. For these, and for all potato measurements, single salts were used without adjustment of pH, unless stated otherwise.

Figure 4.

CW potentials of potato tuber in response to solute transitions among KCl, NaCl, Na₂SO₄, and K₂SO₄ (A) and in response to concentration changes in KCl (B). Arrows indicate the times of solution changes. Concentrations were 0.1 mm unless otherwise labeled.

The ψ_Wall was more sensitive to low concentrations of multivalent cations such as Ca²⁺ and various Al species (Fig. 3, B and C) than to monovalent cations (Fig. 3A). ψ_Wall increased by about 37 mV from about -59 mV over the 30-fold concentration change in CaCl₂ from 0.1 to 3 mm. ψ_Wall was sensitive to AlCl₃ at much lower concentrations. It increased by about 30 mV from about -59 mV over the 5-fold concentration change in AlCl₃ from 0.01 to 0.05 mm. However, [AlCl₃] ≠ [Al³⁺] because of the formation of hydroxo-Al that was variable because the pH decreased as [AlCl₃] increased (Kinraide and Parker, 1989).

Transitions from NaCl to KCl in the bathing solution induced less negative ψ_Wall and vice versa (Fig. 4, A and B). These changes in ψ_Wall were more pronounced with divalent anions, as when K₂SO₄ replaced Na₂SO₄ (Fig. 4A). A similar pattern was observed with divalent cations, as when CaCl₂ replaced MgCl₂ (Fig. 5B). Sulfate salts were more depolarizing than chloride salts (Fig. 5, A and B). The ψ_Wall was also sensitive to pH changes (Fig. 5C). In the present study, each pH change was followed by CW equilibration with 0.1 mm NaCl solution. The potentials measured for pH 5.24 and 6.87 were -67.5 and -80.0 mV, respectively.

Figure 5.

CW potentials of potato tuber in response to solute transitions between CaSO₄ and CaCl₂ (A) and between Ca²⁺ and Mg²⁺ salts (B) and to changes in phosphate-buffered pH (C). Arrows indicate the times of solution changes. Concentrations were 0.1 mm unless otherwise labeled.

Figure 6 expresses ψ_Wall for potato cells as a function of log₁₀ of salt concentrations. Figures 4 through 6 demonstrate that the salts depolarize the CW with effectiveness in the order AlCl₃ > CaCl₂ ≥ MgCl₂ > KCl ≥ NaCl. This is the expected trend—multi-charged ions were more effective at electrostatic screening, and binding strength probably declines in the same order, as it does in the case of PMs (Kinraide et al., 1998). Thus depolarization in the stated order is expected for two reasons: screening and charge elimination by binding.

Figure 6.

Measured and computed CW potentials of potato tuber in response to single-salt solutions. Because of hydrolysis, the pH of the AlCl₃ solutions declined as the concentration increased.

Wheat Root Cells

Figures 7, 8, and 9 express ψ_Wall for wheat cv Scout 66 root cells as a function of log₁₀ concentration of salt solutions or log₁₀{H⁺}. For each of the solutions, the response was linear or nearly linear, and the observed responses agree closely to a Donnan-plus-binding model to be described. Depolarizing effectiveness is in the order trivalent salts > H⁺ > divalent salts > monovalent salts. Our measurements indicate that positive potentials are rarely achieved in artificial solutions and would appear to be extremely rare in nature. For that to occur, pH would need to be less than 3 or other ions would need to exceed values commonly encountered. In a soil solution, where pH = 4.5, [Ca²⁺] = 1,000, and [Al³⁺] = 20 μm, ψ_PM = +4.3 mV (Kinraide et al., 1998), but ψ_Wall would be strongly negative.

Figure 7.

CW potentials of wheat root in response to H⁺ and Na⁺. Parameters for the Donnan-plus-binding model were R_Total = 0.0211 m and K_R,H = 9,450.

Figure 8.

CW potentials of wheat root in response to divalent cations. NaCl = 0.1 mm; pH = 5.6. Model parameters are as in Figure 7.

Figure 9.

CW potentials of wheat root in response to trivalent cations and H⁺. NaCl = 0.1 mm throughout. Model parameters are as in Figure 7. D, Chart record of LaCl₃ added at time zero followed by transitions to AlCl₃ to LaCl₃ to AlCl₃. For D, concentrations of LaCl₃ and AlCl₃ (the latter hydrolyzing slightly at pH 4.3) were selected to yield equal concentrations (108 μm) of Al³⁺ and La³⁺.

Using the method of solute substitutions, illustrated in Figures 4, 5B, and 9D, the following order of depolarizing effectiveness has been obtained for wheat CWs: Al³⁺ > La³⁺ > H⁺ > Cu²⁺ > Ni²⁺ > Ca²⁺ > Co²⁺ > Cd²⁺ > Mg²⁺ > Zn²⁺ > hexamethonium²⁺ > Rb⁺ > K⁺ > Cs⁺ >Na⁺. Compare this with the results from potato where Al³⁺ > Ca²⁺ > Mg²⁺ > K⁺ > Na⁺. This order indicates a possible role for ion size in depolarizing effectiveness: H⁺ was much more effective than other, larger, monovalent ions; Al³⁺ was more effective than the larger La³⁺; and each of the metallic divalent ions was more effective than the much larger hexamethonium²⁺. These examples refer to large size differences. Smaller size differences had no obvious effect.

The order of ions presented above resembles substantially the order of binding strength to CW pectinates (Franco et al., 2002). In addition, the following ions inhibit root elongation in wheat, in a basal medium of CaCl₂, in this order: AlO₄Al₁₂(OH)₂₄ (H₂O)₁₂⁷⁺ > Sc³⁺ (may include some more highly charged polynuclear species) > Cu²⁺ > spermine⁴⁺ > Al³⁺ > La³⁺ > H⁺ > AlF²⁺ > Cs⁺ > Rb⁺ > tris(ethylenediamine)cobalt³⁺ > Zn²⁺ > AlF₂⁺ > Li⁺ > Mg²⁺ > Ca²⁺ > K⁺ > Na⁺ (Kinraide, 1997, 1999; citations in the preceding and unreported results), indicating once again a role for charge and size.

Modeling and Comparisons among Studies

The present studies with potato tubers and wheat roots were performed independently (see “Materials and Methods”), so these and three published studies were compared. One of the studies employed electrophoresis, the others, microelectrodes. O'Shea et al. (1990) measured ζ-potentials in CW fragments of petiolar cells of Nymphoides peltata and Regnellidium diphyllum in a range of pH, [CaCl₂], and [KCl]. Nagai and Kishimoto (1964) measured ψ_Wall in Nitella flexilis in 0.01 to 100 mm KCl. Saftner and Raschke (1981) measured ψ_Wall in guard cells of Commelina communis in 1 to 800 mm KCl at pH 7 and in 30 mm KCl at pH 2 to 7.

Preliminary inspection indicated that ψ_Wall responses to solutes were similar among the studies, except that in the study of Saftner and Raschke (1981), values for ψ_Wall were more negative. For example, in 1 mm KCl at pH 6 to 7, ψ_Wall = -155 mV compared with ψ_Wall ≈ -55 mV in the other studies. The principal difference among the other four studies is that plots of ψ_Wall versus log₁₀[NaCl] remained linear down to 0.1 mm in wheat (Fig. 7), whereas considerable curvature was seen in potato (Fig. 6) and in the study of Nagai and Kishimoto (1964).

We applied the Donnan-plus-binding model to 101 ψ_Wall measurements from the five studies using a technique reported previously for the assessment of ψ_PM. In that study, ζ-potential measurements of PMs from eight studies were compiled (Kinraide et al., 1998; Kinraide, 2001), and parameter values for a Gouy-Chapman-Stern model were computed to minimize the sum of squared differences between calculated ψ_PM and measured ζ-potentials (see Fig. 10B). The parameters consisted of a universal set of optimized binding constants, but the intrinsic surface density of negative charge on the PM surface (σ₀) was optimized separately for each of the eight studies. σ₀ used in the Gouy-Chapman-Stern model is similar in function to R_Total in the Donnan-plus-binding model. The computed binding constants for the PM were these: K_R,Na = K_R,K = 0, K_R,Mg = 23.8, K_R,Ca = 29.1, K_R,La = 2,030, K_R,H = 20,200 m^-1. These values, derived from electrophoretic studies of diverse species and tissues, agreed remarkable well with values determined by a sorption study of wheat root PMs (Yermiyahu et al., 1997).

Figure 10.

A comparison of studies in which CW and PM potentials were measured and computed. For A, parameters for the Donnan-plus-binding model were evaluated for five studies. Optimized values for R_Total were computed for each study, but binding constants (K_R,H = 9,450; all others equal to zero) were evaluated for the pooled data. For B, parameters for the Gouy-Chapman-Stern model were evaluated similarly for eight studies. B is reproduced from Kinraide (2001) with permission.

Figure 10A presents measured versus computed ψ_Wall for the five CW studies. The parameter values for R_Total are presented in the figure and confirm the preliminary observation that one of the studies differs from the others. The only other parameter to achieve a significant value was K_R,H = 9,450 m^-1, indicating an intrinsic pK_a = 4.0 for the negative binding site. No significant value could be obtained for K_P,H, indicating no binding of H⁺ to neutral sites. Weak or negligible binding of H⁺ to neutral sites may be concluded without computer modeling: Our studies indicated no reliable conversion of ψ_Wall from negative to positive at pH 3 (Fig. 7A), and Saftner and Raschke (1981) obtained no charge conversion as pH was reduced to 2.

The failure of the model to detect binding of divalent and trivalent cations to the negative sites of the CWs was surprising given the readily modeled binding of these ions to the PMs, but Figures 7, 8, and 9 demonstrate that model-computed values for ψ_Wall are in close agreement with observed values, usually. Exceptions are that in two studies, the measured values for ψ_Wall were more positive than modeled for 0.1 mm NaCl at pH >5.5. These exceptions can be seen in Figure 10A as three outliers corresponding to y axis values between -60 to -80 mV. As mentioned above, these values give curvature to some plots that is not observed in others.

Figure 8 illustrates a generally close agreement between measured and computed values for ψ_Wall in divalent cations. Nevertheless, the consistent tendency for the ions to depolarize ψ_Wall in the order Cu²⁺ > Ca²⁺ > Zn²⁺ may be interpreted to mean some, perhaps small, binding in the same order. In addition, consistent differences between the depolarizing effectiveness of Na⁺ and K⁺ and between Al³⁺ and La³⁺ were observed too.

A Comparison of ψ_Wall and ψ_PM

Of interest to those who seek to understand electrostatic effects across the whole cell surface (wall and membrane) is the similarity of response of ψ_Wall and ψ_PM to solutes. Table I presents measured and computed ψ_Wall and computed ψ_PM. A detailed look at the values is instructive. The third row from bottom presents the most negative values in what may be considered to be the “basal” medium. Additions of LaCl₃ to this medium, or reductions of pH, reduce the negativity of ψ_PM much more than ψ_Wall, as would be expected from the PM-binding constants K_R,La = 2,200 and K_R,H = 215,000. Additions of CaCl₂ have very similar effects on both ψ_Wall and ψ_PM, but additions of NaCl reduce the negativity of ψ_Wall more than ψ_PM. These latter effects are somewhat coincidental. If the parameters σ₀ and K_R,H for the Gouy-Chapman-Stern model were reduced, then ψ_Wall and ψ_PM responded similarly to changes in NaCl. In any case, measured ψ_Wall and computed ψ_PM are correlated (R = 0.771), and the deviations can be interpreted readily.

Table I.

Measured and computed electrical potentials in some solutions

Values for ψ_{Wall, measured} were taken from the fitted curves in Figures 7 and 9 and from a curve fitted to the pooled data from Figure 8, A through C. Concentrations are in millimolar and potentials in millivolts.

LaCl3	pH	CaCl2	NaCl	ψWall, measured	ψWall, computeda	ψPM, computedb
0.001	5.6	0	0.1	−78.9	−72.0	−44.6
0.01	5.6	0	0.1	−55.7	−54.2	−25.4
0.1	5.6	0	0.1	−32.5	−35.5	−6.0
1	5.6	0	0.1	−9.3	−16.9	12.7
0	5.00	0	0.1	−87.4	−94.7	−71.0
0	4.00	0	0.1	−54.0	−59.1	−16.5
0	3.00	0	0.1	−9.4	−13.1	34.6
0	5.6	0.01	0.1	−88.6	−81.2	−85.1
0	5.6	0.1	0.1	−60.1	−56.6	−62.8
0	5.6	1	0.1	−31.6	−29.5	−36.1
0	5.6	0	0.1	−98.6	−110.6	−101.3
0	5.6	0	1	−57.5	−70.2	−85.5
0	5.6	0	10	−16.4	−22.5	−59.0

^a Parameter values for the Donnan-plus-binding model: R_Total = 0.0211 m and K_R,H = 9450.

^b ψ_{PM, computed} was computed by a Gouy-Chapman-Stern model (Kinraide et al., 1998) in which negative-site binding constants are K_R,Na = I, K_R,Ca = 30, K_R,La = 2,200, K_R,H = 21,500 m⁻¹.

DISCUSSION

The values for ψ_Wall measured independently in four laboratories were similar whether measured by electrophoresis of CW fragments (O'Shea et al., 1990) or by microelectrode placement against the CWs of whole cells that were living or heat killed (Nagai and Kishimoto, 1964; present study). ψ_Wall responses to H⁺ and to monovalent, divalent, and trivalent cations were described successfully by Donnan theory combined with H⁺ binding to a negative CW site.

Measured values for ψ_Wall were often similar to computed values for ψ_PM, and differences can be interpreted mainly on the basis of differences in the strength of ion binding to CWs and PMs. We conclude that ion binding, at least to readily accessible sites, is stronger at PM surfaces than to CW components. This follows from the evaluation of parameters for the electrostatic models and from the fact that ψ_Wall was more resistant than ψ_PM to conversion to positive values.

An advantage of continuous potentiometric measurements with microelectrodes is that small differences in the depolarizing effectiveness of the ions can be determined. That effectiveness follows the order Al³⁺ > La³⁺ > H⁺ > Cu²⁺ > Ni²⁺ > Ca²⁺ > Co²⁺ > Cd²⁺ > Mg²⁺ > Zn²⁺ > hexamethonium²⁺ > Rb⁺ > K⁺ > Cs⁺ > Na⁺. We did not attempt to model all ion effects such as the differences between SO₄^2- and Cl^- as counter ions or differences among some ions within a charge class (e.g. Na⁺ versus K⁺ or Ca²⁺ versus Mg²⁺). These differences may reflect different binding strengths at similar binding sites or access to a greater number of binding sites by some ions. In any case, the sequence of depolarizing effectiveness was readily determined by monitoring ψ_Wall as one salt solution was substituted for another. Furthermore, this sequence resembles, but is not identical to, binding to CW pectinates and to the intoxication of roots.

An item of concern is the low value for estimated charge concentration (R_Total) for four of the studies. Estimates by other methods yielded values ranging from 0.1 to 1.5 m, as reviewed by Grignon and Sentenac (1991). We offer three hypotheses for low values for R_Total. The first is a dilution effect. A microelectrode may accesses simultaneously the Donnan phase and the bulk phase of the medium. Problematical to the hypothesis of a dilution effect is that unbroken and deliberately broken microelectrodes yielded similar readings as do readings taken from different positions (see “Some Features of the Potentiometric Measurements” under “Results”).

Perhaps even the sharpest electrodes fail to embed entirely within the CW as illustrated in the second from left diagram in Figure 1. Perhaps all electrodes merely touch the surface of the CW. The important factor may be the contact between the rim of the electrode orifice and the CW, and a large-circumference electrode may work just as well as a small one, provided the entire rim makes contact with the CW surface. This thinking leads to the second hypothesis: The measured potential is a CW surface potential, not an interior potential. This concept could explain the fact that the ζ-potentials measured by O'Shea et al. (1990) also appear to be insufficiently negative for R_Total > 0.1 m.

The third hypothesis for low computed values for R_Total may be that some of the negative sites were not in equilibrium with the bathing medium. Perhaps some carboxyl groups were bridged by Ca²⁺ within a lattice so that the Ca²⁺ and the negative charges were inaccessible to exchange with other ions or were unable to dissociate freely. This is in accordance with the calcium-pectate egg-box model (Grant et al., 1973) and the localization of various pectin fractions including high or low methoxyl pectin and calcium-pectate (Bush and McCann, 1999). In that case, R_Accessible < R_Total. Consistent with this view is that additions or withdrawals of solutes caused decreases or increases in ψ_Wall negativity that were complete within 1 or 2 min. After that, ψ_Wall remained constant. Additions of 0.1 or 1 mm EDTA adjusted to pH 5.6 with NaOH did not alter ψ_Wall beyond the effects attributable to Na⁺. This almost certainly indicates that some of the CW-bound Ca²⁺ was not readily accessible.

We cannot explain the more highly negative values presented by Saftner and Raschke (1981). Perhaps the leaf cells really did have a more negative R_Total. In a side study in Kinraide's laboratory, ψ_Wall was measured in roots of monocots and dicots. It is well documented that the latter have a higher cation exchange capacity than the former (Marschner, 1995). In each of the concentrations 0.1, 1, and 10 mm KCl, ψ_Wall was unvaryingly negative in the order radish (Raphanus sativus) > turnip > maize (Zea mays) > wheat. The greater negativity of dicot CWs was statistically significant according to measurements obtained and compiled by a naïve observer. Thus the electrodes accessed potentials related to the expected Donnan potentials.

Despite the concerns just mentioned (inability to model the binding of ions other than H⁺ and a low value for computed R_Total), a simple model with only one universal adjustable parameter (K_R,H) and one adjustable parameter for each of the five studies (R_Total) generated values for ψ_Wall that correlate highly with measured values (R = 0.964; Fig. 10A). We consider it likely that both measured or computed values for ψ_Wall are at least proportional to, if not equal to, actual ψ_Wall. Consequently, computed ion activities in the Donnan phase are likely to be proportional to, if not equal to, actual Donnan-phase activities. Proportional, of course, means that actual ψ_Wall = 0 when measured ψ_Wall = 0. This is almost certainly correct because reduced access to the Donnan phase will reduce the magnitude of but will not change the sign of ψ_Wall.

Cell-surface electrostatic effects influence ion uptake, ion-induced intoxication, and ion alleviation of intoxication, but less-studied physiological effects are under electrostatic control as well. Changes in the valence and concentration of the exchangeable ions, as well as the dielectric constant of the aqueous medium, play a role in the CW swelling pressure (Shomer et al., 1991). Reductions in the negativity of ψ_Wall and the thickness of the electric double layer decrease the electrostatic repulsion between CW units. This decreases the swelling pressure and retards the CW swelling, thus resulting in smaller cells and organs as a whole. These morphological changes, as well as the changes in ion activity, may play a role in CW-specific plant responses to salinity and a variety of other environmental challenges. Some practical consequences of changes in ψ_Wall may include food tissue responses important to nutrient status, ripening, storage, pathogen resistance, and texture.

MATERIALS AND METHODS

The ψ_Wall responses were measured in two different tissues (potato [Solanum tuberosum] tuber and wheat [Triticum aestivum L. cv Scout 66] root) of either viable or heat-killed (ghost) cells. The measurements of ψ_Wall in potato were performed at the University of Missouri. Later, measurements of ψ_Wall in wheat began at the Appalachian Farming Systems Research Center. After the Missouri work had been completed, and while the Appalachian work was in progress, the investigators became aware of each other's studies and decided to conflate their reports.

The ψ_Wall was measured by adapting methods used for measuring transmembrane electrical potentials (Lüttge and Higinbotham, 1979). Potato tuber cells were especially suitable for this purpose because heating (at 100°C) inactivates the protoplast, whereas the gelatinized starch inflates the cell lumen, cushions the CW, and stabilizes the inserted microelectrode tip in the CW for the duration of the measurement. Ghost cells were prepared by boiling peeled tuber dices (approximately 3 cm³ including cortex and parenchyma tissues) for 20 min, mashing, and rinsing several times with distilled water. The macerate was strained through a 0.1-mm mesh under a stream of distilled water. The sieved macerate was rinsed and suspended in a column of distilled water. Large, quick-settling and small, slow-settling cells and aggregates were discarded, leaving a suspension of medium-sized cells (4-5 × 10^-3 mm³ [Shomer, 1995]) for ψ_Wall measurements.

The microelectrodes were prepared from microcapillaries with glass microfibers (WP Instruments, Sarasota, FL) that were drawn into micropipettes with a vertical pipette puller (D. Kopf Company, Tujunga, CA). Tip diameter was <0.5 μm, tip potential was -5 to -15 mV, and resistance was 5 to 15 mΩ. The micropipette was filled with 3 m KCl representing one salt bridge, and a 3 m KCl/3% (w/v) agar salt bridge was used as reference. Both bridges were connected via Ag/AgCl electrodes to an electrometer (WPI Intra 767) and strip chart recorder.

The electrical measurements were conducted in a 35-× 5-× 16-mm Plexiglas chamber containing electrolytic solution with a fine sponge attached to the bottom (Fig. 2). One drop of cells suspended in water (1:10, v/v; Shomer et al., 1995) was added to the bath. The cells settled in the Plexiglas chamber, and each cell was held stationary in a separate sponge cavity. The micropipette was inserted into the CW of a visible single ghost cell (biologically inactive) using a micromanipulator under a horizontal microscope. The microelectrode tip was stabilized in the CW as shown in Figure 1, State 2, where the gelatinized starch cushioned the CW against collapse under the pressure exerted by the microelectrode.

The chamber was perfused with various test solutions at a constant flow rate of 1 mL s^-1, thereby accelerating the response when the electrolyte was changed and minimizing interfacial concentration gradients and possible interference from the 3 m KCl of the microelectrode. Each ψ_Wall measurement in each solution was held, if possible, until the reading stabilized. The microelectrode tip was very sensitive to ψ_Wall; no matter where the tip contacted the CW (Fig. 1, States 1, 2, and 4), there was no difference in ψ_Wall. Therefore, the penetration of the microelectrode tip into the CW did not cause aberrations in the electrical measurements. Nevertheless, the ψ_Wall differed somewhat from cell to cell (in the range of -65 to -75 mV without added salts). Unless stated otherwise, the pH of the solutions was about 5.6.

The method of ψ_Wall measurement in wheat roots was similar in most respects to the method used in potato. Whole seedling were mounted in a clear plastic chamber and perfused with test solutions. Electrodes, filled with 2 m KCl, were pushed against the surfaces of root-surface cells. Some seedlings were dipped into boiling water for a few seconds, but a large number of measurements were made on living roots too. The reason for using boiled tissue (a technique adopted independently in Missouri and West Virginia) was that an electrode at the CW surface often penetrated the PM, thereby measuring a transmembrane potential difference. Furthermore, the continuing elongation of live roots caused instabilities in the measurements. Aluminum solutions for the wheat work were adjusted so that the ion activity ratio {Al³⁺}/{H⁺}³ # 10^8.8 (activities in m), thereby ensuring the absence of solid-phase or polynuclear Al (Kinraide and Parker, 1989).

We evaluated the parameters for the model (see “Theory”) so as to minimize the sum of squares of the differences between observed and computed ψ_Wall. The method consisted of an automated assessment of trial values for one parameter while holding all others constant. That parameter was then held constant at its temporary optimum, and trial values for another parameter were assessed. The process was iterated with increasing precision until the sum of squares was minimized. False terminations of the program sometimes occurred, but these could be detected by using different starting values for the parameters.

Distribution of Materials

Upon request, all novel materials described in this publication will be made available in a timely manner for noncommercial research, subject to the requisite permission, obtained by the requestor, from any third-party owners of the materials.