From micro to nano contacts in biological attachment devices

Abstract

Animals with widely varying body weight, such as flies, spiders, and geckos, can adhere to and move along vertical walls and even ceilings. This ability is caused by very efficient attachment mechanisms in which patterned surface structures interact with the profile of the substrate. An extensive microscopic study has shown a strong inverse scaling effect in these attachment devices. Whereas μm dimensions of the terminal elements of the setae are sufficient for flies and beetles, geckos must resort to sub-μm devices to ensure adhesion. This general trend is quantitatively explained by applying the principles of contact mechanics, according to which splitting up the contact into finer subcontacts increases adhesion. This principle is widely spread in design of natural adhesive systems and may also be transferred into practical applications.

Attachment structures have independently developed several times in animal evolution (1, 2). Setose or hairy systems of various animal groups, such as insects, spiders, and lizards contain surfaces covered by fine patterns of protuberances of different origin. These highly specialized structures are not restricted to one particular area of the leg and may be located on different derivatives of the tarsus and pretarsus (3). Even among insects, the protuberances belong to different types: representatives of the Coleoptera and Dermaptera have setae with sockets providing additional mobility of setae, whereas representatives of Diptera have setae without sockets (acanthae). Setae range in their length from several millimeters to a few micrometers (4).

Despite >300 years of studies on hairy attachment systems, there is still a debate concerning the attachment mechanism of animals walking on smooth walls or ceilings. Different hypotheses have been proposed to explain the mechanism of attachment: sticking fluid, microsuckers, and electrostatic forces (5). Based on experimental data, some of these theories have been rejected, and adhesion has been attributed to a combination of molecular interactions and capillary attractive forces mediated by secretions (6) or purely van der Waals interactions (7). Because some animals produce secretory fluids (insects) (8–10) in the contact area, whereas others do not (spiders, geckos) (11, 12), one can expect different basic physical forces contributing to the overall adhesion. Recently, strong evidence has been presented (13) that the adhesion of gecko setae is caused by van der Waals interaction, rejecting mechanisms relying on capillary adhesion. Elements of contact mechanics have also been applied to this problem (13, 14); it was predicted that arrays with smaller setae endings should result in greater adhesive strength. In the present study, we combine an extensive microscopical study¶ of biological surface devices with the theory of contact mechanics based on molecular adhesion. We will show that the scaling of the surface protuberances, for animals differing in weight by 6 orders of magnitude, can be quantitatively explained by this approach.

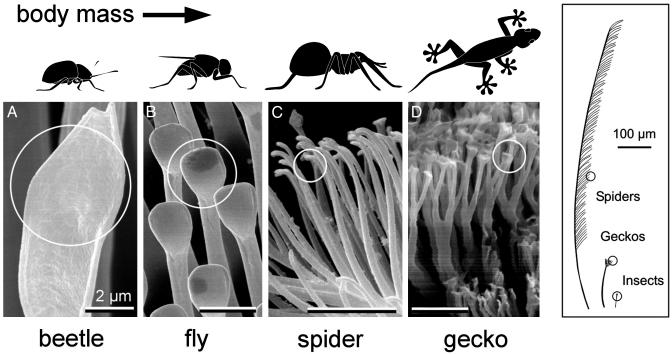
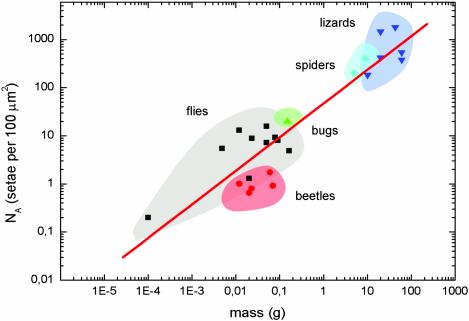
The setae of animals studied∥ are finely structured down to the μm and sub-μm levels. The diameters of their spatula-like terminal elements (Fig. 1) have been measured to range from 0.2 to 5.0 μm. Comparative structural data clearly show that the areal density N_A of these terminal elements strongly increases with increasing body mass m (Fig. 2). It is remarkable that a single master curve exists for the different species; it is given by log·N_A(m^–2) = 13.8 + 0.699·log·m(kg), R = 0.919. Downscaling of the contact elements, which results in a multiplication of the number of single contact, thus appears to be a strong design principle.

Fig. 1.

Terminal elements (circles) in animals with hairy design of attachment pads. Note that heavier animals exhibit finer adhesion structures.

Fig. 2.

Dependence of the terminal element density (N_A) of the attachment pads on the body mass (m) in hairy-pad systems of diverse animal groups (log·N_A(m^–2) = 13.8 + 0.699·log·m(kg), R = 0.919).

We want to interpret these findings in light of theoretical contact mechanics. Consider a geometry in which a seta terminates in a hemispherical shape. In the purely elastic case, the diameter d of the area of contact with a flat substrate is given by the Hertz equation:

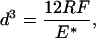[1]

where R is the radius of the hemisphere, E* an average plain strain modulus, and F the compressive contact load.

The Hertz theory has been extended to include surface attraction effects by Johnson, Kendall, and Roberts (15). Their result for the diameter of the contact area is

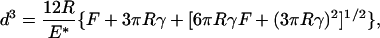[2]

where γ is the adhesion energy per area. One of the consequences of their analysis is the prediction of a finite pull-off force given by

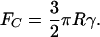[3]

Let us apply this formalism to the attachment pad of the fly Eristalis (16). Assume first that no hairy structure is present and that R = 100 μm is given by the radius of the complete surface of the attachment organ. To support the weight (80 mg) of the fly when hanging from the ceiling on one leg, an adhesion energy in excess of 1 J/m² would be required according to Eq. 3; this is clearly unrealistic for van der Waals interaction forces.

However, in reality, the animal takes advantage of an important consequence of contact theory: inspection of Eq. 3 shows that the adhesion force is proportional to a linear dimension of the contact; therefore, by splitting up the contact into n subcontacts (setae), each with radius 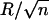(self-similar scaling), the total adhesion force is increased to

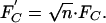[4]

Van der Waals forces (with typical adhesion energies in the range from 50 to 10 mJ/m²) now create sufficient attachment strength, provided the number of setae is of order 10³ to 10⁴ per fly pulvillus. This is indeed in accordance with our microscopic observations (Fig. 1).

It is interesting that such an approach allows some simple predictions to be made about scaling of attachment devices between small and large animals: for dimensionality reasons, the weight of the animal increases more rapidly than the area of the foot-to-substrate contact. This has to be compensated by a simultaneous increase in the setal density. It is shown in the Appendix that two simple cases can be considered:

(i) For self-similar scaling, the contact radius of the terminal elements is linearly related to their size. The setal areal density N_A is then expected to scale as

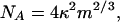[5]

where κ = (2kp^2/3ρ^2/3g/3πγ) is a geometry-insensitive parameter, ρ is the average mass density, g is the gravitational acceleration, k is a “safety” factor, and p is a shape factor.

(ii) For curvature invariance, the contact radius R is assumed to be independent of seta size. This leads to

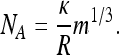[6]

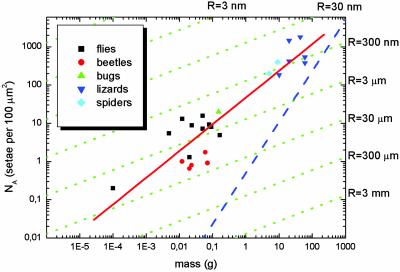
Lines of these slopes are included in Fig. 3 and can now be compared with the experimental data. It is striking that the assumption of self-similarity (Eq. 5), leading to a slope of 2/3, explains the scaling, from the fruit fly to the gecko, very well. Also a value for κ can be extracted; the best fit is obtained for κ = 3.8 × 10⁶ m^–1·kg^–1/3.

Fig. 3.

Interpretation of Fig. 2 in light of contact theory. A fit to all data (red line) gives a slope of ≈2/3, corresponding to the self-similarity criterion. Within each lineage, a lower slope of ≈1/3 is found, suggesting curvature invariance of the contacts with radius R (green lines). The approximate limit for such attachment devices (limit of maximum contact) is shown as a blue line.

Closer inspection of Fig. 3 reveals some additional subtleties. Whereas the relationship between body mass and density of single contacts is well borne out for the complete sample of animals from different evolutionary lineages (red line), the slope appears to be lower within each lineage and approaches the value 1/3 predicted for curvature invariance (green lines). Especially within lineages of beetles and flies this modified dependence renders an improved description of the data. Using the above value for κ, values of contact radius R can be extracted from the data: R ≈ 1.6 μm for the flies (excluding the ultra-light fruit fly) and R ≈ 0.3 μm for the lizards. It may be suggested that in heavier animals within a given lineage adhesion is improved by increasing the seta density slightly at a given radius of curvature of the terminal elements. In lineages with much larger body mass, both the seta diameter and the radius of curvature have to be reduced. The curvature-invariant mechanism of increasing adhesion has a natural limit: For curvature invariance the setae density can only be increased until the seta diameter approaches the contact diameter for a given curvature R. This limit of maximum contact can approximately be calculated by the equations given here; as indicated by a blue line in Fig. 3, it lies well outside the biological regime.

An additional advantage of the patterned surfaces is the reliability of contact on various surface profiles and the increased tolerance to defects at individual contacts (17). In the real situation, failure of some microcontacts because of dust particles or mechanical damage of single seta would minimally influence contact adhesion. In the case of a solitary contact, even a little damage of the contact caused by the presence of dirt or surface asperities will immediately lead to contact breakage.

The present approach, of course, neglects several additional contributions, such as the secretion of sticky fluids (18, 19); however, we note that capillary forces scale in the same way as the Johnson–Kendall–Roberts force (Eq. 3) so that the scaling behavior would remain largely unchanged. Also, biological materials in general and attachment systems in particular (20) exhibit pronounced viscoelastic effects, which requires a more complete treatment of the problem using viscoelastic contact mechanics [e.g., Johnson and Greenwood (21)]. In the light of these simplifications, it may be surprising that this approach reproduces the scaling of the attachment devices from the fruit fly to the gecko, covering 6 orders of magnitude in body mass. This finding suggests that contact splitting is the overriding design principle. Overall, it comes as no surprise that the concepts of contact theory are reflected in the evolutionary design of biological attachment systems.

Appendix: Derivation of the Scaling Relations

We want to derive the dependence of seta density on animal mass, as required by contact theory. The mass m is given by

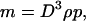[A1]

where D is a size parameter that we choose to be the total apparent contact diameter (i.e., size of one pulvillus); ρ is the average mass density, and p is a dimensionless shape factor. The adhesion force necessary to support this weight is written as

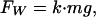[A2]

where g is the gravitational acceleration and k is a safety factor.

Consider a pulvillus with n contacts (setae) of diameter s. The areal density of setae can be expressed as

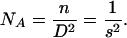[A3]

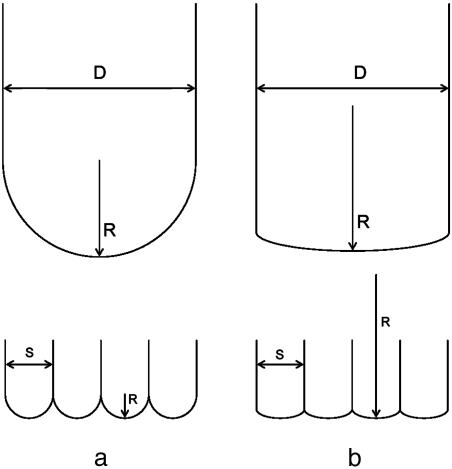
For the calculation of the adhesion force, two cases are distinguished (Fig. 4).

Fig. 4.

Two cases of contact scaling. (a) Self-similarity: contact radius R scales with contact size s.(b) Curvature invariance: contact radius is independent of contact size.

Self-Similarity. If the contract radius R scales with seta diameter s (i.e., R = s/2 for hemispherical shape), then we obtain for the Johnson–Kendall–Roberts adhesion force

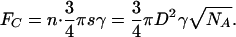[A4]

Equating Eqs. A4 and A2 yields

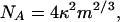[A5]

where

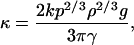[A6]

which we assume to be, to first order, independent of the animal and its size. Eq. A5 predicts plots of log·N_A vs. log·m lines of slope 2/3 (Fig. 3).

Curvature Invariance. If the contact radius R is fixed and does not scale with seta diameter, the adhesion force is approximately given by

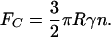[A7]

Equating Eqs. A7 and A2 leads to

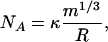[A8]

which corresponds to lines of slope 1/3 in Fig. 3.