Local Context Finder (LCF) reveals multidimensional relationships among mRNA expression profiles of Arabidopsis responding to pathogen infection

Abstract

A major task in computational analysis of mRNA expression profiles is definition of relationships among profiles on the basis of similarities among them. This is generally achieved by pattern recognition in the distribution of data points representing each profile in a high-dimensional space. Some drawbacks of commonly used pattern recognition algorithms stem from their use of a globally linear space and/or limited degrees of freedom. A pattern recognition method called Local Context Finder (LCF) is described here. LCF uses nonlinear dimensionality reduction for pattern recognition. Then it builds a network of profiles based on the nonlinear dimensionality reduction results. LCF was used to analyze mRNA expression profiles of the plant host Arabidopsis interacting with the bacterial pathogen Pseudomonas syringae. In one case, LCF revealed two dimensions essential to explain the effects of the NahG transgene and the ndr1 mutation on resistant and susceptible responses. In another case, plant mutants deficient in responses to pathogen infection were classified on the basis of LCF analysis of their profiles. The classification by LCF was consistent with the results of biological characterization of the mutants. Thus, LCF is a powerful method for extracting information from expression profile data.

An important aspect of expression profile analysis is identification of relationships among multiple profiles on the basis of similarities: comparing either profiles of different samples, which consist of expression values for numerous genes as parameters, or profiles of different genes, which consist of expression values for different samples as parameters. Interesting relationships may be defined by the investigator (e.g., find samples in which genes A and B are up-regulated and gene C is down-regulated). Alternatively, computer algorithms may be used to find relationships that are not strictly defined (e.g., find samples that have similar profiles, regardless of what the similarity might be). When the expression profiles of different samples are compared, computer algorithms treat each expression profile as a data point in a high-dimensional linear space, such that the expression value for each gene is its coordinate in one of the dimensions, and the number of dimensions is equal to the number of genes. In other words, if m profiles, each consisting of expression values for n genes, are to be analyzed, m data points are placed in an n-dimensional linear space. The problem of identifying relationships among expression profiles is thus translated into a problem of recognizing patterns in the distribution of m data points within the n-dimensional space. Similarly, when the expression profiles of n different genes (with m different samples as parameters) are compared, the problem is handled as the distribution of n data points in the m-dimensional space. Thus, the mathematical principle is the same for comparison of profiles of different samples or different genes.

Some drawbacks of conventional algorithms, such as hierarchical clustering (1), Self-Organizing Maps (2, 3), K-means clustering (4), and principal component analysis (5, 6), stem from the facts that they use artificially imposed distance measures such as a distance measure defined in a globally linear space and/or that they consider only very limited degrees of freedom. There is no reason to assume that an artificially imposed space or a space with artificially imposed degrees of freedom can describe the distribution of expression profile data points well. Nonlinear dimensionality reduction (7, 8) is an improvement in both of these aspects. It defines the structure of the global space that contains all the data points and the degree of freedom in the global space, on the basis of the local geometric context of the data point distribution.

Tenenbaum et al. (7) and Roweis and Saul (8) developed two different algorithms, Isomap and Locally Linear Embedding (LLE), respectively, to perform nonlinear dimensionality reduction for the purpose of pattern recognition. A nonlinear dimensionality reduction procedure identifies a globally nonlinear manifold (a space with the degree of freedom defined by the distribution of data points), on the basis of local geometric contexts defined in locally linear spaces. For example, a Swiss roll structure requires three dimensions for description in a linear space but only two for description in a nonlinear space (see figure 3 of ref. 7 and figure 1 of ref. 8). This example clearly demonstrates that a linear dimensionality reduction procedure, such as principal component analysis, is not able to capture such globally nonlinear manifolds.

The model plant–pathogen system consisting of the plant host Arabidopsis and the bacterial pathogen Pseudomonas syringae has been crucial for deepening our understanding of plant–pathogen interactions due to the genetic and genomic tractability of both organisms (9). Gene-for-gene resistance is conditioned by a resistance (R) gene in a plant and the corresponding avirulence (avr) gene in a pathogen. When corresponding R and avr genes are present in the system, the plant exhibits strong resistance to the pathogen (10). Otherwise, the plant is susceptible. Several R–avr combinations were identified in the Arabdiopsis-P. syringae system, including RPS2 for avrRpt2 (11, 12) and RPMI for avrB (13). The ndr1 mutation compromises both RPS2-and RPMI-mediated resistance but has a stronger effect on RPS2-mediated resistance (14, 15).

Even when a plant is susceptible to a pathogen, the plant shows a limited level of resistance to the pathogen (general resistance) (9). Salicylic acid (SA) is an important plant-signaling molecule for general resistance and at least some types of gene-for-gene resistance. The NahG transgene encodes an SA hydroxylase, so plants expressing NahG have very low SA levels. NahG plants show defects in general resistance against P. syringae and in RPS2-mediated resistance (16). Similarly, mutations that reduce the SA level, such as pad4, eds5, and sid2, and a mutation that affects responses to SA, npr1, have defects in general resistance against P. syringae (9). Jasmonic acid (JA) and ethylene (ET) are also important for plant signaling in response to pathogens (9). Plant responses mediated by SA or JA/ET pathways have differential effects on different spectra of pathogens. For example, the JA response mutant coi1 is more susceptible to Alternaria brassicicola than wild-type plants (17), but coi1 is more resistant to P. syringae (18). The ET response mutant ein2 is affected in disease symptom development but is similar to wild type with respect to P. syringae growth (19).

We have been using expression profiling as a massive phenotyping method to characterize biological systems (expression phenotyping) (20–22). When the state of a cell changes, it is likely that expression levels of some genes change. Such expression changes can be used as markers for a particular state of the cell, regardless of whether the expression changes have functional significance. Therefore, an expression profile of a biological sample can be used as a broad-spectrum phenotype of cell state. Although in principle any global profiling technologies can be used for this purpose, mRNA expression profiling currently has an advantage in sensitivity, accuracy, and breadth of coverage.

We recently reported expression phenotyping of Arabidopsis responses after P. syringae infections. Resistant and susceptible responses were compared in one case (20), and several defense mutants were compared in another (21). Hierarchical clustering was the main analytical method used. Although this analysis provided valuable information, we also noticed its limitations, one of which is that the method can handle only one degree of freedom. We need a method that can handle multiple degrees of freedom.

Here, we report development of Local Context Finder (LCF), which uses nonlinear dimensionality reduction for pattern recognition and translates the result into a network. In LCF, globally nonlinear space is generated on the basis of local contexts, and analysis of the multidimensional relationships among profiles is accomplished by using principles of network analysis. LCF was applied to the analysis of Arabidopsis expression profiles from plants infected with P. syringae.

Materials and Methods

mRNA Expression Profile Data. The data used were generated by using the Affimetrix (Santa Clara, ca) AtGenome1 GeneChip, which represents ≈8,000 Arabidopsis genes; these data are available as supplements to refs. 20 and 21. Only probe sets showing significant expression changes, as defined in the references, were chosen for analysis.

LCF. Programs for LCF were written in perl and are available for noncommercial research conducted in nonprofit organizations on request to F.K. The network output of LCF was visualized and analyzed by using pajek (http://vlado.fmf.uni-lj.si/pub/networks/pajek) (23). For visualization, the Kamada–Kawai free energy optimization option was used in Fig. 1 C–E, and the Fruchterman–Reingold 3D option was used in Fig. 2 B–D. The pajek files for Fig. 2 B and C and 2D are published as Data Set 1 and Data Set 2, respectively, as supporting information on the PNAS web site, www.pnas.org.

Fig. 1.

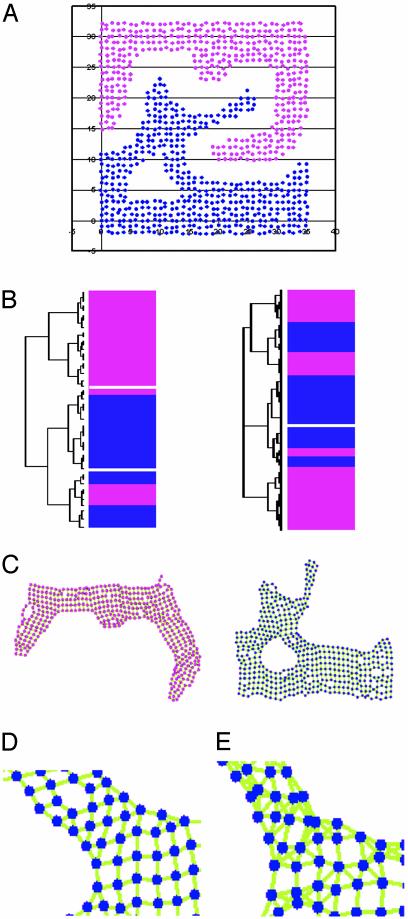
Performance of LCF in pattern recognition. (A) Initial data points for pattern recognition tests. Pattern recognition performance was compared between hierarchical clustering (B; Left, complete linkage; Right, average linkage) (1), and LCF (k = 7) (C). The colors of the bars in B and the vertices in C represent cluster assignment of the colored data points in A.(D) A magnified image of a part of the blue pattern in C. The direction of links is not shown, and the links are not color-coded according to the uncentered Pearson correlation coefficient value (all green). (E) The part corresponding to D when linear reconstruction (Step 2) of LCF is omitted (k = 5), i.e., each point is connected to five neighbors indiscriminately. Note that the links are not always mutual, so some vertices have more than five links.

Fig. 2.

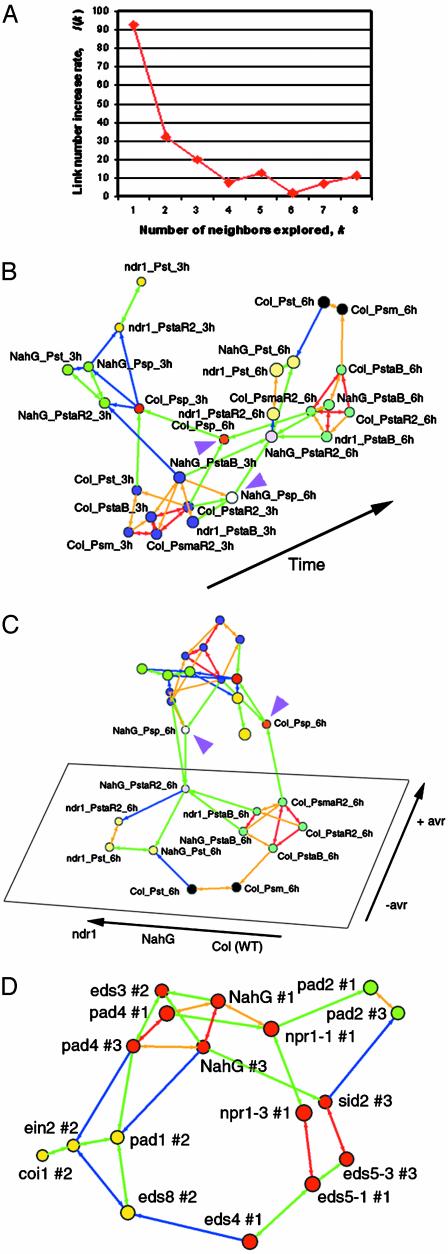
LCF analysis of Arabidopsis responses to pathogen infections. (A–C) Analysis of resistant and susceptible responses of Arabidopsis (Case 1). (A) The link increase rate function I(k). B and C are two different views of the same network generated by LCF. Each profile is shown as a vertex. Vertex size indicates 3D position in embedding, with larger vertices closer to the viewer. The vertices are classified into clusters on the basis of strongly connected components, and the groups are indicated by different colors of the vertices. The color of each arrow indicates the similarity between the data sets defined by the uncentered Pearson correlation coefficient. Red indicates 0.92–0.97; orange, 0.83–0.92; green, 0.72–0.83; and blue, 0.59–0.72. The orientation of each arrow points to a data set from each of its informative neighbors. (B) In this view, profiles are well separated according to time points, except profiles for Psp. (C) In this view, within the set of the 6-h profiles (except those for Psp; labeled vertices), the network can be well described by two independent dimensions. The name of each profile is indicated as “(plant)_(bacteria strain)_(time after inoculation, 3 or 6 h).” (plant); Col (wild-type), NahG or ndr1 (bacteria strain); Pst (P. syringae pv. tomato DC3000, virulent strain); Psm (P. syringae pv. maculicola ES4326, virulent strain); PstaR2 (Pst/avrRpt2, avirulent strain); PsmaR2 (Psm/avrRpt2, avirulent strain); PstaB (Pst/avrB, avirulent strain); and Psp (P. syringae pv. phaseolicola NPS3121, nonhost strain). Purple arrowheads indicate profiles with Psp at 6 h. (D) Relationships determined by LCF among Arabidopsis defense mutants on the basis of their responses 30 h after infection by Psm (Case 2). Representation of the network is similar to B and C. The vertices are classified into three groups on the basis of strongly connected components: red, SA plus central group; green, pad2; yellow, JA/ET group. The color of each arrow indicates the similarity between the data sets defined by uncentered Pearson correlation coefficient. Red indicates 0.77–0.87; orange, 0.65–0.77; green, 0.51–0.65; and blue, 0.36–0.51. For mutants tested in more than one experiment, the experiment number is shown as “#1” or “#3.”

Results and Discussion

Principle of LCF. The LLE procedure (8) for nonlinear dimensionality reduction was adapted to LCF. We chose LLE for LCF rather than Isomap (7), because the algorithm is simpler. The beginning of the LCF procedure is based on the first two steps of LLE (see figure 2 of ref. 8). In LCF, the data points in a high-dimensional space are described as vectors in the space: a data point representing an expression profile is the end point of an n-dimensional vector, where n is equal to the number of expression values, and the origin is the start point of the vector. There is no mathematical restriction on what isotropic local distance measure should be used in LLE (8). LCF uses the uncentered Pearson correlation coefficient (i.e., normalized dot product), because LCF is designed to compare only the shapes of profiles, not the amplitudes.

In mathematical terms:

For profile i, we can define a normalized unit vector, 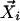, corresponding to a point in n dimensional space:

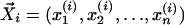and

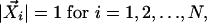where x⁽ⁱ⁾ l is the lth expression measurement in profile i, and N is the total number of profiles.

The uncentered Pearson correlation coefficient between two points i and j is defined as:

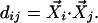For each data point 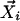, Steps 1 and 2 are performed.

Step 1. Selection of neighbor data points. For 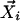, k closest neighbor data points, 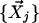, are selected such that for any point, 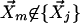, d_im < d_ij. The number of closest data points, k, is used as the primary measure to define the neighbors, instead of a fixed cutoff value for the uncentered Pearson correlation coefficient, because it enables the algorithm to adapt to differences in the local density of the data points. See How the number of neighbors, k, is determined, below, for determination of k.

Step 2. Reconstruction with linear weights. The context-dependent correlation D_i is defined as the uncentered Pearson correlation coefficient between 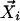and a linear convex combination of neighboring data points .

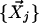where a_ij ≥ 0 for all j, and is chosen to maximize D_i.

In LCF, the linear combination is restricted to a convex one (a_ij ≥ 0). This restriction makes this step equivalent to finding the point closest to within a space confined by .

Building networks. The difference between LCF and LLE lies in the way the data points are embedded in a low-dimensional space. Spaces defined by more than three dimensions are not easily visualized, yet the number of dimensions resulting from a nonlinear dimensionality reduction procedure could be more than three for a particular data set. One way to deal with this situation is to choose three or fewer dimensions at a time. Then embedding of the data points can be optimized for the chosen dimensions and visualized, as in LLE (8). A disadvantage of this LLE-type embedding method for analysis of profiling data is that it may be difficult to grasp overall relationships, because only three dimensions can be viewed at once; therefore, if the data require more than three dimensions, they cannot be displayed in a single view. In LCF, the relationships identified in Step 2 are translated into a network. In this way, the entire network structure can be viewed at once.

Step 3. Translation of the relationships among data points into a network.

Once Steps 1 and 2 have been performed for each data point , if the parameter a_il satisfies a_il/Σ_j a_ij > 0.001, the corresponding point, 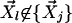, is considered to contribute to the reconstruction significantly, and a directed link is made from vertex l to vertex i. The cutoff value of 0.001 was chosen in the cases below on the basis of the stability of the outcome (see Appendix 1, which is published as supporting information on the PNAS web site). If the cutoff value is too small, the results may be overly sensitive to noise in the data. The strength of each link is defined as d_il. Embedding the results into a low-dimensional space is associated with alteration of the length of the links. To give a sense of distance between vertices, the links are color coded according to their strength.

Step 4. Visualization and analysis of the network. pajek (23) was used for visualization and analysis of the network. When the final number of dimensions for a particular data set is three or fewer, visualizing the network by using energy optimization in three dimensions has an effect similar to embedding the data points in a three-dimensional space in LLE. In other words, the manifold structure can be observed in the network. In LCF, more than three links to one vertex suggest that the local area requires more than three dimensions. Consequently, LCF gives a sense of local dimensionality.

An advantage of translating the results into a network is that relationships among vertices (data points) can be analyzed by network analysis methods on the basis of graph theory. For example, the first analysis would be to see whether the data generate more than one disconnected network. For the next level, “strongly connected components” can be used to define subnetworks or clusters. When it is possible to proceed according to the directions of links from vertex A to vertex B and vice versa, vertices A and B are defined to be strongly connected. A data point closely related to a group of data points is likely to be strongly connected to the members of the group, whereas a data point not closely related to the group is not. Although they were not used in this study, there are other network analysis methods that can be used to define subnetworks. Observing relationships among subnetworks (each subnetwork is defined by consolidation of its member data points) or focusing on the data point relationships within a single subnetwork at a time are powerful ways to simplify the network structure and are crucial for analyzing networks composed of a large number of data points, such as expression profiles of numerous genes with multiple samples as parameters.

How the number of neighbors, k, is determined. If k is too small, LCF cannot capture enough local dimensionality information. If k is too large, contexts considered by the algorithm are more global than local. The optimal value for k is determined for each set of data on the basis of the stability of the outcome network structure. When k is scanned from 1 to a larger integer, the number of directed links L(k) is recorded. The percent increase of the link number I(k) = 100·{L(k + 1) – L(k)}/L(k) is plotted against k. When I(k) stops decreasing consistently with increasing k, our interpretation is that k is large enough to capture most local contexts, and that the resulting network structure is relatively stable. We choose the minimum k value that satisfies this condition. Refer to the examples of actual cases below.

Implementation of bootstrap analysis. Data collection in a global profiling experiment could be biased. For example, the microarray used in the cases below covers only about one-third of Arabidopsis genes. There could be a bias in selection of the genes covered by the microarray. To reduce the effects of such bias in data collection on pattern recognition, bootstrapping of the data was implemented in the analysis. In addition, bootstrapping can reduce some types of noise that affect values for a small fraction of the total number of parameters, e.g., noise caused by small defects in the microarray, without requiring replicate data sets. In the first case below, the initial data had 26 columns (profiles) and 1,606 rows (probesets). To generate a set of bootstrapped data, rows were randomly sampled 1,606 times with replacement. The new bootstrapped data were analyzed by LCF, and the resulting directed links were recorded. This process of generating and analyzing bootstrapped data was performed 1,000 times. A histogram of the occurrence of each directed link was made, and the cutoff value was selected at a clear valley in the histogram shape (see supporting information for details). In this case, the links with a 90% or higher occurrence were chosen as links well supported by bootstrapping. The bootstrap analysis was also performed similarly in the second case, and the links with a 85% or higher occurrence were chosen (see Appendix 1).

Comparison of LCF and Other Methods Commonly Used for Pattern Recognition in Expression Profiling Data. Methods such as hierarchical clustering (1), Self-Organizing Maps, (2), and the K-means method (4) do not perform well in pattern recognition when the patterns are not comprised of nonoverlapping convex sets (24), because they do not consider local contexts. Fig. 1 demonstrates the performance of LCF with overlapping nonconvex patterns. Patterns are easily recognized visually so long as the dimension number of the space is three or lower. Computer algorithms used for expression profile analysis, including LCF, are unaffected by the dimension number of the space. Therefore, to compare pattern recognition performance, it makes sense to perform comparisons by using patterns in a low-dimensional space so results can be easily evaluated visually. For this reason, data points are distributed in a 2D space in this figure (Fig. 1 A). To allow these data points to be analyzed by using normalized unit vectors, an arbitrary large number was assigned as the third-dimension coordinate to all the data points (the coordinates for these data points are provided in Data Set 3, which is published as supporting information on the PNAS web site). It is immediately apparent that these data points should be clustered into two groups, indicated by pink and blue. However, as expected, hierarchical clustering by using average or complete linkage failed to recognize the patterns (Fig. 1B). In contrast, as shown in Fig. 1C, LCF (with k = 7; in this case, k was intentionally set much higher than necessary to demonstrate the power of dimensionality reduction described below) recognized the patterns and separated them into two disconnected networks (in Fig. 1, the directions of the links are not shown). In addition, LCF kept essential geometric relational information in the two dimensions: the shapes of the networks represent the original shapes of the groups well. Recognition of two colored patterns depends on the determination of neighbors. Methods in which a limited number of neighbors are simply chosen (e.g., hierarchical clustering by using single linkage connects the closest neighbors) can also recognize two colored patterns. When a sufficient number of neighbors are chosen, such a method also seems to be able to keep geometric information when embedded in two dimensions (e.g., Fig. 1E shows part of the blue pattern when five neighbors are indiscriminately connected).

An advantage of LCF over these methods, in which a fixed number of neighbors are simply chosen, is that LCF can capture geometric relational information with the actual degree of freedom, which is achieved by dimensionality reduction. To illustrate this point, LCF (Fig. 1D) was compared with a method that connects a fixed number of neighbors without dimensionality reduction (LCF Step 2 is omitted; Fig. 1E). To demonstrate the power of dimensionality reduction, the k value for LCF was chosen to be larger (k = 7) than the fixed number for the second method (five neighbors). A part of the blue pattern in Fig. 1C is magnified in Fig. 1D. It is clear that LCF captures the true 2D nature (i.e., two degrees of freedom) of the pattern, because there are no links crossing each other in this 2D embedded image. In this case, k = 7, so links with seven closest neighbors are considered for each point, but only links necessary to describe the 2D nature of the pattern are selected through linear reconstruction. In contrast, Fig. 1E shows the corresponding part of the pattern when all five closest neighbors are connected to each point without any selection. Although this still separated the pink and blue patterns of Fig. 1 A (not shown) and kept superficial geometric relational information, it is evident that many links cross each other: this procedure without the selection by linear reconstruction resulted in geometric relational information with the degree of freedom higher than the actual degree, 2. Therefore, methods with neighbor selection without dimensionality reduction are inefficient in extracting essential information.

In this particular example, principal component analysis (PCA) can identify two base dimensions to describe these data points, because the initial 2D space is linear, but visual inspection is required to identify the patterns in the 2D space. However, in nonlinear spaces, nonlinear dimensionality reduction methods are generally superior to linear dimensionality reduction methods like PCA, as exemplified by the Swiss roll structure described above (7, 8).

Case 1: Resistant and Susceptible Responses of Arabidopsis. Expression profile data for resistant and susceptible responses (incompatible and compatible interactions, respectively) of Arabidopsis during infection with P. syringae strains (20) were analyzed by LCF including bootstrapping. The value used for analysis is log₂-transformed ratio between the sample and the corresponding control. Because the results from 6 and 9 h after inoculation were similar (20), the 9-h data were omitted from the analysis. The data consist of 26 samples with expression values of 1,606 probesets each. The number of neighbors to explore in LCF, k, was determined by using the function I(k) (Fig. 2 A). In this case, when k ≥ 4, the I(k) value does not decrease consistently. We chose k = 4 to capture the local context. Fig. 2 B and C show two different views of the same network generated by LCF and visualized by pajek. Clusters of profiles defined by strongly connected components are indicated by commonly colored vertices. In Fig. 2B, the dimension that separates profiles between 3 and 6 h is evident, confirming that the shapes of the profiles for resistant and susceptible responses are similar within the same time point (20). The 6-h profiles for infection by the nonhost strain P. syringae pv. phaseolicola (Psp) (indicated by purple arrowheads in Fig. 2 B and C) locate between the 3- and 6-h planes consisting of other profiles, suggesting that the response to Psp has slower kinetics, as we pointed out previously (20). The view in Fig. 2C exhibits the relationships among the 6-h profiles. Within this set of profiles, excluding the profiles with Psp, it is clear that the major trend can be described by two independent dimensions (i.e., two degrees of freedom). One dimension is defined by whether the bacterial strains carry avr genes (+/–avr). The other dimension is defined by effects of NahG and ndr1 (WT-NahG-ndr1). This network structure indicates that (i) the effects of NahG and ndr1 were qualitatively similar when plants were infected with P. syringae pv. tomato (Pst) or Pst/avrRpt2, but ndr1 has a stronger effect; (ii) these effects were weaker but approximately along the sameWTNahG-ndr1 dimension when plants were infected with Pst/avrB; (iii) in ndr1, avrRpt2-dependent responses were not totally eliminated, because the difference between the profiles of Pst_ndr1_6h and Pst/aR2_ndr1_6h is along the +/–avr dimension; and (iv) the profile of Pst/aR2_ndr1_6h is clustered with those of Pst_ndr1_6h and Pst_NahG_6h but not with that of Pst/aR2_NahG_6h. Points i and ii indicate that both NahG and ndr1 strongly affect general resistance responses when Pst or Pst/avrRpt2 is used, and that they weakly affect general resistance responses when Pst/avrB is used. Although both ndr1 and NahG were reported to affect the RPS2-avrRpt2 gene-for-gene interaction (14, 16), point (iv) suggests that the effect on the interaction is stronger with ndr1, and that the ways they affect the interaction are qualitatively different.

In Case 1, LCF provided an easy way to visually identify the global nonlinear dimensions of the data. Note that such visual identification of global dimensions is meaningful only when the numbers of local dimensions do not exceed three. When they do, extracting part of a subnetwork or consolidating some subnetworks could help reduce the numbers and enable visual identification of dimensions. For example, in this case, the entire network required three dimensions, but the 6-h subnetwork required only two. We previously proposed a quantitative model to roughly explain the data for resistant and susceptible responses and the effects of NahG and ndr1 on them (20). We pointed out a limitation of the model due to its single degree of freedom. LCF analysis revealed that two degrees of freedom are required to explain the 6-h data. Although ndr1 was initially described as a mutation that specifically suppresses some resistance mediated by certain R genes (14), it clearly affects general resistance (20). avrRpt2-dependent responses were not totally eliminated in ndr1 (point iii above). A comparison of these profiles with a profile of ndr1 rps2 double-mutant plants infected with Pst/avrRpt2 will determine whether the remnant avrRpt2-dependent responses in ndr1 are RPS2-dependent (i.e., results of a gene-for-gene interaction) or are caused by the virulence function of avrRpt2.

Case 2: Relationships Among Arabidopsis Defense Mutants. We have conducted expression profile analysis of Arabidopsis defense mutants responding to Psm (21). In this work, we analyzed the data from wild-type, sid2, eds5-1, eds5-3, eds4, npr1-1, npr1-3, pad2, NahG, pad4, eds3, pad1, ein2, coi1, and eds8. The data were analyzed by using LCF including bootstrap analysis. The value used in the analysis is a log₂-transformed ratio between an infected mutant and the infected wild-type. The data consist of 17 samples with expression values of 519 probesets each. On the basis of the I(k) function curve, k = 4 was chosen (see Fig. 3, which is published as supporting information on the PNAS web site). Fig. 2D shows a view of the network generated by LCF and visualized by pajek. Clusters of profiles defined by strongly connected components are indicated by commonly colored vertices.

The results are generally in agreement with those obtained by hierarchical clustering, but LCF provides more information. Hierarchical clustering classified the mutants into three major groups: sid2, eds5-1, eds5-3, eds4, and npr1-3 to the SA group; npr1-1, pad2, NahG, pad4, and eds3 to the central group; pad1, ein2, coi1, and eds8 to the JA/ET group. The JA/ET cluster defined by LCF (yellow in Fig. 2D) is the same as the JA/ET group defined by hierarchical clustering. LCF combined the SA and central groups into one group (red in Fig. 2D), except for pad2. However, it is easy to grasp several interesting aspects of this red cluster from its network structure. NahG, pad4, and eds3 are closely related to each other because of high degrees of connection within their profiles (degree of a vertex). This central group core, composed of NahG, pad4, and eds3, is located on the end opposite the part containing the SA group members in the red cluster, which agrees with the separation of the central and SA groups by hierarchical clustering (21). The network structure also shows that npr1-1 is located in the position that connects the central group core to the SA group members. In addition, that the major difference between the central group core members, npr1-1, and the SA group is described along a single nonlinear dimension (the arc shape spanning from pad4 and eds3 to eds4) suggests the difference can be explained by a single factor. pad2 was classified as a cluster (green in Fig. 2D) separate from the red cluster by LCF, and the difference between pad2 and the red cluster was represented by a dimension different from the one representing the major difference among the red cluster members. These observations suggest that pad2 is very different from members of the SA and central groups, which is consistent with the biological observation that pad2 is not impaired in either the SA or JA/ET pathways (21). This aspect of pad2 was not correctly predicted by hierarchical clustering analysis. With assignments of eds3 to the red cluster (SA, central group), pad1 and eds8 to the JA/ET cluster, and pad2 to its own cluster, LCF correctly predicted the characteristics of all these mutants.

There are links from the central group core to pad1 and ein2 and from eds4 to eds8 (Fig 2D), indicating that the way the central group core members are similar to JA/ET cluster members is distinct from the way eds4 is similar to JA/ET cluster members. With these links, the overall network consisting of the red and JA/ET cluster members (except coi1) has a circular 2D structure. This circular connection pattern indicates that at least two degrees of freedom are required to explain differences among these mutants.

LCF also detected experiment-to-experiment variations. The plane defined by pad4 #1, NahG #1, npr1-1 #1, pad2 #1, npr1-3 #1, eds5-1 #1, and eds4 #1 is approximately parallel to the plane defined by pad4 #3, NahG #3, sid2 #3, pad2 #3, and eds5-3 #3 (Fig. 2D). Note that the size of a vertex represents the depth in the 3D imaging, and that the number after “#” labels each experimental set. It is important that the dimension for the experiment-to-experiment variations can be separated from the dimensions representing biological differences, which are the one along the arc from pad4 and eds3 to eds4 and the one representing the difference between the red cluster and pad2. It will be interesting to see whether experiment-to-experiment variations among many different experiments can generally be represented by a single dimension, similar to the one detected in this study.

In Case 2, we demonstrated the usefulness of applying network analysis to LCF results. The profiles can be classified into clusters defined by the nature of their links, such as strongly connected components. In addition, features in the network structure, such as the degree of a vertex, could be used in interpretation of their biological significance. Network analysis is independent of dimension numbers. Therefore, translation of the results of nonlinear dimensionality reduction into networks in LCF can aid analysis of complex profile data involving many degrees of freedom.

Conclusion

With the advance of genomic technologies and the rapid increase of data generated by them, pattern recognition in high-dimensional spaces (i.e., multivariate analysis) is becoming increasingly important in biology research. Accurate pattern information captured from large data sets allows researchers to build testable hypotheses with a high probability of being correct. Therefore, an advanced pattern recognition method like LCF will be a crucial tool for pursuing hypothesis-driven research that exploits the availability of large data sets.