Configuration-dependent diffusion can shift the kinetic transition state and barrier height of protein folding

Abstract

We show that diffusion can play an important role in protein-folding kinetics. We explicitly calculate the diffusion coefficient of protein folding in a lattice model. We found that diffusion typically is configuration- or reaction coordinate-dependent. The diffusion coefficient is found to be decreasing with respect to the progression of folding toward the native state, which is caused by the collapse to a compact state constraining the configurational space for exploration. The configuration- or position-dependent diffusion coefficient has a significant contribution to the kinetics in addition to the thermodynamic free-energy barrier. It effectively changes (increases in this case) the kinetic barrier height as well as the position of the corresponding transition state and therefore modifies the folding kinetic rates as well as the kinetic routes. The resulting folding time, by considering both kinetic diffusion and the thermodynamic folding free-energy profile, thus is slower than the estimation from the thermodynamic free-energy barrier with constant diffusion but is consistent with the results from kinetic simulations. The configuration- or coordinate-dependent diffusion is especially important with respect to fast folding, when there is a small or no free-energy barrier and kinetics is controlled by diffusion. Including the configurational dependence will challenge the transition state theory of protein folding. The classical transition state theory will have to be modified to be consistent. The more detailed folding mechanistic studies involving phi value analysis based on the classical transition state theory also will have to be modified quantitatively.

Studying the kinetics of protein folding is key to understanding the fundamental underlying mechanism. Levinthal posed the so-called Levinthal paradox in 1969 (1). If protein folding proceeds with every possible state, then it takes cosmological time to reach the native state. In nature, protein folding is completed on a time scale from milliseconds to seconds. The recent energy landscape theory of protein folding (2–6) resolves the issue by assuming the underlying energy landscape is funneled toward the native state. Superimposed on the funnel are the bumps and wiggles that form local traps. For folding to be completed in a biological time scale under physiological temperature (300 K), the slope of the funnel must be steep enough to overcome the local traps. Energy landscape theory is successful in qualitatively and quantitatively explaining many folding experiments (2–7).

Both theoretical and experimental investigations on folding and reaction kinetics have explored kinetics in different ranges of temperature and other environmental conditions (2–26). By varying environmental conditions, the underlying energy landscape structures can be probed in different levels, from locally to globally detailed perspectives (19, 20). The relationship between the dynamics and the functions of the biomolecules can be revealed.

The kinetics of protein folding is conventionally expected to be determined by the free-energy barrier or so-called transition state. Transition state theory first was proposed by Eyring in 1935 to explain the chemical reaction rates (27). In normal chemical kinetics, the transition state is defined as the thermodynamic bottleneck in reaching the product state from the reactant state (27). From the free-energy profile, we can locate the position of the barrier or the transition state by free-energy optimization in the reaction coordinate space. Then we can calculate the value of the free energy at the location of the transition state, which determines the barrier height from reactant to product. The position of the transition state in the reaction coordinate determines how close the transition state (or the nucleation seed) is to the product (or reactant) state. Thus, the kinetic rate is determined by the free-energy difference between the transition state and reactant state formulated in the transition state theory. Characterizing the transition state ensemble is very important in determining the underlying kinetic mechanism and identifying the nucleation seeds from reactant to product. Transition state theory has been successfully applied to many molecular systems. There since have been many theoretical extensions and modifications (28–34). For example, Kramers' rate theory takes into account the effect of the prefactors and the influences of the frictional effects from solvents. The variational transition state theory (31–34) takes into account some other important degrees of freedom.

It is important to realize that the picture of the transition state theory will be modified when we take the dependence of the diffusion coefficient on the configuration or reaction coordinates into consideration. The origin of the configuration- or reaction coordinate-dependent diffusion is the fact that the underlying protein-folding energy landscape is multidimensional in nature. In real experiments, we can only probe or trace finite degrees of freedom or dimensions. When we project the multidimensional landscape into one or a few dimensions or coordinates Q (for example, Q can be chosen as the number of native spatial contacts), each position of Q will experience different local environments or local conformational landscapes from the other coordinates. Therefore, the local escape time or diffusion in general is coordinate- or position-dependent (2, 22, 23, 25, 35–41, 55, 56). Furthermore, we typically have different energy barrier distributions because of the roughness of the local energy landscape, resulting in different time scales in each position of the coordinate. When we project the multidimensional landscape into one or a few dimensions, distribution of energy barriers or multi-time scales often emerges, then the diffusion also is in general time-dependent (2, 22–26). In the case of coordinate-dependent diffusion, the transition state theory will be modified in the sense that although the expression and functional form of the transition state theory may or may not change significantly, the actual location and the height of the transition state barrier will change. In other words, the presence of the spatial dependence of the diffusion coefficient effectively contributes to the free energy so that the height and the position of the effective barrier are changed. Thus, the kinetics is controlled by both the thermodynamic free energy and the diffusion. The diffusion acts as an effective driving force in addition to the thermodynamic free energy to contribute to kinetics. It also is possible that the actual kinetic paths may not go through the thermodynamic transition state, instead they pass through the effective transition state determined by both thermodynamics and diffusion.

Including the configurational dependence therefore will challenge the transition state theory of protein folding. The classical transition state theory will have to be modified to be consistent. The more detailed folding mechanistic studies involving phi value analysis based on the classical transition state theory (14) also will have to be quantitatively modified.

Here we show explicitly that diffusion plays an important role in protein-folding kinetics. We explicitly calculate the diffusion coefficient of protein folding in a 3 × 3 × 3 lattice model (36). We found that diffusion is reaction coordinate-dependent. The diffusion coefficient is found to be decreasing with respect to the progression of folding toward the native state, and we showed that this is because of the confinement from rapid collapse of the available configurational space. We found that the position dependence of the diffusion coefficient on the reaction coordinate has a significant contribution to the kinetics in addition to the thermodynamic free-energy barrier. It changes (increases) the effective free-energy barrier and modifies the folding kinetic routes. The resulting folding time with the combined effects of kinetic diffusion and thermodynamic folding free-energy profile thus is slower than the estimation from the thermodynamic free-energy barrier with constant diffusion but is consistent with the results from kinetic simulations. The configuration- or coordinate-dependent diffusion is especially important to consider for fast folding when there is a small or no free-energy barrier and the kinetics is controlled by the diffusion.

Diffusion for specific fast-folding protein such as the λ repressor and its fast mutant, as well as others, has been extensively explored experimentally (21, 42–51). For fast folding, because the inherent thermodynamic barrier is low or comparable with the thermal energy k_BT, the effect of diffusion on the kinetic barrier can be significant. Thus, the theoretical explorations here will contribute to the full understanding of the interplay between thermodynamics and diffusion on the protein-folding kinetics.

Results and Discussion

In this study, we intend to describe the effects of a varying diffusion coefficient as a function of the order parameter on the folding process for a lattice model protein. We will compare our results with the study of Socci et al. (36) in which the diffusion coefficient was treated as constant calculated by the quasi-harmonic diffusive approximation D = ΔQ(T)²/τ(T). The numerator is the mean square dispersion of the reaction coordinate fluctuations, and the denominator is the autocorrelation time of the reaction coordinate (Q, the number of native contacts) that characterizes the decay of the correlation function defined as:

In this study, we will consider the diffusion coefficient D as a function of the reaction coordinate Q, i.e., D = D(Q). In the work of Socci et al. (36), the diffusion coefficient as calculated by the above equation is a constant, and it is determined for values of Q in the interval 0 < Q < 16. In the present study, we added a harmonic term of the form E = K(Q − Q*)² to the interaction energy between monomers, which biased the simulation to have a value of < Q > close to Q*. Then, by changing Q*, it is possible to change the values of < Q > as well as the correlation times. The value of K should be high enough to make the landscape locally harmonic, in order to use the quasiharmonic diffusive approximation. Inspection of Fig. 1a shows that values of K > 0.08 can make the lanscape harmonic in a region where it is clearly not harmonic for K = 0. On the other hand, the harmonic term should not significantly restrict the conformational space, which could cause the diffusion coefficient D to decrease to very low values. Inspection of Fig. 1b shows that values of K > 0.1 cause the diffusion coefficient to decrease significantly. We therefore chose K = 0.1 for our simulations.

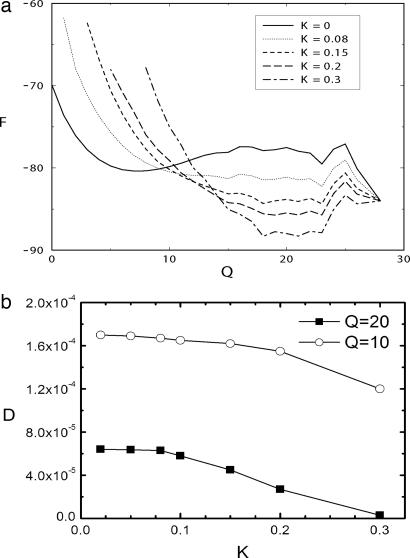
Fig. 1.

Free energy versus reaction coordinate and diffusion coefficient versus spring constant K. (a) The free energy as a function of the reaction coordinate Q (number of native spatial contacts) for biased and an unbiased simulations are shown. (b) Calculated diffusion coefficients versus spring constant K of the harmonic constrained well.

In Fig. 1a, the free energy as a function of the reaction coordinate for biased and an unbiased simulations at a chosen Q* = 20 is shown. The biased and unbiased simulations produce similar values of the diffusion coefficient for K < 0.1 (as shown in Fig. 1b), calculated by D = ΔQ(T)²/τ(T), which means that the calculated value of the fluctuations ΔQ(T)² (which is smaller than the unbiased case) scales in a similar manner to that of τ_corr(T) (also smaller than the unbiased case). It is not possible to ascertain whether this will happen in the entire range; nevertheless, we will make this assumption.

We also see from Fig. 1b that the estimation of diffusion coefficient will be influenced significantly by K when K > 0.1. It clearly is shown that for Q = 10, where the free energy already is quasi-harmonic, the diffusion coefficient D is nearly independent of K until K = 0.2. But for Q = 20, in the region where the free energy does not have a quasi-harmonic shape, the value of K should be at most equal to 0.1. This value may be enough, according to Fig. 1a. For higher values, the conformational space is reduced drastically by the force constant, constraining the reaction coordinate Q to be approximately Q = 20, which severely reduces the value of ΔQ(T)² and thus the estimation of diffusion coefficient D.

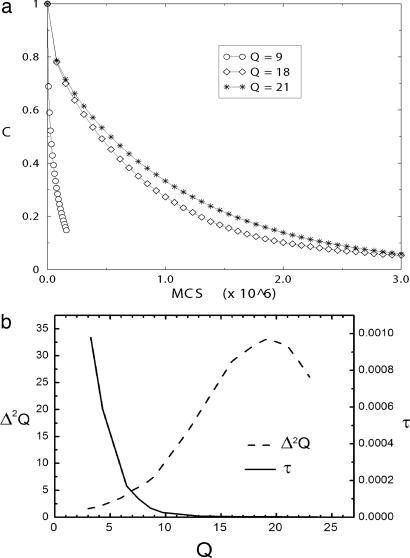
Fig. 2a shows the correlation function for three different values of < Q >. It decreases slower, i.e., with a higher correlation time τ(T), as < Q > increases. Because ΔQ(T)² changes moderately with Q (increase up to certain point) (Fig. 2b), it is implied that D = ΔQ(T)²/τ(T) decreases as Q increases. The configurational dependence of the diffusion coefficient was expected from the earlier analytical studies of Bryngelson and Wolynes (2) as well as Monte Carlo studies of Socci, Onuchic, and Wolynes (36).

Fig. 2.

The correlations and dispersions of Q. (a) The correlation functions for T = 1.5 as a function of time, in Monte Carlo steps (×10⁶), for different values of Q: 9, 18, and 21. (b) Correlation time as well as dispersion Δ²Q of reaction coordinate Q as a function of Q. The diffusion coefficient is dominated by the trend in correlation time.

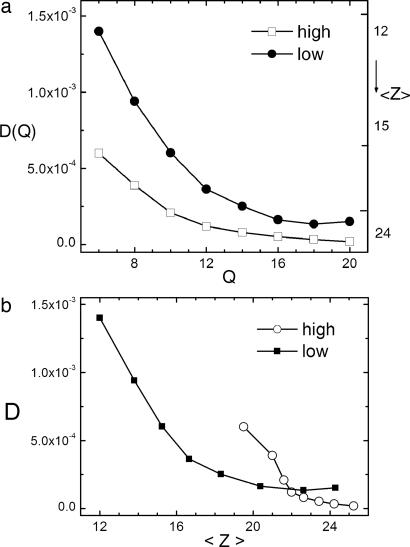
Fig. 3a shows the diffusion coefficient as function of Q (horizontal axis) and the mean value of Z, the number of any contact between monomers (right axis). When Z becomes large, the system becomes more compact. Two regimes of hydrophobicity are shown. The high hydrophobic limit is characterized by an overall attraction between monomers toward the native state, which induces a collapse before folding (52). In the low hydrophobic limit, the interaction parameters are such that there is no overall biased interaction between monomers toward the folded state. In this case, folding is not preceded by a collapse; instead, they occur simultaneously.

Fig. 3.

Diffusion coefficients versus Q and compactness < Z >. (a) Diffusion coefficient D (left axis) and average number of nonbonded contacts (< Z >) (right axis) as a function of reaction coordinate Q (number of native spatial contacts) for low- and high-hydrophobicity cases. For a given Q, it shows that the decrease in D is caused by the increase of < Z >. (b) Diffusion constant D as a function of average number of nonbonded contacts (< Z >) for low- and high-hydrophobicity cases.

The thermodynamic free-energy profile has two minima (one nonnative and one native) separated by a free-energy barrier at Q = 16. The diffusion coefficient is found to be decreasing with respect to the progression of folding toward the native state (as Q increases), which is caused by the confinement from rapid collapse of the available configurational space, as suggested by Fig. 3b. When Z is roughly a constant, such as in the late stage of folding when the compactness of proteins does not change significantly, the diffusion coefficient does not change much either (beyond Q = 16 in Fig. 3a). The collapse can be shown to be important by comparing diffusion coefficients of the high hydrophobicity with low hydrophobicity of the same value of Q (Fig. 3 a and b). It suggests that collapse, which increases the value of < Z >, is responsible for the decreasing values of the diffusion coefficient.

We can study the mean first passage time for folding τ from any particular Q from energy landscape theory once the diffusion coefficient is given (2, 22, 23):

where D(Q) is the diffusion coefficient as a function of the reaction coordinate and F(Q) is the thermodynamic free energy. Q_u and Q_f represent unfolded and folded states, respectively. In the work of Socci et al. (36), D(Q) was taken as constant, and in this study it depends on the reaction coordinate as described above.

It important to point out that for quasi-equilibrium condition, the friction and diffusion coefficients are related closely through Dζ = kT (the fluctuation–dissipation theorem), where ζ is the friction coefficient. The resulting steady probability distribution does not depend on diffusion coefficient D. However, the kinetics depends on the diffusion coefficient explicitly. In other words, configurational diffusion will not influence the equilibrium probability distribution but instead will influence the flux or kinetic rate (2, 22, 23).

The first integral of τ is dominated by the minimum of F(Q″) (in unfolded denatured state, Q″ = 7 in this case). When D is a constant, the second integral is dominated by the maximum of F(Q′). Then, we recover the usual transition state expression for τ. The kinetic time is determined mainly by the thermodynamic free-energy barrier height at the transition state. When the diffusion coefficient is Q-dependent, D = D(Q), then the second integral is dominated by maximum of exp[F(Q′)/kT]/D(Q′). Because D(Q) is monotonically decreasing as a function of Q from the results of our simulations, it is obvious that τ with D = D(Q) is slower than τ with D = D₀ (D₀ is the diffusion coefficient at unfolded denatured state, Q = 7 in this case). On the other hand, it is not hard to see that the position of the maximum of exp[F(Q′)/kT]/D(Q′) is right-shifted relative to the maximum of exp[F(Q)/kT] (that is, the kinetic transition state is right-shifted relative to the thermodynamic transition state).

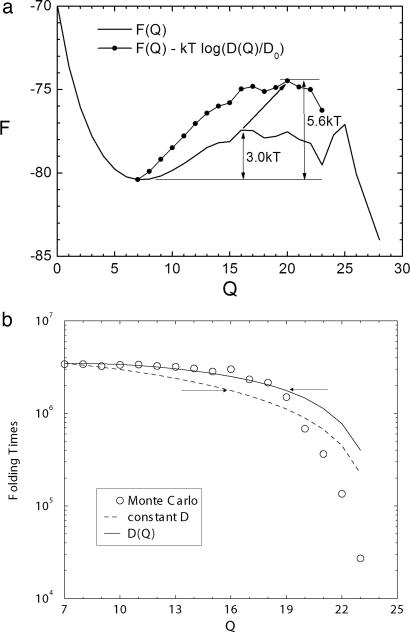
The shiftand the increase of the kinetic transition state barrier are clearly shown in Fig. 4a. The thermodynamic transition state is at Q = 16, and the barrier height is 3 kT. The equation exp[F(Q)/kT]/D(Q) = exp[F(Q)/kT − lnD(Q)], which determines the kinetic time, has an effective barrier height of 5.6 kT, implying a higher kinetic barrier compared with the thermodynamic one. The kinetic barrier coming purely from diffusion is 5.6 kT − 3 kT = 2.6 kT, which is quite significant compared with the thermodynamic barrier height (3 kT), which means that configuration-dependent diffusion can play a significant role in kinetics, especially when the thermodynamic barrier is relatively small (fast-folding proteins). On the other hand, it is clear that the maximum of exp[F(Q)/kT]/D(Q) = exp[F(Q)/kT − lnD(Q)] is right-shifted relative to the thermodynamic transition state from Q = 16 to Q = 20. Thus, the kinetic route or path does not have to follow the equilibrium path dictated by the underlying thermodynamics and may not go through the thermodynamic transition state. Instead, the kinetic path can go through a short cut.

Fig. 4.

Free energy and folding times versus reaction coordinate Q. (a) Free energy F(Q) and F(Q) − kTln(D(Q)/D₀) profiles (controlling the kinetic first passage time with Q-dependent diffusion relative to constant diffusion) as a function of reaction coordinate Q. (b) First passage time of folding from specific Q from Monte Carlo results, constant, and Q-dependent diffusion.

Fig. 4b shows τ(Q) (the first passage time from any particular Q to folded state) as a function of Q with constant and Q-dependent diffusion compared with Monte Carlo results. Notice that the kinetic time drops significantly after certain Q because of the downhill motion beyond, which naturally defines the position of the kinetic transition state. We can see that the kinetic time with Q-dependent diffusion agrees with Monte Carlo results much better compared with the constant diffusion case up to the position of kinetic transition state (indicated by the right arrow in Fig. 4b), which is right-shifted from the thermodynamic transition state (indicated by the left arrow in Fig. 4b).

We also can see from Fig. 4b that the points above the arrows are nearly the same in folding time at T = 1.5 through the Monte Carlo method by Socci et al. (36). The folding time therefore comes mainly from configurations that precede the transition state ensemble. Also, going from Q up to the transition state region, the free-energy barrier decreases, then diffusion also must decrease to maintain the folding times constant in the mentioned portion of the conformational space shown in Fig. 3a.

Although configuration-dependent diffusion does not disturb the equilibrium distribution, it modifies the kinetic rate or flux through the increase of the kinetic barrier height and the kinetic route or path through the right shift of the kinetic barrier position.

In Fig. 5a, we show the temperature dependence of diffusion coefficients. In Fig. 5b, we show the temperature dependence of the folding times calculated from direct Monte Carlo results, from constant diffusion (open squares and open circles), and from coordinate (Q)-dependent diffusion (filled circles) by using the formula mentioned above for folding time τ.

Fig. 5.

Diffusion coefficients versus Q and folding times versus temperature. (a) Diffusion coefficient as a function of Q for several different temperatures: T = 2.0, 1.5, and 1.25. (b) The kinetic folding time obtained from Monte Carlo simulations are shown as a function of temperature (solid line). The open squares are the results of Socci et al. (36) with constant diffusion. The results of our work with configuration-dependent diffusion are shown in filled circles at T = 2.0, 1.5, and 1.25.

Fig. 5a shows that as temperature increases, typically the diffusion coefficient increases near or above folding temperature. For high temperature at T = 2.0 (folding temperature is 1.5), the diffusion is significant even until Q = 16, where the thermodynamic transition state is located. The rate-limiting step, or folding time, is determined mainly by the thermodynamic barrier height when the diffusion is fast. At the lower temperature T = 1.25, the rate-limiting time for folding is more likely to be determined by the slow diffusion coefficient. And at the folding temperature, there should be a balance between the barrier and diffusion in the calculation of the folding time.

Fig. 5b shows that our results of the mean first passage time for folding from a coordinate-dependent diffusion coefficient compare well with those of Monte Carlo data [Socci et al. (36)]. At folding temperature T = 1.5, folding time from the coordinate-dependent diffusion is significantly larger than the one obtained from a constant diffusion (36), which means the effect of the coordinate-dependent diffusion is to increase the effective free-energy barrier and therefore the kinetic folding time. At other temperatures, the difference between the constant and spatial-dependent diffusion is small. At a higher temperature of T = 2.0, the barrier for folding is higher, the effect of Q-dependent diffusion is thus small. At a lower temperature of T = 1.25, the average barrier for folding is lower, but the free-energy landscape becomes rougher than that of higher temperatures and trapping starts to become important, which leads to higher effective barrier and slower kinetics. The difference between the constant and spatial-dependent diffusion at T = 1.25 is less significant, as shown in Fig. 5a, compared with higher temperatures, thus it does not seem to lead to much discrimination in kinetics, as shown in Fig. 5b.

The end of the conformational space was taken as Q = 23 rather than Q = 28. As discussed (36), there are Monte Carlo movements that take the reaction coordinate directly from Q = 23 to the native value Q = 28. Indeed, the kinetic values in Fig. 4b show that the folding time is negligible for Q = 23.

In the work of Socci et al. (36), the double integral for kinetic time is taken from Q = 0 to Q = 23, but the diffusion (constant) is calculated in a more restricted conformational space (Q < 16), which delimits the region before the transition state. In principle, there is no reason for not using the whole conformational space to calculate the coordinate-dependent diffusion coefficient, as we did here.

Conclusions

We have explored the effects of kinetic diffusion on the dynamics of protein folding. We found that kinetic diffusion clearly plays an important role in determining the rate of folding in addition to the thermodynamic free-energy barrier. The effective kinetic barrier is increased, and the position of the barrier is shifted. This feature is especially important for the fast-folding process in which the thermodynamic free-energy barrier is either small or zero (downhill process). The kinetics thus is strongly controlled by the diffusion, which reflects the ability of escaping from the local free-energy landscape. Through the experimental and theoretical studies, we can detect and map more details of the local intrinsic features and topology of the underlying energy landscape.

Our findings that the effective free-energy barrier shifts both in height and position with configuration-dependent diffusion challenge the transition state theory of protein folding. The transition state theory worked well for constant diffusion but might not be accurate enough to describe the kinetics of protein folding when configurational diffusion is taken into account. We expect that when the folding thermodynamic barrier is high, the diffusion will play a less important role in determining the kinetics. The classical transition state theory will be more accurate in describing the dynamic process. On the other hand, when the folding thermodynamic barrier is small or comparable with the thermal energy such as in the fast-folding proteins, the configuration-dependent diffusion can play significant role in determining the kinetics of folding process.

Furthermore, for detailed folding mechanistic studies, the phi value analysis based on the transition state theory may need to be modified quantitatively (14). The phi value is determined by the ratio of free-energy change between transition state and unfolded state upon mutations versus free-energy change between folded and unfolded state. So it sensitively depends on the kinetic barrier at the transition state and its associated changes. If the effective kinetic barrier is changed, then the phi value also will be changed. Because the position of the effective kinetic barrier also is shifted, then the average phi value, which often is correlated with the position, also will be shifted.

The theory and methodology outlined in this study provide a basis for comparing and connecting with the models/simulations and experiments (21, 26, 44–51) and can be applied to a wide variety of other biological as well as condensed-phase systems and problems.

Materials and Methods

The lattice model used for the kinetic simulations has been used extensively in previous studies (4, 5, 35, 53). The protein is modeled by a 27-mer polymer chain on a three-dimensional cubic lattice. The 27-mer lattice is a renormalized (or reduced) description of small globular proteins. We use a Monte Carlo algorithm with standard polymer local moves: end moves, corner flip moves, and 90° crankshaft moves (35) (see Fig. 1). The energy for the heteropolymer is given by:

where E_l is the nonbonded contact energy between monomers of the same type, E_u is the energy between monomers of different types, N_l is the number of contacts between monomers of similar type, and N_u is the number of contacts between monomers of dissimilar types. There are only two types of monomers with hydrophobic or hydrophilic nature. High hydrophobicity parameters are used (E_l = −3 and E_u = −1 in arbitrary units, chosen so that typical temperatures are of order one), where biasing toward the folded state is strong and the roughness of the landscape is weak. Low hydrophobic parameters are used (E_l = −3 and E_u = 3), where biasing toward the folded state is weak and the roughness of the landscape is strong.

We use the previously designed sequence (54): ABABBBBBABBABABAAABBAAAAAAB. In this study, only one good folding sequence is used. Effects of sequence variations are not analyzed here. Monte Carlo sampling with a local move set is used to determine the density of states and to define the kinetics of the model (5, 35, 52). The density of states is determined as a function of energy E, number of native nonbonded contacts Q, and the total number of nonbonded contacts Z. Within the microcanonical ensemble, the free energy of the system can be obtained as a function of Q and Z, and the complete thermodynamics can be determined. Four phases typically are found: the noncompact unfolded states (so-called random-coil states), compact unfolded states, trapping states, and the native state. The transition temperatures T_f (folding) and T_g (local trapping) are determined.

We can measure the mean first passage time to reach the native state for the designed sequence starting from random-coil configurations. By repeating the dynamic Monte Carlo simulations with different initial conditions, we can obtain information about the statistical average of these folding times.