Temperature-dependent heme kinetics with nonexponential binding and barrier relaxation in the absence of protein conformational substates

Abstract

We present temperature-dependent kinetic measurements of ultrafast diatomic ligand binding to the “bare” protoheme (L₁-FePPIX-L₂, where L₁ = H₂O or 2-methyl imidazole and L₂ = CO or NO). We found that the binding of CO is temperature-dependent and nonexponential over many decades in time, whereas the binding of NO is exponential and temperature-independent. The nonexponential nature of CO binding to protoheme, as well as its relaxation above the solvent glass transition, mimics the kinetics of CO binding to myoglobin (Mb) but on faster time scales. This demonstrates that the nonexponential kinetic response observed for Mb is not necessarily due to the presence of protein conformational substates but rather is an inherent property of the solvated heme. The nonexponential kinetic data were analyzed by using a linear coupling model with a distribution of enthalpic barriers that fluctuate on slower time scales than the heme–CO recombination time. Below the solvent glass transition (T_g ≈ 180 K), the average enthalpic rebinding barrier for H₂O-PPIX-CO was found to be ≈1 kJ/mol. Above T_g, the barrier relaxes and is ≈6 kJ/mol at 290 K. Values for the first two moments of the heme doming coordinate distribution extracted from the kinetic data suggest significant anharmonicity above T_g. In contrast to Mb, the protoheme shows no indication of the presence of “distal” enthalpic barriers. Moreover, the wide range of Arrhenius prefactors (10⁹ to 10¹¹ s⁻¹) observed for CO binding to heme under differing conditions suggests that entropic barriers may be an important source of control in this class of biochemical reactions.

The binding and release of diatomic ligands in heme proteins is one of the simplest and most fundamental chemical reactions taking place in living systems. Since the pioneering study of the temperature dependence of CO rebinding in myoglobin (Mb) by Austin et al. (1), great progress has been made in understanding the ligand binding process, and Mb has become an important prototype for this reaction (2–19). However, the origin(s) of the final enthalpic barrier for CO binding in Mb as well as the diminished prefactors in the Arrhenius expression for the rate remain somewhat obscure. The reduced prefactor has been ascribed to the spin-forbidden (ΔS = 2) nature of CO binding to ferrous heme (14, 20, 21), whereas the enthalpic barrier can be attributed to a combination of proximal and distal effects (19). Various theoretical models, usually involving protein conformational substates, have been put forward to explain the barriers and the nonexponential kinetic response observed at temperatures below the solvent glass transition (1, 2, 19). In addition, the significant decrease in the MbCO rebinding rates as the temperature is increased above T_g (glycerol–water glass transition) has led to quantitative models of protein relaxation and fluctuational averaging that focus on the role of the protein and its evolution between the ligand-bound and unbound conformations (2, 19, 22).

Investigations using protein samples are complicated by the fact that there is high probability for the CO to escape from the protein into solution when the temperature exceeds T_g ≈ 180 K. Thus, ligand migration and protein relaxation are found to couple with the ligand rebinding process, sometimes making interpretation of the kinetic data problematic. For the present study, we eliminated the complexity of the protein material and investigated CO and NO binding to the bare heme group [iron protoporphyrin IX (FePPIX)] with either water or 2-methyl imidazole (2MeIm) as the heme axial ligand.

Kinetic studies of MbCO have suggested that the enthalpic barrier for CO binding to the heme in Mb is ≈18 kJ/mol near room temperature (23, 24), whereas analysis of kinetic data below the glass transition (T < T_g) suggest that the average barrier is ≈11 kJ/mol (25). In either temperature range, the corresponding Arrhenius prefactor for MbCO is found to be ∼10⁹ s⁻¹ (1, 23–25). The increase in the enthalpic rebinding barrier for T > T_g is thought to be due to the relaxation (or diffusion) of Mb from its bound state conformation (frozen in at low temperature) to its unbound conformation after ligand photolysis (2, 19, 22).

Earlier studies of CO rebinding to heme model compounds with and without proximal imidazole ligation at room temperature have revealed that imidazole coordination leads to a significantly increased rebinding barrier (26). The faster CO rebinding for H₂O-FePPIX-CO is described by a highly nonexponential kinetic response, suggesting that a distribution of transition state barriers exists on the kinetic time scale. In contrast, the much slower CO geminate rebinding kinetics observed for 2MeIm-FePPIX-CO are found to be well described by an exponential fitting function (26), suggesting that the slower rebinding allows for fluctuational averaging of the transition state barriers (e.g., heme geometries) on time scales that are faster than the kinetics. Here we explore further the rebinding kinetics of heme-CO (and heme-NO) as a function of temperature.

Temperature-dependent kinetics of CO binding to protoheme have been reported before (27–29). Below the solvent glass transition (T < T_g ≈ 180 K), we obtain a constant enthalpic rebinding barrier (≈1 kJ/mol) that is similar to an earlier report (28). When T > T_g, we find that heme relaxation increases the enthalpic barrier, independent of the presence of protein material. In contrast, an earlier analysis assumed a fixed enthalpic barrier at all temperatures and used a ligand diffusion model with an entropic preexponential distribution to explain the nonexponential rebinding kinetics at higher temperatures (29). A key observation that leads us to revisit these experiments is the temperature-independent exponential rebinding of NO to FePPIX (30), which is not predicted by a diffusive model. As an alternative, we present an analysis based on a distribution of heme conformations and reorganization energies (19) that quantitatively explains both the highly nonexponential FePPIX-CO rebinding process and the slowing of the rates as the temperature is increased above T_g. For NO binding, we have previously discussed how a “harpoon” mechanism decouples the electronic binding reaction from the heme conformation, leading to an exponential kinetic response at all temperatures (30).

We also present measurements of the temperature dependence of the near-infrared transitions of H₂O-FePPIX. The main absorption feature near 780 nm is assigned to the analogous band III seen in deoxyMb and deoxyHb (31), whereas another weaker band near 850 nm corresponds to band II. Band III is a weak iron-to-porphyrin charge-transfer transition that is sensitive to iron–porphyrin displacement (32–34). An analysis of the spectral moments of this band as a function of temperature indicates a close correlation between the kinetics and heme structural evolution. This observation clearly demonstrates how different conformations of the heme group, and their temperature-dependent structural evolution, can lead to nonexponential CO rebinding that is analogous to MbCO, even in the absence of protein conformational substates.

An important additional question raised by these observations is whether the various models for CO binding to heme in Mb can be extended to explain the ultrafast subnanosecond geminate rebinding of CO to protoheme (3, 26, 35) and to various other heme proteins, such as CooA (36) or carboxymethyl cytochrome c (37), for which the Arrhenius prefactor must be ∼10¹¹ s⁻¹ (instead of 10⁹ s⁻¹ as found for MbCO). If the Arrhenius prefactors for CO binding can differ by several orders of magnitude between different heme proteins and heme environments, it suggests that entropic factors (rather than spin selection rules) may turn out to be an important and underappreciated source of biochemical control in this class of protein reactions.

Kinetic Data Analysis.

Here we use a distributed linear coupling model for the CO binding reaction that has been described in detail by Srajer, Reinish, and Champion (SRC) (19, 33, 38). The SRC model separates the enthalpic barrier for CO rebinding into two parts:

where the term H_p denotes the “proximal” barrier due to heme “doming” and a is the generalized iron out-of-plane displacement associated with this heme distortion. The “effective” force constant associated with moving the iron into the heme plane is denoted as K, and H₀ represents the remaining (mostly distal) contributions to the barrier. The quantity H₀ contains energies involving ligand docking and steric constraints associated with the distal pocket as well as a small a-independent term from the linearly coupled heme potential surfaces (19, 33, 38). The distribution of the iron out-of-plane displacements, P(a), is assumed Gaussian with a₀*(T) denoting the average out-of-plane coordinate displacement in the photolyzed deoxy state at temperature T, and σ_a(T) its variance. This results in an asymmetric distribution of barrier heights (H > H₀) that goes as

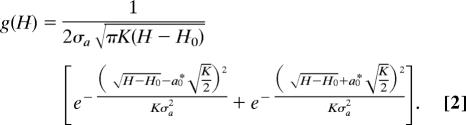The survival population after photolysis, which is the measured kinetic observable, is given by

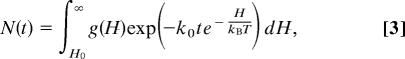where k₀ is the Arrhenius prefactor in the expression for the rate and k_B is Boltzmann's constant.

To efficiently fit the kinetic data, N(t) can be simplified by using a transformation of variables:

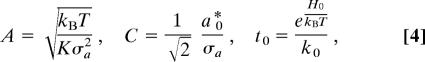and x = (H − H₀)/k_BT. These substitutions lead to

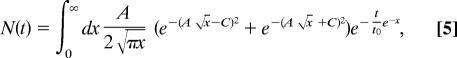so there are only three independent fitting parameters: {A, C, t₀}.

After fitting the kinetic data, the average proximal barrier can be recovered as

We can also invert the remaining parameters in Eq. 4 to find

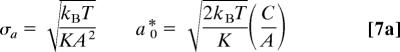Experimental Results

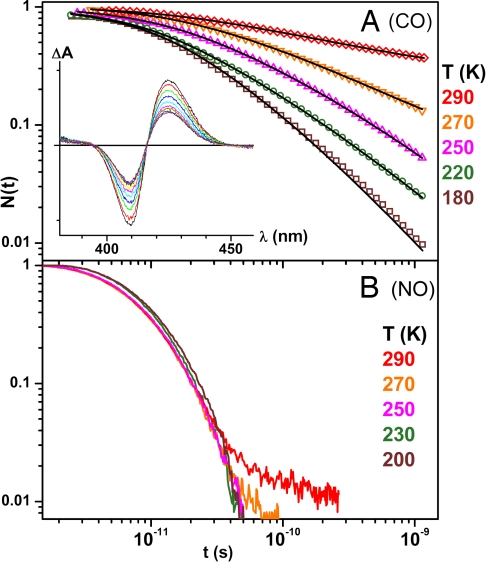
Fig. 1 presents the kinetics of CO and NO rebinding to H₂O-FePPIX at temperatures above the glycerol–water solvent glass transition. The kinetics are essentially temperature-independent and exponential for NO binding but highly nonexponential and temperature-dependent for CO rebinding. The solid lines through the heme-CO data are obtained by applying Eq. 5 at each temperature. Fig. 1A Inset shows the transient spectral evolution for CO binding.

Fig. 1.

Ligand rebinding to heme. (A) The CO rebinding kinetics for H₂O-FePPIX above the glass transition temperature. (Inset) Transient absorption spectra at room temperature. The delays are 10, 20, 40, 80, 160, 300, 500, 1,000, 2,000, and 4,000 picoseconds. (B) NO rebinding to H₂O-FePPIX.

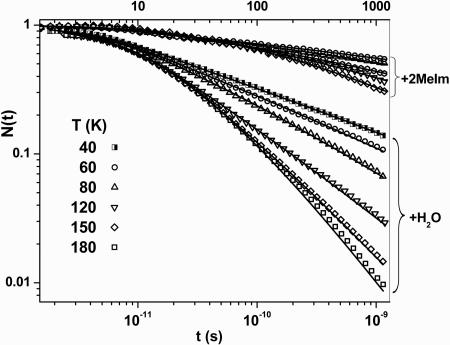
In Fig. 2, the CO rebinding kinetics are presented for temperatures below the glass transition, and the effect of replacing the H₂O ligand with 2MeIm is shown. The solid lines are again derived from fitting each highly nonexponential curve using the SRC model (Eq. 5). We want to emphasize that the three parameter SRC fits are distinctly superior to what we obtained with a stretched exponential function with offset, which also has three free parameters. The poorer fit using a stretched exponential function can be understood because the kinetics display power law behavior at long times, which is a characteristic of an underlying barrier distribution. The stretched exponential function is more typical of a relaxation process and cannot follow this behavior over such a large dynamic range.

Fig. 2.

The CO rebinding kinetics for 2MeIm-FePPIX and H₂O-FePPIX below the glass transition temperature.

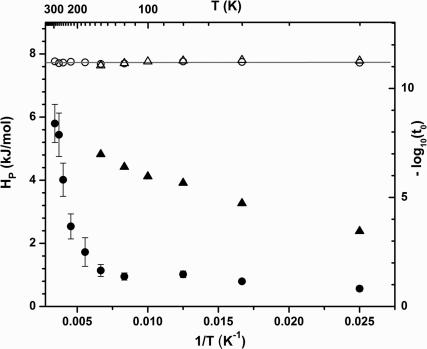
In Fig. 3, we plot the extracted values for −log₁₀(t₀) as a function of inverse temperature. From Eq. 7b, the slope of this plot yields H₀ ∼ 0, and the intercept gives the Arrhenius prefactor, k₀ = 1.5 × 10¹¹ s⁻¹. The temperature dependence of H̅_p found from Eq. 6 also is plotted in Fig. 3 for both the 2MeIm-FePPIX-CO and H₂O-FePPIX-CO complexes. The slower kinetics associated with the 2MeIm complex at low temperature do not allow for a complete sample reset to equilibrium between pulse pairs (see Fig. 2). As a result, the distribution of enthalpic barriers that gives rise to the nonexponential kinetic response changes with temperature due to “pumping” (39) of the 2MeIm-FePPIX-CO ensemble. The longer-lived dissociated states do not rebind before the arrival of the next pump–probe pulse pair and are selectively removed from the kinetic response as the temperature is lowered. As seen in Fig. 3, this leads to values for H̅_p that appear to decrease with temperature below the glass transition temperature.

Fig. 3.

Eq. 7b was used to extract the distal enthalpic barrier (H₀) and Arrhenius prefactor by plotting −log₁₀(t₀) vs. 1/T (open symbols). The proximal enthalpic barrier H_p (filled symbols) was extracted from the fits by using Eq. 6. The circles correspond to the heme without 2MeIm, and the triangles correspond to heme with 2MeIm.

In contrast, the H₂O-FePPIX-CO sample shows a constant value for H̅_p ≈ 1 kJ/mol below T_g, followed by a distinct relaxation to larger values, H̅_p ≈ 6 kJ/mol, as room temperature is approached. The constant value for H̅_p below T_g is consistent with the “freezing in” of a more planar distribution of heme geometries and the fact that H₂O-FePPIX rebinds CO fast enough to reset between the arrival of the pump–probe pulse pairs (whereas 2MeIm-FePPIX does not).

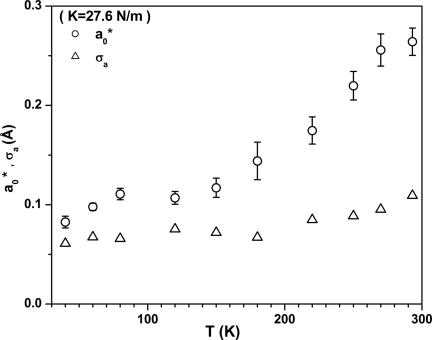
In Fig. 4 we plot the values of the mean iron displacement, a₀*, and its variance, σ_a, extracted from the H₂O-FePPIX-CO kinetics by using Eq. 7. [For MbCO below T_g we find (19, 33) a₀* ≈ 0.2 Å and σ_a ≈ 0.1 Å.] The absolute values of these quantities depend on the doming force constant, K, which is taken here to be 27.6 N/m. The value of K is based on the observed up-shift of the H₂O-FePPIX low-frequency vibrational modes compared with 2MeIm-FePPIX (see Discussion).

Fig. 4.

Distribution parameters for H₂O-FePPIX-CO obtained from the kinetic fits and Eq. 7a.

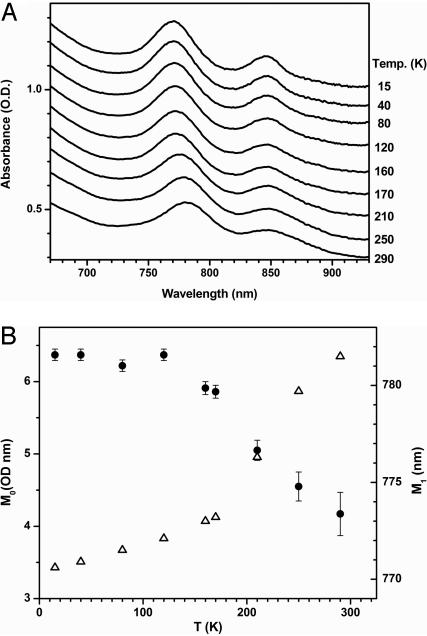
In Fig. 5 we present the near-infrared absorption spectra of H₂O-FePPIX as a function of temperature. The spectral moments, M₀ and M₁, corresponding to the area and position of the major feature in Fig. 5A, are extracted from the data and presented in Fig. 5B. The red-shift of the absorption band as the temperature is raised through the glass transition, along with the decreasing intensity of the transition, signals a shift in the heme structure, presumably due to anharmonicity in the potential energy surface that leads to movement of the iron farther out of the heme plane (32).

Fig. 5.

Temperature dependence of band III. (A) Temperature dependence of the near-infrared spectra of the band III region of H₂O(Fe²⁺)PPIX. (B) The temperature dependence of the 0th moment (integrated intensity; solid circles) and first moment (center wavelength; open triangles) of band III.

Discussion

The slowing down of the heme-CO kinetics at temperatures above the solvent glass transition can be seen in Fig. 1. This non-Arrhenius behavior signals a relaxation-induced increase of the rebinding barrier distribution as the temperature is raised. The contrasting exponential behavior observed for heme-NO demonstrates that diatomic ligand diffusion (28, 29) is not the source of either the nonexponential behavior or the relaxation phenomenon. (Note that within the first 20 ps at 180 K the NO is 90% bound with pure exponential kinetics, whereas CO is 60% bound but with highly nonexponential kinetics. Moreover, at longer times there is no indication of an independent diffusive phase for either ligand, so it is difficult to attribute the nonexponential kinetics of CO to diffusion, whereas the NO kinetics remain exponential on the same time scale.) Additionally, the evolution of the heme structure sensitive band III shown in Fig. 5 is strong evidence that heme structural change underlies the observed temperature dependent kinetic relaxation response for CO rebinding.

In contrast to Fig. 1, the data in Fig. 2 show that when T < T_g, the CO rebinding rates increase with increasing temperature and are characteristic of a quenched distribution of rebinding barriers (1, 2, 19). The data in Fig. 2 also contrast the binding of CO to heme with and without a 2MeIm ligand, indicating the importance of H_p. The nonexponential CO rebinding kinetics of FePPIX are analogous to what has been observed for MbCO (1). Clearly, protein conformational substates are not a requirement for this type of kinetic behavior, which apparently is an inherent property of the solvated heme.

The CO rebinding at all temperatures can be fitted well by using the SRC model (Eq. 5), and the fundamental dynamic parameters can be extracted at each temperature (Figs. 3 and 4). When the value of −log₁₀(t₀) is plotted vs. 1/T in Fig. 3, the flat slope demonstrates that H₀ ∼ 0 (see Eq. 7b), so that heme doming is the dominant enthalpic contribution to the rebinding barrier for FePPIX (with or without 2MeIm). Evidently, the removal of the protein distal pocket leads to a significant reduction in the value of H₀, which is found to be ≈7 kJ/mole for MbCO (19). A summary of approximate CO rebinding barriers and prefactors is given in Table 1 for T < T_g and for T = 293 K.

Table 1.

Enthalpic barriers and Arrhenius prefactors

Complex	T < Tg			T = 293 K
	H0	Hp	k0	H0	Hp	k0	H0+ Hp
MbCO	7	5	1.6 × 109	—	—	1.6 × 109	18
H2O-FePPIXCO	0	1	1.5 × 1011	0	6	1.5 × 1011	6
2MeIm-FePPIXCO	0	≈4	1.5 × 1011	—	—	1.5 × 1011†	⪝16‡

The units of measure are kJ/mol for barriers (H₀, H_p) and s⁻¹ for prefactors (k₀). —, not determined. The values for MbCO are taken from refs. 22 and 23.

^‡If the entropic barrier and prefactor at 293 K are taken to be the same as for H₂O-FePPIX, the enthalpic barrier is increased by 10 kJ/mol (26) to16 kJ/mol. If the entropic barrier is larger (smaller prefactor), the enthalpic barrier is <16 kJ/mol.

The intercept of the −log₁₀(t₀) plot gives the prefactor (k₀) for CO rebinding in protoheme. The value of k₀ is 1.5 × 10¹¹ s⁻¹, which is two orders of magnitude larger than what is found for Mb (23, 25). This strongly suggests that, in addition to the distal enthalpic barrier (H₀ ≈ 7 kJ/mol), there are significant entropic barriers that are presented by the protein, which are absent in the model systems. Based on the significant variations in the Arrhenius prefactors between MbCO (1.6 × 10⁹ s⁻¹) and FePPIX-CO (1.5 × 10¹¹ s⁻¹), and what can be deduced for other heme proteins (36, 37), it appears to us that the role of entropic control in heme proteins may have been underestimated. The Arrhenius prefactor can be approximated as

where ν₀ is an “attempt” frequency (k_BT/h ≈ 10^12–13 s⁻¹) and S^† − S₀ is the entropic barrier. Significant differences in the number of accessible states of the ligand–protein system after dissociation (Ω₀) or in the rebinding transition state (Ω^†) may be required to account for the wide variation in prefactors observed for CO binding under different conditions.

Spin can potentially play a role; however, it is an unlikely source of the dramatic variation in k₀. For example, the transient spectra in Fig. 1 are typical of the S = 2 to S = 0 transition seen in MbCO, so that altered spin selection rules cannot be responsible for the large increase in k₀ observed for the bare heme.

The quantities a₀* and σ_a(T) plotted in Fig. 4 describe the first two moments of the heme geometry distribution (namely, the iron out-of-plane displacement and its variance) after photolysis. The absolute magnitudes of these parameters depend on the effective doming force constant, K, which is approximated to be independent of temperature and taken to be twice that of Mb (19). The value 27.6 N/m is consistent with measurements using femtosecond coherence spectroscopy, which show an upshift of ≈40% in the low-frequency modes when water replaces 2MeIm as the axial heme ligand (F.G., unpublished data). Obviously, the choice of a softer force constant will lead to increased values for a₀* and σ_a, which scale weakly as the inverse square-root of K. The average iron out-of-plane displacement for the water ligated protoheme is unknown; however, the increased value for K indicated by the femtosecond coherence spectroscopy experiments predicts smaller values for a₀ and σ_a than are observed for the imidazole bound heme systems.

A key observation associated with Fig. 4 is the clear break point between 150–180 K for the values of a₀*. Evidently the heme potential is anharmonic (40) and coupled to the surrounding solvent matrix. As the glass transition is reached and the matrix begins to melt, the iron out-of-plane displacement increases, due to vibronic coupling (32) [direct thermal excitations of the d(t_2g) iron orbitals may also have an affect on the structure of the heme core].

The temperature-dependent, near-infrared spectral changes of the equilibrium deoxy state of H₂O-FePPIX are displayed in Fig. 5. As the temperature is raised through the glass transition, band III shifts systematically from 770 to 780 nm, showing a distinctive break point near the glass transition temperature. Previous studies conclude that the intensity of band III is sensitive to the iron–porphyrin distance, with larger distance resulting in a weaker band intensity (32). As the temperature is raised in Fig. 5, the band III intensity shows relatively little change below the glass transition but begins to decrease near 180 K, indicating that the iron–porphyrin distance is increasing with temperature above the glass transition temperature.

We conclude that a change in the heme structure, mainly the iron out-of-plane displacement, increases the enthalpic rebinding barrier and causes the abnormal slowing down of the CO rebinding kinetics as the temperature is increased above T_g. By fitting the kinetic data using the SRC model, we obtained an estimate of how the underlying heme configuration is changing as the temperature is raised above the glass transition. The kinetics for CO binding to protoheme are well explained if the iron out-of-plane distance increases with temperature above 180 K as shown in Fig. 4. Protein relaxation cannot be invoked to explain this observation because there is no protein present.

In contrast to CO rebinding, the temperature-independent exponential kinetics of FePPIX-NO demonstrates the absence of a proximal heme rebinding barrier, and insensitivity to the iron out-of-plane distance. We explain this using a “harpoon” model (30), based on the extra unpaired electron of NO, which allows it to bind without waiting for a thermal fluctuation to bring the heme into the more planar configuration that depopulates the d_z² orbital (see figure 9 in ref. 30).

Flash photolysis generates an initial nonequilibrium distribution of unligated conformations, which relaxes and undergoes equilibrium fluctuational averaging when T > T_g. There are two limiting cases concerning the speed of the initial relaxation. One limiting case involves a fast heme doming relaxation that precedes ligand rebinding and fluctuational averaging. This possibility is supported by time-resolved resonance Raman and coherence studies, which suggest that heme doming takes place on subpicosecond time scales (41, 42). In this scenario, the photodissociated heme quickly relaxes to a new equilibrium configuration above the glass transition. Because the iron–porphyrin displacement increases with temperature, it suggests that the observed slowing-down of the rebinding kinetics arises due to a larger rebinding barrier associated with increased heme doming.

The other limiting case involves a slower relaxation of the heme doming process that is stretched in time. For example, the heme relaxation in MbCO was monitored by using the position of band III and was reported to involve timescales that stretched from hundreds of picoseconds to nanoseconds (43). Because the SRC model assumes a static inhomogeneous barrier distribution, the fits presented here would represent an average of a slowly evolving distribution. However, the interconnected nature and “frustration” associated with the protein conformation of Mb might be expected to slow down the heme doming process in comparison to the bare heme compounds under investigation here. The poorer fits of the stretched exponential relaxation function also indicate that an underlying distribution, rather than slow relaxation, is the source of the observed nonexponential behavior. Moreover, it has been suggested (44) that the longer time scale processes observed in band III evolution (43) are due to slow protein relaxation, whereas the heme is fully relaxed within 2.5 ps. As a result, it is likely that the fast doming relaxation limit is operative when T > T_g, with possible exceptions for temperatures very close to T_g.

The nonexponential kinetics observed for H₂O-FePPIX-CO suggests that, after photolysis, the equilibrium fluctuational averaging within the ensemble of hemes takes place on a slower time scale than either the fast-doming relaxation or the ligand-rebinding process. The doming relaxation is subpicosecond because it is spontaneously driven by ultrafast nonequilibrium electronic forces, associated with the Fe d-electron redistribution that accompanies photolysis. In contrast, the equilibrium averaging of the various heme nuclear configurations is much slower because it involves thermally activated transitions that must surmount free-energy barriers involving solvent and heme structural rearrangements.

An interesting observation is that the 2MeIm-FePPIX-CO kinetics are exponential at room temperature (26) with a rebinding time constant of τ_BA ∼ 3 × 10⁻⁹ s. In contrast, the H₂O-FePPIX-CO room temperature kinetics remain highly nonexponential with an average time scale of 〈τ_BA〉 ∼ 7 × 10⁻¹¹ s, which requires that, in 80% glycerol at 290 K, the fluctuational averaging time for the various heme-doming geometries is faster than 3 × 10⁻⁹ s (to explain the exponential kinetics with the 2MeIm ligand) but slower than ≈7 × 10⁻¹¹ s (to explain the nonexponential kinetics without the 2MeIm ligand). This requirement is in excellent agreement with the 3 × 10⁻¹⁰ s solvent relaxation time scale observed for 80% glycerol–water at 290 K (45). Moreover, as might be expected at lower temperatures (200–220 K), the time scale for fluctuational averaging as measured by the loss of kinetic hole-burning in band III (46) is even slower (approximately tens of nanoseconds). These results provide additional evidence that a heterogeneous distribution of heme conformations, rather than diffusion, underlies the heme-CO rebinding kinetics reported here.

Prior studies of Mb reported a slowing down of the CO rebinding kinetics above 170 K that was attributed (22) to a protein relaxation process (Mb*→Mb). The relaxation was shown to be independent of solvent viscosity, implying that only internal parts of the protein are involved in the process (22). The present study demonstrates that the heme geometry itself plays a central role in the relaxation process and that the structural parameter associated with heme doming is a key reaction coordinate that can be well quantified using the SRC model (19). Another surprising and somewhat paradigm-shifting conclusion is that protein conformational substates are not required to generate highly nonexponential CO rebinding analogous to what is seen in Mb (1, 27).

The current study clearly reveals the potentially significant role of protein-specific entropic factors in the determination of the CO rebinding rate. The prefactor for the CO rebinding rate in protoheme (with or without a proximal imidazole ligand) is found to be 1.5 × 10¹¹ s⁻¹ at all temperatures studied, whereas the prefactor for CO rebinding to Mb is found to be ≈2 × 10⁹ s⁻¹ (25). Thus, in addition to the ≈7 kJ/mol value for H₀, the heme surroundings in Mb evidently provide a significant entropic barrier for CO binding. These additional protein-specific entropic and enthalpic barriers are what shift the nonexponential kinetics seen in Fig. 2 to the longer time scales observed for Mb.

We also note that for NO binding to Mb, the prefactor is ≈10¹¹ s⁻¹, indicating a much smaller entropic barrier than for CO. One possible explanation for this surprising observation is that the entropic barrier may depend on the time scale for the rebinding process and, thus, on the very different enthalpic barriers that the heme presents to the two ligands. For NO binding, H_p ∼ 0 because there is no need for a heme thermal fluctuation to vacate the d_z² orbital, which speeds up the NO rebinding process and may not allow enough time to fully explore the available system states, Ω₀. This explanation would predict a decreased (nonequilibrium) entropic barrier (and increased k₀) for NO compared to CO. A more formal treatment of such nonequilibrium thermodynamic effects would improve our understanding of ultrafast (bio)chemical reactions.

In fact, biological systems may have evolved entropic architectures and dynamics that take advantage of relatively small enthalpic barriers, which can tune the lifetimes of metastable states relative to their entropy production times (48). In this way, the system can very effectively discriminate between desired outcomes (e.g., efficient NO and O₂ rebinding to heme with low entropic barriers) vs. undesired outcomes (e.g., retarded CO rebinding with high entropic barriers) by using much smaller enthalpic barriers than would otherwise be necessary.

Experimental Methods

Hemin (FePPIX chloride) was purchased from Porphyrin Products (Logan, UT) and glycerol was obtained from Acros Organics (Geel, Belgium). Hemin was dissolved in 1 M NaOH and then diluted into an 80% (vol/vol) glycerol solution with the final sample pH adjusted to 12 by using aliquots of 1 M HCl. After flushing with argon, the sample was reduced by addition of a small amount of degassed sodium dithionite solution. The CO adduct was formed from the reduced sample by flushing with CO for at least 30 min. The equilibrium absorption spectra at 293 K were obtained by using a U-3410 spectrophotometer (Hitachi, Tokyo, Japan). Equilibrium spectra at cryogenic temperatures were measured with a fiber-coupled CCD array spectrophotometer (Spectral Instruments, Tucson, AZ) using a homemade cryogenic gas-tight sample holder under an argon atmosphere (30).

Details of the ultrafast laser system and detection technique have been described elsewhere (26, 30, 47). The pulse train was passed through a “pulse-picker” (Conoptics, Danbury, CT) to lower the repetition rate of the laser (to 38 MHz) to help overcome the possibility that at lower temperatures the recombination rates might become slower than the repetition rate of the laser. Fast optical scanning across the sample was performed by using a technique based on an off-axis spinning lens (46) that creates a common focal point moving in a circle of adjustable radius (1–4 mm). This methodology allows us to probe stationary samples at cryogenic temperatures and helps to minimize the thermal lensing background signals.

The error bars in Fig. 3 and 4 are a measure of goodness-of-fit resulting from the least squares application of Eq. 5 to the data. Errors less than the symbol size are not shown, and the errors for 2MeIm-FePPIX are not presented because of incomplete sample reset.

Abbreviations

Mb

myoglobin

FePPIX

iron protoporphyrin IX

2MeIm

2-methyl imidazole.