Real-time observations of single bacteriophage λ DNA ejections in vitro

Abstract

The physical, chemical, and structural features of bacteriophage genome release have been the subject of much recent attention. Many theoretical and experimental studies have centered on the internal forces driving the ejection process. Recently, Mangenot et al. [Mangenot S, Hochrein M, Rädler J, Letellier L (2005) Curr Biol 15:430–435.] reported fluorescence microscopy of phage T5 ejections, which proceeded stepwise between DNA nicks, reaching a translocation speed of 75 kbp/s or higher. It is still unknown how high the speed actually is. This paper reports real-time measurements of ejection from phage λ, revealing how the speed depends on key physical parameters such as genome length and ionic state of the buffer. Except for a pause before DNA is finally released, the entire 48.5-kbp genome is translocated in ≈1.5 s without interruption, reaching a speed of 60 kbp/s. The process gives insights particularly into the effects of two parameters: a shorter genome length results in lower speed but a shorter total time, and the presence of divalent magnesium ions (replacing sodium) reduces the pressure, increasing ejection time to 8–11 s. Pressure caused by DNA–DNA interactions within the head affects the initiation of ejection, but the close packing is also the dominant source of friction: more tightly packed phages initiate ejection earlier, but with a lower initial speed. The details of ejection revealed in this study are probably generic features of DNA translocation in bacteriophages and have implications for the dynamics of DNA in other biological systems.

The transfer of bacteriophage DNA from a capsid into the host cell is an event of great importance to biology and physics. In biology, DNA ejection was a key piece of evidence demonstrating that the genetic material was DNA and not protein (1), phages have long been used to insert foreign genes into bacteria (2), and phage-mediated DNA transfer between species is a challenge to theories of evolution (3). In physics, the translocation of DNA through a pore has been studied from the theoretical and experimental points of view (4–8). Because phage DNA ejection is such a well known example of this process, it is important to understand it from a quantitative point of view.

This paper addresses a longstanding, quantitative puzzle about phage DNA ejection: How fast is the ejection process? We use bacteriophage λ, a typical tailed phage, to answer this question. In a λ infection, first the phage tail binds to the Escherichia coli outer membrane protein LamB, triggering ejection. Then the genome, 48.5 kbp of double-stranded DNA, moves out of the phage head, through the tail, and into the cytoplasmic space, which requires force on the DNA directed into the cell. A force of tens of piconewtons (pN) is produced by the highly bent and compressed DNA within the capsid (9–11), but not much is known about how fast the DNA transfer occurs, except that ejection reaches completion in vivo in <2 min (12). One study used lipid vesicles incorporating LamB and filled with ethidium bromide: the DNA was ejected into the vesicles, causing an increase in fluorescence over ≈30 s (13). However, the ≈1,000 molecules of ethidium bromide in each vesicle were enough for only the first 1 kbp of DNA (14). Also, because the ejections could have started at different times, that experiment says very little about the DNA translocation process. This paper aims to resolve these challenges in describing the λ ejection process.

An important insight from theory is that frictional forces limit the speed of ejection, due to DNA rearrangement in the phage head or sliding forces in the tail (15, 16). Because the DNA is in a liquid state (17), we expect friction to behave at least somewhat like macroscopic hydrodynamic drag: stronger at higher speed or at smaller spacings between the moving parts. The DNA-tail interaction does not change during the ejection process, so we expect friction in the tail to remain constant. In contrast, friction in the head should be stronger when the spacing between the loops of DNA is small, i.e., at the beginning of ejection.

To quantify the rate of ejection, a single-phage technique is necessary. Single-phage ejections were first observed with fluorescence microscopy on phage T5, revealing an effect of the unique structure of the T5 genome: nicks in the DNA resulted in predefined stopping points and a stepwise translocation process, with speeds that were too high to be quantified, so that further analysis of the speed and source of friction was not possible (18). As we will show here, λ ejects its DNA differently from T5, following a continuous process that we can quantify with single-molecule measurements. This allows us to clarify the earlier vesicle-ejection results and study the speed of the ejection process. In fact, knowledge of the forces involved in ejection makes λ an ideal subject for study at the single-molecule level. By comparing the forces to the rate of ejection, we are able to quantify the friction and determine which source of friction actually dominates. Furthermore, we argue that only through systematic analysis of different phages is it possible to develop a complete picture of the DNA translocation process.

The key to checking quantitative ideas about bacteriophage ejection is to vary parameters that affect the process. Earlier, the genome length of λ was varied to investigate how it affects ejection force (11). In this paper we exploit the same strategy, using genome length as a control parameter, but this time to control the ejection dynamics. We expected that the dynamics only depends on the amount of DNA within the capsid, not on the length of the genome that was originally enclosed. A second parameter is the ionic composition of the solution, because monovalent cations lead to higher pressures than divalent cations (19). In fact, Mg²⁺ ions are commonly used to stabilize λ, but these ions are less important for the stability of mutants with shorter genomes (20). Here, we will compare a buffer containing Mg²⁺ to one containing Na⁺. The goal of the paper is to use these tunable parameters to dissect the DNA translocation process.

The paper is organized as follows: in Results, we describe what we have observed about λ ejection using the single-molecule assay. In Discussion, we analyze these results, looking specifically at what they can tell us about the source of friction during ejection. We conclude by summarizing what we have learned about the ejection process, with recommendations for further work. Detailed procedures are give in Methods, and further details are available in supporting information (SI) Text, SI Movies 1–4, SI Figs. 6–11, and SI Table 1.

Results

To reveal details of the λ ejection process, we measured the rate of ejection as a quantitative velocity with units of kbp/s, following recent work in which single phage T5 ejections could be seen by fluorescence microscopy (18): The λ capsids were bound to a microscope coverslip and washed with a dye/LamB solution to initiate ejection, with a high enough dye concentration to stain the DNA immediately after ejection. An oxygen-scavenging system reduced photodamage, allowing high frame-rate (4 s⁻¹) real-time measurement of the amount of DNA leaving the capsid (see Methods for details). As mentioned in Introduction, we can compare our results to models of the ejection process by varying the phage genome length and ion type. The genome length dependence was addressed by using two λ mutants, λb221 (38 kbp) and λcI60 (48.5 kbp), which together represent a range close to the maximum allowable range of DNA lengths for λ (21). To gain an understanding of the effects of various ions on the ejection process, we compared ejection in two buffers, with either Mg²⁺ or Na⁺ ions at a concentration of 10 mM (see Methods). What we expected to see is that the force driving ejection is significantly reduced in the Mg buffer as compared with the Na buffer. These ions are significantly less concentrated than those within an E. coli cell, but the cytoplasmic concentrations are not relevant for the ejection process, which takes place when the capsid is bound to the outer surface of the cell.

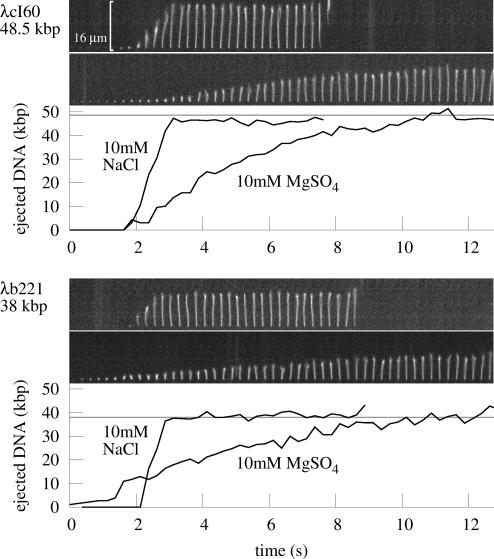
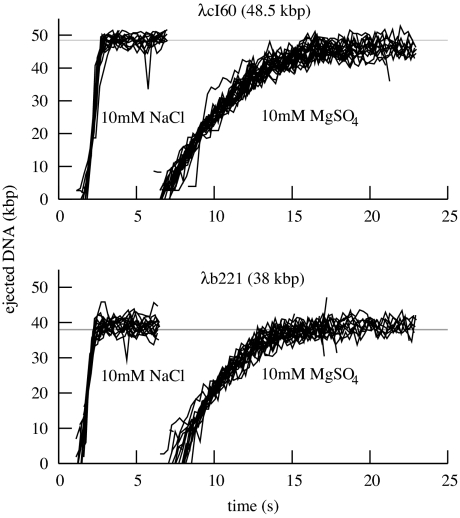
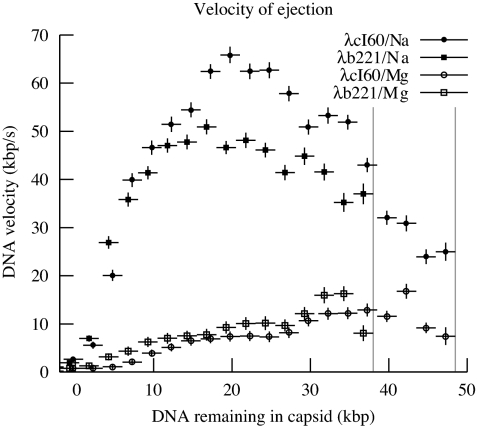
Fig. 1 shows real-time views of genome ejection from λ. A total of 81 such single-molecule trajectories were selected from the video data and processed, representing different solution conditions, flow rates, and genome lengths. For each set of experimental conditions, the ejection followed a reproducible trajectory: except for experimental noise or photodamage, there were no apparent differences between events, as shown in Fig. 2. Fig. 3 shows the speed of the ejection process. As these graphs show, the translocation of DNA reaches a high rate of up to 60 kbp/s, slowing as it approaches a maximum extension near 100% ejection, after a total of 1–11 s. This is to be contrasted with the T5 genome, which exhibited multiple random pauses during the ejection process (18). At its maximum extension, however, the λ DNA remained attached for a random amount of time, seconds to minutes, often a long enough time that it was destroyed by photodamage before the release could be measured. Just as the pauses in the case of T5 were due to a feature of the T5 genome, this effect could be due to a unique feature of the λ genome: the 12-bp overhang at the end of the DNA might form nonspecific hydrogen bonds with the capsid protein. However, the present experimental technique does not have the resolution to address exactly how large the piece of DNA remaining within the capsid is.

Fig. 1.

Images: time series of single genome ejections from λcI60 and λb221, taken at a frame rate of 4 s⁻¹. For each of the phages, the ejection in buffer with 10 mM NaCl (Upper) is significantly faster than ejection in 10 mM MgSO₄ (Lower). The 16-μm scale bar is approximately the contour length of a 48.5-kbp piece of DNA. Graphs show length of the DNA that has emerged from the capsid at each time point, as computed by using a computer image-processing algorithm together with DNA length standards as described in the text.

Fig. 2.

Graphs of ejection trajectories, comparing NaCl and MgSO₄ buffers and two genome lengths. Single-ejection events were analyzed as described in the text, resulting in trajectories giving the length of DNA out of the capsid as a function of time. These trajectories are aligned and plotted for visual comparison; the offset of the starting time of the ejection is not used in further analysis. The graphs show that ejection proceeds on a time scale of ≈1 s in NaCl buffer, or ≈10 s in MgSO₄ buffer. The ejection speeds of phages with different genome lengths appear similar in this view.

Fig. 3.

Averaged speeds of DNA ejection for λcI60 and λb221. The plot shows the DNA ejection speed as a function of the amount of DNA within the capsid, averaged in bins of width 2.5 kbp (shown as the horizontal error bars.) Vertical error bars are computed from the standard deviation of the calibration data; there are additional systematic deviations in all curves due to inaccuracies in calibration at the different ionic conditions. The curves for phages of different genome lengths lie close to each other, whereas most of the variation is caused by the difference in buffer conditions. A maximum of ≈60 kbp/s is reached in NaCl buffer, whereas the maximum in MgSO₄ buffer is ≈17 kbp/s. Vertical gray lines represent the genome lengths of λcI60 and λb221.

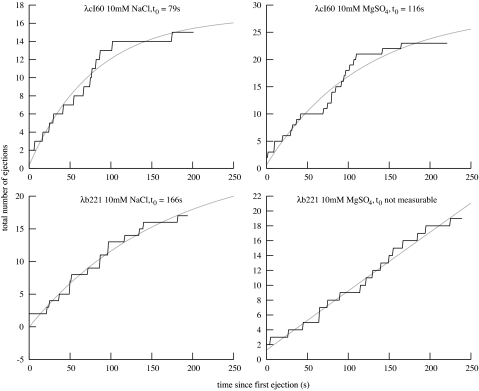
Another important feature of the ejection process is the waiting time before translocation begins. Although all ejections proceed nearly identically once they have started, λ exhibits a random waiting time of seconds to minutes, during which time no visible DNA has emerged from the capsid. Fig. 4 shows the number of ejections that have been triggered as a function of time, with exponential fits to determine the approximate time constant t₀ of the waiting process.

Fig. 4.

The number of ejections that have been triggered as a function of time. For each experiment, the total number of ejections that had been observed was plotted as a function of time; these are the same ejections that were used for the analysis above. Also plotted are exponential least-squares fits of the form a(1 − exp(−t/t₀)) + b, where t₀ is the time constant of triggering. To take into account the delay before LamB entered the flow chamber, we set t = 0 at the time of the first observed ejection.

Discussion

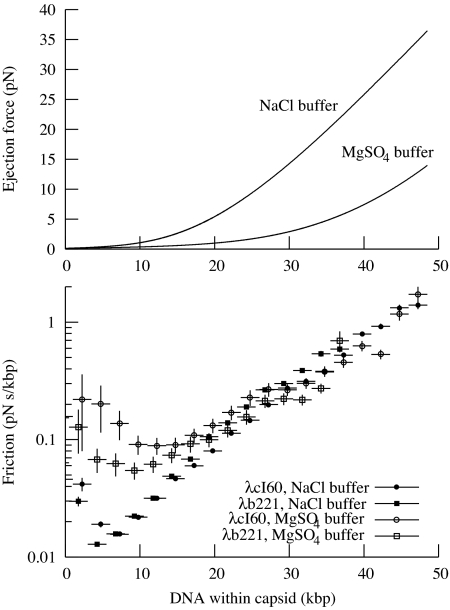
The previous section described the general features of the λ ejection process: a stochastic initiation process followed by a continuous, reproducible translocation. Now we will discuss the quantitative details in light of recent theories that model the phage genome, predicting the forces that will be produced by compressed DNA during ejection, as shown in Fig. 5.

Fig. 5.

The relationship between force and velocity. (Upper) Force on the DNA, as a function of the amount of DNA left within the capsid, according to theoretical calculations (M. Inamdar, personal communication). Calculations for both buffers were run according to the method of Purohit et al. (33), which requires two parameters, F₀ and c, that must be determined experimentally. We used F₀ = 12,000 pN/nm²; c = 0.30 nm for Mg buffer and F₀ = 660 pN/nm²; c = 0.52 nm for Na buffer, based on fitting to experimental data from Rau et al. (19). The calculations for Mg buffer were identical to those reported earlier (11). The force in Na buffer is significantly higher than that in Mg buffer. (Lower) Computed friction coefficient φ, showing the relationship between DNA packing within the capsid and its friction. The graph shows that φ generally increases with increasing DNA density. For low concentrations of DNA, φ is much lower for Na buffer than for Mg buffer. However, with more than ≈20 kbp in the capsid, φ becomes independent of the type of buffer. The value of φ appears to increase to a very high value when 100% of the DNA is packed. Error bars are computed as in Fig. 3.

For DNA translocation to initiate, some kind of molecular door that blocks the exit of the DNA must first open. Fig. 4 shows that the parameters known to affect pressure and velocity affect the waiting time before ejection, denoted by t₀. For example, in Na buffer, λcI60 has t₀ = 79 s and λb221 has t₀′ = 166 s. Here we have chosen to use an exponential function corresponding to a one-step kinetic process, because this is the simplest form that is supported by the data. In this case, the Arrhenius relation holds

where E and E′ are the energies of the transition state for initiation of ejection in the two phages. This results in

As shown in Fig. 5, the force F on the DNA with 48.5 kbp of DNA in the capsid is predicted to be 36 pN, whereas it is 23 pN with 38 kbp of DNA. How could the transition state energy be coupled to F? In the transition state, the door may be partially open, having moved a distance Δx along the phage axis. In that case, we find

Similarly, in Mg buffer, we find forces of 14 and 6.2 pN. For λcI60, we find t₀ = 116 s, whereas the t₀ value for λb221 is unmeasurable. Comparing λcI60 in the two buffers, we get Δ x = 0.07 nm, of the same order of magnitude as the value above. However, this method predicts a value of t₀ for λb221 of ≈100 s, which should have been observable. It is possible that the change in buffer conditions has altered the details of the mechanism that initiates ejection.

The values of Δ x given above have the right order of magnitude for a transition that involves, for example, the breaking of hydrogen bonds, suggesting that the waiting time distribution can tell us about the mechanics of the initiation process. However, we do not have enough data to make a claim about exactly what this process is.

After initiation, the DNA begins translocation through the phage tail, proceeding continuously with a varying speed until the entire genome has exited. We would like to understand the details of this process, with particular attention to the source of friction that limits the speed of translocation. Figs. 1 and 2 show that the presence of Mg²⁺ has a dramatic effect on the overall speed, with λcI60 taking ≈1.5 s to eject its DNA in Na buffer, which should be compared with 8–11 s in Mg buffer. The most obvious interpretation of this result, in agreement with the findings of bulk DNA pressure measurements (19), is that the higher pressure in Na buffer is responsible for the faster ejection. However, this simplistic view is not entirely correct, as we discuss below.

Fig. 3 shows v for each set of parameters. As expected, v is a function only of the ionic conditions and the amount of DNA inside the capsid, independent of the original genome length. The graph shows that the maximum v is actually reached at an intermediate stage of ejection, whereas it is reduced by ≈50% when the capsid is fully packed. The maximum of F is when the capsid is fully packed, so we know that v cannot simply be proportional to F. This suggests a modification to the simplistic idea of v being proportional to the force F with which the DNA is being ejected. The ratio of the two values represents the strength of the friction, which we denote by φ = F/v.

Apparently, φ depends on the amount of DNA within the capsid. A reasonable interpretation is that when the capsid is fully packed, contact between strands of DNA or the capsid walls increases φ, slowing translocation below the maximum. It is also possible that φ will be different for Na and Mg buffers.

In Fig. 5 we plot φ as a function of the amount of DNA within the capsid, showing that the value of φ strongly depends on the amount of DNA in the capsid, increasing to ≈100 times its initial value as the phage becomes fully packed. In fact, over most of this range, φ is independent of all parameters except for the amount of DNA in the capsid. As discussed in Introduction, this dependence on DNA density strongly points to friction originating from hydrodynamic drag within the phage head rather than in the phage tail. The question now becomes whether we can understand the magnitude of φ theoretically. However, two challenges limit the development of models: First, the DNA remaining in the capsid will rearrange as it becomes progressively less dense; it is important to know how its structure changes to estimate how fast these changes can occur. The second is that the forces between DNA strands, water, ions, and the protein capsid are not well understood and are particularly difficult to calculate for the interaction of DNA with the narrowest part of tail. As a result, most theoretical modelers have “deliberately avoided” explicit calculations of the time scale of DNA translocation (15, 16, 22, 23). We believe that the data presented here will encourage the development of models that can quantitatively account for the actual ejection velocity.

In this paper, we have shown that the ejection of DNA from bacteriophage λ can reach speeds of up to 60 kbp/s, comparable to the lower bound of 75 kbp/s found for the translocation speed in T5 (18) and clarifying an earlier bulk experiment (13). The speed may also be compared with the slips of 10 kbp/s or greater observed during φ29 DNA packaging under force (24). This assay provides a quantitative way to look at parameters that might affect the ejection process: here, we have examined the effects of ions and the phage genome length, comparing them to expectations from theory. Other factors could be incorporated into the assay, such as external osmotic pressure, DNA-condensing agents, or DNA-binding proteins, in an effort to develop a better theoretical understanding of the ejection process. Additionally, because we have seen the ejection process from so many different points of view in λ, it would be interesting to know more about the forces and dynamics of DNA packaging in that phage. The ejection assay could also be replicated with other phages, to provide points of comparison to λ. In particular, φ29 has been shown to experience forces of up to 100 pN during packaging; its ejection could be significantly different from that of λ (24, 25).

We used SYBR Gold as a fluorescent marker for visualizing DNA, which may affect the translocation velocity, because the dye penetrated the capsid on a time scale of ≈10 min. The lowest possible dye concentration was used for this experiment, and dye was added immediately before ejection, which should minimize any dye-related effects. We did not notice any systematic difference between earlier or later ejections in each recording. Despite the low dye concentration, staining of ejected DNA occurred on a time scale faster than the video frame rate: otherwise, the position of the DNA at the fixed end would have appeared to change during the ejection process.

Finally, it should be noted that the DNA ejection process in vivo may be quite different from what we observe here, due to osmotic pressure in the bacterial cytoplasm and the presence of proteins that can bind to and actively translocate DNA. No matter how high the internal force is when a phage is fully packed, it will drop to zero as the DNA exits the capsid, so it cannot be sufficient to complete ejection against the internal osmotic pressure of E. coli, which produces an outward force of several pN (11). A first attempt to mimic the cell interior could be made by including an osmotic stressing agent such as PEG in the ejection buffer. Several other forces potentially playing a role in ejection include proteins such as RNA polymerase that bind to DNA and produce an effective inward force by translocation or ratcheting (26), channels opened during the ejection process that allow water to rush in and produce drag on the DNA (27), and even molecular motors found in the phage capsid (28). For λ, it is not known what part of the process depends on the pressure in the capsid and what part relies on active transport. Further work to visualize the ejection process in vivo is probably the only way that this information could be revealed.

Methods

Buffers and Strains.

Several buffers were used for in vitro ejection: Na buffer (10 mM Tris/10 mM NaCl, pH 7.8) was considered representative of buffers containing 100% monovalent cations, whereas Mg buffer (10 mM Tris/10 mM MgSO₄, pH 7.8) was considered representative of buffers containing ≈100% divalent cations. TM buffer (50 mM Tris/10 mM MgSO₄, pH 7.4) was used in earlier ejection experiments (9, 11); we use it here for the preparation of the phages. Buffer A was used earlier for experiments on the DNA packaging process (24). Because of the 10-fold excess of NaCl, it is not clear which type of ion will dominate within the bacteriophage capsid. We found, in fact, that buffer A had an intermediate behavior: calibration DNA behaved identically to DNA in Mg buffer, but DNA translocation required ≈4 s, between the values for the Na and Mg buffers (see SI Table 1).

Phages λb221cI26 (λb221) and λcI60 were extracted from single plaques and grown on E. coli C600 cells with the plate-lysis method on 50-ml supplemented tryptone-thiamine plates (20 g/liter agar, 10 g/liter tryptone, 5 g/liter NaCl, 2.5 g/liter MgSO₄, 13 mg/liter CaCl₂, 20 mg/liter FeSO₄, 2 mg/liter thiamine), which were covered with 20 ml of TM buffer after confluent lysis and incubated at room temperature for several hours or 4°C overnight. Phages were then purified by differential sedimentation and equilibrium CsCl gradients, resulting in 10¹² to 10¹³ infectious particles, as determined by titering on LB agar. After purification, the CsCl buffer was replaced with TM using 100,000 MWCO spin columns (Amicon).

The λ receptor LamB (maltoporin), required to trigger ejection, was extracted from the membranes of E. coli pop154 cells: these cells express a lamB gene from S. sonnei known to be compatible with a variety of λ strains, allowing ejection in the absence of chloroform (29, 30). An overnight culture was sonicated, then the membranes were pelleted, homogenized, and washed in 0.3% n-octyl-oligo-oxyethylene (oPOE; Alexis Biochemicals catalog no. 500-002-L005) at 40°C for 50 min. A second wash was performed in 0.5% oPOE, followed by extraction in 3% oPOE at 37°C. LamB was affinity-purified in amylose resin and spin-filtered to replace the buffer with TM buffer containing 1% oPOE. Based on the sequence of LamB, it follows that a 1-cm absorbance of 1.0 at 280 nm corresponds to 0.34 mg/ml protein, which we use for computing LamB concentrations in the experiment. Accordingly, from 2 liters of cells we were able to obtain at least 1 mg of protein, enough for many ejection experiments.

Single-Molecule Measurement.

Our single molecule ejection assay essentially uses an earlier technique (18), with modifications for use with phage λ. A 5-mm-wide, 120-μm-thick channel was constructed from double-sided adhesive sheets (Grace Biolabs). The channels were produced with laser cutting to assure reproducible dimensions (Pololu Corporation). Tygon tubing (inner diameter: 0.02 in) was epoxied to holes at each end of a glass slide. Before each observation, we cleaned a no. 1 coverslip by heating to 95°C in 0.5% Alconox detergent for 30–60 min, rinsing twice with water, and drying in a stream of air. Chambers were assembled, placed on a warm hot-plate for several seconds to seal, and used immediately after cooling. This cleaning process is critical for good imaging, and we noticed a significant degradation in image quality due to SYBR Gold/protein/glass interactions if the chambers were used just a few hours later.

Mg buffer containing 10¹⁰ pfu/ml λcI60 or λb221 was incubated with 4 μg/ml DNase I at 37°C for 15 min to remove any prematurely released DNA. As a focusing aid, 0.1-μm fluorescent beads were included at a dilution of ≈10⁷. This phage-bead solution was added to the chamber and left at room temperature for 15 min or more, to allow the phages and beads to adhere to the surface of the coverslip. Then, at the microscope, the left end of the channel was coupled to a reservoir and the right end to a syringe pump, allowing a controlled left-to-right fluid flow along the channel that stretched out the DNA for visualization. To make the observations, the following three solutions were drawn through in succession: first, 800 μl of Mg or Na buffer containing 1% oPOE to wash away unbound phage particles; second, 40 μl of the same Mg or Na buffer plus 1% oPOE, 10⁻⁵ diluted SYBR Gold, and an oxygen-scavenging system containing 1% gloxy [gloxy: 17 mg of glucose oxidase (Sigma G2133–10KU) and 60 μl of catalase (Roche 10681325) in 140 μl Mg buffer], 0.4% glucose, and 1% 2-mercaptoethanol (31); and third (after sufficient dye was present for observation of the earliest ejections), the same buffer with 2.5 μg/ml LamB added. This concentration of LamB was required to make binding occur faster than ≈10 s (data not shown). Single ejections were observed on a Nikon inverted microscope using a 100×, 1.4 NA oil immersion objective at ambient temperature (≈28°C). The illumination source was a 100-W mercury lamp, used at full intensity. Images were acquired at 4 s⁻¹ with a Photometrics Coolsnap FX camera. Example movies are available in SI Movies 1–4.

Many individual DNA ejections were visible in each acquired image sequence. Before analysis, each ejection was checked for various artifacts that would interfere with processing: overlap with other strands or the edge of the field of view, sticking of DNA ends to the glass, or breaking of the DNA strand. Overlap is unavoidable, whereas the sticking and breaking were caused by the intense illumination and greatly ameliorated by the oxygen-scavenging system. The ejections were analyzed by using a custom difference-of-gaussians filter running within the GNU Octave programming language; for each frame, the program identified the shape of the DNA and recorded its extension in the direction of the flow. See SI Text for details of the image processing routine, including source code.

Lengths were calibrated by using λ DNAs tethered to specially prepared chambers. The goal was to examine the function that relates the size of a DNA image in pixels to three variables: its length in base pairs, the flow rate, and the ionic composition of the solution. We obtained λ DNA (New England Biolabs) and modified it by using Klenow exo⁻ (New England Biolabs) to add biotin-11-dUTP (Roche) to one end, as a length standard equivalent to an entire piece of ejected DNA from λcI60. Other length standards were then prepared by digesting aliquots of the DNA with restriction enzymes. The DNAs were attached to streptavidin (Sigma) on the surface of a coverslip, and flows of various magnitudes were applied. Images were collected and analyzed identically to the images from the ejection videos. It was found that the DNA fit well to the form

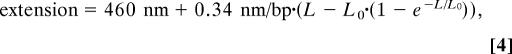where 460 nm was the minimum feature size observable by our technique and L is the length of the DNA fragment in base pairs (data shown in SI Text) The parameter L₀ is a function of flow rate; at L = L₀, the DNA is stretched out to 37% of its contour length by the flow. When L ≪ L₀, there is no observable stretching, and when L ≫ L₀, the DNA will appear shorter than its actual length by L₀. The equation we used for fitting is not derived from any physical principles, it is just intended to be a smooth curve having the above properties without introducing any parameters other than L₀. We found L₀ = 18 kbp for Mg buffer and 8 kbp for Na buffer at a flow rate of 40 μl/min. This flow was determined to have no significant effect on the ejection process (see SI Text) so it was used throughout the experiment. We note that the physics of tethered DNA in a shear flow is an interesting physical problem in its own right that may have interesting dynamics that would not be completely captured by a time-independent expression like Eq. 4 (32).